| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Теорема существования Тейхмюллера
4.1. Римановы метрики на компактных поверхностях
Риманова метрика на многообразии  это положительно определенная симметричная билинейная форма на слоях касательного расслоения многообразия
это положительно определенная симметричная билинейная форма на слоях касательного расслоения многообразия  .
.
В случае поверхности  удобно представлять локально риманову метрику в виде формы, введенной Гауссом:
удобно представлять локально риманову метрику в виде формы, введенной Гауссом:

 Несложная, но скучная выкладка позволяет выразить
Несложная, но скучная выкладка позволяет выразить  через локальную координату
через локальную координату  в виде
в виде

Здесь  Из условия инвариантности относительно замены локальной координаты следует, что
Из условия инвариантности относительно замены локальной координаты следует, что  преобразуется как
преобразуется как  -форма, т. е.
-форма, т. е.  инвариантно. При этом
инвариантно. При этом  служит коэффициентом растяжения, постоянным относительно изменения направления в точке
служит коэффициентом растяжения, постоянным относительно изменения направления в точке  и X есть
и X есть  -форма, т. е.
-форма, т. е.  инвариантно. Множитель
инвариантно. Множитель  описывает изменение направления при инфинитезимальном искажении расстояний.
описывает изменение направления при инфинитезимальном искажении расстояний.
Если  римановы метрики на поверхности
римановы метрики на поверхности  то тождественное отображение
то тождественное отображение  конформно тогда, когда
конформно тогда, когда  Таким образом, скалярные множители X оказываются несущественными, и множители
Таким образом, скалярные множители X оказываются несущественными, и множители  можно использовать для того, чтобы параметризовать классы конформной эквивалентности римановых метрик. В случае более общих диффеоморфизмов следует перейти к универсальной накрывающей и воспользоваться следующей леммой.
можно использовать для того, чтобы параметризовать классы конформной эквивалентности римановых метрик. В случае более общих диффеоморфизмов следует перейти к универсальной накрывающей и воспользоваться следующей леммой.
Лемма 1. Пусть  диффеоморфизм, и пусть
диффеоморфизм, и пусть  метрика Пуанкаре на
метрика Пуанкаре на  Пусть
Пусть  другая риманова метрика на
другая риманова метрика на  Следующие свойства эквивалентны:
Следующие свойства эквивалентны:
 конформно как отображение
конформно как отображение  ,
,
 удовлетворяет уравнению Бельтрами
удовлетворяет уравнению Бельтрами 
Доказательство. Отображение  конформно тогда и только тогда, когда
конформно тогда и только тогда, когда  не зависит от направления. Если
не зависит от направления. Если  удовлетворяет уравнению Бельтрами, то
удовлетворяет уравнению Бельтрами, то

где  зависит только от
зависит только от  Поэтому
Поэтому  не зависит от направления как отображение из (
не зависит от направления как отображение из ( Таким образом,
Таким образом,  Обращая это рассуждение, получим обратную импликацию.
Обращая это рассуждение, получим обратную импликацию. 
Простое вычисление показывает, что  накрывает отображение
накрывает отображение  тогда и только тогда, когда X является
тогда и только тогда, когда X является  -формой относительно
-формой относительно  является
является  -формой относительно
-формой относительно  т. е.
т. е.  и
и
 всех Vе Каждая гиперболическая поверхность допускает гладкую метрику, а именно метрику Пуанкаре. Если
всех Vе Каждая гиперболическая поверхность допускает гладкую метрику, а именно метрику Пуанкаре. Если  локальная координата на римановой поверхности
локальная координата на римановой поверхности  то мы видим, что деформация Тейхмюллера
то мы видим, что деформация Тейхмюллера  порождает метрику с особенностями
порождает метрику с особенностями

Лемма 2. Если  есть
есть  -координата на
-координата на  -есть
-есть  -координата на
-координата на  то
то  где
где  есть линейный элемент на
есть линейный элемент на  а множитель С не зависит от направления,
а множитель С не зависит от направления,
Доказательство.

так как 
Формы называются коэффициентами Бельтрами. Коэффициент Бельтрами вида  и
и  называется дифференциалом Тейхмюллера.
называется дифференциалом Тейхмюллера.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
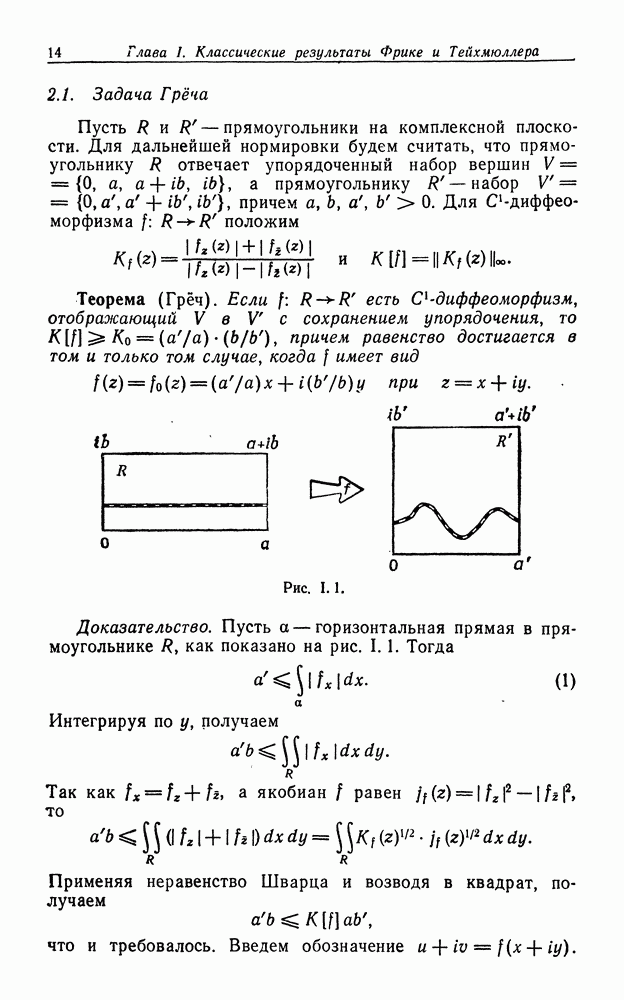
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
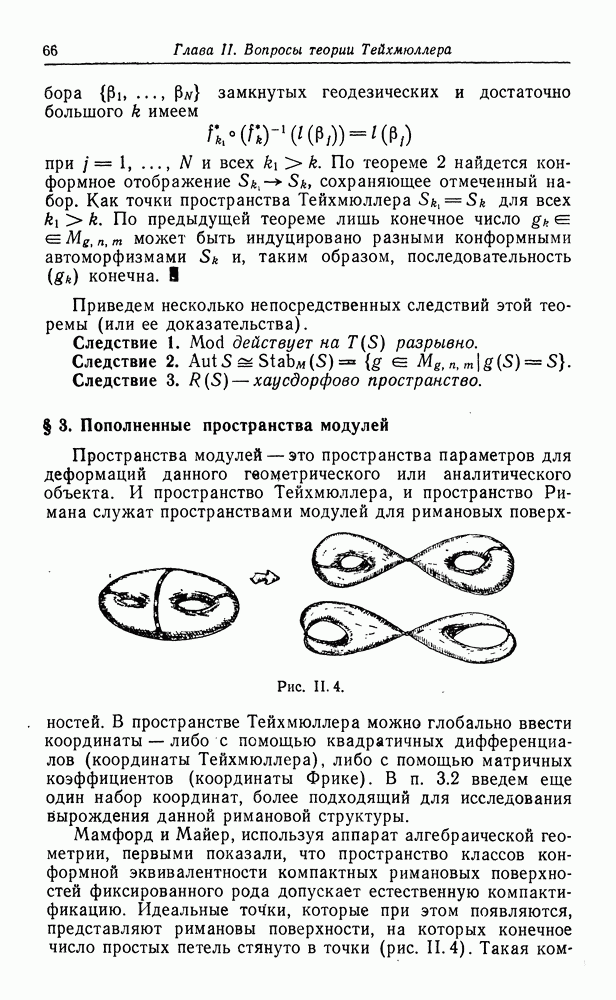
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания