| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Пополненные пространства модулей
Пространства модулей — это пространства параметров для деформаций данного геометрического или аналитического объекта. И пространство Тейхмюллера, и пространство Римана служат пространствами модулей для римановых поверхностей.

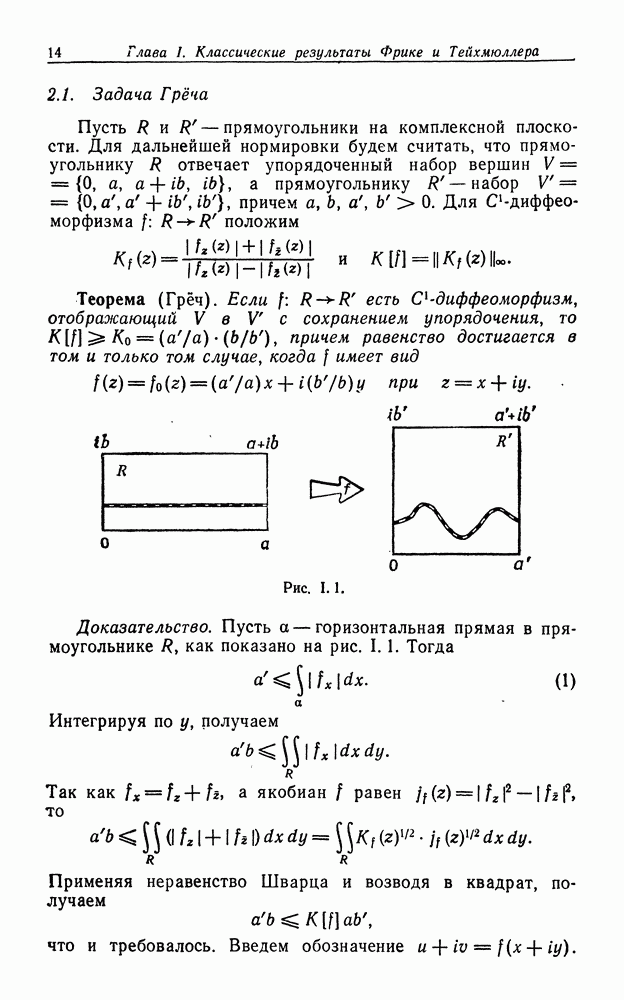
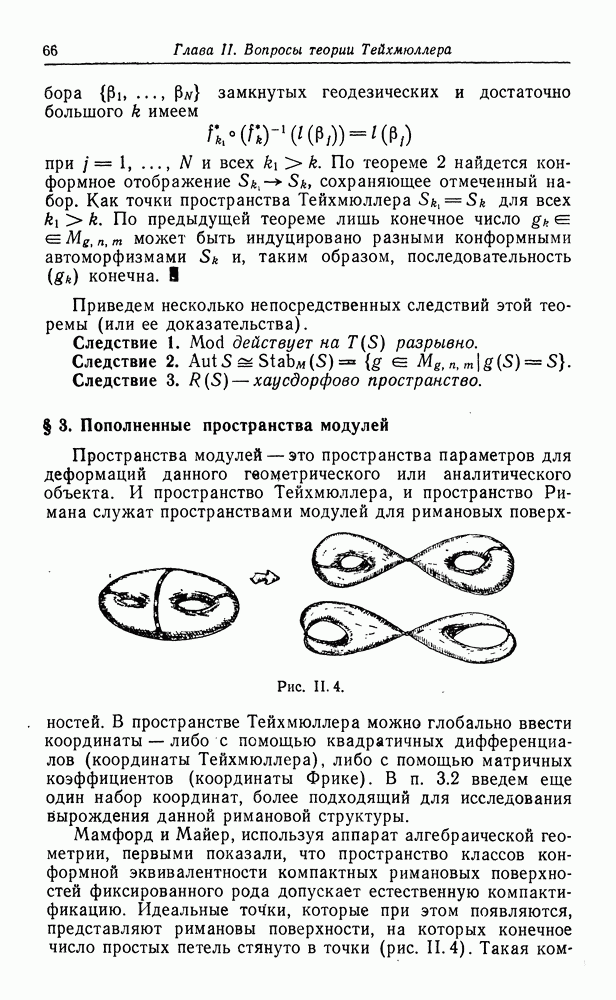
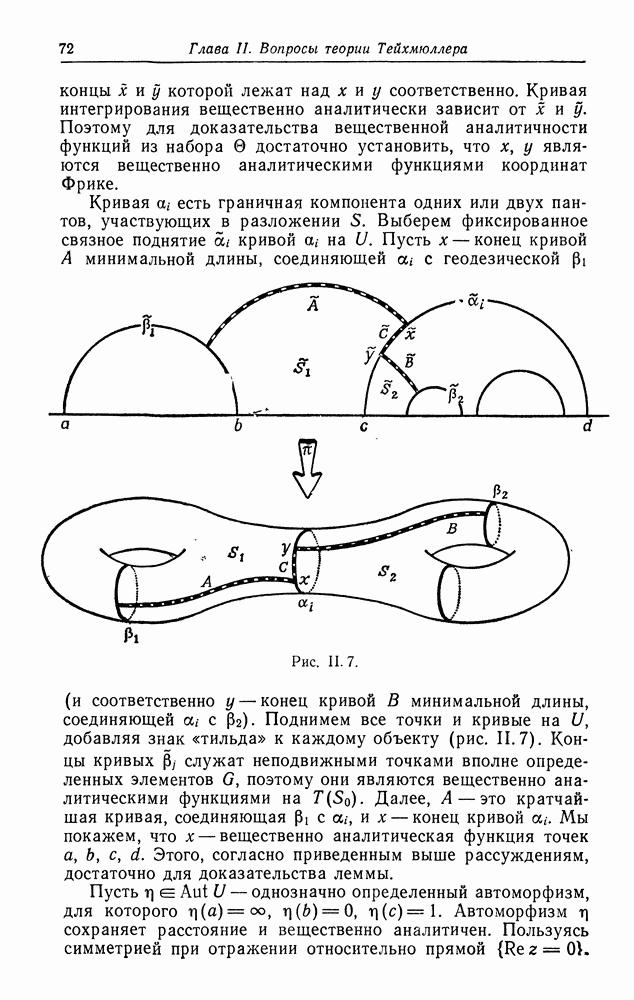
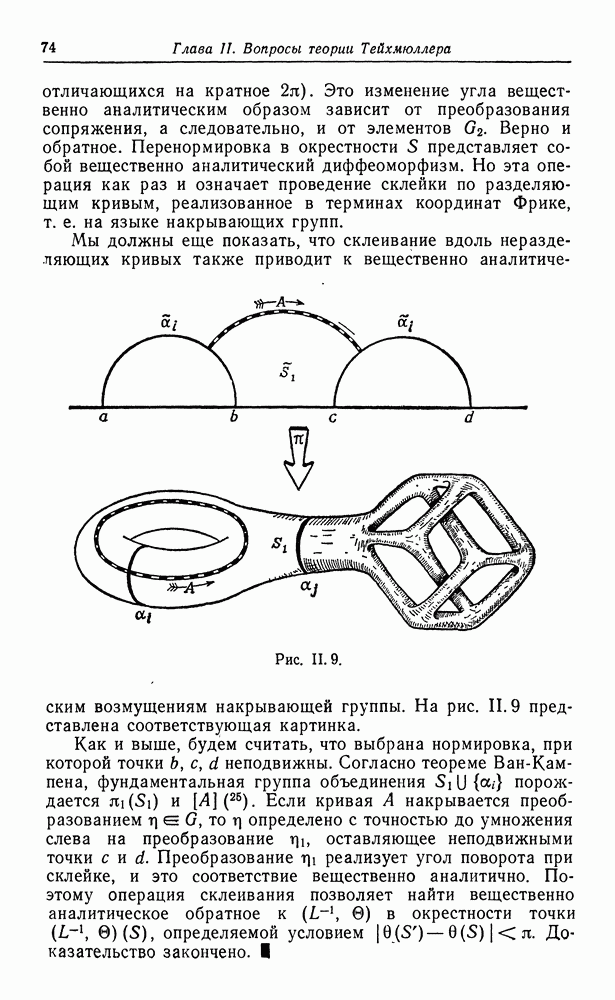
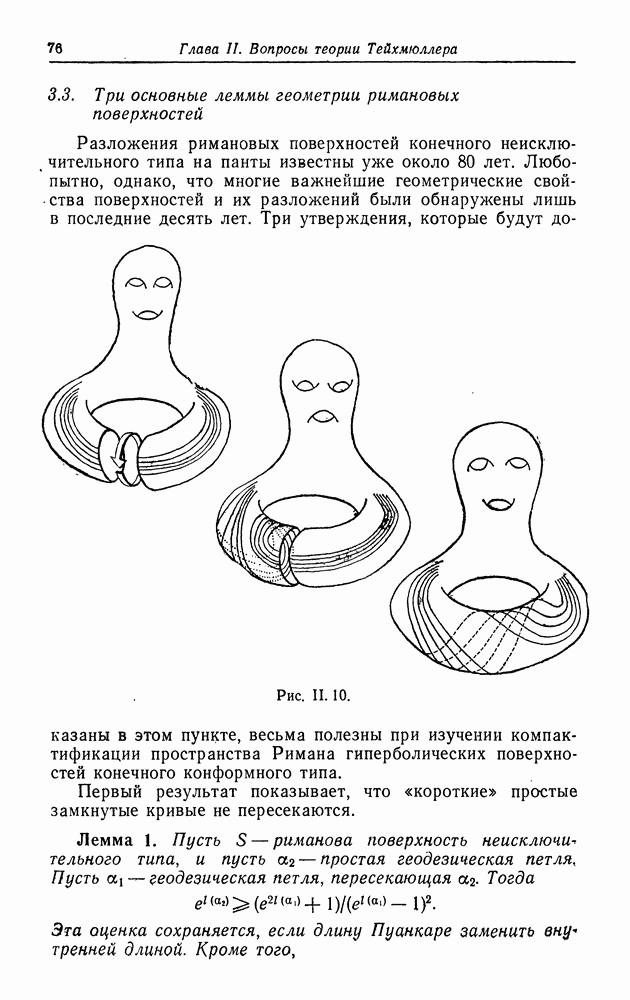
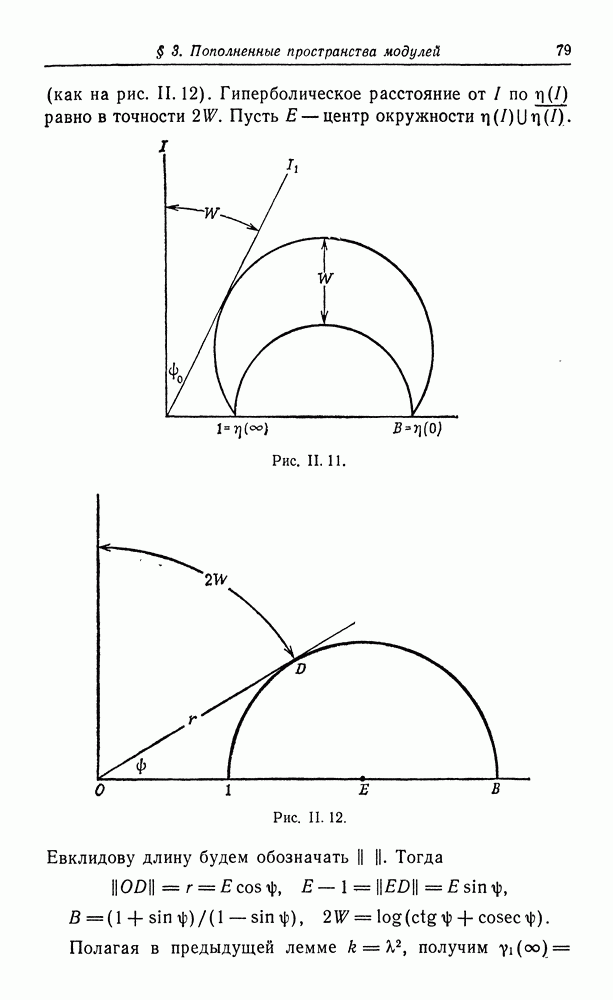
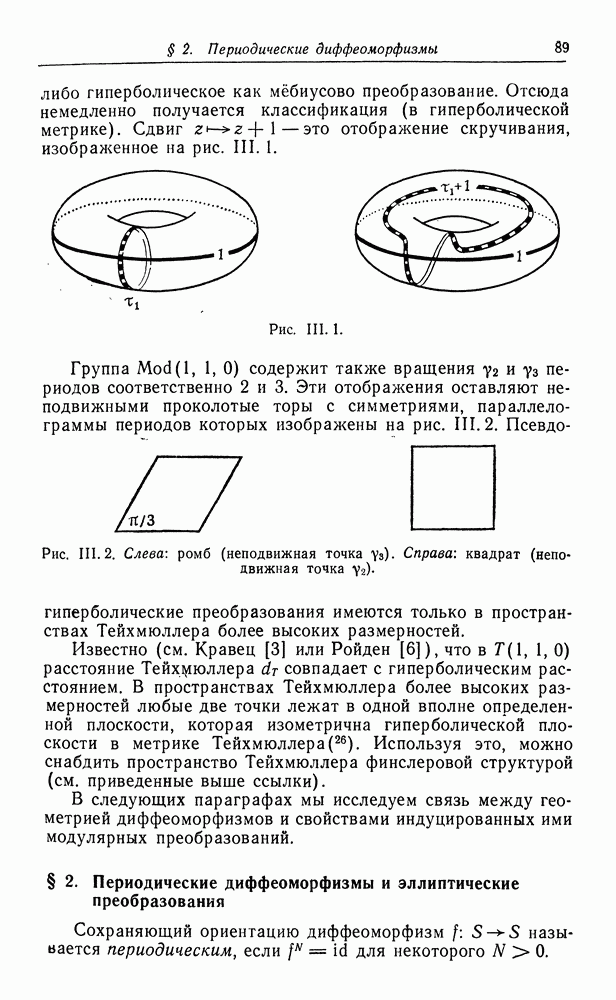
Рис. 
В пространстве Тейхмюллера можно глобально ввести координаты — либо с помощью квадратичных дифференциалов (координаты Тейхмюллера), либо с помощью матричных коэффициентов (координаты Фрике). В п. 3.2 введем еще один набор координат, более подходящий для исследования вырождения данной римановой структуры.
Мамфорд и Майер, используя аппарат алгебраической геометрии, первыми показали, что пространство классов конформной эквивалентности компактных римановых поверхностей фиксированного рода допускает естественную компактификацию. Идеальные точки, которые при этом появляются, представляют римановы поверхности, на которых конечное число простых петель стянуто в точки (рис. II. 4).
Такая компактификация пространства  обозначается
обозначается  и называется пополненным пространством Римана. Идеальная граница
и называется пополненным пространством Римана. Идеальная граница  соответствует идеальным граничным точкам, которые могут быть добавлены к любому разветвленному накрытию
соответствует идеальным граничным точкам, которые могут быть добавлены к любому разветвленному накрытию  . В частности, мы получаем пополнение
. В частности, мы получаем пополнение  пространства Тейхмюллера
пространства Тейхмюллера  Группа
Группа  действует на
действует на 
3.1. Панты и их конформные структуры
Простым следствием классификации поверхностей является тот хорошо известный факт, что каждая ориентируемая поверхность конечного неисключительного типа может быть представлена в виде конечной связной суммы трехсвязных областей. Склеивание происходит вдоль одной или нескольких граничных кривых (23). В этом пункте мы опишем конформную структуру таких трехсвязных областей, или, в нашей терминологии, пантов. В следующем пункте будет описан процесс конформного склеивания. Это позволит нам параметризовать пространство Тейхмюллера длинами идеальных граничных кривых трехсвязных областей и некоторых углов склейки.
Следуя Тёрстону, будем называть пантами (от французского  такие поверхности
такие поверхности  с краем, внутренность которых гомеоморфна трехсвязной области
с краем, внутренность которых гомеоморфна трехсвязной области  Панты, у которых одна или несколько граничных компонент С являются проколами, будем называть сжатыми (вокруг С). Граничные компоненты пантов удобно называть поясом
Панты, у которых одна или несколько граничных компонент С являются проколами, будем называть сжатыми (вокруг С). Граничные компоненты пантов удобно называть поясом  левым вырезом
левым вырезом  и правым вырезом
и правым вырезом  Отметим, что
Отметим, что  свободная группа с двумя образующими. В качестве образующих можно взять гомотопические классы двух из трех граничных кривых.
свободная группа с двумя образующими. В качестве образующих можно взять гомотопические классы двух из трех граничных кривых.
Пусть  универсальное накрытие. Возьмем точку
универсальное накрытие. Возьмем точку  и выпустим из
и выпустим из  гиперболические геодезические
гиперболические геодезические  соединяющие ее с каждой из граничных компонент. Дополнение
соединяющие ее с каждой из граничных компонент. Дополнение  представляет собой односвязную риманову поверхность, и, следовательно, его прообраз
представляет собой односвязную риманову поверхность, и, следовательно, его прообраз  односвязная область
односвязная область  Если для какой-нибудь точки
Если для какой-нибудь точки  выбрать прообраз
выбрать прообраз  то
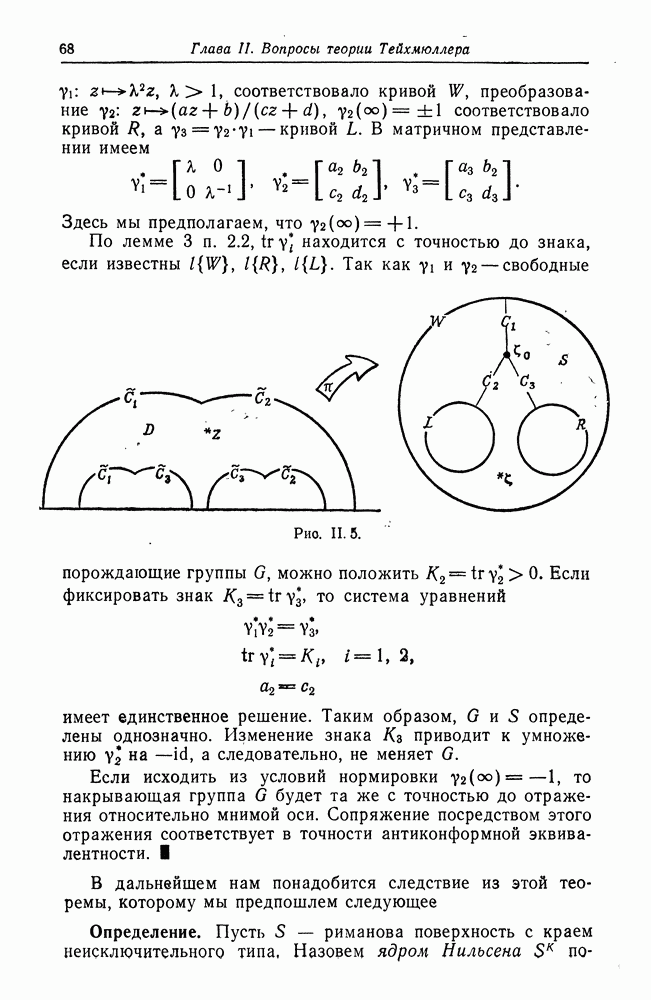
то  определяется однозначно (рис. II. 5).
определяется однозначно (рис. II. 5).
Теорема. Если  панты, то конформная структура
панты, то конформная структура  определяется с точностью до конформной или антиконформной эквивалентности набором чисел
определяется с точностью до конформной или антиконформной эквивалентности набором чисел 
Доказательство. Прежде всего выберем ориентацию на кривых  Нормализуем группу
Нормализуем группу  преобразований наложения накрытия
преобразований наложения накрытия  так, чтобы преобразование
так, чтобы преобразование
 соответствовало кривой
соответствовало кривой  преобразование
преобразование  соответствовало кривой
соответствовало кривой  кривой
кривой  . В матричном представлении имеем
. В матричном представлении имеем

Здесь мы предполагаем, что 
По лемме 3 п. 2.2,  находится с точностью до знака, если известны
находится с точностью до знака, если известны  Так как
Так как  — свободные имеет единственное решение.
— свободные имеет единственное решение.

Рис. 
порождающие группы  можно положить
можно положить  Если фиксировать знак
Если фиксировать знак  то система уравнений
то система уравнений

Таким образом,  определены однозначно. Изменение знака
определены однозначно. Изменение знака  приводит к умножению
приводит к умножению  на
на  а следовательно, не меняет
а следовательно, не меняет 
Если исходить из условий нормировки  то накрывающая группа
то накрывающая группа  будет та же с точностью до отражения относительно мнимой оси. Сопряжение посредством этого отражения соответствует в точности антиконформной эквивалентности.
будет та же с точностью до отражения относительно мнимой оси. Сопряжение посредством этого отражения соответствует в точности антиконформной эквивалентности. 
В дальнейшем нам понадобится следствие из этой теоремы, которому мы предпошлем следующее
Определение. Пусть  риманова поверхность с краем неисключительного типа, Назовем ядром Нильсена
риманова поверхность с краем неисключительного типа, Назовем ядром Нильсена 
поверхности  такую связную подповерхность с краем поверхности
такую связную подповерхность с краем поверхности  что:
что:
 есть деформационный ретракт поверхности
есть деформационный ретракт поверхности  если
если  простая геодезическая петля, стягиваемая на границу
простая геодезическая петля, стягиваемая на границу  то
то 
Отметим, что  единственная поверхность, для которой
единственная поверхность, для которой  является расширением Нильсена.
является расширением Нильсена.
Следствие 1. Пусть  панты. Если а — замкнутая кривая на поверхности
панты. Если а — замкнутая кривая на поверхности  пусть
пусть  -внутренняя длина
-внутренняя длина 

Тогда поверхность  определяется величинами
определяется величинами  однозначно с точностью до конформной или антиконформной эквивалентности.
однозначно с точностью до конформной или антиконформной эквивалентности.
Доказательство. Достаточно заметить, что  есть в точности ядро Нильсена поверхности
есть в точности ядро Нильсена поверхности  рассмотренной в теореме. I
рассмотренной в теореме. I
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания