| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5. Пространство Тейхмюллера
До сих пор наша конструкция существенно зависела от выбора исходной для  поверхности
поверхности  Однако Тейхмюллер показал, что на
Однако Тейхмюллер показал, что на  имеется структура метрического пространства, параметризующего конформные структуры на отмеченной поверхности
имеется структура метрического пространства, параметризующего конформные структуры на отмеченной поверхности  Метрика (по определению) не зависит от выбора базисной поверхности
Метрика (по определению) не зависит от выбора базисной поверхности  Пусть род
Пусть род  равен
равен 
Будем отождествлять точки  с поверхностями, которые они представляют. Для
с поверхностями, которые они представляют. Для  положим
положим

где  Пространство Тейхмюллера
Пространство Тейхмюллера  это метрическое пространство
это метрическое пространство 
Теорема.  полное метрическое пространство, гомеоморфное пространствам
полное метрическое пространство, гомеоморфное пространствам 
Доказательство. Из результатов п. 3.5 и теоремы единственности Тейхмюллера следует, что  метрика. Если
метрика. Если  последовательность Коши в метрике
последовательность Коши в метрике  то
то  -последовательность Коши в топологии
-последовательность Коши в топологии  Следовательно,
Следовательно,  полно. Если
полно. Если  то легко показать, что
то легко показать, что  и обратно.
и обратно.
Много интересных результатов о геометрии пространства Тейхмюллера получил С. Кравец [8]. Однако в его работе содержится и ошибочное утверждение. Этот вопрос обсуждался в диссертации  Линч в Колумбийском университете и в работе
Линч в Колумбийском университете и в работе  Мазура [24]
Мазура [24]
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
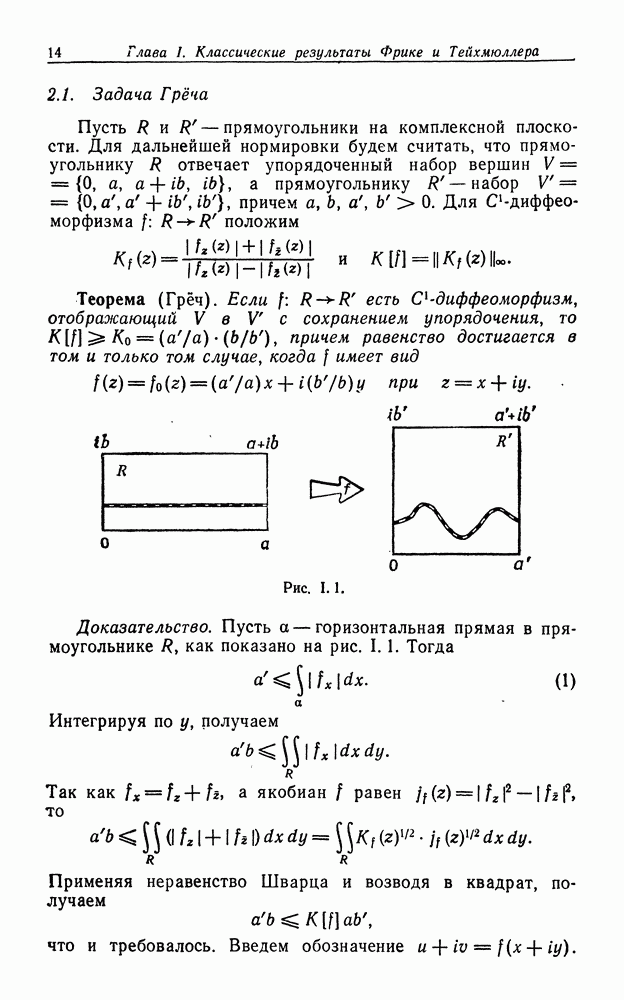
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
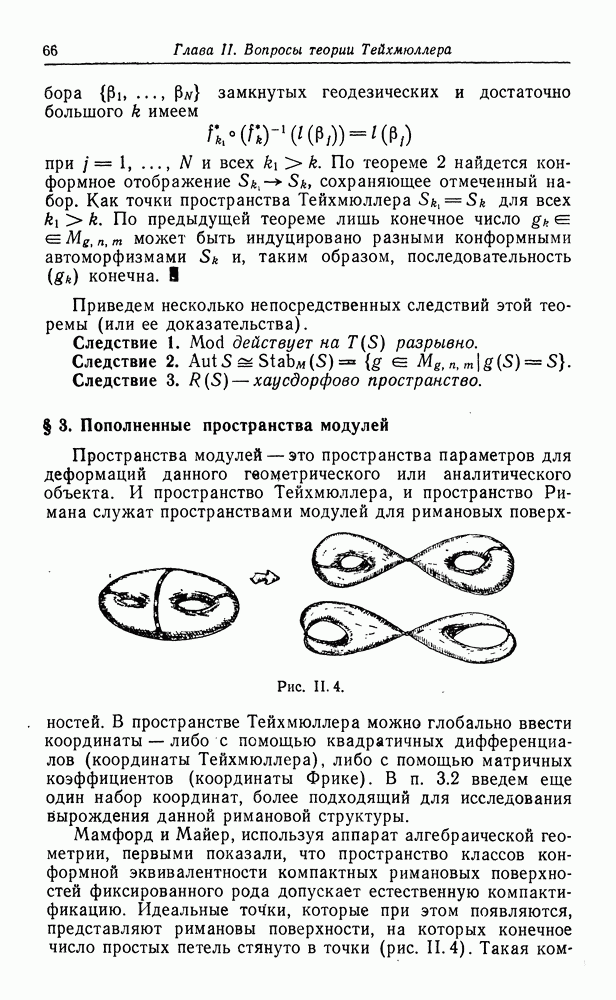
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания