| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. Дубль поверхности и расширения Нильсена
Пусть  риманова поверхность с краем,
риманова поверхность с краем,  ее зеркальный образ. Дубль (Шоттки)
ее зеркальный образ. Дубль (Шоттки)  поверхности
поверхности  есть, по определению, объединение
есть, по определению, объединение  в котором отождествлены соответствующие точки краев
в котором отождествлены соответствующие точки краев  и 5. Точнее говоря, каждой точке
и 5. Точнее говоря, каждой точке  сопоставляется точка
сопоставляется точка  При этом если
При этом если  то в окрестности
то в окрестности  точки
точки  введем локальную карту
введем локальную карту  . В качестве соответствующей карты в окрестности
. В качестве соответствующей карты в окрестности  точки
точки  возьмем
возьмем  где
где  комплексное сопряжение. Для точек края
комплексное сопряжение. Для точек края  используем очевидную топологию. Это определяет поверхность
используем очевидную топологию. Это определяет поверхность  зеркальный образ поверхности
зеркальный образ поверхности  Полагаем теперь
Полагаем теперь 
Конформная структура  определяется в точках очевидным образом. Пусть теперь
определяется в точках очевидным образом. Пусть теперь  окрестность точки
окрестность точки  и пусть функция
и пусть функция  непрерывна в IV и голоморфна в
непрерывна в IV и голоморфна в  Вложим
Вложим  посредством отображения
посредством отображения  такого, что
такого, что  голоморфно и
голоморфно и  подобно тому, как это делалось в п. 1.1. Так как прямые линии представляют собой устранимые особенности для голоморфных отображений с непрерывным продолжением (см., например, Картан [3, с. 71, 74]) (14), то отображение
подобно тому, как это делалось в п. 1.1. Так как прямые линии представляют собой устранимые особенности для голоморфных отображений с непрерывным продолжением (см., например, Картан [3, с. 71, 74]) (14), то отображение  голоморфно продолжается на
голоморфно продолжается на  Отсюда следует, что
Отсюда следует, что  голоморфно продолжается на все
голоморфно продолжается на все  значит,
значит,  имеет в окрестности точки
имеет в окрестности точки  единственную конформную структуру. Таким образом,
единственную конформную структуру. Таким образом,  риманова поверхность без края.
риманова поверхность без края.
Имеется другой способ построения дубля римановой поверхности. Пусть  поверхность с краем,
поверхность с краем, 
универсальное накрытие  соответствующая ему группа накрывающих преобразований. Можно предполагать, что точка
соответствующая ему группа накрывающих преобразований. Можно предполагать, что точка  является неподвижной для некоторого элемента группы
является неподвижной для некоторого элемента группы  Группа
Группа  действует разрывно на открытом подмножестве
действует разрывно на открытом подмножестве  при это
при это  где
где  нижняя полуплоскость в С. Кроме того,
нижняя полуплоскость в С. Кроме того,  действует разрывно на открытых подынтервалах оси
действует разрывно на открытых подынтервалах оси  Тогда
Тогда  Отображение
Отображение  накрывается сопряжением
накрывается сопряжением  на
на  имеется каноническая антиконформная инволюция, меняющая местами
имеется каноническая антиконформная инволюция, меняющая местами  и оставляющая неподвижными все точки
и оставляющая неподвижными все точки 
Пусть  риманова поверхность с краем типа
риманова поверхность с краем типа  причем
причем  Если
Если  ) или (0, 1, 1), то
) или (0, 1, 1), то  гиперболическая поверхность. Вложение
гиперболическая поверхность. Вложение  накрывается изометрией универсальной накрывающей поверхности
накрывается изометрией универсальной накрывающей поверхности  Поэтому каждая компонента края
Поэтому каждая компонента края  геодезическая в своем классе свободной гомотопии на
геодезическая в своем классе свободной гомотопии на  Чтобы в этом убедиться, достаточно выяснить, какие кривые в А остаются на месте при антиконформной изометрии порядка два, а затем спроектировать их на
Чтобы в этом убедиться, достаточно выяснить, какие кривые в А остаются на месте при антиконформной изометрии порядка два, а затем спроектировать их на 
Определение. Пусть  риманова поверхность с краем, и пусть
риманова поверхность с краем, и пусть  ее дубль. Предположим, что
ее дубль. Предположим, что  гииерболическая поверхность. Ограничение на
гииерболическая поверхность. Ограничение на  гиперболической метрики
гиперболической метрики  называется внутренней метрикой
называется внутренней метрикой 
Рассуждения, предшествующие определению, доказывают следующую лемму.
Лемма 1. Граничные кривые являются геодезическими для внутренней метрики.
Представим  в виде
в виде  с накрывающей группой
с накрывающей группой  При этом
При этом  вкладывается в
вкладывается в  и ее образ
и ее образ  стабилизирует односвязную компоненту
стабилизирует односвязную компоненту  дополнения
дополнения  Далее,
Далее,  есть деформационный ретракт поверхности
есть деформационный ретракт поверхности  Поверхность
Поверхность  называется расширением Нильсена поверхности
называется расширением Нильсена поверхности  (см. Берс [2]). При построении расширения Нильсена к поверхности
(см. Берс [2]). При построении расширения Нильсена к поверхности  приклеивается по бесконечному рогу вдоль каждой кривой края, и таким образом осуществляется пополнение
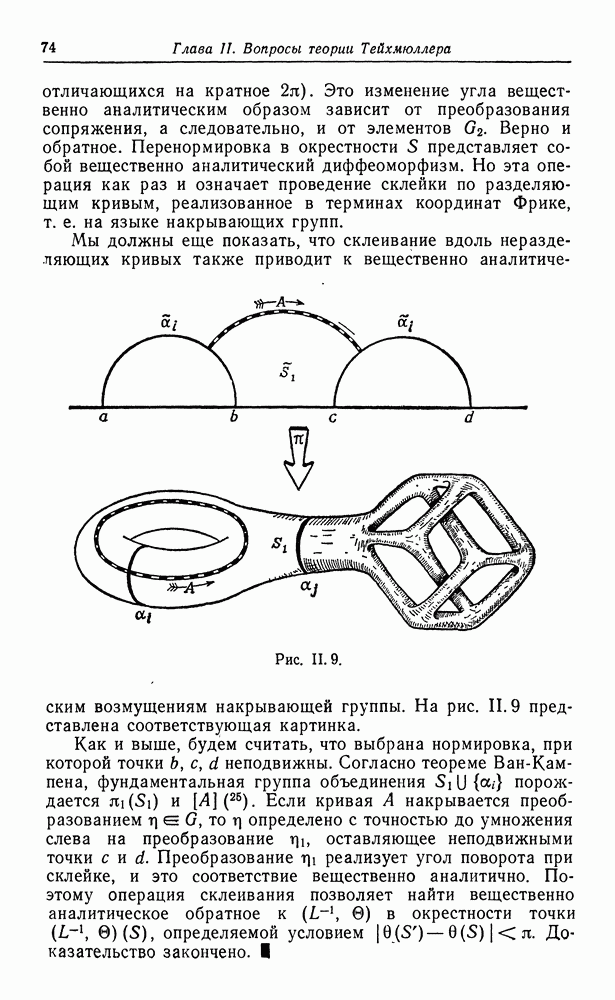
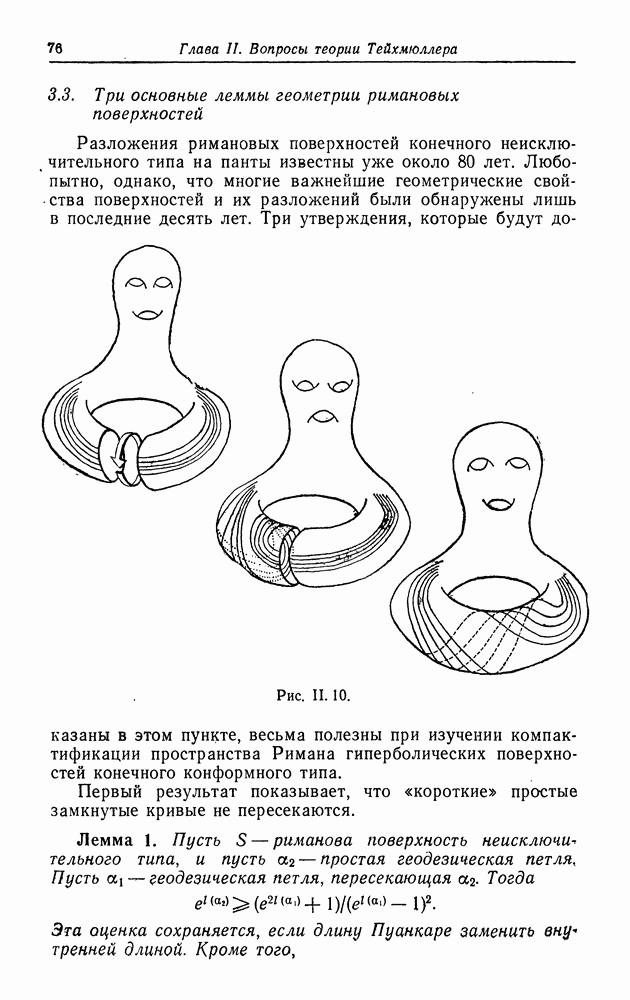
приклеивается по бесконечному рогу вдоль каждой кривой края, и таким образом осуществляется пополнение  по внутренней метрике (рис. И. 1) (15).
по внутренней метрике (рис. И. 1) (15).
Элементарные рассуждения показывают, что любой элемент  накрывающий компоненту края
накрывающий компоненту края  гиперболичен. Поэтому, согласно следствию 1 п.
гиперболичен. Поэтому, согласно следствию 1 п.  имеет граничные кривые, соответствующие каждой из ее идеальных граничных компонент. Далее можно применить к
имеет граничные кривые, соответствующие каждой из ее идеальных граничных компонент. Далее можно применить к  процесс построения расширения Нильсена и получить
процесс построения расширения Нильсена и получить  и т. д.
и т. д.
Граничные кривые поверхности  будут геодезическими в (полной) гиперболической метрике на
будут геодезическими в (полной) гиперболической метрике на 
Определение. Бесконечным расширением Нильсена поверхности  называется
называется


Рис. 11.1.
Следующая лемма также доказывается с помощью обобщенной леммы Шварца.
Лемма 2. Пусть С — граничная кривая поверхности  граничная кривая расширения Нильсена
граничная кривая расширения Нильсена  поверхности
поверхности  свободно гомотопная кривой С. Если I — длина С в гиперболической метрике
свободно гомотопная кривой С. Если I — длина С в гиперболической метрике  на
на  длина
длина  в гиперболической метрике
в гиперболической метрике  на
на  то
то 
Доказательство. Мы показали выше, что  но
но  Из теоремы п. 1.2 следует, что при этих условиях
Из теоремы п. 1.2 следует, что при этих условиях  Далее,
Далее,  есть геодезическая (относительно
есть геодезическая (относительно  в классе свободной гомотопии кривой С. Поэтому
в классе свободной гомотопии кривой С. Поэтому

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
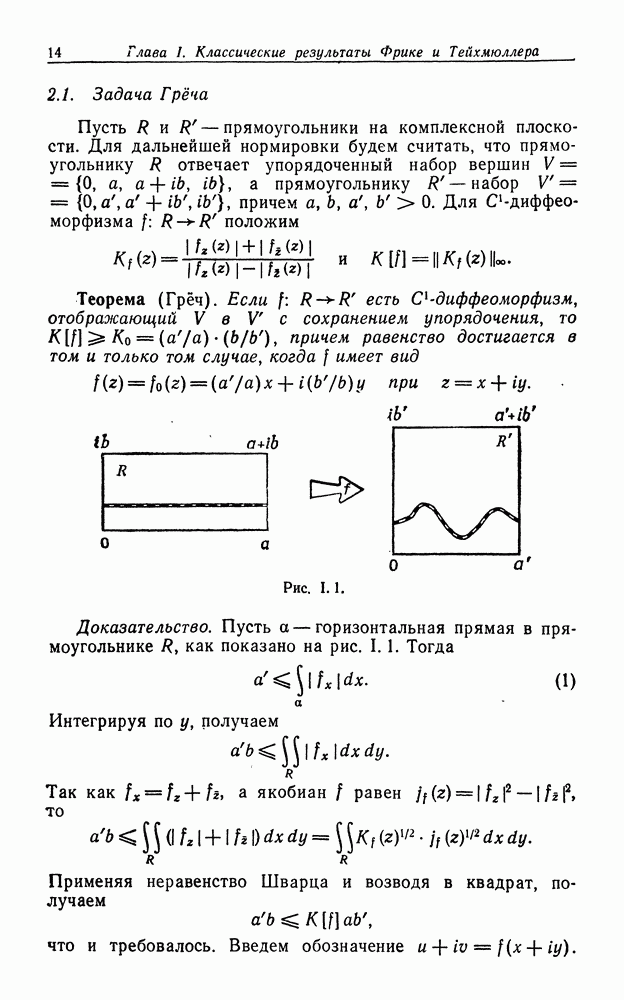
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
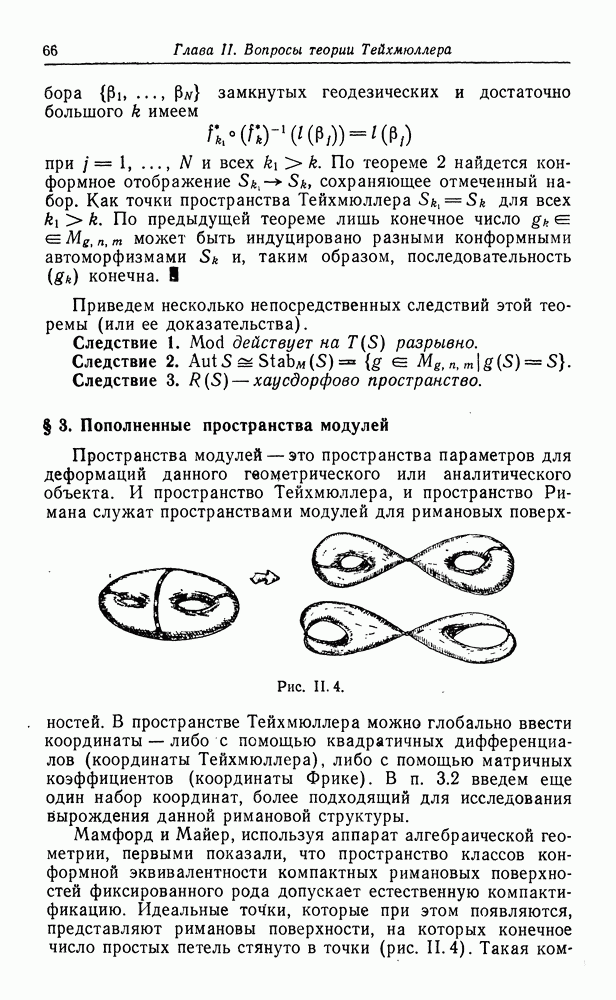
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания