| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. Деформации Тейхмюллера
Пусть  . Определим деформацию комплексной структуры поверхности
. Определим деформацию комплексной структуры поверхности  следующим образом. Пусть и пусть
следующим образом. Пусть и пусть  есть
есть  -координата в окрестности точки
-координата в окрестности точки  такая, что
такая, что  Обозначим через
Обозначим через  кольцо ростков голоморфных в исходной структуре функций в окрестности
кольцо ростков голоморфных в исходной структуре функций в окрестности  Назовем росток
Назовем росток  непрерывной в окрестности
непрерывной в окрестности  функции голоморфным относительно структуры
функции голоморфным относительно структуры  , если
, если  где
где  росток голоморфной функции в окрестности нуля комплексной плоскости,
росток голоморфной функции в окрестности нуля комплексной плоскости,  Если
Если  то это условие эквивалентно тому, что
то это условие эквивалентно тому, что  . В терминах
. В терминах  -координаты на
-координаты на  имеем
имеем

Здесь  квадратичный дифференциал на поверхности
квадратичный дифференциал на поверхности  индуцированный деформацией
индуцированный деформацией 
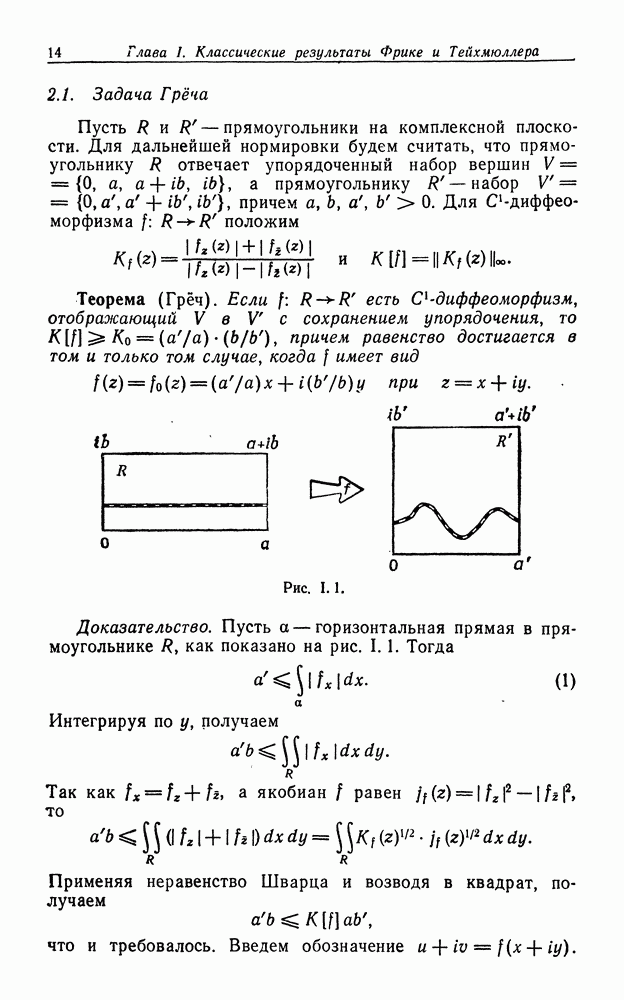
Переход от координаты  на 5 к координате на
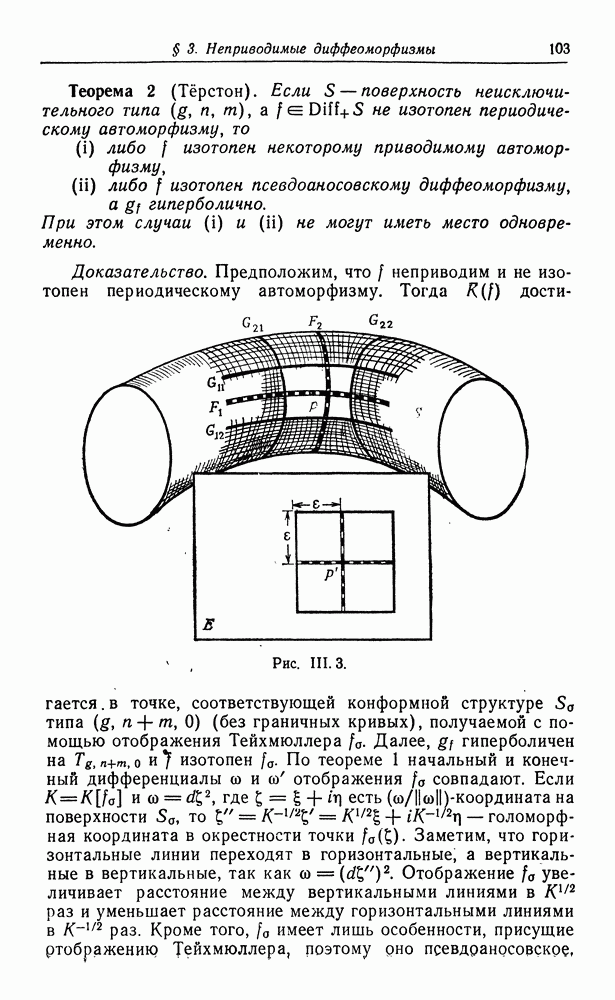
на 5 к координате на  сохраняет длину вертикальных линий, но растягивает горизонтальные линии в К раз.
сохраняет длину вертикальных линий, но растягивает горизонтальные линии в К раз.
Структура  как римановой поверхности определена таким образом только в окрестностях точек
как римановой поверхности определена таким образом только в окрестностях точек  Для того чтобы показать, что
Для того чтобы показать, что  есть на самом деле риманова поверхность, осталось установить, что малый проколотый диск
есть на самом деле риманова поверхность, осталось установить, что малый проколотый диск  с центром в точке
с центром в точке  конформно эквивалентен проколотому диску на
конформно эквивалентен проколотому диску на  но не кольцу. Предположим, что со имеет в точке
но не кольцу. Предположим, что со имеет в точке  нуль четного порядка
нуль четного порядка  т. е.
т. е.  для некоторой локальной координаты
для некоторой локальной координаты  Положим
Положим  т. е. перейдем к локальному
т. е. перейдем к локальному  -листному накрытию
-листному накрытию  Поднимая со на это накрытие, получим квадратичный дифференциал
Поднимая со на это накрытие, получим квадратичный дифференциал  Горизонтальная (соответственно вертикальная) линия дифференциала со есть поднятие горизонтальной (соответственно вертикальной) линии для
Горизонтальная (соответственно вертикальная) линия дифференциала со есть поднятие горизонтальной (соответственно вертикальной) линии для  Заданная
Заданная  -координата
-координата  в окрестности
в окрестности  поднимается до
поднимается до  -координаты в окрестности прообраза точки
-координаты в окрестности прообраза точки  Введем
Введем  Проектируя в
Проектируя в  получим
получим

— требуемую  -координату в окрестности точки
-координату в окрестности точки  Если
Если  нечетно, нужно сначала поднять со на ориентирующее накрытие, а затем, повторив предыдущую процедуру, получить аналогичное выражение для Таким образом мы ввели локальную координату в окрестности каждой точки
нечетно, нужно сначала поднять со на ориентирующее накрытие, а затем, повторив предыдущую процедуру, получить аналогичное выражение для Таким образом мы ввели локальную координату в окрестности каждой точки  и тем самым определили на
и тем самым определили на  структуру римановой поверхности
структуру римановой поверхности 
Определение. Структура римановой поверхности  называется деформацией Тейхмюллера структуры римановой поверхности
называется деформацией Тейхмюллера структуры римановой поверхности 
Предложение. Пусть  . Тогда
. Тогда  росток голоморфной функции в точке
росток голоморфной функции в точке  (относительно
(относительно  в том и только том случае, когда
в том и только том случае, когда  где
где  удовлетворяет уравнению
удовлетворяет уравнению

Доказательство. По определению,  росток функции, голоморфной на
росток функции, голоморфной на  если
если  где
где  росток голоморфной функции от Последнее эквивалентно условию
росток голоморфной функции от Последнее эквивалентно условию  Применяя правило дифференцирования сложной функции (цепное правило), получаем
Применяя правило дифференцирования сложной функции (цепное правило), получаем

Отметим, что выражения квадратичных дифференциалов со и  отличаются в соответствующих им координатах лишь скалярным множителем. Деформация римановой структуры не зависит, очевидно, от величины этого множителя. Поэтому деформации Тейхмюллера данной комплексной структуры можно параметризовать парами
отличаются в соответствующих им координатах лишь скалярным множителем. Деформация римановой структуры не зависит, очевидно, от величины этого множителя. Поэтому деформации Тейхмюллера данной комплексной структуры можно параметризовать парами  где
где  а со лежит на единичной (относительно какой-нибудь нормы) сфере
а со лежит на единичной (относительно какой-нибудь нормы) сфере  пространства
пространства  Исходная структура
Исходная структура  соответствует значению
соответствует значению 
Определение. Множество

с естественной топологией называется пространством Тейхмюллера с базисной точкой 
При  имеем
имеем  Фиксируем
Фиксируем  и рассмотрим луч
и рассмотрим луч  Вертикальное измеримое слоение
Вертикальное измеримое слоение  меняется при 1 (точнее, вырождается). Однако, и это весьма существенно, горизонтальное слоение
меняется при 1 (точнее, вырождается). Однако, и это весьма существенно, горизонтальное слоение  не зависит от
не зависит от  Поэтому пространство деформаций Тейхмюллера допускает компактификацию измеримыми слоениями. Суммируем полученные результаты в следующей теореме.
Поэтому пространство деформаций Тейхмюллера допускает компактификацию измеримыми слоениями. Суммируем полученные результаты в следующей теореме.
Теорема. Пусть  компактная риманова поверхность рода
компактная риманова поверхность рода  и пусть
и пусть  для некоторых
для некоторых  . Если со
. Если со  индуцирован дифференциалом
индуцирован дифференциалом  то
то  -горизонтальное слоение
-горизонтальное слоение  не зависит от
не зависит от  . В частности,
. В частности,  допускает компактификацию
допускает компактификацию  граничные точки которой представляют собой
граничные точки которой представляют собой  -горизонтальные измеримые слоения поверхности
-горизонтальные измеримые слоения поверхности 
Из теоремы Римана — Роха следует, что  Доказательство этого утверждения на языке автоморфных форм можно найти в книге Ленера
Доказательство этого утверждения на языке автоморфных форм можно найти в книге Ленера  или в монографии
или в монографии  Шимуры «Введение в арифметическую теорию автоморфных функций» (Пер. с англ. — М.: Мир, 1973). Таким образом,
Шимуры «Введение в арифметическую теорию автоморфных функций» (Пер. с англ. — М.: Мир, 1973). Таким образом,  представляет собой открытый
представляет собой открытый  -мерный диск,
-мерный диск,  есть
есть  -мерный замкнутый диск.
-мерный замкнутый диск.
Остальная часть этой главы посвящена изучению связи  с конформными структурами на
с конформными структурами на  и иному, не использующему базисных точек, метрическому описанию
и иному, не использующему базисных точек, метрическому описанию 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания