| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Теорема существования Тейхмюллера
В этом пункте мы введем естественную топологию на множестве деформаций Тейхмюллера и определим естественное отображение этого множества — его гомеоморфизм  на пространство
на пространство  Отсюда, в частности, следует, что любая конформная структура на поверхности
Отсюда, в частности, следует, что любая конформная структура на поверхности  может быть получена деформацией Тейхмюллера исходной структуры.
может быть получена деформацией Тейхмюллера исходной структуры.
Пусть опять  компактная риманова поверхность рода
компактная риманова поверхность рода  — голоморфная универсальная накрывающая поверхности
— голоморфная универсальная накрывающая поверхности  Мы будем также использовать обозначения (возможно, с добавлением индексов)
Мы будем также использовать обозначения (возможно, с добавлением индексов)  где
где  есть сама поверхность
есть сама поверхность  , снабженная
, снабженная  -структурой, поднятой с
-структурой, поднятой с  Применяя теорему униформизации, получаем коммутативную диаграмму
Применяя теорему униформизации, получаем коммутативную диаграмму

где  конформные отображения,
конформные отображения,  определяется из условия коммутативности верхнего квадрата. Группа накрывающих преобразований
определяется из условия коммутативности верхнего квадрата. Группа накрывающих преобразований  для проекции (соответственно группа
для проекции (соответственно группа  для определена с точностью до автоморфизма
для определена с точностью до автоморфизма  Если
Если  то пусть
то пусть  порождающие элементы группы
порождающие элементы группы  определенные фиксированным изоморфизмом
определенные фиксированным изоморфизмом  (см. § 1) (соответственно
(см. § 1) (соответственно  порождающие группы
порождающие группы  определенные изоморфизмом
определенные изоморфизмом  индуцированным тождественным отображением
индуцированным тождественным отображением  Нормируем
Нормируем  так, чтобы точка
так, чтобы точка  была отталкивающей, а
была отталкивающей, а  притягивающей неподвижной точкой
притягивающей неподвижной точкой  неподвижной точкой Соответственно этому будут нормированы и отображения
неподвижной точкой Соответственно этому будут нормированы и отображения  Определим отображение
Определим отображение

где  нормированная группа накрывающих преобразований для
нормированная группа накрывающих преобразований для  Как мы видели выше, это отображение не инъективно.
Как мы видели выше, это отображение не инъективно.
Введем в  норму
норму  и обозначим через
и обозначим через  открытый единичный шар в этой норме в
открытый единичный шар в этой норме в  Рассмотрим отображение
Рассмотрим отображение

Тогда  гомеоморфизм пространства Тейхмюллера
гомеоморфизм пространства Тейхмюллера  на
на  Возьмем теперь отображение
Возьмем теперь отображение 
Лемма. Отображение  инъективно.
инъективно.
Доказательство. Если  то
то  конформно эквивалентны, причем эта эквивалентность осуществляется отображением, гомотопным тождественному. Согласно следствию из теоремы единственности Тейхмюллера,
конформно эквивалентны, причем эта эквивалентность осуществляется отображением, гомотопным тождественному. Согласно следствию из теоремы единственности Тейхмюллера,  т. е.
т. е. 
Как мы уже отмечали ранее,  есть
есть  -мерное комплексное векторное пространство. Используя свойство инвариантности области, мы установим, что
-мерное комплексное векторное пространство. Используя свойство инвариантности области, мы установим, что  гомеоморфизм, простой проверкой того, что это непрерывная сюръекция. Нам понадобится следующая теорема существования и единственности.
гомеоморфизм, простой проверкой того, что это непрерывная сюръекция. Нам понадобится следующая теорема существования и единственности.
Теорема. Пусть и  Существует единственный гомеоморфизм
Существует единственный гомеоморфизм  такой, что
такой, что

 оставляет неподвижными точки
оставляет неподвижными точки 
 — гладкое отображение в точках гладкости
— гладкое отображение в точках гладкости 
 при
при  если
если  зависит
зависит  -гладко (соответственно комплексно аналитически) от каких-нибудь параметров, то
-гладко (соответственно комплексно аналитически) от каких-нибудь параметров, то  зависит от этих параметров также
зависит от этих параметров также  -гладко (соответственно комплексно аналитически).
-гладко (соответственно комплексно аналитически).
Доказательство. См. Альфорс [2, гл. V].
Сделаем несколько замечаний по поводу этой теоремы.
1) Вообще говоря, производные, о которых идет речь в  понимаются как локально интегрируемые обобщенные производные. Однако для наших целей это не существенно.
понимаются как локально интегрируемые обобщенные производные. Однако для наших целей это не существенно.
2) Утверждения  были получены с постепенным снижением ограничений на
были получены с постепенным снижением ограничений на  Гауссом, Корном и Лихтенштейном, а для
Гауссом, Корном и Лихтенштейном, а для  Морри (1938) (10). Дальнейший вклад внесли Альфорс и Берс. Они выяснили характер зависимости от параметров. Используя свойство
Морри (1938) (10). Дальнейший вклад внесли Альфорс и Берс. Они выяснили характер зависимости от параметров. Используя свойство  легко показать, что пространство Тейхмюллера есть комплексное многообразие. Сам Тейхмюллер утверждал, что он получил лишь вещественно аналитическую параметризацию
легко показать, что пространство Тейхмюллера есть комплексное многообразие. Сам Тейхмюллер утверждал, что он получил лишь вещественно аналитическую параметризацию  (но в его доказательствах имеются пробелы).
(но в его доказательствах имеются пробелы). 
3) Если  удовлетворяет дополнительно условию
удовлетворяет дополнительно условию  то из единственности
то из единственности  следует, что его ограничение на
следует, что его ограничение на  есть гомеоморфизм
есть гомеоморфизм  на себя. Поэтому
на себя. Поэтому  определяет автоморфизм
определяет автоморфизм  причем
причем  для всех
для всех  . В дальнейшем, если
. В дальнейшем, если  определена на 0, будем считать ее продолженной на всю плоскость С равенством
определена на 0, будем считать ее продолженной на всю плоскость С равенством 
Следствие 1. Отображение  непрерывно.
непрерывно.
Доказательство. Положим

где  — поднятие
— поднятие  Так как
Так как  компактна, то сходимость в
компактна, то сходимость в  индуцированная нормой, влечет за собой сходимость в топологии равномерной сходимости. Поэтому если
индуцированная нормой, влечет за собой сходимость в топологии равномерной сходимости. Поэтому если  то
то  нормально. Однако если
нормально. Однако если  то
то

Поэтому сходимость  к равномерна всюду, исключая нули
к равномерна всюду, исключая нули  и стало быть,
и стало быть,  непрерывно.
непрерывно.
Положим  Снабдим группу автоморфизмов
Снабдим группу автоморфизмов  топологией равномерной сходимости. Из теоремы Альфорса — Берса следует, что отображение 42 непрерывно в этой топологии.
топологией равномерной сходимости. Из теоремы Альфорса — Берса следует, что отображение 42 непрерывно в этой топологии.
Пусть  . Вне точек
. Вне точек  функция
функция  удовлетворяет уравнению Бельтрами
удовлетворяет уравнению Бельтрами

(предложение 3.4). Вспомним теперь, что  голоморфная функция от
голоморфная функция от  . Короткое вычисление в локальной координате показывает, что
. Короткое вычисление в локальной координате показывает, что

Из утверждения теоремы о единственности нормированного отображения получаем 
Отсюда следует, что компоненты матричного представления конечного множества порождающих группы  также непрерывно зависят от
также непрерывно зависят от  значит,
значит,  непрерывно.
непрерывно.
Следствие 2. Отображение  есть сюръекция на компоненту связности множества
есть сюръекция на компоненту связности множества 
Доказательство. Допустим, что  и
и  как отмеченная поверхность. Пусть
как отмеченная поверхность. Пусть  дифференцируемое отображение
дифференцируемое отображение  накрывающее
накрывающее  Тогда
Тогда  Так как образ
Так как образ  плотен в
плотен в  а открыто, то существуют дифференцируемые отображения
а открыто, то существуют дифференцируемые отображения  такие, что
такие, что  и следующая диаграмма коммутативна:
и следующая диаграмма коммутативна:

Предполагается, что  сохраняют отмеченные наборы и что
сохраняют отмеченные наборы и что  конформно. Если
конформно. Если  дифференциал Тейхмюллера, соответствующий
дифференциал Тейхмюллера, соответствующий  , то
, то

С другой стороны, по теореме единственности Тейхмюллера

поскольку  Полученное противоречие показывает, что
Полученное противоречие показывает, что  значит,
значит,  сюръекция
сюръекция  на компоненту связности
на компоненту связности 
Следствие 3. Множество  связно.
связно.
Доказательство. Пусть  фиксированная отмеченная поверхность. Каждая точка
фиксированная отмеченная поверхность. Каждая точка  определяет мономорфизм
определяет мономорфизм  Положим
Положим  Ясно, что
Ясно, что  также отмеченная поверхность. Сглаженное
также отмеченная поверхность. Сглаженное  -отображение
-отображение  определяет диффеоморфизм
определяет диффеоморфизм  сохраняющий отмеченный набор. Поднимем
сохраняющий отмеченный набор. Поднимем  до
до  Тогда
Тогда  более гого,
более гого,  Пусть
Пусть  нормированное решение уравнения Бельтрами
нормированное решение уравнения Бельтрами  Ввиду единственности нормированного решения имеем
Ввиду единственности нормированного решения имеем 
Пусть  и пусть
и пусть  нормированное решение уравнения
нормированное решение уравнения  Вычисляя
Вычисляя  -производные, мы видим, что
-производные, мы видим, что  и отображение
и отображение

где  определено условием
определено условием  непрерывно. Таким образом,
непрерывно. Таким образом,  линейно связно.
линейно связно. 
Из доказанных лемм следует
Теорема (Тейхмюллер).  — гомеоморфизм.
— гомеоморфизм.
Следствие 1 (теорема существования Тейхмюллера). Если  компактная поверхность рода
компактная поверхность рода  то каждая комплексная структура на ней (если
то каждая комплексная структура на ней (если  рассматривается как отмененная поверхность) может быть получена из исходной структуры деформацией Тейхмюллера.
рассматривается как отмененная поверхность) может быть получена из исходной структуры деформацией Тейхмюллера.
Это утверждение нужно понимать в том смысле, что любая деформация конформной структуры на  гомотопна деформации Тейхмюллера (либо тривиальна).
гомотопна деформации Тейхмюллера (либо тривиальна).
Таким образом, Доказательство теорем Тейхмюллера завершено.
Из теоремы существования непосредственно вытекает
Следствие 2. Пусть  гомеоморфизм. В гомотопическом классе отображения
гомеоморфизм. В гомотопическом классе отображения  найдется отображение вида
найдется отображение вида  где
где  деформация Тейхмюллера поверхности
деформация Тейхмюллера поверхности  конформное отображение.
конформное отображение.
Отображение  из следствия 2 называется отображением Тейхмюллера в классе
из следствия 2 называется отображением Тейхмюллера в классе 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
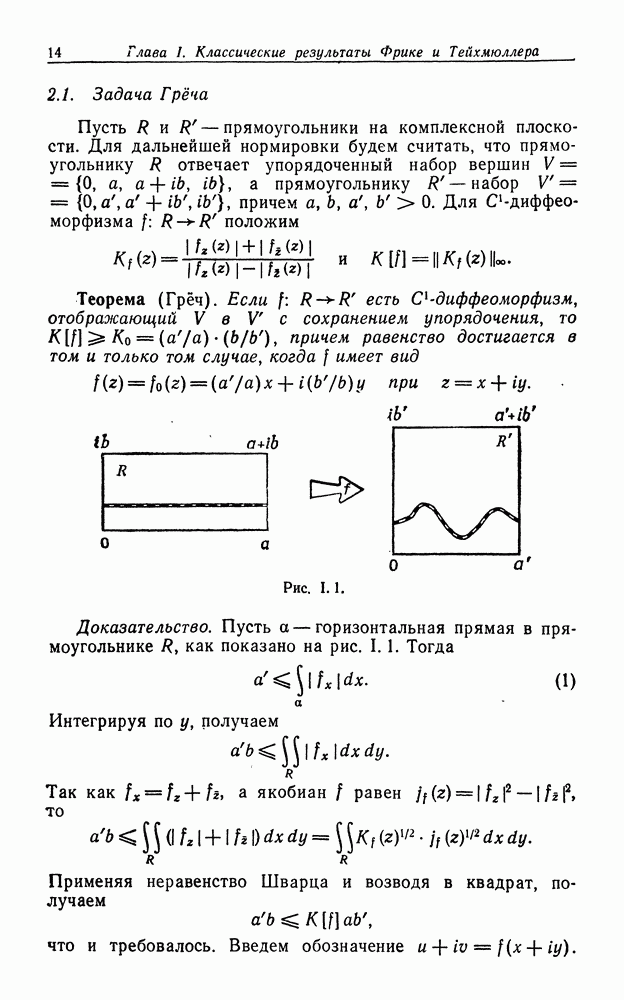
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
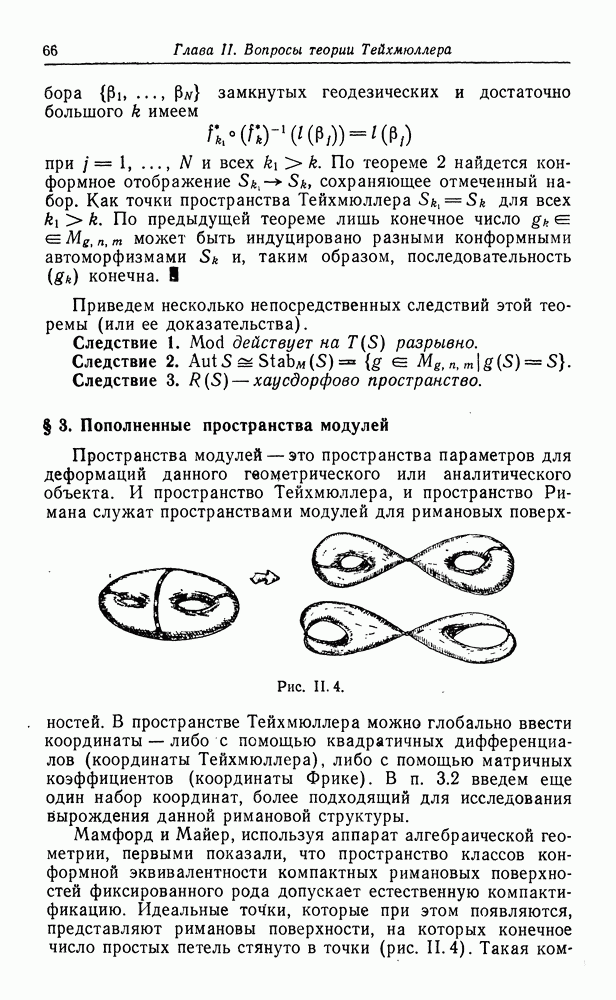
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания