Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА

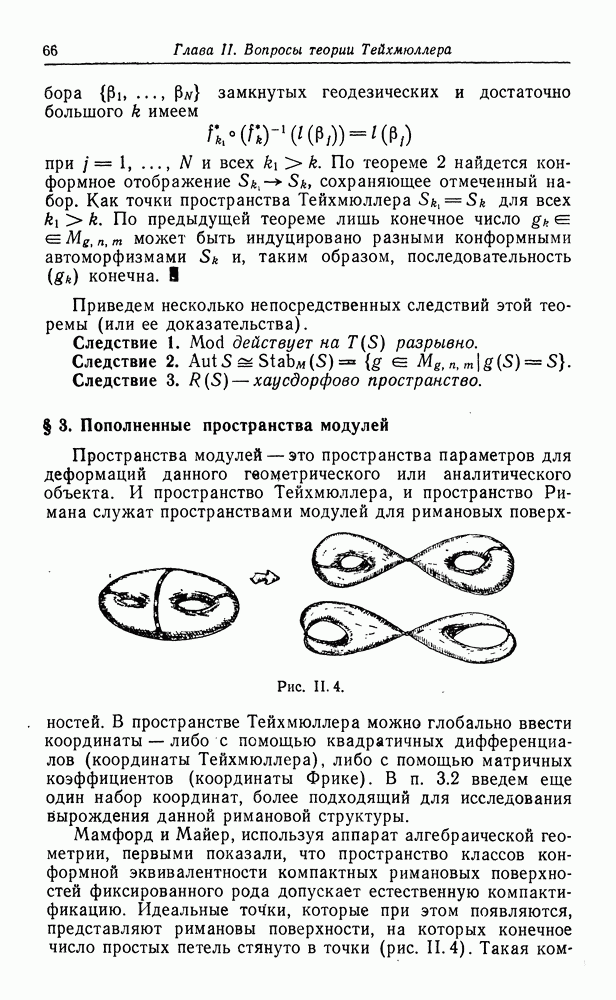
В предыдущей главе излагались теоремы Тейхмюллера для компактных поверхностей. Эти результаты не новы — единственное важное утверждение, которое не было известно в сороковых годах, — это принадлежащая Альфорсу и Берсу часть теоремы, приведенной в п. 4.2 гл. Эта глава имеет двоякую цель. Во-первых, мы строим компактификацию пространства Римана конформно конечной римановой поверхности Точки соответствуют римановым поверхностям с узлами; такие поверхности получаются после стягивания в точку на топологической поверхности конечного числа различных гомотопически независимых простых замкнутых кривых. Во-вторых, мы излагаем результаты, которые будут использованы в третьей главе при классификации диффеоморфизмов поверхностей и изучении действия непрерывной группы на пространстве Тейхмюллера.

Результаты § 1 этой главы принадлежат, в основном, Тейхмюллеру. Здесь доказываются (с использованием техники Альфорса) теоремы Тейхмюллера для топологически конечных римановых поверхностей. В § 2 определена модулярная группа Тейхмюллера и показано, что она действует разрывно на пространстве Тейхмюллера. Третий параграф посвящен пополненным пространствам модулей и координатам Фенхеля — Нильсена в них. Параграф заканчивается доказательством компактности

§ 1. Проколотые поверхности с краем и их пространства Тейхмюллера

Поверхность назовем топологически (соответственно дифференцируемо) конечной, если группа конечно порождена, или, что эквивалентно, найдется компактная поверхность и непрерывная (соответственно дифференцируемая) инъекция такая, что множество конечно. Родом поверхности называется род и число точек дополнения полностью определяют классы гомеоморфности (соответственно диффеоморфности) ориентируемых конечных поверхностей. Если снабжена конформной

структурой, то можно различать два типа ее идеальных граничных компонент, т. е., в данном случае, точек Именно, пусть достаточно малый диск с центром такой, что Тогда по теореме униформизации есть либо проколотый диск, либо кольцо. В первом случае точка называется проколом. Будем говорить, что имеет тип если имеет род состоит из точек и из этих точек — проколы. Поверхность называется конформно конечной, если топологически конечна и Все рассматриваемые нами поверхности предполагаются ориентируемыми.

1.1. Поверхности с краем

Пусть поверхность типа Покажем, что можно рассматривать как внутренность поверхности с краем, который состоит из граничных кривых. По ходу доказательства, основанного на лемме Шварца будет получено несколько других результатов, которые пригодятся нам впоследствии.

Допустим, что две гиперболические римановы поверхности с универсальной накрывающей причем Накрывающая проекция позволяет снабдить полной гиперболической метрикой постоянной отрицательной кривизны. Введя локальную координату в окрестности точки запишем эту метрику в виде

Величина преобразуется как -форма, т. е. если другая локальная координата в окрестности точки и

Нетрудно доказать следующее утверждение.

Теорема (обобщенная лемма Шварца), Если гиперболическая, то

причем равенство достигается в том и только том случае, когда

Доказательство. Согласно классификации негиперболических римановых поверхностей, имеем Пусть причем Последнего можно добиться, применяя, если нужно, подходящий автоморфизм к прообразу

Легко найти голоморфную инъекцию для которой диаграмма

коммутативна, причем Классическая лемма Шварца дает Обозначим через а гиперболическую метрику в А и положим Значения для близких к служат локальной координатой в окрестности точки . С ее помощью можно записать в виде

Если коэффициент в локальной координате то, применяя формулу (2), найдем

Полагая получим

Для того чтобы здесь достигалось равенство, необходимо, чтобы а с ним и было сюръективным. Тем самым теорема доказана для локальной координаты в окрестности точки Но можно выбрать произвольно, а замена локальной координаты приводит к умножению обеих частей неравенства на один и тот же множитель. Теорема доказана.

Следствие 1. Пусть прокол на Преобразование наложения у круга накрывающее простую петлю С вокруг параболично.

Доказательство. Обозначим через достаточно малую окрестность точки конформно эквивалентную проколотому диску, а через -универсальную накрывающую окрестности Отождествим с верхней полуплоскостью и пусть

есть соответствующее универсальное накрытие. Если гиперболическая метрика в то длина кривой С, лежащей равна Простая петля вокруг прокола накрывается разомкнутой кривой в , соединяющей некоторую точку с точкой При стягивании кривой С в точку прокола ее длина в гиперболической метрике стремится

к нулю. Длина той же кривой С в гиперболической метрике на задается интегралом Поэтому нижняя грань -длин кривых С, взятая по всему гомотопическому классу кривой С, равна нулю.

Пусть теперь проекция универсального накрытия, преобразование наложения, накрывающее С. Покажем, что не может быть гиперболическим. Если бы 71 было гиперболическим, то оно имело бы две неподвижные точки, и можно считать, что это точки и Кривая С поднимается до дуги, идущей из точки в точку Так как гиперболическая метрика в есть то нижняя грань длин в соответствующем гомотопическом классе достигается на вертикальной прямой, проходящей через 0, и эта нижняя грань положительна.

Верно и обратное утверждение.

Следствие 2. Пусть идеальная граничная компонента поверхности которая не является проколом. Тогда преобразование наложения круга А, накрывающее достаточно малую петлю С вокруг гиперболическое.

Доказательство. Так как С разбивает на компоненты связности, то любая компонента С поднятия С на должна разбивать Будь параболическим, оно имело бы единственную неподвижную точку, которую можно считать точкой . В одной из компонент накрывающее отображение должно было бы быть экспоненциальным, а проколом.

В доказательствах следствий 1 и 2 неявно содержится утверждение, что гомотопический класс, определенный параболическим накрывающим преобразованием, не имеет геодезического представителя. С другой стороны, класс, определенный гиперболическим накрывающим преобразованием 7, содержит геодезическую. Это проекция гиперболической прямой проходящей через неподвижные точки у.

Пусть С — простая замкнутая петля на поверхности окружающая идеальную граничную компоненту которая не является проколом. Пусть С определяет накрывающее преобразование у для накрытия Петля С поднимается до -инвариантной кривой связывающей неподвижные точки . Одна из компонент, скажем В, дополнения проектируется в окрестность точки конформно эквивалентную кольцу, а именно Граница В в содержит замкнутую дугу А — часть границы такую, что

концами А являются неподвижные точки у. Накрывающая группа разрывно действует на орбите дополнения {концевые точки}. При этом представляет собой поверхность с краем. Такую компоненту края можно найти для любой идеальной граничной компоненты которая не является проколом. Полученная поверхность, имеющая границу, называется римановой поверхностью с краем. Более общо, римановой поверхностью с краем называется поверхность с краем, внутренность которой снабжена структурой римановой поверхности. Будем называть краем поверхности

Конечную риманову поверхность с краем часто компактифицируют, заклеивая проколы. Добавленные точки называются выделенными точками. В современной литературе термины «прокол» и «выделенная точка» используются как взаимозаменяемые.