| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
Результаты Тёрстона об измеримых слоениях поверхностей и его компактификация пространства Тейхмюллера естественно приводят к классификации диффеоморфизмов топологически конечных ориентируемых поверхностен. В работе [1] Берс рассмотрел экстремальную проблему в теории Тейхмюллера и показал, что ее решение — либо несуществование решения — приводит к той же классификации. Ниже мы излагаем метод Берса. Иной подход к получению классификации принадлежит Харви [4]. Харви применил к модулярной группе Тейхмюллера технику комплексов Титса и графов групп.
В § 4 этой главы изучается непрерывное действие некоторой группы на пространстве Тейхмюллера. Это действие аналогично действию группы автоморфизмов единичного диска  порожденной орициклическими потоками. Показано, что действие этой группы транзитивно на пространстве Тейхмюллера.
порожденной орициклическими потоками. Показано, что действие этой группы транзитивно на пространстве Тейхмюллера.
В § 5 делаются некоторые заключительные замечания и формулируются открытые проблемы.
§ 1. Экстремальная проблема Берса и вычисления для проколотых торов
Пусть  дифференцируемая ориентированная поверхность конечного неисключительного типа
дифференцируемая ориентированная поверхность конечного неисключительного типа  Если
Если  риманова поверхность и
риманова поверхность и  диффеоморфизм, то
диффеоморфизм, то  можно снабдить конформной структурой
можно снабдить конформной структурой  поднимая ее с помощью а. В гомотопическом классе
поднимая ее с помощью а. В гомотопическом классе  диффеоморфизма
диффеоморфизма  выберем отображение
выберем отображение  экстремальное в следующем смысле:
экстремальное в следующем смысле:

Из теорем Тейхмюллера, относящихся к поверхностям конечного неисключительного типа, следует, что такое  существует и единственно, а
существует и единственно, а  либо конформно, либо является отображением Тейхмюллера. Берс рассматривал проблему
либо конформно, либо является отображением Тейхмюллера. Берс рассматривал проблему
минимизации  по всем возможным конформным структурам а. Положим
по всем возможным конформным структурам а. Положим

и поставим следующие вопросы:  Будет ли
Будет ли 
Существует ли на  конформная структура а, для которой
конформная структура а, для которой 
Конформную структуру, для которой достигается  назовем
назовем  -минимальной. Так как любая экстремальная функция
-минимальной. Так как любая экстремальная функция  либо конформна, либо является отображением Тейхмюллера, то проблема Берса относится к классам диффеоморфизмов, действующих на пространстве Тейхмюллера. Действительно, вопрос
либо конформна, либо является отображением Тейхмюллера, то проблема Берса относится к классам диффеоморфизмов, действующих на пространстве Тейхмюллера. Действительно, вопрос  можно перефразировать так:
можно перефразировать так:
 Пусть
Пусть  индуцирует
индуцирует  Существует ли
Существует ли  такая, что
такая, что

Эта переформулировка следует сразу из определения расстояния Тейхмюллера (см. § 5 гл. I). Для того чтобы классифицировать элементы  выберем
выберем  индуцирующие
индуцирующие  Результаты классификации приведены в следующей таблице:
Результаты классификации приведены в следующей таблице:
(см. скан)
Эта классификация есть обобщение классификации элементов модулярной группы Тейхмюллера для торов с одним проколом. Этот случай является классическим, и вычисления, набросок которых мы даем ниже, в этом случае элементарны. Пусть  решетка в
решетка в  Отождествим
Отождествим  с набором точек
с набором точек  где
где  Предположим, что
Предположим, что  Фактор
Фактор  есть проколотый тор, и по теореме униформизации, рассматривая различные те
есть проколотый тор, и по теореме униформизации, рассматривая различные те  мы получим все торы с одним проколом. Поэтому
мы получим все торы с одним проколом. Поэтому  является моделью для
является моделью для  Две точки
Две точки  определяют конформно эквивалентные торы тогда и только тогда, когда
определяют конформно эквивалентные торы тогда и только тогда, когда  Это в свою очередь эквивалентно равенству
Это в свою очередь эквивалентно равенству  где
где  Таким образом, модулярной группой Тейхмюллера
Таким образом, модулярной группой Тейхмюллера  является классическая эллиптическая модулярная группа. Если
является классическая эллиптическая модулярная группа. Если  то
то  либо параболическое, либо эллиптическое,
либо параболическое, либо эллиптическое,
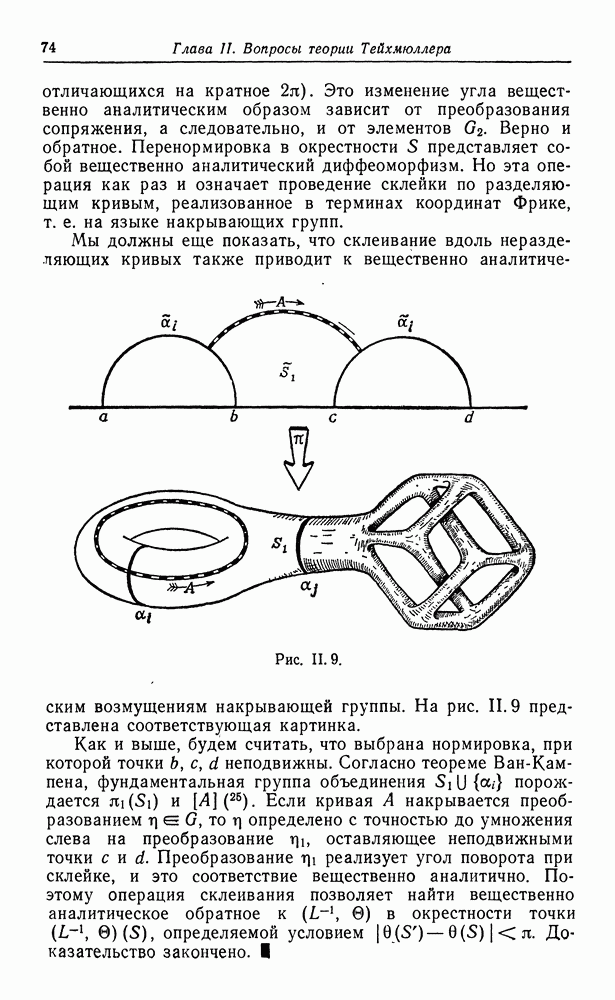
либо гиперболическое как мёбиусово преобразование. Отсюда немедленно получается классификация (в гиперболической метрике). Сдвиг  отображение скручивания, изображенное на рис. III. 1.
отображение скручивания, изображенное на рис. III. 1.

Рис. III.1.
Группа  содержит также вращения
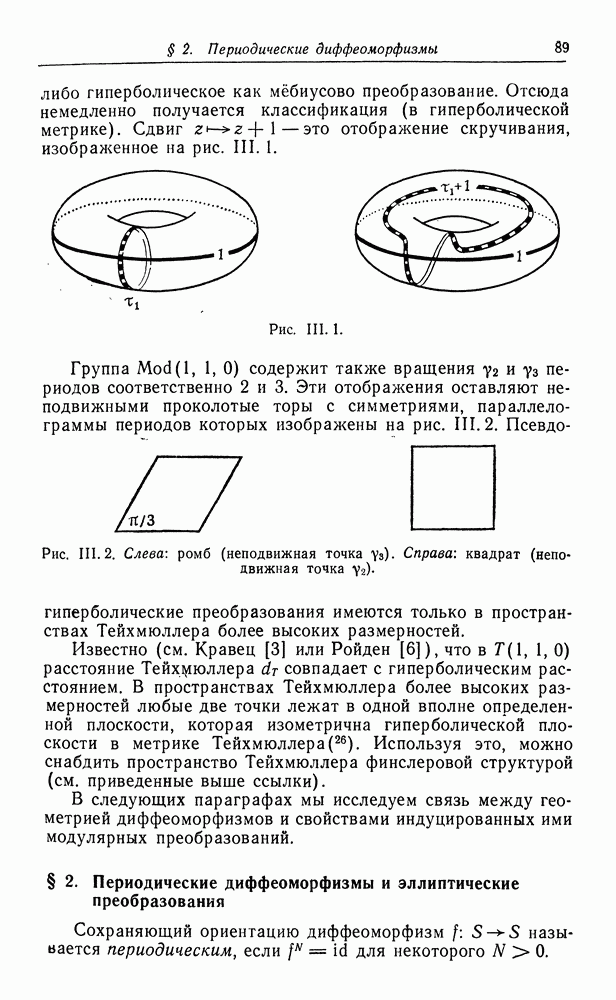
содержит также вращения  периодов соответственно 2 и 3. Эти отображения оставляют неподвижными проколотые торы с симметриями, параллелограммы периодов которых изображены на рис. III. 2.
периодов соответственно 2 и 3. Эти отображения оставляют неподвижными проколотые торы с симметриями, параллелограммы периодов которых изображены на рис. III. 2.

Рис. III. 2. Слева: ромб (неподвижная точка  Справа: квадрат (неподвижная точка
Справа: квадрат (неподвижная точка 
Псевдогиперболические преобразования имеются только в пространствах Тейхмюллера более высоких размерностей.
Известно (см. Кравец [3] или Ройден [6]), что в  расстояние Тейхмюллера
расстояние Тейхмюллера  совпадает с гиперболическим расстоянием. В пространствах Тейхмюллера более высоких размерностей любые две точки лежат в одной вполне определенной плоскости, которая изометрична гиперболической плоскости в метрике
совпадает с гиперболическим расстоянием. В пространствах Тейхмюллера более высоких размерностей любые две точки лежат в одной вполне определенной плоскости, которая изометрична гиперболической плоскости в метрике  Используя это, можно снабдить пространство Тейхмюллера финслеровой структурой (см. приведенные выше ссылки).
Используя это, можно снабдить пространство Тейхмюллера финслеровой структурой (см. приведенные выше ссылки).
В следующих параграфах мы исследуем связь между геометрией диффеоморфизмов и свойствами индуцированных ими модулярных преобразований.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
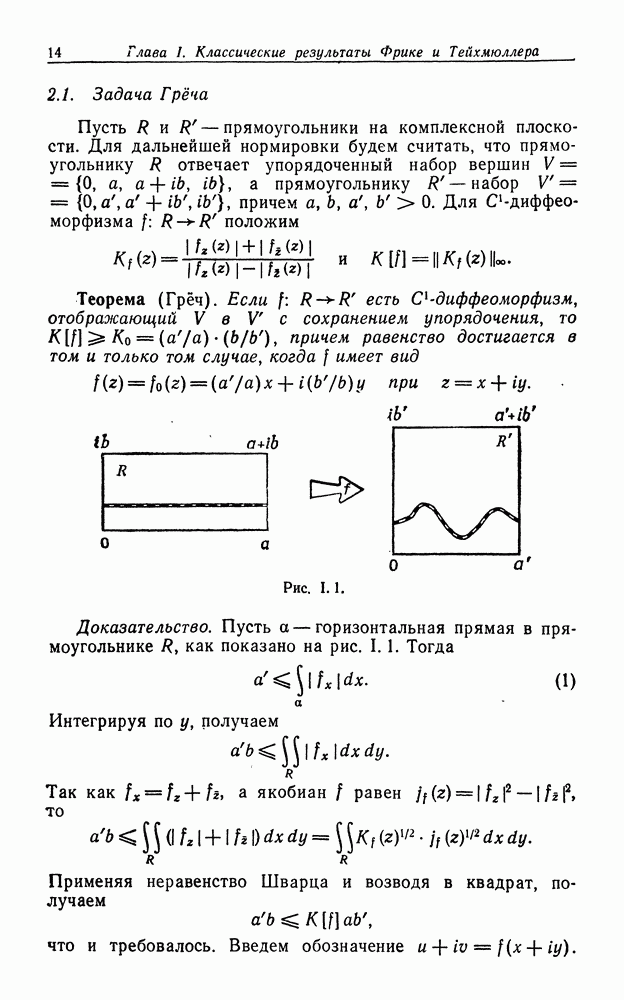
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
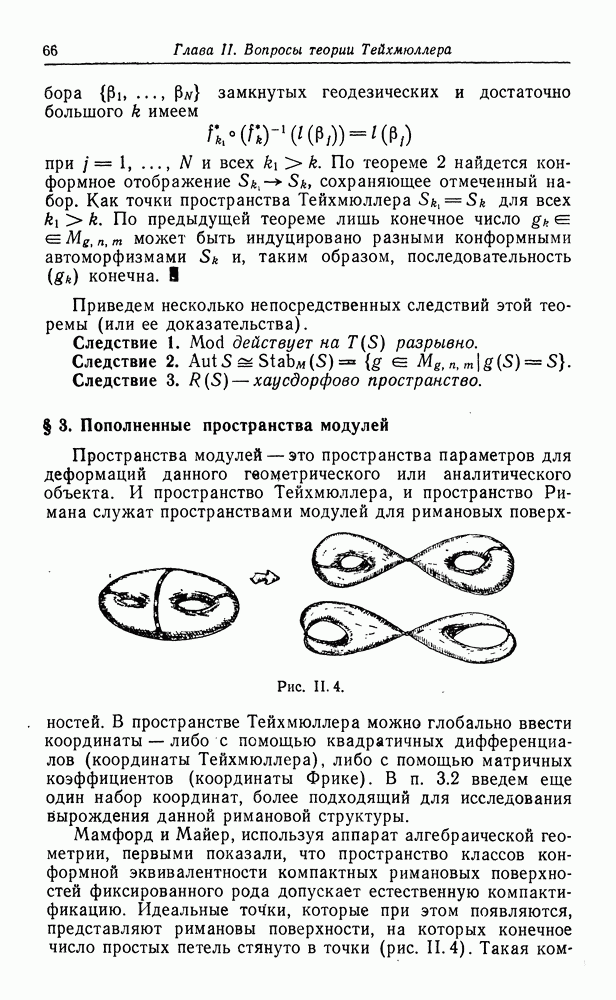
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания