| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Проблема Грёча
В конце 20-х гг. Г. Грёч поставил и решил элементарную экстремальную задачу для конформных отображений. Экстремальное отображение оказалось аффинным. Ту же экстремальную задачу можно поставить для компактных поверхностей рода больше 1. Решение этой задачи дают теоремы Тейхмюллера, составляющие содержание этой главы. Доказательства утверждений Тейхмюллера гораздо сложнее рассуждений Грёча по двум причинам. Первая заключается в том, что на многообразии отображение будет аффинным только при определенном выборе локальной координаты, т. е. аффинность не является внутренним (инвариантным) свойством. Вторая причина состоит в том, что у компактной поверхности нет границы, в то время как в задаче Грёча имеются граничные условия. Первую трудность Тейхмюллер преодолел, пользуясь квадратичными дифференциалами, а вторую при помощи соображений эргодичности.
2.1. Задача Грёча
Пусть  прямоугольники на комплексной плоскости. Для дальнейшей нормировки будем считать, что прямоугольнику
прямоугольники на комплексной плоскости. Для дальнейшей нормировки будем считать, что прямоугольнику  отвечает упорядоченный набор вершин
отвечает упорядоченный набор вершин  а прямоугольнику
а прямоугольнику  набор
набор  причем
причем  Для
Для  -диффео-морфизма
-диффео-морфизма  положим
положим

Теорема (Грёч). Если  есть
есть  -диффеоморфизм, отображающий
-диффеоморфизм, отображающий  с сохранением упорядочения, то
с сохранением упорядочения, то  причем равенство достигается в том и только том случае, когда
причем равенство достигается в том и только том случае, когда  имеет вид
имеет вид


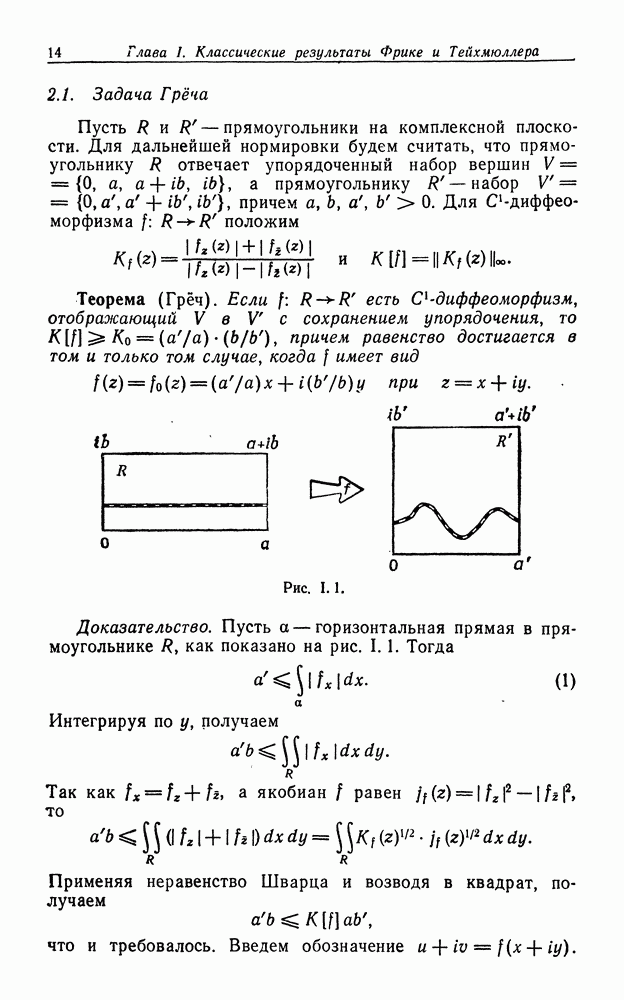
Рис. 1.1.
Доказательство. Пусть а — горизонтальная прямая в прямоугольнике  как показано на рис.
как показано на рис.  Тогда
Тогда

Интегрируя по у, получаем

Так как  якобиан
якобиан  равен
равен  то
то

Применяя неравенство Шварца и возводя в квадрат, получаем

что и требовалось. Введем обозначение и 
Выясним теперь, при каких условиях достигается равенство. Если в (1) имеет место равенство, то  при фиксированном
при фиксированном  Фиксируя
Фиксируя  видим, что
видим, что  на вертикальных линиях. Далее
на вертикальных линиях. Далее  Так как
Так как  то
то  Кроме того,
Кроме того,  Неравенство Шварца превращается в равенство тогда и только тогда, когда
Неравенство Шварца превращается в равенство тогда и только тогда, когда  где с — некоторая постоянная. В этом случае
где с — некоторая постоянная. В этом случае  с некоторыми константами
с некоторыми константами  Теперь легко показать, что константы
Теперь легко показать, что константы  имеют требуемый вид. I
имеют требуемый вид. I
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
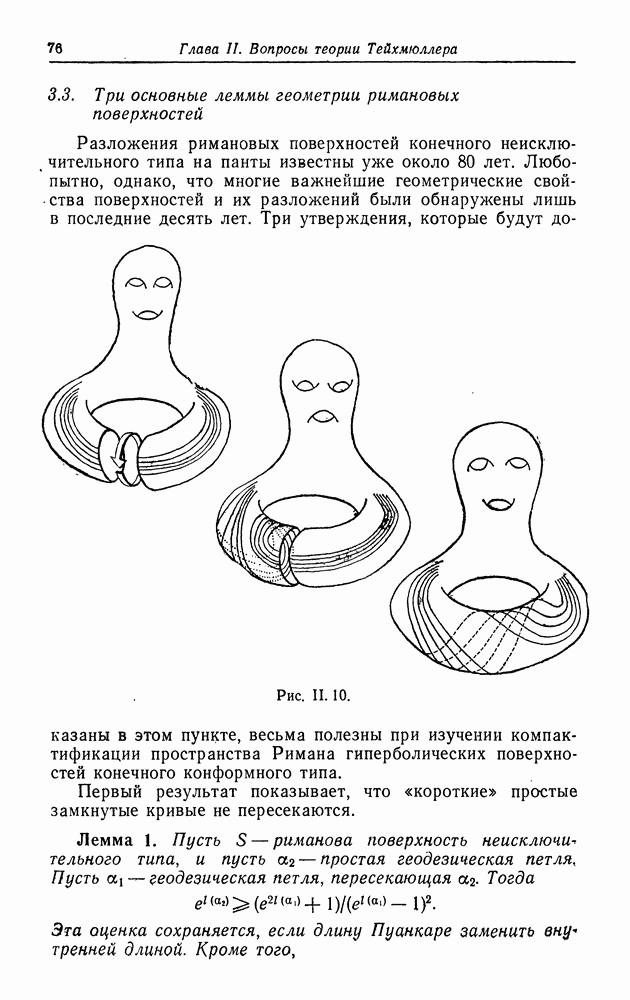
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
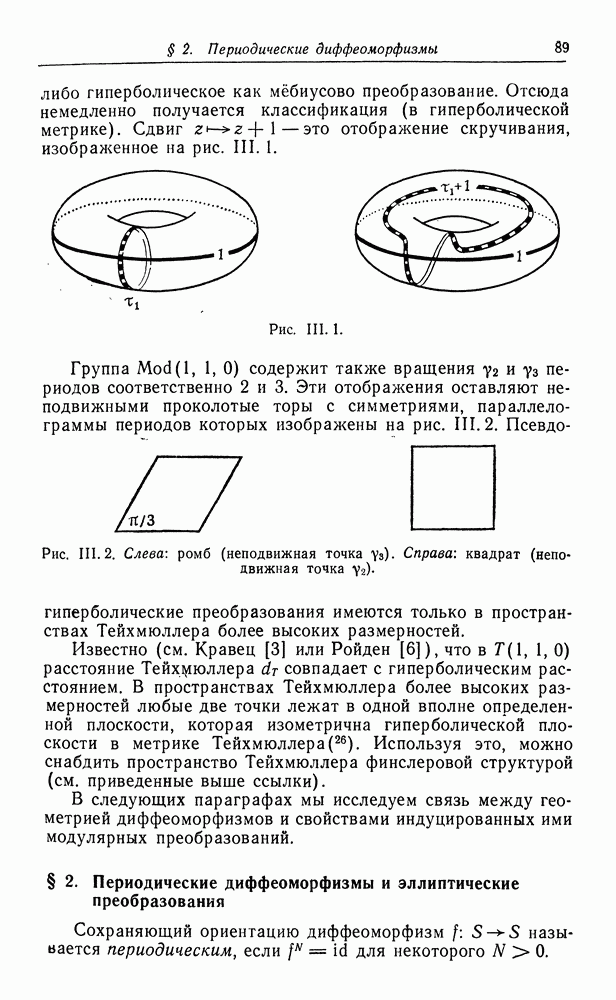
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания