| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3. Кольца и проколотые диски: метод экстремальных длин
Пусть  риманова поверхность с краем, гомеоморфная проколотому диску
риманова поверхность с краем, гомеоморфная проколотому диску  Тогда
Тогда  имеет тип (0, 0, 2) или (0, 1, 1), причем
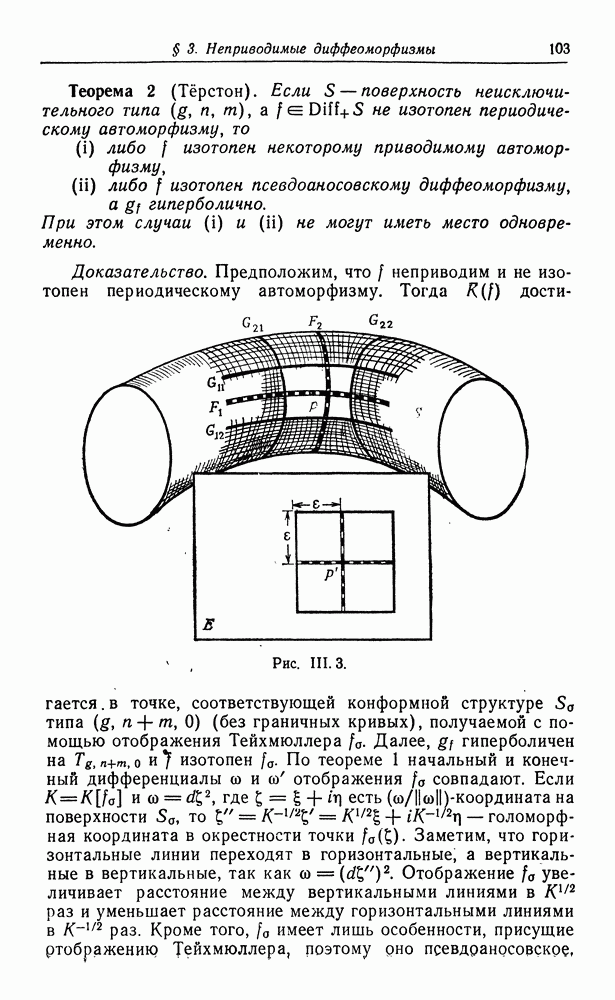
имеет тип (0, 0, 2) или (0, 1, 1), причем  всегда гиперболична. В первом случае накрывающая группа для
всегда гиперболична. В первом случае накрывающая группа для  имеет вид
имеет вид  с некоторым вещественным
с некоторым вещественным  Второму случаю соответствует группа
Второму случаю соответствует группа  Остановимся на поверхности типа (0, 0, 2). Число X можно использовать для параметризации классов голоморфной эквивалентности поверхностей типа (0, 0, 2). Накрывающая проекция
Остановимся на поверхности типа (0, 0, 2). Число X можно использовать для параметризации классов голоморфной эквивалентности поверхностей типа (0, 0, 2). Накрывающая проекция

отображает  в кольцо
в кольцо  Другой способ описания состоит в том, что классы эквивалентности
Другой способ описания состоит в том, что классы эквивалентности
параметризуются числом  при этом поверхность
при этом поверхность  конформно эквивалентна кольцу
конформно эквивалентна кольцу  Число
Число  называется модулем кольца
называется модулем кольца  Несколько иную характеристику модуля кольца доставляет метод экстремальных длин, принадлежащий Альфорсу и Бёрлингу.
Несколько иную характеристику модуля кольца доставляет метод экстремальных длин, принадлежащий Альфорсу и Бёрлингу.
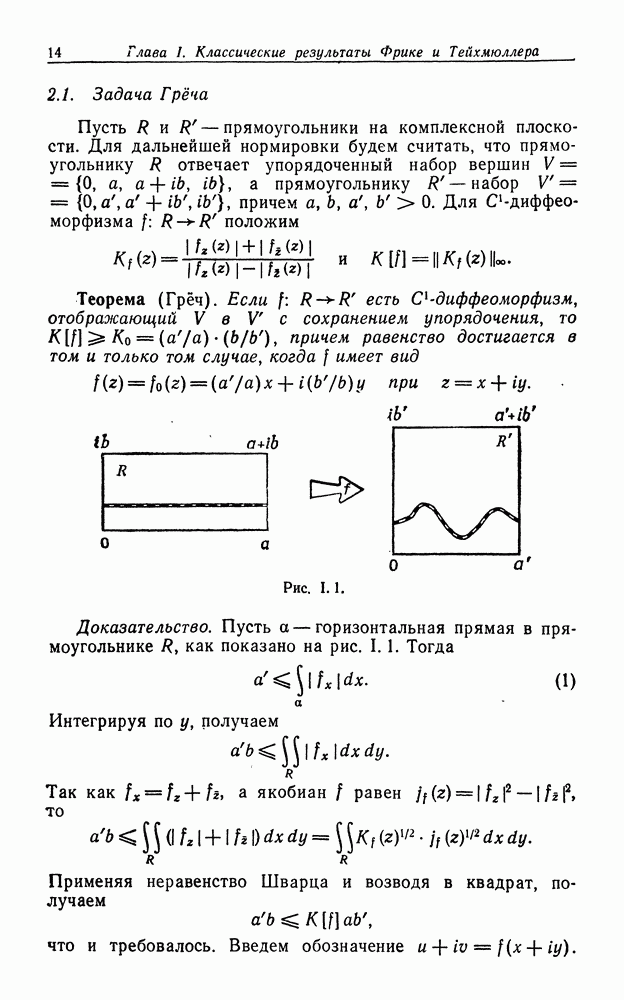
Теорема 1. Пусть А — кольцо  измерима и
измерима и 
Обозначим через  множество простых замкнутых кривых, разделяющих граничные компоненты кольца А. Положим
множество простых замкнутых кривых, разделяющих граничные компоненты кольца А. Положим

и пусть  Тогда
Тогда

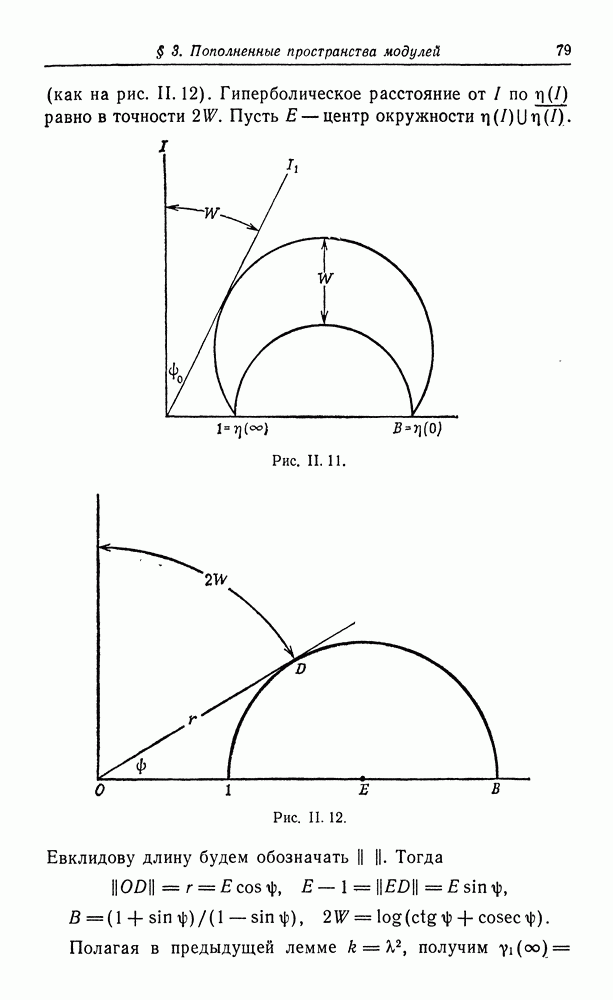
Доказательство. В полярных координатах имеем неравенства

Интегрируя по  получаем
получаем

Применяя неравенство Шварца, приходим к следующему результату:

или

Осталось заметить, что для  это неравенство превращается в равенство. I
это неравенство превращается в равенство. I
Если отображение  конформно и инъективно, то можно поднять на
конформно и инъективно, то можно поднять на  кривые семейства
кривые семейства  и плотности
и плотности 
Так как  конформный инвариант, то этим свойством обладает и правая часть равенства (3). Это наблюдение приводит к неравенству Грёча, которое мы сформулируем в виде следующей теоремы.
конформный инвариант, то этим свойством обладает и правая часть равенства (3). Это наблюдение приводит к неравенству Грёча, которое мы сформулируем в виде следующей теоремы.
Теорема 2 (супераддитивность модуля). Пусть  кольцо, а с — простая замкнутая кривая, разделяющая граничные компоненты
кольцо, а с — простая замкнутая кривая, разделяющая граничные компоненты  Если
Если  две компоненты
две компоненты  то
то

Доказательство. Пусть  семейство кривых,
семейство кривых,  множество плотностей для
множество плотностей для  Ясно, что
Ясно, что  Для
Для  положим
положим

Пусть  Тогда
Тогда  для
для  и
и

Отсюда следует неравенство

Точная нижняя грань левой части есть  Для 1, 2 каждую плотность
Для 1, 2 каждую плотность  можно продолжить до плотности
можно продолжить до плотности  полагая
полагая  для
для  Следовательно,
Следовательно,

и, взяв  в полученном неравенстве, придем к требуемому результату.
в полученном неравенстве, придем к требуемому результату. 
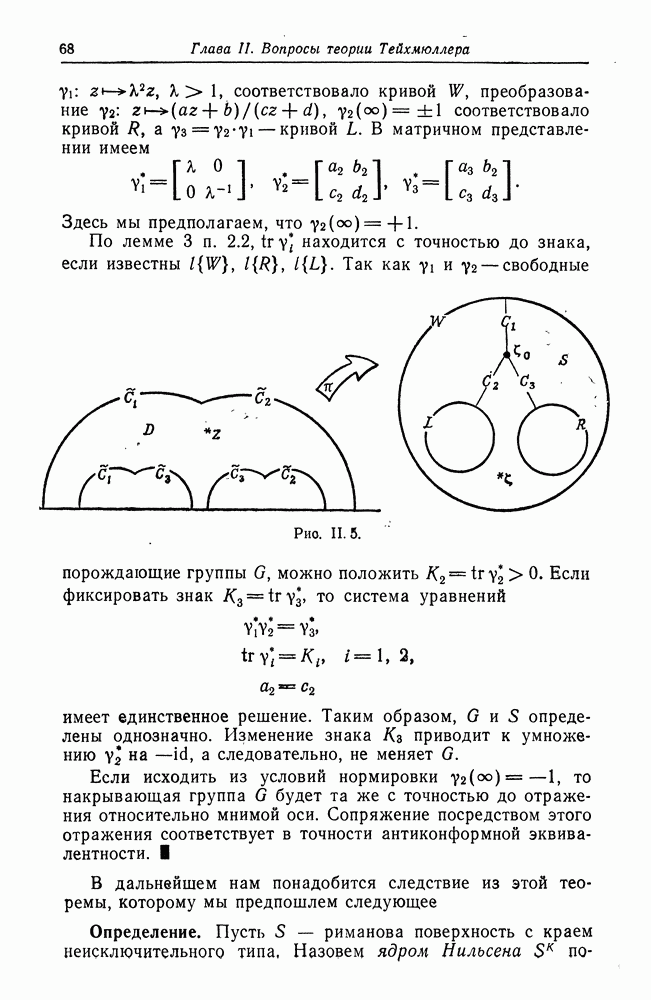
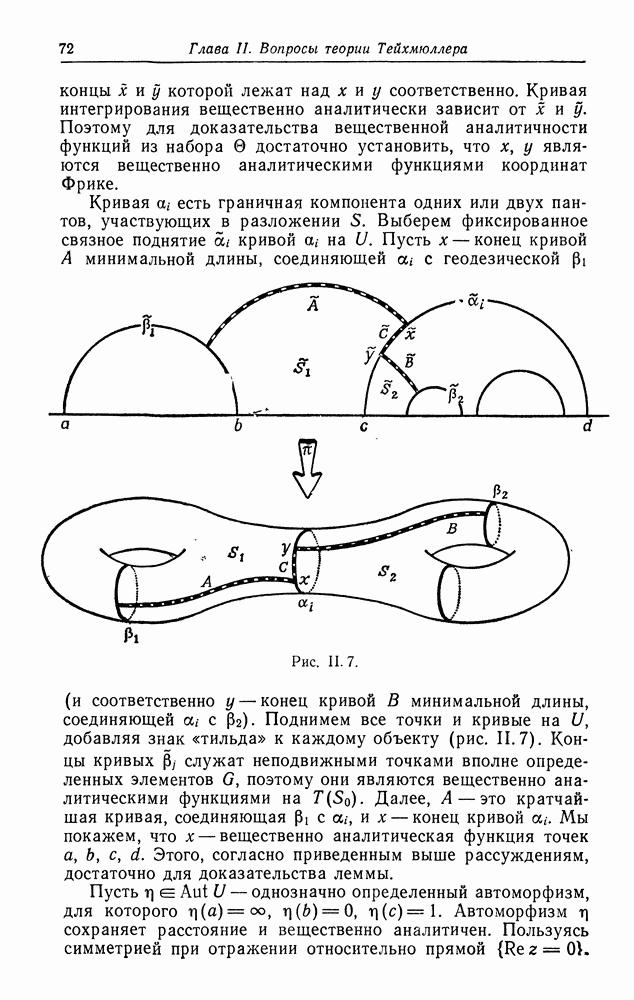
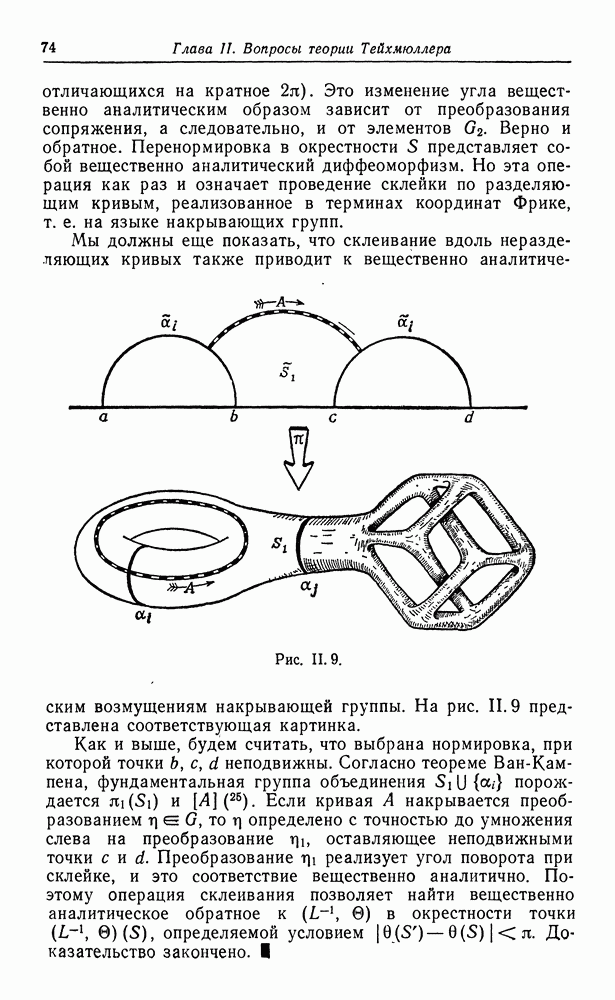
Применим теперь эти теоремы к процессу расширения Нильсена. Пусть  риманова поверхность с краем типа
риманова поверхность с краем типа  расширение Нильсена поверхности
расширение Нильсена поверхности  Ограничение на
Ограничение на  полной гиперболической метрики поверхности
полной гиперболической метрики поверхности  есть внутренняя метрика поверхности
есть внутренняя метрика поверхности  Поэтому, согласно лемме 2 п. 1.2, каждая компонента дополнения топологически эквивалентна кольцу а. Вычислим теперь
Поэтому, согласно лемме 2 п. 1.2, каждая компонента дополнения топологически эквивалентна кольцу а. Вычислим теперь
Лемма.  где
где  -длина кривой
-длина кривой  в гиперболической метрике на
в гиперболической метрике на 
Доказательство. Обозначим через  проекцию универсального накрытия
проекцию универсального накрытия  а через
а через  — автоморфизм
— автоморфизм  накрывающий Предположим, что кривая
накрывающий Предположим, что кривая  ориентирована таким образом, что
ориентирована таким образом, что  Очевидно, что это допустимое предположение. Повторяя вычисления из доказательства теоремы 1, приходим к формуле
Очевидно, что это допустимое предположение. Повторяя вычисления из доказательства теоремы 1, приходим к формуле 
Теорема 3. Если  риманова поверхность с краем, имеющая тип
риманова поверхность с краем, имеющая тип  то ее бесконечное расширение Нильсена
то ее бесконечное расширение Нильсена  не имеет граничных кривых, т. е.
не имеет граничных кривых, т. е.  конформно конечная поверхность.
конформно конечная поверхность.
Доказательство. Достаточно показать, что каждая компонента А дополнения  конформно эквивалентна проколотому диску. Для этого в свою очередь достаточно установить, что
конформно эквивалентна проколотому диску. Для этого в свою очередь достаточно установить, что  Так как
Так как  то
то

где через  обозначена длина
обозначена длина  относительно внутренней метрики
относительно внутренней метрики  По лемме 2 п. 1.2 последовательность
По лемме 2 п. 1.2 последовательность  неограниченно возрастает и, следовательно,
неограниченно возрастает и, следовательно, 
Исследуем теперь деформации конформной структуры колец, индуцированные допустимыми отображениями.
Лемма 2. Пусть  два кольца и
два кольца и  диффеоморфизм с изолированными особенностями. Если
диффеоморфизм с изолированными особенностями. Если  то
то

Доказательство. Перейдем к дублю  кольца
кольца  который представляет собой тор с параллелограммом периодов
который представляет собой тор с параллелограммом периодов  Диффеоморфизм
Диффеоморфизм  поднимается до отображения
поднимается до отображения  при подходящем выборе
при подходящем выборе  Приведенное в предыдущей главе решение задачи Грёча показывает, что
Приведенное в предыдущей главе решение задачи Грёча показывает, что  минимизирует
минимизирует  среди всех допустимых отображений
среди всех допустимых отображений  в том и только том случае, когда
в том и только том случае, когда  аффинно.
аффинно.
С точностью до конформной эквивалентности  можно представить в виде
можно представить в виде  Отобразим множество
Отобразим множество  с помощью выбранной ветви логарифма. Теперь экстремальное допустимое отображение
с помощью выбранной ветви логарифма. Теперь экстремальное допустимое отображение  принимает вид
принимает вид  где
где 
Так как отображение, осуществляемое логарифмом, конформно на  то
то

Заключение леммы следует теперь из того, что 
Теорема 4 (Волперт). Пусть  гиперболические поверхности,
гиперболические поверхности,  диффеоморфизм с изолированными особенностями и
диффеоморфизм с изолированными особенностями и  Если
Если  замкнутая гиперболическая геодезическая на поверхности
замкнутая гиперболическая геодезическая на поверхности  то гиперболическая геодезическая в классе кривой
то гиперболическая геодезическая в классе кривой  удовлетворяет неравенству
удовлетворяет неравенству 
Доказательство. Пусть  группа накрывающих преобразований универсального накрытия
группа накрывающих преобразований универсального накрытия  Сопрягая, если потребуется,
Сопрягая, если потребуется,  мёбиусовым автоморфизмом, можно считать, что
мёбиусовым автоморфизмом, можно считать, что  накрывается геодезической, идущей из
накрывается геодезической, идущей из  в
в  Тогда
Тогда  определяет преобразование
определяет преобразование  Диффеоморфизм
Диффеоморфизм  накрывается допустимым отображением
накрывается допустимым отображением  причем
причем  Обозначим через
Обозначим через  циклическую группу, порожденную
циклическую группу, порожденную  Ясно, что
Ясно, что  накрывает и отображение
накрывает и отображение  При этом
При этом  кольцо. Применяя предыдущую лемму, получаем неравенство
кольцо. Применяя предыдущую лемму, получаем неравенство

Так как дилатация отображения — чисто локальная характеристика,  Простые вычисления, проделанные ниже в п. 2.2 при доказательстве леммы 3, показывают, что
Простые вычисления, проделанные ниже в п. 2.2 при доказательстве леммы 3, показывают, что  Учитывая замечание, сделанное в начале п. 1.3, имеем
Учитывая замечание, сделанное в начале п. 1.3, имеем

Комбинируя это неравенство с неравенством (4), получаем требуемый результат. 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
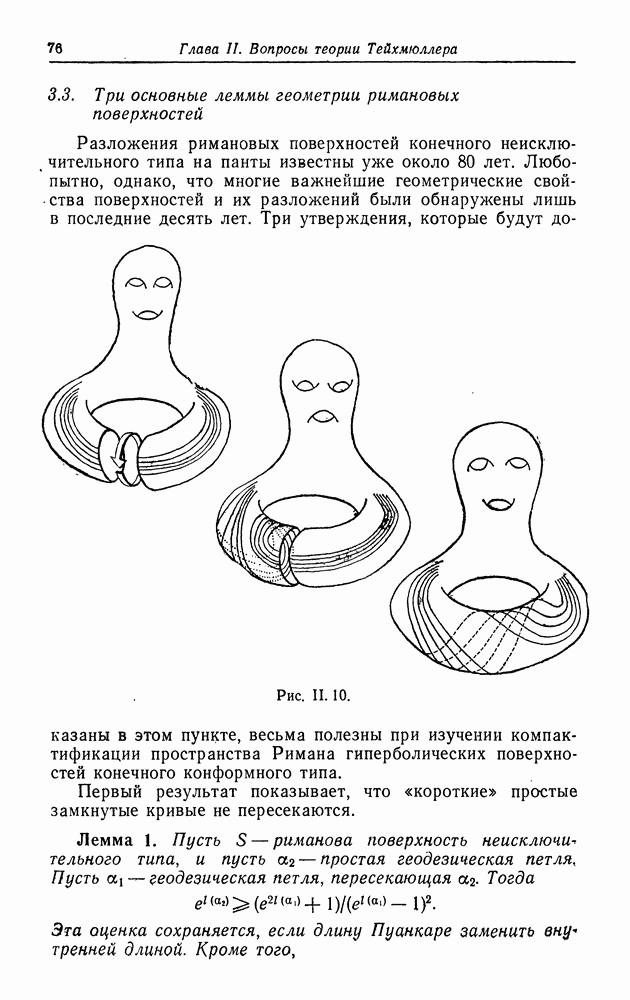
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
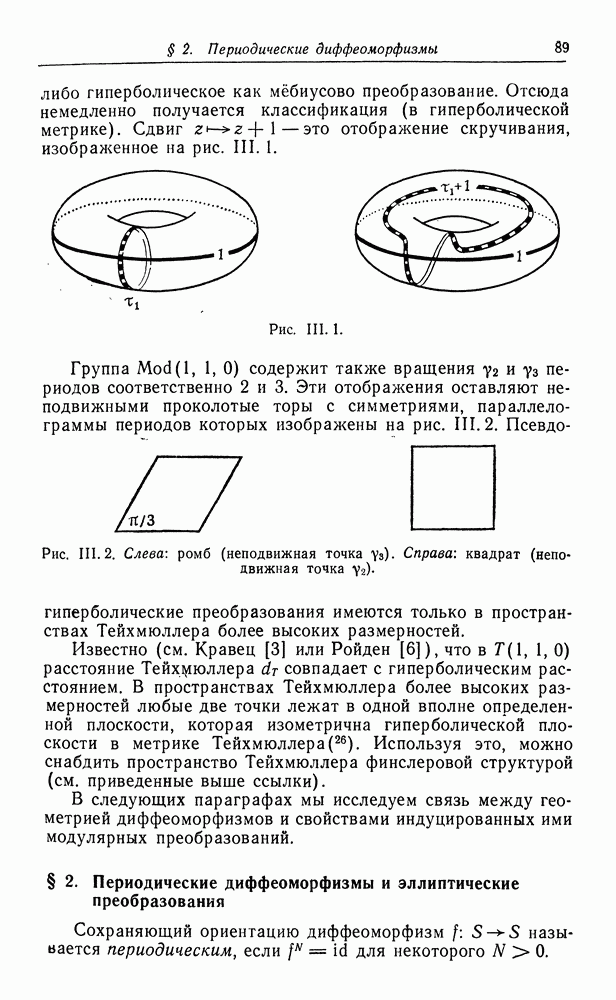
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания