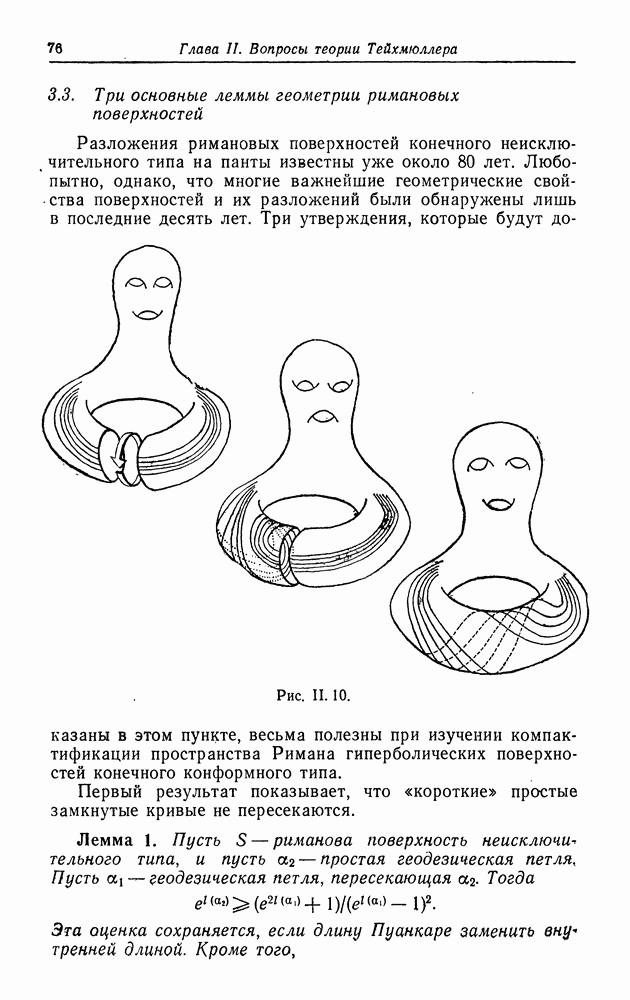
3.3. Три основные леммы геометрии римановых поверхностей

Разложения римановых поверхностей конечного неисключительного типа на панты известны уже около 80 лет. Любопытно, однако, что многие важнейшие геометрические свойства поверхностей и их разложений были обнаружены лишь в последние десять лет.

Рис.

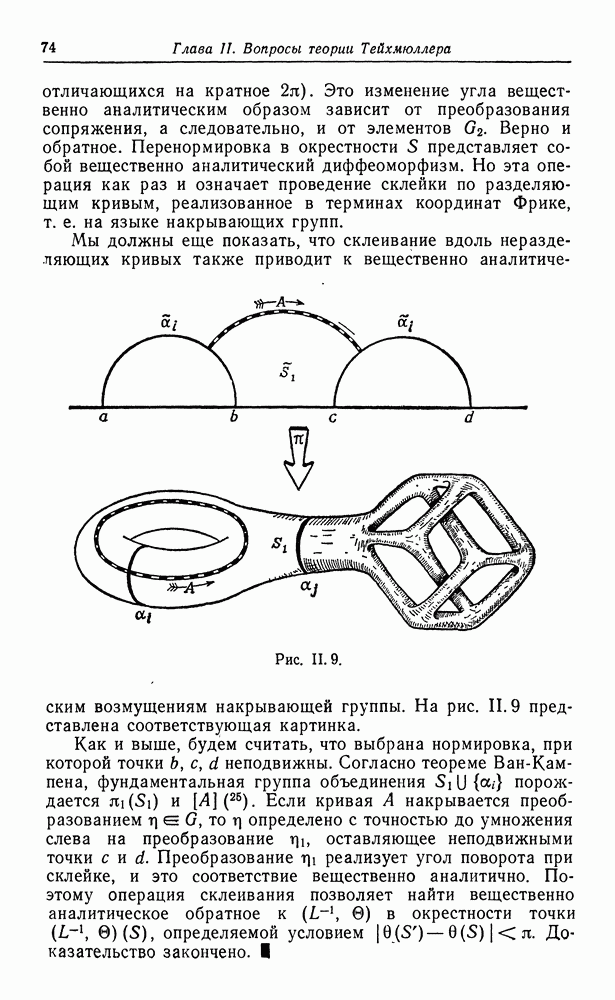
Три утверждения, которые будут доказаны в этом пункте, весьма полезны при изучении компактификации пространства Римана гиперболических поверхностей конечного конформного типа.

Первый результат показывает, что «короткие» простые замкнутые кривые не пересекаются.

Лемма 1. Пусть риманова поверхность неисключительного типа, и пусть простая геодезическая петля, Пусть геодезическая петля, пересекающая Тогда

Эта оценка сохраняется, если длину Пуанкаре заменить внутренней длиной. Кроме того,

Доказательство. Пусть универсальное накрывающее отображение. Сопрягая, если необходимо, в группе можно считать, что кривой соответствует преобразование где а кривой преобразование

Преобразование оставляет неподвижными точки 1 и (отметим, что не нормировано). Допустим, что геодезическая, соединяющая 1 и 5, пересекает значит, Имеем Так как не пересекает ни одной из кривых, полученных из нее самой сдвигом относительно то Аналогично получаем или, что то же самое,

или еще

Поэтому

Заключение теперь очевидно. Чтобы получить тот же результат для внутренней длины, достаточно перейти к дублю поверхности а затем повторить проведенные выше рассуждения для накрытия

Из леммы 1 непосредственно вытекает

Следствие. Существует универсальная постоянная такая, что если геодезические простые петли на мановой поверхности неисключительного типа и или то

Простая замкнутая геодезическая петля а на поверхности имеет трубчатую окрестность Эта окрестность будет односторонней, если граничная кривая, и двусторонней в противном случае. Соответствующее расположение гомеоморфно стандартному, на плоскости, для кривой . В первом случае имеем во втором

Компонента С дополнения называется воротником кривой а. Если а — геодезическая кривая (относительно внутренней метрики), то воротником ширины кривой

а называется такой воротник а, что внутреннее расстояние между а и другой компонентой постоянно и равно Можно говорить также о внутренней площади воротника С. В силу компактности, каждая замкнутая простая геодезическая имеет воротник положительной ширины и площади. Каждый воротник вокруг а имеет две граничные компоненты: одна из них есть а, другую мы обозначим Наш следующий результат — «лемма о воротнике» — утверждает, что нижние границы для и верхняя граница для зависят только от Точные оценки были найдены Мательски [8].

Лемма 2. Пусть риманова поверхность неисключительного типа, и пусть а — граничная кривая поверхности Обозначим через I внутреннюю длину кривой а. Тогда существуют такие постоянные что а имеет воротник С ширины площади А и При этом ограничен сверху числом

Доказательство. Пусть кривая а накрывается мёбиусовым преобразованием По соображениям симметрии можно считать, что воротник С вокруг поднимается до сектора Единственные отождествления, которые нужно сделать в С при возвращении в производятся степенями у. В терминах имеем

Далее, в этих обозначениях

Для того чтобы получить максимальные площадь и ширину С, необходимо взять максимальное значение Ясно, что будет максимальным, если найдется мёбиусово преобразование такое, что для имеем Концы являются неподвижными точками элемента сопряженного преобразованию у (рис. II 11).

Применяя, если необходимо, гомотетию, можно считать, что Если положить то -геодезическая, соединяющая точки 1 и В. Проведем касательную к кривой проходящую через

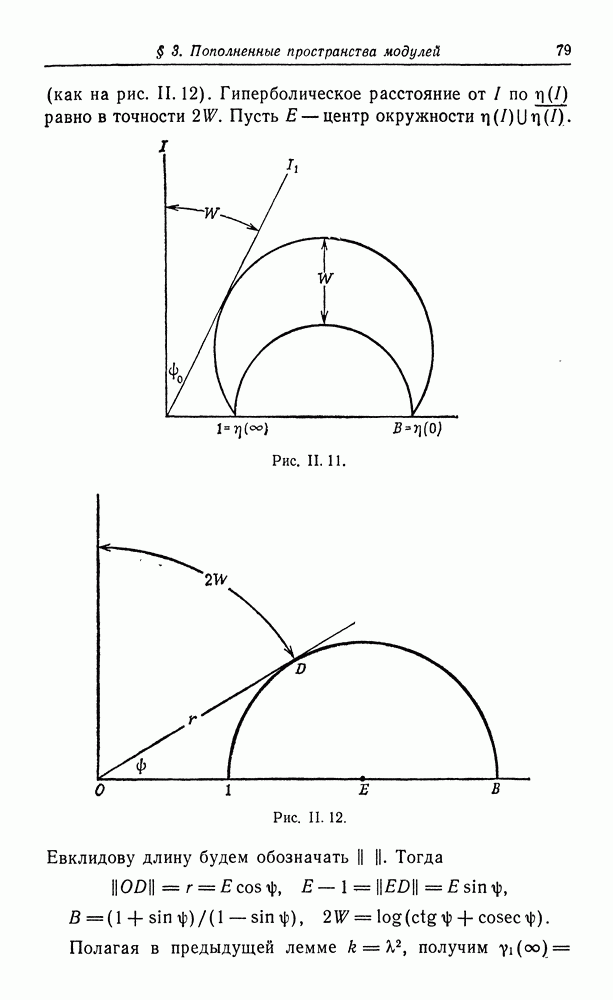
(как на рис. II. 12). Гиперболическое расстояние от по равно в точности Пусть центр окружности

Рис. и.

Рис.

Евклидову длину будем обозначать Тогда

Полагая в предыдущей лемме получим

а следовательно, Но -монотонные функции Поэтому

При фиксированном величина № имеет минимум. Этим доказано существование констант Ясно, что 1 при Кроме того, при этом и

Если близко к то поэтому, согласно (3.2) и (3.3), асимптотически стремится к вблизи Так как поверхность конечного неисключительного типа, подмножество то

Это завершает доказательство леммы.

Известно (см. Л. Кин [5]), что воротник можно выбрать таким образом, чтобы

Лемма 3. Существует разложение поверхности на панты такое, что длина каждой кривой а на границе ограничена константой зависящей только от типа поверхности и внутренних длин ее граничных кривых.

Доказательство. Если панты, то доказывать нечего, поэтому будем предполагать, что это не так. Пусть граничные кривые 5, геодезические во внутренней метрике. Для доказательства леммы достаточно найти еще одну кривую, вдоль которой мы рассечем поверхность и такую, что ее длина ограничена числом, зависящим только от типа и величин

Обозначим через ширину воротника вокруг доставляемую предыдущей леммой. Пусть Если удастся найти нетривиальную не стягиваемую на простую петлю а длины меньшей то доказательство будет закончено. Такая нетривиальная кривая должна существовать, иначе каждая простая петля а, не стягиваемая на и такая, что была бы гомотопна нулю. Выберем простую петлю лежащую в дополнении и не стягиваемую на Положим Вдоль на расстоянии друг от друга вырежем диски радиуса . В силу выбора эти диски содержатся в Число дисков равно приблизительно и для малых площадь каждого диска близка к Поэтому сумма площадей всех дисков равна приблизительно По теореме Гаусса — Бонне внутренняя

площадь конечна и определяется типом . Следовательно, либо

диски перекрываются.

Альтернатива немедленно приводит к нужному результату. Из следует, что в можно найти такие замкнутые петли что свободно гомотопна некоторому произведению этих петель.

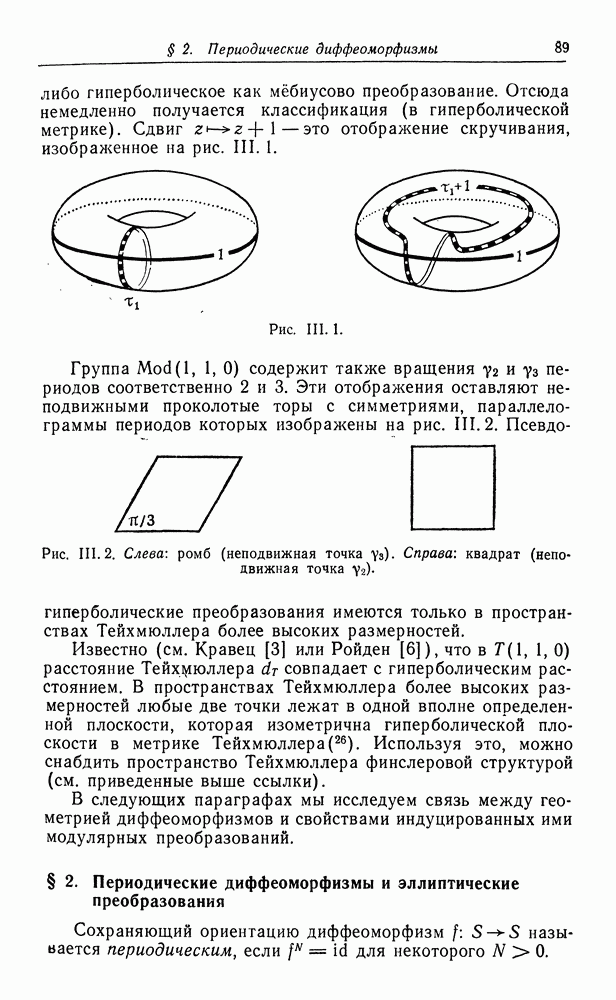
Рассмотрим теперь отдельно случаи

Случай 1. Если то в качестве возьмем простую петлю вокруг ручки.

Рис.

В этом случае не может быть свободно гомотопна произведению граничных кривых, и, значит, по индукции можно найти такую простую петлю не стягиваемую на что (Это рассуждение можно сделать строгим, если заметить, что гомологический класс кривой нетривиален, а любое произведение кривых, гомотопных граничным кривым, всегда гомологично нулю.)

Случай 2. Пусть тогда свободно порождается гомотопическими классами граничных кривых и малых петель вокруг проколов. Вырезая воротники вокруг граничных кривых и орициклические окрестности проколов, получим подповерхность поверхности Пусть ограничение на функции внутреннего расстояния на Обозначим через минимальное -расстояние между граничными кривыми

поверхности Величина достигается вдоль некоторой внутренней геодезической Проделаем теперь следующее построение: вдоль на расстоянии друг от друга вырежем диски радиуса 8. Как и раньше, зависит только от внутренних длин граничных кривых. Диски не могут пересекаться, поэтому Таким образом, ограничено константой, зависящей только от исходных данных. Дуга идет от одной граничной кривой на поверхности до другой, которую мы обозначим через По предыдущей лемме причем С зависит только от Рассмотрим кривую она представляет собой замкнутую кривую на поверхности и гомотопна простой геодезической петле Так как и определяется исходными данными, то лемма доказана.