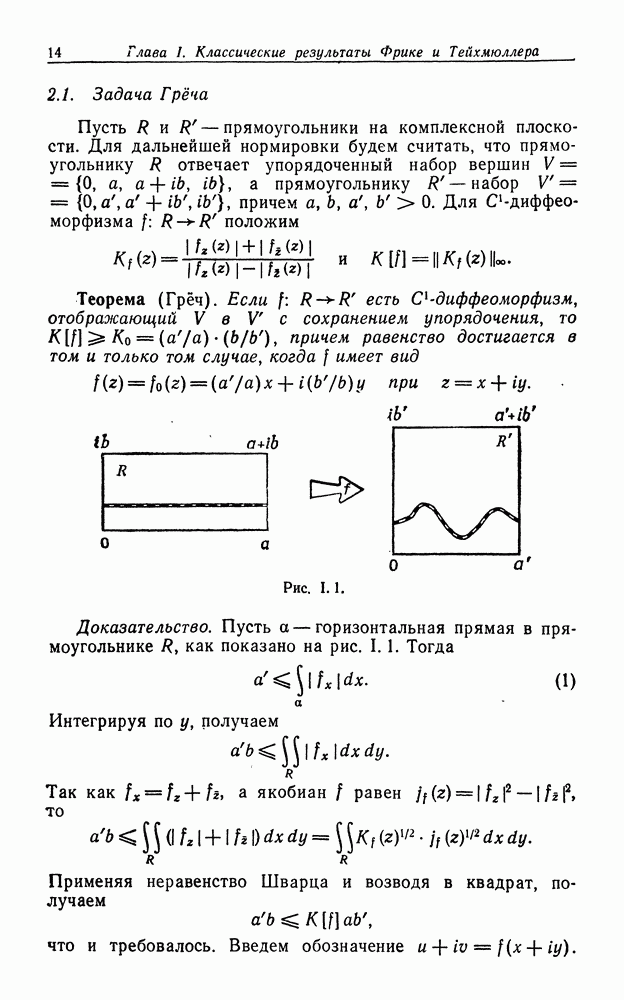
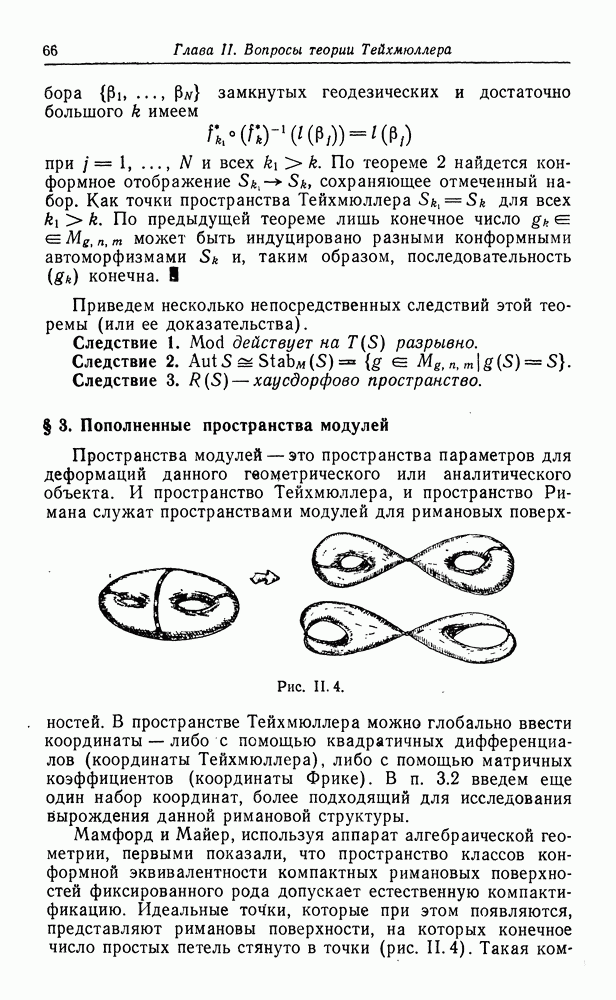
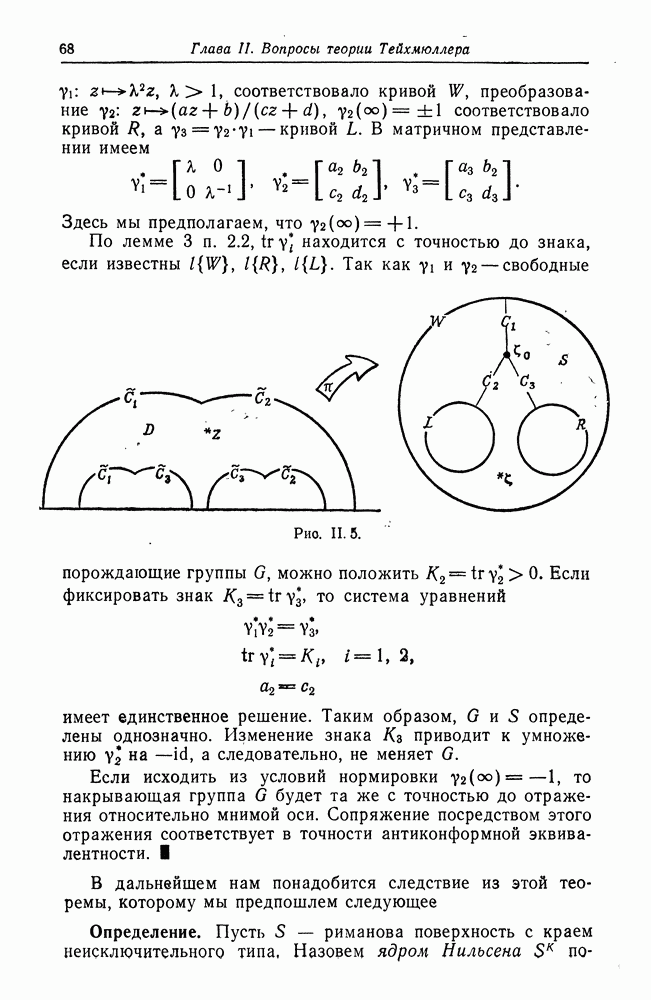
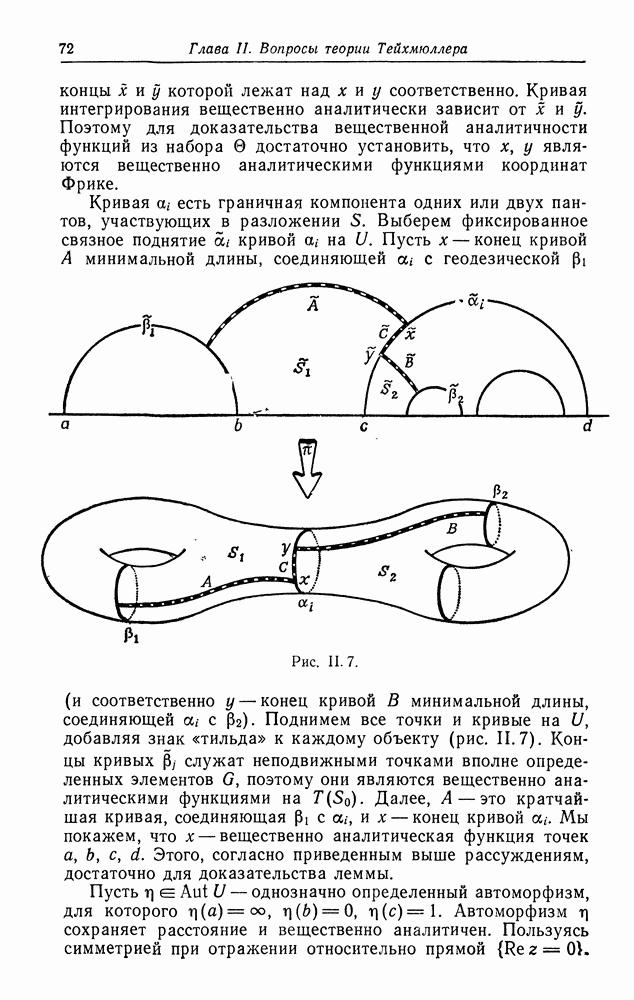
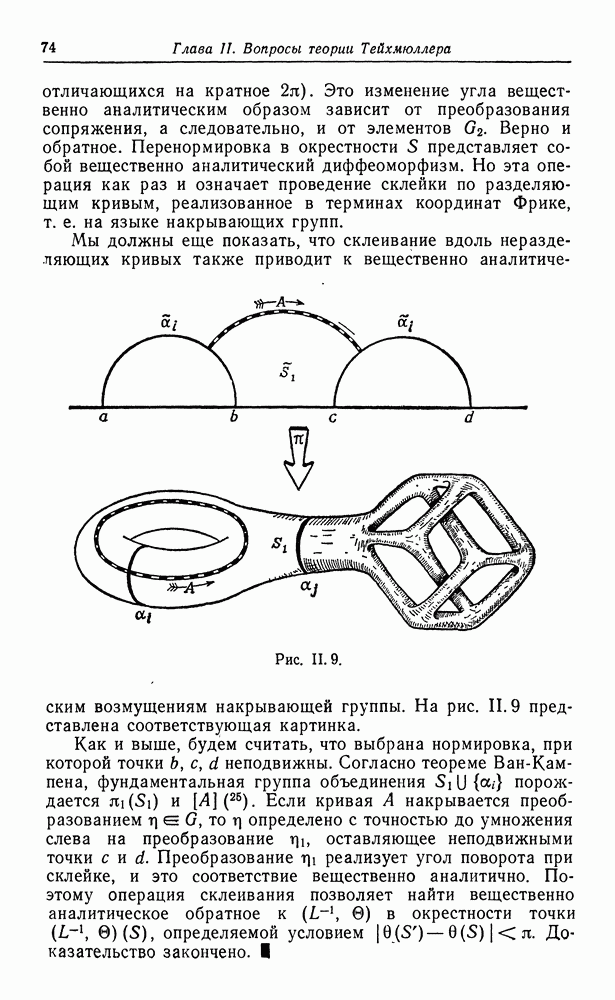
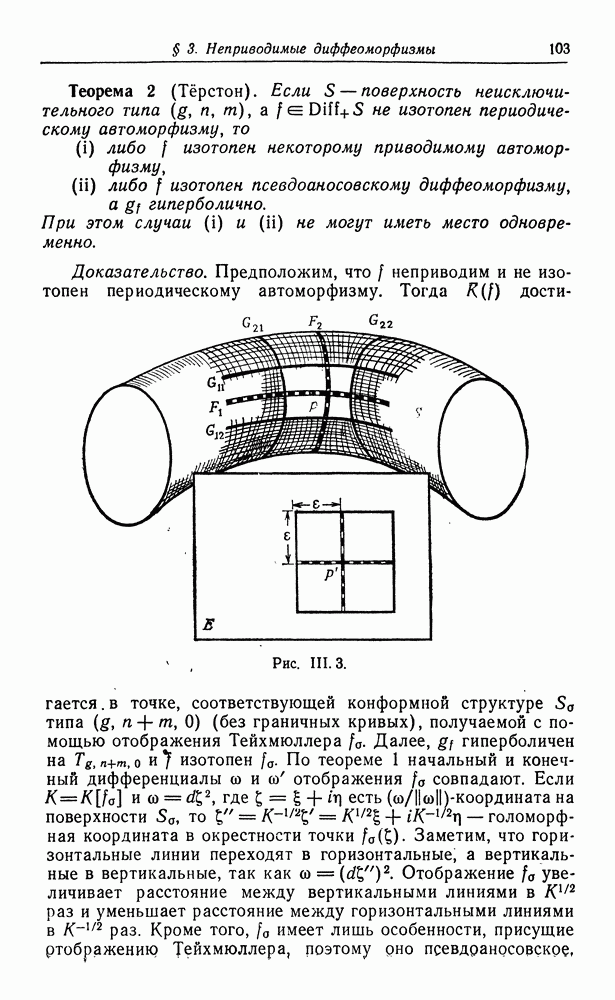
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1. Униформизация и фуксовы группы
1.1. Теорема униформизации
Считается общепризнанным, что теория римановых поверхностей выделяется в общей теории комплексных многообразий двумя основными теоремами и их следствиями. Вторая из этих теорем составляет предмет всей этой главы, а первая — это следующая теорема униформизации.
Теорема. Пусть  произвольная риманова поверхность; тогда
произвольная риманова поверхность; тогда  голоморфно эквивалентна одной из следующих поверхностей:
голоморфно эквивалентна одной из следующих поверхностей:

В качестве первого приложения этого результата мы классифицируем голоморфные универсальные накрывающие компактных римановых поверхностей. Если род  равен 0, то
равен 0, то  односвязна и, следовательно, голоморфно эквивалентна С. Если род
односвязна и, следовательно, голоморфно эквивалентна С. Если род  равен 1, то
равен 1, то  свободная абелева группа ранга 2 и с точностью до голоморфной эквивалентности
свободная абелева группа ранга 2 и с точностью до голоморфной эквивалентности  где
где  группа накрывающих преобразований универсального голоморфного накрытия
группа накрывающих преобразований универсального голоморфного накрытия  Так как накрытие голоморфно, то
Так как накрытие голоморфно, то  где
где  группа голоморфных автоморфизмов 3. Поверхность 3 не может быть голоморфно эквивалентна С, поскольку группа голоморфных автоморфизмов для С есть в точности группа мёбиусовых преобразований
группа голоморфных автоморфизмов 3. Поверхность 3 не может быть голоморфно эквивалентна С, поскольку группа голоморфных автоморфизмов для С есть в точности группа мёбиусовых преобразований

Каждое мёбиусово преобразование имеет по крайней мере одну неподвижную точку в С. Поэтому группа  не может действовать собственно разрывно в С, если только
не может действовать собственно разрывно в С, если только  не тривиальна.
не тривиальна.
Группа голоморфных автоморфизмов полуплоскости  которую мы обозначаем
которую мы обозначаем  состоит из мёбиусовых преобразований с вещественными коэффициентами и изоморфна
состоит из мёбиусовых преобразований с вещественными коэффициентами и изоморфна  Разрывные подгруппы группы
Разрывные подгруппы группы  называются
называются
фуксовыма группами и представляют собой кристаллографические группы сохраняющих ориентацию преобразований гиперболической плоскости (плоскости Пуанкаре). Вещественные мёбиусовы преобразования классифицируются следующим образом: преобразование  называется соответственно эллиптическим, параболическим или гиперболическим, если
называется соответственно эллиптическим, параболическим или гиперболическим, если  или
или  Любое параболическое преобразование сопряжено в группе
Любое параболическое преобразование сопряжено в группе  сдвигу
сдвигу  любое гиперболическое преобразование сопряжено подобию
любое гиперболическое преобразование сопряжено подобию  с некоторым
с некоторым  Эллиптическое преобразование имеет в
Эллиптическое преобразование имеет в  неподвижную точку; поэтому группа накрывающих преобразований неразветвленного накрытия не может содержать эллиптических элементов.
неподвижную точку; поэтому группа накрывающих преобразований неразветвленного накрытия не может содержать эллиптических элементов.
Предположим теперь, что 5 голоморфно эквивалентна  Согласно теореме униформизации, это верно для всех поверхностей рода
Согласно теореме униформизации, это верно для всех поверхностей рода  Гиперболическая метрика Пуанкаре на
Гиперболическая метрика Пуанкаре на  имеет вид
имеет вид  и
и  -инвариантна. Поэтому она проектируется в гладкую метрику на
-инвариантна. Поэтому она проектируется в гладкую метрику на  в случае любой собственно разрывной группы
в случае любой собственно разрывной группы  Пусть
Пусть  соответствующая проекция.
соответствующая проекция.
Лемма 1. Если  компактна, то каждый элемент
компактна, то каждый элемент  гиперболичен.
гиперболичен.
Доказательство. Предположим, что  параболичен. Сопрягая
параболичен. Сопрягая  можно считать, что у — сдвиг:
можно считать, что у — сдвиг:  Отображение у определяет класс
Отображение у определяет класс  свободно гомотопных замкнутых кривых на
свободно гомотопных замкнутых кривых на  Так как 5 компактна, то
Так как 5 компактна, то

где  длина кривой а в метрике Пуанкаре. Для любого
длина кривой а в метрике Пуанкаре. Для любого 

и  Полученное противоречие доказывает лемму.
Полученное противоречие доказывает лемму. 
Таким образом, можно считать, что каждый нетривиальный элемент  имеет в
имеет в  неподвижные точки. Так как
неподвижные точки. Так как  разрывна, то она является дискретной подгруппой
разрывна, то она является дискретной подгруппой  следовательно, счетна.
следовательно, счетна.
Лемма 2. Пусть  гиперболические преобразования. Тогда
гиперболические преобразования. Тогда  коммутируют в том и только том случае, когда они имеют одни и те же неподвижные точки.
коммутируют в том и только том случае, когда они имеют одни и те же неподвижные точки.
Доказательство. Свойство элементов группы коммутировать инвариантно относительно сопряжения, поэтому можно
считать, что у: где  где
где  Суперпозиции мёбиусовых преобразований соответствует произведение матриц. Поэтому условие коммутативности
Суперпозиции мёбиусовых преобразований соответствует произведение матриц. Поэтому условие коммутативности  принимает вид
принимает вид

Простое вычисление показывает, что это условие эквивалентно равенствам  т. е. тому, что
т. е. тому, что  имеет вид
имеет вид 
Из этой леммы непосредственно следует, что  не имеет свободных абелевых разрывных подгрупп ранга 2 с гиперболическими порождающими. В частности, для поверхности
не имеет свободных абелевых разрывных подгрупп ранга 2 с гиперболическими порождающими. В частности, для поверхности  рода 1 имеем
рода 1 имеем 
Риманова поверхность  называется гиперболической (соответственно параболической или эллиптической), если 5 голоморфно эквивалентна
называется гиперболической (соответственно параболической или эллиптической), если 5 голоморфно эквивалентна  (соответственно С, или С). Имеет место следующее
(соответственно С, или С). Имеет место следующее
Предложение 1. Пусть род компактной римановой поверхности  равен
равен  Тогда
Тогда  (соответственно
(соответственно  в том и только том случае, когда
в том и только том случае, когда  эллиптическая (соответственно параболическая или гиперболическая).
эллиптическая (соответственно параболическая или гиперболическая).
Предложение 2. Если  имеет род больше
имеет род больше  — голоморфный автоморфизм
— голоморфный автоморфизм  гомотопный тождественному, то
гомотопный тождественному, то 
Доказательство. Представим  в виде
в виде  и пусть
и пусть  гомотопия
гомотопия  к тождественному автоморфизму. Автоморфизм
к тождественному автоморфизму. Автоморфизм  накрывается мёбиусовым преобразованием у, которое принадлежит нормализатору
накрывается мёбиусовым преобразованием у, которое принадлежит нормализатору  При этом
При этом  тогда и только тогда, когда
тогда и только тогда, когда  Пусть
Пусть  геодезическая в метрике Пуанкаре в классе свободной гомотопии кривой
геодезическая в метрике Пуанкаре в классе свободной гомотопии кривой  Тогда
Тогда  Кривой
Кривой  соответствует некоторый элемент
соответствует некоторый элемент  неподвижные точки которого совпадают с концевыми точками множества
неподвижные точки которого совпадают с концевыми точками множества  Поэтому у оставляет эти концевые точки неподвижными. Так как группа
Поэтому у оставляет эти концевые точки неподвижными. Так как группа  не циклическая, у оставляет на месте более двух точек. Следовательно,
не циклическая, у оставляет на месте более двух точек. Следовательно, 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава I. КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ФРИКЕ И ТЕЙХМЮЛЛЕРА ПО ПРОБЛЕМЕ МОДУЛЕЙ РИМАНОВЫХ ПОВЕРХНОСТЕЙ
- § 1. Униформизация и фуксовы группы
- 1.2. Отмеченные римановы поверхности и пространство Фрике
- § 2. Проблема Грёча
- § 3. Теорема единственности Тейхмюллера
- 3.2. Меры на горизонтальном и вертикальном слоениях
- 3.3. Дифференциальная геометрия квадратичных дифференциалов
- 3.4. Деформации Тейхмюллера
- 3.5. Теорема единственности Тейхмюллера
- § 4. Теорема существования Тейхмюллера
- 4.2. Теорема существования Тейхмюллера
- § 5. Пространство Тейхмюллера
- § 6. Замечания
- Глава II. ВОПРОСЫ ТЕОРИИ ТЕЙХМЮЛЛЕРА
- § 1. Проколотые поверхности с краем и их пространства Тейхмюллера
- 1.2. Дубль поверхности и расширения Нильсена
- 1.3. Кольца и проколотые диски: метод экстремальных длин
- 1.4. Деформации Тейхмюллера поверхностей конечного топологического типа
- 1.5. Теорема Тейхмюллера для поверхностей конечного топологического типа
- 1.6. Пространства Фрике и Тейхмюллера конечной гиперболической поверхности
- § 2. Модулярная группа Тейхмюллера и пространство Римана
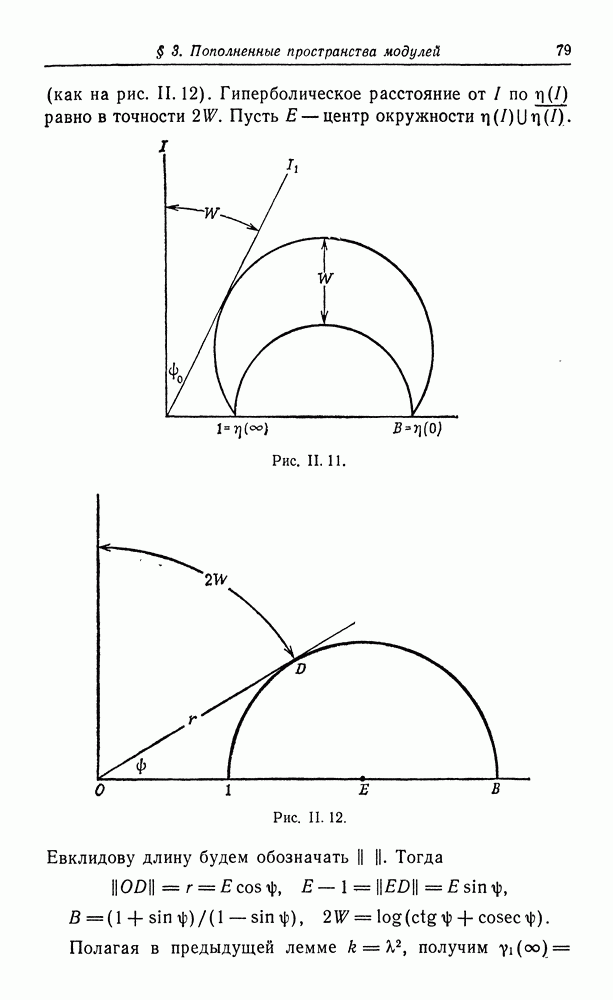
- § 3. Пополненные пространства модулей
- 3.2. Координаты Фенхеля — Нильсена в пространстве Тейхмюллера
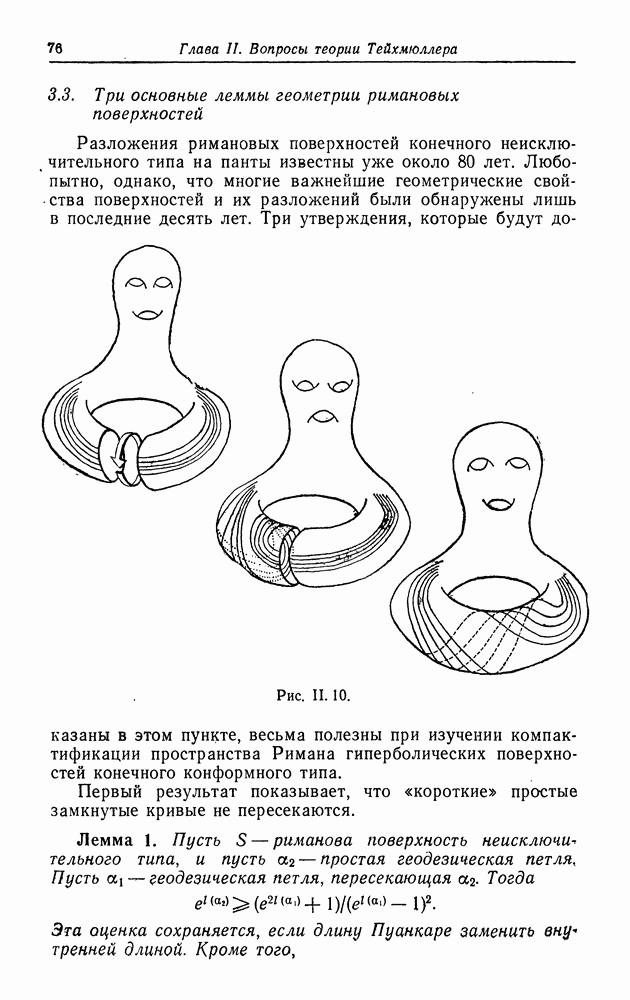
- 3.3. Три основные леммы геометрии римановых поверхностей
- 3.4. Римановы поверхности с узлами и пополненные пространства модулей
- Глава III. КЛАССИФИКАЦИЯ ДИФФЕОМОРФИЗМОВ ПОВЕРХНОСТЕЙ КОНЕЧНОГО ТИПА И ДЕЙСТВИЯ ГРУПП НА ПРОСТРАНСТВЕ ТЕЙХМЮЛЛЕРА
- § 1. Экстремальная проблема Берса и вычисления для проколотых торов
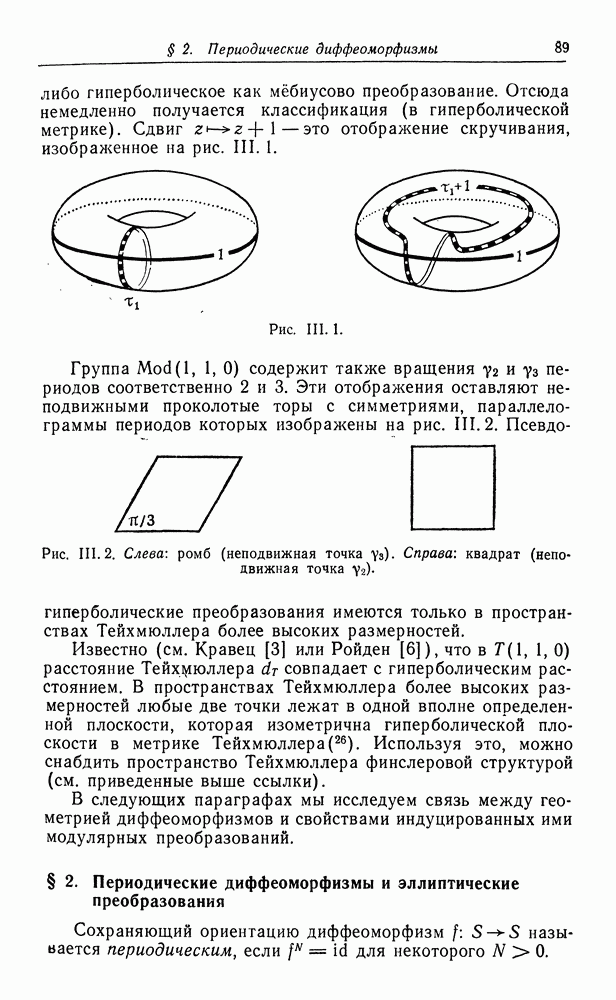
- § 2. Периодические диффеоморфизмы и эллиптические преобразования
- § 3. Неприводимые диффеоморфизмы и гиперболические преобразования
- 3.2. Метрическая геометрия пространства Тейхмюллера
- 3.3. Гиперболические преобразования и инвариантные прямые
- 3.4. Псевдоаносовские диффеоморфизмы
- § 4. Относительные пространства Тейхмюллера и группа дробного скручивания
- 4.2. Асимптотическое поведение длин кривых
- 4.3. Транзитивность группы дробного скручивания
- § 5. Заключительные замечания