| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 17. Примеры применения первого закона термодинамики
Первый закон термодинамики, как и закон сохранения энергии в механике, часто дает возможность исследовать тепловые процессы в макроскопических системах даже в тех случаях, когда нам не известны детали микроскопической картины изучаемых явлений.
Энергетический баланс. Первый закон универсален, он применим ко всем без исключения тепловым процессам в любых системах. Как и всякий закон сохранения, он не дает детальной информации о ходе процесса, но позволяет составить уравнение баланса, если заранее известно, какие энергетические превращения происходят в рассматриваемой системе. В этом параграфе мы рассмотрим примеры использования первого закона термодинамики.
Теплота и внутренняя энергия. Прежде всего сделаем несколько замечаний о смысле входящих в уравнение первого закона величин. Количество переданной теплоты было определено как мера изменения внутренней энергии системы при теплопередаче. Но не всегда подведение к системе теплоты приводит к изменению ее внутренней энергии. Например, при изотермическом расширении идеального газа подведение теплоты не сопровождается увеличением внутренней энергии газа. Внутренняя энергия идеального газа зависит только от температуры и при изотермическом процессе не меняется, но газ совершает работу, и величина этой работы равна подводимому к системе количеству теплоты.
Теплота и работа. Совершение внешними силами механической работы над системой также может не сопровождаться изменением ее внутренней энергии. Если сжимать идеальный газ, принимая меры к тому, чтобы его температура при этом не увеличивалась, то внутренняя энергия газа останется без изменения, а окружающим телам перейдет некоторое количество теплоты, равное совершенной над газом при его сжатии работе.
Пример применения первого закона термодинамики. Применяя первый закон термодинамики, нужно всегда внимательно следить за тем, к каким изменениям в самой системе может привести подведение к ней теплоты и совершение работы. Поясним это на следующем примере. Представьте себе, что в комнате на некоторое время включили электрический нагреватель, в результате чего температура воздуха увеличилась от  до
до  Может показаться, что в результате этого внутренняя энергия воздуха в комнате увеличилась. Проверим, так ли это. Будем считать воздух идеальным газом. В состоянии теплового равновесия внутренняя энергия одного моля пропорциональна абсолютной температуре, а энергия всего воздуха в комнате пропорциональна количеству (числу молей) газа, находящегося в комнате. Поэтому выражение для энергии можно записать в виде
Может показаться, что в результате этого внутренняя энергия воздуха в комнате увеличилась. Проверим, так ли это. Будем считать воздух идеальным газом. В состоянии теплового равновесия внутренняя энергия одного моля пропорциональна абсолютной температуре, а энергия всего воздуха в комнате пропорциональна количеству (числу молей) газа, находящегося в комнате. Поэтому выражение для энергии можно записать в виде

где  — масса воздуха, М — его молярная масса,
— масса воздуха, М — его молярная масса,  — молярная теплоемкость при постоянном объеме.
— молярная теплоемкость при постоянном объеме.
Воспользовавшись уравнением Менделеева—Клапейрона  замечаем, что выражению для внутренней энергии воздуха
замечаем, что выражению для внутренней энергии воздуха  можно придать вид
можно придать вид

Объем V комнаты не изменяется при работе нагревателя, не изменяется и давление  воздуха в комнате. Оно равно атмосферному, поскольку комната не герметична. Тогда из формулы (2) видно, что внутренняя энергия воздуха в комнате не изменяется при протапливании. Сразу возникают вопросы: что происходит с потребляемой от сети электроэнергией и зачем мы вообще включаем электронагреватель? Отвечая на второй вопрос, отметим, что для человека имеет значение не энергия воздуха, а его температура, которая повышается при протапливании. Что касается энергии, потребляемой нагревателем от сети, то она целиком «выходит» наружу: масса воздуха в комнате при нагревании при постоянном давлении уменьшается.
воздуха в комнате. Оно равно атмосферному, поскольку комната не герметична. Тогда из формулы (2) видно, что внутренняя энергия воздуха в комнате не изменяется при протапливании. Сразу возникают вопросы: что происходит с потребляемой от сети электроэнергией и зачем мы вообще включаем электронагреватель? Отвечая на второй вопрос, отметим, что для человека имеет значение не энергия воздуха, а его температура, которая повышается при протапливании. Что касается энергии, потребляемой нагревателем от сети, то она целиком «выходит» наружу: масса воздуха в комнате при нагревании при постоянном давлении уменьшается.
Итак, внутренняя энергия воздуха в комнате при работе нагревателя не меняется, несмотря на повышение температуры. Но никакого парадокса в этом нет. Первый закон термодинамики, разумеется, справедлив и в этом случае. Просто при нагревании изменяется сама рассматриваемая система: количество воздуха в комнате уменьшается.
Еще один пример применения первого закона термодинамики. Рассмотрим теперь стационарный поток идеального газа, протекающего через длинную спиральную трубку — змеевик (рис. 55). На входе змеевика поддерживаются постоянные давление  и температура
и температура  На выходе змеевика поддерживаетсяостоянное давление
На выходе змеевика поддерживаетсяостоянное давление  и измеряется температура
и измеряется температура  Прежде всего подсчитаем работу, совершаемую при прохождении через змеевик одного моля газа.
Прежде всего подсчитаем работу, совершаемую при прохождении через змеевик одного моля газа.
О какой работе идет речь? Мы знаем, что газ, а точнее, сила давления газа, совершает работу при перемещении поршня или любого другого тела, ограничивающего занимаемый газом объем. Таким телом является, например, оболочка резинового шарика, деформирующаяся при его наполнении газом. Общее выражение для работы силы давления газа дается формулой (12) предыдущего параграфа:

Отметим, что наличие тела, ограничивающего объем газа, совершенно необходимо для того, чтобы можно было говорить о совершаемой газом работе: газ, расширяющийся в пустоту, работы не совершает!
Поясним это. Представим себе сосуд, разделенный перегородкой на две части: по одну сторону от перегородки находится газ, по
другую — вакуум. При внезапном удалении перегородки газ заполняет весь сосуд, объем газа увеличивается  давление газа
давление газа  однако работы газ не совершает:
однако работы газ не совершает:  Формула (3) в этом случае неприменима.
Формула (3) в этом случае неприменима.
Наряду с работой, совершаемой газом, можно рассматривать работу внешних сил, совершаемую над газом при перемещении поршня. Очевидно, что при равномерном перемещении поршня работа  совершаемая над газом, противоположна по знаку и равна по модулю работе газа
совершаемая над газом, противоположна по знаку и равна по модулю работе газа  т. е.
т. е.  Так о какой же работе идет речь? Ведь никаких поршней здесь нет! Однако на самом деле «поршни», т. е. внешние тела, поддерживающие заданные давления на входе и выходе змеевика, здесь есть, и они-то и совершают работу над протекающим газом. Эту работу можно подсчитать следующим образом.
Так о какой же работе идет речь? Ведь никаких поршней здесь нет! Однако на самом деле «поршни», т. е. внешние тела, поддерживающие заданные давления на входе и выходе змеевика, здесь есть, и они-то и совершают работу над протекающим газом. Эту работу можно подсчитать следующим образом.
Рассмотрим газ, заключенный между входным  и выходным
и выходным  сечениями змеевика (рис. 55). Вследствие стационарности потока масса этого газа не меняется со временем, т. е. если за время
сечениями змеевика (рис. 55). Вследствие стационарности потока масса этого газа не меняется со временем, т. е. если за время  через входное сечение прошла масса газа
через входное сечение прошла масса газа  то точно такая же масса вышла из змеевика.
то точно такая же масса вышла из змеевика.
Пусть объем, занимаемый массой  на входе при давлении
на входе при давлении  и температуре
и температуре  равен
равен  а объем на выходе из змеевика равен
а объем на выходе из змеевика равен  Газ, находившийся между сечениями
Газ, находившийся между сечениями  теперь занимает новое положение: идущая за ним порция газа действовала на него с силой
теперь занимает новое положение: идущая за ним порция газа действовала на него с силой  идущий впереди газ оказывал сопротивление
идущий впереди газ оказывал сопротивление  Таким образом, работа внешних сил над рассматриваемым газом
Таким образом, работа внешних сил над рассматриваемым газом  Поскольку во время процесса давления газа на входе и выходе остаются постоянными, то работа внешних сил при проталкивании через змеевик одного моля газа равна
Поскольку во время процесса давления газа на входе и выходе остаются постоянными, то работа внешних сил при проталкивании через змеевик одного моля газа равна

где  и
и  — объемы, занимаемые одним молем газа при условиях, существующих на входе и на выходе змеевика соответственно. Согласно уравнению Менделеева—Клапейрона можно написать
— объемы, занимаемые одним молем газа при условиях, существующих на входе и на выходе змеевика соответственно. Согласно уравнению Менделеева—Клапейрона можно написать


Рис. 55. Прохождение газа через змеевик
Поэтому совершаемая над одним молем газа работа равна

Теперь обратим внимание на одну особенность рассматриваемого примера: в то время как температура газа на входе в змеевик 
задается, температура на выходе  измеряется. Напомним, что давление в обоих случаях задается. От чего же зависит температура газа на выходе? Очевидно, от условий его прохождения через змеевик. Чем же могут различаться эти условия? Только интенсивностью теплообмена протекающего по змеевику газа с окружающей средой. Рассмотрим вначале случай, когда теплообмен вообще отсутствует — змеевик адиабатически изолирован от окружающей среды. Какова при этом температура газа
измеряется. Напомним, что давление в обоих случаях задается. От чего же зависит температура газа на выходе? Очевидно, от условий его прохождения через змеевик. Чем же могут различаться эти условия? Только интенсивностью теплообмена протекающего по змеевику газа с окружающей средой. Рассмотрим вначале случай, когда теплообмен вообще отсутствует — змеевик адиабатически изолирован от окружающей среды. Какова при этом температура газа  на выходе? Используя первый закон термодинамики
на выходе? Используя первый закон термодинамики

получаем  так как
так как  Поскольку внутренняя энергия идеального газа пропорциональна термодинамической температуре, имеем
Поскольку внутренняя энергия идеального газа пропорциональна термодинамической температуре, имеем

Подставляя выражения (5) и (7) в уравнение (6) и учитывая, что в отсутствие теплообмена  получаем
получаем

а так как  то отсюда немедленно следует
то отсюда немедленно следует 
Таким образом, температура идеального газа при адиабатическом прохождении через змеевик не меняется, а совершаемая при этом работа, как видно из (5), равна нулю. Для того чтобы работа была отлична от нуля, необходим теплообмен. Легко убедиться, что, когда газ получает теплоту  совершаемая над ним работа отрицательна и, наоборот, при
совершаемая над ним работа отрицательна и, наоборот, при  совершаемая над газом работа положительна:
совершаемая над газом работа положительна:  Действительно, подставляя в уравнение первого закона (6) выражения (5) и (7), получаем
Действительно, подставляя в уравнение первого закона (6) выражения (5) и (7), получаем

Сумма  равна молярной теплоемкости идеального газа при постоянном давлении
равна молярной теплоемкости идеального газа при постоянном давлении  поэтому формулу (8) можно записать и так:
поэтому формулу (8) можно записать и так:

Из этого выражения видно, что знак  совпадает со знаком
совпадает со знаком  Если, например,
Если, например,  т. е. газ при прохождении через змеевик отдает теплоту, то
т. е. газ при прохождении через змеевик отдает теплоту, то  и из выражения (5) видно, что совершаемая при этом над газом работа положительна:
и из выражения (5) видно, что совершаемая при этом над газом работа положительна: 
Змеевик как тепловая машина. Исходя из полученных результатов попытаемся представить себе, как происходит протекание газа через змеевик. Если в змеевике газ охлаждается, т. е. отдает теплоту  то совершаемая над газом работа положительна — внешние силы «проталкивают» газ через змеевик. Если теплота
то совершаемая над газом работа положительна — внешние силы «проталкивают» газ через змеевик. Если теплота
подводится к газу  то наш змеевик подобен тепловой машине — газ сам совершает работу над внешними телами. И обратите внимание, что этот результат не зависит от того, какова величина давления газа на выходе и на входе. Единственное условие при этом — давление на входе должно быть больше давления на выходе, иначе газ просто потечет в обратную сторону.
то наш змеевик подобен тепловой машине — газ сам совершает работу над внешними телами. И обратите внимание, что этот результат не зависит от того, какова величина давления газа на выходе и на входе. Единственное условие при этом — давление на входе должно быть больше давления на выходе, иначе газ просто потечет в обратную сторону.
Как было выяснено, при адиабатическом протекании газа через змеевик совершаемая над ним работа равна нулю. Не кажется ли вам странным этот результат? Легко придумать такой опыт, в котором над газом работа совершается, а теплообмена с окружающей средой нет. Действительно, попробуем при помощи компрессора прокачивать через змеевик газ в вакуум. Для того чтобы процесс можно было считать стационарным, сечение выходного отверстия сделаем много меньше сечения входного. Змеевик теплоизолируем от окружающей среды.
Совершаемая компрессором над газом работа положительна и равна полной совершаемой над газом работе, ибо, как уже отмечалось, выходя в вакуум, газ работы не совершает. Так как нет обмена теплотой, налицо противоречие с утверждением о том, что при адиабатическом протекании работа равна нулю.
Это противоречие возникло потому, что при прокачивании газа в вакуум происходят и такие энергетические превращения, которые были совершенно несущественны в разобранном выше примере. Действительно, первый закон термодинамики использовался в виде  где
где  — внутренняя энергия газа. Поэтому при использовании такой формулировки первого закона термодинамики заранее молчаливо предполагается, что в рассматриваемых процессах не происходит изменения механической энергии системы, т. е. не меняется потенциальная энергия газа как целого во внешнем поле, не меняется и кинетическая энергия движения газа как целого, не возникает в газе никаких макроскопических потоков. Теперь уже становится ясно, что при прокачивании газа в вакуум возникает макроскопический направленный поток, кинетическую энергию которого необходимо учитывать. Работа компрессора в этом случае как раз и определяет кинетическую энергию этого потока.
— внутренняя энергия газа. Поэтому при использовании такой формулировки первого закона термодинамики заранее молчаливо предполагается, что в рассматриваемых процессах не происходит изменения механической энергии системы, т. е. не меняется потенциальная энергия газа как целого во внешнем поле, не меняется и кинетическая энергия движения газа как целого, не возникает в газе никаких макроскопических потоков. Теперь уже становится ясно, что при прокачивании газа в вакуум возникает макроскопический направленный поток, кинетическую энергию которого необходимо учитывать. Работа компрессора в этом случае как раз и определяет кинетическую энергию этого потока.
Если вход и выход змеевика расположены на разной высоте, то в уравнении закона сохранения энергии необходимо учитывать и изменение потенциальной энергии газа в поле тяжести, подобно тому как это делалось в гидродинамике при выводе уравнения Бернулли.
Измерение теплоемкости газа. Змеевик, помещенный в калориметр, можно использовать для измерения теплоемкости газа. Дело в том, что непосредственное измерение теплоемкости газа при постоянном объеме  затруднительно, так как для заключенного в сосуд газа масса, а следовательно, и теплоемкость всегда малы по сравнению с их значениями для сосуда и калориметра. Через змеевик
затруднительно, так как для заключенного в сосуд газа масса, а следовательно, и теплоемкость всегда малы по сравнению с их значениями для сосуда и калориметра. Через змеевик
можно пропустить большую массу газа, так что температура воды в калориметре может заметно измениться. Таким образом удается преодолеть отмеченную выше трудность.
Зная теплоемкость калориметра с водой, по изменению его температуры можно подсчитать количество переданной газу теплоты  (в пересчете на один моль прошедшего газа). Это количество теплоты связано с изменением температуры газа формулой (9), что позволяет рассчитать величину С — теплоемкость газа при постоянном давлении. Теплоемкость
(в пересчете на один моль прошедшего газа). Это количество теплоты связано с изменением температуры газа формулой (9), что позволяет рассчитать величину С — теплоемкость газа при постоянном давлении. Теплоемкость  можно затем найти с помощью уравнения Майера:
можно затем найти с помощью уравнения Майера: 
Задача
В вертикальном цилиндрическом сосуде под массивным поршнем находится 1 моль идеального газа. Приложим к поршню некоторую силу и сожмем газ настолько, чтобы эта сила совершила заданную работу А. Затем поршень отпускаем и через некоторое время он устанавливается в новом положении равновесия. Определить, на сколько градусов температура газа в конечном состоянии отличается от начальной температуры, считая газ адиабатически изолированным.
Решение. До приложения внешней силы поршень находился в механическом равновесии: разность сил давления газа под поршнем и атмосферы над ним уравновешивала действующую на поршень силу тяжести. Приложив дополнительную силу, мы нарушаем это равновесие, и поршень перемещается вниз. При перемещении поршня все действующие на него внешние силы совершают положительную работу: кроме заданной в условии работы А приложенной силы это еще работа действующей на поршень сверху силы атмосферного давления и работа силы тяжести. Работа всех этих сил равна изменению внутренней энергии газа и кинетической энергии поршня.
При сжатии адиабатически изолированного газа его температура и давление возрастают. Поэтому после прекращения действия приложенной силы газ начинает расширяться, и поршень будет перемещаться вверх. При этом сила атмосферного давления и сила тяжести совершают отрицательную работу. В конце концов кинетическая энергия поршня обратится в нуль, и он установится в новом положении равновесия. Это новое положение равновесия поршня будет расположено выше исходного на некоторую величину 
Полная работа, складывающаяся из работы А приложенной силы, работы силы тяжести и работы Латм силы атмосферного давления на всем перемещении поршня от начального положения, в соответствии со сказанным выше, равна изменению внутренней энергии газа 

Так как конечное положение поршня на  выше начального, то очевидно, что
выше начального, то очевидно, что

где  — масса поршня,
— масса поршня,  — его площадь,
— его площадь,  — атмосферное давление. Изменение внутренней энергии
— атмосферное давление. Изменение внутренней энергии  находящегося под поршнем одного моля идеального газа определяется только изменением его температуры
находящегося под поршнем одного моля идеального газа определяется только изменением его температуры 

Подставляя (11) и (12) в (10), получаем

Во втором слагаемом левой части (13) вынесем за скобки площадь поршня  Тогда
Тогда  равно изменению объема газа
равно изменению объема газа  — давление газа
— давление газа  одинаковое в начальном и конечном состояниях. Поэтому (13) переписывается в виде
одинаковое в начальном и конечном состояниях. Поэтому (13) переписывается в виде

Применяя уравнение Менделеева—Клапейрона к начальному и конечному состояниям газа, имеем

Теперь соотношение (14) принимает вид

Так как  то для изменения температуры
то для изменения температуры  имеем:
имеем:  .
.
• Можно ли применять первый закон термодинамики к процессам, в которых изменяется химический состав или количество вещества в рассматриваемой системе?
• Всегда ли подведение теплоты к системе приводит к увеличению ее внутренней энергии?
• По показаниям какого прибора — термометра или барометра — можно судить о внутренней энергии всего воздуха, находящегося в вашей комнате?
• При прохождении газа через змеевик мы составляем уравнение энергетического баланса, в котором не учитываем кинетическую энергию потока газа, считая малой его скорость. При этом мы не заботимся о законе сохранения импульса. Медленность протекания газа можно обеспечить, например, с помощью пористой перегородки внутри змеевика. Поясните, почему такая перегородка, обеспечивая сохранение импульса, не влияет на энергетический баланс.
• Почему теплоемкость газа при постоянном объеме  трудно измерить на опыте непосредственно? Как эту трудность можно преодолеть на практике?
трудно измерить на опыте непосредственно? Как эту трудность можно преодолеть на практике?
• В приведенном решении задачи утверждалось, что конечное положение поршня расположено выше начального. Докажите, что это действительно так.
• В условии задачи предполагалось, что приложенная сила перемещает поршень вниз. Изменится ли ответ, если считать, что она перемещает поршень вверх? Опишите процессы, происходящие в системе в этом случае.
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
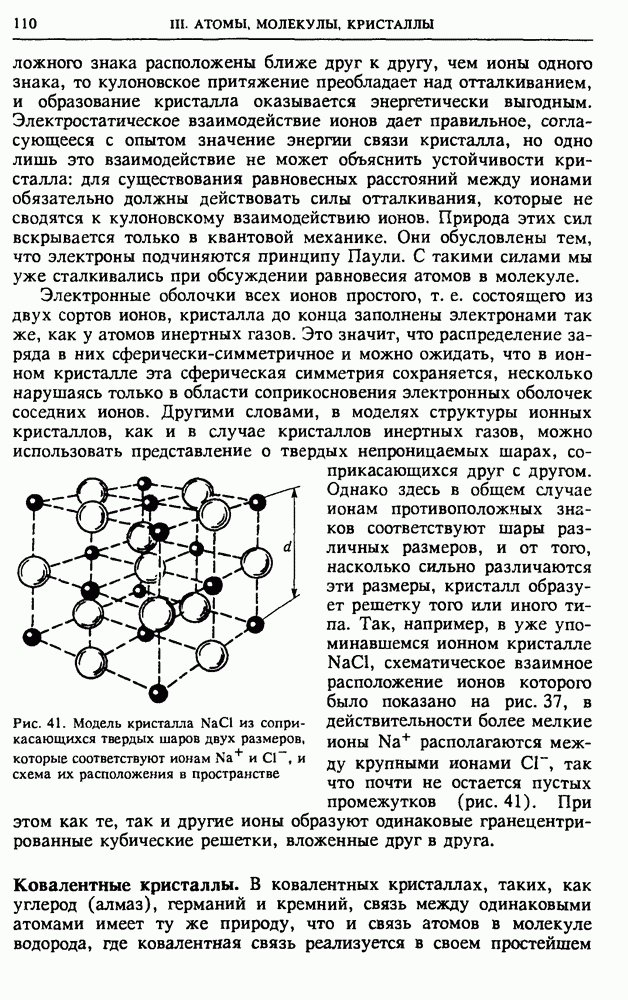
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
- § 13. Кристаллы
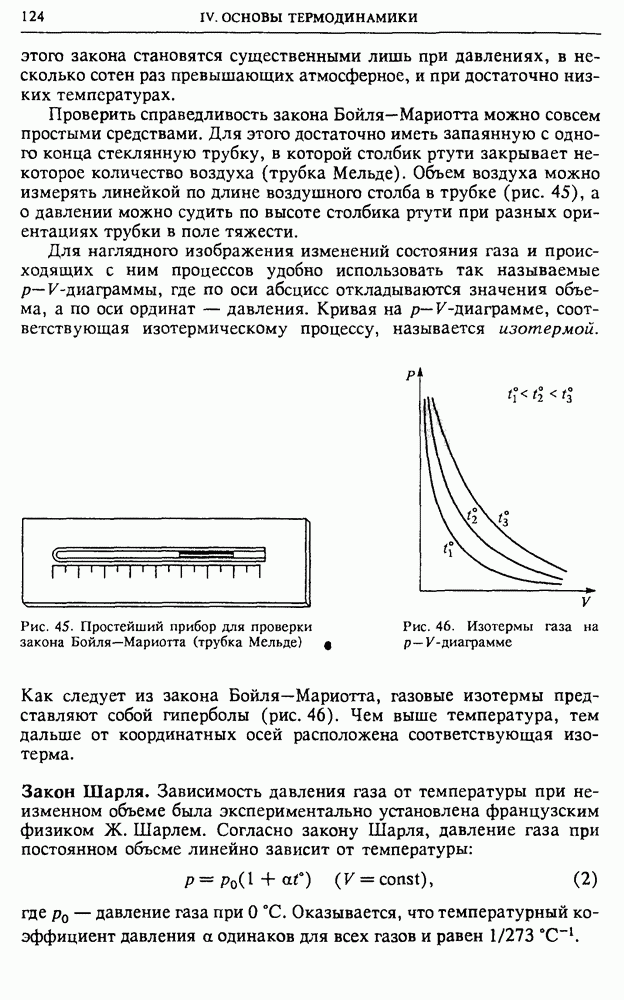
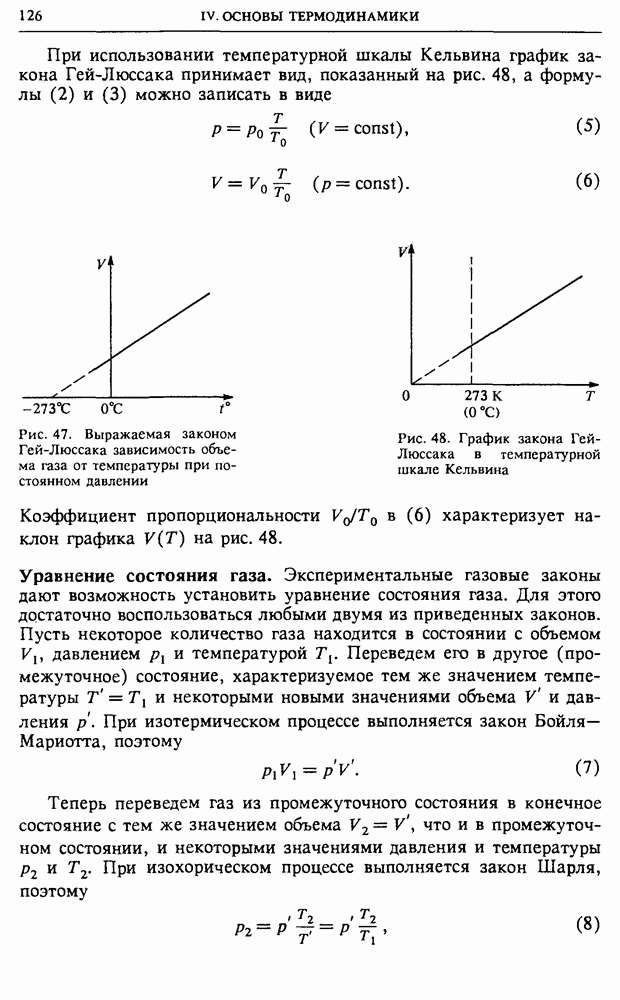
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
- § 15. Уравнение состояния газа
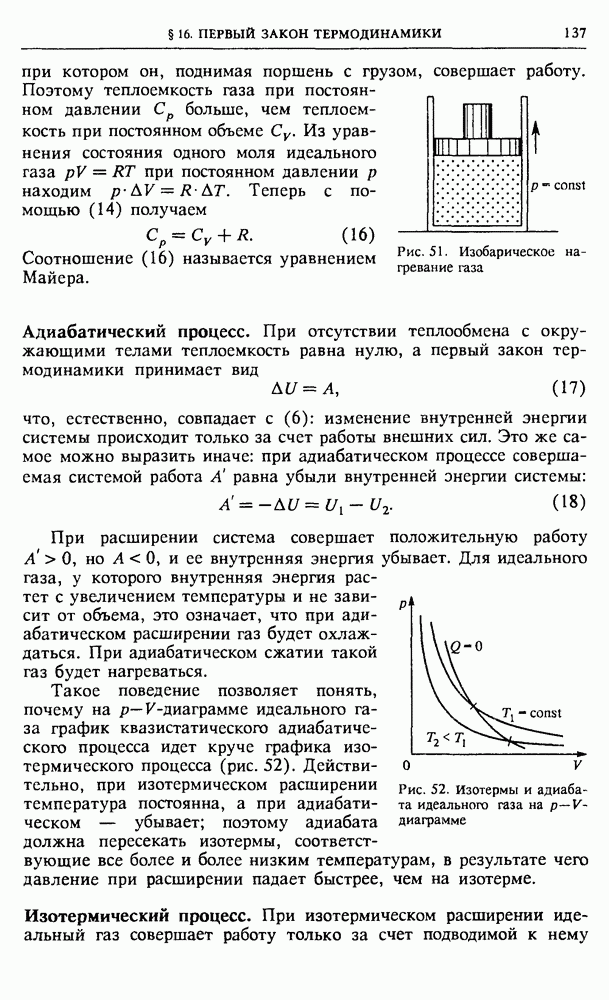
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы