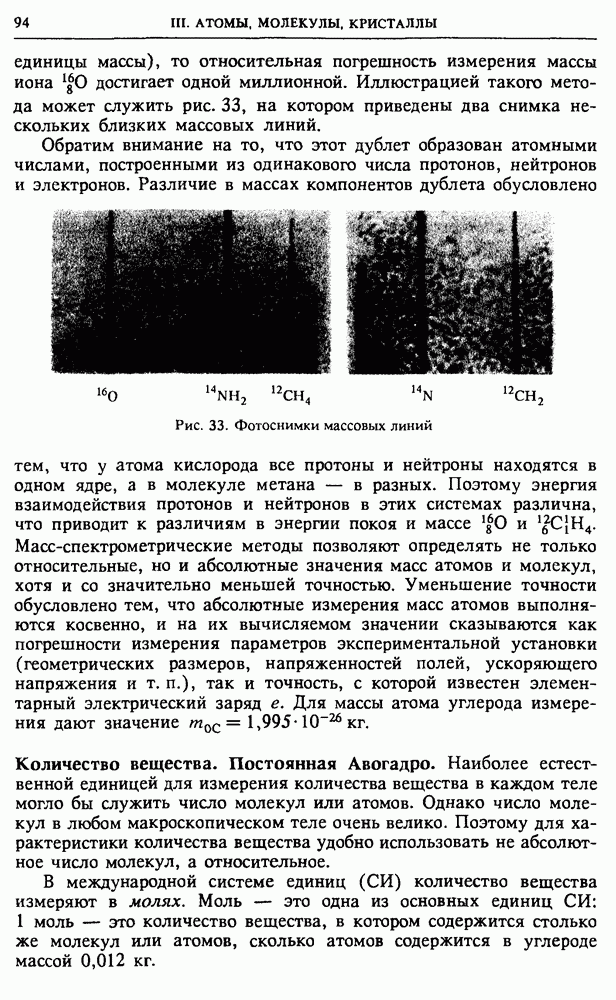
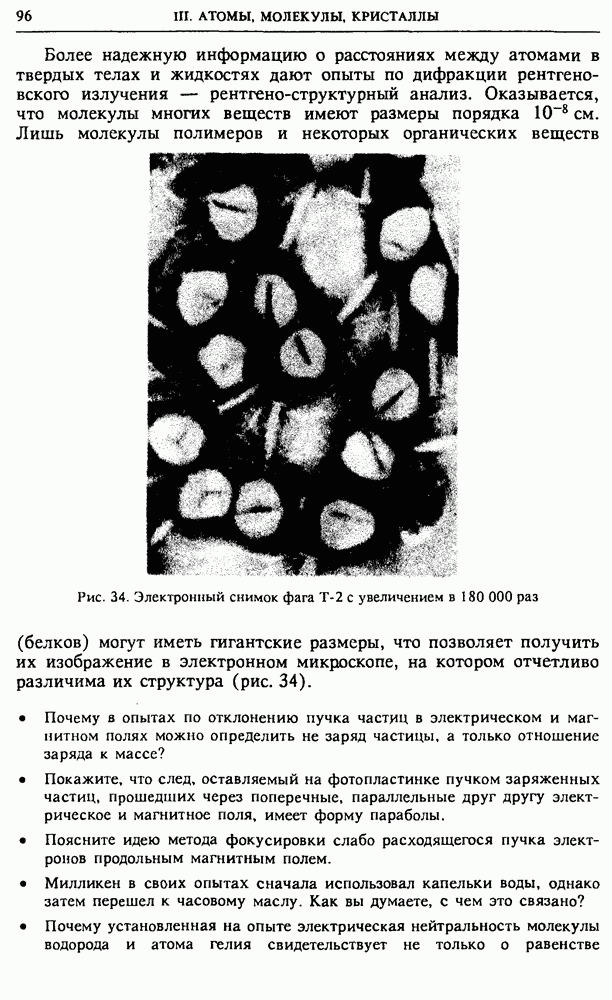
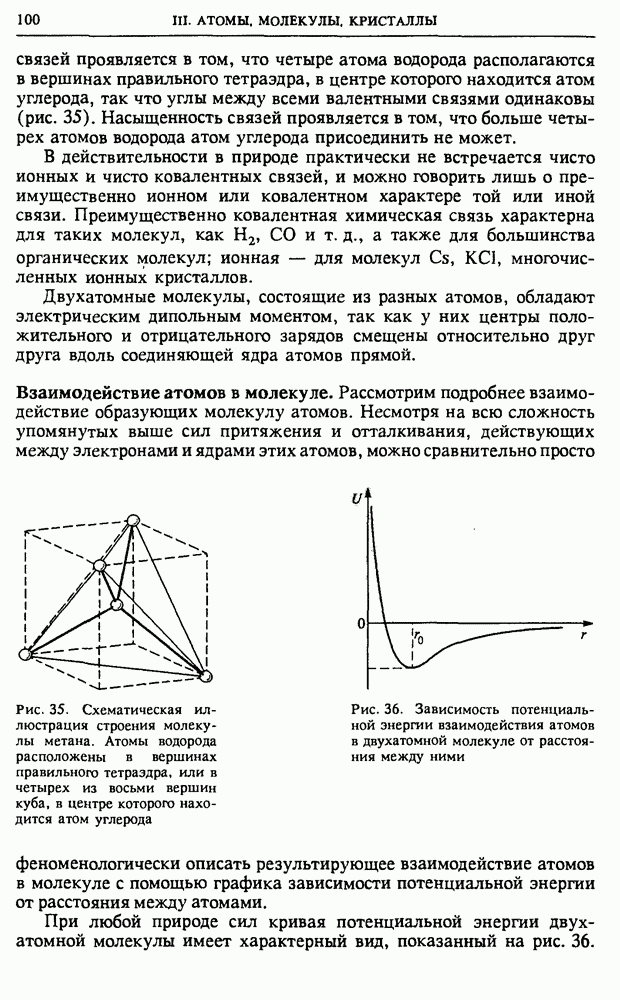
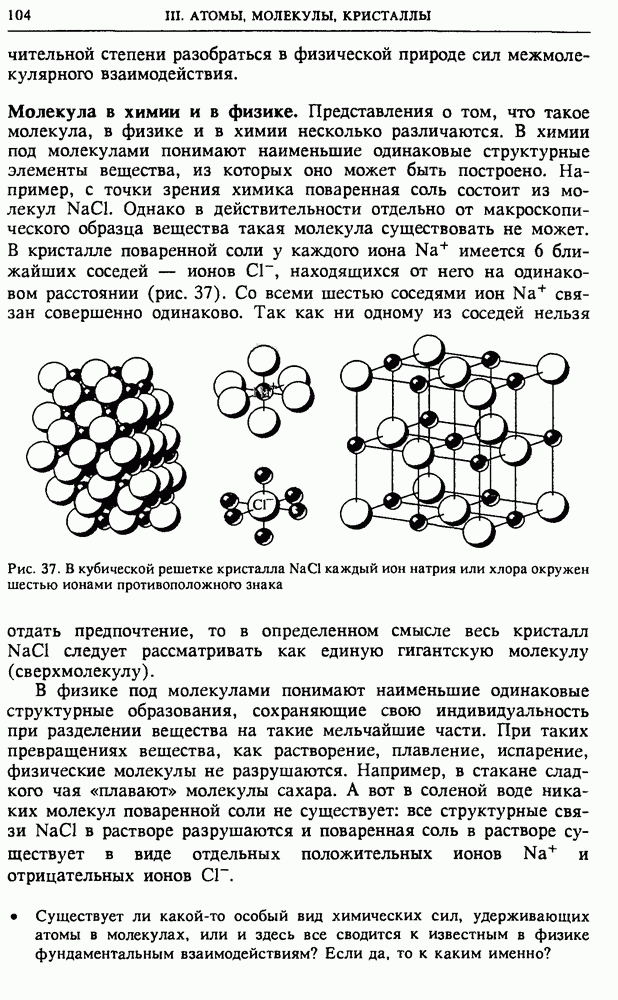
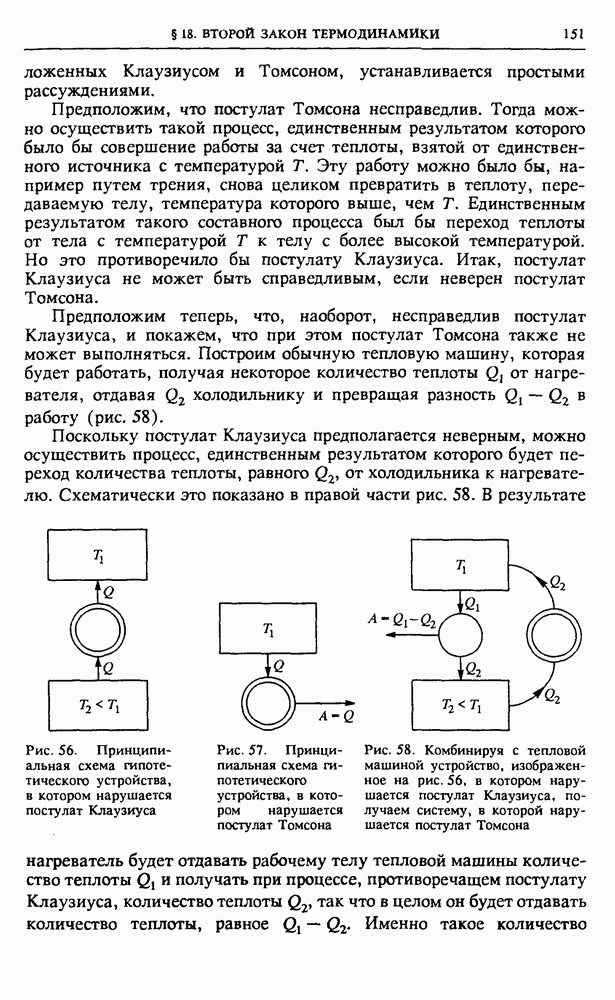
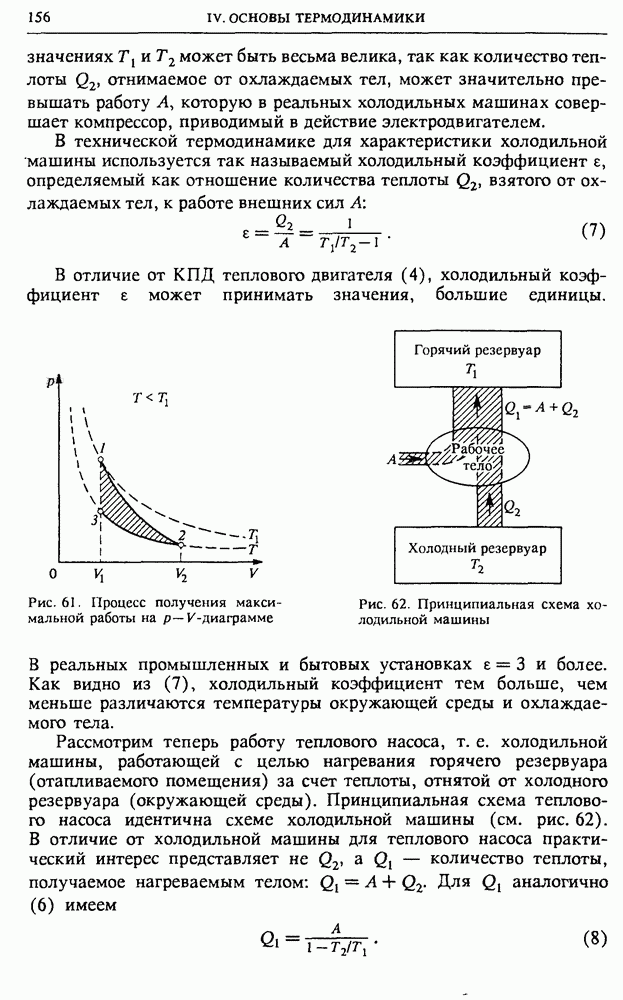
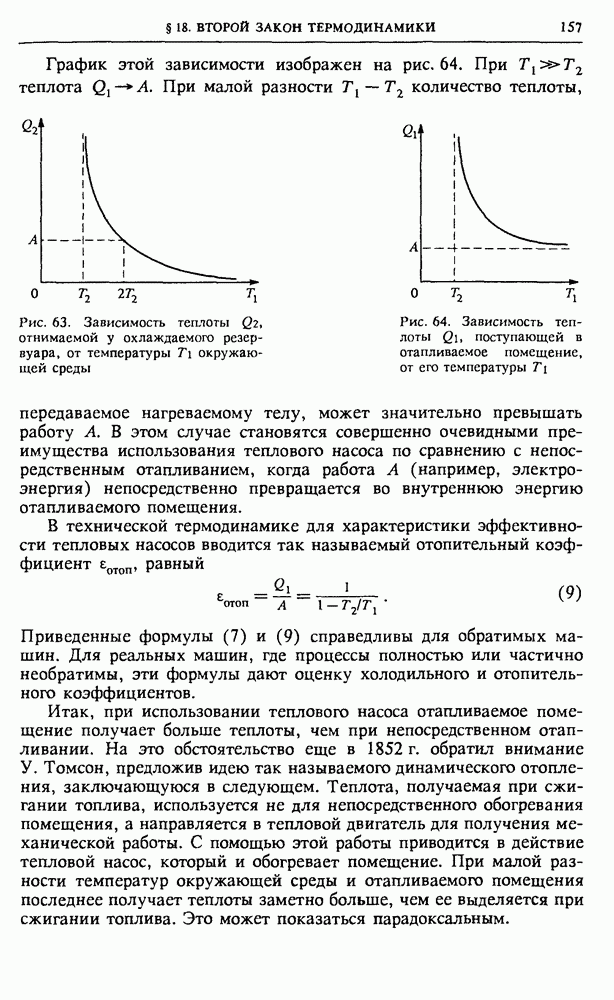
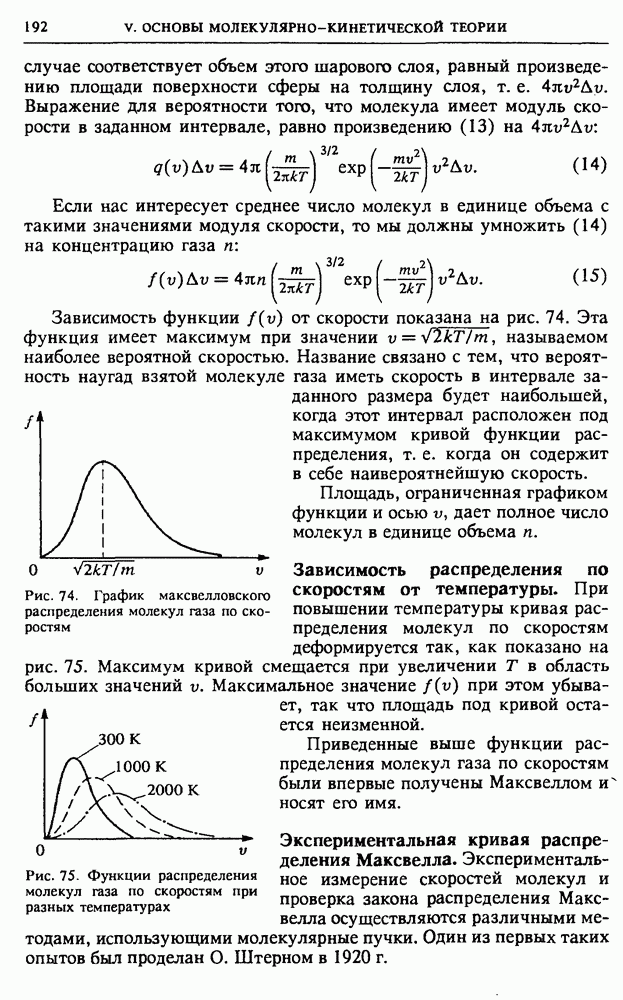
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 35. Электронные свойства металлов
Многие макроскопические свойства металлов, обусловленные наличием в них электронов проводимости, невозможно объяснить на основе классической статистической механики. Объяснение поведения
коллектива электронов проводимости требует обязательного привлечения квантовых закономерностей.
Принцип Паули и электроны в металлах. Рассмотрим подробнее свойства электронов проводимости в металлах, считая для простоты, что их эффективная масса изотропна, а число электронов проводимости в образце равно числу атомов металла  Именно так обстоит дело, например, у щелочных металлов. Хотя поведение отдельного электрона проводимости в кристалле очень сходно с поведением классической свободной частицы, свойства коллектива таких электронов резко отличаются от свойств классического газа. Причина этому — принцип Паули, согласно которому в каждом квантовом состоянии может находиться не более одного электрона.
Именно так обстоит дело, например, у щелочных металлов. Хотя поведение отдельного электрона проводимости в кристалле очень сходно с поведением классической свободной частицы, свойства коллектива таких электронов резко отличаются от свойств классического газа. Причина этому — принцип Паули, согласно которому в каждом квантовом состоянии может находиться не более одного электрона.
Принцип Паули приводит к тому, что даже при абсолютном нуле температуры электроны не могут находиться в состоянии покоя, так как нельзя все электроны поместить в состояние с равным нулю импульсом. Оказывается, что уровню энергии с нулевым импульсом соответствуют только два различных квантовых состояния. Поэтому только два из  электронов могут иметь равные нулю импульс и энергию. Всем остальным электронам придется занимать состояния с отличным от нуля импульсом и энергией.
электронов могут иметь равные нулю импульс и энергию. Всем остальным электронам придется занимать состояния с отличным от нуля импульсом и энергией.

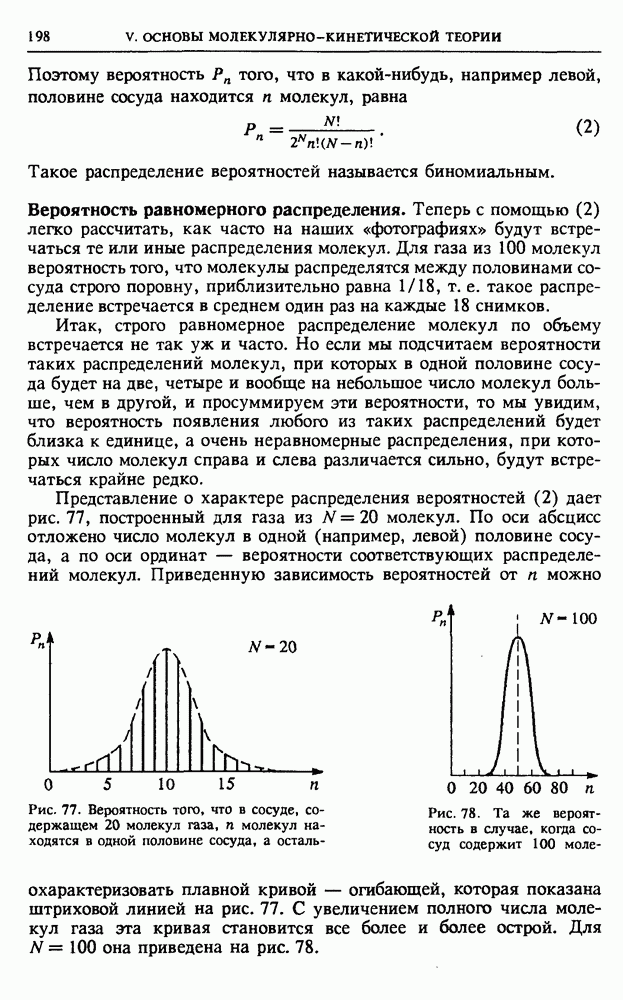
Рис. 113. Функция распределения электронов при абсолютном нуле температуры
Импульс Ферми. При температуре  система электронов будет иметь наименьшую возможную энергию, если все состояния с импульсами, меньшими некоторого предельного значения, называемого импульсом Ферми
система электронов будет иметь наименьшую возможную энергию, если все состояния с импульсами, меньшими некоторого предельного значения, называемого импульсом Ферми  будут заняты, а все состояния с ббльшими импульсами — пусты. Функция распределения электронов по состояниям
будут заняты, а все состояния с ббльшими импульсами — пусты. Функция распределения электронов по состояниям  дающая вероятность заполнения данного состояния с импульсом
дающая вероятность заполнения данного состояния с импульсом  будет, следовательно, при
будет, следовательно, при  равна единице при
равна единице при  и равна нулю при
и равна нулю при  (рис. 113).
(рис. 113).
Значение импульса Ферми зависит от объемной концентрации электронов в зоне проводимости  где V — объем образца. Характер этой зависимости можно установить на основании соотношений неопределенностей Гейзенберга. Пусть образец металла имеет форму прямоугольного параллелепипеда со сторонами
где V — объем образца. Характер этой зависимости можно установить на основании соотношений неопределенностей Гейзенберга. Пусть образец металла имеет форму прямоугольного параллелепипеда со сторонами  Для электрона, находящегося внутри образца, наибольшая неопределенность в значении х-координаты равна размеру образца в этом направлении; поэтому наименьшая неопределенность его х-компоненты импульса
Для электрона, находящегося внутри образца, наибольшая неопределенность в значении х-координаты равна размеру образца в этом направлении; поэтому наименьшая неопределенность его х-компоненты импульса  определяется соотношением
определяется соотношением

Такие же соотношения справедливы и для  Поэтому для произведения неопределенностей имеем
Поэтому для произведения неопределенностей имеем

Поскольку  есть наименьшая неопределенность значения
есть наименьшая неопределенность значения  совместимая с условием пребывания электрона внутри образца, то это — та наименьшая величина, на которую следует изменить значение
совместимая с условием пребывания электрона внутри образца, то это — та наименьшая величина, на которую следует изменить значение  для того, чтобы можно было считать, что электрон находится в другом квантовом состоянии. Поэтому произведение
для того, чтобы можно было считать, что электрон находится в другом квантовом состоянии. Поэтому произведение  дает объем ячейки в пространстве импульсов, в пределах которой при изменении импульса электрона его состояние не меняется. Это означает, что
дает объем ячейки в пространстве импульсов, в пределах которой при изменении импульса электрона его состояние не меняется. Это означает, что  электронов в соответствии с принципом Паули занимают в пространстве импульсов объем, пропорциональный
электронов в соответствии с принципом Паули занимают в пространстве импульсов объем, пропорциональный  . В соответствии с (2)
. В соответствии с (2)

В основном состоянии энергия системы электронов имеет наименьшее возможное значение. Энергия каждого электрона  если эффективная масса
если эффективная масса  изотропна. Поэтому при
изотропна. Поэтому при  будут заполнены все состояния в пространстве импульсов, лежащие внутри сферы радиуса
будут заполнены все состояния в пространстве импульсов, лежащие внутри сферы радиуса  Этот радиус можно найти, приравнивая объем части пространства импульсов, даваемой формулой (3), объему шара радиуса
Этот радиус можно найти, приравнивая объем части пространства импульсов, даваемой формулой (3), объему шара радиуса  с центром в начале координат:
с центром в начале координат:  Поэтому
Поэтому  откуда
откуда

Энергия Ферми. Наибольшая энергия, которую может иметь электрон, проводимости в металле при  это энергия электрона с
это энергия электрона с 

Она называется энергией Ферми. Интересно сравнить энергию Ферми  с характерной тепловой энергией
с характерной тепловой энергией  Для типичных металлов концентрация электронов проводимости составляет около
Для типичных металлов концентрация электронов проводимости составляет около  а эффективная масса
а эффективная масса  близка к массе свободного электрона. Поэтому по формуле (5) легко подсчитать, что
близка к массе свободного электрона. Поэтому по формуле (5) легко подсчитать, что  оказывается порядка нескольких электронвольт. Легко убедиться, что тепловая энергия
оказывается порядка нескольких электронвольт. Легко убедиться, что тепловая энергия  становится сравнимой с энергией Ферми только при температурах приближающихся к
становится сравнимой с энергией Ферми только при температурах приближающихся к  Для всех металлов при всех температурах вплоть до точки плавления
Для всех металлов при всех температурах вплоть до точки плавления 
Нетрудно подсчитать скорость электрона, обладающего энергией  Она оказывается равной примерно
Она оказывается равной примерно  Таким образом, вследствие принципа Паули электроны проводимости в металле при абсолютном нуле температуры отнюдь не покоятся. Но все же их максимальная скорость в сотни раз меньше скорости света, что оправдывает использование для электронов в металлах представлений нерелятивистской физики.
Таким образом, вследствие принципа Паули электроны проводимости в металле при абсолютном нуле температуры отнюдь не покоятся. Но все же их максимальная скорость в сотни раз меньше скорости света, что оправдывает использование для электронов в металлах представлений нерелятивистской физики.
О вкладе электронов в теплоемкость металла. При повышении температуры от абсолютного нуля до некоторого значения Т средняя энергия каждой частицы, согласно представлениям классической статистической механики, должна возрасти на величину порядка  Но для подчиняющихся принципу Паули электронов в металле это не так. При температуре абсолютного нуля электроны проводимости уже имеют энергию порядка
Но для подчиняющихся принципу Паули электронов в металле это не так. При температуре абсолютного нуля электроны проводимости уже имеют энергию порядка  которая всегда много больше
которая всегда много больше  . Эта энергия не связана с тепловым движением электронов. При повышении температуры
. Эта энергия не связана с тепловым движением электронов. При повышении температуры  отнюдь не каждый электрон может увеличить свою энергию на величину порядка
отнюдь не каждый электрон может увеличить свою энергию на величину порядка  так как для большинства электронов все состояния, отстоящие от данного по энергии на величину порядка
так как для большинства электронов все состояния, отстоящие от данного по энергии на величину порядка  заняты другими электронами.
заняты другими электронами.

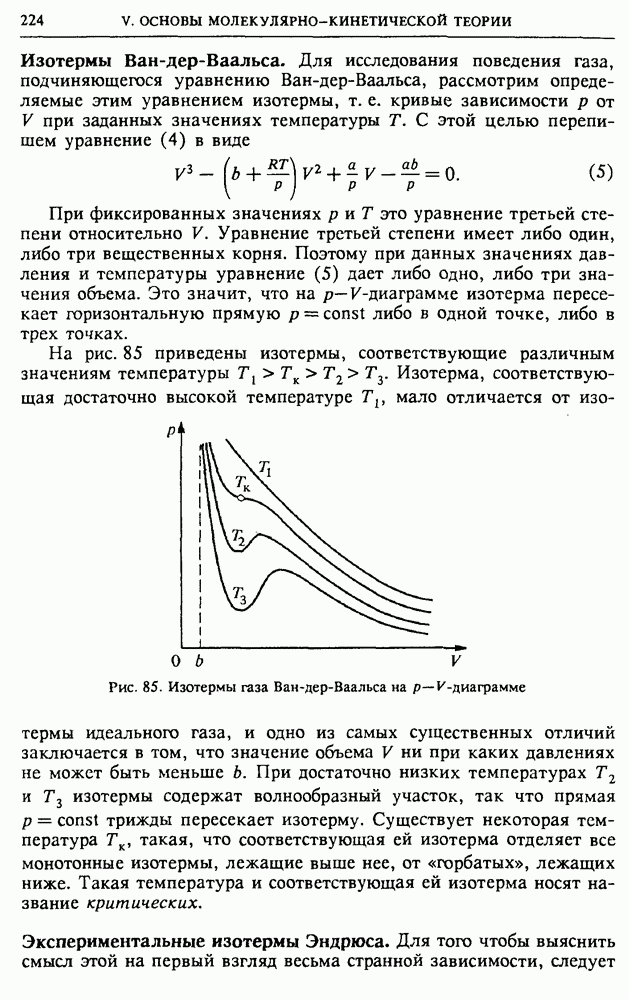
Рис. 114. Температурное размытие края функции распределения электронов в металле
Увеличить свою энергию смогут только электроны, занимающие состояния в интервале шириной примерно  около
около  Поэтому тепловое движение при конечной температуре приводит к размытию ступеньки функции распределения
Поэтому тепловое движение при конечной температуре приводит к размытию ступеньки функции распределения  в узком интервале значений энергии порядка
в узком интервале значений энергии порядка  (рис. 114). Основная часть электронов будет занимать те же состояния, что и при абсолютном нуле. О таких свойствах функции распределения говорят как о сильном вырождении электронного газа в металлах.
(рис. 114). Основная часть электронов будет занимать те же состояния, что и при абсолютном нуле. О таких свойствах функции распределения говорят как о сильном вырождении электронного газа в металлах.
Отличие функции распределения электронов проводимости в металле от максвелловской функции распределения классического газа объясняет особенности наблюдаемых электронных свойств металлов. Сравним, например, теплоемкости классического одноатомного газа и вырожденного газа электронов проводимости. В состоянии теплового равновесия в одноатомном классическом газе средняя энергия хаотического движения одной частицы равна  Поэтому внутренняя энергия всего газа из
Поэтому внутренняя энергия всего газа из  частиц равна
частиц равна  а его теплоемкость при постоянном объеме равна
а его теплоемкость при постоянном объеме равна  к и не зависит от температуры.
к и не зависит от температуры.
В вырожденном электронном газе в тепловом движении может участвовать лишь часть электронов порядка  поскольку именно такая доля полного их числа
поскольку именно такая доля полного их числа  содержится в интервале шириной
содержится в интервале шириной
около  вблизи энергии Ферми
вблизи энергии Ферми  Каждый из этих электронов приобретает дополнительную энергию порядка
Каждый из этих электронов приобретает дополнительную энергию порядка  , следовательно, полная энергия хаотического теплового движения электронов Е по порядку величины равна
, следовательно, полная энергия хаотического теплового движения электронов Е по порядку величины равна

По своему смыслу эта энергия представляет собой вклад электронов проводимости во внутреннюю энергию металла. Поэтому для теплоемкости электронного газа получаем выражение

(с точностью до числового множителя порядка единицы).
Поскольку  (например, при комнатной температуре это отношение равно всего лишь 1/200), то теплоемкость вырожденного электронного газа примерно на два порядка меньше теплоемкости классического одноатомного газа с тем же числом частиц. Поэтому при комнатной температуре молярная теплоемкость металлов практически целиком определяется вкладом решетки и почти не отличается от молярной теплоемкости диэлектриков, в которых электроны проводимости отсутствуют.
(например, при комнатной температуре это отношение равно всего лишь 1/200), то теплоемкость вырожденного электронного газа примерно на два порядка меньше теплоемкости классического одноатомного газа с тем же числом частиц. Поэтому при комнатной температуре молярная теплоемкость металлов практически целиком определяется вкладом решетки и почти не отличается от молярной теплоемкости диэлектриков, в которых электроны проводимости отсутствуют.
Другое важное отличие теплоемкости электронного газа (7) заключается в том, что она пропорциональна температуре, в то время как теплоемкость классического газа от температуры не зависит.
Электропроводность металлов. Наряду со свойствами коллектива электронов проводимости, которые он проявляет в состоянии равновесия, большой интерес представляет изучение поведения электронов проводимости в металле в неравновесном состоянии, когда они движутся под действием приложенных внешних полей. Такие процессы называются явлениями переноса. Примерами явлений переноса могут служить теплопроводность, электропроводность, эффект Холла, термоэлектрические явления и т. д.
Остановимся подробнее на одном из наиболее важных неравновесных процессов — прохождении электрического тока в металле, описываемом законом Ома. Закон Ома является одним из самых ранних экспериментальных открытий в области электрического тока в веществе. Согласно этому закону плотность электрического тока пропорциональна напряженности приложенного электрического поля:  Это уравнение описывает наблюдаемое поведение очень многих веществ в широком диапазоне условий.
Это уравнение описывает наблюдаемое поведение очень многих веществ в широком диапазоне условий.
Закон Ома нельзя вывести только из законов электродинамики, описывающих электрическое поле. Его можно получить на основе изучения процессов, происходящих в веществе при приложении электрического поля. Интересно отметить, что в разных веществах эти процессы могут сильно различаться, но независимо от характера
процессов рассеяния носителей связь между плотностью тока и напряженностью поля при не слишком сильных полях всегда оказывается линейной.
В металлах сопротивление электрическому току обусловлено рассеянием электронов проводимости на тепловых колебаниях решетки и хаотически расположенных дефектах кристалла — в идеальной решетке сопротивление отсутствует. Феноменологически описать процессы рассеяния электронов проводимости можно путем введения так называемого времени релаксации.
Будем рассуждать следующим образом. В состоянии равновесия функция распределения электронов по импульсам сферически-симметрична. Поэтому средняя скорость электронов равна нулю и никакого направленного переноса заряда, т. е. электрического тока, нет.

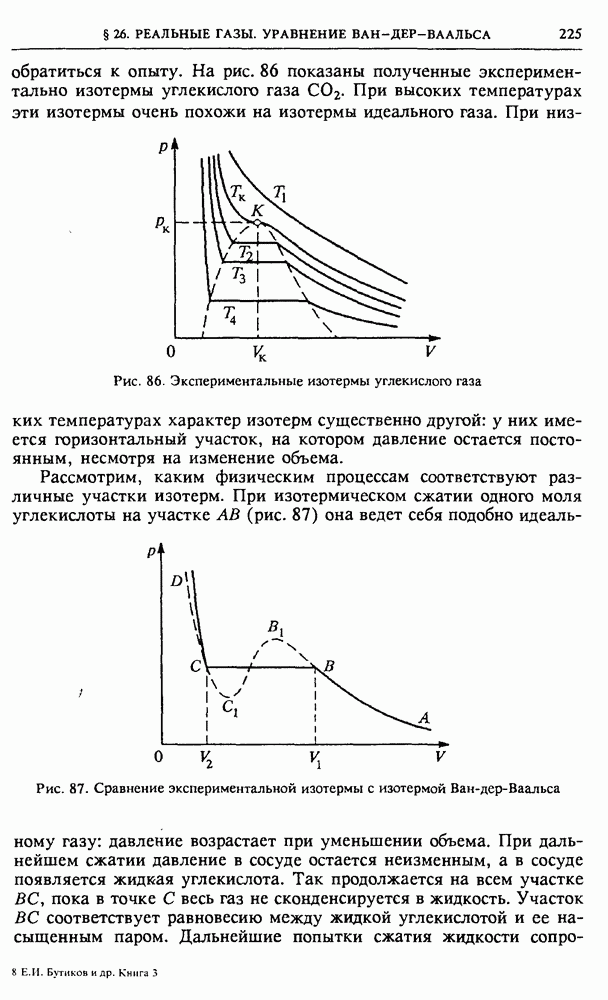
Рис. 115. Смещение сферической поверхности Ферми под действием приложенного электрического поля
Приложенное электрическое поле вызывает искажение функции распределения. В отличие от изотропного теплового воздействия, которое могло только размыть край распределения, не нарушая его сферической симметрии, направленное действие внешнего поля вызывает сдвиг всего распределения (рис. 115). На этом рисунке показано, как под действием электрического поля смещается в пространстве импульсов сфера радиуса  внутри которой расположены занятые электронами состояния. Средняя заштрихованная область соответствует состояниям, которые заполнены электронами как до приложения электрического поля, так и после. Незаштрихованная часть соответствует состояниям, которые до приложения поля были заполнены, а после приложения поля оказались не занятыми. Наконец, дважды заштрихованная область соответствует состояниям, которые оказались заполненными после приложения поля. Видно, что теперь число электронов, движущихся в направлении действия силы электрического поля, больше, чем движущихся в противоположном направлении. Для такого сдвинутого в пространстве импульсов распределения средняя скорость уже отлична от нуля, что означает наличие тока в образце.
внутри которой расположены занятые электронами состояния. Средняя заштрихованная область соответствует состояниям, которые заполнены электронами как до приложения электрического поля, так и после. Незаштрихованная часть соответствует состояниям, которые до приложения поля были заполнены, а после приложения поля оказались не занятыми. Наконец, дважды заштрихованная область соответствует состояниям, которые оказались заполненными после приложения поля. Видно, что теперь число электронов, движущихся в направлении действия силы электрического поля, больше, чем движущихся в противоположном направлении. Для такого сдвинутого в пространстве импульсов распределения средняя скорость уже отлична от нуля, что означает наличие тока в образце.
Пусть в некоторый момент времени внешнее электрическое поле выключается. Очевидно, что система электронов будет возвращаться в состояние теплового равновесия. Предположим, что скорость приближения к равновесию в каждый момент пропорциональна величине отклонения от равновесия. Тоща и изменение средней скорости направленного движения электронов будет происходить по такому же закону. Так как в равновесии средняя скорость равна
нулю, то изменение скорости происходит пропорционально самой средней скорости:

Поскольку решение этого уравнения имеет вид

то х есть время, в течение которого скорость направленного движения убывает в  раз. Оно называется временем релаксации.
раз. Оно называется временем релаксации.
Закон изменения средней скорости  направленного движения электронов проводимости (9) имеет в точности такой же вид, что и уравнение движения тела в вязкой среде под действием силы трения, пропорциональной скорости:
направленного движения электронов проводимости (9) имеет в точности такой же вид, что и уравнение движения тела в вязкой среде под действием силы трения, пропорциональной скорости:

Это наводит на мысль, что взаимодействие электронов проводимости с колебаниями решетки и примесями, приводящее к описываемой уравнением (9) релаксации средней скорости, можно учесть путем введения некоторой эффективной, непрерывно действующей на электрон силы трения 
При наличии постоянного электрического поля Е на электрон, кроме силы трения, действует еще сила — еЕ, где  — абсолютная величина заряда электрона. В стационарном состоянии электрон движется с такой постоянной скоростью, при которой эти силы уравновешиваются:
— абсолютная величина заряда электрона. В стационарном состоянии электрон движется с такой постоянной скоростью, при которой эти силы уравновешиваются:  Такой же будет средняя скорость
Такой же будет средняя скорость  движения электронов в металле под действием поля Е:
движения электронов в металле под действием поля Е: 
Плотность тока  обусловленного направленным движением электронов со скоростью
обусловленного направленным движением электронов со скоростью  равна
равна  Подставляя сюда значение
Подставляя сюда значение  находим 2
находим 2

Это и есть закон Ома. Вычисление времени релаксации  , следовательно, удельной электрической проводимости
, следовательно, удельной электрической проводимости  требует детального рассмотрения механизмов рассеяния электронов проводимости.
требует детального рассмотрения механизмов рассеяния электронов проводимости.
Описанная выше физическая картина электропроводности металлов основывалась на предположении, что перенос заряда обусловлен только электронами зоны проводимости. Во многих металлах, однако, электропроводность определяется электронами нескольких энергетических зон. Например, электропроводность железа создается как электронами зоны проводимости, возникшей из  -уровней изолированного атома железа, так и дырками из заполненной на
-уровней изолированного атома железа, так и дырками из заполненной на  энергетической зоны, возникшей из З-уровней атома железа. Но и в случае
энергетической зоны, возникшей из З-уровней атома железа. Но и в случае
дырочной проводимости остаются справедливыми развитые представления о роли рассеяния носителей тока для объяснения закона Ома.
Плазменные свойства металлов. При изучении электронных свойств металлов, таких, как теплоемкость и электропроводность, систему свободных электронов можно было рассматривать как совокупность невзаимодействующих между собой частиц. Все наблюдаемые свойства объяснялись взаимодействием электронов проводимости с колебаниями кристаллической решетки и дефектами ее структуры — примесями, вакансиями и т. д.
Однако существует целый ряд явлений, в которых взаимодействие электронов играет определяющую роль. В таких случаях говорят о проявлении электронами плазменных свойств.
Выше при изучении плазмы мы считали, что к частицам, из которых состоит плазма, можно применять законы классической физики. В газоразрядной и тем более в ионосферной плазме это действительно так, ибо там расстояние между электронами много больше их дебройлевской длины волны.
Но для плазмы, представляющей собой электроны в металлах или полупроводниках, ситуация совсем иная. Сильное вырождение электронного газа в металле означает, что среднее расстояние между электронами одного порядка с их дебройлевской длиной волны  для электронов с импульсом Ферми
для электронов с импульсом Ферми  Строгая теория плазменных свойств металлов очень сложна, однако основные закономерности можно установить с помощью анализа размерностей.
Строгая теория плазменных свойств металлов очень сложна, однако основные закономерности можно установить с помощью анализа размерностей.
Поведение электронов проводимости описывается квантовой механикой. Поэтому мы должны ожидать, что в формулах, выражающих свойства такой плазмы, наряду с параметрами  появится постоянная Планка
появится постоянная Планка  Теперь наряду с безразмерным параметром
Теперь наряду с безразмерным параметром  , даваемым формулой (7) § 33 и характеризующим классическую плазму, появится еще один безразмерный параметр Г:
, даваемым формулой (7) § 33 и характеризующим классическую плазму, появится еще один безразмерный параметр Г:

Физический смысл этого параметра легко уяснить, обращаясь к формуле (5): Г представляет собой отношение энергии Ферми  к характерной тепловой энергии
к характерной тепловой энергии  Если
Если  , т. е.
, т. е.  то электронный газ по своим свойствам близок к рассмотренной выше классической плазме. Так бывает в полупроводниках при не слишком больших концентрациях электронов проводимости и достаточно высоких температурах.
то электронный газ по своим свойствам близок к рассмотренной выше классической плазме. Так бывает в полупроводниках при не слишком больших концентрациях электронов проводимости и достаточно высоких температурах.
Как мы видели, для электронов в металлах при всех температурах вплоть до точки плавления  , следовательно,
, следовательно,  Для такой плазмы потенциальную энергию кулоновского взаимодействия электронов
Для такой плазмы потенциальную энергию кулоновского взаимодействия электронов  следует сравнивать не с кинетической энергией теплового движения
следует сравнивать не с кинетической энергией теплового движения  а с энергией Ферми
а с энергией Ферми
 Степень близости электронной плазмы в металлах к идеальному газу характеризуется отношением энергии взаимодействия к энергии Ферми, т. е. безразмерным параметром, который принято обозначать
Степень близости электронной плазмы в металлах к идеальному газу характеризуется отношением энергии взаимодействия к энергии Ферми, т. е. безразмерным параметром, который принято обозначать 

Нетрудно видеть, что параметр  пропорционален отношению среднего расстояния между электронами
пропорционален отношению среднего расстояния между электронами  к боровскому радиусу
к боровскому радиусу  Электронный газ в металле был бы близок к идеальному газу при
Электронный газ в металле был бы близок к идеальному газу при 
Из формулы (12) также видно, что в противоположность классической плазме электронный газ тем ближе к идеальному газу, чем выше его концентрация. Конечно, при увеличении концентрации электронов  потенциальная энергия их взаимодействия возрастает. В случае классической плазмы, где кинетическая энергия не зависит от концентрации, плазма с ростом концентрации по своим свойствам все меньше напоминала бы идеальный газ.
потенциальная энергия их взаимодействия возрастает. В случае классической плазмы, где кинетическая энергия не зависит от концентрации, плазма с ростом концентрации по своим свойствам все меньше напоминала бы идеальный газ.
Для электронов в металле, как мы видели, вследствие принципа Паули кинетическая энергия растет с увеличением концентрации как  Поэтому, несмотря на увеличение потенциальной энергии, которая растет как
Поэтому, несмотря на увеличение потенциальной энергии, которая растет как  отношение потенциальной энергии к кинетической убывает. Другими словами, относительная роль взаимодействия электронов при увеличении их концентрации становится все меньше и меньше. Оказывается, что для реальных металлов параметр
отношение потенциальной энергии к кинетической убывает. Другими словами, относительная роль взаимодействия электронов при увеличении их концентрации становится все меньше и меньше. Оказывается, что для реальных металлов параметр  больше единицы, т. е. концентрация электронов все-таки недостаточно высока для того, чтобы электронный газ можно было считать идеальным. Для электронов в металле более подходящим является название «электронная жидкость», чем «электронный газ». Тем не менее последовательная теория электронной жидкости металлов показала, что многие свойства, полученные в модели свободных электронов, качественно остаются справедливыми и при учете электронного взаимодействия.
больше единицы, т. е. концентрация электронов все-таки недостаточно высока для того, чтобы электронный газ можно было считать идеальным. Для электронов в металле более подходящим является название «электронная жидкость», чем «электронный газ». Тем не менее последовательная теория электронной жидкости металлов показала, что многие свойства, полученные в модели свободных электронов, качественно остаются справедливыми и при учете электронного взаимодействия.
Как и для классической плазмы, для электронов проводимости в металле характерно существование плазменных колебаний, обусловленных кулоновским взаимодействием электронов и ионов кристаллической решетки. В выражение (3) § 33 для частоты плазменных колебаний  не входит ни температура Т, ни постоянная Планка
не входит ни температура Т, ни постоянная Планка  Это соответствует физической причине возможности существования плазменных колебаний: они обусловлены кулоновским взаимодействием заряженных частиц, а не тем, какими законами
Это соответствует физической причине возможности существования плазменных колебаний: они обусловлены кулоновским взаимодействием заряженных частиц, а не тем, какими законами  классическими или квантовыми должно описываться движение.
классическими или квантовыми должно описываться движение.
Энергия кванта плазменных колебаний (плазмона)  при характерных для металлов концентрациях электронов проводимости
при характерных для металлов концентрациях электронов проводимости
оказывается больше энергии Ферми  максимальной энергии электронов для металла в основном состоянии. Поэтому плазменные колебания в металлах не могут возникать за счет энергии движения отдельных электронов, в противоположность классической плазме. Плазменные колебания в металлах могут возбуждаться только пролетающими через образец быстрыми заряженными частицами или падающими электромагнитными волнами. Роль плазменных колебаний в состоянии равновесия сводится по существу только к экранированию кулоновского взаимодействия электронов. Именно поэтому модель свободных электронов качественно верно объясняет многие электронные свойства металлов.
максимальной энергии электронов для металла в основном состоянии. Поэтому плазменные колебания в металлах не могут возникать за счет энергии движения отдельных электронов, в противоположность классической плазме. Плазменные колебания в металлах могут возбуждаться только пролетающими через образец быстрыми заряженными частицами или падающими электромагнитными волнами. Роль плазменных колебаний в состоянии равновесия сводится по существу только к экранированию кулоновского взаимодействия электронов. Именно поэтому модель свободных электронов качественно верно объясняет многие электронные свойства металлов.
Частота плазменных колебаний сор представляет собой граничную частоту для электромагнитных волн, которые могут распространяться в плазме. Волны с частотой, меньшей сор, не могут проникать в плазму, так как низкочастотные электромагнитные поля таких волн экранируются заряженными частицами плазмы. Падающая на границу плазмы волна при  отражается от границы. Если же частота электромагнитной волны выше плазменной частоты, то такая волна проникает в плазму.
отражается от границы. Если же частота электромагнитной волны выше плазменной частоты, то такая волна проникает в плазму.
Концентрация свободных электронов в щелочных металлах такова, что частота плазменных колебаний соответствует ультрафиолетовой области спектра. Поэтому в ультрафиолетовой области щелочные металлы прозрачны, хотя в видимой и инфракрасной областях спектра хорошо отражают падающее на них излучение. Напомним, что для ионосферной плазмы граница прозрачности попадает в диапазон метровых радиоволн.
• Поясните, почему распределение электронов проводимости в металле по разрешенным энергетическим уровням резко отличается от соответствующего распределения для газа классических частиц, хотя поведение отдельного электрона проводимости в кристалле сходно с поведением классической свободной частицы.
• Что такое импульс Ферми? Как эта величина связана с концентрацией электронов проводимости в металле?
• Что такое энергия Ферми? Как оценить скорость электрона в металле, обладающего энергией, равной энергии Ферми?
• Чем объясняется малый по сравнению с кристаллической решеткой вклад электронов проводимости в теплоемкость металлов?
• Поясните, почему теплоемкость вырожденного электронного газа пропорциональна температуре, в то время как теплоемкость классического газа от температуры не зависит.
• Что такое время релаксации для электронов в металле? Разъясните смысл этого понятия на примере затухания направленного движения электронов.
• Как объясняется закон Ома на основе представлений об эффективной силе трения, действующей на электроны проводимости при их направленном движении под действием электрического поля?
• Почему, в противоположность классической плазме, электронный газ в металлах с увеличением концентрации приближается по своим свойствам к идеальному газу?
• Покажите, что энергия кванта плазменных колебаний в реальном металле превосходит максимальную энергию отдельного электрона. К каким следствиям это приводит?
• Почему, строго говоря, свободные электроны в металле некорректно рассматривать как идеальный газ?
• Чем объясняется прозрачность щелочных металлов в ультрафиолетовой области спектра?
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
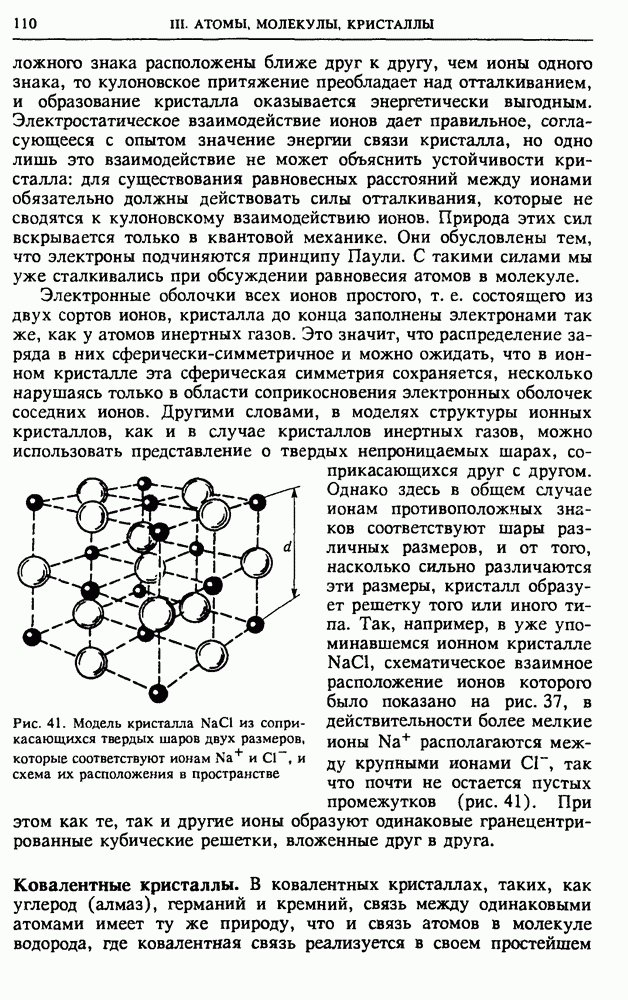
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
- § 13. Кристаллы
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
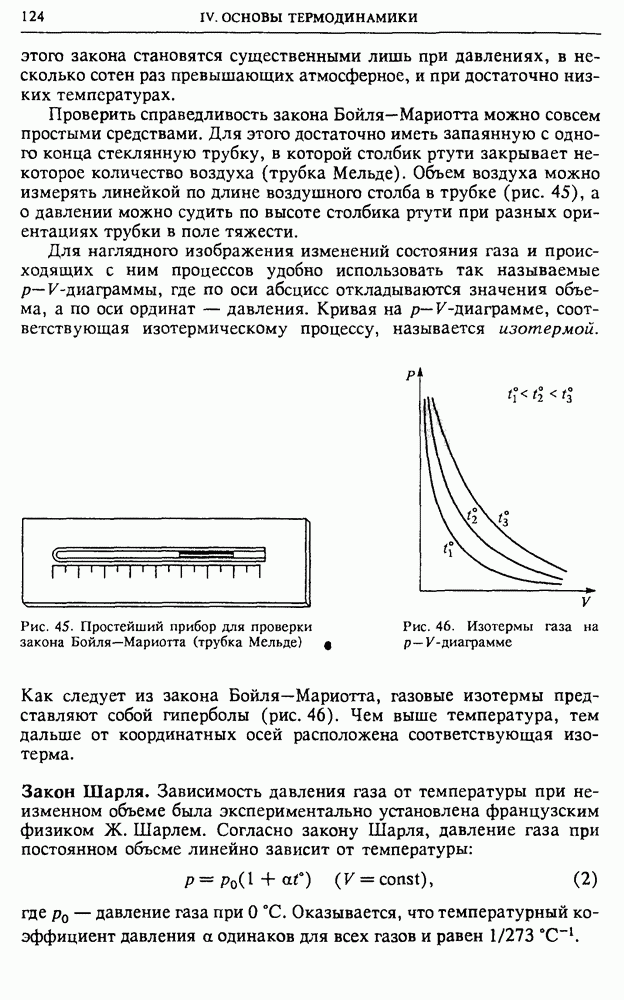
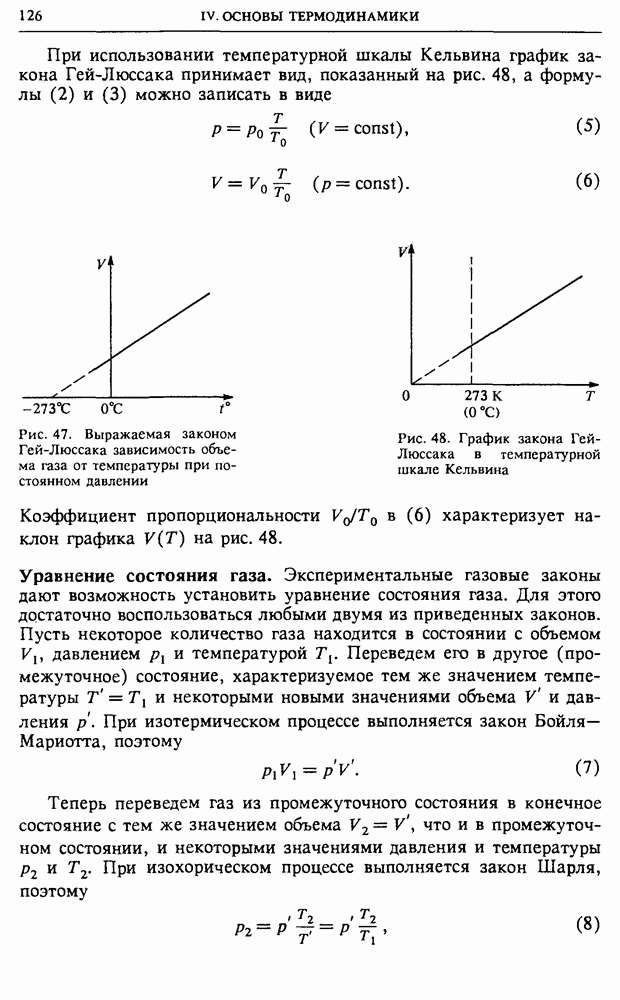
- § 15. Уравнение состояния газа
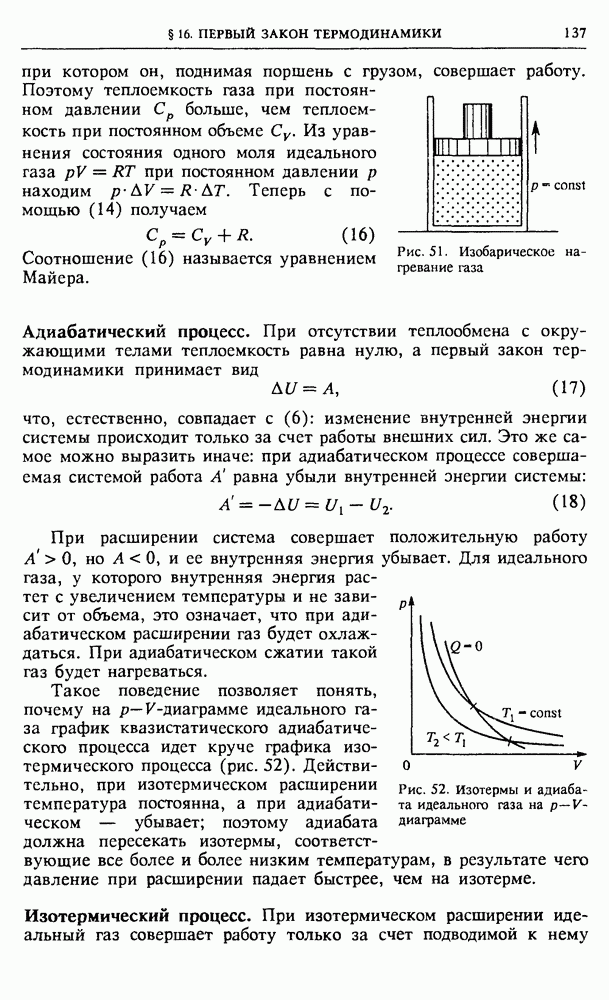
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
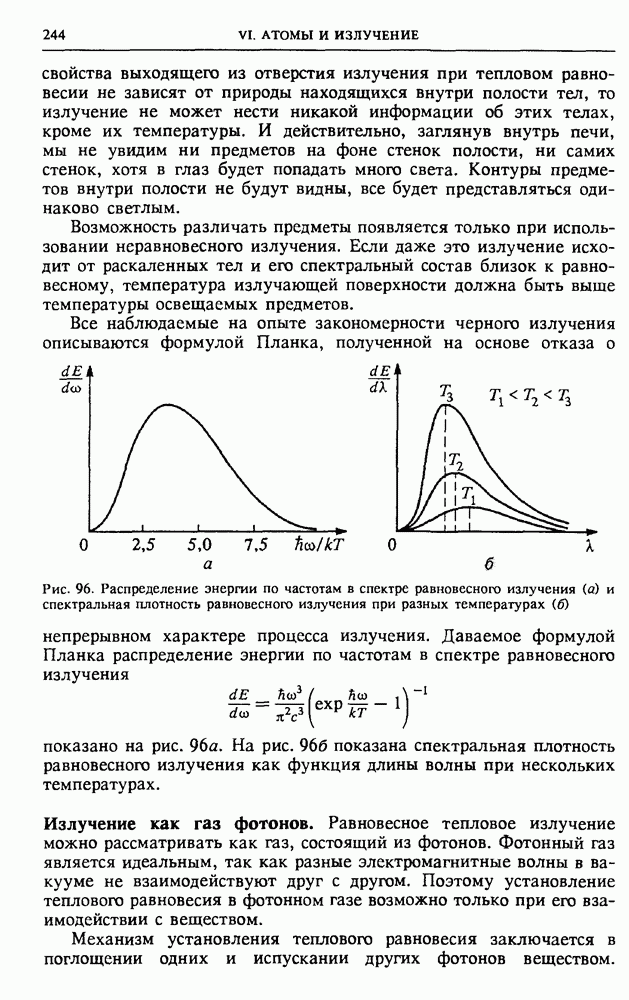
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
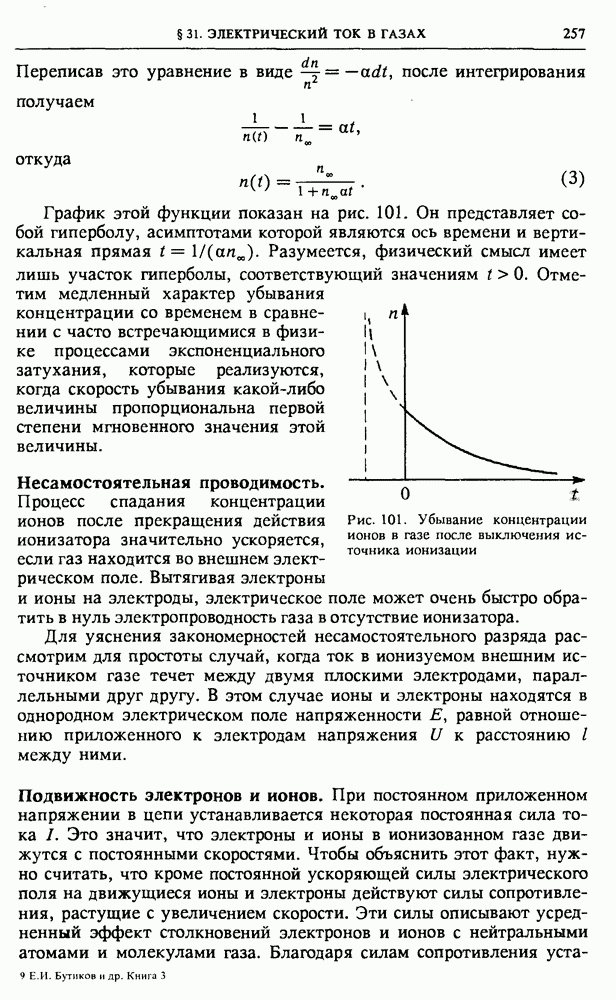
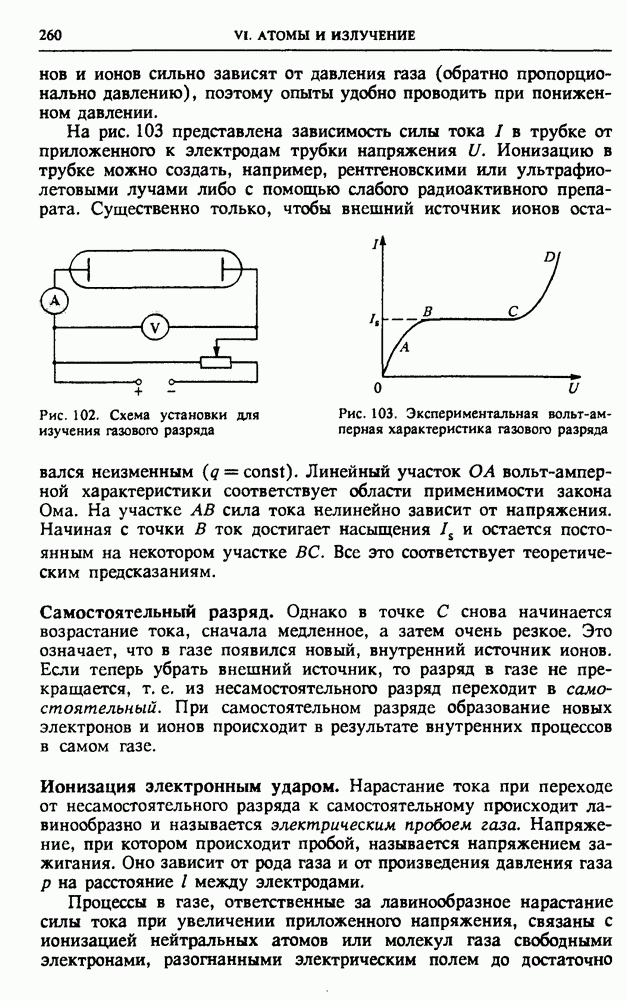
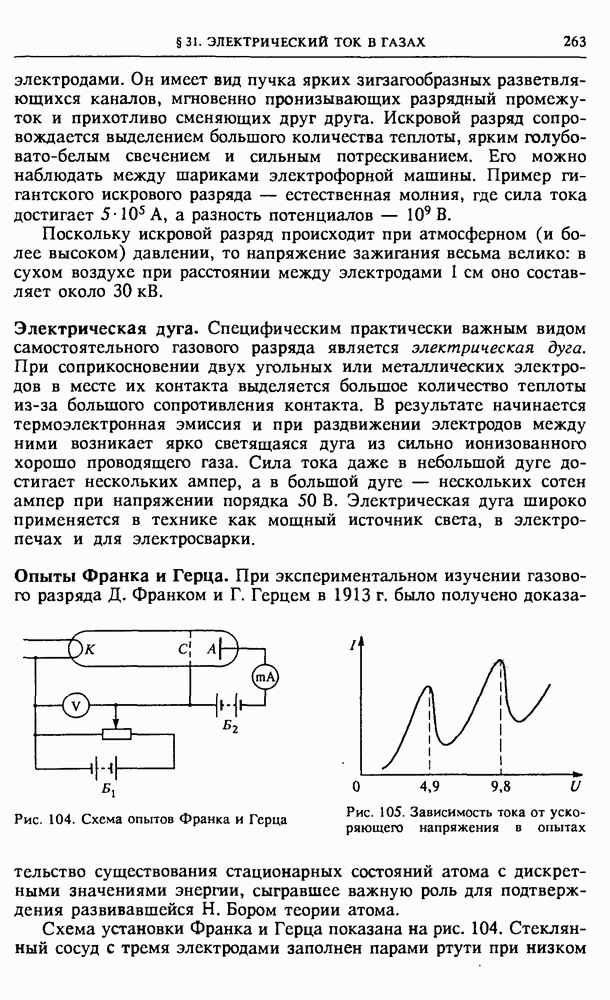
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы