| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
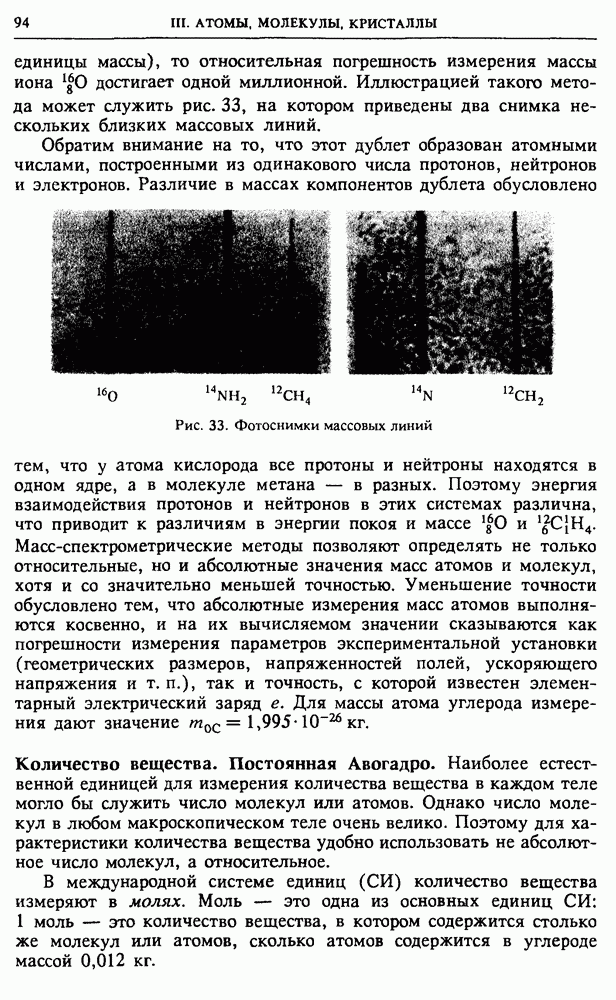
§ 36. Электронные свойства полупроводников
Как уже отмечалось, электрические свойства полупроводников очень сильно зависят от наличия и концентрации тех или иных примесей. Чтобы разобраться в этих вопросах, нужно иметь представление о природе и энергетическом спектре состояний электронов, связанных с атомами примесей.
Роль примесей в полупроводниках. Наибольшее влияние на свойства полупроводников оказывают так называемые донорные и акцепторные примеси (или доноры и акцепторы). О донорах мы уже упоминали в § 34 при классификации полупроводников. Наличие донорных примесей в кристалле приводит к появлению дополнительных разрешенных электронных уровней энергии, лежащих в запрещенной зоне вблизи дна зоны проводимости. Акцепторные примеси приводят к появлению дополнительных уровней в запрещенной зоне, лежащих вблизи потолка валентной зоны. Важно, что в обоих случаях примесные уровни отделены от соответствующих разрешенных зон энергетическими интервалами, малыми по сравнению с шириной запрещенной зоны.
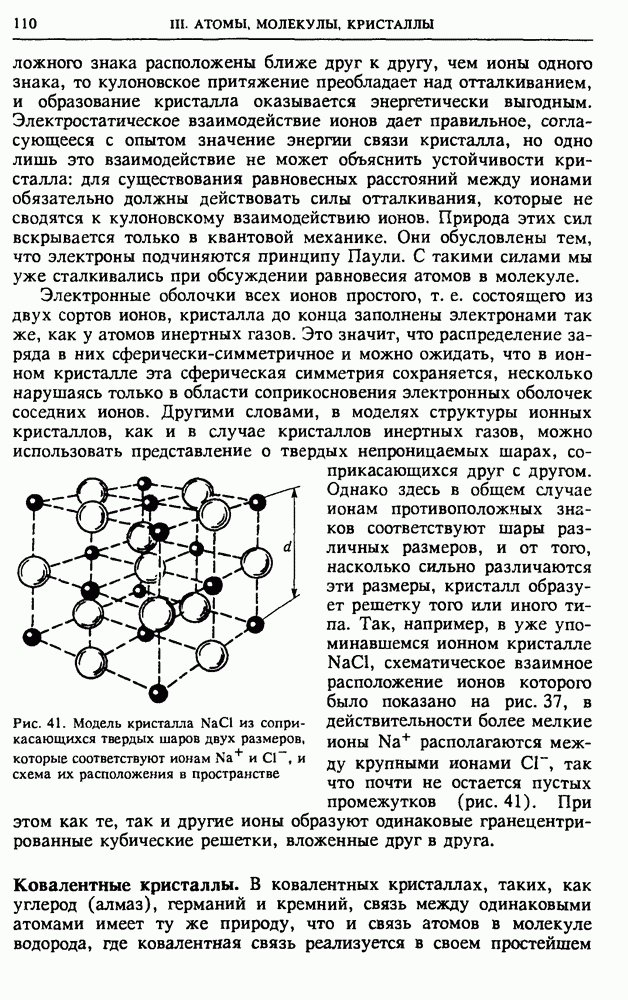
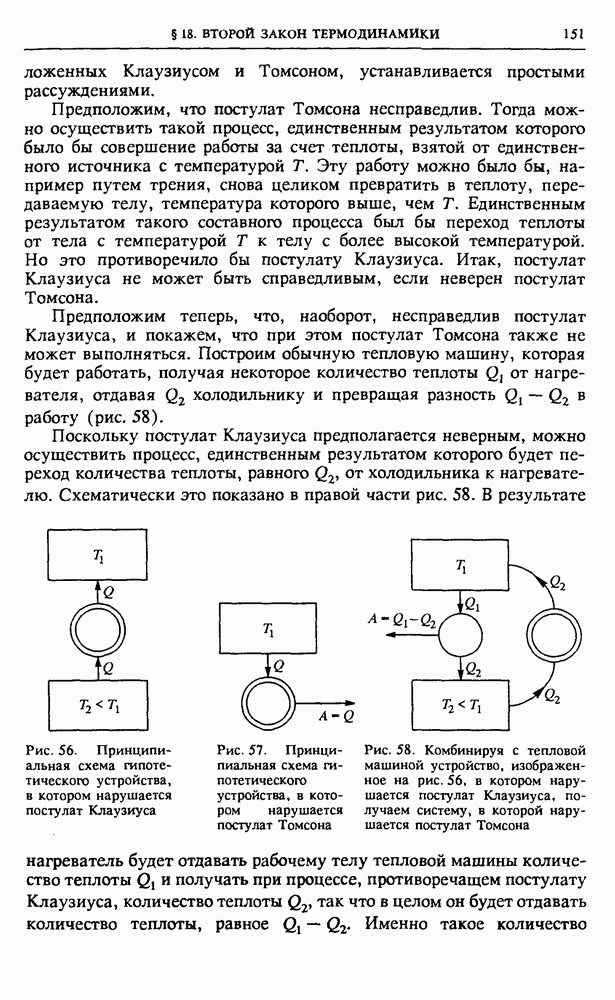
Доноры. В качестве простого примера донорного центра в полупроводнике рассмотрим кристалл кремния, в котором один из узлов решетки занят атомом фосфора (рис. 116). Кремний кристаллизуется в решетке типа алмаза, где каждый атом имеет четыре ближайших соседа, расположенных в вершинах правильного тетраэдра, в центре которого находится рассматриваемый атом. Четыре электрона из внешней электронной оболочки каждого атома участвуют в образовании направленных ковалентных связей с четырьмя окружающими его такими же атомами кремния. В картине энергетических зон кристалла кремния эти электроны занимают
квантовые состояния валентной зоны, причем при абсолютном нуле температуры эта зона оказывается полностью заполненной.
Примесный атом фосфора, занимающий соседнюю ячейку в таблице Менделеева, имеет пять электронов во внешней оболочке. Четыре из них участвуют в образовании ковалентных связей с соседними атомами кремния. Пятый электрон фосфора оказывается лишним, он не нужен для образования ковалентных связей. Этот электрон не вполне свободен, потому что ядро атома фосфора обладает положительным зарядом, на единицу большим, чем ядро атома кремния. В результате этот электрон движется в кристалле по большой орбите вокруг примесного атома, подобно тому, как движется электрон вокруг ядра в атоме водорода. На рис. 116 эта орбита показана. Размеры такой орбиты велики по сравнению с межатомным расстоянием в кристалле.

Рис. 116. Схематическое двумерное изображение донорного центра в кристалле кремния
Большой размер орбиты и малая энергия связи такого электрона объясняются тем, что сила взаимодействия его с ядром атома фосфора ослаблена диэлектрическими свойствами среды кристаллической решетки кремния, и тем, что эффективная масса электрона в зоне проводимости кремния меньше массы свободного электрона.
Таким образом, электрически нейтральное состояние примесного центра можно представить как локализованное состояние электрона (электрон связан с примесным центром), причем энергия этого состояния на диаграмме электронных уровней энергии кристалла лежит в запрещенной зоне вблизи дна зоны проводимости (рис. 117). Из такого локализованного состояния электрон может быть переведен в нелокализованное состояние зоны проводимости, если ему сообщить дополнительную энергию, не меньшую  При этом донорный центр становится ионизованным, так как на нем локализован избыточный положительный заряд.
При этом донорный центр становится ионизованным, так как на нем локализован избыточный положительный заряд.

Рис. 117. Уровни энергии доноров и акцепторов
Энергия электрона на донорном центре составляет около 0,01 эВ, поэтому при обычных температурах практически все донорные центры ионизованы.
Акцепторы. В кристаллах кремния и германия донорами могут служить не только атомы фосфора, но и атомы других элементов пятой
группы таблицы Менделеева. В противоположность этому примеси элементов третьей группы в таких кристаллах являются акцепторами. В этом случае при замещении одного из основных атомов кристалла, например атомом бора, для образования направленных ковалентных связей с соседями не хватает одного электрона.
Представляется естественным, что одна из четырех валентных связей, направленных к бору, должна остаться ненасыщенной. Это соответствует отсутствию электрона в заполненной валентной зоне, т. е. положительной дырке. Пространственное положение отсутствующей связи может изменяться, переходя от одного из соседних с примесью атомов кремния к другому.
Наиболее просто такую ситуацию можно описать, используя представление о связанной дырке, движущейся в кулоновском поле, создаваемом эффективным отрицательным зарядом  происхождение которого связано с тем, что заряд ядра примесного атома на единицу меньше заряда ядра атома кремния. Как и в случае доноров, это поле ослаблено диэлектрической проницаемостью кристаллической решетки. Поскольку и для дырки эффективная масса в данном случае меньше массы свободного электрона, то радиус боровской орбиты дырки, движущейся вокруг примесного центра, простирается на большое (по сравнению с постоянной решетки) расстояние. Энергия связи дырки невелика, поэтому соответствующий акцепторному центру энергетический уровень электрона лежит в запрещенной зоне немного выше потолка валентной зоны (рис. 117).
происхождение которого связано с тем, что заряд ядра примесного атома на единицу меньше заряда ядра атома кремния. Как и в случае доноров, это поле ослаблено диэлектрической проницаемостью кристаллической решетки. Поскольку и для дырки эффективная масса в данном случае меньше массы свободного электрона, то радиус боровской орбиты дырки, движущейся вокруг примесного центра, простирается на большое (по сравнению с постоянной решетки) расстояние. Энергия связи дырки невелика, поэтому соответствующий акцепторному центру энергетический уровень электрона лежит в запрещенной зоне немного выше потолка валентной зоны (рис. 117).
Дырка, связанная с акцепторным центром, может быть переведена из локализованного состояния в нелокализованное состояние валентной зоны, если ей сообщить дополнительную энергию, превосходящую энергию ионизации акцепторного центра  . Акцепторный центр при этом становится отрицательно заряженным.
. Акцепторный центр при этом становится отрицательно заряженным.
Энергия связи дырки на акцепторном центре, как и в случае донорных центров, также измеряется сотыми долями электронвольта. Поэтому при обычных температурах и акцепторные центры практически полностью ионизованы.
Электропроводность полупроводников. Проводимость кристалла, обусловленная наличием доноров, поставляющих электроны в зону проводимости, называется проводимостью n-типа (от англ. negative — отрицательный), а проводимость, обусловленная акцепторными примесями, поставляющими положительные дырки в валентную зону, — проводимостью  -типа (от англ. positive).
-типа (от англ. positive).
Электропроводность металла при изменении внешних условий меняется только из-за изменения времени релаксации, которое зависит от температуры и концентрации дефектов кристаллической решетки. Однако число носителей зарядов — свободных электронов — остается постоянным. В полупроводнике дело обстоит
совершенно иначе. Главная причина изменения электропроводности полупроводника заключается в изменении концентрации носителей заряда.
Собственный полупроводник при абсолютном нуле температуры, как и диэлектрик, не содержит свободных носителей, так как валентная зона заполнена целиком, а зона проводимости пуста. С повышением температуры часть электронов переходит из валентной зоны в зону проводимости. Концентрация свободных носителей при этом зависит от отношения характерной тепловой энергии  к ширине запрещенной зоны.
к ширине запрещенной зоны.
В примесных полупроводниках появление свободных носителей при низких температурах связано в основном не с переходом электронов в зону проводимости из валентной зоны, а с ионизацией локализованных электронных состояний, энергии которых лежат в запрещенной зоне.
Реальные кристаллы всегда содержат примеси. Поэтому собственная проводимость преобладает только в очень чистых полупроводниковых кристаллах при сравнительно высоких температурах. При глубоком охлаждении собственный полупроводник неизбежно должен стать примесным.
Распределение носителей тока по энергиям. Как распределены электроны в зоне проводимости полупроводника и дырки в валентной зоне по уровням энергии? Это нужно знать для построения микроскопической теории электропроводности и других наблюдаемых свойств, обусловленных электронами. Качественно ответ на этот вопрос можно дать, основываясь на значении безразмерного параметра Г, определяемого формулой (11) предыдущего параграфа:

Легко видеть, что этот параметр представляет собой квадрат отношения дебройлевской длины волны частицы  имеющей характерный тепловой импульс
имеющей характерный тепловой импульс  к среднему расстоянию между частицами
к среднему расстоянию между частицами  При
При  поведение носителей тока определяется законами классической физики и их функция распределения по энергиям и скоростям такая же, как у газа классических частиц. При
поведение носителей тока определяется законами классической физики и их функция распределения по энергиям и скоростям такая же, как у газа классических частиц. При  необходимо учитывать принцип Паули, ибо среднее расстояние между частицами много меньше дебройлевской длины волны. В этом случае, как и у металлов, распределение носителей тока по уровням энергии имеет вид ступеньки: почти все состояния с импульсами, меньшими импульса Ферми, заполнены, с большими импульсами — свободны. Все физические свойства при этом обусловлены вкладом носителей с энергиями, соответствующими области размытия этой ступеньки.
необходимо учитывать принцип Паули, ибо среднее расстояние между частицами много меньше дебройлевской длины волны. В этом случае, как и у металлов, распределение носителей тока по уровням энергии имеет вид ступеньки: почти все состояния с импульсами, меньшими импульса Ферми, заполнены, с большими импульсами — свободны. Все физические свойства при этом обусловлены вкладом носителей с энергиями, соответствующими области размытия этой ступеньки.
В полупроводниках со смешанной проводимостью, где одновременно есть и электроны в зоне проводимости, и дырки в валентной
зоне, параметр Г для каждого типа носителей имеет свое значение. Может быть, например, так, что распределение электронов описывается ступенчатой функцией, а дырок — максвелловской. В обычных условиях в полупроводниках, используемых во многих электронных устройствах, распределение носителей тока описывается классической максвелловской функцией.
Эффект Холла. Представление о дырках как о свободных носителях тока с положительными зарядами было введено для того, чтобы наглядно описать вклад в электропроводность валентной зоны, почти целиком заполненной электронами. Убедительное доказательство реальности положительных дырок дает эффект Холла, открытый в 1879 г., задолго до возникновения представлений о самих дырках.
Эффект Холла можно наблюдать при прохождении электрического тока в любых твердых проводящих телах, помещенных во внешнее магнитное поле. Он заключается в появлении внутри проводящего тела электрического поля, напряженность Е которого перпендикулярна как индукции В внешнего магнитного поля, так и плотности  пропускаемого через образец тока.
пропускаемого через образец тока.

Рис. 118. К объяснению эффекта Холла
Рассмотрим прямоугольную пластинку из проводящего вещества, помещенную в однородное магнитное поле с индукцией В (рис. 118). Пусть ток I пропускается через образец слева направо, как показано на рисунке, и осуществляется одним типом носителей с зарядом  который может быть как положительным, так и отрицательным. Обозначив концентрацию носителей через
который может быть как положительным, так и отрицательным. Обозначив концентрацию носителей через  а их дрейфовую скорость через
а их дрейфовую скорость через  запишем выражение для силы тока I в виде
запишем выражение для силы тока I в виде

При наложении магнитного поля В на движущиеся в пластине носители тока действует сила Лоренца

направленная перпендикулярно как магнитному полю В, так и скорости  направленного движения носителей. В результате на боковых гранях пластины скапливаются заряды противоположного знака, создающие электрическое поле Е. Действующая со стороны этого поля сила
направленного движения носителей. В результате на боковых гранях пластины скапливаются заряды противоположного знака, создающие электрическое поле Е. Действующая со стороны этого поля сила

уравновешивает силу Лоренца, обеспечивая направленное движение носителей тока параллельно боковым граням пластины. Наличие электрического поля Е, перпендикулярного направлению движения зарядов, означает, что между точками А и С на противоположных гранях образца, которые в отсутствие магнитного поля имели одинаковый потенциал, теперь появляется некоторая разность потенциалов  пропорциональная напряженности поля Е:
пропорциональная напряженности поля Е:

Приравнивая правые части выражений (3) и (4) и подставляя в получившееся равенство  из (2) и Е из (5), находим
из (2) и Е из (5), находим

Формула (6) справедлива как для положительных, так и для отрицательных носителей заряда. Зависящий только от свойств материала пластины (но не от ее размеров) коэффициент пропорциональности в (6)

называется постоянной Холла. Знак постоянной Холла совпадает со знаком носителей заряда. Поэтому для образцов с электронной и дырочной проводимостью постоянная Холла имеет противоположные знаки.
Измерения постоянной Холла недвусмысленно подтвердили существование полупроводников как с электронной, так и с дырочной проводимостью. Более того, постоянная Холла оказалась положительной и для некоторых металлов, например для железа, что обусловлено 80%-ным заполнением энергетической зоны, возникшей из З-уровня энергии изолированного атома железа.
• Почему электрические свойства полупроводников очень сильно зависят от наличия примесей?
• Поясните аналогию между локализованным состоянием электрона на примесном центре и состоянием электрона в атоме водорода. Почему радиус орбиты электрона, связанного с примесным центром, много больше воровского радиуса  ?
?
• Что является аналогом ионизации атома водорода для нейтрального донорного примесного центра в кристалле?
• Опишите физическую модель примесного акцепторного центра в полупроводниковом кристалле. Почему в рамках такой модели энергетические уровни локализованных электронных состояний лежат в запрещенной зоне вблизи потолка валентной зоны?
• Как объяснить ионизацию акцепторного центра, не прибегая к концепции положительных дырок, а рассматривая переход электрона из состояния в валентной зоне на примесный уровень?
• В чем состоит принципиальное различие причин изменения электропроводности металлов и полупроводников при изменении внешних условий?
• Поясните, почему в реальных образцах собственных полупроводников при очень низких температурах преобладает примесная проводимость.
• Почему при низкой концентрации носителей тока в полупроводниках их распределение по энергиям будет классическим, а при высокой концентрации функция распределения имеет вид ступеньки? Как изменится функция распределения при повышении температуры?
• Что такое эффект Холла? Каким образом он позволяет судить о знаке носителей заряда в исследуемом образце?
• Объясните, почему на противоположных боковых гранях образца в магнитном поле при пропускании тока скапливаются заряды противоположного знака, хотя электрический ток переносится зарядами одного знака.
| << Предыдущий параграф | Следующий параграф >> |
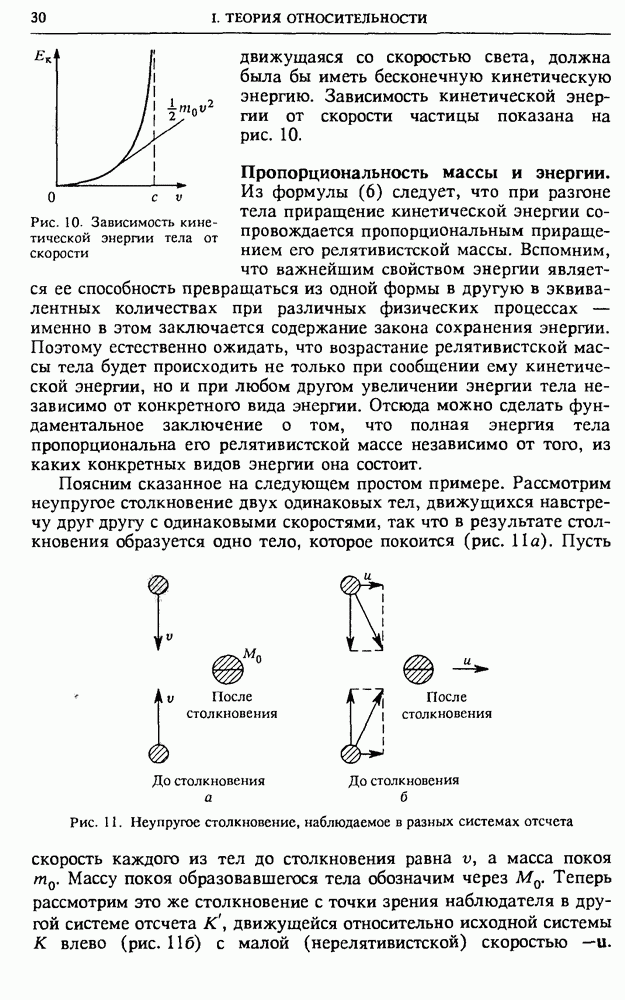
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
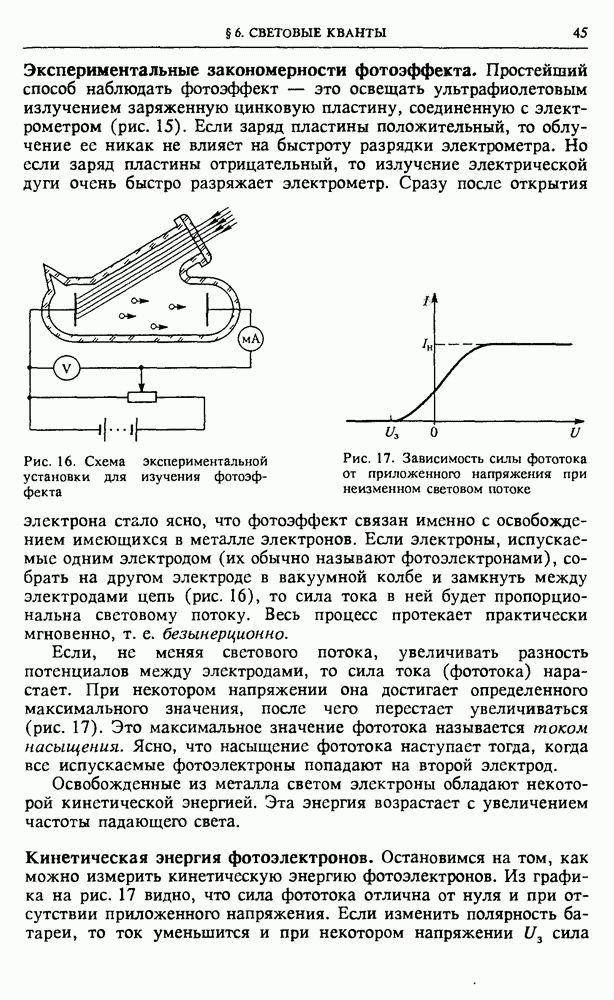
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
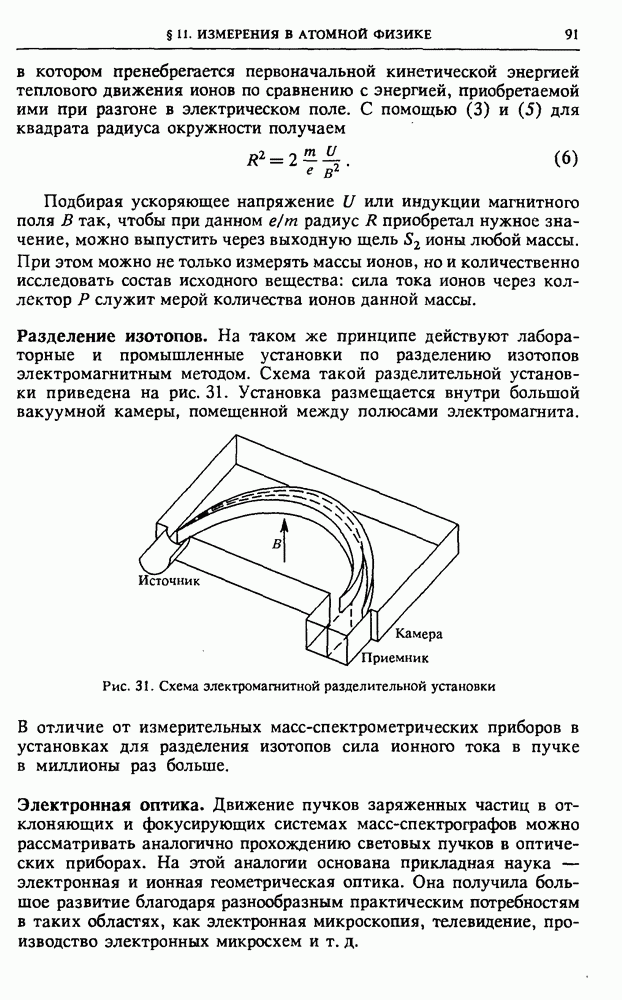
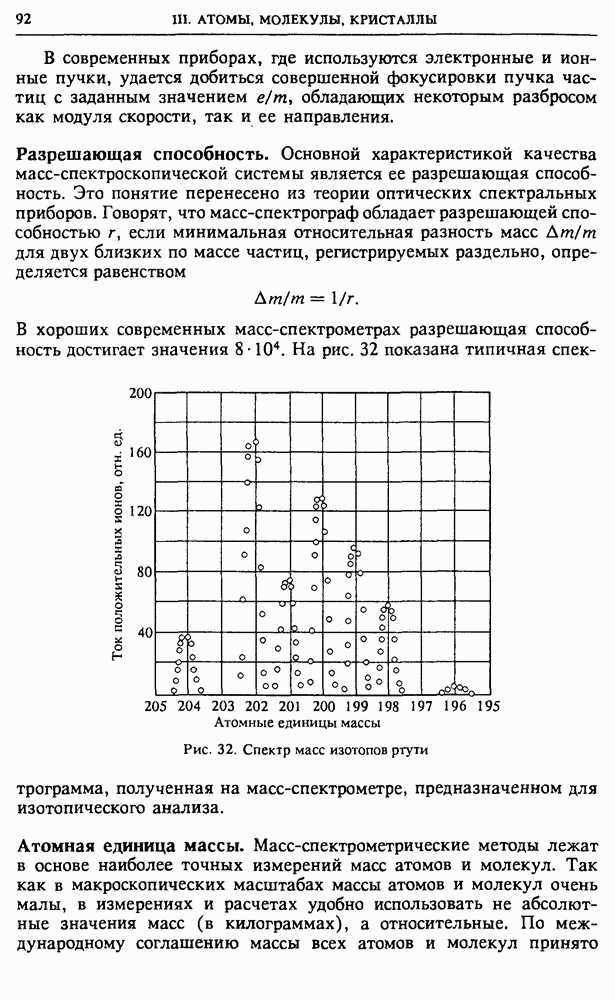
- § 11. Измерения в атомной физике
- § 12. Молекулы
- § 13. Кристаллы
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
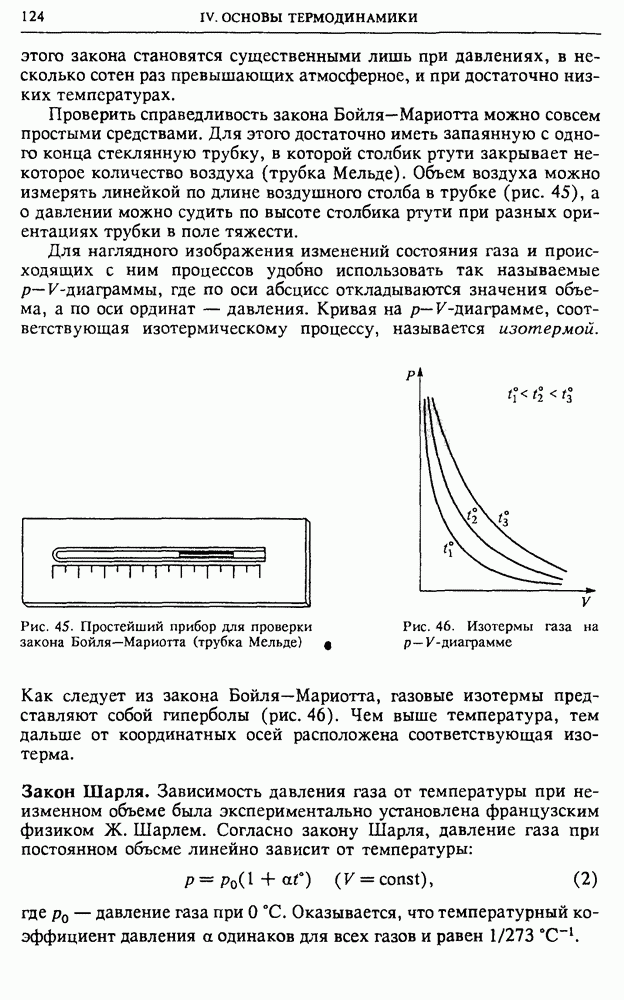
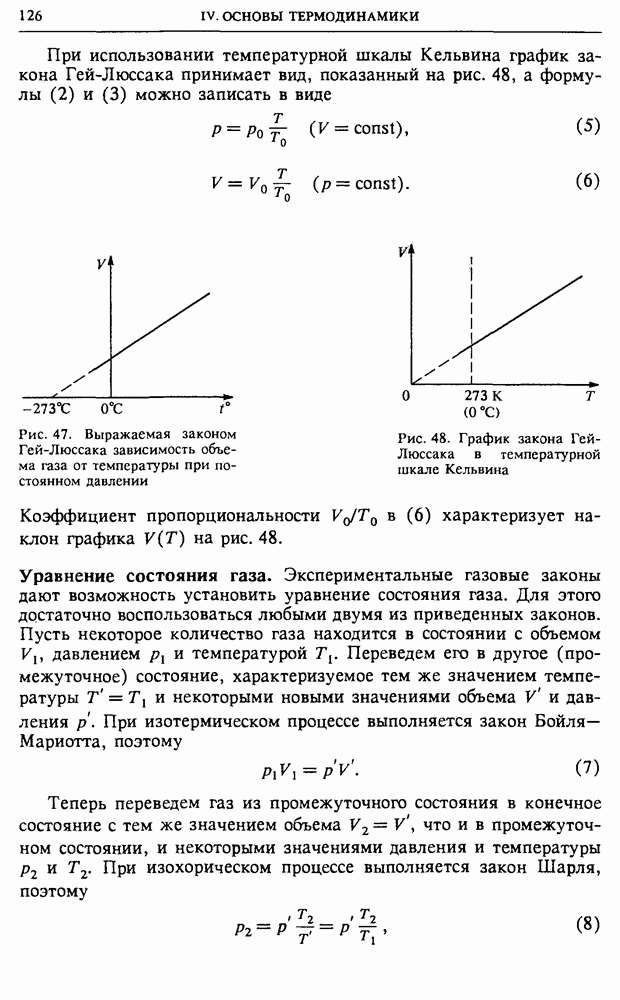
- § 15. Уравнение состояния газа
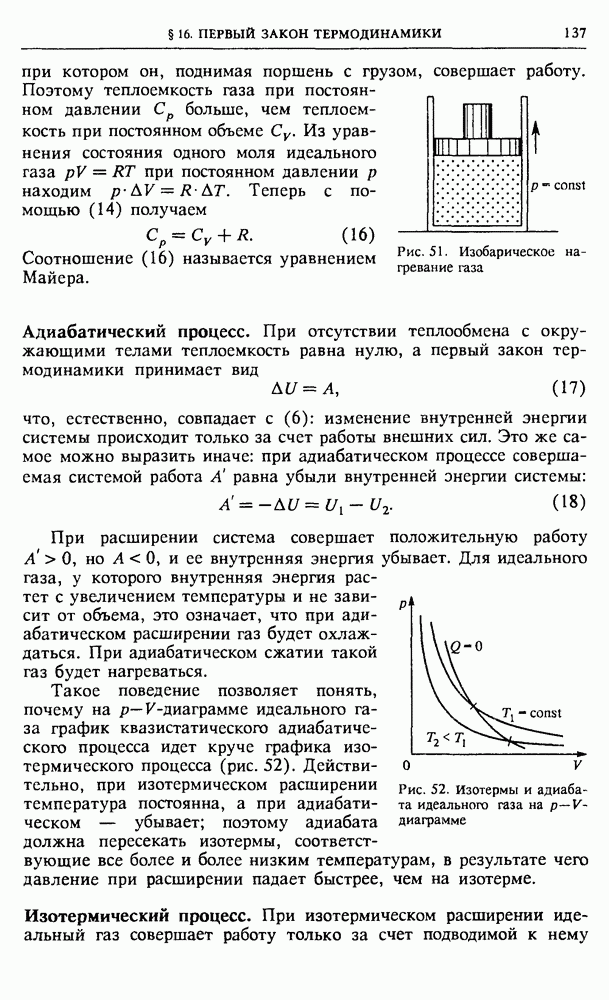
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
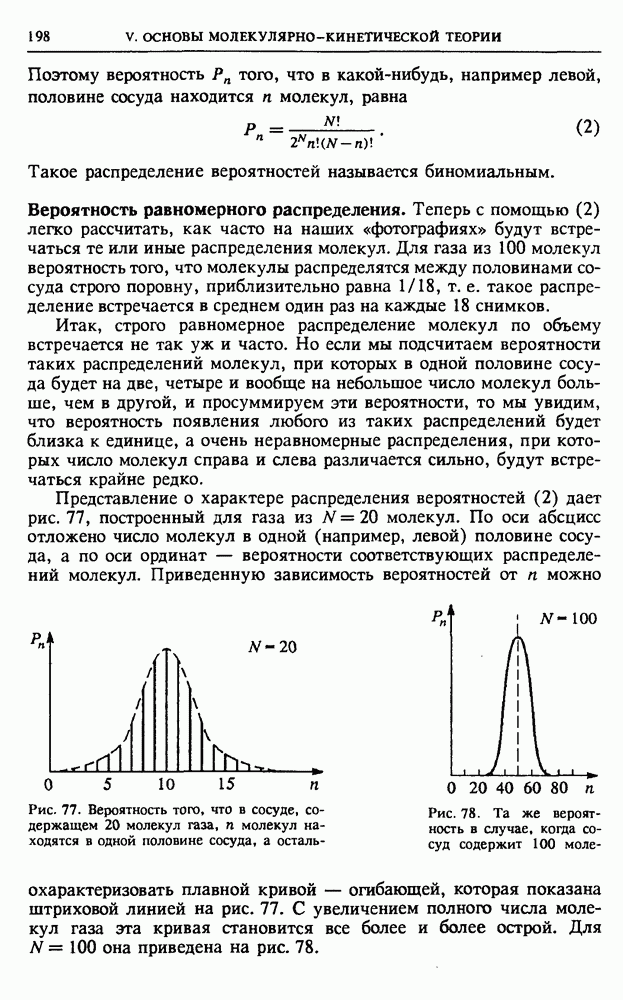
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
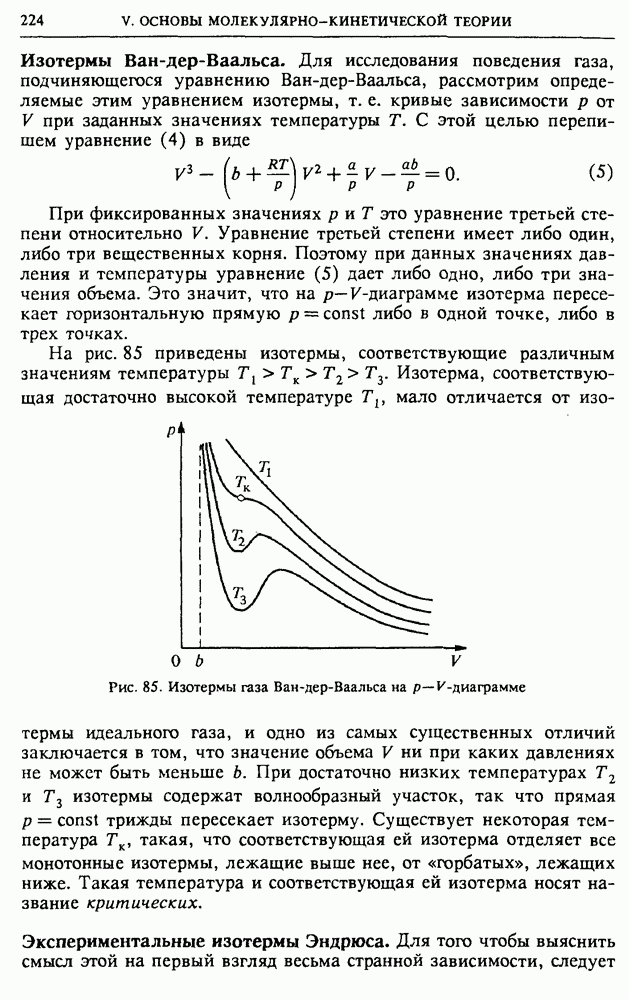
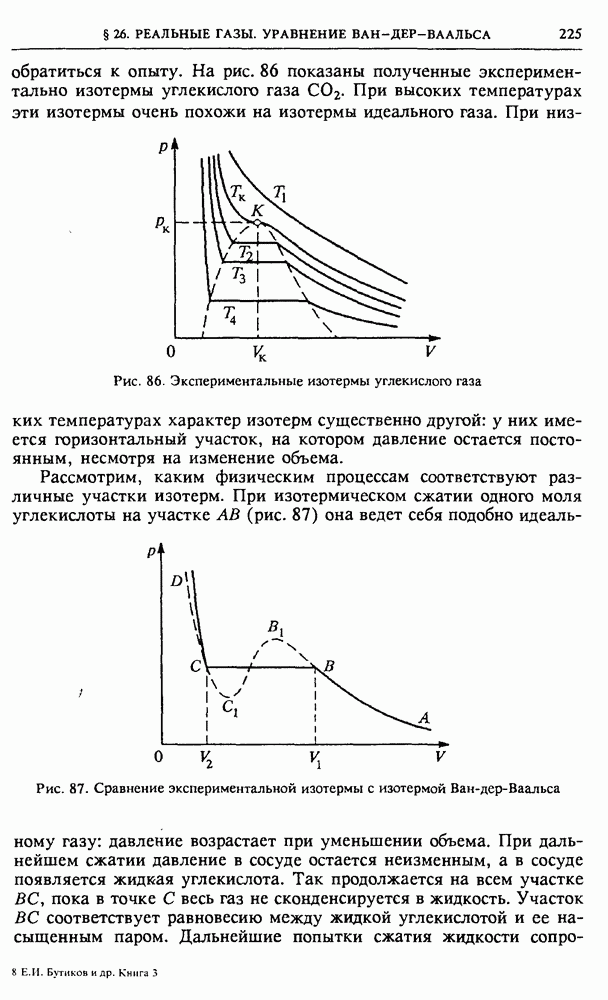
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
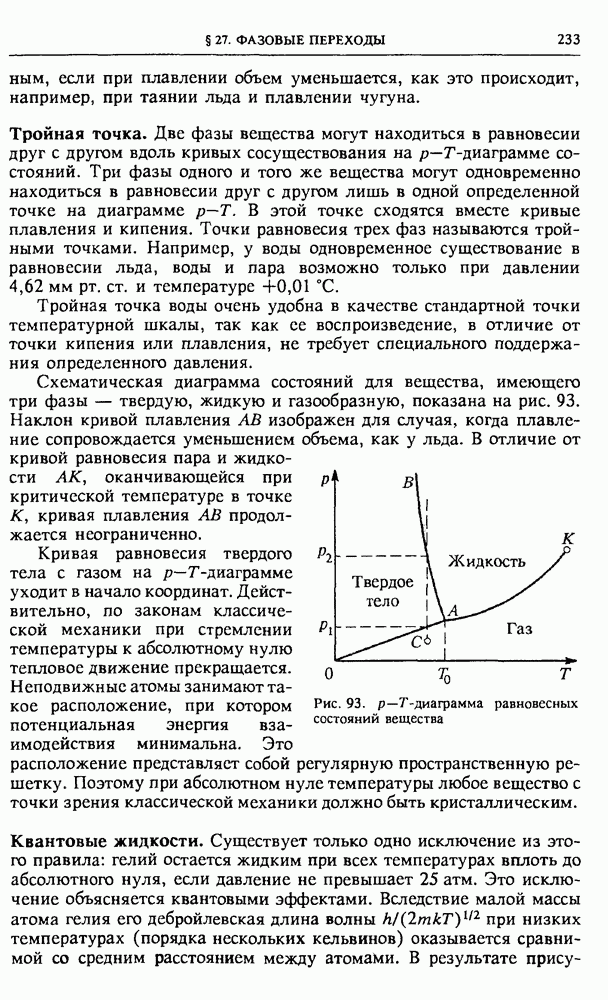
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
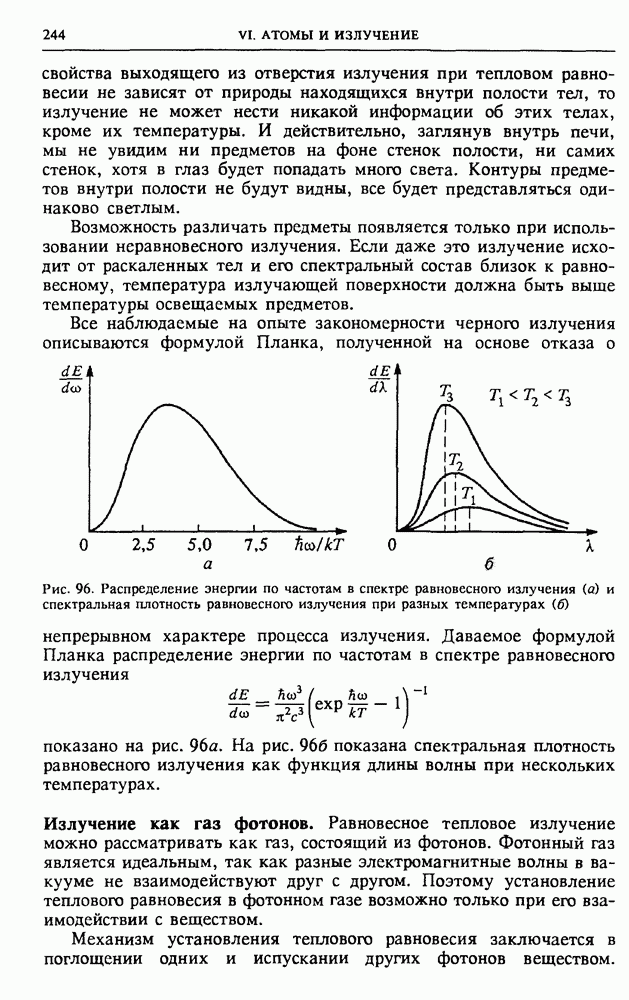
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
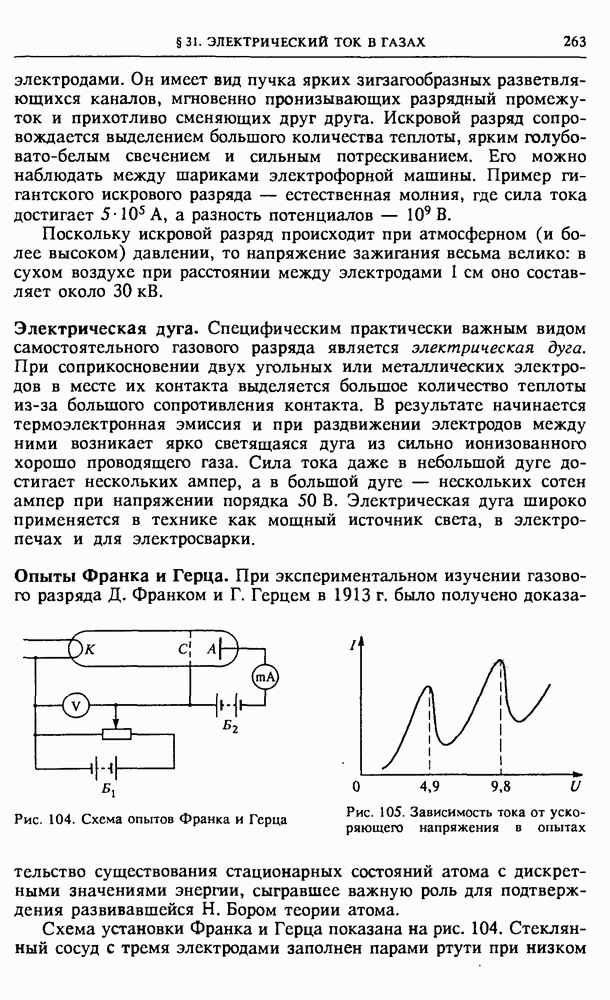
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы