| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Примеры релятивистского движения частиц
Формулы (1) предыдущего параграфа вместе с уравнениями (2), выражающими закон их изменения, служат основой для рассмотрения любых задач релятивистской механики. Вместо этих формул можно использовать две другие формулы, которые получаются из них исключением скорости 

и почленным делением формул (1) § 4:

Связь энергии и импульса. Соотношение (1) устанавливает связь между энергией и импульсом частицы в релятивистской механике. Энергия и импульс частицы зависят от системы отсчета. Но правая часть в (1) представляет собой релятивистский инвариант. Это значит, что и стоящая в левой части комбинация  изменяющихся при переходе от одной системы отсчета к другой энергии и импульса остается при таком переходе неизменной.
изменяющихся при переходе от одной системы отсчета к другой энергии и импульса остается при таком переходе неизменной.
Для ультрарелятивистских частиц, энергия Е которых много больше энергии покоя  соотношение (1) можно приближенно переписать в виде
соотношение (1) можно приближенно переписать в виде

Формула (2) выражает скорость релятивистской частицы через ее энергию и импульс. В отличие от формул (1) § 4 эти формулы не теряют смысла даже при  и поэтому пригодны для всех без исключения релятивистских объектов. Часто они оказываются более удобными и в практических приложениях.
и поэтому пригодны для всех без исключения релятивистских объектов. Часто они оказываются более удобными и в практических приложениях.
Движение под действием постоянной силы. В качестве первого примера рассмотрим движение первоначально покоившейся частицы с зарядом  и массой покоя
и массой покоя  в однородном электрическом поле напряженности Е. Действующая на частицу сила
в однородном электрическом поле напряженности Е. Действующая на частицу сила  постоянна и равна
постоянна и равна  . Поэтому из закона изменения импульса
. Поэтому из закона изменения импульса  немедленно следует, что
немедленно следует, что


Рис. 13. Скорость частицы при движении в однородном электрическом поле
Подставляя это выражение для импульса частицы в формулу (1), получим

Теперь с помощью (2) находим скорость частицы  спустя промежуток времени
спустя промежуток времени  после начала движения:
после начала движения:

Если  т. е. электрическое поле слабое или мало время движения, то в подкоренном выражении в (6) можно пренебречь вторым слагаемым, и для скорости получается обычное нерелятивистское выражение:
т. е. электрическое поле слабое или мало время движения, то в подкоренном выражении в (6) можно пренебречь вторым слагаемым, и для скорости получается обычное нерелятивистское выражение:

Если  то под корнем в (6) можно пренебречь единицей по сравнению со вторым слагаемым. Видно, что при этом скорость
то под корнем в (6) можно пренебречь единицей по сравнению со вторым слагаемым. Видно, что при этом скорость  стремится к с. На рис. 13 показана зависимость скорости
стремится к с. На рис. 13 показана зависимость скорости  от времени.
от времени.
Движение в магнитном поле. Перейдем к рассмотрению движения заряженной частицы в однородном магнитном поле. Поскольку действующая на частицу со стороны магнитного поля сила Лоренца перпендикулярна скорости частицы, то скорость не меняется по модулю и, следовательно, не меняется и релятивистская масса частицы  . Поэтому закон изменения импульса частицы запишется в виде
. Поэтому закон изменения импульса частицы запишется в виде

Если скорость  перпендикулярна вектору индукции магнитного поля В, то частица движется по окружности и ее ускорение равно
перпендикулярна вектору индукции магнитного поля В, то частица движется по окружности и ее ускорение равно  где
где  — радиус окружности. В этом случае уравнение (8) дает
— радиус окружности. В этом случае уравнение (8) дает

Для угловой скорости обращения  , связанной с линейной скоростью
, связанной с линейной скоростью  обычным соотношением
обычным соотношением  с помощью (9) находим
с помощью (9) находим

Выражение (10) имеет такой же вид, как и нерелятивистская формула для угловой скорости обращения в магнитном поле, только в знаменателе стоит релятивистская масса частицы  связанная с ее массой покоя
связанная с ее массой покоя  соотношением
соотношением

Ускоритель на встречных пучках. В качестве третьего примера рассмотрим ускоритель заряженных частиц на встречных пучках. Выясним, в чем преимущество таких ускорителей по сравнению с обычными ускорителями с неподвижной мишенью, и установим соответствие между кинетической энергией частицы  в обычном ускорителе и эквивалентной энергией
в обычном ускорителе и эквивалентной энергией  в ускорителе со встречными пучками.
в ускорителе со встречными пучками.
Одной из важнейших характеристик ускорителя является та доля кинетической энергии разогнанных элементарных частиц, которая может быть использована для реакции образования новых частиц. В обычных ускорителях, когда частица-мишень неподвижна, требование сохранения импульса исключает возможность превращения всей кинетической энергии частицы-снаряда в энергетический эквивалент массы покоя новых частиц, образующихся при столкновении. В самом деле, до столкновения суммарный импульс снаряда и мишени отличен от нуля. Такой же суммарный импульс должен быть и после
столкновения. Поэтому образовавшиеся в результате столкновения частицы не могут находиться в покое и, следовательно, часть начальной кинетической энергии снаряда переходит в кинетическую энергию частиц после столкновения.
Однако если сталкивающиеся частицы с равными массами летят навстречу друг другу с одинаковыми скоростями, то в результате неупругого удара вся кинетическая энергия налетающих частиц может быть использована для рождения новых частиц: поскольку начальный импульс системы равен нулю, то ничто не запрещает покоиться образовавшимся в результате столкновения частицам.
Оценим вначале «выигрыш» в энергии для простого случая столкновения одинаковых нерелятивистских частиц. Используя закон сохранения импульса, легко убедиться, что в этом случае при неподвижной мишени для реакции образования новых частиц может быть использована только половина кинетической энергии налетающей частицы  Если же столкнутся движущиеся навстречу друг другу частицы с кинетическими энергиями
Если же столкнутся движущиеся навстречу друг другу частицы с кинетическими энергиями  то для реакции может быть использована вся их кинетическая энергия
то для реакции может быть использована вся их кинетическая энергия  Таким образом, используя ускоритель, способный разогнать частицы до кинетической энергии
Таким образом, используя ускоритель, способный разогнать частицы до кинетической энергии  мы можем с помощью накопительных колец повысить эффективность использования кинетической энергии в четыре раза.
мы можем с помощью накопительных колец повысить эффективность использования кинетической энергии в четыре раза.
Идея устройства накопительных колец показана на рис. 14. Пучок частиц из ускорителя с помощью быстродействующего магнита-переключателя А разделяется на два пучка, каждый из которых с помощью системы отклоняющих магнитов А и Б направляется в свое кольцо, где обращается по орбите благодаря удерживающему магнитному полю, перпендикулярному плоскости рисунка. На общем участке  происходят столкновения движущихся навстречу друг другу частиц.
происходят столкновения движущихся навстречу друг другу частиц.

Рис. 14 Накопительные кольца
Итак, в нерелятивистском случае неупругого столкновения частиц одинаковой массы, одна из которых покоится, т. е. при использовании неподвижной мишени, только половина первоначальной энергии может перейти в энергию покоя рождающихся частиц. А как обстоит дело в случае релятивистских частиц, с которыми имеет дело физика высоких энергий? Оказывается, что для неподвижной мишени дело обстоит еще хуже. Чтобы убедиться в этом, придется тщательно рассмотреть законы сохранения энергии и импульса при столкновении релятивистских частиц.
Рассмотрим неупругое столкновение релятивистской частицы с массой покоя  с такой же покоящейся частицей.
с такой же покоящейся частицей.
Будем искать энергию  которая может быть использована для образования новых частиц в этом случае. Обозначим через
которая может быть использована для образования новых частиц в этом случае. Обозначим через  полную массу покоя системы после столкновения. Тогда
полную массу покоя системы после столкновения. Тогда  есть не что иное, как увеличение энергии покоя частиц, которое произошло в рассматриваемом столкновении:
есть не что иное, как увеличение энергии покоя частиц, которое произошло в рассматриваемом столкновении:

Найдем теперь  — массу покоя частиц системы после столкновения. Применим к столкновению законы сохранения энергии и импульса. Из формулы (1) выразим квадрат импульса любой частицы
— массу покоя частиц системы после столкновения. Применим к столкновению законы сохранения энергии и импульса. Из формулы (1) выразим квадрат импульса любой частицы  через ее полную энергию Е:
через ее полную энергию Е:

Полная энергия релятивистской частицы Е есть сумма энергии покоя частицы и ее кинетической энергии:

Энергия, которой характеризуют ускорители, — это кинетическая энергия разогнанных частиц  Учитывая, что до столкновения одна из частиц покоилась
Учитывая, что до столкновения одна из частиц покоилась  запишем квадрат импульса всей системы до удара
запишем квадрат импульса всей системы до удара  равный квадрату импульса налетающей частицы
равный квадрату импульса налетающей частицы  в виде
в виде

Согласно закону сохранения энергии полная энергия системы после столкновения Е такая же, как и до столкновения, т. е. равна сумме энергий покоя обеих частиц и кинетической энергии налетающей частицы:

Запишем теперь квадрат импульса системы после столкновения с помощью (12) и (15):

Полный импульс системы до удара (14) и после удара (16) обозначены одной и той же буквой Р, так как полный импульс системы сохраняется. Приравнивая правые части равенств (14) и (16), после простых преобразований находим 

Теперь для  в (11) получим
в (11) получим

Легко видеть, что для нерелятивистской частицы, кинетическая энергия которой много меньше энергии покоя  выражение (18) дает результат, полученный ранее элементарным путем:
выражение (18) дает результат, полученный ранее элементарным путем:  Для этого достаточно воспользоваться приближенной формулой
Для этого достаточно воспользоваться приближенной формулой 

В противоположном ультрарелятивистском случае, когда кинетическая энергия частицы много больше энергии покоя:  в формуле (18) можно пренебречь единицами по сравнению с
в формуле (18) можно пренебречь единицами по сравнению с  Тогда выражение (18) принимает вид
Тогда выражение (18) принимает вид

Если, например, мы хотим иметь  ГэВ при столкновении протонов (энергия покоя протона
ГэВ при столкновении протонов (энергия покоя протона  ГэВ), то с помощью формулы (19) убеждаемся, что необходим ускоритель, разгоняющий протоны до энергии
ГэВ), то с помощью формулы (19) убеждаемся, что необходим ускоритель, разгоняющий протоны до энергии  ГэВ. Таким образом, в рассматриваемом примере может быть использована только десятая часть кинетической энергии протона (а не половина, как было бы в нерелятивистском случае).
ГэВ. Таким образом, в рассматриваемом примере может быть использована только десятая часть кинетической энергии протона (а не половина, как было бы в нерелятивистском случае).
Итак, из-за релятивистских эффектов доля кинетической энергии разогнанных частиц, которая может быть использована для реакции, у ускорителей с неподвижной мишенью падает с ростом энергии. В ускорителе же на встречных пучках и в релятивистском случае вся кинетическая энергия сталкивающихся частиц может перейти в энергию покоя рождающихся частиц.
Интересно получить соотношение, связывающее кинетические энергии частиц в ускорителе обычного типа  и в ускорителе на встречных пучках
и в ускорителе на встречных пучках  при которых получается одна и та же энергия
при которых получается одна и та же энергия  способная превратиться в энергию покоя рождающихся частиц. В ускорителе на встречных пучках
способная превратиться в энергию покоя рождающихся частиц. В ускорителе на встречных пучках  ускорителе с неподвижной мишенью
ускорителе с неподвижной мишенью  определяется формулой (18). Подставляя в нее
определяется формулой (18). Подставляя в нее  находим
находим

В ультрарелятивистском случае, когда  эта формула принимает вид
эта формула принимает вид

Из приведенных формул видно, что выигрыш при использовании ускорителей на встречных пучках особенно велик для легких частиц, например электронов, для которых  МэВ. Так, для установки со встречными пучками, ускоряющей электроны до энергии
МэВ. Так, для установки со встречными пучками, ускоряющей электроны до энергии  МэВ, энергия
МэВ, энергия  эквивалентного ускорителя с неподвижной мишенью составляет, согласно формуле (21), примерно 70 ГэВ, т. е. в 520 раз больше!
эквивалентного ускорителя с неподвижной мишенью составляет, согласно формуле (21), примерно 70 ГэВ, т. е. в 520 раз больше!
• При каких условиях энергия частицы пропорциональна импульсу?
• Покажите, что при ускорении частицы под действием постоянной силы ее скорость стремится к конечному пределу.
• Почему в ускорителях, разгоняющих частицы до высоких энергий, период обращения в магнитном поле не остается постоянным?
• В чем заключается преимущество использования встречных пучков в физике высоких энергий?
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
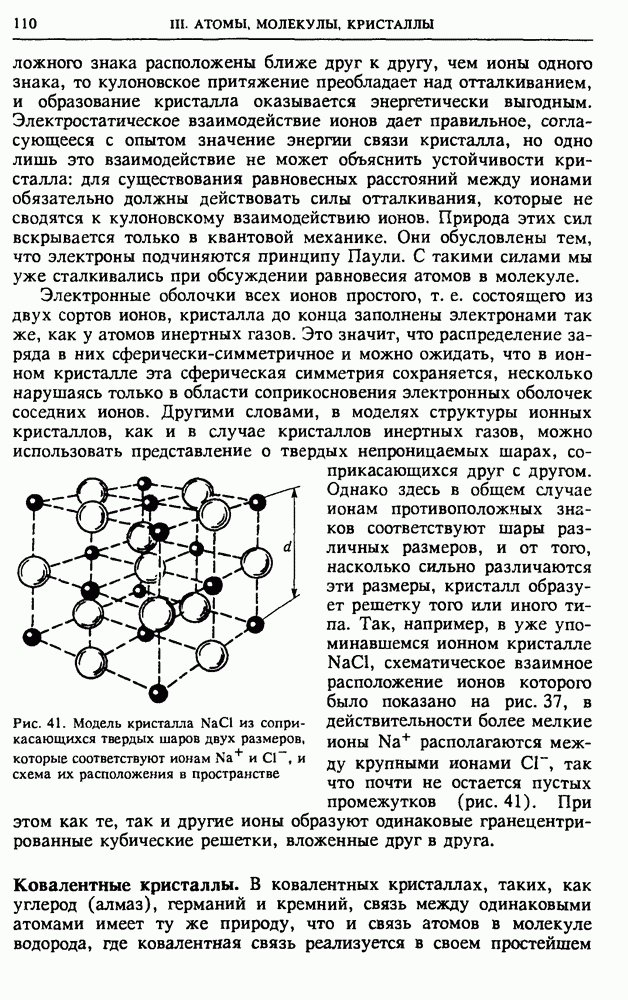
- § 13. Кристаллы
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
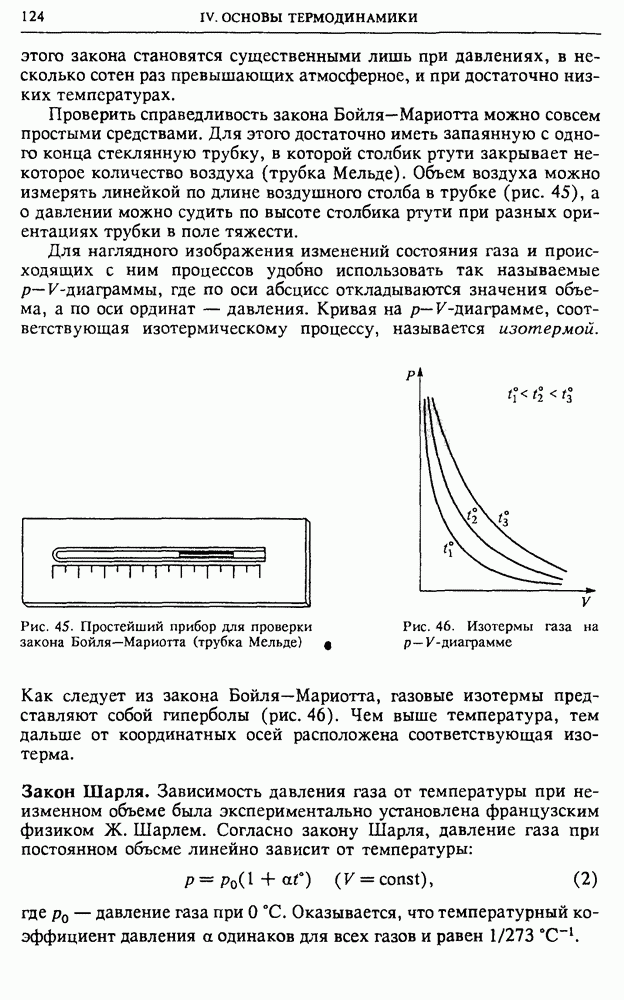
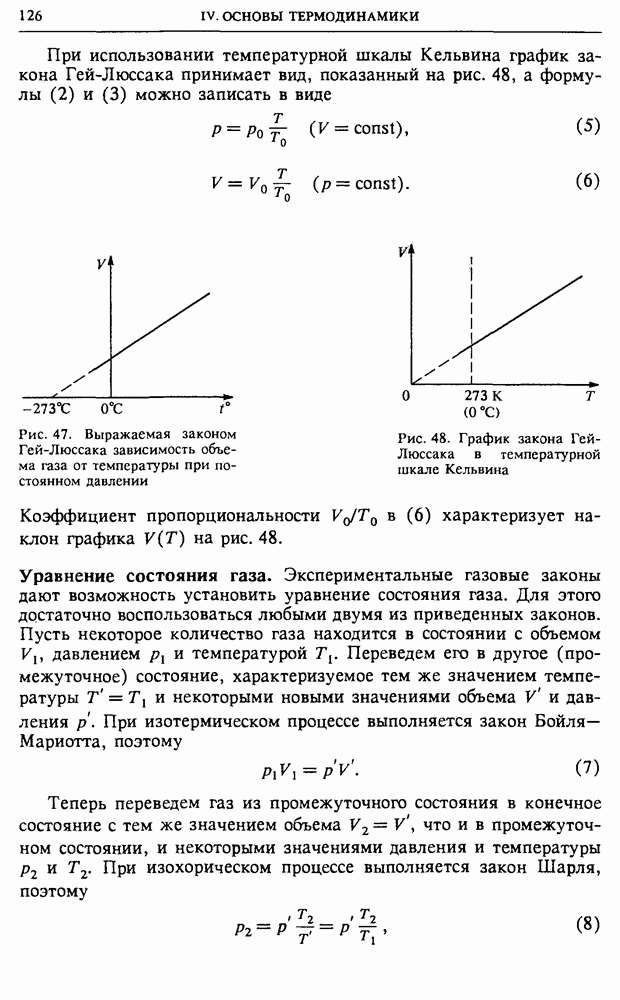
- § 15. Уравнение состояния газа
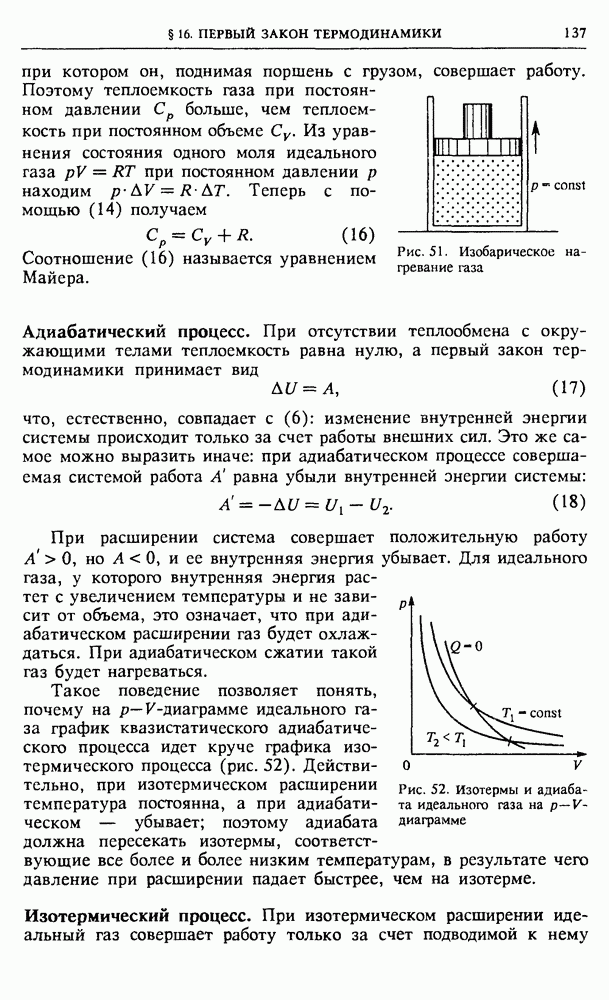
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы