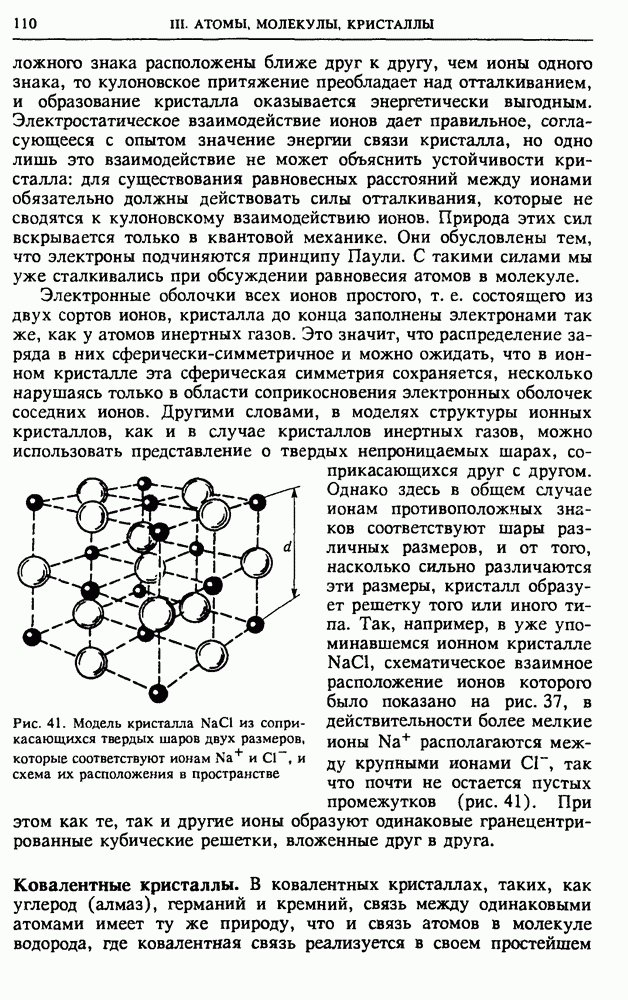
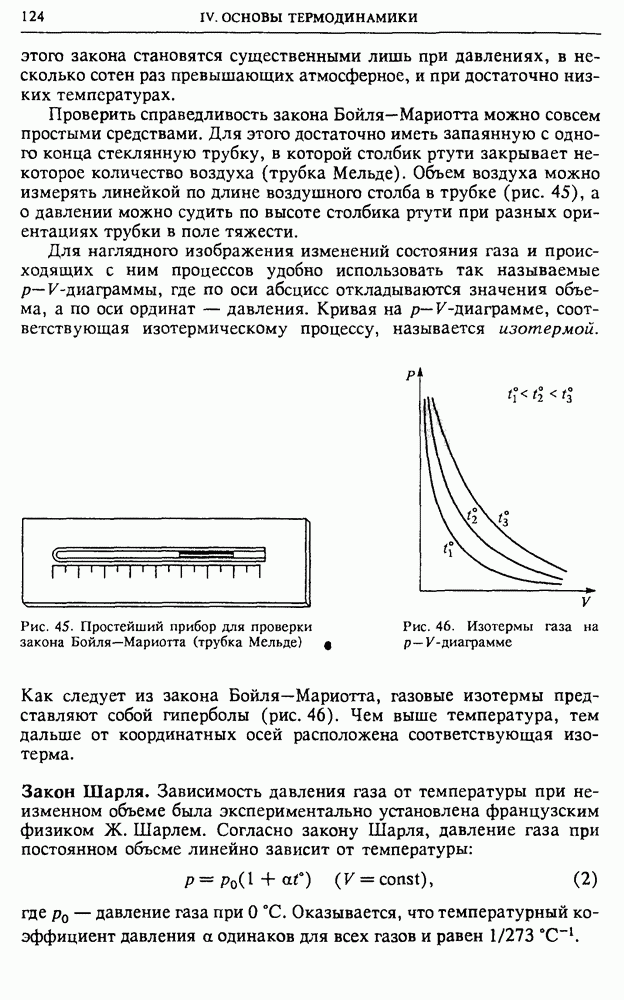
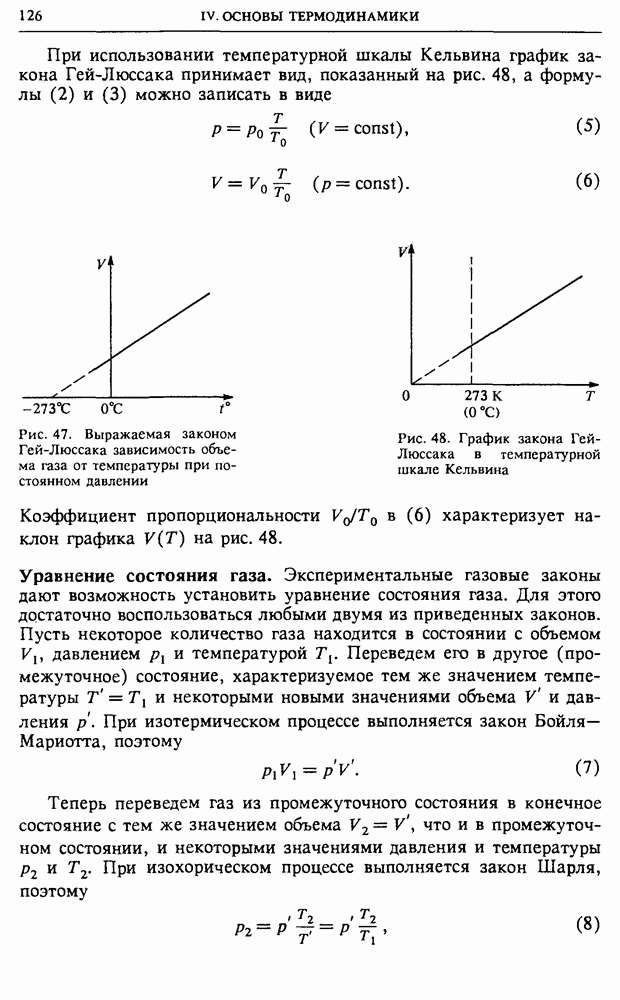
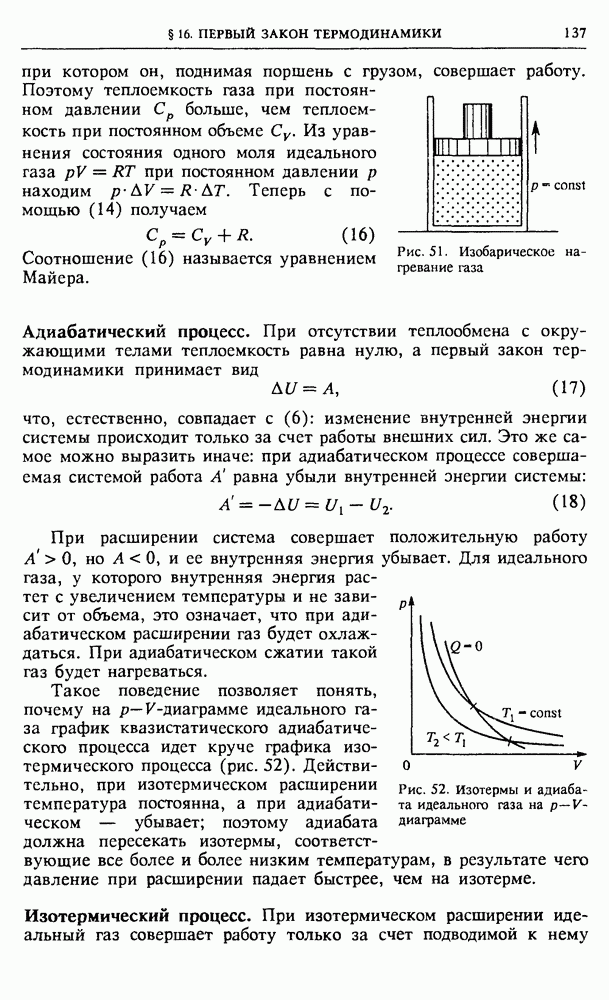
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
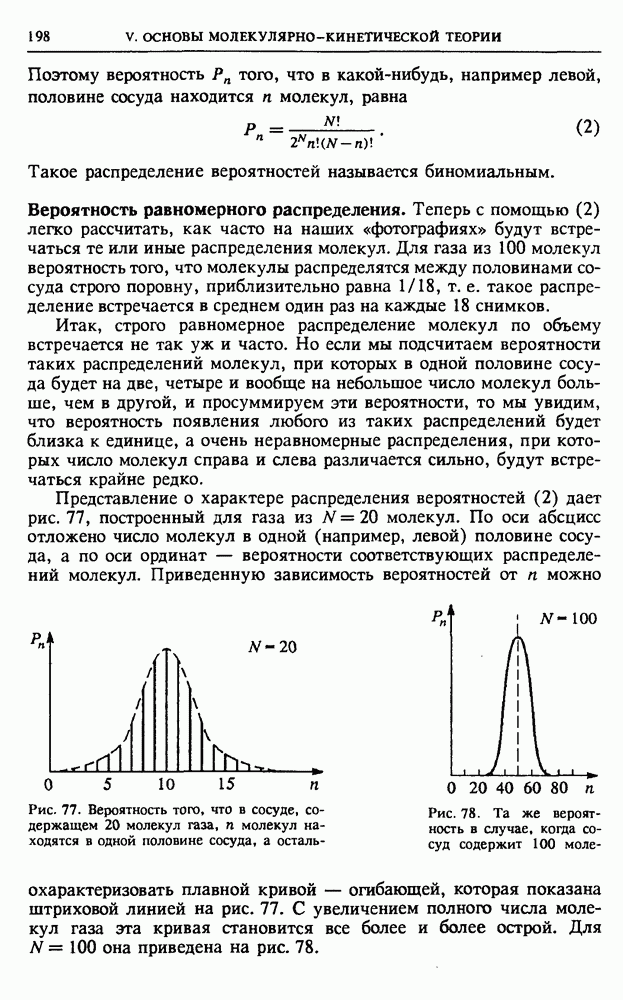
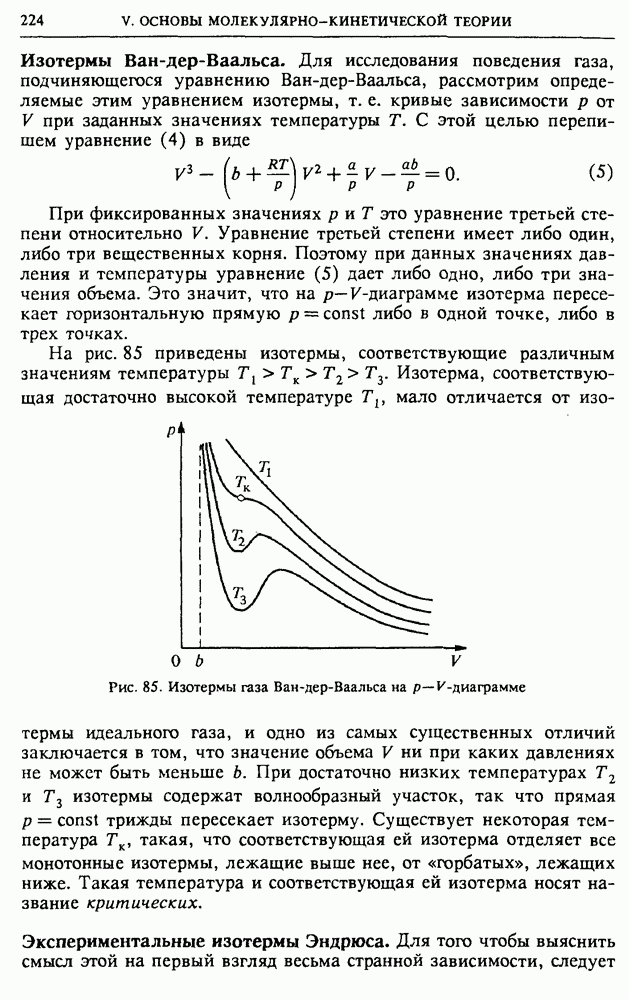
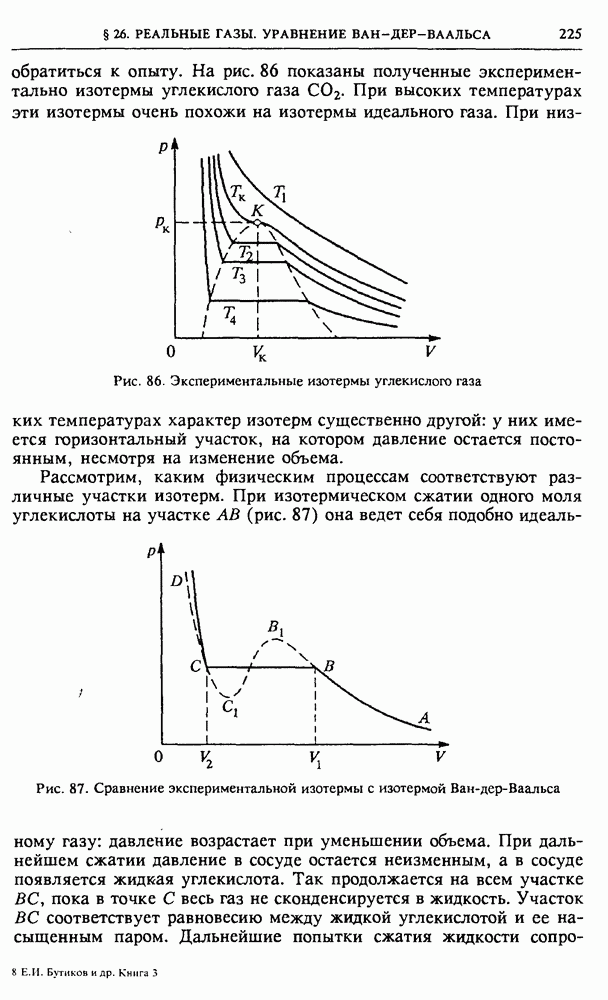
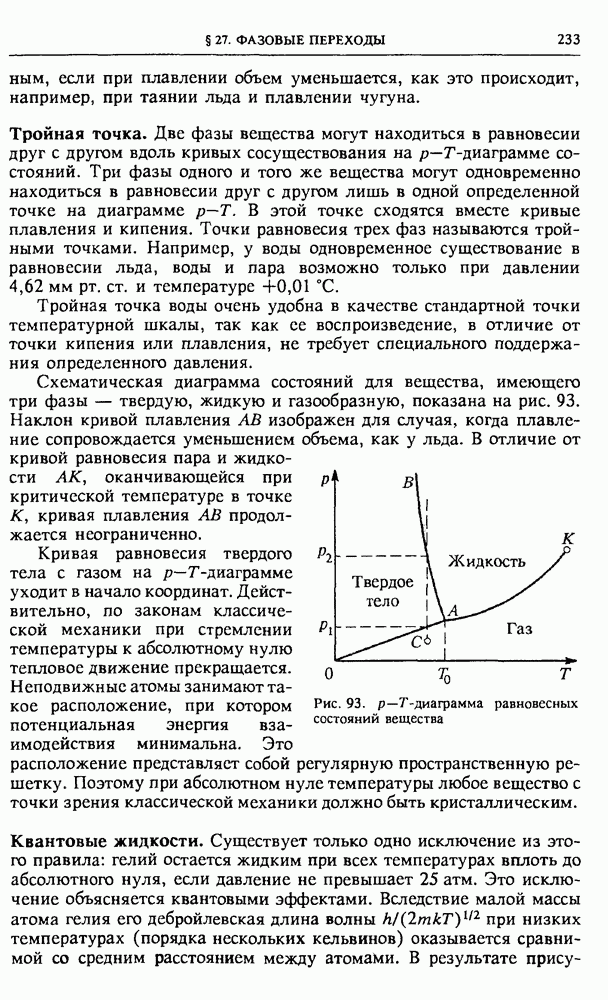
V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
§ 20. Экспериментальные основания статистической механики
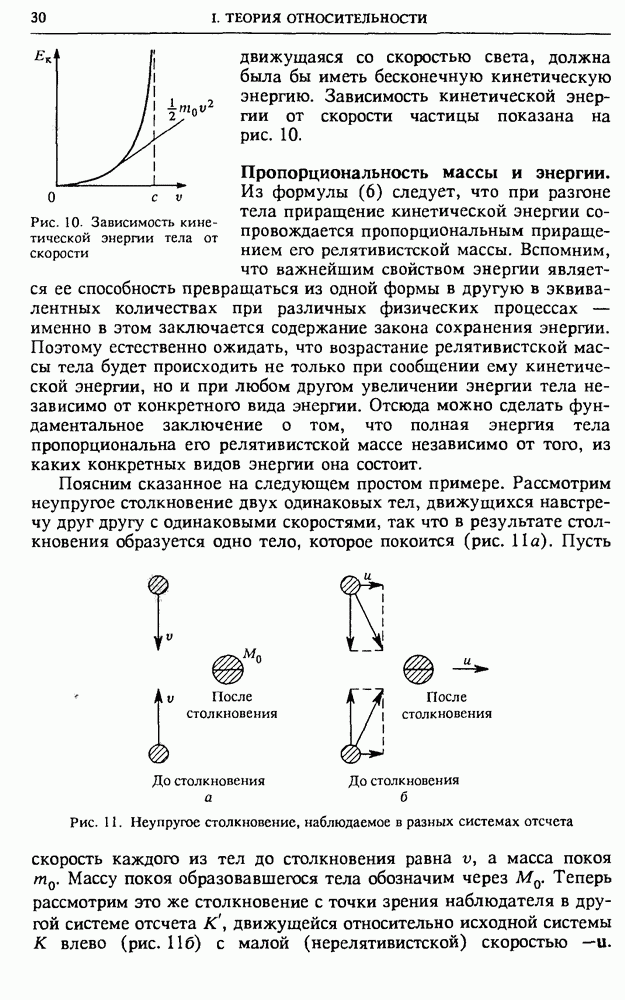
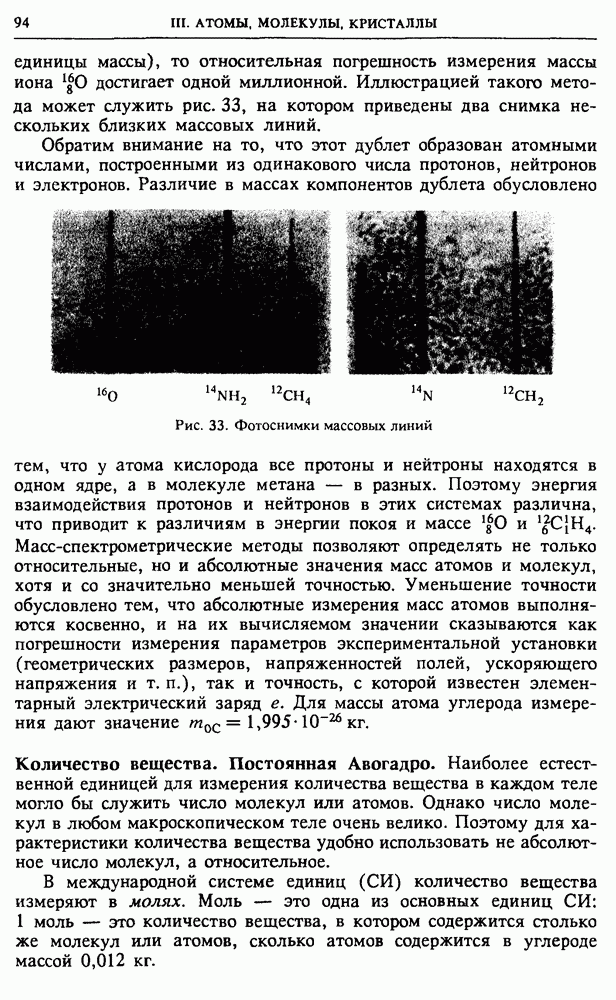
Основное положение молекулярно-кинетической теории строения вещества, вытекающее из опытных фактов, заключается в том, что атомы и молекулы, из которых состоят все макроскопические тела, находятся в состоянии непрерывного хаотического теплового движения.
Тепловое движение молекул. Наиболее убедительным опытным фактом, наглядно подтверждающим хаотический характер теплового движения и зависимость интенсивности этого движения от температуры, является броуновское движение.
Впервые это явление наблюдал английский ботаник Р. Броун в 1827 г., рассматривая в микроскоп взвешенные в воде крошечные сферические частички — споры плауна. Броуновское движение можно наблюдать и в газе. Его совершают, например, взвешенные в воздухе мелкие частицы пыли или дыма. Молекулярно-кинетическая теория броуновского движения была создана А. Эйнштейном только в 1905 г. В настоящее время термин «броуновское движение» используется в более широком смысле. Броуновским движением называют, в частности, дрожание стрелок чувствительных приборов, которое происходит из-за теплового движения молекул в самом приборе и в окружающей среде.
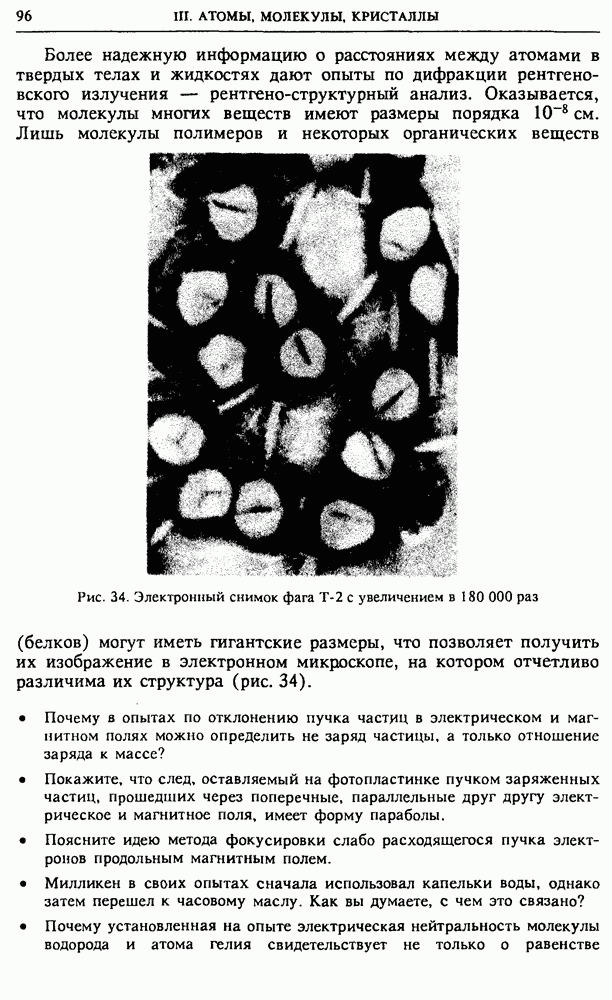
Наблюдая в микроскоп за движением взвешенных в жидкости мелких частиц, можно обнаружить, что каждая частица совершает хаотическое движение. Представление о характере блужданий частицы можно получить, если фиксировать ее положение в поле зрения измерительного микроскопа через равные промежутки времени. Соединив последовательные положения частицы прямыми, мы получим ломаную линию, подобную изображенной на рис. 65. Направления соседних участков ломаной линии составляют всевозможные углы друг с другом, так что не удается подметить никакой закономерности в изменении направления ломаной линии. Чем короче промежутки времени, через которые фиксируется положение частицы, тем более изломанной будет выглядеть «траектория» частицы:
точки А, В, С, ... фиксируют положение частицы через 30 секунд, а точки  соединенные штриховой линией, фиксируют ее положение через каждые 5 секунд.
соединенные штриховой линией, фиксируют ее положение через каждые 5 секунд.
Наблюдение броуновского движения. Если наблюдать за движением сразу нескольких взвешенных в жидкости частиц, то можно заметить, что они движутся то в одну сторону, то в противоположные, то под углом друг к другу. Отсюда можно сделать вывод, что наблюдаемое броуновское движение не связано с перемещением потоков жидкости, так как в этом случае соседние частицы всегда перемещались бы вместе.
На опыте же в условиях термодинамического равновесия никакой согласованности в движении соседних частиц не наблюдается, движутся они совершенно независимо друг от друга.

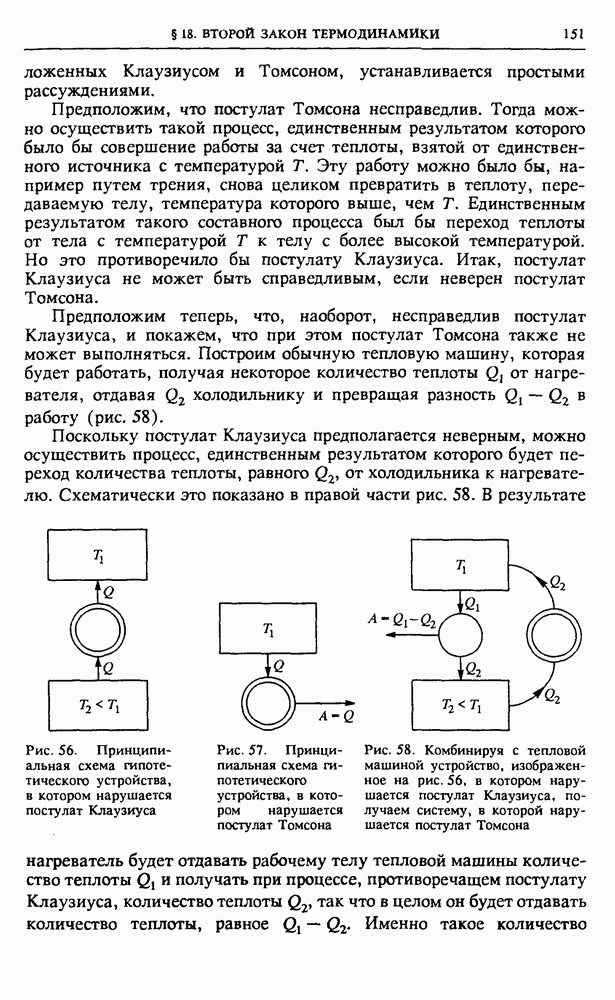
Рис. 65. Броуновское движение
Изменяя температуру, при которой проводится опыт, можно заметить, что с увеличением температуры интенсивность броуновского движения растет, с понижением температуры оно замирает.
Такой характер движения позволяет предположить, что броуновская частица движется под действием ударов, получаемых от молекул жидкости, в которой она находится. Если при этом считать, что тепловое движение молекул жидкости является хаотическим, то можно объяснить все наблюдаемые на опыте закономерности броуновского движения.
Закономерности броуновского движения. На первый взгляд могло бы показаться, что совершенно хаотический, беспорядочный характер ударов отдельных молекул должен был бы приводить к тому, что броуновская частица, масса которой во много раз больше массы молекулы, вообще не должна была бы заметно перемещаться. В самом деле, действие ударов, полученных броуновской частицей с одной стороны, должно полностью компенсироваться ударами с противоположной стороны. В такой ситуации, казалось бы, броуновская частица может только «дрожать» на месте. Ошибка такого рассуждения заключается в том, что случайный процесс подменяется, по существу, регулярным чередованием воздействий с противоположных сторон. Но такое чередование уже не является случайным процессом, а обладает высокой степенью упорядоченности. Степень упорядоченности такого чередования не отличается от степени упорядоченности процесса, в котором все
испытываемые частицей толчки происходят в одном направлении. Если, например, результат одного толчка характеризуется некоторым расстоянием  то результат последовательности
то результат последовательности  упорядоченных толчков пропорционален величине
упорядоченных толчков пропорционален величине  Если же последовательность этих
Если же последовательность этих  толчков носит случайный характер, то их результат пропорционален
толчков носит случайный характер, то их результат пропорционален  Покажем это.
Покажем это.
Будем с помощью измерительного микроскопа определять расстояние, на которое броуновская частица удаляется от начала координат за время  многократно повторяя этот опыт. Всякий раз мы будем получать разные значения этого расстояния, однако в большинстве опытов будут получаться близкие друг к другу значения и лишь изредка заметно отличающиеся от остальных. Можно ввести среднее расстояние, на которое уходит частица от начала координат. Направления перемещений в отдельных опытах могут быть совершенно различными, поскольку все направления равновероятны.
многократно повторяя этот опыт. Всякий раз мы будем получать разные значения этого расстояния, однако в большинстве опытов будут получаться близкие друг к другу значения и лишь изредка заметно отличающиеся от остальных. Можно ввести среднее расстояние, на которое уходит частица от начала координат. Направления перемещений в отдельных опытах могут быть совершенно различными, поскольку все направления равновероятны.
Зависимость среднего перемещения от времени. Задача состоит в том, чтобы найти зависимость от времени среднего расстояния, которое будем обозначать 
Разделим интересующее нас время наблюдения  на большое число равных малых промежутков
на большое число равных малых промежутков  таких, что в течение каждого промежутка частица испытывает огромное число ударов со стороны молекул жидкости. По существу, такое рассуждение означает многократное повторение опыта по измерению среднего расстояния, пройденного частицей за время
таких, что в течение каждого промежутка частица испытывает огромное число ударов со стороны молекул жидкости. По существу, такое рассуждение означает многократное повторение опыта по измерению среднего расстояния, пройденного частицей за время  причем каждый раз мы совмещаем начало координат с положением частицы в конце предыдущего промежутка времени
причем каждый раз мы совмещаем начало координат с положением частицы в конце предыдущего промежутка времени  Другими словами, это такой же опыт, как и рассмотренный выше, только осуществляемый за промежуток времени
Другими словами, это такой же опыт, как и рассмотренный выше, только осуществляемый за промежуток времени  а не
а не  Поскольку и за промежуток
Поскольку и за промежуток  частица испытывает огромное число ударов, все приведенные выше рассуждения остаются в силе: направление перемещения за каждый «шаг»
частица испытывает огромное число ударов, все приведенные выше рассуждения остаются в силе: направление перемещения за каждый «шаг»  совершенно произвольно и никак не связано с направлением перемещений в другие промежутки, а расстояние, проходимое частицей за
совершенно произвольно и никак не связано с направлением перемещений в другие промежутки, а расстояние, проходимое частицей за  будет примерно одинаковым для большинства промежутков.
будет примерно одинаковым для большинства промежутков.
Для простоты будем считать это расстояние одинаковым для всех шагов и обозначим его через 
Пусть в результате  таких последовательных шагов частица оказалась в точке с радиусом-вектором
таких последовательных шагов частица оказалась в точке с радиусом-вектором  Тогда после очередного шага она попала в точку
Тогда после очередного шага она попала в точку

где  — вектор перемещения за
— вектор перемещения за  шаг, имеющий произвольное направление и определенную длину
шаг, имеющий произвольное направление и определенную длину  Расстояние частицы от начала координат после
Расстояние частицы от начала координат после  шага равно
шага равно

Здесь  угол между векторами и
угол между векторами и  Найти среднее значение правой части этого выражения затруднительно, ибо усреднять нужно квадратный корень, а в общем случае среднее значение функции не равно этой функции от среднего значения аргумента:
Найти среднее значение правой части этого выражения затруднительно, ибо усреднять нужно квадратный корень, а в общем случае среднее значение функции не равно этой функции от среднего значения аргумента:  Легко заметить, что если возвести (1) или (2) в квадрат:
Легко заметить, что если возвести (1) или (2) в квадрат:

то среднее значение квадрата смещения может быть легко найдено. Поэтому будем использовать для характеристики удаления броуновской частицы от начала координат не  Усредняя левую и правую части (3) и учитывая, что угол с равной вероятностью принимает любые значения от 0 до
Усредняя левую и правую части (3) и учитывая, что угол с равной вероятностью принимает любые значения от 0 до  получаем
получаем

Используя метод математической индукции, на основе соотношения (4) легко показать, что

Таким образом, среднее значение квадрата смещения пропорционально числу шагов, а поскольку шаги совершаются за одинаковые промежутки времени  то
то

Это, конечно, не означает, что среднее смещение пропорционально времени. Броуновское движение частицы таково, что средний квадрат смещения растет пропорционально времени. Другими словами, квадратный корень из  растет со временем пропорционально
растет со временем пропорционально  Эта величина, т. е.
Эта величина, т. е.  называемая средним квадратичным значением
называемая средним квадратичным значением  не равна среднему значению расстояния
не равна среднему значению расстояния  частицы от начала координат спустя промежуток времени
частицы от начала координат спустя промежуток времени  которое мы хотели определить. Однако можно показать, что эти величины отличаются только постоянным множителем. Поэтому среднее расстояние броуновской частицы от начала координат также пропорционально
которое мы хотели определить. Однако можно показать, что эти величины отличаются только постоянным множителем. Поэтому среднее расстояние броуновской частицы от начала координат также пропорционально 

Совершенно очевидно, что коэффициенты а и  в формулах (6) и (7) зависят от интенсивности теплового движения молекул жидкости, удары которых приводят к броуновскому движению взвешенной частицы, т. е. в конечном счете от температуры.
в формулах (6) и (7) зависят от интенсивности теплового движения молекул жидкости, удары которых приводят к броуновскому движению взвешенной частицы, т. е. в конечном счете от температуры.
Эксперимент и статистическая механика. Изучение броуновского движения сыграло большую роль в развитии молекулярно-кинетической теории строения вещества. Именно броуновское движение не только принесло неопровержимое доказательство реальности атомов и молекул, но и позволило впервые подсчитать количество молекул
в макроскопическом объеме вещества, т. е. определить значение постоянной Авогадро:  . Таким образом, было окончательно установлено, что тепловая форма движения материи обусловлена хаотическим движением атомов или молекул, из которых состоят макроскопические тела. Последнюю точку в этом вопросе поставили опыты французского физика
. Таким образом, было окончательно установлено, что тепловая форма движения материи обусловлена хаотическим движением атомов или молекул, из которых состоят макроскопические тела. Последнюю точку в этом вопросе поставили опыты французского физика  Перрена, выполненные в начале XX века. Тем самым была подведена надежная экспериментальная база под статистическую механику, которая изучает свойства макроскопических систем исходя из определенных модельных представлений о внутренней структуре вещества.
Перрена, выполненные в начале XX века. Тем самым была подведена надежная экспериментальная база под статистическую механику, которая изучает свойства макроскопических систем исходя из определенных модельных представлений о внутренней структуре вещества.
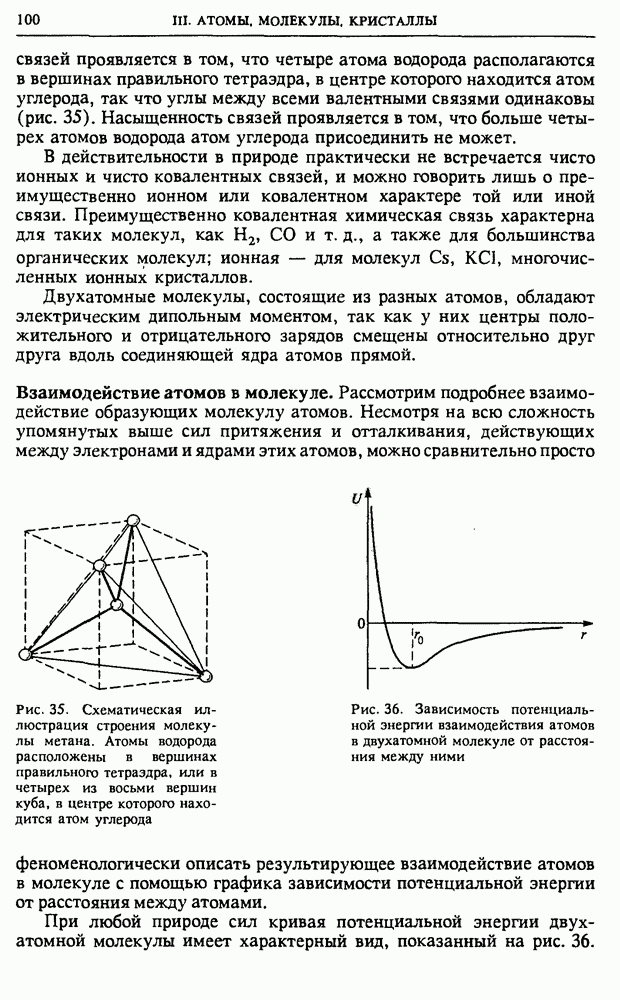
Постановка задачи в статистической механике. Задачей статистической механики является установление законов поведения макроскопических систем, состоящих из огромного числа частиц, на основе известных динамических законов поведения отдельных частиц. Другими словами, статистическая механика устанавливает связь между экспериментально измеряемыми макроскопическими величинами, характеризующими систему в целом, такими, как давление, объем, температура, напряженность электрического поля и т. д., и микроскопическими характеристиками системы, такими, как массы и заряды составляющих систему частиц, их координаты и импульсы и т. д.
Поясним сказанное на примере. Простейшей системой, состоящей из большого числа частиц, является газ, занимающий некоторый объем. С точки зрения механики состояние такой системы (т. е. ее микросостояние) определяется заданием положений и скоростей всех молекул газа, число которых в макроскопическом объеме огромно. Например, всего  воздуха при нормальных условиях содержит
воздуха при нормальных условиях содержит  молекул. Из-за движения молекул механическое состояние непрерывно изменяется. Однако опыт показывает, что при неизменных внешних условиях любая макроскопическая система рано или поздно приходит в стационарное состояние, при котором, несмотря на изменение механического состояния, такие макроскопические параметры, как, например, температура, плотность, давление, характеризующие макросостояние системы, остаются неизменными. Для изолированной макроскопической системы это будет состояние теплового равновесия.
молекул. Из-за движения молекул механическое состояние непрерывно изменяется. Однако опыт показывает, что при неизменных внешних условиях любая макроскопическая система рано или поздно приходит в стационарное состояние, при котором, несмотря на изменение механического состояния, такие макроскопические параметры, как, например, температура, плотность, давление, характеризующие макросостояние системы, остаются неизменными. Для изолированной макроскопической системы это будет состояние теплового равновесия.
Таким образом, определение состояния системы в статистической механике является гораздо менее детализированным, чем в механике, так как опирается лишь на небольшое число макроскопических параметров, измеряемых на опыте. В большинстве случаев такое сокращенное описание системы является вполне достаточным, ибо нас, как правило, совершенно не интересует детальная информация о движении отдельных молекул.
Но значения макроскопических параметров, разумеется, зависят от движения молекул, и задача статистической механики — выразить свойства системы в целом через характеристики отдельных молекул, т. е. перекинуть мост между макро- и микроскопическими
описаниями системы. При этом требуется установить связь макроскопических параметров системы со средними значениями микроскопических величин и дать способ вычисления этих средних значений на основе законов движения отдельных молекул.
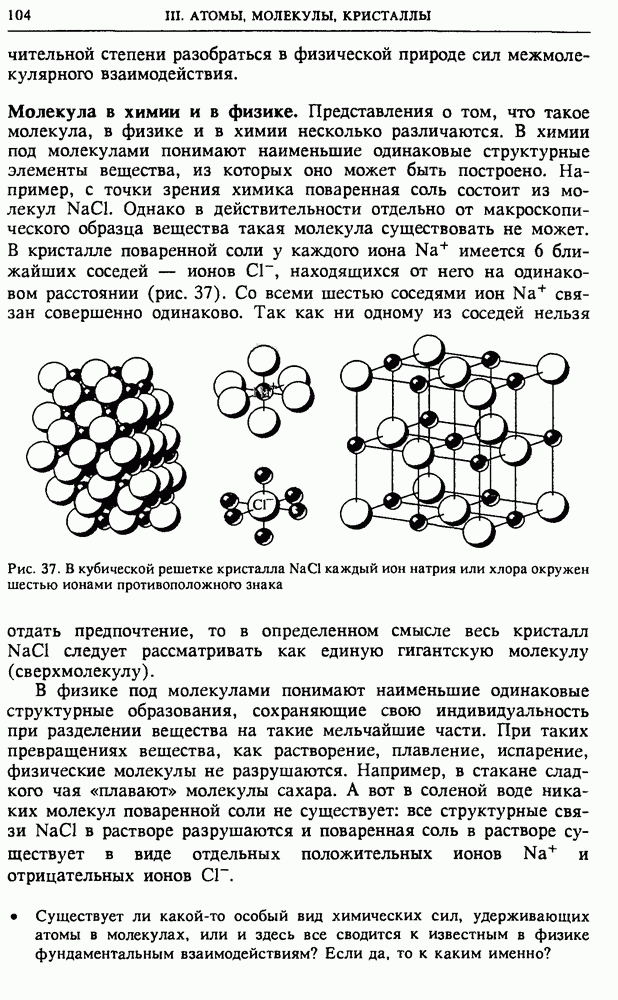
Статистическая механика и термодинамика. Напомним, что в отличие от молекулярно-кинетической теории термодинамический подход не опирается ни на какие модельные представления об атомно-молекулярной структуре вещества. Основные понятия термодинамики вводятся на основе физического эксперимента, и поэтому она оперирует только макроскопическими величинами: давлением, температурой, объемом и т. п. Термодинамический подход отличается большой общностью и простотой. Он дает возможность решать многие конкретные задачи, не требуя никаких сведений о свойствах атомов или молекул.
Недостатком термодинамического метода можно считать то, что при его использовании остается невыявленной связь между наблюдаемым явлением и обусловливающим это явление поведением молекул. Если мы, например, термодинамическим методом установим, что металлический стержень при нагревании должен удлиняться, а растянутый резиновый жгут — сокращаться, то мы не сможем объяснить, какие особенности строения вещества приводят к такому различию в поведении при нагревании. Если же это нас не удовлетворяет и мы хотим понять, почему так происходит, то мы должны обратиться к статистической механике, так как в рамках термодинамики невозможно вскрыть глубокий физический смысл макроскопических параметров и их связь с микроскопическими параметрами.
Статистическая механика и термодинамика долгое время развивались независимо, ибо термодинамика основывалась на экспериментальных фактах, в то время как в основе статистической механики лежали гипотезы об атомно-молекулярном строении вещества и кинетической природе теплоты, достоверность которых вызывала сомнение до тех пор, пока эти гипотезы не были подтверждены экспериментально. С тех пор отпала необходимость в резком разграничении между термодинамикой и молекулярно-кинетической теорией, и в настоящее время они фактически слились в единую науку — статистическую термодинамику.
Действительно, как мы увидим, наиболее полные представления о свойствах систем большого числа частиц дает совместное использование термодинамики и статистической механики.
• Объясните, почему броуновская частица не «топчется» на месте, а систематически смещается из начального положения, несмотря на то, что молекулы окружающей среды в равной мере бомбардируют ее со всех сторон.
• Почему среднее значение  равно нулю, если аргумент
равно нулю, если аргумент  принимает с равной вероятностью любые значения от 0 до
принимает с равной вероятностью любые значения от 0 до 
• Докажите, используя метод математической индукции, что средний квадрат смещения броуновской частицы за  шагов пропорционален числу шагов
шагов пропорционален числу шагов 
Как зависит среднее смещение броуновской частицы от числа шагов  от времени наблюдения?
от времени наблюдения?
• Почему коэффициенты пропорциональности а и (3 в формулах (6) и (7) зависят от температуры?
• В чем состоит принципиальное отличие подхода к изучению макроскопических систем в термодинамике и в статистической механике?
• Как в статистической механике макроскопические параметры системы связаны с микроскопическими характеристиками используемых физических моделей строения вещества?
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
- § 13. Кристаллы
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
- § 15. Уравнение состояния газа
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы