| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
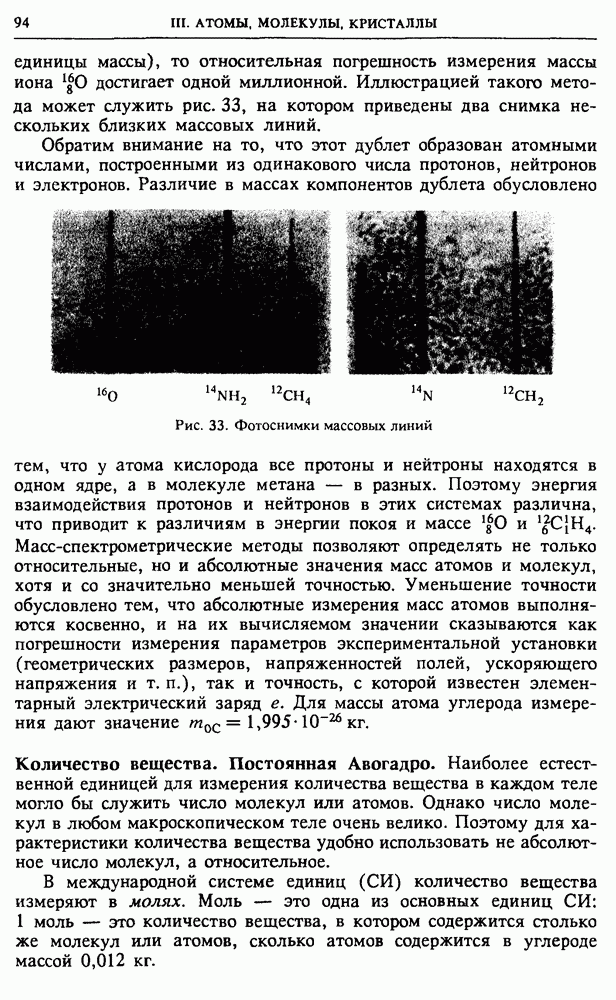
§ 23. Тепловое равновесие в статистической механике
Тепловое равновесие — это всегда динамическое равновесие. Тепловое движение атомов или молекул, из которых состоит макроскопическая система, никогда не прекращается. Поэтому макроскопические величины, характеризующие систему в целом, строго говоря, никогда не остаются постоянными, а испытывают малые беспорядочные колебания вблизи некоторых средних значений. Такие хаотические отклонения от средних значений тех или иных величин, происходящие в течение малых промежутков времени, называются флуктуациями. Относительная величина флуктуаций тем больше, чем меньше размеры изучаемой системы.
Флуктуации макроскопических параметров. Яркий пример флуктуаций — это дрожание зеркальца чувствительного гальванометра. Макроскопическая система, состоящая из подвижной катушки гальванометра, подвешенной на упругой кварцевой нити, в состоянии механического равновесия была бы совершенно неподвижной, если бы не тепловое движение. Удары молекул воздуха, совершающих
тепловое движение, приводят к тому, что угол поворота зеркальца испытывает хаотические колебания вблизи положения механического равновесия. Фактически это то же броуновское движение, которое отличается от рассмотренного выше движения взвешенной в жидкости частицы только тем, что здесь рассматривается не поступательное, а вращательное движение вблизи устойчивого, а не безразличного положения равновесия. Интенсивность такого движения зависит от температуры, оно принципиально неустранимо и ставит предел чувствительности измерительной аппаратуры.
Пространственное распределение молекул. Основные закономерности флуктуаций можно подметить, рассматривая пространственное распределение молекул идеального газа внутри сосуда в состоянии теплового равновесия. В среднем газ равномерно заполняет весь сосуд, т. е. концентрация молекул всюду одинакова. Разделим мысленно сосуд на две равные части. Пусть число молекул слева равно  справа —
справа —  Сумма
Сумма  есть полное число молекул в сосуде.
есть полное число молекул в сосуде.
В равновесии в среднем  но так как это равновесие динамическое, то в каждый момент времени вследствие хаотического движения это верно лишь приближенно, потому что молекулы непрерывно переходят из одной половины сосуда в другую и обратно. В принципе ничто не мешает им вообще в какой-то момент времени собраться в одной половине сосуда. Однако такое событие будет крайне маловероятным.
но так как это равновесие динамическое, то в каждый момент времени вследствие хаотического движения это верно лишь приближенно, потому что молекулы непрерывно переходят из одной половины сосуда в другую и обратно. В принципе ничто не мешает им вообще в какой-то момент времени собраться в одной половине сосуда. Однако такое событие будет крайне маловероятным.
Чтобы убедиться в этом, рассмотрим, какими способами молекулы могут распределяться между половинами сосуда. Одну молекулу можно разместить в сосуде двумя способами — либо в левой, либо в правой его половине. Исходя из симметрии, естественно предположить, что вероятность найти молекулу в какой-то одной половине сосуда равна 1/2, если, конечно, сосуд разделен на строго равные части. Две молекулы можно распределить в сосуде четырьмя (22) способами, ибо для каждого из двух способов распределения одной молекулы существует два способа распределения другой. Для трех молекул число способов распределения равно восьми (23), так как для каждого из четырех возможных вариантов распределения первых двух молекул есть две возможности распределения третьей молекулы, и т. д. В случае  молекул число способов распределения равно
молекул число способов распределения равно 
Вероятности распределений молекул по половинам сосуда. Будем считать, что вероятность нахождения любой наугад взятой молекулы в определенной половине сосуда не зависит от того, где в этот момент находятся все остальные молекулы. Это верно для идеального газа, молекулы которого не взаимодействуют между собой и имеют пренебрежимо малые размеры, так что их собственный
объем значительно меньше объема сосуда. В этом случае каждый из  способов распределения
способов распределения  молекул в сосуде имеет одну и ту же вероятность, равную (1/2). Разъясним это подробнее.
молекул в сосуде имеет одну и ту же вероятность, равную (1/2). Разъясним это подробнее.
Молекулы газа находятся в тепловом движении, и их расположение в сосуде непрерывно изменяется. Предположим, что мы можем делать мгновенные «фотографии» положения молекул в сосуде. На каждой такой «фотографии» мы увидим один из мыслимых способов распределения молекул. Распределения на любых двух снимках считаются одинаковыми, если в какой-либо половине сосуда, например левой, на обоих снимках находятся одни и те же молекулы. Утверждение о равной вероятности всех  распределений означает, что какое-либо распределение будет встречаться на снимках не чаще и не реже других, в среднем один раз в каждой серии, содержащей
распределений означает, что какое-либо распределение будет встречаться на снимках не чаще и не реже других, в среднем один раз в каждой серии, содержащей  «фотографий».
«фотографий».
Разместить все  молекул в одной половине сосуда можно только одним способом. Поэтому вероятность того, что весь газ самопроизвольно соберется в одной половине сосуда, равна (1/2). При больших
молекул в одной половине сосуда можно только одним способом. Поэтому вероятность того, что весь газ самопроизвольно соберется в одной половине сосуда, равна (1/2). При больших  это очень малая величина. Например, для газа, содержащего всего 100 молекул, вероятность такого события равна
это очень малая величина. Например, для газа, содержащего всего 100 молекул, вероятность такого события равна  . В среднем только на одном из 1030 снимков мы бы увидели, что одна из половин сосуда пуста. (Чтобы представить себе, насколько велико это число, вспомним, что, по преданию, изобретатель шахматной игры потребовал в награду «всего»
. В среднем только на одном из 1030 снимков мы бы увидели, что одна из половин сосуда пуста. (Чтобы представить себе, насколько велико это число, вспомним, что, по преданию, изобретатель шахматной игры потребовал в награду «всего»  зерен пшеницы. Это оказалось больше, чем количество зерен, которое может уместиться в амбаре высотой
зерен пшеницы. Это оказалось больше, чем количество зерен, которое может уместиться в амбаре высотой  и шириной
и шириной  протянувшемся от Земли до Солнца.) И это для газа, состоящего всего из ста молекул! А для одного моля газа, где число молекул составляет
протянувшемся от Земли до Солнца.) И это для газа, состоящего всего из ста молекул! А для одного моля газа, где число молекул составляет  , вероятность всем молекулам оказаться в одной половине сосуда настолько мала, что просто невозможно найти для нее подходящее сравнение в мире образов, доступных человеческому воображению.
, вероятность всем молекулам оказаться в одной половине сосуда настолько мала, что просто невозможно найти для нее подходящее сравнение в мире образов, доступных человеческому воображению.
Разместить  молекул в сосуде так, чтобы в определенной половине сосуда была только одна молекула, а в другой остальные
молекул в сосуде так, чтобы в определенной половине сосуда была только одна молекула, а в другой остальные  можно, очевидно,
можно, очевидно,  способами, поскольку в первой половине сосуда может при этом находиться любая из
способами, поскольку в первой половине сосуда может при этом находиться любая из  молекул. Вероятность такого распределения молекул равна
молекул. Вероятность такого распределения молекул равна 
Подсчитаем теперь вероятность того, что в определенной половине сосуда находится заданное число  молекул. Эта вероятность равна отношению числа способов распределения, при которых в выбранной половине сосуда находятся любые
молекул. Эта вероятность равна отношению числа способов распределения, при которых в выбранной половине сосуда находятся любые  молекул, к 2 — полному числу возможных распределений.
молекул, к 2 — полному числу возможных распределений.
Число таких распределений, очевидно, равно числу способов, которыми можно выбрать  молекул из совокупности
молекул из совокупности  молекул, т. е. числу сочетаний из
молекул, т. е. числу сочетаний из  по
по  Это число сочетаний равно
Это число сочетаний равно

Поэтому вероятность  того, что в какой-нибудь, например левой, половине сосуда находится
того, что в какой-нибудь, например левой, половине сосуда находится  молекул, равна
молекул, равна

Такое распределение вероятностей называется биномиальным.
Вероятность равномерного распределения. Теперь с помощью (2) легко рассчитать, как часто на наших «фотографиях» будут встречаться те или иные распределения молекул. Для газа из 100 молекул вероятность того, что молекулы распределятся между половинами сосуда строго поровну, приблизительно равна 1/18, т. е. такое распределение встречается в среднем один раз на каждые 18 снимков.
Итак, строго равномерное распределение молекул по объему встречается не так уж и часто. Но если мы подсчитаем вероятности таких распределений молекул, при которых в одной половине сосуда будет на две, четыре и вообще на небольшое число молекул больше, чем в другой, и просуммируем эти вероятности, то мы увидим, что вероятность появления любого из таких распределений будет близка к единице, а очень неравномерные распределения, при которых число молекул справа и слева различается сильно, будут встречаться крайне редко.
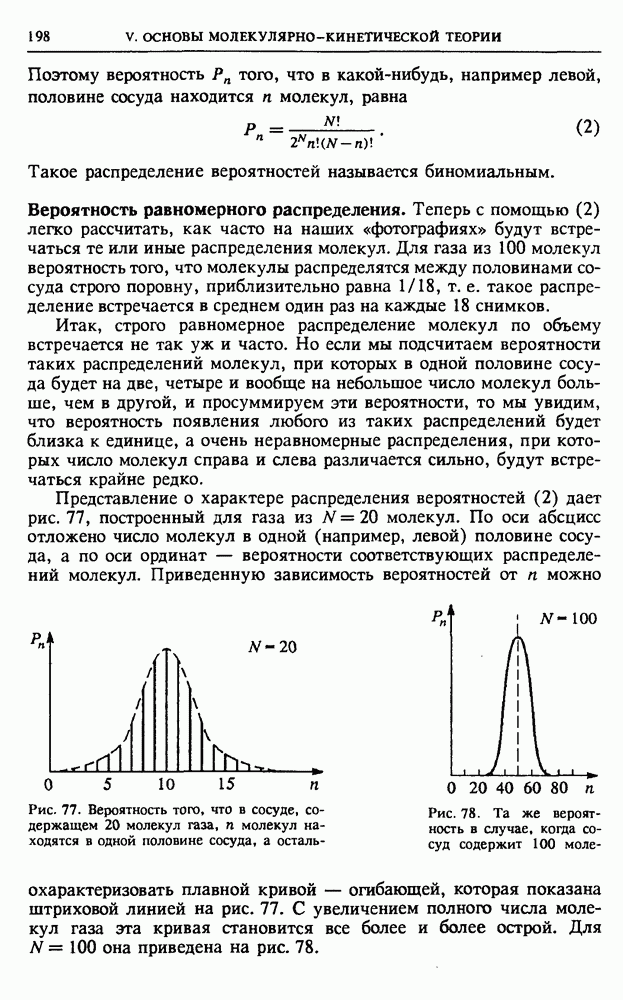
Представление о характере распределения вероятностей (2) дает рис. 77, построенный для газа из  молекул. По оси абсцисс отложено число молекул в одной (например, левой) половине сосуда, а по оси ординат — вероятности соответствующих распределений молекул.
молекул. По оси абсцисс отложено число молекул в одной (например, левой) половине сосуда, а по оси ординат — вероятности соответствующих распределений молекул.

Рис. 77. Вероятность того, что в сосуде, содержащем 20 молекул газа,  молекул находятся в одной половине сосуда
молекул находятся в одной половине сосуда

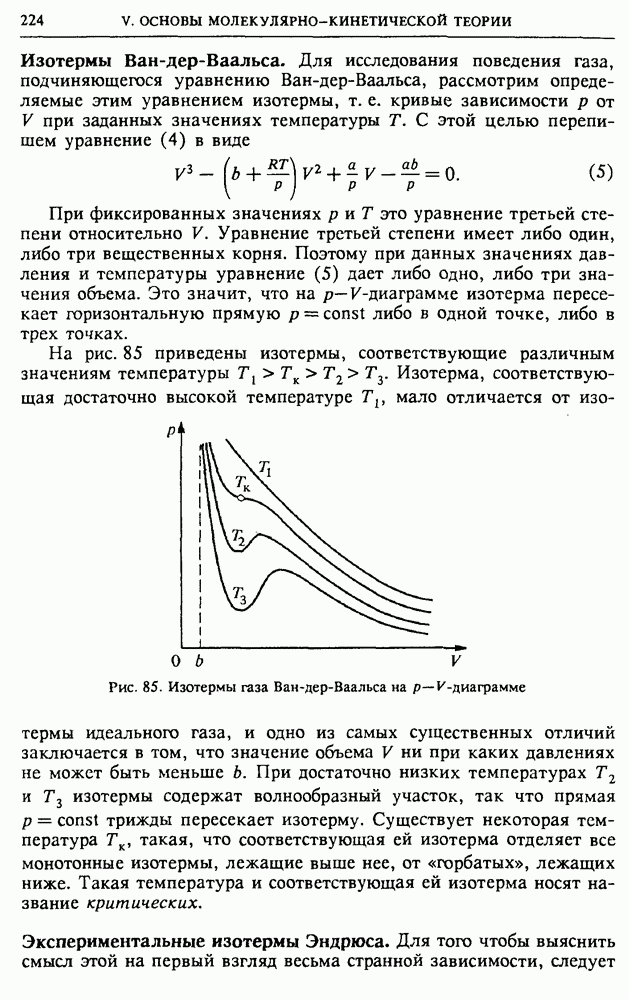
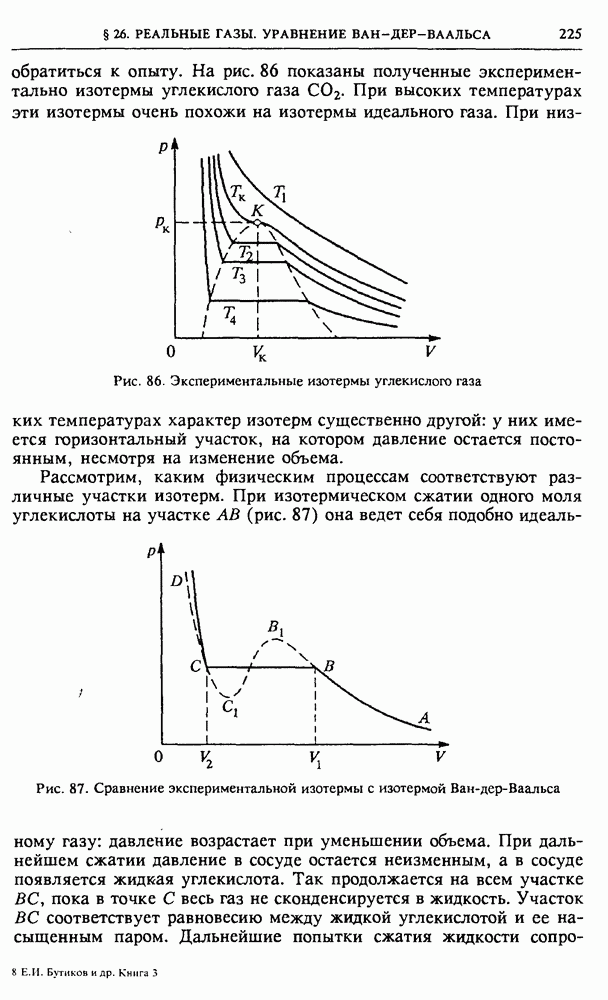
Рис. 78. Та же вероятность в случае, когда сосуд содержит 100 молекул
Приведенную зависимость вероятностей от  можно охарактеризовать плавной кривой — огибающей, которая показана штриховой линией на рис. 77. С увеличением полного числа молекул газа эта кривая становится все более и более острой. Для
можно охарактеризовать плавной кривой — огибающей, которая показана штриховой линией на рис. 77. С увеличением полного числа молекул газа эта кривая становится все более и более острой. Для  она приведена на рис. 78.
она приведена на рис. 78.
Таким образом, знание функции распределения вероятностей позволяет не только вычислять средние значения макроскопических параметров, но и находить характерные отклонения этих величин от своих средних значений, дающие представление о величине флуктуаций.
Общие закономерности флуктуаций. Теперь мы можем сделать следующий общий вывод: если полное число молекул в изучаемой системе велико, то флуктуации плотности, соответствующие существенно неоднородному распределению, почти никогда не возникают.
Описанные выше закономерности справедливы не только для флуктуаций плотности, но и для флуктуаций других макроскопических параметров. Если число частиц в системе очень велико, то относительная величина флуктуаций любого параметра очень мала по сравнению со средним значением этого параметра и ею почти всегда можно пренебречь. Поэтому мы обычно не осознаем факта существования флуктуаций, когда имеем дело с большими макроскопическими системами. Но если система достаточно мала, то флуктуации могут быть легко обнаружены и часто имеют большое значение.
Как уже упоминалось, тепловые флуктуации ставят предел чувствительности любых измерительных приборов. При измерении малых значений физических величин или слабых сигналов флуктуации в чувствительном элементе измерительного прибора могут оказаться сравнимыми с измеряемой величиной. Флуктуации, возникающие в самом измерительном приборе, затрудняют измерения и поэтому называются шумами.
• Почему при хаотическом тепловом движении все молекулы макроскопического количества газа не могут самопроизвольно собраться в одной половине сосуда?
• Что такое флуктуации макроскопических параметров? Приведите примеры появления флуктуаций в физическом эксперименте.
• Какие соображения вы можете привести в пользу предположения о равной вероятности каждой молекуле идеального газа оказаться в одной из половин сосуда?
• Как подсчитать вероятность того, что в определенной половине сосуда находится  молекул газа из полного числа W?
молекул газа из полного числа W?
• Чему равна сумма вероятностей  даваемых формулой (2), по всем значениям и от 0 до W?
даваемых формулой (2), по всем значениям и от 0 до W?
• Как изменяется вид функции распределения этих вероятностей с увеличением полного числа  молекул газа?
молекул газа?
• Каковы максимальные значения вероятностей  на рис. 77 и 78?
на рис. 77 и 78?
• Как относительная флуктуация макроскопических параметров зависит от размеров системы, т. е. от числа молекул 
Статистический подход. На приведенном выше примере расчета вероятностей распределения молекул идеального газа по половинам сосуда можно проиллюстрировать основные идеи Гиббса построения равновесной статистической механики. При этом все макроскопические характеристики рассматриваемой молекулярной модели термодинамической системы должны вводиться без ссылок на термодинамику, и только затем можно найти их термодинамические эквиваленты.
Основное понятие статистического метода — это микроскопическое состояние. Задать его — значит задать механическое состояние системы, т. е. координаты и скорости всех молекул в один момент времени. Но в некоторых случаях достаточно в определение микросостояния включать только часть характеристик отдельных молекул. Так, в приведенном примере мы под микросостоянием фактически понимали только информацию о том, в какой половине сосуда находится каждая молекула. Под макросостоянием в этом случае понимается информация о том, сколько молекул находится в левой, а тем самым и сколько в правой половине сосуда.
Равные вероятности микросостояний. Основной гипотезой в методе Гиббса является предположение о равной вероятности реализации любых возможных микроскопических состояний замкнутой системы, для которой зафиксированы энергия, объем и число частиц. Именно это предположение в рассмотренном выше примере приводило к биномиальному распределению вероятностей  Гипотеза равной вероятности различных микросостояний считается справедливой не только для идеального газа, но и для любых сколь угодно сложных термодинамических систем.
Гипотеза равной вероятности различных микросостояний считается справедливой не только для идеального газа, но и для любых сколь угодно сложных термодинамических систем.
Статистический вес макросостояния. Вероятности реализации различных макросостояний при этом, в отличие от микросостояний, уже не равны друг другу, поскольку каждое макросостояние может быть реализовано своим вполне определенным числом микросостояний. Так, макросостояние, в котором все молекулы находятся в одной (левой) половине сосуда, реализуется единственным микросостоянием, а макросостояние, когда в левой половине находится одна из  молекул, реализуется
молекул, реализуется  различными микросостояниями.
различными микросостояниями.
Статистическим весом или термодинамической вероятностью некоторого макросостояния системы называется число различных микросостояний, которыми может быть реализовано данное макросостояние. В рассмотренном примере статистический вес макросостояния с определенным числом  молекул в левой половине — это число способов такого распределения
молекул в левой половине — это число способов такого распределения  молекул газа по половинам сосуда. Оно равно числу сочетаний
молекул газа по половинам сосуда. Оно равно числу сочетаний 
Как определить понятие теплового равновесия при статистическом подходе? Рассмотрим две термодинамические системы, находящиеся в тепловом контакте и образующие вместе замкнутую систему с определенной энергией Е. Число частиц и объем обеих подсистем фиксированы, но они могут обмениваться энергией в форме теплопередачи. Пусть на долю первой подсистемы приходится энергия  а на долю второй — остальная энергия
а на долю второй — остальная энергия  Число микросостояний всей замкнутой системы
Число микросостояний всей замкнутой системы  равно при этом произведению числа различных микросостояний первой подсистемы
равно при этом произведению числа различных микросостояний первой подсистемы  на число микросостояний второй подсистемы
на число микросостояний второй подсистемы 

Значение  будет разным в зависимости от того, какая часть
будет разным в зависимости от того, какая часть  полной энергии Е приходится на первую подсистему.
полной энергии Е приходится на первую подсистему.
Тепловое равновесие между подсистемами определяется как макроскопическое состояние с наибольшим статистическим весом, т. е. состояние с таким распределением энергии между подсистемами, при котором  как функция
как функция  имеет максимальное значение. В разобранном примере состоянию равновесия соответствовало распределение молекул между половинами сосуда поровну.
имеет максимальное значение. В разобранном примере состоянию равновесия соответствовало распределение молекул между половинами сосуда поровну.
Найдем, при каком условии статистический вес  максимален. Приравняем нулю производную
максимален. Приравняем нулю производную 

Производная от  по
по  равна взятой с противоположным знаком производной от
равна взятой с противоположным знаком производной от  по ее аргументу
по ее аргументу  Поэтому (4) можно записать в виде
Поэтому (4) можно записать в виде

Равенство (5), выражающее условие максимума статистического веса, равносильно равенству производных от логарифмов:

Энтропия и температура. В статистической механике энтропия  и термодинамическая температура Т определяются следующими равенствами:
и термодинамическая температура Т определяются следующими равенствами:

При вычислении производной в (8) объем системы V и число частиц в ней  следует считать фиксированными параметрами.
следует считать фиксированными параметрами.
Определение температуры (8) обусловлено тем, что в состоянии теплового равновесия, характеризующимся равенством температур, именно такая величина, как видно из (6), одинакова у обеих подсистем.
Определенная равенством (7) энтропия как характеристика макросостояния термодинамической системы обладает следующими свойствами.
Во-первых, энтропия аддитивна: энтропия всей системы равна сумме энтропий составляющих ее частей. Это непосредственно следует из равенства (3).
Во-вторых, энтропия системы максимальна в состоянии теплового равновесия. Это значит, что введенная определением (7) энтропия обладает таким же свойством, что и энтропия, введенная в термодинамике: согласно второму закону термодинамики энтропия замкнутой системы имеет максимальное значение в состоянии теплового равновесия.
Покажем согласованность определений энтропии (7) и температуры (8) с определениями этих величин в термодинамике. Пусть два тела с разными температурами Г, и  приводятся в тепловой контакт. В результате теплообмена они приходят в состояние теплового равновесия. Энтропия
приводятся в тепловой контакт. В результате теплообмена они приходят в состояние теплового равновесия. Энтропия  всей системы при этом увеличивается. Запишем выражение для изменения
всей системы при этом увеличивается. Запишем выражение для изменения 

Пусть некоторое количество теплоты  переходит от тела с температурой
переходит от тела с температурой  к телу с температурой Т При этом энергия
к телу с температурой Т При этом энергия  первого тела возрастает, а энергия
первого тела возрастает, а энергия  убывает:
убывает:  В соответствии с определением (8) производные в (9) равны обратным температурам тел:
В соответствии с определением (8) производные в (9) равны обратным температурам тел: 

Теперь (9) переписывается в виде

Отсюда следует, что  т. е. что при теплообмене энергия переходит от тела с более высокой температурой к телу с более низкой температурой.
т. е. что при теплообмене энергия переходит от тела с более высокой температурой к телу с более низкой температурой.
Задача о расширении газа в пустоту. Покажем, что статистическое определение (7) энтропии  приводит при решении задачи о необратимом расширении газа при разрушении перегородки
приводит при решении задачи о необратимом расширении газа при разрушении перегородки
в сосуде (см. § 19) к тому же результату, что и термодинамическое определение. Напомним условие задачи.
Идеальный газ находится в одной половине теплоизолированного сосуда, разделенного перегородкой на две равные части. Определить изменение энтропии газа, если перегородка внезапно разрушается и газ заполнит весь сосуд.
Статистический вес начального состояния газа равен единице:  так как существует лишь одно микросостояние, при котором все молекулы находятся в одной половине сосуда. В конечном состоянии молекулы распределены по половинам сосуда почти поровну (строго поровну, если отвлечься от флуктуаций). Вследствие исключительной остроты максимума кривой распределения вероятностей различных распределений молекул газа по половинам сосуда приближенно можно считать, что все остальные
так как существует лишь одно микросостояние, при котором все молекулы находятся в одной половине сосуда. В конечном состоянии молекулы распределены по половинам сосуда почти поровну (строго поровну, если отвлечься от флуктуаций). Вследствие исключительной остроты максимума кривой распределения вероятностей различных распределений молекул газа по половинам сосуда приближенно можно считать, что все остальные  микросостояний системы соответствуют конечному макросостоянию:
микросостояний системы соответствуют конечному макросостоянию:

Поэтому в соответствии с (7)

При строгом решении следует воспользоваться формулой (1) при 

и формулой Стирлинга

В результате имеем

Поскольку  то
то  и для энтропии получаем прежнее значение
и для энтропии получаем прежнее значение

Распределение Гиббса. Гипотеза Гиббса о равной вероятности всех микросостояний замкнутой системы позволяет получить функцию распределения вероятностей для любой малой подсистемы, находящейся в тепловом контакте с очень большой системой — термостатом.
Рассмотрим замкнутую систему, состоящую из рассматриваемой подсистемы и термостата. Пусть  — энергия всей замкнутой системы,
— энергия всей замкнутой системы,  энергия выделенной подсистемы. Тогда на долю термостата приходится энергия
энергия выделенной подсистемы. Тогда на долю термостата приходится энергия  Очевидно, что
Очевидно, что
вероятность  подсистеме иметь энергию Е пропорциональна числу микросостояний
подсистеме иметь энергию Е пропорциональна числу микросостояний  термостата с энергией
термостата с энергией  Поэтому для отношения двух вероятностей
Поэтому для отношения двух вероятностей  можно написать
можно написать

Используя определение энтропии (7), перепишем это отношение в виде

где  Учитывая, что энергии подсистемы
Учитывая, что энергии подсистемы  малы по сравнению с энергией термостата, выражение для
малы по сравнению с энергией термостата, выражение для  можно приближенно записать следующим образом:
можно приближенно записать следующим образом:

или, с учетом (8),

Подставляя  в (12), находим
в (12), находим

Итак, мы получаем, что вероятность того, что малая подсистема, находящаяся в тепловом контакте с термостатом при температуре Т, будет иметь энергию Е, пропорциональна экспоненте 

Формула (13) дает распределение вероятностей для любой физической величины, характеризующей подсистему. При этом в показателе экспоненты играет роль лишь та часть энергии подсистемы, которая зависит от этой величины.
Если, например, в качестве подсистемы взять одну молекулу, то (13) дает распределение для ее координат, скорости, магнитного или электрического момента, и т. д. В частности, рассматривая распределение вероятностей для проекции скорости  нужно взять в качестве Е ту часть кинетической энергии, которая зависит от
нужно взять в качестве Е ту часть кинетической энергии, которая зависит от  . В результате сразу приходим к формуле (12) § 22. При этом коэффициент пропорциональности перед экспонентой получается из условия нормировки: сумма всех вероятностей должна быть равна единице.
. В результате сразу приходим к формуле (12) § 22. При этом коэффициент пропорциональности перед экспонентой получается из условия нормировки: сумма всех вероятностей должна быть равна единице.
• Приведите соображения, обосновывающие выражение (3) для числа микросостояний составной замкнутой системы. При каких условиях это выражение справедливо?
• Как понимается условие теплового равновесия в статистической механике?
• Объясните, почему состоянию теплового равновесия идеального газа в сосуде соответствует распределение молекул поровну между половинами сосуда.
• Как определяются энергия и температура в статистической механике на основе представления о статистическом весе макроскопического состояния системы?
• Поясните, почему энтропия  определяемая равенством (7), увеличивается при переходе замкнутой системы в состояние термодинамического равновесия.
определяемая равенством (7), увеличивается при переходе замкнутой системы в состояние термодинамического равновесия.
• Приведите доводы, свидетельствующие о том, что статистические определения энтропии (7) и температуры (8) согласуются с определениями этих величин в термодинамике.
• Поясните, почему в приведенном выводе распределения Гиббса считалось, что вероятность подсистеме иметь энергию Е пропорциональна числу состояний термостата с энергией 
• Где в выводе распределения Гиббса использовалось предположение о том, что выделенная подсистема много меньше термостата?
• Покажите, как из общего распределения Гиббса (13) получить барометрическую формулу.
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
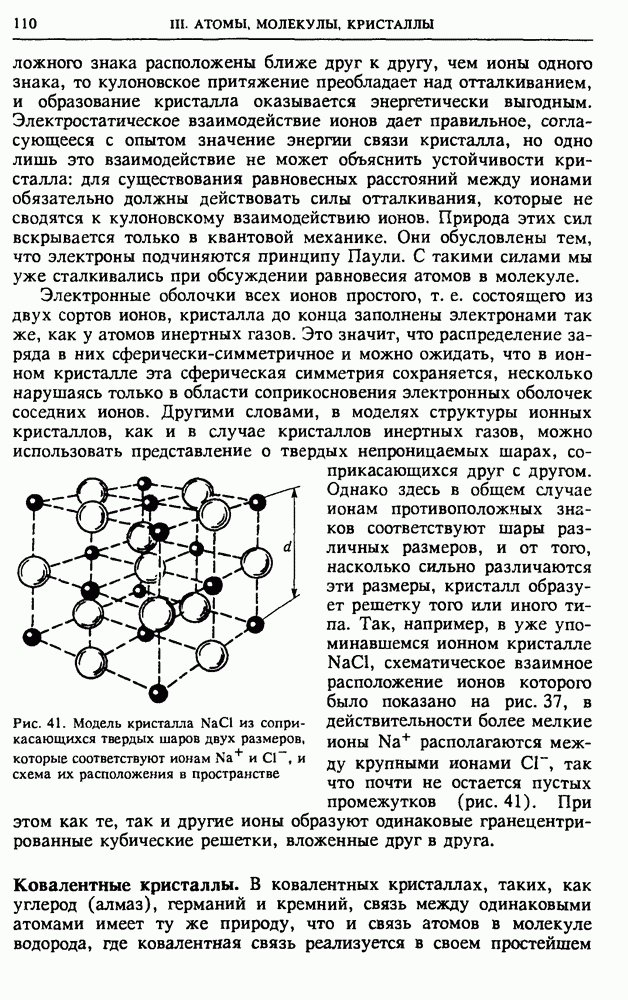
- § 13. Кристаллы
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
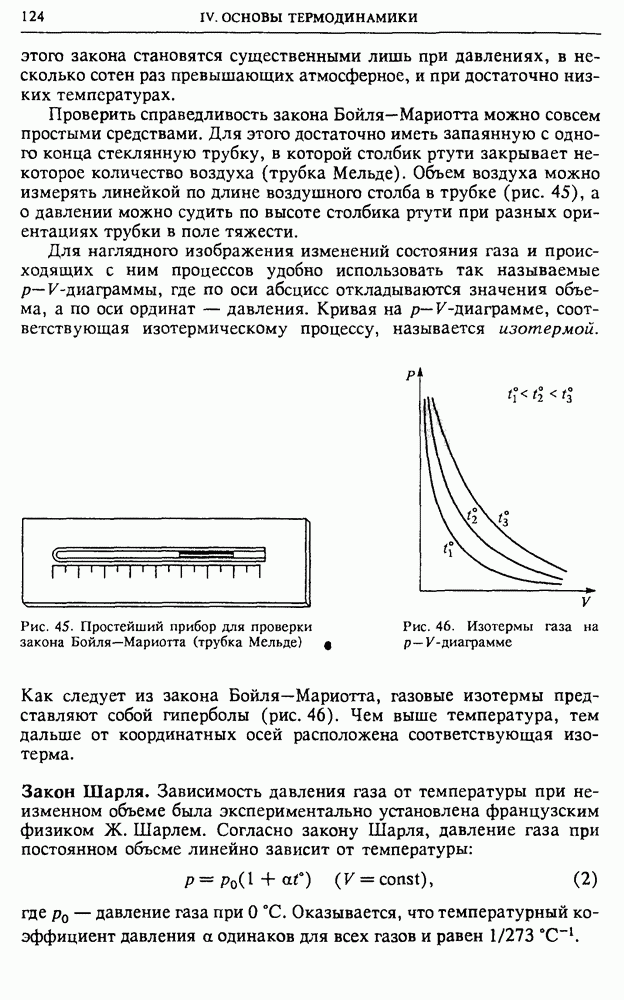
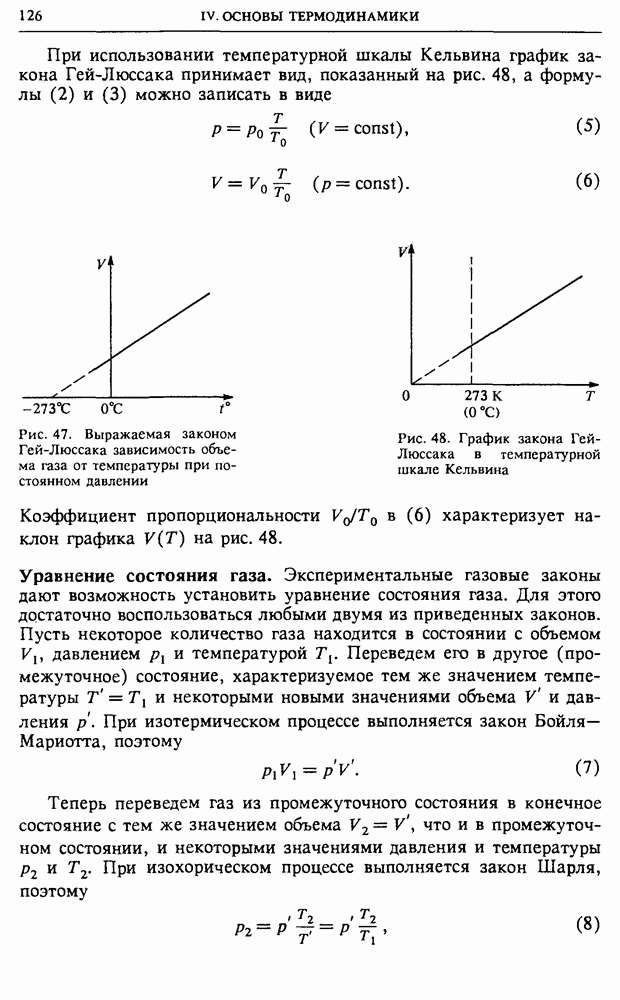
- § 15. Уравнение состояния газа
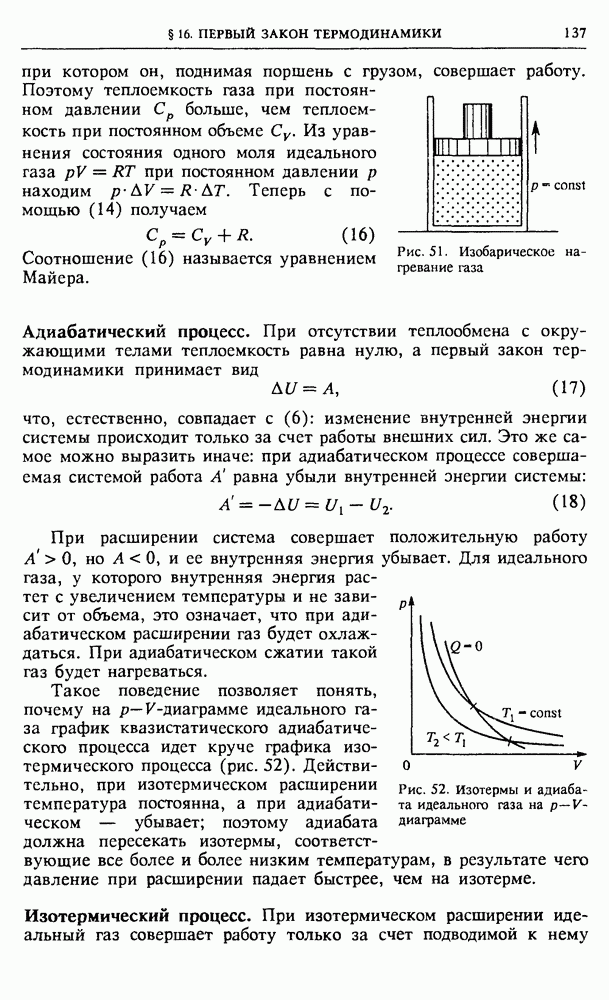
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
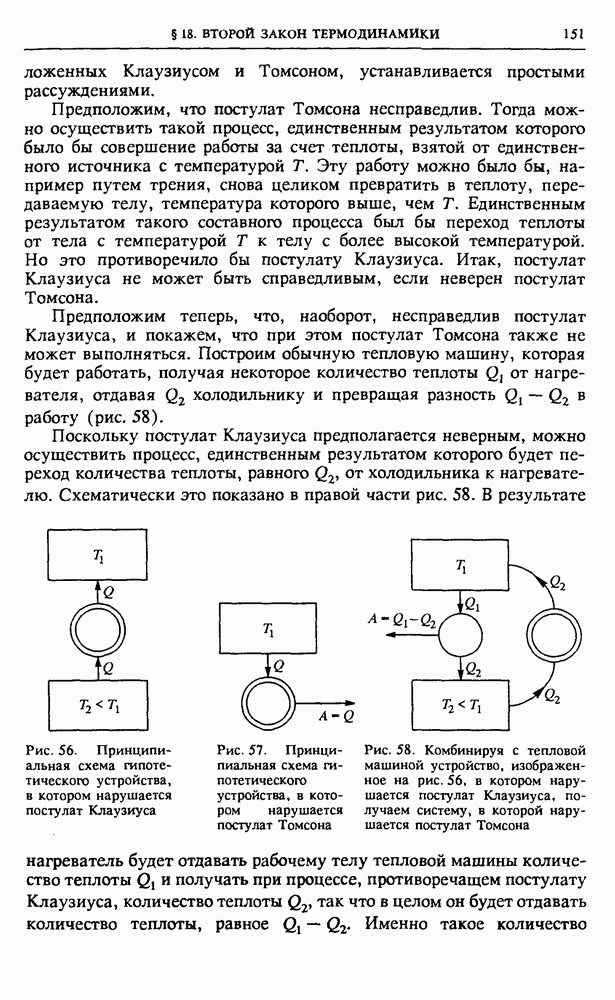
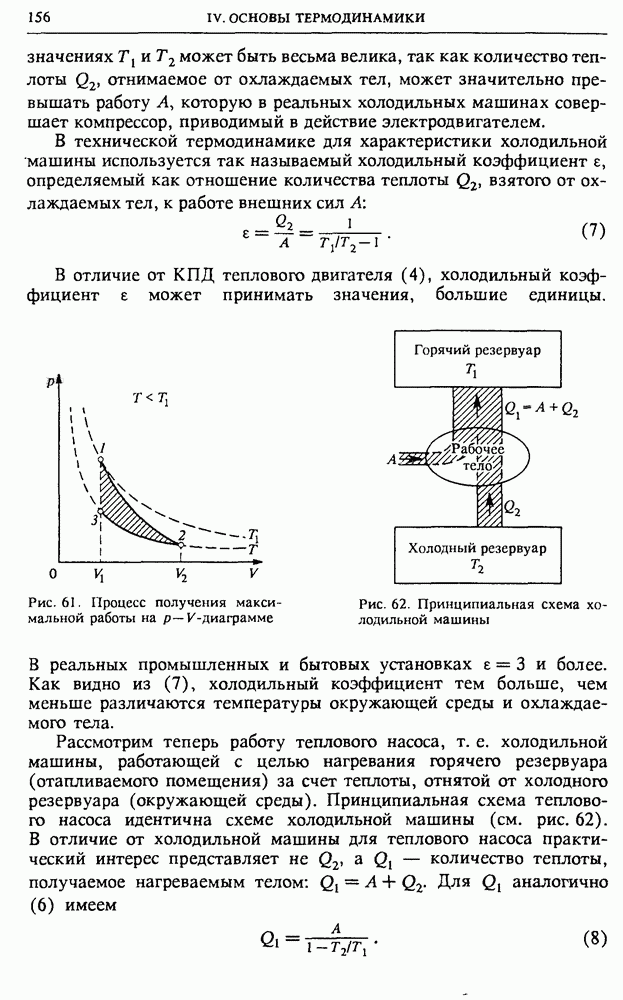
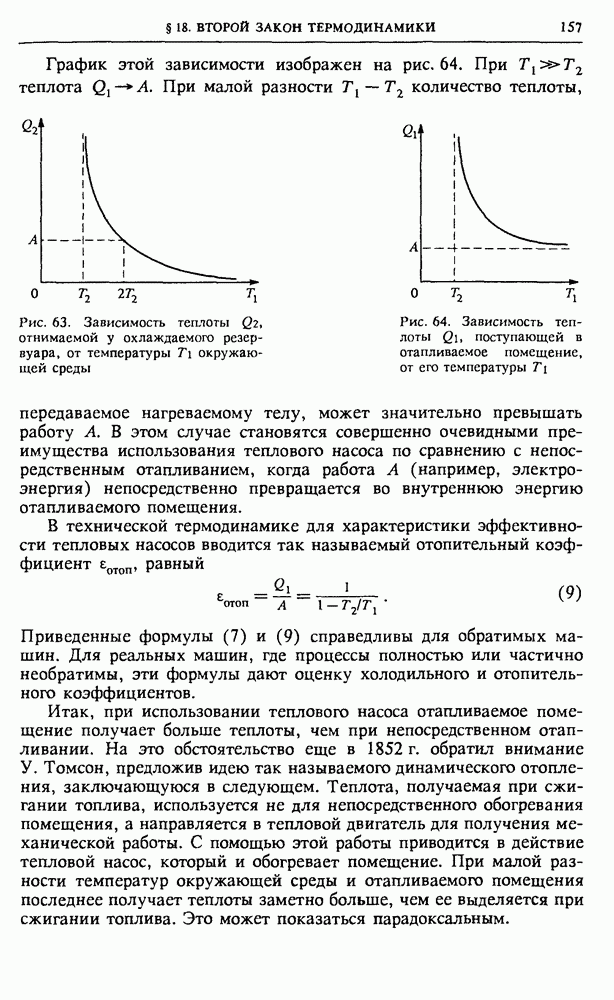
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
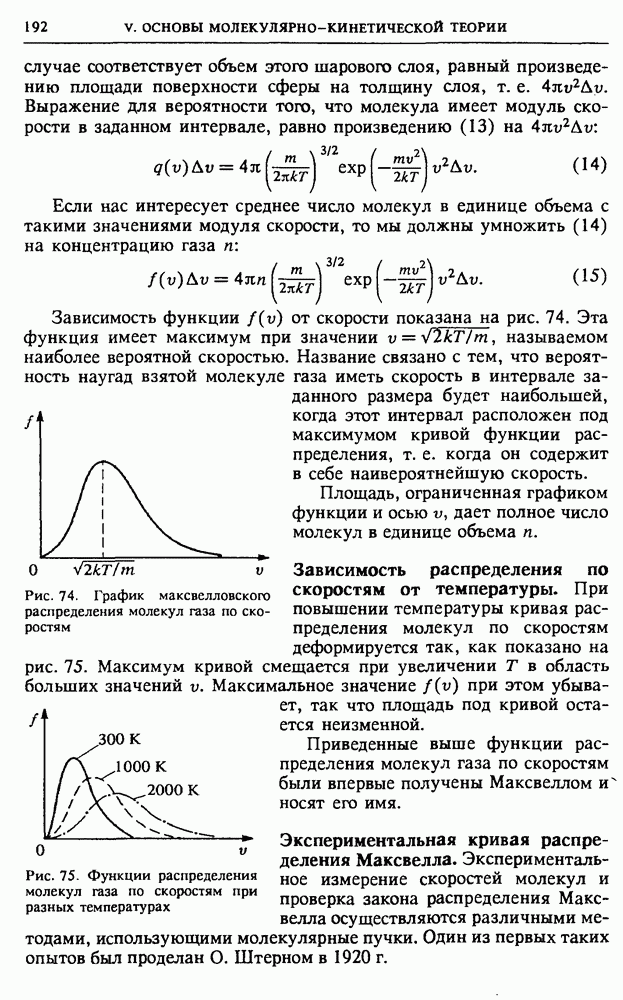
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы