| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 19. Методы термодинамики и их применения
В предыдущем параграфе была приведена без доказательства теорема Карно, выражающая максимально возможный коэффициент полезного действия теплового двигателя через температуры горячего и холодного тепловых резервуаров:

Из второго закона термодинамики следует, что КПД тепловой машины, работающей по обратимому циклу, не зависит от того, какое вещество используется в качестве рабочего тела.
КПД всех обратимых тепловых машин одинаков. Убедиться в этом можно с помощью следующих рассуждений. Предположим
противное, т. е. что КПД у одной из двух обратимых машин, работающих при заданных температурах  больше, чем у другой:
больше, чем у другой:  Допустим, что за один цикл обе машины отдают холодильнику одинаковые количества теплоты:
Допустим, что за один цикл обе машины отдают холодильнику одинаковые количества теплоты:  Тогда машина, у которой КПД выше, за цикл превращает в работу большее количество теплоты:
Тогда машина, у которой КПД выше, за цикл превращает в работу большее количество теплоты: 
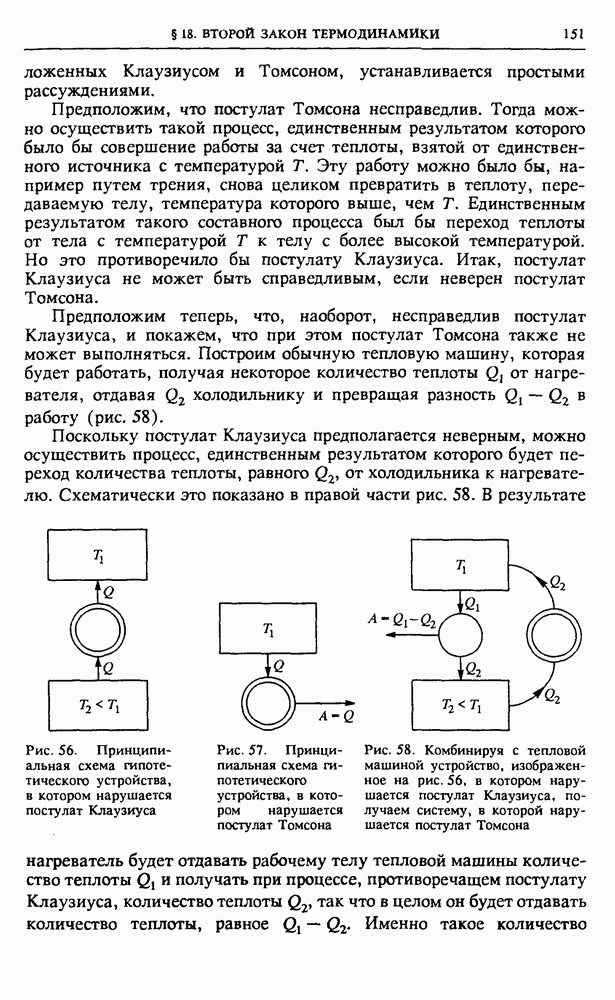
Пусть теперь машина с большим КПД работает в прямом, а с меньшим КПД — в обратном направлении, т. е. как холодильная машина. За счет совершения работы А внешними телами от холодного резервуара отнимается теплота  и передается горячему резервуару теплота
и передается горячему резервуару теплота  В результате их совместного действия за цикл получается следующий результат. Холодильник получает от рабочего тела первой машины столько же теплоты, сколько отдает рабочему телу второй
В результате их совместного действия за цикл получается следующий результат. Холодильник получает от рабочего тела первой машины столько же теплоты, сколько отдает рабочему телу второй  т. е. в холодильнике никаких изменений не происходит. Поскольку
т. е. в холодильнике никаких изменений не происходит. Поскольку  то лишь части работы
то лишь части работы  достаточно для приведения в действие холодильной машины. Нагреватель отдает теплоту
достаточно для приведения в действие холодильной машины. Нагреватель отдает теплоту  а получает меньшую теплоту
а получает меньшую теплоту  т. е. в целом отдает только
т. е. в целом отдает только  Итак, теплота
Итак, теплота  взятая от нагревателя, целиком превращается в полезную работу
взятая от нагревателя, целиком превращается в полезную работу  — а холодильнику при этом никакой теплоты не передается. Это противоречит второму закону термодинамики в форме постулата Томсона. Значит, предположение, что
— а холодильнику при этом никакой теплоты не передается. Это противоречит второму закону термодинамики в форме постулата Томсона. Значит, предположение, что  неверно.
неверно.
Точно такие же рассуждения покажут, что для обратимых машин окажется неверным и предположение, что  Мы приходим к выводу, что все обратимые машины имеют одинаковый КПД.
Мы приходим к выводу, что все обратимые машины имеют одинаковый КПД.
Приведенное доказательство теоремы Карно основывалось на предположении об обратимости обеих тепловых машин, означающем, что любую из них можно было заставить действовать в обратном направлении. Если одна из машин, например с  необратима, то из приведенных рассуждений следует только, что
необратима, то из приведенных рассуждений следует только, что  любой необратимой тепловой машины меньше КПД обратимой машины, работающей при тех же температурах
любой необратимой тепловой машины меньше КПД обратимой машины, работающей при тех же температурах 
Независимость КПД обратимой тепловой машины от рода рабочего тела позволяет для получения формулы (1) выбрать простейшее рабочее тело — идеальный газ.
Для расчета КПД цикла Карно с идеальным газом нам понадобятся выражение для работы, совершаемой идеальным газом в изотермическом процессе, и уравнение адиабаты идеального газа.
Работа идеального газа в изотермическом процессе. Пусть один моль идеального газа изотермически расширяется от объема  до
до
объема  . Совершаемая при этом работа выражается определенным интегралом:
. Совершаемая при этом работа выражается определенным интегралом:

Давление газа  можно выразить с помощью уравнения состояния:
можно выразить с помощью уравнения состояния:  Поскольку в изотермическом процессе температура постоянна, то выражение (2) принимает вид
Поскольку в изотермическом процессе температура постоянна, то выражение (2) принимает вид

Вывод уравнения адиабаты. Уравнение адиабаты идеального газа можно получить, используя первый закон термодинамики и уравнение состояния. Так как в адиабатическом процессе теплообмен не происходит, то первый закон термодинамики записывается в виде

Приращение внутренней энергии  поскольку внутренняя энергия идеального газа не зависит от объема. Выражение для
поскольку внутренняя энергия идеального газа не зависит от объема. Выражение для  можно получить из уравнения состояния
можно получить из уравнения состояния 

С учетом приведенных выражений для  уравнение (4) переписывается в виде
уравнение (4) переписывается в виде

где мы воспользовались тем, что  Введем обозначение для отношения теплоемкостей
Введем обозначение для отношения теплоемкостей 

Разделив обе части (6) на произведение  получаем дифференциальное уравнение, выражающее зависимость давления идеального газа от объема в адиабатическом процессе:
получаем дифференциальное уравнение, выражающее зависимость давления идеального газа от объема в адиабатическом процессе:

Интегрируя (8), получаем

где константа С сохраняет свое значение в течение адиабатического процесса. Это и есть уравнение адиабаты идеального газа.
Его можно записать и в других переменных, например V и Г. Для этого можно просто подставить в  из уравнения состояния:
из уравнения состояния:

Аналогично уравнение адиабаты можно записать и в переменных  и Г.
и Г.
КПД цикла Карно. Теперь у нас есть все необходимое для получения формулы (1). Рассмотрим цикл Карно с идеальным газом, показанный на рис. 59. Газ получает количество теплоты от нагревателя с температурой 71 на изотермическом участке 1—2 и отдает холодильнику с температурой  количество теплоты
количество теплоты  на изотермическом участке 3—4. На адиабатических участках 2—3 и 4—1 теплообмена нет. Поскольку внутренняя энергия идеального газа при изотермическом процессе не меняется, то теплота
на изотермическом участке 3—4. На адиабатических участках 2—3 и 4—1 теплообмена нет. Поскольку внутренняя энергия идеального газа при изотермическом процессе не меняется, то теплота  равна совершаемой газом работе при изотермическом расширении от
равна совершаемой газом работе при изотермическом расширении от  до
до  . Поэтому в соответствии с (3) имеем
. Поэтому в соответствии с (3) имеем

Аналогично для теплоты  можно написать
можно написать

Теперь для КПД цикла Карно имеем

Легко видеть, что отношение логарифмов в (13) равно единице. В самом деле, с помощью (10) для адиабат 2—3 и 4—1 имеем

Из этих равенств следует, что  . Итак, для КПД цикла Карно с идеальным газом получаем формулу (1):
. Итак, для КПД цикла Карно с идеальным газом получаем формулу (1):

В силу доказанной выше теоремы это выражение для КПД через температуры  справедливо для цикла Карно с любым рабочим телом.
справедливо для цикла Карно с любым рабочим телом.
Формулу (1) можно использовать для определения термодинамической температуры, не зависящей от свойств конкретных термометрических тел. Чтобы однозначно определить термодинамическую шкалу, необходимо задать значение температуры в
некоторой реперной точке. В качестве такой точки выбирается тройная точка воды.
Неравенство Клаузиуса. Приведенные результаты позволяют дать второму закону термодинамики количественную формулировку в виде некоторого неравенства. Для любого кругового процесса между тепловыми резервуарами с температурами  справедливо соотношение, называемое неравенством Клаузиуса:
справедливо соотношение, называемое неравенством Клаузиуса:

Здесь  — количество теплоты, полученное от резервуара с температурой
— количество теплоты, полученное от резервуара с температурой  — количество теплоты, отданное резервуару с температурой
— количество теплоты, отданное резервуару с температурой  Знак равенства достигается в случае обратимого процесса, которым, как мы видели, может быть только цикл Карно.
Знак равенства достигается в случае обратимого процесса, которым, как мы видели, может быть только цикл Карно.
Энтропия как функция состояния. Из (15) следует, что

Если условиться считать теплоту, получаемую рабочим телом, положительной, а отдаваемую — отрицательной, то (16) можно переписать в виде

где
Неравенство (17) можно обобщить на случай любого кругового процесса, в котором рабочее тело обменивается теплотой с несколькими тепловыми резервуарами с различными температурами 

Если температура на протяжении кругового процесса изменяется непрерывно, то сумма в (18) обычным образом превращается в интеграл по замкнутому пути, так как рабочее тело, пройдя через ряд промежуточных состояний, возвращается в исходное состояние:

где под  понимается получаемая (или отдаваемая) теплота на элементарном участке кругового процесса, настолько малом, чтобы температуру можно было считать постоянной.
понимается получаемая (или отдаваемая) теплота на элементарном участке кругового процесса, настолько малом, чтобы температуру можно было считать постоянной.
В случае обратимого кругового процесса в (19) фигурирует знак равенства, т. е. интеграл по замкнутому контуру равен нулю:

Это означает, что под интегралом стоит дифференциал некоторой функции состояния термодинамической системы: сумма ее приращений вдоль замкнутого пути обращается в нуль при возвращении системы в исходное состояние. Ситуация здесь такая же, как и при введении понятия потенциальной энергии в механике, где независимость работы от формы траектории (а следовательно, равенство нулю работы по любому замкнутому контуру) свидетельствовала о существовании функции состояния механической системы — потенциальной энергии. Итак,

где  — некоторая функция состояния термодинамической системы. Ее называют энтропией. Энтропия в каждом состоянии системы имеет вполне определенное значение, не зависящее от того, каким образом (обратимо или необратимо) система попала в данное состояние. При обратимом процессе изменение энтропии на элементарном участке, где температура Т считается постоянной, равно отношению количества передаваемой теплоты
— некоторая функция состояния термодинамической системы. Ее называют энтропией. Энтропия в каждом состоянии системы имеет вполне определенное значение, не зависящее от того, каким образом (обратимо или необратимо) система попала в данное состояние. При обратимом процессе изменение энтропии на элементарном участке, где температура Т считается постоянной, равно отношению количества передаваемой теплоты  к абсолютной температуре. Формула (21) позволяет для каждой конкретной системы с известным уравнением состояния найти явный вид этой функции. При необратимом процессе
к абсолютной температуре. Формула (21) позволяет для каждой конкретной системы с известным уравнением состояния найти явный вид этой функции. При необратимом процессе 
Задача
Идеальный газ находится в одной половине теплоизолированного сосуда, разделенного перегородкой на две равные части. Определить изменение энтропии газа, если перегородка внезапно разрушается и газ заполняет весь сосуд.
Решение. Поскольку газ не получает теплоты (сосуд теплоизолирован) и не совершает работы (он расширяется в вакуум и никакого перемещения окружающих тел не происходит), его внутренняя энергия остается неизменной. Внутренняя энергия идеального газа пропорциональна его температуре и не зависит от объема, поэтому температура газа в результате описанного процесса не изменяется. Происходящий с газом процесс необратим. Однако энтропия конечного состояния газа, являясь функцией состояния, не зависит от того, каким путем попал газ в это конечное состояние. Поэтому можно рассмотреть обратимый изотермический процесс, при котором газ расширяется, перемещая перегородку, пока не займет весь объем сосуда.
Количество теплоты, получаемое идеальным газом при изотермическом процессе, равно совершаемой им работе:

так как 
Вследствие постоянства температуры изменение энтропии системы записывается в виде

Объединенное уравнение первого и второго законов. Используя (21), можно записать равенство, выражающее и первый, и второй законы термодинамики. Для обратимых процессов из (21) следует, что

Подставляя в уравнение первого закона термодинамики

количество теплоты  выраженное с помощью (22) через приращение энтропии
выраженное с помощью (22) через приращение энтропии  получаем
получаем

Если система изотропна и совершает только механическую работу, то  и (24) записывается в виде
и (24) записывается в виде

Формула (25), объединяющая первый и второй законы термодинамики, называется фундаментальным равенством Гиббса.
Свободная энергия. Соотношение (25) выражает приращение внутренней энергии при изменении состояния системы. В качестве независимых переменных, задающих состояние термодинамической системы, могут использоваться разные макроскопические параметры. В (25) такими независимыми переменными выступают объем V и энтропия  . В практических приложениях использовать энтропию как независимую переменную неудобно. Более удобной физической величиной была бы температура, которую можно, как и объем, измерять непосредственно.
. В практических приложениях использовать энтропию как независимую переменную неудобно. Более удобной физической величиной была бы температура, которую можно, как и объем, измерять непосредственно.
Перейти к независимым переменным Т и V можно следующим образом. Введем еще одну функцию состояния  связанную с внутренней энергией
связанную с внутренней энергией  соотношением
соотношением

Функцию  называют свободной энергией системы. Для установления ее физического смысла запишем ее приращение при малом изменении состояния системы:
называют свободной энергией системы. Для установления ее физического смысла запишем ее приращение при малом изменении состояния системы:

Подставляя сюда  из (25), получаем
из (25), получаем

Видно, что независимыми переменными, определяющими состояние, для функции  являются температура и объем. Если изменить состояние системы изотермически, т. е. считать
являются температура и объем. Если изменить состояние системы изотермически, т. е. считать  то, как видно из (28),
то, как видно из (28),

Величина  представляет собой работу внешних сил над системой при изменении ее объема на
представляет собой работу внешних сил над системой при изменении ее объема на  Таким образом, работа внешних сил при изотермическом процессе равна изменению свободной энергии системы.
Таким образом, работа внешних сил при изотермическом процессе равна изменению свободной энергии системы.
Термодинамика диэлектриков и магнетиков. Полученные выше термодинамические соотношения позволяют исследовать энергетические превращения в самых разных физических системах. В частности, можно рассмотреть роль тепловых явлений в различных электромагнитных процессах. Оказывается, что, как и в случае реальных механических систем, практически любые энергетические превращения связаны с необратимым выделением теплоты.
Пусть, например, заполненный диэлектриком конденсатор заряжается от некоторого источника питания. При изменении заряда конденсатора на  внешние силы (источник питания) совершают над ним работу
внешние силы (источник питания) совершают над ним работу

где через  обозначено напряжение на конденсаторе, т. е. разность потенциалов между его обкладками. Это напряжение в каждый момент пропорционально заряду конденсатора
обозначено напряжение на конденсаторе, т. е. разность потенциалов между его обкладками. Это напряжение в каждый момент пропорционально заряду конденсатора 

В этом выражении  — емкость конденсатора, равная произведению диэлектрической проницаемости
— емкость конденсатора, равная произведению диэлектрической проницаемости  диэлектрика в зазоре между обкладками на емкость
диэлектрика в зазоре между обкладками на емкость  того же конденсатора в отсутствие диэлектрика. В нашем случае основное соотношение (24), выражающее первый и второй законы термодинамики, записывается в виде
того же конденсатора в отсутствие диэлектрика. В нашем случае основное соотношение (24), выражающее первый и второй законы термодинамики, записывается в виде

или, после подстановки  из (30),
из (30),

Отметим, что внутренняя энергия  рассматриваемой системы (заряженного конденсатора) включает в себя и электростатическую энергию. В принципе с помощью (32) можно было бы получить выражение для этой внутренней энергии, сначала проинтегрировав
рассматриваемой системы (заряженного конденсатора) включает в себя и электростатическую энергию. В принципе с помощью (32) можно было бы получить выражение для этой внутренней энергии, сначала проинтегрировав
(32) при постоянной энтропии и добавив затем изменение внутренней энергии при постоянном зараде. Однако практически сделать это затруднительно, поскольку при адиабатическом процессе  меняется температура системы, а вместе с ней и диэлектрическая проницаемость е.
меняется температура системы, а вместе с ней и диэлектрическая проницаемость е.
Обойти эту трудность можно, воспользовавшись вместо (32) аналогичным соотношением для свободной энергии F. В рассматриваемом случае вместо (28) имеем для 

Это соотношение уже легко проинтегрировать при  так как при постоянной температуре диэлектрическая проницаемость
так как при постоянной температуре диэлектрическая проницаемость  также неизменна. В результате получаем
также неизменна. В результате получаем

Здесь  — свободная энергия системы в отсутствие электрического заряда. Мы не рассматриваем ее зависимость от объема, поскольку считаем, что в интересующих нас процессах изменение объема мало.
— свободная энергия системы в отсутствие электрического заряда. Мы не рассматриваем ее зависимость от объема, поскольку считаем, что в интересующих нас процессах изменение объема мало.
С помощью полученного выражения (34) можно вернуться к внутренней энергии. Из (26) имеем

где энтропию  можно найти с помощью (33):
можно найти с помощью (33):

Здесь  — энтропия системы в отсутствие заряда (незаряженного конденсатора), получаемая в результате дифференцирования первого члена в правой части (34). Подставляя (34) и (36) в (35), получаем
— энтропия системы в отсутствие заряда (незаряженного конденсатора), получаемая в результате дифференцирования первого члена в правой части (34). Подставляя (34) и (36) в (35), получаем

Первое слагаемое в правой части (37) — это внутренняя энергия незаряженного конденсатора  явное выражение для которой нас здесь не интересует. Второе слагаемое дает вклад во внутреннюю энергию системы, связанный с наличием заряда на конденсаторе.
явное выражение для которой нас здесь не интересует. Второе слагаемое дает вклад во внутреннюю энергию системы, связанный с наличием заряда на конденсаторе.
В электростатике при выводе выражения для энергии заряженного конденсатора мы пренебрегали тепловыми процессами и считали, что энергия заряженного конденсатора равна работе электрических сил, совершаемой при его зарядке. При этом для энергии конденсатора получалось выражение  Из выражения (37)
Из выражения (37)
видно, что это справедливо только в том случае, когда диэлектрическая проницаемость  не зависит от температуры. В общем случае энергетические превращения в процессе зарадки конденсатора имеют более сложный характер.
не зависит от температуры. В общем случае энергетические превращения в процессе зарадки конденсатора имеют более сложный характер.
Предположим, что процесс зарядки конденсатора происходит изотермически. В этом случае изменение внутренней энергии, определяемое вторым слагаемым в правой части (37), не равно работе внешних сил  Когда диэлектрическая проницаемость
Когда диэлектрическая проницаемость  убывает с ростом температуры (т. е.
убывает с ростом температуры (т. е.  запасаемая конденсатором зависящая от
запасаемая конденсатором зависящая от  энергия меньше работы внешних сил. Это означает, что в процессе адиабатической зарядки температура конденсатора будет повышаться, а при разрядке — понижаться. К выводу о понижении температуры мы пришли, рассматривая обратимые процессы. Поэтому такой эффект может наблюдаться лишь тогда, когда необратимым выделением джоулевой теплоты в веществе можно пренебречь.
энергия меньше работы внешних сил. Это означает, что в процессе адиабатической зарядки температура конденсатора будет повышаться, а при разрядке — понижаться. К выводу о понижении температуры мы пришли, рассматривая обратимые процессы. Поэтому такой эффект может наблюдаться лишь тогда, когда необратимым выделением джоулевой теплоты в веществе можно пренебречь.
Совершенно аналогично можно рассмотреть тепловые процессы, сопровождающие намагничивание и размагничивание магнетиков. Адиабатическое размагничивание парамагнитных солей используется в криогенной технике как метод получения наиболее низких температур, близких к абсолютному нулю.
Зависимость внутренней энергии от объема. Информацию о связи различных термодинамических характеристик можно получать из общих соотношений типа (25) и (28) с помощью формальных математических приемов. Например, с помощью этих соотношений легко найти закон зависимости внутренней энергии системы от ее объема. Действительно, разделив (25) на приращение объема  находим
находим

Но из (28) следует, что  Поэтому (38) переписывается в виде
Поэтому (38) переписывается в виде

Если известно уравнение состояния  , то (39) позволяет найти явный вид зависимости внутренней энергии от объема. Например, для идеального газа
, то (39) позволяет найти явный вид зависимости внутренней энергии от объема. Например, для идеального газа  внутренняя энергия идеального газа не зависит от объема.
внутренняя энергия идеального газа не зависит от объема.
• Проведите доказательство теоремы Карно с помощью таких рассуждений от противного, в которых использовался бы второй закон термодинамики в формулировке Клаузиуса.
• Почему при выводе уравнения адиабаты (9) величину у в дифференциальном уравнении (8) можно считать постоянной?
• Почему при выборе общей формулы (1) для КПД теплового двигателя рассматривается частный случай — цикл Карно с идеальным газом?
• Поясните, почему неравенство Клаузиуса (15) или (16) можно рассматривать как альтернативную формулировку второго начала термодинамики.
• Поясните, каким образом из соотношения (20) следует вывод о существовании некоторой функции состояния.
• Почему выражение (21), связывающее приращение энтропии с передаваемой теплотой, справедливо только для обратимых процессов?
• Почему уравнение (24) или (25) можно рассматривать как соотношение, выражающее и первый и второй законы термодинамики?
• Покажите, что работа идеального газа при адиабатическом расширении может быть найдена по формуле

• При каких условиях работа внешних сил над термодинамической системой равна изменению свободной энергии?
• Почему при формулировке закона сохранения энергии в термодинамике используют понятие внутренней энергии, а не свободной энергии?
• Поясните, почему при адиабатической зарядке конденсатора с диэлектриком его температура повышается, когда  .
.
• Поясните, как методами термодинамики доказать, что внутренняя энергия идеального газа не зависит от его объема.
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
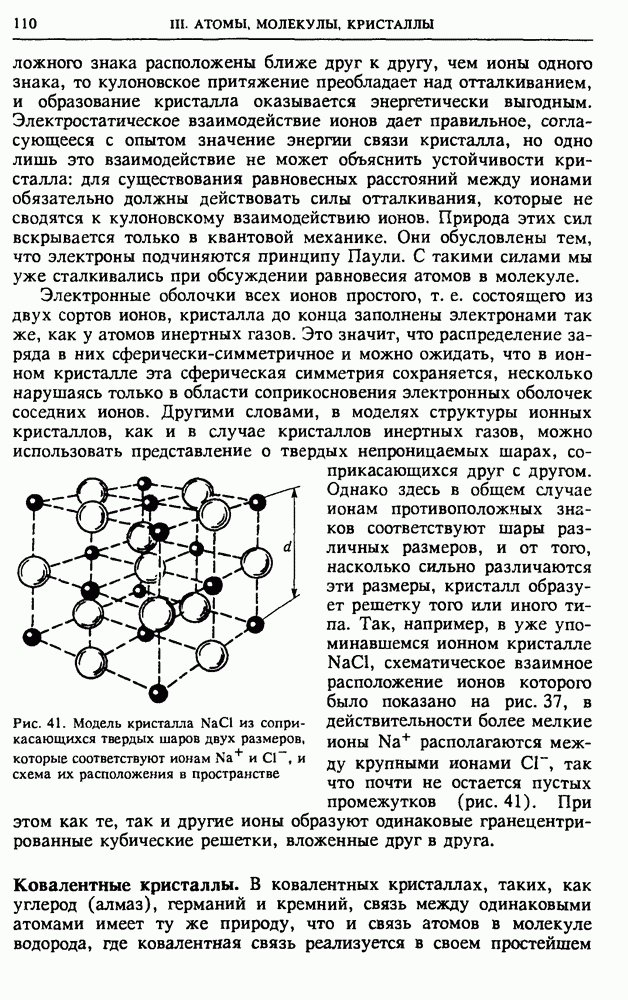
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
- § 13. Кристаллы
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
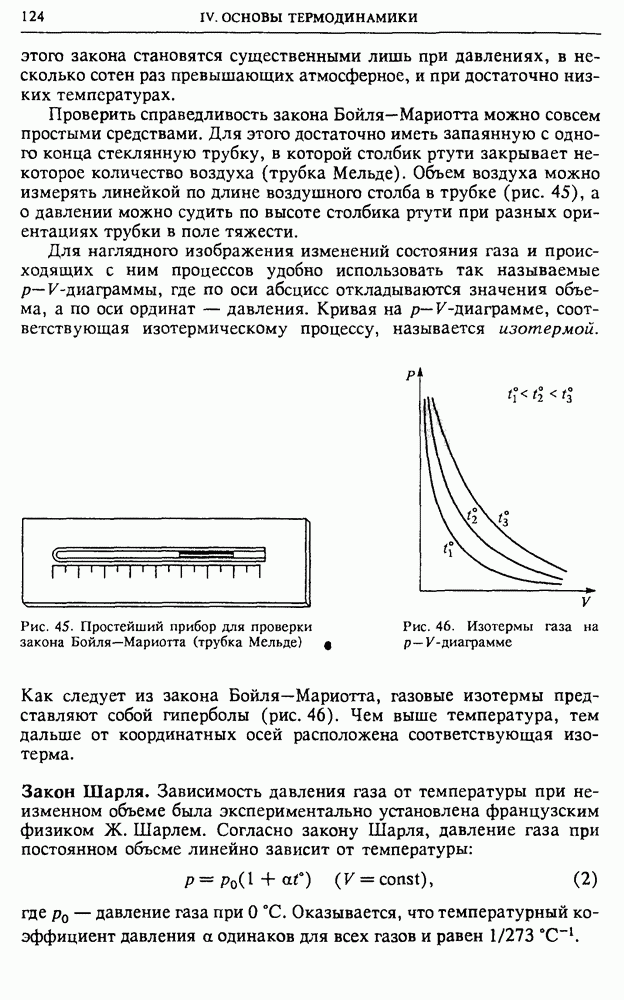
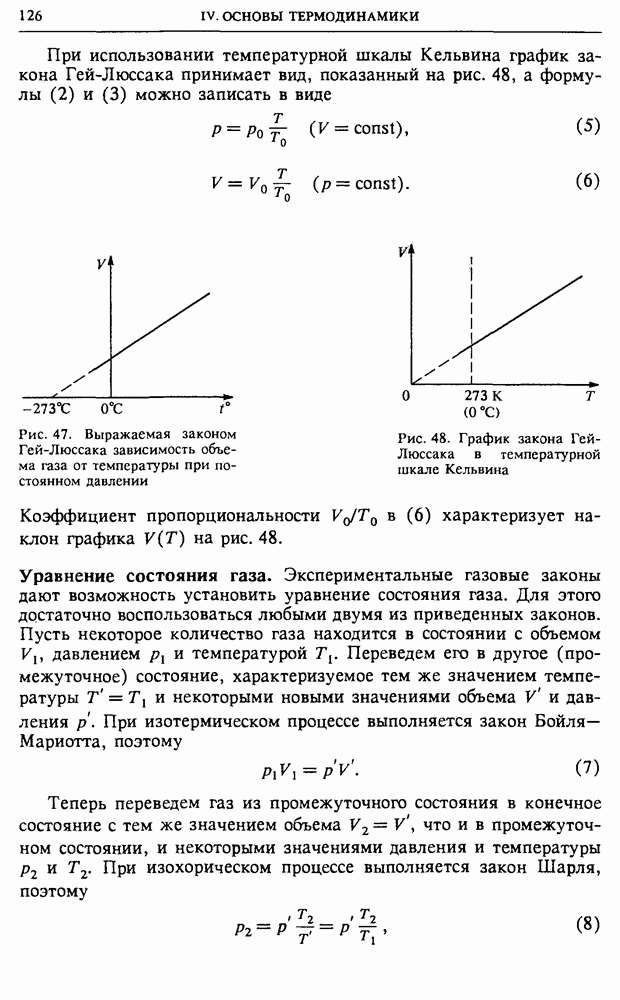
- § 15. Уравнение состояния газа
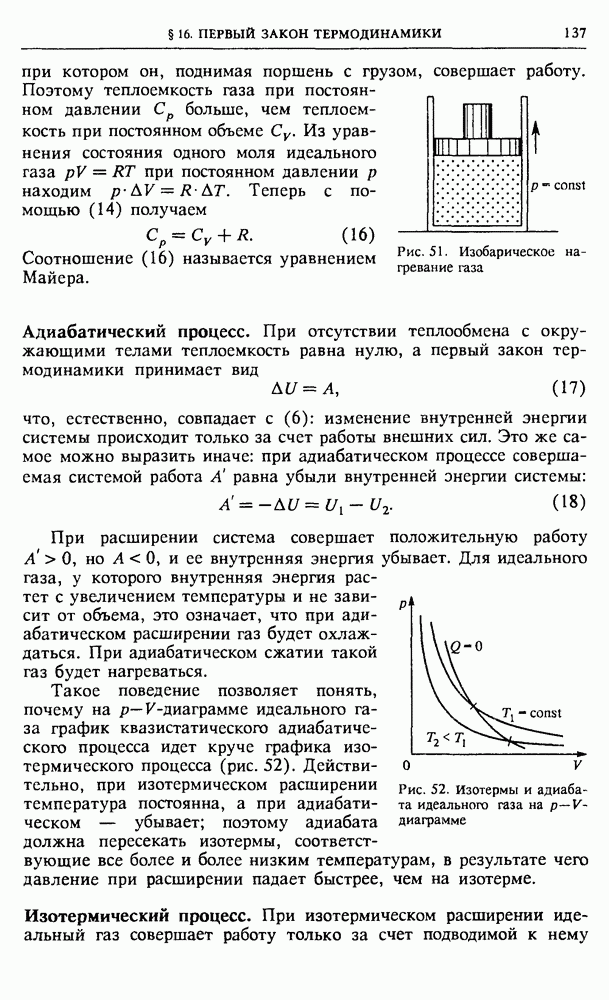
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы