| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Преобразования Лоренца
Полученные в § 2 на основе постулатов теории относительности формулы (1) и (2), связывающие промежутки времени и расстояния между точками в разных системах отсчета, позволяют написать релятивистский закон преобразования координат и времени произвольного события при переходе от одной системы отсчета к другой. Этот закон должен заменить основанные на классических представлениях о пространстве и времени преобразования Галилея.
Рассмотрим, как и в § 1, описание некоторого события А в двух инерциальных системах отсчета К и К. Пусть координаты и время этого события в системе К есть х, у, z и  а в системе
а в системе  и
и  (рис. 7). Как и прежде, считаем, что при
(рис. 7). Как и прежде, считаем, что при  точки О и о совпадают. Расстояния в направлении, перпендикулярном относительной скорости
точки О и о совпадают. Расстояния в направлении, перпендикулярном относительной скорости  систем отсчета, как уже было показано, одинаковы в К и К, поэтому
систем отсчета, как уже было показано, одинаковы в К и К, поэтому 

Рис. 7. Координаты одного и того же события А в двух системах отсчета
Координата х есть собственная длина  отрезка
отрезка  неподвижного в К-системе. Длина
неподвижного в К-системе. Длина  этого же отрезка в
этого же отрезка в  -системе, где измерение производится в момент времени
-системе, где измерение производится в момент времени  есть
есть  Учитывая соотношение (2) предыдущего параграфа между собственной длиной некоторого отрезка
Учитывая соотношение (2) предыдущего параграфа между собственной длиной некоторого отрезка  и длиной
и длиной  этого же отрезка в системе отсчета, относительно которой он движется со скоростью
этого же отрезка в системе отсчета, относительно которой он движется со скоростью 

мы можем написать 

откуда

Но можно рассуждать и иначе. Координата х есть собственная длина отрезка  неподвижного в
неподвижного в  -системе. Длина этого же отрезка в
-системе. Длина этого же отрезка в  -системе, измеряемая в момент времени
-системе, измеряемая в момент времени  по часам К, равна
по часам К, равна  Снова учитывая соотношение между длиной одного и того же отрезка в двух системах отсчета, можем написать
Снова учитывая соотношение между длиной одного и того же отрезка в двух системах отсчета, можем написать

Формулы (1) и (2) представляют собой искомый закон преобразования координаты х при переходе от К к К и обратно. Взятые вместе, они позволяют найти связь между временем  и V одного и того же события в обеих системах отсчета. Исключая из (1) и (2) сначала
и V одного и того же события в обеих системах отсчета. Исключая из (1) и (2) сначала  а затем х, найдем
а затем х, найдем

Преобразования Лоренца. Интервал между событиями. Таким образом, релятивистские формулы преобразования координат некоторого события при переходе от одной инерциальной системы отсчета к другой имеют вид

Эти формулы называют преобразованиями Лоренца. Они заменяют преобразования Галилея, справедливые лишь в предельном случае малых по сравнению со скоростью света относительных скоростей. При  преобразования Лоренца (4) переходят в преобразования Галилея. Это означает, что теория относительности не отвергает полностью классические представления о пространстве и времени, а включает их в себя как предельный случай, справедливый для медленных движений. Теория относительности не отвергает классическую физику, а определяет границы ее применимости.
преобразования Лоренца (4) переходят в преобразования Галилея. Это означает, что теория относительности не отвергает полностью классические представления о пространстве и времени, а включает их в себя как предельный случай, справедливый для медленных движений. Теория относительности не отвергает классическую физику, а определяет границы ее применимости.
Преобразования Лоренца выражают относительный характер промежутков времени между событиями и расстояний между точками в пространстве. Однако наиболее характерной чертой теории относительности является не утверждение относительного характера пространства и времени, а установление абсолютных, не зависящих от выбора систем отсчета законов природы.
Задача нахождения абсолютного выражения законов природы тесно связана с отысканием абсолютных, инвариантных величин. Одна из таких величин упоминается уже в основных постулатах — это максимальная скорость распространения взаимодействий, равная скорости света в вакууме с. Другой важной инвариантной
величиной является пространственно-временной интервал между событиями, определяемый следующим соотношением:

где  — промежуток времени между событиями в некоторой системе отсчета, а
— промежуток времени между событиями в некоторой системе отсчета, а  — выраженное в той же системе расстояние между точками, в которых происходят рассматриваемые события. В частности, если одному из происходящих событий соответствуют координаты
— выраженное в той же системе расстояние между точками, в которых происходят рассматриваемые события. В частности, если одному из происходящих событий соответствуют координаты  и момент времени
и момент времени  а второму — координаты х, у, z и момент
а второму — координаты х, у, z и момент  то интервал между ними
то интервал между ними

Пусть, например, первое событие представляет собой вспышку света, происходящую в начале координат при  а второе — приход фронта этой световой волны в точку с координатами
а второе — приход фронта этой световой волны в точку с координатами  в момент времени
в момент времени  Тогда
Тогда  и интервал для такой пары событий
и интервал для такой пары событий  Координаты и время второго события в другой системе отсчета К будут другими, но и для них в силу инвариантности скорости света будет выполняться такое же соотношение
Координаты и время второго события в другой системе отсчета К будут другими, но и для них в силу инвариантности скорости света будет выполняться такое же соотношение  , следовательно,
, следовательно,  Таким образом, если два события связаны между собой световым сигналом, то интервал между ними равен нулю во всех инерциальных системах отсчета. Этот результат является математическим выражением абсолютного характера скорости света.
Таким образом, если два события связаны между собой световым сигналом, то интервал между ними равен нулю во всех инерциальных системах отсчета. Этот результат является математическим выражением абсолютного характера скорости света.
Инвариантность интервала. Для любой другой пары событий, не связанных световым сигналом, интервал отличен от нуля, но величина его во всех инерциальных системах отсчета одинакова:

В этом легко убедиться с помощью преобразований Лоренца (4), подставив в левую часть выражения для х, у, z и  через координаты и время этого же события
через координаты и время этого же события  и
и  в другой системе отсчета. Инвариантность интервала означает, что утверждение «два события разделены интервалом
в другой системе отсчета. Инвариантность интервала означает, что утверждение «два события разделены интервалом  имеет абсолютный характер, т. е. оно справедливо во всех инерциальных системах отсчета.
имеет абсолютный характер, т. е. оно справедливо во всех инерциальных системах отсчета.
Классификация интервалов. Понятие интервала между событиями является обобщением понятий промежутка времени и расстояния между точками. В зависимости от того, какая составляющая — временная или пространственная — преобладает в рассматриваемом интервале, возникает деление интервалов на времениподобные и пространственноподобные. Для времениподобного интервала  . В этом случае всегда можно найти такую систему отсчета К, в которой рассматриваемые события происходят
. В этом случае всегда можно найти такую систему отсчета К, в которой рассматриваемые события происходят
в одной точке, т. е.  и промежуток времени между ними в такой системе отсчета является собственным временем
и промежуток времени между ними в такой системе отсчета является собственным временем 

Таким образом, для событий, разделенных времениподобным интервалом, всегда существует такая система отсчета, в которой этот интервал (с точностью до постоянного множителя с) представляет собой просто промежуток времени  между этими событиями. Для этих событий понятия «раньше», «позже» имеют абсолютный характер. Очевидно, что между такими событиями может иметь место причинно-следственная связь.
между этими событиями. Для этих событий понятия «раньше», «позже» имеют абсолютный характер. Очевидно, что между такими событиями может иметь место причинно-следственная связь.
Для событий, разделенных пространственноподобным интервалом,  а интервал является мнимым числом. В этом случае всегда можно найти такую систему отсчета К, в которой эти события происходят одновременно, т. е.
а интервал является мнимым числом. В этом случае всегда можно найти такую систему отсчета К, в которой эти события происходят одновременно, т. е. 

Абсолютная величина пространственноподобного интервала представляет собой пространственное расстояние между событиями в той системе отсчета, в которой эти события произошли одновременно. Понятия «одновременно», «раньше», «позже» для таких событий относительны: всегда можно указать такие системы отсчета, в которых первое событие происходит раньше второго, и такие, в которых второе происходит раньше первого. Ясно, что между событиями, для которых теряют абсолютный смысл понятия «раньше» и «позже», не может быть причинно-следственной связи.
Впрочем, невозможность причинной связи между событиями, разделенными пространственноподобным интервалом, для которых  непосредственно видна из того, что никакой сигнал, никакое взаимодействие не может распространяться со скоростью, большей с.
непосредственно видна из того, что никакой сигнал, никакое взаимодействие не может распространяться со скоростью, большей с.
Равный нулю интервал между событиями, связанными световым сигналом, называют светоподобным.
Подчеркнем еще раз, что разделение интервалов между событиями на времениподобные и пространственноподобные вследствие инвариантности интервала является абсолютным, т. е. не зависящим от системы отсчета.
Закон преобразования скорости. Преобразования Лоренца для координат и времени события при переходе от одной инерциальной системы отсчета к другой позволяют сразу получить и закон преобразования скорости частицы. Пусть некоторая частица за малый промежуток времени  по часам системы отсчета К переместилась из точки с радиус-вектором
по часам системы отсчета К переместилась из точки с радиус-вектором  в точку с радиусом-вектором
в точку с радиусом-вектором  Тогда по определению скоростью и этой частицы относительно системы К
Тогда по определению скоростью и этой частицы относительно системы К
называется предел отношения  при
при  . Скоростью
. Скоростью  этой же частицы в системе отсчета
этой же частицы в системе отсчета  будет предел отношения
будет предел отношения  где
где  промежуток времени и изменение радиуса-вектора в К для той же пары событий, т. е. для конечного и начального положений частицы. Применяя преобразования Лоренца (4) к конечному и начальному положениям частицы и вычитая их почленно, получим
промежуток времени и изменение радиуса-вектора в К для той же пары событий, т. е. для конечного и начального положений частицы. Применяя преобразования Лоренца (4) к конечному и начальному положениям частицы и вычитая их почленно, получим

Разделив почленно первые три равенства на четвертое, находим

Переходя в этих формулах к пределу при  получим
получим

Выражения (7) представляют собой закон преобразования скорости частицы при переходе от одной инерциальной системы отсчета к другой. Отметим, что поперечные к направлению относительной скорости систем отсчета компоненты скорости частицы  в отличие от поперечных координат
в отличие от поперечных координат  не остаются неизменными. Это связано с тем, что при переходе от одной системы отсчета к другой время преобразуется.
не остаются неизменными. Это связано с тем, что при переходе от одной системы отсчета к другой время преобразуется.
В предельном случае  релятивистские формулы (7) переходят в формулы классической механики:
релятивистские формулы (7) переходят в формулы классической механики:

Релятивистский закон преобразования скорости согласуется, разумеется, с исходным постулатом об инвариантности скорости света. Рассмотрим, например, в системе отсчета К световой импульс, распространяющийся вдоль оси х. Для такого импульса  Тогда, согласно (7), для скорости этого же импульса в системе отсчета К получим
Тогда, согласно (7), для скорости этого же импульса в системе отсчета К получим

т. е. импульс и в системе К распространяется вдоль оси х со скоростью с.
Аберрация света. В качестве примера применения релятивистского преобразования скорости рассмотрим точечный источник света, покоящийся в системе К и равномерно излучающий свет по всем направлениям (рис. 8).
Рассмотрим те  светового потока, которые источник излучает в переднюю полусферу в системе отсчета К. С точки зрения наблюдателя в системе К, относительно которой источник движется со скоростью
светового потока, которые источник излучает в переднюю полусферу в системе отсчета К. С точки зрения наблюдателя в системе К, относительно которой источник движется со скоростью  излучение уже отнюдь не будет изотропным: эти
излучение уже отнюдь не будет изотропным: эти  будут излучаться преимущественно вперед в конус с углом 6 (рис. 9), причем
будут излучаться преимущественно вперед в конус с углом 6 (рис. 9), причем 

Рис. 8. Неподвижный источник света излучает равномерно по всем направлениям
В самом деле, в системе К луч света, ограничивающий рассматриваемый пучок, направлен вдоль оси у и для него 
Переходя в систему отсчета К, мы для этого же луча получим, согласно формулам (7),

откуда

При скорости источника к, близкой к скорости света, пучок света сконцентрируется в узкий конус, направленный вперед по движению, с осью, совпадающей с направлением движения источника.

Рис. 9. Для наблюдателя, относительно которого источник света движется, излучение не является изотропным
Совершенно аналогично с помощью релятивистского закона преобразования скорости объясняется явление звездной аберрации. Движущийся наблюдатель обнаружит искажение картины звездного неба: для него Вселенная «сжата» в направлении его движения по сравнению с картиной, которую видит в том же направлении неподвижный относительно звезд наблюдатель. Если движущийся наблюдатель будет менять свою скорость, то он обнаружит, что звездное небо «переливается» вокруг него: направления, в которых он видит звезды, будут все время меняться, не образуя постоянных углов друг с другом. Именно в таком положении находится наблюдатель на Земле, обращающейся вокруг Солнца. Каждые полгода скорость Земли в ее годичном движении  меняет направление на противоположное. В аберрации света звезд обнаруживается, конечно, не сама скорость Земли, а тот факт, что эта
меняет направление на противоположное. В аберрации света звезд обнаруживается, конечно, не сама скорость Земли, а тот факт, что эта
скорость изменяется: в разное время года положения звезд сдвинуты по-разному.
• Покажите, что в предельном случае малых скоростей  с преобразования Лоренца переходят в преобразования Галилея.
с преобразования Лоренца переходят в преобразования Галилея.
• Получите из формул преобразований Лоренца выражения для релятивистского преобразования промежутков времени между двумя событиями и для лоренцева сокращения длины движущегося стержня.
• Что такое интервал между двумя событиями? Докажите его инвариантность.
• В каких случаях интервал между двумя событиями называется светоподобным? времениподобным? пространственноподобным? Поясните связь этой классификации интервалов с возможностью причинно-следственной связи между событиями.
• Почему при движении системы отсчета  вдоль оси х системы преобразуются не только х-проекция скорости частицы, но также и
вдоль оси х системы преобразуются не только х-проекция скорости частицы, но также и  и
и  -проекции?
-проекции?
• Как релятивистская кинематика объясняет явление звездной аберрации?
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
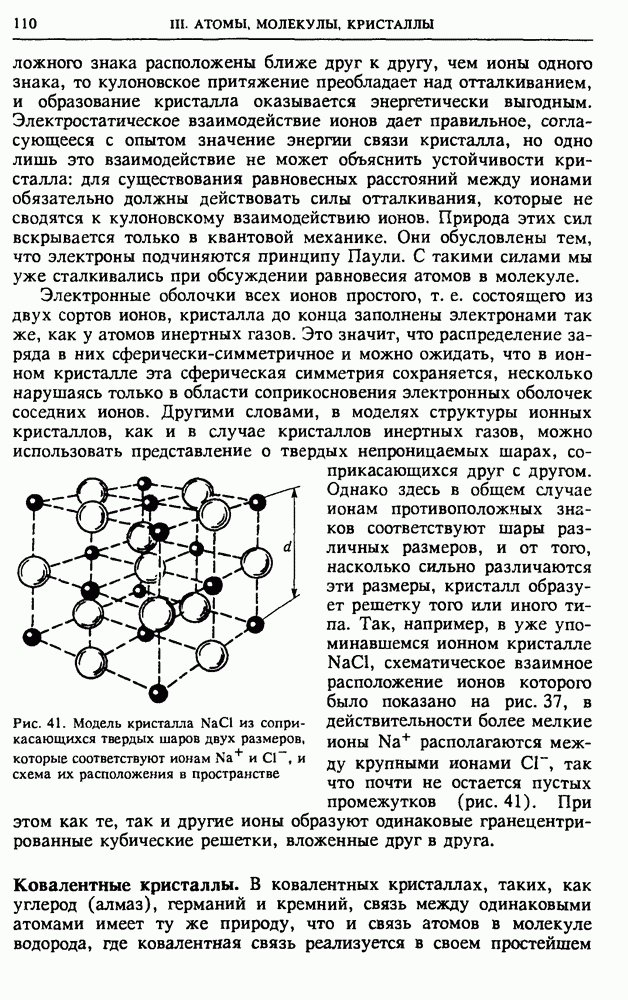
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
- § 13. Кристаллы
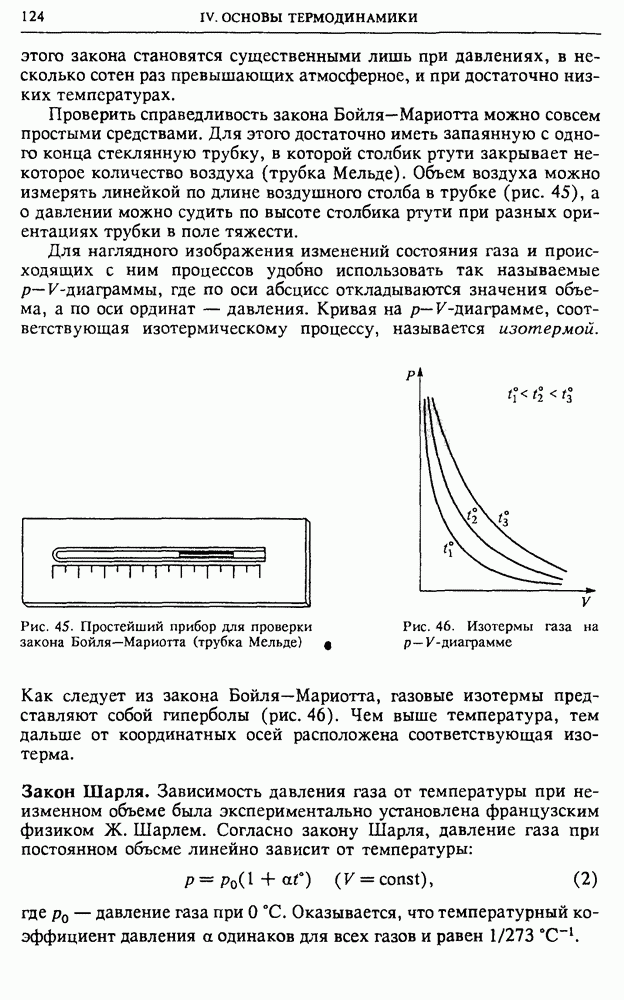
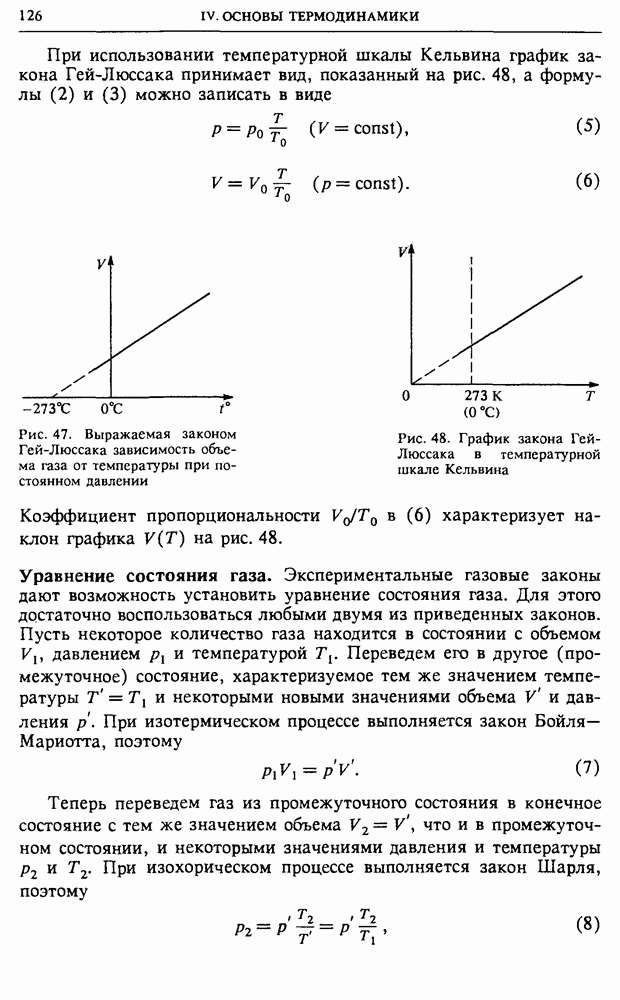
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
- § 15. Уравнение состояния газа
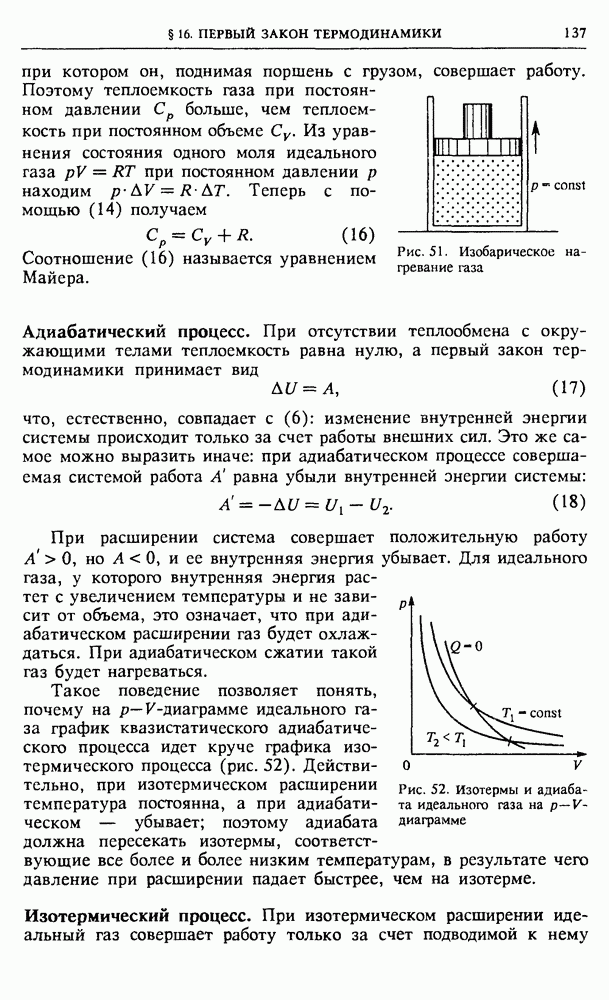
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы