| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Свет — частицы или волны?
Корпускулярно-волновой дуализм. Попробуем использовать соотношения неопределенностей, чтобы разобраться в вопросе: что же все-таки такое свет частицы или волны? Как мы видели, некоторые оптические явления свидетельствуют в пользу волновых представлений, другие могут быть объяснены только с корпускулярной точки зрения. Наконец, существует целый ряд оптических явлений, которые допускают объяснение как с точки зрения волновых, так и с точки зрения корпускулярных представлений о свете.
Рассмотрев несколько примеров, мы могли убедиться, что при анализе конкретных явлений эта двойственная природа света никак не мешала нашим рассуждениям и не приводила к логическим противоречиям. Нам только нужно было выбрать, на волновом или корпускулярном языке вести рассмотрение, и последовательно придерживаться выбранного способа описания.
Противоречие возникает только тогда, когда мы пытаемся составить общее представление о свете. Действительно, соотношение  или
или  связывает волновые и корпускулярные свойства фотона: правые части содержат величину
связывает волновые и корпускулярные свойства фотона: правые части содержат величину  определяемую из интерференционных явлений, а левые части, Е и
определяемую из интерференционных явлений, а левые части, Е и  характеризуют фотон как частицу. Но именно эти то свойства света и не могут быть логически непротиворечиво объяснены классической физикой, ибо с точки зрения классической физики понятия волны и частицы являются взаимоисключающими.
характеризуют фотон как частицу. Но именно эти то свойства света и не могут быть логически непротиворечиво объяснены классической физикой, ибо с точки зрения классической физики понятия волны и частицы являются взаимоисключающими.
Частицы и волны в классической физике. Действительно, в классической физике частица всегда движется по определенной траектории и в каждый момент времени имеет определенные координаты и скорость. Если вблизи траектории расположить преграды, которых траектория не задевает, то частица просто «не заметит» таких преград, если, разумеется, они не оказывают на нее силового воздействия посредством каких-либо полей. Для волнового движения характерно понятие протяженного фронта волны (или волновой поверхности), и тем самым отсутствует представление о какой-либо траектории. Помещение преград на пути волны принципиально изменяет условия ее распространения. Различия в свойствах частиц и волн настолько существенны, что не возникает даже мысли о возможности сочетания этих свойств у одного объекта. И тем не менее, в явлениях микромира оказалось, что эти свойства проявляются у одних и тех же объектов.
Мысленный опыт, снимающий логические противоречия. Для иллюстрации возникающих логических трудностей, а также для демонстрации того, как они преодолеваются квантовой теорией, рассмотрим подробнее уже упоминавшийся выше простой мысленный дифракционный опыт, схематически представленный на рис. 21.

Рис. 21. Дифракция света на двух щелях
Реальные опыты, которые могут быть осуществлены, более сложны, но их результаты подтверждают справедливость заключений, сделанных в результате анализа обсуждаемого здесь мысленного опыта.
Источник света  освещает экран А, в котором прорезаны две щели. Расстояние от А до Б велико по сравнению с расстоянием
освещает экран А, в котором прорезаны две щели. Расстояние от А до Б велико по сравнению с расстоянием  между щелями, которое в свою очередь много больше длины световой волны. На светочувствительном экране В возникает дифракционная картина, причем в местах дифракционных максимумов вырывается наибольшее число фотоэлектронов. Как и в разобранном выше опыте с дифракцией на одной щели, эксперимент показывает, что дифракционная картина сохранится и в том случае,
между щелями, которое в свою очередь много больше длины световой волны. На светочувствительном экране В возникает дифракционная картина, причем в местах дифракционных максимумов вырывается наибольшее число фотоэлектронов. Как и в разобранном выше опыте с дифракцией на одной щели, эксперимент показывает, что дифракционная картина сохранится и в том случае,
если в каждый момент времени между источником и экраном в среднем будет находиться только один фотон. Распределение множества фотонов, попавших на экран за достаточно большой промежуток времени, по-прежнему будет определяться классической картиной дифракции от двух щелей, хотя при вырывании фотоэлектронов из экрана В фотоны ведут себя как частицы, каждая из которых выбивает электрон в определенном месте экрана.
Если закрыть одну из щелей, то интерференционные полосы пропадают — распределение интенсивности на экране становится таким же, как при дифракции на одной щели, и при очень узкой щели становится практически равномерным. Поэтому мы вынуждены считать, что при движении от источника света через щели до экрана В излучение ведет себя как волна. Если попытаться объяснить результаты опыта с помощью представления о свете как о частицах, то нужно считать, что каждый фотон, по-видимому, проходит только через одну из щелей. Но тогда, в рамках чисто корпускулярных представлений, можно было бы спросить: каким образом поток независимых фотонов, каждый из которых проходит только через одну из щелей, может образовать дифракционную картину, наблюдаемую лишь при наличии обеих щелей? Или, другими словами, каким образом щель, через которую фотон не проходит, не позволяет ему попасть на те места экрана, куда он мог бы попасть, если бы эта щель была закрыта?
В этой формулировке вопроса предполагается, что фотон действительно проходит через одну из щелей. С точки зрения классической теории это допущение является естественным, ибо предполагается, что в любой момент времени фотон (как и любая другая частица) движется по определенной траектории, т. е. имеет определенные координаты, доступные измерению. Современная квантовая теория отказывается от этого допущения, утверждая, что говорить о положении фотона имеет смысл лишь в том случае, если при постановке опыта мы позаботимся об определении его координаты. Значит, если мы хотим считать, что каждый фотон действительно, подобно частице, проходит только через одну из щелей, мы должны поставить какой-либо измерительный прибор, который бы фиксировал нам факт прохождения фотона через определенную щель. Если мы попробуем с помощью специальных счетчиков С и  фиксировать, через какое отверстие проходит каждый фотон, то обнаружим, что дифракционная картина на экране В размоется. Попробуем объяснить этот экспериментальный факт, используя соотношения неопределенностей Гейзенберга. Выясним, можно ли в принципе наблюдать на экране В интерференционные полосы, если точно определять, через какие отверстия проходит фотон.
фиксировать, через какое отверстие проходит каждый фотон, то обнаружим, что дифракционная картина на экране В размоется. Попробуем объяснить этот экспериментальный факт, используя соотношения неопределенностей Гейзенберга. Выясним, можно ли в принципе наблюдать на экране В интерференционные полосы, если точно определять, через какие отверстия проходит фотон.
Если с помощью счетчиков, установленных непосредственно вблизи отверстий в экране А, мы будем определять, через какое именно отверстие проходит каждый фотон, то тем самым мы
действительно заставим свет проявлять корпускулярные свойства, ибо только для частицы имеет смысл утверждение, что она прошла через определенное отверстие, для волны вопрос о том, через какое отверстие она прошла (разумеется, если открыты оба), вообще лишен смысла.
Для того чтобы уверенно судить о том, через какое отверстие прошел фотон, нужно с помощью счетчиков определять его координату х с достаточной точностью, так чтобы ошибка  в определении координаты фотона была бы меньше половины расстояния между отверстиями:
в определении координаты фотона была бы меньше половины расстояния между отверстиями:

Однако не следует стремиться определять х-координату фотона слишком точно, так как в силу соотношения неопределенностей Гейзенберга

это приводит к слишком большой неопределенности в значении х-компоненты импульса фотона и дифракционная картина на экране В заведомо размажется, т. е. нам тогда не удастся наблюдать в этом опыте проявление волновых свойств света.
Итак, для наблюдения одновременного проявления светом корпускулярных и волновых свойств необходимо определять координату фотона с максимальной неопределенностью, совместимой с выражением (1), т. е. с возможностью установления, через какое отверстие прошел фотон, надеясь при этом, что вносимая при измерении координаты неопределенность в значении импульса  еще не приведет к полному размытию интерференционных полос. Выясним, совместимы ли эти условия.
еще не приведет к полному размытию интерференционных полос. Выясним, совместимы ли эти условия.
Какова максимально допустимая неопределенность в значении импульса  которая еще не приводит к полному уничтожению дифракционной картины? Дифракционная картина от двух отверстий, наблюдаемая на экране В, состоит из чередующихся светлых и темных полос. Угловое расстояние
которая еще не приводит к полному уничтожению дифракционной картины? Дифракционная картина от двух отверстий, наблюдаемая на экране В, состоит из чередующихся светлых и темных полос. Угловое расстояние  между направлениями на соседние максимум и минимум определяется из условия
между направлениями на соседние максимум и минимум определяется из условия  поскольку максимумы расположены в тех точках экрана В, разность хода до которых от отверстий в экране А равна целому числу длин волн. Неопределенность в значении импульса
поскольку максимумы расположены в тех точках экрана В, разность хода до которых от отверстий в экране А равна целому числу длин волн. Неопределенность в значении импульса  можно выразить через неопределенность направления импульса
можно выразить через неопределенность направления импульса  Интерференционные полосы, очевидно, не будут полностью размыты, только если
Интерференционные полосы, очевидно, не будут полностью размыты, только если  т. е.
т. е.

Используя соотношение между импульсом фотона и длиной волны  можно переписать это неравенство в виде
можно переписать это неравенство в виде

Таким образом, для проявления волновых свойств света в этом опыте должно выполняться неравенство (3), а для проявления корпускулярных свойств — неравенство (1). Объединяя эти неравенства, получаем условие одновременного проявления светом корпускулярных и волновых свойств:

Но это условие противоречит соотношению неопределенностей, а потому не может быть выполнено. Итак, установив, через какие отверстия проходят фотоны, мы теряем дифракционную картину и не можем говорить о проявлении фотонами волновых свойств. Мы рассмотрели упрощенный мысленный опыт. В более сложном варианте подобные опыты действительно были поставлены и полностью подтвердили результаты приведенного здесь анализа.
Подведем некоторые итоги. Как мы видели, отдельные фотоны обнаруживают волновое поведение, заключающееся в том, что каждый фотон проявляет интерференционные свойства независимо от других фотонов. Но, попадая на экран, фотоны обнаруживают корпускулярное поведение, заключающееся в том, что они взаимодействуют с веществом только в определенных точках. Если при этом не делать попытки экспериментально наблюдать траектории фотонов до попадания их на экран, то, пропустив большое число фотонов, мы будем наблюдать на экране дифракционную картину, предсказываемую волновой теорией. Но предсказать, в какое место экрана попадет определенный фотон, невозможно. Это можно сделать только в вероятностном смысле: вероятность попасть фотону в область минимума мала. Для проверки такого предсказания нужно большое число фотонов. Если же фиксировать траектории фотонов до попадания на экран, то фотоны вовсе не проявляют волновых свойств.
Фотон — квантовый объект. Как же понимать тот факт, что фотоны выступают иногда в облике частиц, а иногда в облике волн? Квантовая теория отвечает на этот вопрос так: фотон представляет собой квантовый объект, а когда мы описываем его поведение как поведение частицы или волны, мы навязываем классическое описание этому объекту, имеющему существенно неклассическую природу. Рассматривать поведение фотона имеет смысл, только исходя из результатов измерений, совершаемых над ним. Поэтому то, как поведет себя фотон — как частица или как волна, зависит от характера проводимого над ним измерения.
Итак, что же такое свет — частицы или волны? Ни то, ни другое. Мы можем заставить материальный объект, который мы
называем светом, проявлять либо корпускулярные, либо волновые свойства. Но в принципе невозможно осуществить эксперимент, в котором свет одновременно проявлял бы и те, и другие свойства. Этим устраняется логическая трудность. Действительно, нам больше не нужно пытаться представить себе, как это фотон может быть одновременно и волной, и частицей. Теперь корпускулярноволновой дуализм мы понимаем в том смысле, что свет обладает потенциальной возможностью проявлять и волновые, и корпускулярные свойства, но они никогда не проявляются одновременно. Соотношения  означают, что между этими взаимно исключающими друг друга свойствами имеет место эквивалентность в том смысле, что меры этих свойств всегда пропорциональны. Эти свойства дополняют друг друга, ибо только их совокупность дает полное представление о свете. Но, как показывают соотношения неопределенностей, в любом явлении в зависимости от конкретных условий реализуется только одна возможность.
означают, что между этими взаимно исключающими друг друга свойствами имеет место эквивалентность в том смысле, что меры этих свойств всегда пропорциональны. Эти свойства дополняют друг друга, ибо только их совокупность дает полное представление о свете. Но, как показывают соотношения неопределенностей, в любом явлении в зависимости от конкретных условий реализуется только одна возможность.
Корпускулярно-волновой дуализм присущ не только фотонам, но и любым другим микрообъектам.
Волны де Бройля. Мы уже упоминали об экспериментах, в которых наблюдалась дифракция электронов при прохождении их сквозь кристаллы. Но еще до осуществления таких экспериментов, в 1924 г., Луи де Бройль предположил, что все частицы должны обладать волновыми свойствами, подобными волновым свойствам света, и ввел количественное соотношение между длиной сопоставляемой частице волны и импульсом частицы, аналогичное соотношению между длиной волны и импульсом фотона:

Несколько лет спустя Джермер и Дэвиссон, изучая рассеяние электронов кристаллами, обнаружили дифракцию электронов, подобную дифракции света на решетке. Атомы кристалла никеля, который использовался в опыте, образуют регулярную конфигурацию, которая действует подобно дифракционной решетке. Максимумы в распределении рассеянных кристаллом электронов находились на тех местах, для которых выполнялось условие

Но это условие совпадает с известным условием для максимумов при дифракции волн на решетке с периодом  Вычисленное по (5) значение длины волны X совпадало со значением, даваемым (4), с погрешностью до
Вычисленное по (5) значение длины волны X совпадало со значением, даваемым (4), с погрешностью до  Следовательно, электроны, отражаясь от кристалла, дифрагируют точно так же, как если бы они были волнами с длиной, предсказанной де Бройлем.
Следовательно, электроны, отражаясь от кристалла, дифрагируют точно так же, как если бы они были волнами с длиной, предсказанной де Бройлем.
Волновые свойства микрочастиц. Результаты этого опыта имеют фундаментальное значение, ибо они демонстрируют волновые свойства вещества, которые не могут быть поняты в рамках представлений о том, что вещество состоит из классических частиц. Более поздние опыты показали, что и другие частицы вещества, даже такие относительно крупные, как молекулы, также проявляют волновые свойства.
Когда реальность проявления волновых свойств микрочастицами стала очевидной, возникла необходимость как-то интерпретировать волны де Бройля, придать им определенный физический смысл. Появилась концепция «волны-пилота», в которой предполагалось, что волна в каком-то смысле «управляет» движением частицы. Но целый ряд экспериментальных фактов показывал, что такое весьма наглядное представление не приводит к внутренне непротиворечивой картине поведения микрочастиц. Правильное толкование этого вопроса стало возможным только после создания квантовой механики. Пока мы будем просто считать, что соотношение (4) дает нам длину волны, которую следует сопоставлять любому материальному объекту, если опыт показывает проявление этим объектом волновых свойств.
Еще о границах классического описания. Представления о волнах де Бройля можно, наряду с соотношениями неопределенностей Гейзенберга, использовать для выяснения вопроса о том, какой теорией, квантовой или классической, следует описывать конкретное явление. Для этого нужно сравнить сопоставляемую по формуле (4) изучаемому объекту длину волны с характерными размерами в соответствующей задаче, имея в виду, что волновые свойства объекта не играют существенной роли, пока эта длина волны не станет соизмеримой с характерными размерами. Например, длина волны электрона, находящегося в атоме водорода, сравнима с размерами самого атома. Поэтому квантовые эффекты в этом случае будут весьма существенными, и представления классической физики здесь заведомо неприменимы.
Сравним теперь длину волны де Бройля, сопоставляемую Земле, с размерами земной орбиты. Так как масса Земли  скорость Земли на орбите
скорость Земли на орбите  а расстояние от Земли до Солнца
а расстояние от Земли до Солнца  км, то
км, то

Эта величина фантастически мала. Следовательно, движение Земли будет превосходно описываться классической механикой. Любые волновые или квантовые эффекты будут в этом случае меньше, чем, например, эффекты, вызванные столкновением Земли с протоном или электроном, содержащимся в космических лучах.
Задача
Для уменьшения размеров пятна на экране электронно-лучевой трубки можно на пути разогнанного ускоряющим напряжением электронного пучка поместить две диафрагмы с отверстиями (рис. 22). Покажите, что для второго отверстия существует оптимальный диаметр, обеспечивающий наименьший размер пятна на экране.
Решение. После прохождения ускоряющего промежутка с напряжением  электроны в трубке движутся равномерно с практически одинаковыми по модулю импульсами
электроны в трубке движутся равномерно с практически одинаковыми по модулю импульсами  определяемыми из соотношения
определяемыми из соотношения

Будем сначала рассматривать электрон как классическую частицу. Пусть отверстие в первой диафрагме настолько мало, что его можно считать точечным. В этом случае диаметр пятна на экране был бы тем меньше, чем меньше отверстие во второй диафрагме. Угловой размер пятна, как видно из рис. 23, определяется соотношением

где  — диаметр отверстия во второй диафрагме,
— диаметр отверстия во второй диафрагме,  расстояние между диафрагмами. Таким образом, пятно от классических частиц можно было бы сделать сколь угодно малым.
расстояние между диафрагмами. Таким образом, пятно от классических частиц можно было бы сделать сколь угодно малым.

Рис. 22. Для уменьшения размера пятна на экране можно использовать две диафрагмы с отверстиями

Рис. 23. Угловой размер пучка  зависит от диаметра
зависит от диаметра  отверстия во второй диафрагме
отверстия во второй диафрагме
Однако из-за квантовых явлений уменьшение диаметра диафрагмы с некоторого момента приводит к расширению пятна. Оценить критический диаметр отверстия можно с помощью соотношения неопределенностей Гейзенберга.
Если электрон прошел сквозь отверстие во второй диафрагме, то неопределенность в значении его координаты в направлении поперек пучка  определяется размером отверстия
определяется размером отверстия 

Такая локализация электрона приводит к появлению у него неконтролируемой составляющей импульса поперек пучка:

В результате после прохождения диафрагмы появляется неопределенность в направлении движения электрона, характеризуемая углом 

Из (10) следует, что при уменьшении диаметра отверстия  происходит расширение пучка и как следствие увеличение пятна на экране трубки. Уменьшать отверстие в диафрагме следует до тех пор, пока размытие пучка
происходит расширение пучка и как следствие увеличение пятна на экране трубки. Уменьшать отверстие в диафрагме следует до тех пор, пока размытие пучка  не сравняется с его угловым размером 0, определяемым классическими траекториями электронов:
не сравняется с его угловым размером 0, определяемым классическими траекториями электронов:  Отсюда с помощью (7) и (10) определяем оптимальный размер отверстия во второй диафрагме:
Отсюда с помощью (7) и (10) определяем оптимальный размер отверстия во второй диафрагме:

Этот результат можно получить иначе, используя представление о связанной с электроном волне де Бройля

Если классическому представлению о движении электронов по определенным траекториям соответствует приближение геометрической оптики, то проявлению квантовых свойств отвечает дифракция волн де Бройля. Дифракционные явления дают отклонение от геометрического закона распространения лучей на углы порядка отношения длины волны к размеру препятствия или отверстия. Поэтому

Подставляя сюда вместо  де-бройлевское выражение (12) для длины волны электрона, приходим к прежнему соотношению (10).
де-бройлевское выражение (12) для длины волны электрона, приходим к прежнему соотношению (10).
• Оцените оптимальный диаметр отверстия в трубке с такими характеристиками: ускоряющее напряжение  расстояние между диафрагмами
расстояние между диафрагмами  см, расстояние до экрана L = 0,5 м.
см, расстояние до экрана L = 0,5 м.
• Поясните, в каком смысле в соотношениях  левые части характеризуют фотон как частицу, а правые — как волну.
левые части характеризуют фотон как частицу, а правые — как волну.
• Почему в классической физике представления о волне и о частице неприменимы к какому бы то ни было одному и тому же объекту?
• Поясните, каким образом в мысленном опыте по дифракции на двух щелях происходит полное размытие интерференционных полос, если фиксировать щель, через которую проходит каждый из фотонов.
• Покажите, почему возможность проявления электроном взаимоисключающих корпускулярных и волновых свойств не приводит к логическому противоречию.
• Что такое волны де Бройля? Как длина волны де Бройля зависит от массы и скорости частицы?
• Как применить представление о волнах де Бройля к выяснению возможности классического описания?
| << Предыдущий параграф | Следующий параграф >> |
- I. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Релятивистская кинематика
- § 3. Преобразования Лоренца
- § 4. Релятивистская динамика
- § 5. Примеры релятивистского движения частиц
- II. ЗАКОНЫ МИКРОМИРА. ЧАСТИЦЫ И ВОЛНЫ
- § 6. Световые кванты
- § 7. Границы применимости классической физики
- § 8. Свет — частицы или волны?
- § 9. Законы движения в квантовой физике
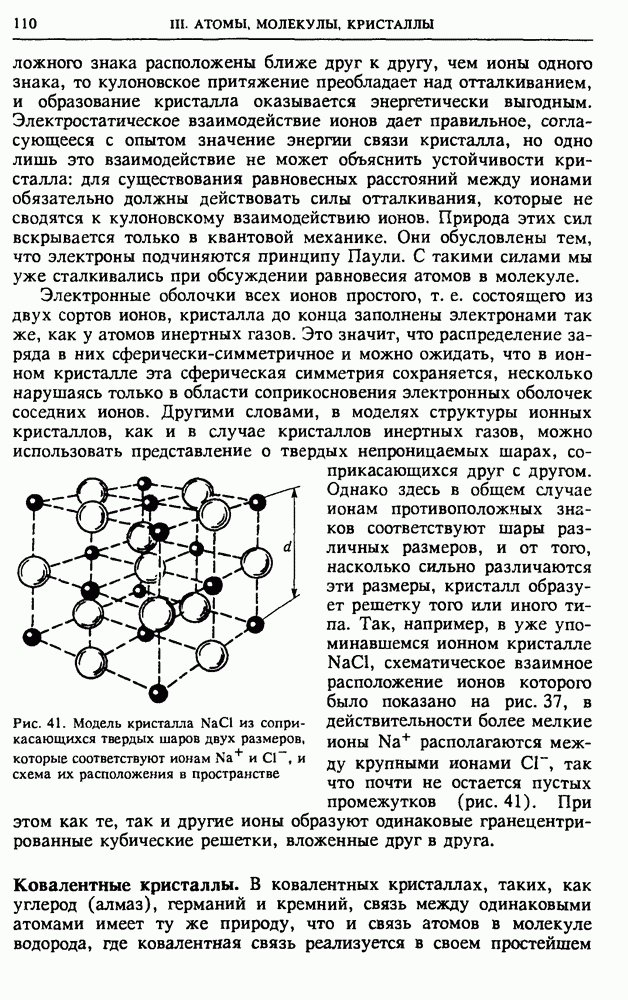
- III. АТОМЫ, МОЛЕКУЛЫ, КРИСТАЛЛЫ
- § 10. Строение атома
- § 11. Измерения в атомной физике
- § 12. Молекулы
- § 13. Кристаллы
- IV. ОСНОВЫ ТЕРМОДИНАМИКИ
- § 14. Основные понятия термодинамики
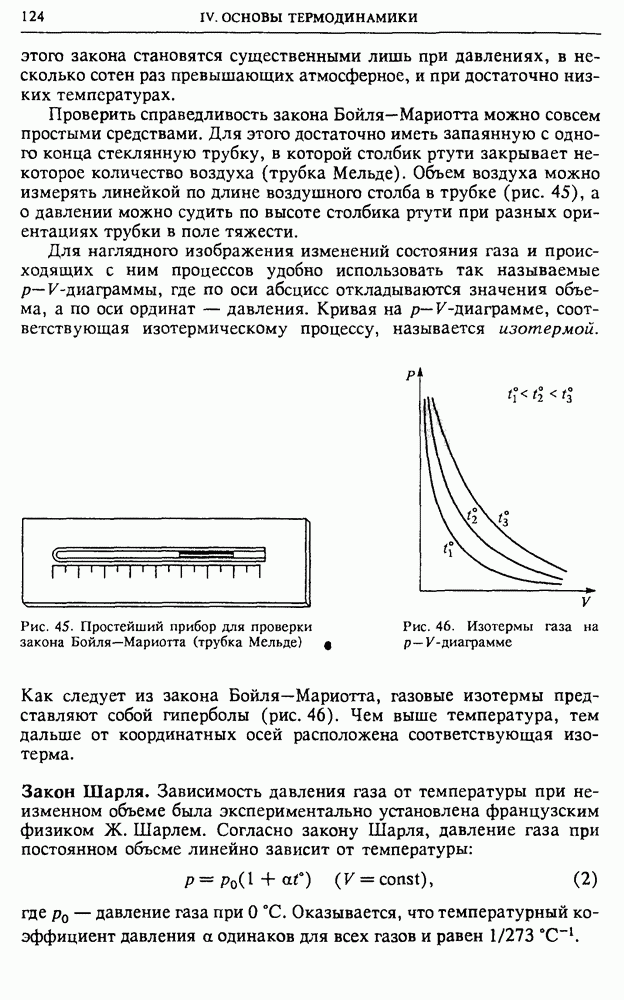
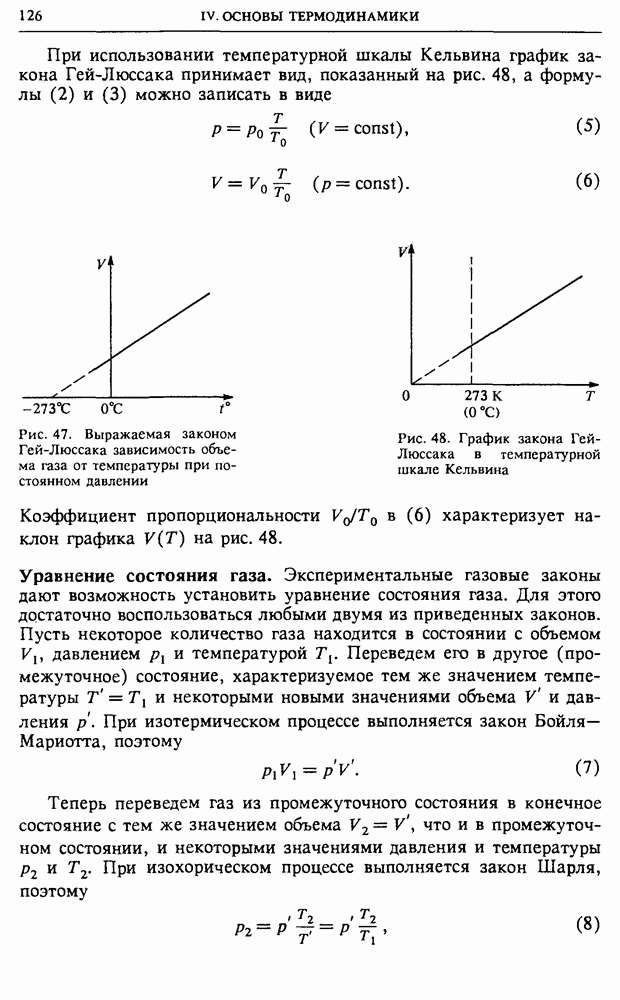
- § 15. Уравнение состояния газа
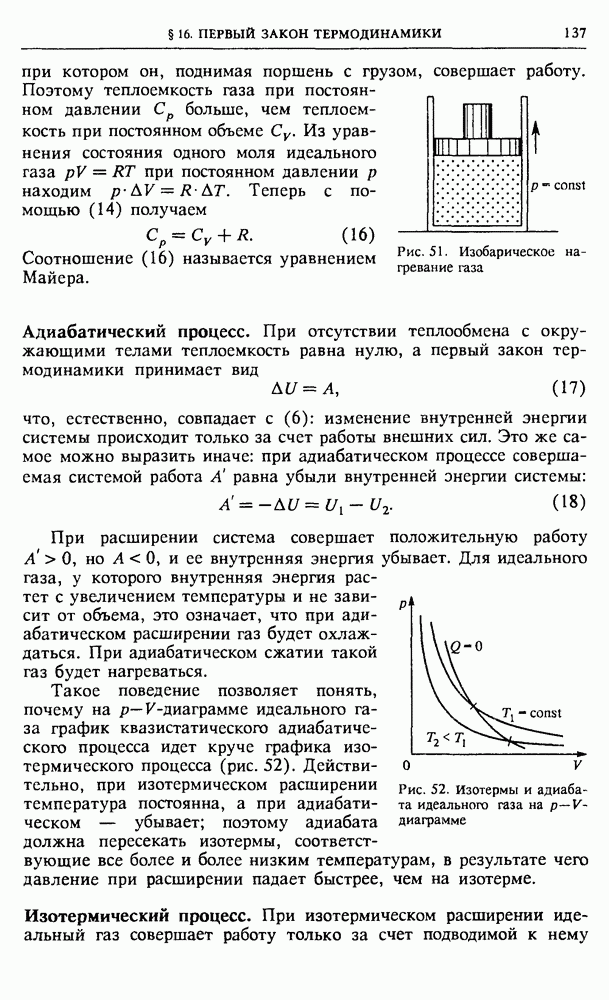
- § 16. Первый закон термодинамики
- § 17. Примеры применения первого закона термодинамики
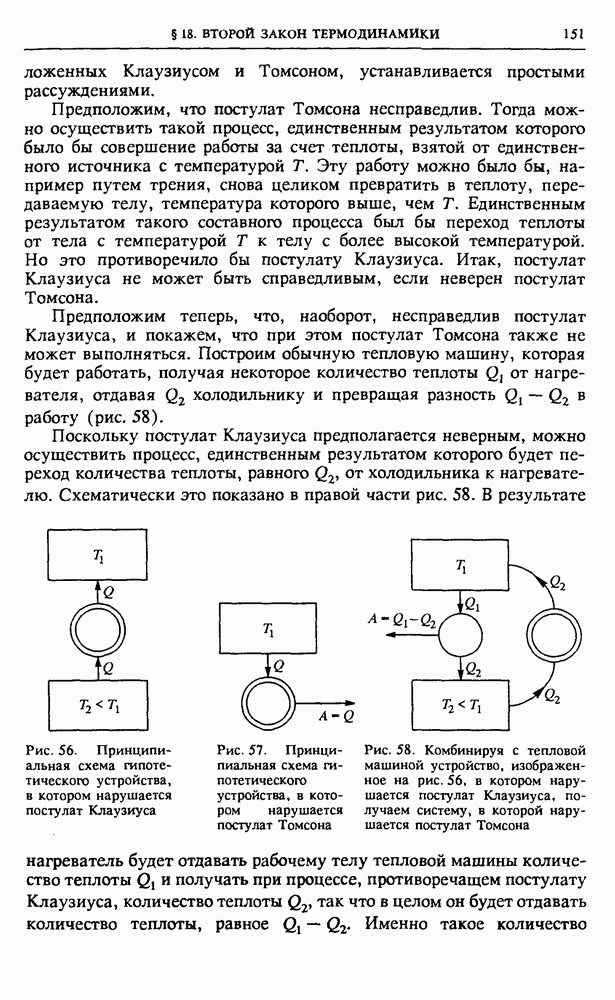
- § 18. Второй закон термодинамики
- § 19. Методы термодинамики и их применения
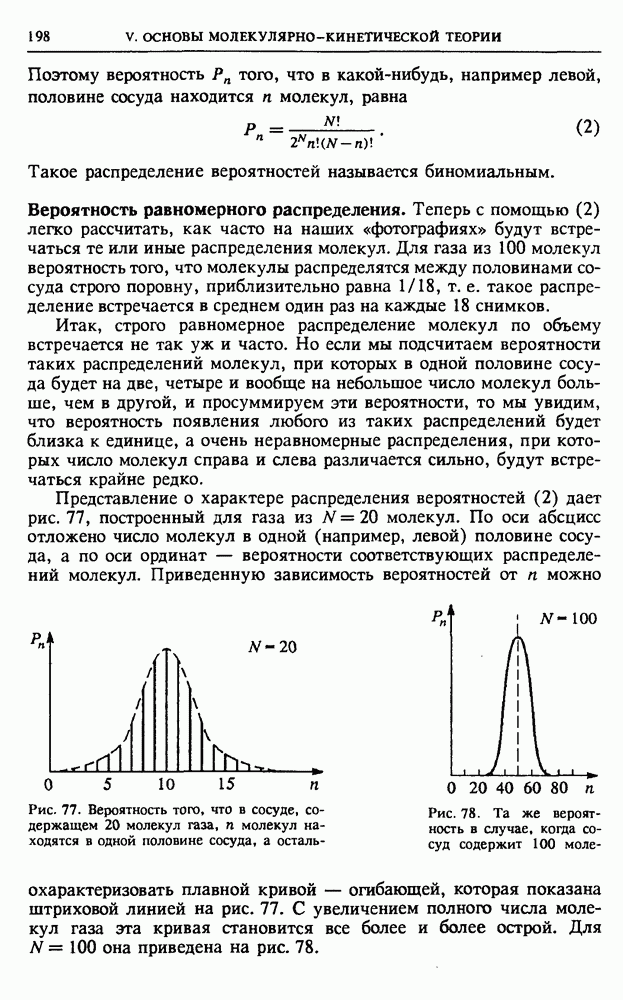
- V. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
- § 20. Экспериментальные основания статистической механики
- § 21. Молекулярно-кинетическая теория идеального газа
- § 22. Статистические распределения
- § 23. Тепловое равновесие в статистической механике
- § 24. Статистическая природа необратимости тепловых процессов
- § 25. Газы, жидкости, фазовые переходы
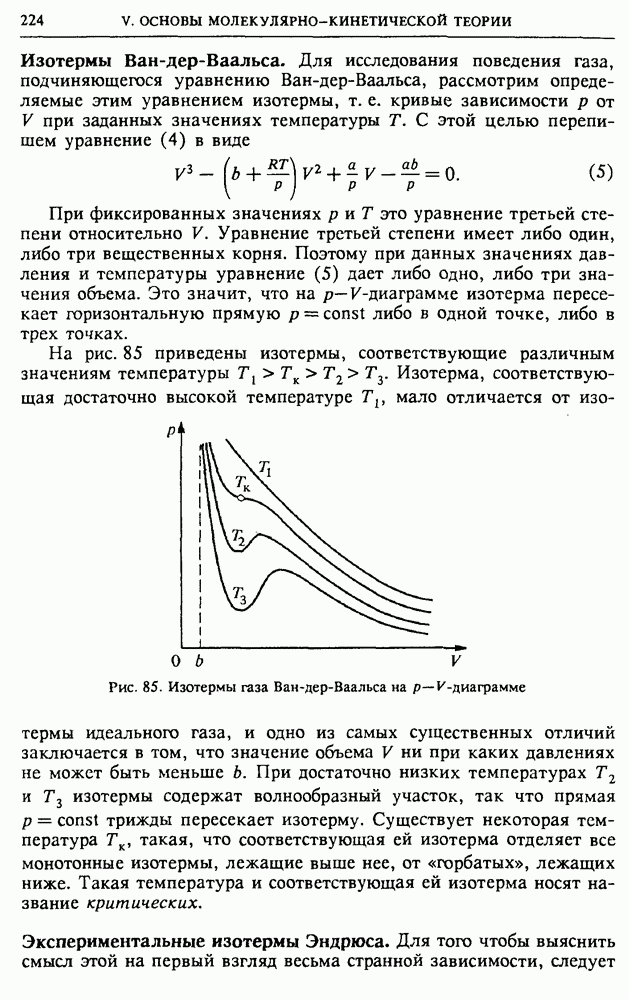
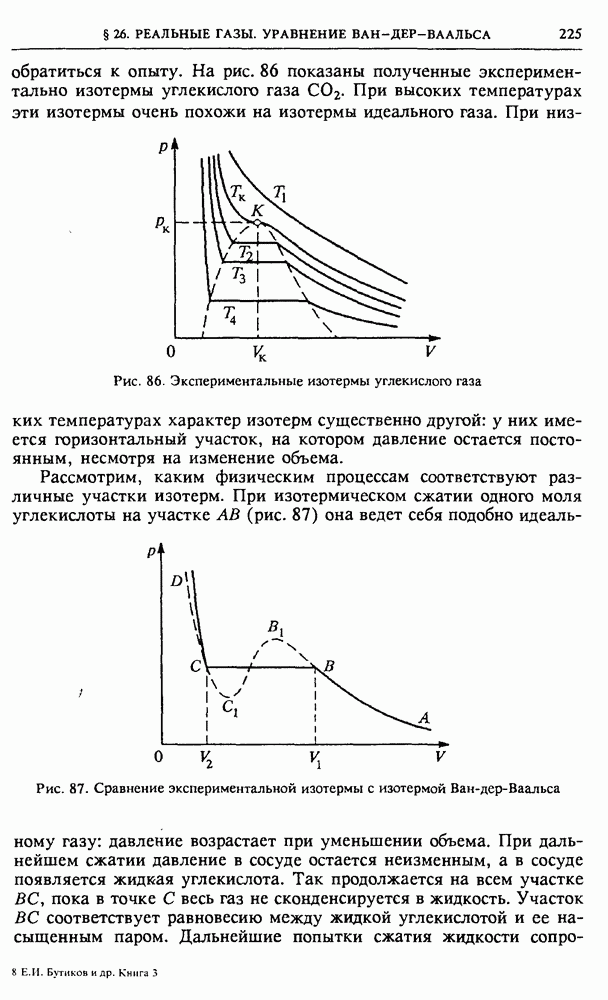
- § 26. Реальные газы. Уравнение Ван-дер-Ваальса
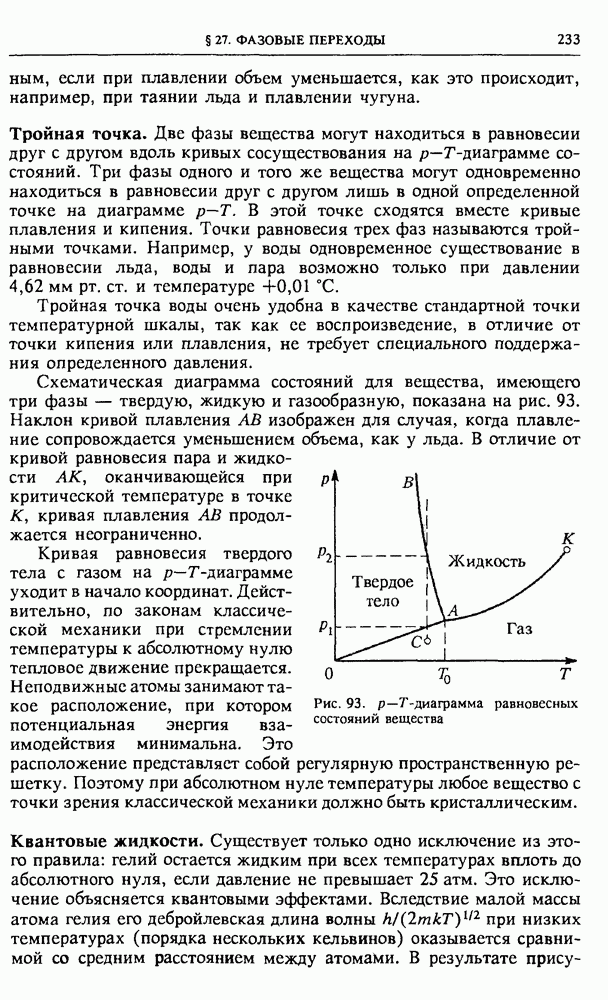
- § 27. Фазовые переходы
- VI. АТОМЫ И ИЗЛУЧЕНИЕ
- § 28. Излучение света атомами
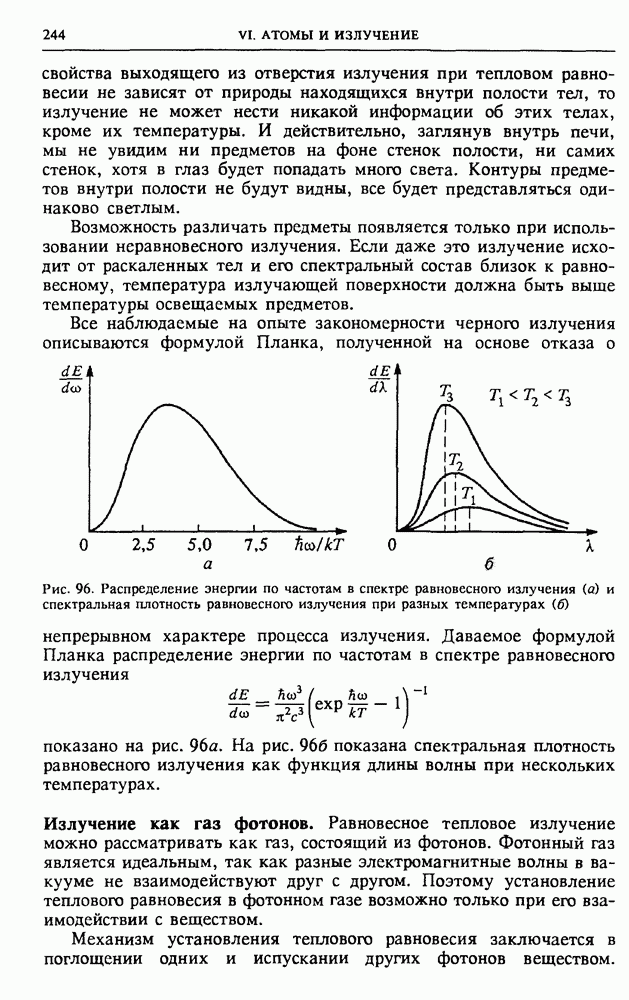
- § 29. Излучение света нагретыми телами
- § 30. Вынужденное излучение. Квантовые усилители и генераторы света
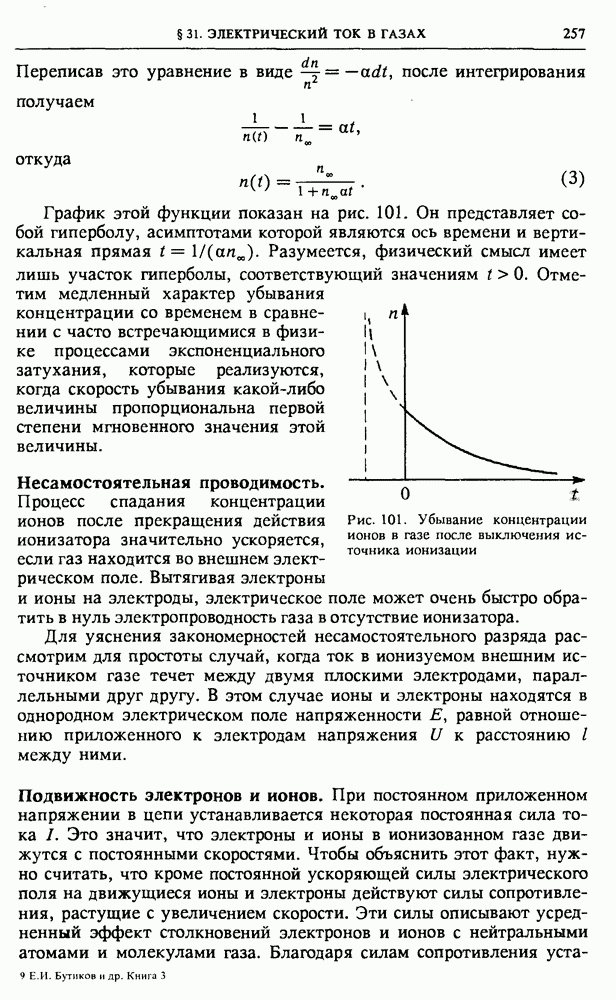
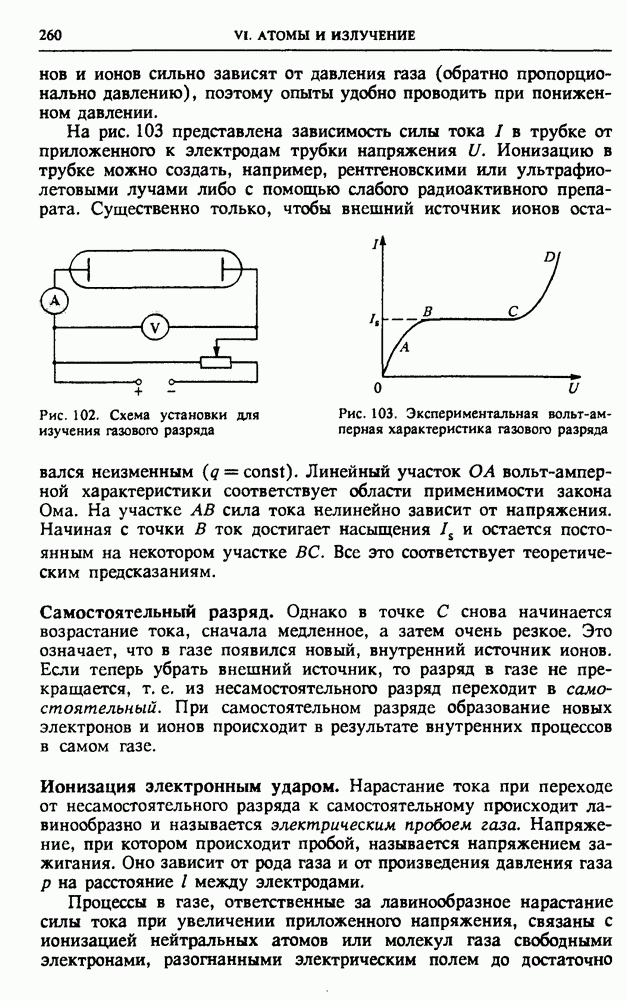
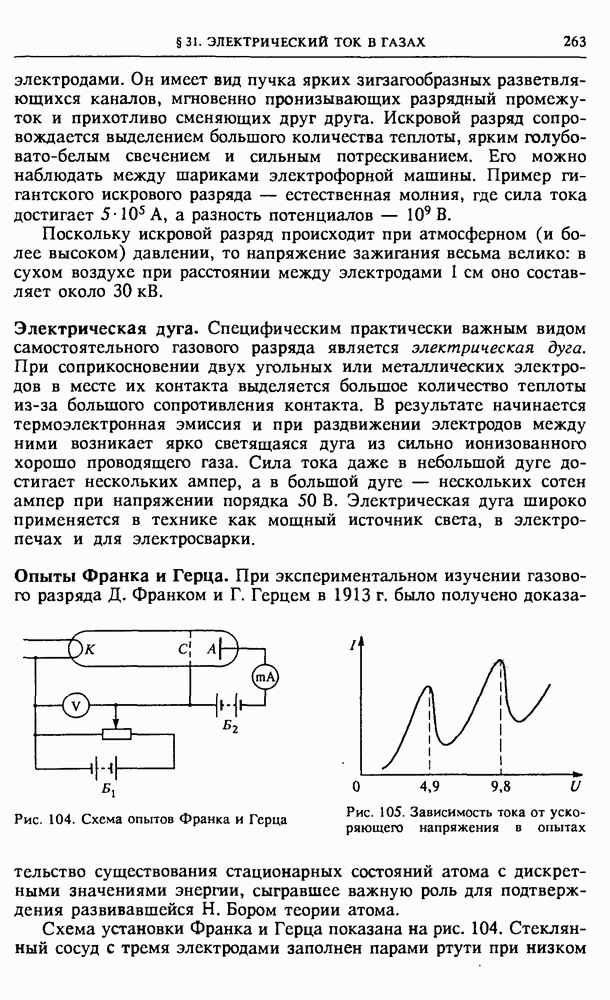
- § 31. Электрический ток в газах
- § 32. Электрический ток в жидкостях
- § 33. Плазма
- VII. ЭЛЕКТРОННЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- § 34. Электронная структура кристаллов
- § 35. Электронные свойства металлов
- § 36. Электронные свойства полупроводников
- § 37. Полупроводниковые приборы
- VIII. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38. Строение атомного ядра
- § 39. Радиоактивность. Ядерные реакции
- § 40. Элементарные частицы