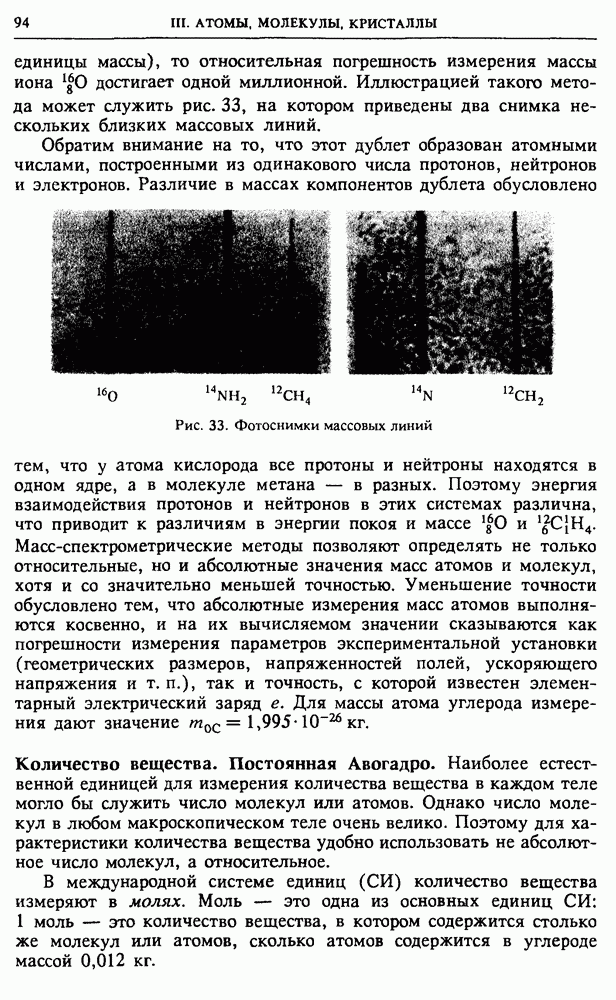
§ 21. Молекулярно-кинетическая теория идеального газа

Статистическая механика дает возможность установить связь между макроскопическими параметрами большой системы и средними значениями микроскопических величин, характеризующих отдельные молекулы. Проиллюстрируем это на простом, но важном примере уравнения состояния идеального газа.

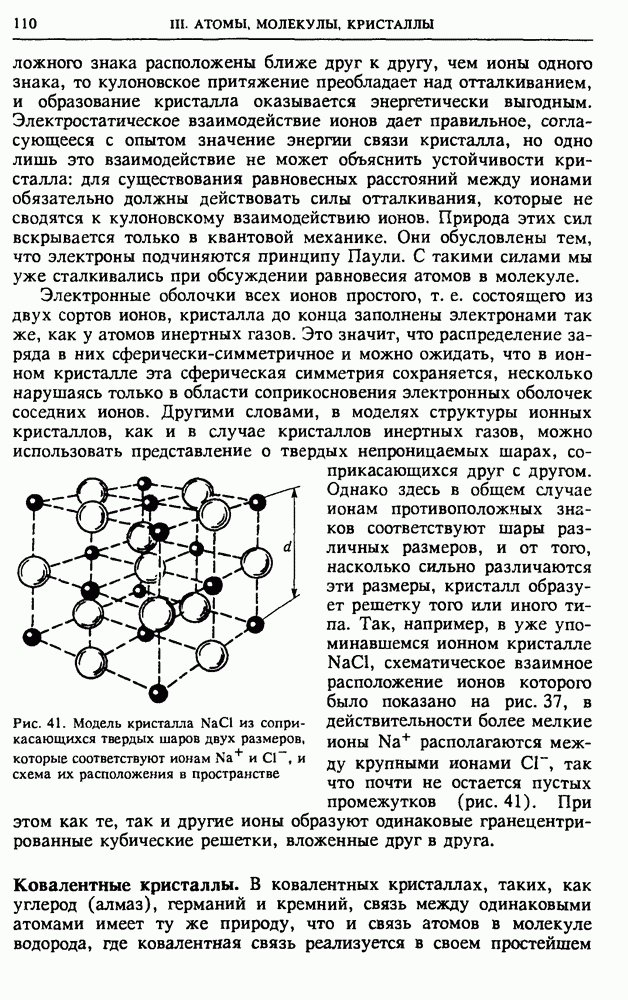
В разреженном газе расстояния между молекулами во много раз превышают их размеры. Так как молекулы электрически нейтральны, их взаимодействие между собой проявляется только на малых расстояниях. Поэтому большую часть времени молекулы газа проводят в свободном движении, и их кинетическая энергия в среднем преобладает над потенциальной.

Физическая модель газа. Вместо того чтобы рассматривать реальный газ, введем его простейшую физическую модель — идеальный газ. Будем считать, что идеальный газ — это совокупность огромного числа одинаковых молекул, размеры которых пренебрежимо малы. В рамках такой модели считается, что молекулы движутся по законам классической механики и взаимодействуют между собой только во время столкновений, которые имеют характер упругого удара.

Вывод основного уравнения кинетической теории идеального газа. Газ заключен в сосуд, и в состоянии теплового равновесия никаких макроскопических движений в нем не происходит. Рассчитаем давление, оказываемое идеальным газом на стенку сосуда. Для этого нужно сопоставить этот макроскопический параметр с результатом бомбардировки стенки отдельными молекулами. Суммарное действие молекул на поверхность можно заменить одной непрерывно действующей силой, так как молекул очень много и их столкновения со стенкой происходят очень часто. Согласно законам динамики Ньютона, эта сила равна модулю изменения

перпендикулярной к стенке составляющей импульса всех молекул, которые испытывают столкновения с ней, за единицу времени.

Столкновение молекулы со стенкой. Хотя место и время удара каждой молекулы о стенку совершенно несущественны, начинать приходится с рассмотрения удара отдельной молекулы. Пока для простоты предположим, что молекулы сталкиваются со стенкой абсолютно упруго. Когда молекула отскакивает от стенки, проекция ее скорости на направление нормали к стенке меняет знак. Направим ось х по нормали к стенке (рис. 66). Обозначим через проекцию скорости молекулы до удара, а через — после удара. Изменение импульса молекулы при столкновении со стенкой равно а передаваемый стенке импульс равен Это относится к единичному столкновению.

Рис. 66. Упругое столкновение молекулы газа со стенкой сосуда

О роли столкновений молекул. При подсчете давления газа можно не думать о столкновениях молекул между собой благодаря хаотичности их теплового движения: если в результате столкновения рассматриваемая молекула изменит свою скорость, то в большом ансамбле молекул в состоянии равновесия на смену ей непременно придет другая молекула, получившая такую же скорость в результате другого столкновения.

Так как давление газа зависит от его температуры и объема и не зависит от формы сосуда, возьмем для простоты сосуд в форме прямоугольного параллелепипеда. Двигаясь как свободная, молекула проходит расстояние между противоположными стенками за время так что второе столкновение с той же стенкой произойдет спустя время Следовательно, за достаточно большое время I молекула нанесет по данной стенке ударов, передавая ей каждый раз импульс . В результате за время эта молекула передаст стенке импульс, равный

Суммирование по всем молекулам. Для нахождения импульса, передаваемого стенке всеми молекулами газа, нужно сложить результаты действия всех молекул. Силу давления на стенку мы получим, разделив полный передаваемый импульс на время а давление — разделив эту силу на площадь стенки:

Здесь — объем сосуда, в котором заключен газ, проекция скорости молекулы на перпендикулярную к стенке сосуда ось х. Обратим внимание на то, что сумма квадратов деленная на число молекул представляет собой среднее значение квадрата проекции скорости одной молекулы:

Поэтому формулу (1) можно переписать в виде

Среднее значение квадрата скорости. Входящую в (3) величину можно выразить через среднее значение квадрата скорости молекулы . В самом деле, Для средних значений, очевидно, справедливо Так как в состоянии равновесия все направления в газе равноправны, то

Теперь выражение (3) принимает вид

или

где — среднее число молекул газа в единице объема, или концентрация молекул.

Выражение (5) или (6) называют основным уравнением кинетической теории идеального газа. Макроскопический параметр, характеризующий газ в целом, — давление — выражен здесь через среднее значение микроскопического параметра — квадрата скорости отдельной молекулы.

Идеальный газ в статистической механике и термодинамике. Рассмотрим подробнее полученное уравнение. В его правой части можно увидеть среднюю кинетическую энергию одной молекулы

Так как внутренняя энергия идеального газа состоит только из кинетической энергии хаотического теплового движения его молекул, то произведение и представляет собой внутреннюю энергию идеального газа из молекул. Поэтому уравнение (5) можно переписать в виде

Таким образом, в рассматриваемой статистической модели идеального газа произведение давления на объем равно (с точностью до множителя 2/3) внутренней энергии

В термодинамике идеальным газом был назван газ, для которого точно выполняется эмпирическое уравнение Клапейрона—Менделеева. Сравнивая (8) с уравнением Клапейрона—Менделеева

получаем выражение для внутренней энергии одного моля идеального газа:

Мы видим, что внутренняя энергия идеального газа пропорциональна термодинамической температуре Т и не зависит от объема. Это значит, что рассмотренная здесь статистическая модель адекватна представлению об идеальном газе, введенному в термодинамике. Эта модель соответствует одноатомному газу, поскольку его молекулы рассматривались как материальные точки, вся кинетическая энергия которых сводится только к энергии поступательного движения. Для двухатомных и многоатомных молекул необходимо было бы учитывать еще и кинетическую энергию их вращения как целого и энергию колебаний входящих в них атомов.

Используя соотношение (10) для внутренней энергии одноатомного газа, можно получить явное выражение для его молярной теплоемкости при постоянном объеме:

Видно, что это универсальная постоянная величина, не зависящая от химического состава газа, его молярной массы и других характеристик газа в условиях, когда к нему применима модель одноатомного идеального газа.

Физический смысл температуры. Соотношению (10) можно придать другой вид, если рассматривать не внутреннюю энергию одного моля газа, а среднюю кинетическую энергию, приходящуюся на одну молекулу

где универсальная постоянная

равная отношению универсальной газовой постоянной к постоянной Авогадро называется постоянной Больцмана в честь выдающегося австрийского физика Больцмана, основоположника теории кинетических явлений.

Формула (2) позволяет установить физический смысл термодинамической температуры Т — физической величины, которая была введена ранее феноменологически. Этот макроскопический параметр, как видно из (12), характеризует среднее значение кинетической энергии хаотического теплового движения одной молекулы в состоянии термодинамического равновесия.

Интересно отметить, что средняя энергия теплового движения молекул зависит только от температуры газа. При данной температуре средняя кинетическая энергия поступательного хаотического движения молекул не зависит ни от химического состава газа, ни от массы молекул, ни от давления газа, ни от объема, занимаемого газом.

Равнораспределение энергии по степеням свободы. Молекула одноатомного идеального газа, рассматриваемая как материальная точка, имеет три степени свободы. Равенство средних значений квадратов проекций скорости молекулы, выражаемое соотношением (4), позволяет сделать вывод о том, что на каждую степень свободы в состоянии термодинамического равновесия в среднем приходится одна и та же энергия. Эта энергия, как следует из (12), равна

Оказывается, что этот результат имеет универсальный характер: средняя кинетическая энергия, приходящаяся на каждую степень свободы, одинакова и равна Это утверждение относится не только к газам, оно справедливо для теплового движения молекул в жидкостях и твердых телах, ионов и электронов в плазме и даже для макроскопических тел, совершающих броуновское движение в результате хаотических ударов молекул окружающей среды.

Давление газа и температура. Соотношения (7) и (12) позволяют переписать основное уравнение кинетической теории идеального газа (6) так, что давление газа выражается только через его концентрацию и температуру:

Смеси различных газов. Поскольку в состоянии теплового равновесия средняя кинетическая энергия молекул зависит только от температуры, то в смеси газов средние кинетические энергии молекул разных сортов одинаковы:

Поэтому легкие молекулы движутся в среднем быстрее тяжелых.

Полное давление смеси идеальных газов равно сумме давлений, которые имел бы каждый из газов, составляющих смесь, если удалить из сосуда остальные газы. В этом можно убедиться, буквально повторяя приведенный вывод уравнения (6) и учитывая, что импульс, передаваемый стенке молекулами каждого сорта, обусловливает то

давление, которое создавал бы один этот газ. Этот закон был открыт

опытным путем Дж. Дальтоном и носит его имя.

• Как вы понимаете утверждение, что в разреженном газе из электрически нейтральных молекул их кинетическая энергия в среднем преобладает над потенциальной?

• Опишите модель идеального газа, используемую в молекулярно-кинетической теории. Какую роль играют в этой модели собственные размеры молекул и их столкновения между собой?

• Чем определяется импульс, передаваемый стенке молекулой в единичном соударении с ней?

• Сформулируйте основные этапы вывода уравнения (5) кинетической теории газа. Какие гипотезы положены в основу вывода?

• Приведите аргументы, подтверждающие заключение о равенстве средних значений квадратов проекций скоростей молекулы на оси х, у, z.

• Приведите соображения, свидетельствующие о соответствии рассмотренной статистической модели идеального газа и модели идеального газа, принятой в термодинамике.

• Поясните, почему формулы (8), (10) и (11) применимы только для одноатомного газа.

• Как средняя энергия хаотического теплового движения молекул связана с температурой системы?

• Каким образом в статистической механике раскрывается физический смысл температуры?

• Какой вывод о скоростях теплового движения молекул разной массы в смеси газов можно сделать на основе представлений о равнораспределении кинетической энергии по степеням свободы?

О микроскопических моделях. Вернемся еще раз к приведенному выше выводу основного уравнения кинетической теории идеального газа. Прежде всего отметим то обстоятельство, что в механике и электродинамике при использовании различных физических моделей мы рассматривали характеристики изучаемой системы, доступные непосредственному наблюдению и измерению в эксперименте. Но в статистической модели газа микроскопические параметры, характеризующие отдельные молекулы, непосредственно не наблюдаются, а с опытом сравниваются только их усредненные по всему ансамблю молекул значения, через которые выражаются макроскопические параметры. Поэтому особое значение здесь приобретает обоснованность предположений относительно микроскопической картины рассматриваемых явлений.

Рассмотрим с этих позиций допущения, которые были сделаны при выводе уравнения (5) или (6).

Другой вывод основного уравнения. Прежде всего могут показаться не вполне убедительными соображения, приведенные для

обоснования возможности пренебречь столкновениями молекул. Поэтому приведем несколько иной вывод, в котором этот вопрос исследуется более тщательно. Будем, как и раньше, удар молекулы о стенку считать абсолютно упругим, так что передаваемый стенке при единичном ударе импульс равен Учтем теперь, что ударяющиеся о стенку молекулы имеют разные значения проекций скорости . Рассмотрим те молекулы, у которых проекция скорости на ось лежит в малом интервале значений от до . Пусть число таких молекул в единице объема равно . За время до стенки долетят и столкнутся с ней только те из них, которые находятся внутри слоя толщиной прилегающего к участку стенки площади (рис. 67).

Рис. 67. К вычислению давления газа

Промежуток времени можно выбрать настолько малым, чтобы толщина слоя была много меньше длины свободного пробега молекул. Тогда столкновений молекул между собой в этом слое практически не будет. Итак, число ударов, наносимых рассматриваемыми молекулами за время равно а передаваемый при этом стенке импульс равен

Отсюда давление на стенку создаваемое этой группой молекул, равно

Полное давление, создаваемое всеми молекулами, получим, просуммировав (16) по всем группам молекул, скорости которых направлены к стенке, т. е. по всевозможным значениям

Вследствие хаотичности теплового движения в состоянии равновесия число летящих к стенке молекул со скоростью, лежащей в интервале от до в среднем равно числу летящих от стенки молекул со скоростью от до

Так как под знаком суммы в (17) стоит квадрат проекции скорости, то сумма только по положительным значениям равна половине суммы по всевозможным

Легко сообразить, что сумма в (18) связана со средним значением квадрата проекции скорости молекулы на ось х. В самом деле, среднее значение по совокупности из молекул определяется формулой (2). Но в (18) фактически стоит та же самая сумма, только суммирование производится не по отдельным молекулам, а по группам молекул в единице объема, имеющих почти одинаковые значения Поэтому (18) можно переписать в виде

где есть среднее число молекул в единице объема с любыми скоростями, т. е. концентрация. Дальнейшие рассуждения не отличаются от использованных ранее. В силу равноправия всех направлений при хаотическом тепловом движении , следовательно, формула (19) принимает вид

что совпадает с формулой (6).

Еще раз о роли столкновений. Теперь мы можем более четко сформулировать соображения о том, что столкновения молекул между собой не влияют на полученный результат. При подсчете числа ударов о площадку мы считали, что все молекулы из выделенной группы со скоростями от до лежащие в слое толщиной достигают стенки в течение промежутка времени Но на самом деле некоторые из них не долетят до стенки, так как в результате столкновений могут изменить направление скорости. Но кроме таких столкновений, в результате которых молекулы «уходят» из выделенной группы, в газе происходят столкновения, пополняющие эту группу молекул. В состоянии теплового равновесия, когда в газе отсутствуют макроскопические потоки, среднее число молекул в каждой группе не меняется со временем, несмотря на частые столкновения молекул. Поэтому столкновения не могут изменить среднего результата ударов молекул о стенки сосуда, выражаемого формулой (6).

Еще один вывод основного уравнения. В обоих приведенных выводах основного уравнения кинетической теории идеального газа фигурировала проекция скорости на направление нормали к стенке сосуда, и давление газа выражалось через среднее значение квадрата этой проекции (формулы (3) и (19)). Затем значение выражалось через благодаря эквивалентности всех направлений в изотропном газе. Можно построить рассуждения таким образом, чтобы с самого начала учесть эту изотропность.

Поскольку давление газа не зависит от формы сосуда, возьмем сосуд сферической формы, в котором сначала имеется только одна молекула. На рис. 68 показано сечение этого сосуда плоскостью, проходящей через траекторию молекулы и центр сосуда. При абсолютно упругом столкновении со стенкой изменение импульса молекулы, как видно из этого рисунка, дается выражением . Именно такой импульс передается стенке по нормали к ней при каждом столкновении, так как угол а при последовательных упругих столкновениях со стенкой остается прежним. Так как давление в газе определяется модулем импульса, передаваемого молекулами стенке по нормали к ней, то можно просуммировать эти модули для последовательных столкновений, невзирая на то, что при каждом соударении нормаль к стенке имеет свое направление. Как видно из рис. 68, расстояние, проходимое молекулой между любыми двумя последовательными соударениями со стенкой, равно , где — радиус сосуда. Поэтому за промежуток времени молекула нанесет по стенке ударов и передаст по нормали к ней импульс

Рис. 68. Столкновение молекулы газа со стенкой сферического сосуда

Видно, что передаваемый по нормали импульс за время не зависит от направления движения молекулы.

Для подсчета импульса, передаваемого стенке по нормали всеми молекулами газа, нужно сложить результаты действия всех молекул. Когда этих молекул много и они движутся хаотически, любой участок стенки испытывает одинаковое воздействие, и для нахождения давления нужно просто разделить суммарный передаваемый по нормали импульс на время и площадь поверхности сосуда

Здесь сумму квадратов скорости всех молекул можно заменить произведением полного числа молекул на среднее значение квадрата их скорости

Учитывая, что объем сферического сосуда равен видим, что (21) совпадает с полученной ранее формулой (5).

Отметим, что в этом выводе коэффициент 1/3 в выражении для появляется не в результате усреднения квадрата проекции скорости а как прямое следствие трехмерности физического пространства.

О характере столкновения со стенкой. Во всех приведенных выводах основного уравнения предполагалось, что столкновение молекулы со стенкой сосуда происходит по законам упругого удара.

На самом деле это предположение также является несущественным. Чтобы убедиться в этом, рассмотрим газ в прямоугольном сосуде (рис. 69), в котором стенки А и В обладают разными свойствами: удар молекул газа о стенку А абсолютно упругий, а о стенку В — неупругий. Если бы давление газа на эти стенки было различным, то в отсутствие трения о подставку сосуд с газом пришел бы в движение под действием внутренних сил. Так как сосуд в движение не приходит, мы должны заключить, что в состоянии теплового равновесия давление газа не зависит от характера взаимодействия его молекул со стенками.

Рис. 69. Стенки сосуда А и В разные: удар молекул о стенку А абсолютно упругий, о стенку В — неупругий

Объясняется это тем, что в стационарном состоянии молекулы не накапливаются на стенках: сколько молекул прилипает к стенке при неупругом ударе, столько же от нее и улетает, причем в среднем с такой же скоростью, так как температуры стенки и газа в состоянии теплового равновесия одинаковы.

В отличие от предположений о характере столкновений молекул между собой и со стенкой сосуда, принципиально важным оказывается допущение о том, что газ идеальный, т. е. его молекулы настолько малы, что их полный собственный объем мал по сравнению с объемом занимаемого газом сосуда, и что молекулы взаимодействуют только во время столкновений. Только для газа с такими свойствами и справедливо уравнение (6). Для реальных газов оно выполняется лишь приближенно.

• В чем специфика молекулярных моделей, используемых в статистической механике, в сравнении с физическими моделями в механике макроскопических тел и электродинамике?

• Поясните, почему при выводе основного уравнения кинетической теории газа учет столкновений между молекулами не влияет на окончательный результат.

• Объясните качественно, почему в сферическом сосуде импульс, передаваемый молекулой по нормали к стенке за большое время, не зависит от

угла падения на стенку. Рассмотрите также предельный случай скользящего падения, соответствующий движению молекулы по окружности радиуса R.

• Рассмотрите неупругое столкновение молекулы со стенкой сосуда. Какие предположения о механизме взаимодействия со стенкой необходимы в этом случае, чтобы модель описывала состояние теплового равновесия?

• В некоторых физических теориях рассматривается модель двумерного идеального газа, молекулы которого могут двигаться только в одной плоскости. Выведите основное уравнение кинетической теории такого газа, понимая под его давлением силу, действующую на единицу длины границы.