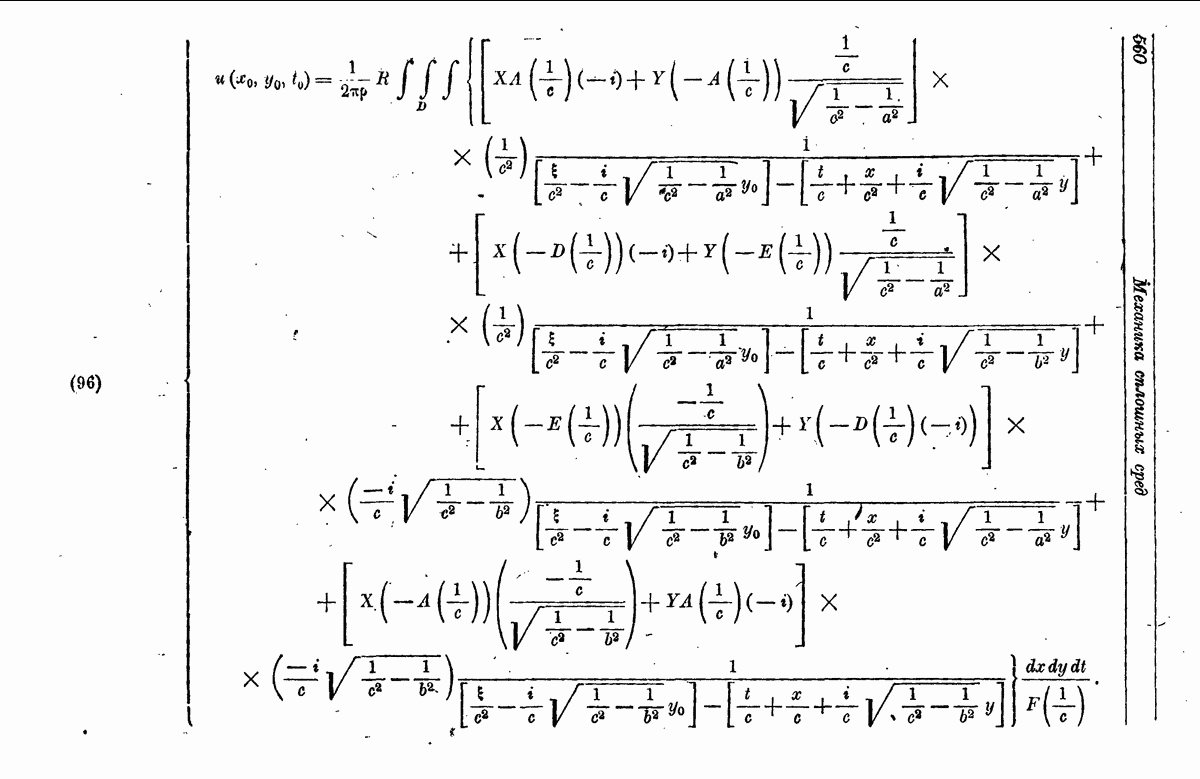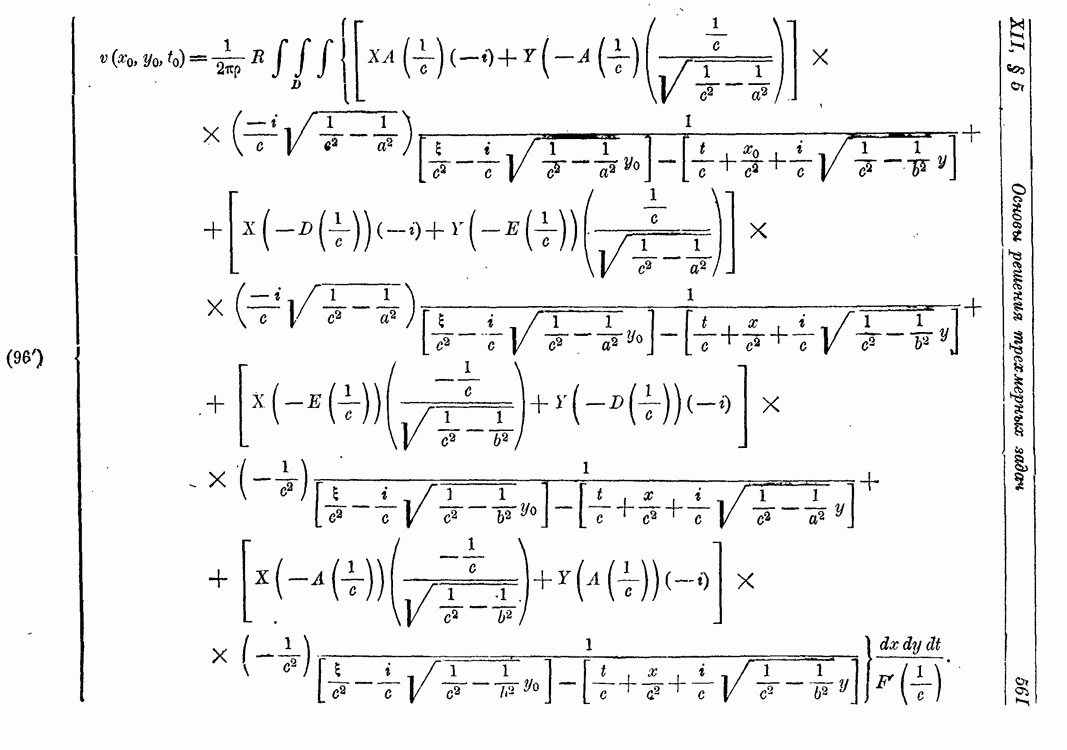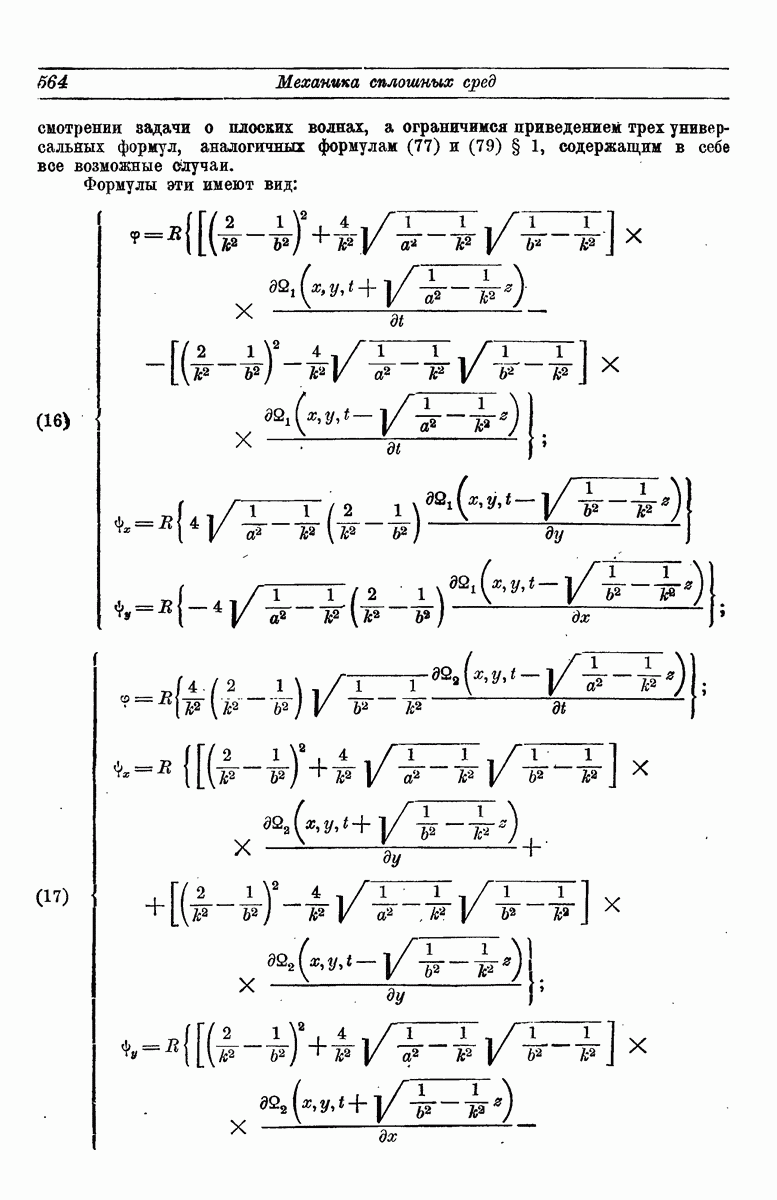| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Движение самолета
1. Вывод уравнений движения.
В случае свободного движения (§ 2) и движения в поле тяжести (§ 3) из системы уравнений движения можно выделить частичную систему, состоящую из трех уравнений, которая содержит только три координаты центра инерции  и позволяет вычислить движение центра инерции, не зная вращательного движения. Но это невозможно в том случае, когда силы
и позволяет вычислить движение центра инерции, не зная вращательного движения. Но это невозможно в том случае, когда силы  к зависят также от углов Эйлера
к зависят также от углов Эйлера  , и их производных
, и их производных
 В этом случае необходимо изучать сразу всю систему девяти совокупных дифференциальных уравнений.
В этом случае необходимо изучать сразу всю систему девяти совокупных дифференциальных уравнений.
В качестве примера рассмотрим движение самолета. Здесь, кроме силы тяжести и тяги пропеллера, которую мы предположим заданной с помощью составляющих  действуют еще сопротивления воздуха, которые зависят
действуют еще сопротивления воздуха, которые зависят  интенсивности и направления воздушного потока относительно самолета. Предположим для упрощения что это действие может быть представлено для каждой самостоятельной части самолета отдельной силой, которая зависит: 1) от скорости
интенсивности и направления воздушного потока относительно самолета. Предположим для упрощения что это действие может быть представлено для каждой самостоятельной части самолета отдельной силой, которая зависит: 1) от скорости  "средней" точки (с координатами
"средней" точки (с координатами  этой части по отношению к покоящемуся воздуху (т. е. по отношению к неподвижной системе); 2) от угла между этой скоростью и определенным направлением, жеотко связанным в средней точке с соответствующей частью самолета, "средней нормалью" с направляющими косинусами
этой части по отношению к покоящемуся воздуху (т. е. по отношению к неподвижной системе); 2) от угла между этой скоростью и определенным направлением, жеотко связанным в средней точке с соответствующей частью самолета, "средней нормалью" с направляющими косинусами  Если ввести еще "угол атаки" соответствующей части
Если ввести еще "угол атаки" соответствующей части  то
то

Результаты опыта заставляют предположить, что составляющие воздушных сопротивлений имеют вид  а координаты точек их приложения
а координаты точек их приложения  и т. д., где
и т. д., где  функции от
функции от  определяемые из опыта. Так как сила тяжести имеет вид § 3, (1), где
определяемые из опыта. Так как сила тяжести имеет вид § 3, (1), где  означает полную массу самолета, то девять уравнений движения получатся из уравнений § 1, (25), (22) и § 3, (5), если в них положить:
означает полную массу самолета, то девять уравнений движения получатся из уравнений § 1, (25), (22) и § 3, (5), если в них положить:

При этом  моменты приложенных сил относительно центра инерции самолета и кроме того предположено, что линия действия тяги пропеллера проходит через центр инерции.
моменты приложенных сил относительно центра инерции самолета и кроме того предположено, что линия действия тяги пропеллера проходит через центр инерции.  как, согласно § 1 (3):
как, согласно § 1 (3):

то мы имеем дело с девятью дифференциальными уравнениями для девяти неизвестных  Мы выполним их интегрирование только при следующих трех допущениях: плоскость
Мы выполним их интегрирование только при следующих трех допущениях: плоскость  есть плоскость симметрии самолета. Она движется все время в одной и той же (неподвижной в пространстве) вертикальной плоскости, а именно в плоскости
есть плоскость симметрии самолета. Она движется все время в одной и той же (неподвижной в пространстве) вертикальной плоскости, а именно в плоскости  Поступательная скорость в направлении
Поступательная скорость в направлении  пропеллера велика по сравнению с остальными составляющими скорости.
пропеллера велика по сравнению с остальными составляющими скорости.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ ИЗДАТЕЛЯ К ПЕРВОМУ НЕМЕЦКОМУ ИЗДАНИЮ
- ЧАСТЬ ПЕРВАЯ. КЛАССИЧЕСКАЯ МЕХАНИКА И ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 1. Световые лучи и волновые поверхности в любых телах
- 2. Принцип Ферма и световые лучи.
- 3. Световые лучи и волновые поверхности.
- 4. Дифференциальное уравнение волновых поверхностей и световых лучей.
- § 2. Оптическое отображение в общей случае анизотропной среды
- 2. Отображение элеиентов линии и элеиентов поверхности.
- 3. Нахождение световых лучей при помощи эйконала, касательные преобразования.
- § 3. Ход луча в различных средах
- 2. Изотропные среды.
- 3. Одноосные кристаллы.
- 4. Движущиеся тела
- 5. Электронный микроскоп.
- § 4. Отображение посредством симметричных оптических приборов
- 2. Диоптрика Гаусса.
- 3. Диоптрика электронных лучей.
- ГЛАВА II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ В ОБЩЕМ СЛУЧАЕ
- § 1. Уравнения движения в прямоугольных координатах
- 2. Пример: влияние сопротивления воздуха на движение точки под влиянием силы тяжести.
- 3. Уравнения движения системы свободных материальных точек и их интегралы.
- 4. Положения равновесия как особые точки.
- 5. Принцип Даламбера.
- § 2. Уравнения движения Лагранжа и Гамильтона
- 2. Примеры.
- 3. Законы энергии и импульса.
- 4. Связь с вариационным исчислением.
- 5. Уравнения движения в форме Гамильтона и Рауза.
- 6. Интегралы уравнений движения Гамильтона.
- § 3. Дифференциальные уравнения траекторий
- 2. Траектории механических систем в общем случае.
- 3. Различные виды траекторий.
- 4. Примеры.
- § 4. Теория преобразований дифференциальных уравнений Гамильтона
- 2. Касательное преобразование, канонические переменные.
- 3. Соответствующие канонические перепенные.
- 4. К интегрированию уравнения Гамильтона-Якоби в частных производных.
- 5. Введение волн, соответствующих движению точки.
- § 5. Метод разделения переменных
- 2. Критерий его применимости.
- 3. Выполнение вычисления.
- 4. Цримеры.
- 5. Свойства периодичности разделяющихся переменных.
- 6. Угловые переменные и переменные действия.
- § 6. Многократно-периодические системы
- 2. Введение общих многократно-периодических систем.
- 3. Вырождение.
- 4. Примеры.
- § 7. Однозначные интегралы и траектории, заполняющие объем
- 2. Системы однозначных интегралов; импримитивные системы.
- 3. Приближенные периоды n-кратно периодических систем.
- § 8. Некоторые сведения из статистической механики
- 2. Вычисление объемов в фазовом пространстве.
- 3. Теорема Лиувилля.
- 4. Теорема Больцмана.
- 5. Время пребывания n-кратно периодической системы.
- 6. Квазиэргодическая система, микрокаяоническое множество.
- ГЛАВА III. УСТОЙЧИВОСТЬ И МАЛЫЕ КОЛЕБАНИЯ
- § 1. Квазистатические движения
- 2. Квазистатическио движения по Раузу.
- 3. Обобщение понятна квазистатического движения по Леви-Чивита.
- § 2. Устойчивость и энергия
- 2. Энергетический критерий устойчивости Рауза.
- 3. Примеры.
- § 3. Малые колебания системы около положения равновесия, или установившегося движения
- 2. Интегрирование дифференциальных уравнений свободных колебаний.
- 3. Частные случаи колебания системы. Колебания около положений равновесия.
- § 4. Вынужденные колебания
- 2. Система с одной степенью свободы.
- § 5. Малые колебания и устойчивость
- 2. Примеры.
- 3. Центробежный регулятор.
- ГЛАВА IV. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДЫХ ТЕЛ
- 2. Скоростные координаты.
- 3. Законы движения твердого тела.
- 4. Уравнения движении Эйлера.
- 5. Формальное обобщение математических выражений (исчисление моторов).
- 6. Уравнения движения Лагранжа.
- § 2. Свободное движение твердого тела
- 2. Явный вид решений в случае периодического движения.
- 3. Квазистатические движения.
- 4. Симмеричный волчок.
- § 3. Движение в поле тяжести
- 2. Симметричный волчок. Квазистатическое движение.
- 3. Симметричный волчок. Самое общее движение.
- 4. Колебательные движения с конечной амплитудой.
- § 4. Движение самолета
- 2. Дифференциальные уравнения продольного движения.
- 3. Постоянные (перманентные) движения и малые колебания.
- 4. Продольная устойчивость горизонтального полета.
- 5. Фигондное движение.
- ГЛАВА V. МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 1. Основные понятия теории возмущений
- 2. Многократно-периодические системы.
- 3. Вырожденные системы.
- 4. Дифференциальные уравнения вековых возмущений.
- § 2. Возмущения упругих колебаний
- 2. Возмущающая сила пропорциональна кубу отклонения.
- 3. Возмущающая сила содержит члены связи.
- 4. Возмущения просто-пориодических траекторий.
- § 3. Выражение энергии для возмущенных систем
- 2. Вычисление выражения энергии.
- 3. Невозмущенная система вырождена.
- § 4. Выражение энергии для негармонических колебаний
- 2. Просто-периодическое основное движение.
- ГЛАВА VI. ЗАДАЧИ НЕБЕСНОЙ И АТОМНОЙ МЕХАНИКИ
- § 1. Движение Кеплера
- 2. Введение угловых переменных и переиенпых действия.
- 3. Вычисление координат положения.
- § 2. Возмущенное движение Кеплера
- § 3. Некоторые введения, касающиеся задачи трех тел
- 2. Приведение задачи трех тел.
- 3. Квазнстатические орбиты в случае плоской задачи трех тел.
- § 4. О касательных преобразованиях (Дополнение редактора)
- ЧАСТЬ ВТОРАЯ. МЕХАНИКА СПЛОШНЫХ СРЕД
- ГЛАВА VII. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ УПРУГОСТИ
- § 2. Анализ напряжений и деформаций
- 2. Тензор нанряженнй.
- 3. Тензор деформации.
- § 3. Закон Гука и основные уравнения теорнн упругости
- 2. Основные уравнения теории упругости.
- 3. Вычисление смещений но данный напряжениям.
- § 4. Минимальные принципы. Теоремы единственности
- 2. Принцип минимума для смещений. Принцип возможных перемещений.
- 3. Принцип минимума для напряжений.
- 4. Единственность решения.
- § 6. Уравнения движения. Единственность решения
- ГЛАВА VIII. ЗАДАЧИ НА УПРУГОЕ РАВНОВЕСИЕ
- § 1. Элементарные решения с лннейныи распределением напряжений
- 2. Растягивающая нагрузка, равномерно распределенная на концах цилиндра.
- 3. Изгиб стержня приложенными на концах его моментами.
- § 2. Кручение призматических стержней
- 2. Простейшие примеры.
- 3. Прямоугольник. Метод разложения в ряды.
- 4. Сечение, ограниченное многоугольником. Применение метода теории функций комплексной переменной.
- 5. Кручение призм, составленных из различных материалов
- § 3. Плоская пластинка, к которой приложены силы, расположенные в этой же плоскости
- 1а. Комплексное представление функции напряжений.
- 2. Сосредоточенная сила, приложенная на границе полуплоскости.
- 3. Круглая шайба (диск) под действием: нормальных: сил, приложенных к ее границе.
- 4. Растяжение полосы с отверстием.
- § 4. Пространственные задачи
- 1. Равновесие тела, ограниченного бесконечной плоскостью.
- 2. Вдавливание цилиндра в горизонтальную плоскость.
- ГЛАВА IX. ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- 1. Дифференциальное уравнение колебаний струны.
- 2. Метод разложения в ряд.
- 3. Определение постоянных по начальному состоянию струны.
- 4. Решение в форме Даламбера.
- 5. Бесконечная струна.
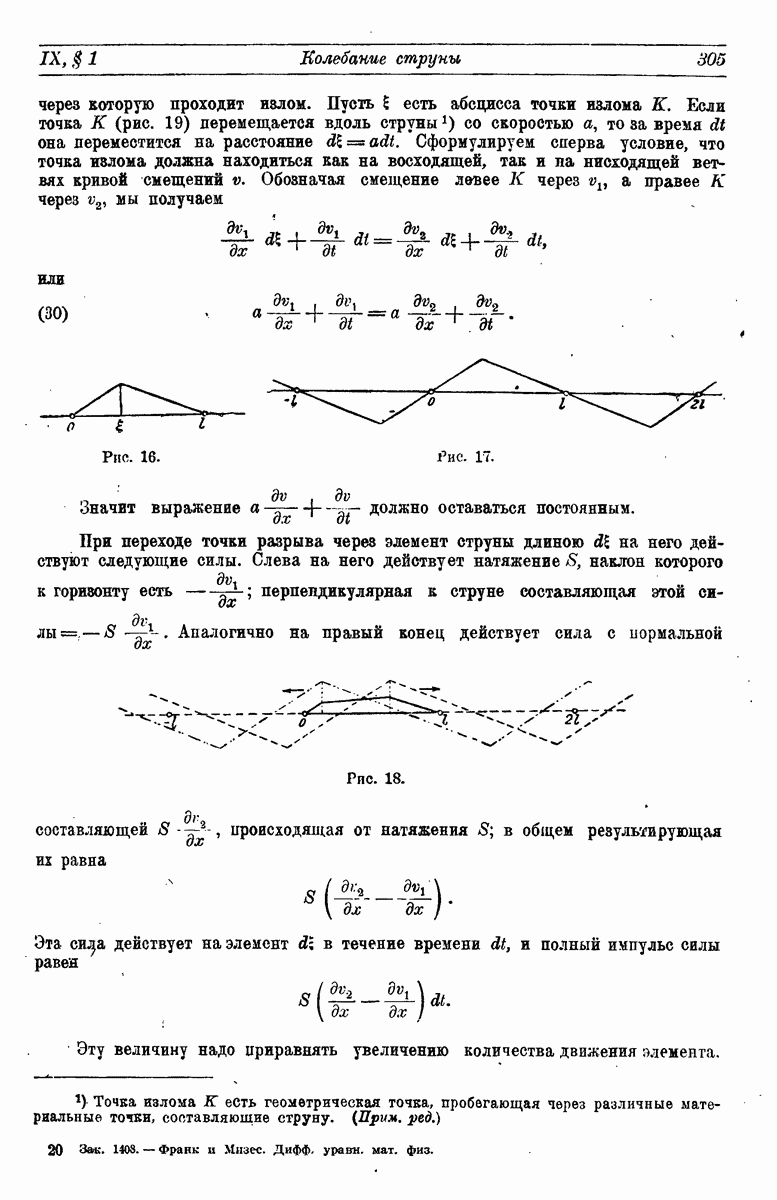
- 6. Разрывы.
- § 2. Приложение интегральных уравнений к задаче колебания
- 2. Потенциальная и кинетическая энергия.
- 3. Решение при данных начальных условиях.
- 4. Вынужденные колебания.
- 5. Колебания стержня.
- § 3. Колебания мембраны
- 1. Дифференциальное уравнение колебаний мембраны.
- 2. Прямоугольная мембрана.
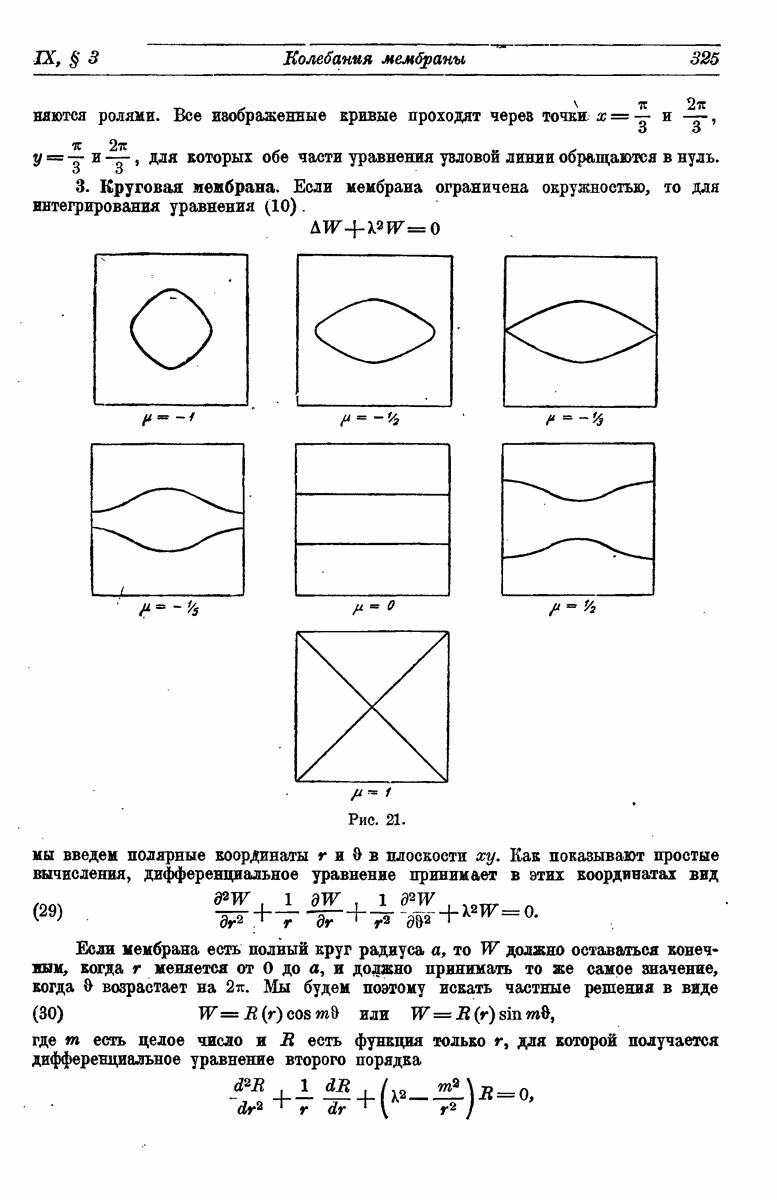
- 3. Круговая мембрана.
- 4. Аналитические свойства решений.
- 5. Интегральное уравнение колебания мембраны.
- § 4. Граничная задача колеблющейся мембраны как задача вариационного исчисления
- 2. Высшие характеристические числа.
- 3. Следствия из минимальных свойств.
- 4. Метод Ритца. Эллиптическая мембрана.
- 5. Асимптотическое распределение характеристических чисел.
- ГЛАВА X. ИДЕАЛЬНЫЕ ЖИДКОСТИ
- 1. Определение идеальной жидкости.
- 2. Поле скоростей.
- 3. Уравнение неразрывности.
- 4. Теорема Гаусса; поток.
- 5. Деформация частицы жидкости.
- 6. Безвихревое движение; потенциал скоростей.
- 7. Примеры
- 8. Уравнения Эйлера.
- 9. Уравнения Лагранжа.
- 10. Гидростатика; плавание.
- 11. Свободная поверхность вращающейся жидкости. Фигуры равновесия.
- 12. Уравнение для давления; уравнение энергии.
- 13. Теоремы о количестве движения для стационарного течения жидкости. Истечение из сосуда.
- 14. Теоремы о количестве движения. Общая формулировка.
- 15. Ток и циркуляция.
- 16. Теорема Стовса. Поток вихря.
- 17. Сохранение циркуляции.
- 18. Теоремы Гельягольца о вихрях.
- 19. Стационарное вихревое движение.
- § 2 Общие методы
- 1. Потенциальное движение; теорема Грина.
- 2. Следствия из теоремы Грина.
- 3. Источники.
- 4. Двойной источник (диполь).
- 5. Поверхностное распределение источников; слои источников.
- 6. Задачи с граничными условиями; функция Грина.
- 7. Метод изображений.
- 8. Вихревое поле; вихревые линии; закон Био-Савара.
- 9. Вихревые слои.
- 10. Представление потока с помощью источников и вихрей.
- 11. Кинетическая энергия потока.
- 12. Геометрические свойства; слои тока.
- 13. Давление в потоке.
- 14. Движение твердых тел в идеальной жидкости.
- § 3. Частные задачи и методы
- 2. Конформное отображение.
- b) ОБРАЗОВАНИЕ СТРУЙ
- 3. Струя в покоящейся («мертвой») воде.
- 4. Плоские струи. Методы Гельмгольца и Кирхгофа.
- 5. Метод Леви-Чивита.
- 6. Учет силы тяжести. Переливание жидкости через плотину.
- 7. Функциональное уравнение для свободной границы струи; перманентные волны.
- 8. Пространственные струи.
- с) ВОЛНЫ
- 9. Общие соображения о волнах жидкости.
- 10. Периодические волны в канале.
- 11. Наложение (суперпозиция) волн в каналах.
- 12. Волны Герстнера.
- 13. Корабельные волны.
- 14. Волны прилива и отлива.
- d) ВИХРИ
- 15. Вихревые точки в неограниченной плоскости.
- 16. Вихревые точки в ограниченной области.
- 17. Вихри Кармана.
- 18. Возникновение вихрей Кармана.
- 19. Вихревые кольца.
- 20. Другие вихревые образования.
- е) ЦИРКУЛЯЦИЯ И ПОДЪЕМНАЯ СИЛА
- 21. Гидродинамическая подъемная сила.
- 22. Теорема Кутта-Жуковского.
- 23. Техническое значение гидродинамической подъемной силы.
- 24. Прандтлевская теория несущего крыла.
- ГЛАВА XI. ДВИЖЕНИЕ ЖИДКОСТЕЙ С ТРЕНИЕМ
- 2. Закон Пуазейля.
- 3. Обозначения.
- 4. Связь между напряжениями и скоростью деформаций.
- 5. Полные дифференциальные уравнения.
- 6. Составляющие напряжения на поверхности покоящегося тела.
- 7. Линеаризованные дифференциальные уравнения.
- § 2. Фундаментальные интегралы линеаризованных дифференциальных уравнений
- 2. Линеаризованные уравнения пространственного движения для случая, когда система координат ииеет постоянную поступательную скорость.
- 3. Линеаризованные уравнения плоского движения для случая, когда система координат имеет постоянную поступательную скорость.
- 4. Движение твердого тела.
- 5. Наиболее общие линеаризованные дифференциальные уравнения.
- § 3. Стоксова формула сопротивления и связанные с ней формулы
- 2. Более точное вычисление потока вокруг шара.
- 3. Поступательное движение тонкого кругового цилиндра в вязкой жидкости.
- § 4. Точные решении уравнений движения вязкой иесжииаеиой жидкости
- § 5. Теория пограничного слоя
- 2. Уравнение движения пограничного слоя.
- 3. Отрыв пограничного слоя.
- 4. Пограничный слой в точной теории Гамеля.
- ГЛАВА XII. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ РАСПРОСТРАНЕНИЯ КОЛЕБАНИЙ
- § 1. Задача об отражении плоских упругих волн
- 2. Плоская задача.
- 3. Граничные (краевые) условия. Полупространство.
- 4. Линейно-поляризованные поперечные волны.
- 5. Звуковые волны.
- 6. Класс комплексных решений волнового уравнения.
- 7. Плоские волны. Отражение плоских продольных волн.
- 8. Отражение поперечных волн.
- 9. Поверхностные волны Рэлея.
- 10. Общие формулы комплексной теории отражения.
- § 2. Общий анализ комплексных решений
- 1. Однородные комплексные решения волнового уравнения. Внутренность основного конуса.
- 2. Внешность основного конуса.
- 3. Кинематические и динамические условия совместности. Характеристики.
- 4. Условия правильности однородных, комплексных решений.
- 5. Анализ комплексных решений общего типа.
- § 3. Задача об источниках колебаний для полупространства
- 2. Задача с однородными смещениями.
- 3. Конформное преобразование типа …
- 4. Задача об отражении продольных волн. Случай комплексных потенциалов.
- 5. Задача об отражении продольных волн. Случай комплексных смещений.
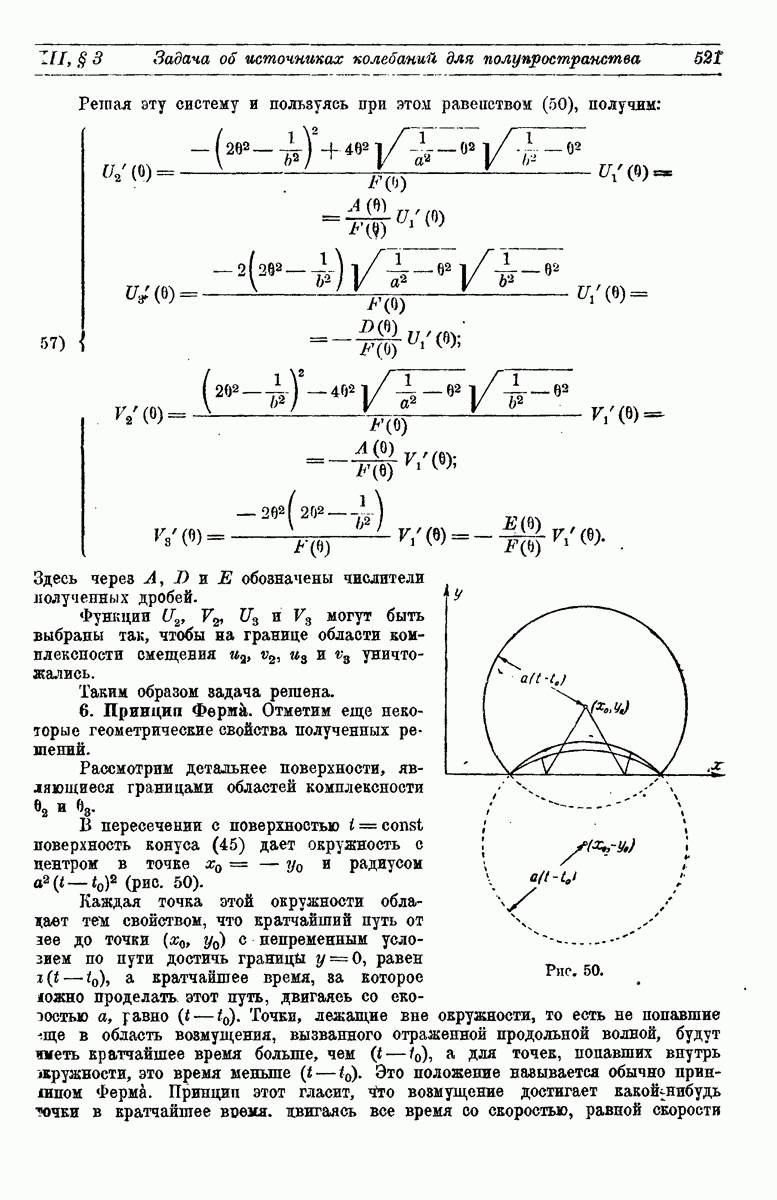
- 6. Принцип Ферма.
- 7. Отражение поперечных волн. Случай комплексных потенциалов.
- 8. Отражение поперечных волн. Случай комплексных смещений.
- 9. Принцип Ферма.
- 10. Волны Рэлея.
- § 4. Задача Коши для упругого полупространства в двух измерениях
- 2. Фундаментальное решение Вольтерра.
- 4. Решение задачи Коши по методу Вольтерра.
- 4. Формула Грнна-Вольтерра.
- 5. Кинематические и динамические условии совместности для уравнений упругости.
- 6. Постановка плоской задачи теории упругости для полупространства.
- 7. Фундаментальные решения.
- 8. Решение общей задачи теории упругости для полупространства в плоском случае.
- 9. Теория точечных источников.
- 10. Задача Лэмба.
- 11. Волны Рэлея.
- § 5. Основы решения трехмерных: задач распространении колебаний методом комплексной переменной
- 2. Отражение упругих примитивных волн.
- 3. Полное внутреннее отражение поперечной волны при …
- 4. Волны Рэлея.
- 5. Принцип наложения.
- 6. Построение первого фундаментального решения для трехмерной задачи теории упругости.
- 7. Задачи с осевой симметрией.
- 8. Построение других фундаментальных решений.
- 9. Основные свойства наложения общих комплексных решений.
- 10. Отражение фундаментальных решений.
- § 6. Задача Коши в трехмерном пространстве
- 2. Формула Грина для волнового уравнения.
- 3. Фундаментальное решение волнового уравнения.
- 4. Решение волнового уравнения.
- 5. Формула Грина для уравнений теории упругости.
- 6. Фундаментальные решения уравнений упругости для полупространства.
- 7. Решение задачи Коши для упругого полупространства.
- 8. Анализ полученных результатов.
- § 7. Обобщение решения волнового уравнения
- 2. Обобщенные решения волнового уравнения.
- 3. Связь с условиями совместности.
- 4. Теорема интегрирования.
- 5. Обобщенные комплексные решения.
- 6. Обобщенные комплексные решения во всей области существования.
- §. 8. Задача о диффракции плоских волн
- 2. Разветвляющиеся комплексные решения волнового уравнения.
- 3. Элементарные плоские волны логарифмической поверхности.
- 4. Диффракция произвольной плоской волны.
- 5. Периодические решения.
- 6. Диффракция относительно угла.
- 7. Трехмерная задача диффракции плоских волн.
- 8. Общая задача диффракции для двухмерного пространства.
- ЧАСТЬ ТРЕТЬЯ. ТЕПЛОПРОВОДНОСТЬ И ДИФФУЗИЯ
- 1. Основные понятия теплопроводности в твердых телах.
- 2. Дифференциальное уравнение теплопроводности.
- 3. Основные понятия диффузии при отсутствии внешних сил.
- 4. Дифференциальное уравнение диффузии.
- § 2. Теплопроводность и диффузия в неограниченных телах
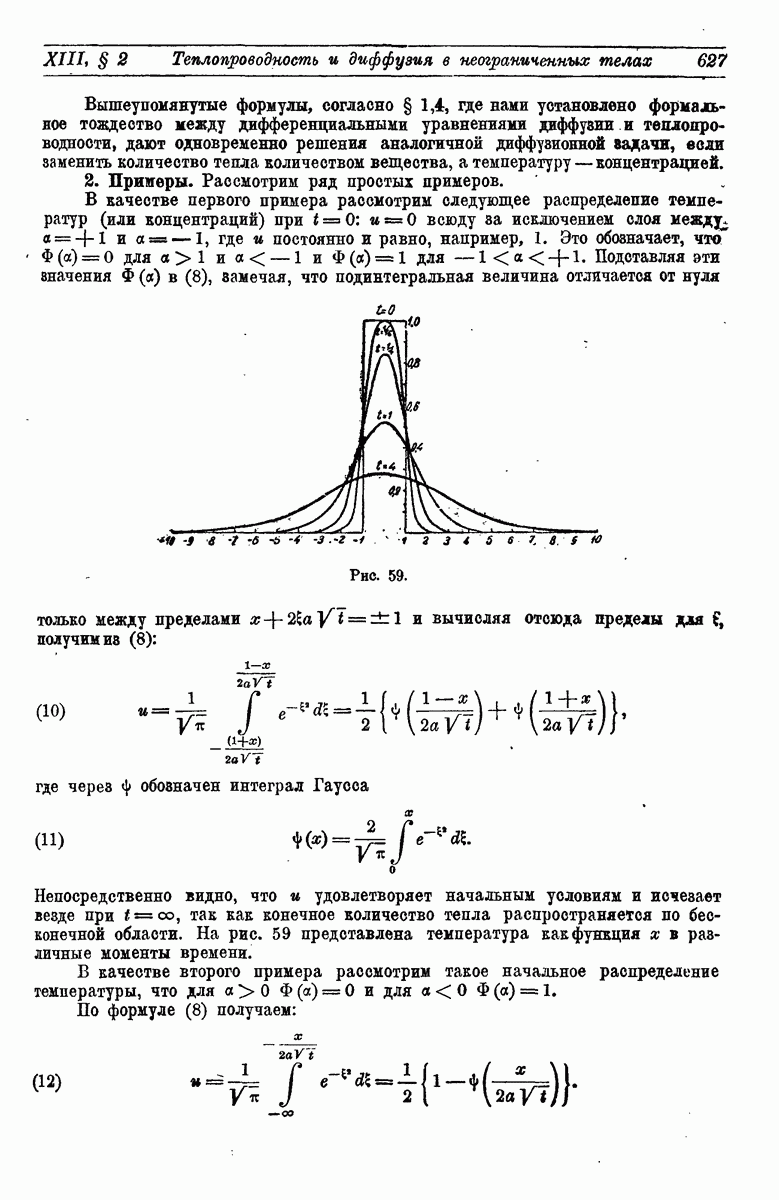
- 2. Примеры.
- 3. Применение к броуновскому движению одной частицы.
- 4. Тела, бесконечно протяженные в двух измерениях.
- 5. Тела, бесконечно протяженные в трех измерениях.
- 6. Интегральное уравнение теплопроводности и диффузии.
- § 3. Теплопроводность и диффузия в ограниченных телах
- 2. Диффузнонный опыт Бриллуэпа и «первые прохождения» при броуновском движении.
- 3. Тело, ограниченное двумя плоскостями.
- 4. «Двухсторонние первые прохождения» при броуновском движении.
- 5. Слоистые тела.
- 6. Теплопроводность в цилиндре.
- 7. Теплопроводность в шаре.
- 8. Распространение холода.
- 9. Температура (концентрация) граничной поверхности есть заданная функция времени.
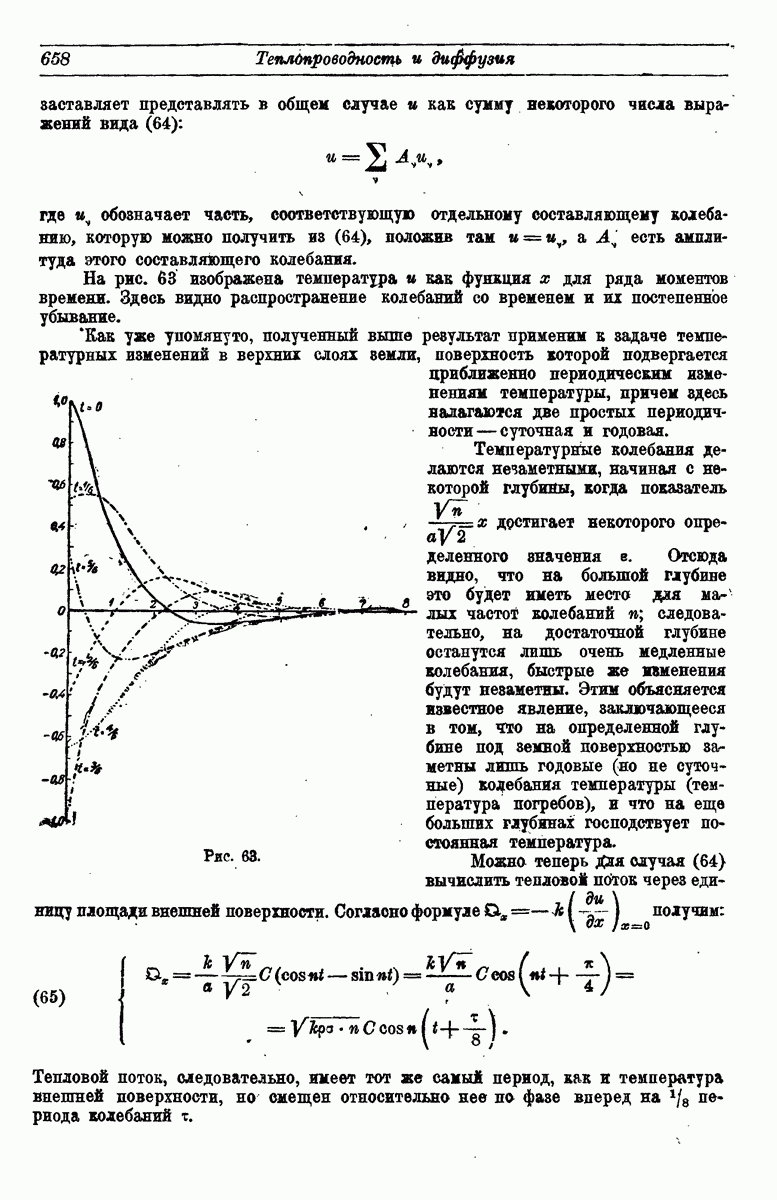
- 10. Тепловые волны.
- 11. Внешняя поверхность — изолятор.
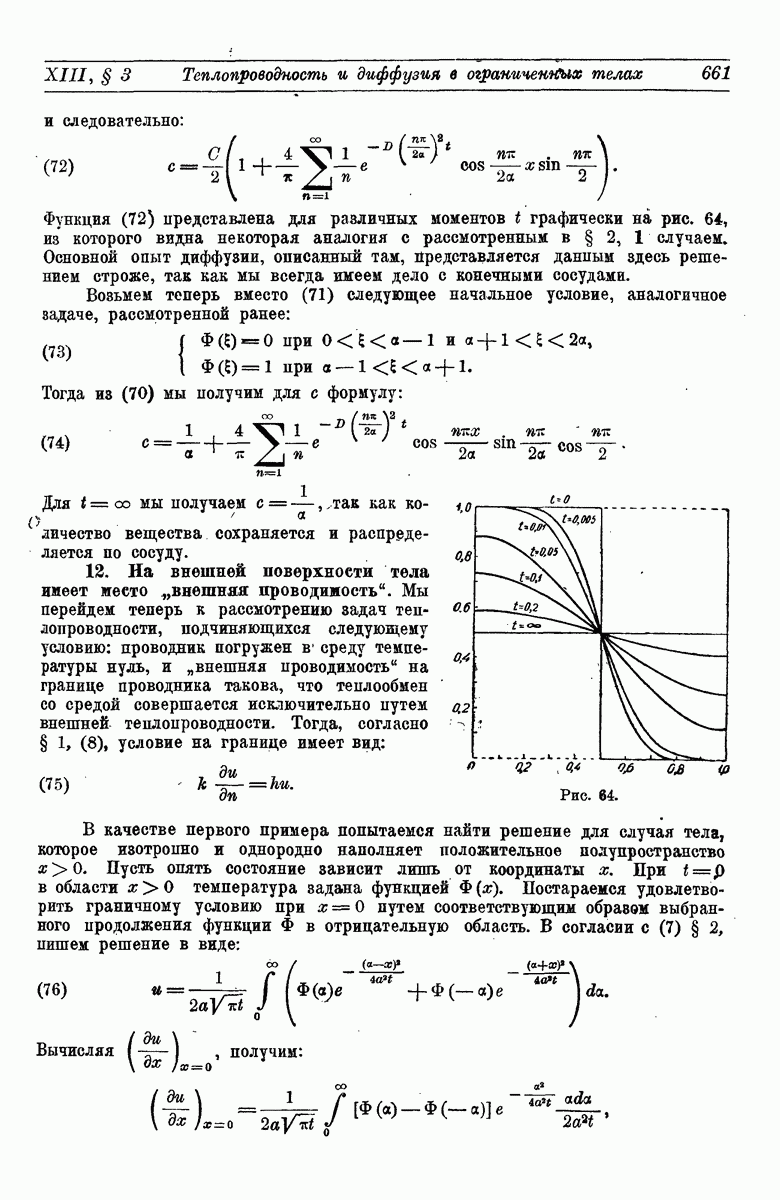
- 12. На внешней поверхности тела имеет место «внешняя проводимость».
- 13. Диффузия сквозь диафрагму.
- 14. Задача внешней теплопроводности в двух измерениях.
- 15. Теплопроводность стержня.
- ГЛАВА XIV. ВЫНУЖДЕННАЯ ТЕПЛОПРОВОДНОСТЬ И ДИФФУЗИЯ
- 2. Дифференциальное уравнение диффузии при действии внешних сил.
- 3. Интегральное уравнение диффузии и его связь со статистикой.
- § 2. Теплопроводность и диффузия при вынужденной конвекции
- 2. Конечный коэффициент теплопередачи.
- 3. Течение сквозь узкие трубы. Холодильник.
- 4. Диффузия в текущих газах и под действием заданных внешних сил.
- 5. Седиментация и броуновское движение в поле силы тяжести.
- 6. Связь с одной теоремой статистической механики.
- 7. Диффузия электролитов.
- 7. Диффузия ионов в газах.
- § 3. Спонтанное конвекционное течение под действием внешних сил
- § 4. Связь между теорией диффузии и волновой механикой
- 2. Движение системы частиц под действием внешних сил.
- 3. Движение по инерции.
- 4. Связь с соотношением неопределенности.
- ЧАСТЬ ЧЕТВЕРТАЯ. СТАЦИОНАРНОЕ (И КВАЗИСТАЦИОНАРНОЕ) ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- ГЛАВА XV. ЭЛЕКТРОСТАТИКА
- 2. Математические уравнения поля.
- § 2. Основные задачи; метод отражений и электрических изображений
- 2. Распределение электричества на эллипсоиде.
- 4. Отражение и электрические изображения.
- § 3. Электростатическое равновесие на двух заряженных сферах
- § 4. Цилиндрические поля. Представление посредством функций комплексной переменной
- 2. Отражение, эксцентрические круговые цилиндры.
- 3. Представление поля посредством функций комплексной переменной.
- § 5. Поле призматических проводников
- 2. Два бесконечных призматических проводника.
- 3. Поле между двумя конечными ограниченными проводниками.
- § 6. Применение электростатики к теории катодных ламп
- ГЛАВА XVI. СТАЦИОНАРНЫЕ ЭЛЕКТРИЧЕСКИЕ ТОКИ
- § 1. Формулировка уравнений поля и простые задачи
- 2. Простые задачи о стационарных полях тока.
- § 2. Прохождение тока между землей и металлическими проводниками
- 3. Решение интегрального уравнения для распределения тока.
- 4. Решение интегродифференциального уравнения для выхода тока.
- § 3. Слой жидкости с металлической границей. Цветные кольца Нобили
- 2. Учет поляризации.
- 3. Однородная вспомогательная задача.
- 4. Общее решение неоднородной задачи.
- 5. Решение в случае тока.
- ГЛАВА XVII. МАГНИТОСТАТИКА
- § 1. Образование магнитных полей
- 2. Постоянный магнит и магнитный момент.
- 3. Стационарное электромагнитное поле.
- § 2. Парамагнитные тела в магнитном поло
- 2. Шар в однородном поле
- 3. Эллипсоид в однородном поле.
- § 3. Силы, испытываемые материальными телами в электрическом или магнитном поле
- 2. Вспомогательная теорема.
- 3. Энергия диэлектрического тела в электрической поле.
- 4. Энергия пара- или диаиагнитиого тела в магнитнои поле.
- 5. Применение в эллипсоиду.
- ГЛАВА XVIII. КВАЗИСТАЦИОНАРНЫЕ ТОКИ И ВОЛНЫ
- § 1. Квазистационарные контуры тока
- 2. Механическое представление системы. Закон индукции Фарадея.
- 3. Колебание цепей. Сопротивление при переменном токе.
- § 2. Квазистационарные волны в проводниках
- 2. Стоячие волны. Свободные колебания.
- 3. Вынужденные колебания.
- 4. Бегущие волны произвольной формы.
- § 3. Квазистационарные волны в катушках
- 2. Гармонические волны.
- 3. Образование преломленных волн.
- ЧАСТЬ ПЯТАЯ. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ И МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Закон сохранения энергии и однозначность решений.
- 3. Замечание о математической трактовке колебательных процессов.
- 4. Электронная теория.
- § 2. Инвариантность уравнений Максвелла по отношению к преобразованию Лоренца
- 2. Антисимметричный тензор поля.
- 3. Группа ортогональных преобразований.
- 4. Частное преобразование Лоренца.
- § 3. Запаздывающие потенциалы и поле ускоренно движущегося заряда
- 2. Запаздывающие потенциалы и приближение Льенарда-Вихерта.
- 3. Поле произвольно движущегося заряда.
- § 4. Вектор Герца и излучение колеблющегося диполя
- 1. Непосредственное рассмотрение электрического диполя.
- 2. Поле линейного гармонического вибратора.
- 3. Излучение энергии.
- 4. Обобщения.
- 5. Вычисление оптической интенсивности по вектору Герца.
- § 5. Условия излучениях). Собственные функции и собственные значения
- ГЛАВА XX. ТЕОРИЯ ДИФФРАКЦИИ
- § 1. Разветвленные решения уравнения колебаний
- 2. Понятие пространства Римана.
- 3. Функция плоской волны, однозначная на поверхности Римана.
- 4. Решения для пространства Римана.
- 5. Приложения и дополнения.
- § 2. Сходящиеся и полусходящиеся разложения разветвленных решений.
- 2. Выражение для разветвленной функции плоской волны в виде сходящихся рядов по Бесселевым функциям.
- 3. Асимптотическое выражение разветвленной функции плоской волны.
- 4. Частный случай n=2.
- § 3. Сравнение с классической теорией диффракции (Френель-Кирхгоф)
- 2. Принцип Гюйгенса.
- 3. Прямоугольное отверстие, щель и полуплоскость.
- 4. Связь между геометрической и волновой оптикой.
- § 4. Диффракция от шара и от других тел. Метод разложения в ряды
- 2. Теоремы сложения.
- 3. Диффракции от цилиндра.
- 4. Диффракции от шара. Коллоидальные частицы.
- ГЛАВА XXI. СОПРОТИВЛЕНИЕ ДЛЯ ПЕРЕМЕННЫХ ТОКОВ И СКИН-ЭФФЕКТ
- § 1. Распределение в проводящей плоскости
- 2. Исследование поля.
- 3. Сопротивление переменному току.
- § 2. Провод с круговым сечением при низких и высоких частотах
- 2. Исследование поля.
- 3. Сопротивление и самоиндукция провода.
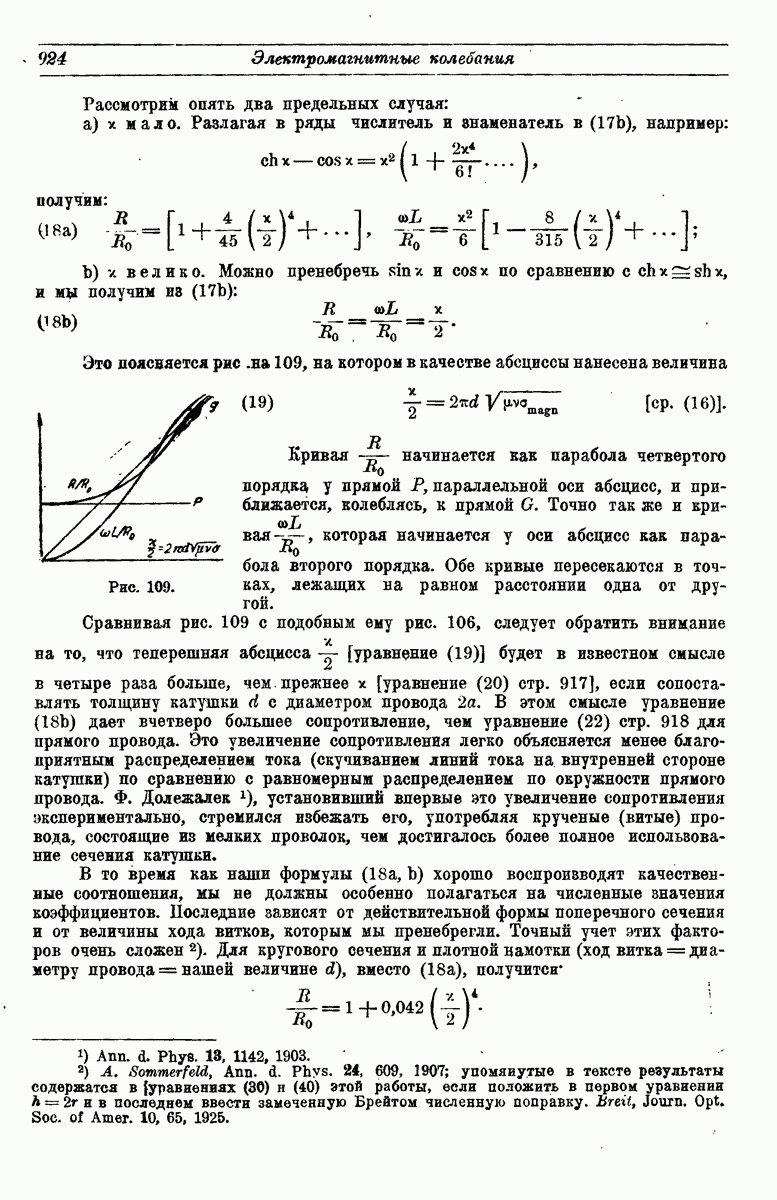
- § 3. Катушка с переменным током
- 2. Исследование поля.
- 3. Сопротивление и самоиндукция катушки.
- ГЛАВА XXII. ВОЛНЫ ВДОЛЬ ПРОВОДОВ
- § 1. Поле и распространение волн вдоль проводов
- 2. Численный пример для одного типичного случая.
- 3. Очень тонкий провод. Аномальный случай распространения и затухания.
- 4. Поток энергии на бесконечности.
- 5. Структура поля.
- § 2. Дополнения
- 1. Побочные волны электрического и магнитного типов. Несимметричные волны.
- 2. Поверхностные волны на непроводниках.
- 3. Случай металлического обратного провода.
- ГЛАВА XXIII. БЕСПРОВОЛОЧНАЯ ТЕЛЕГРАФИЯ
- § 1. Вертикальная антенна на плоской земле
- 2. Преобразование первичного возбуждения.
- 3. Выполнение граничных условий.
- 4. Другие формы решения.
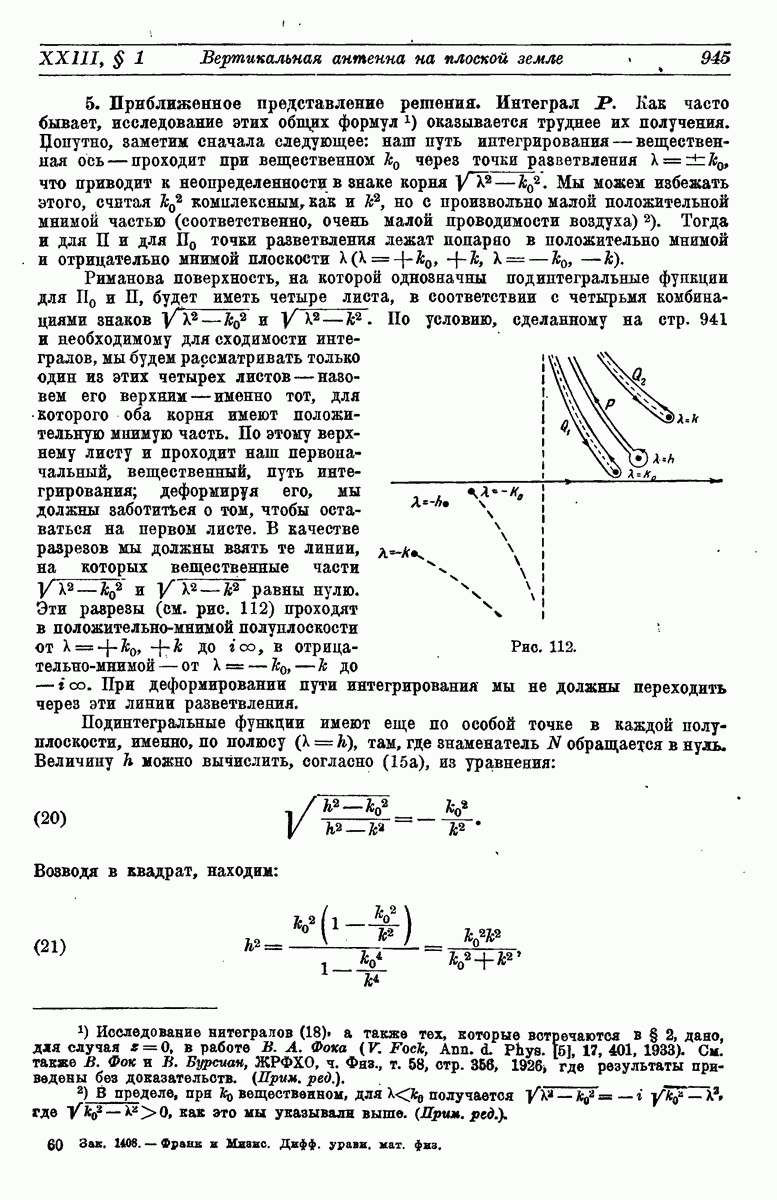
- 5. Приближенное представление решения.
- 6. Приближенное представление решения.
- 7. Вывод приближенной формулы для точек вблизи поверхности земли.
- § 2. Горизонтальная и рамочная антенны
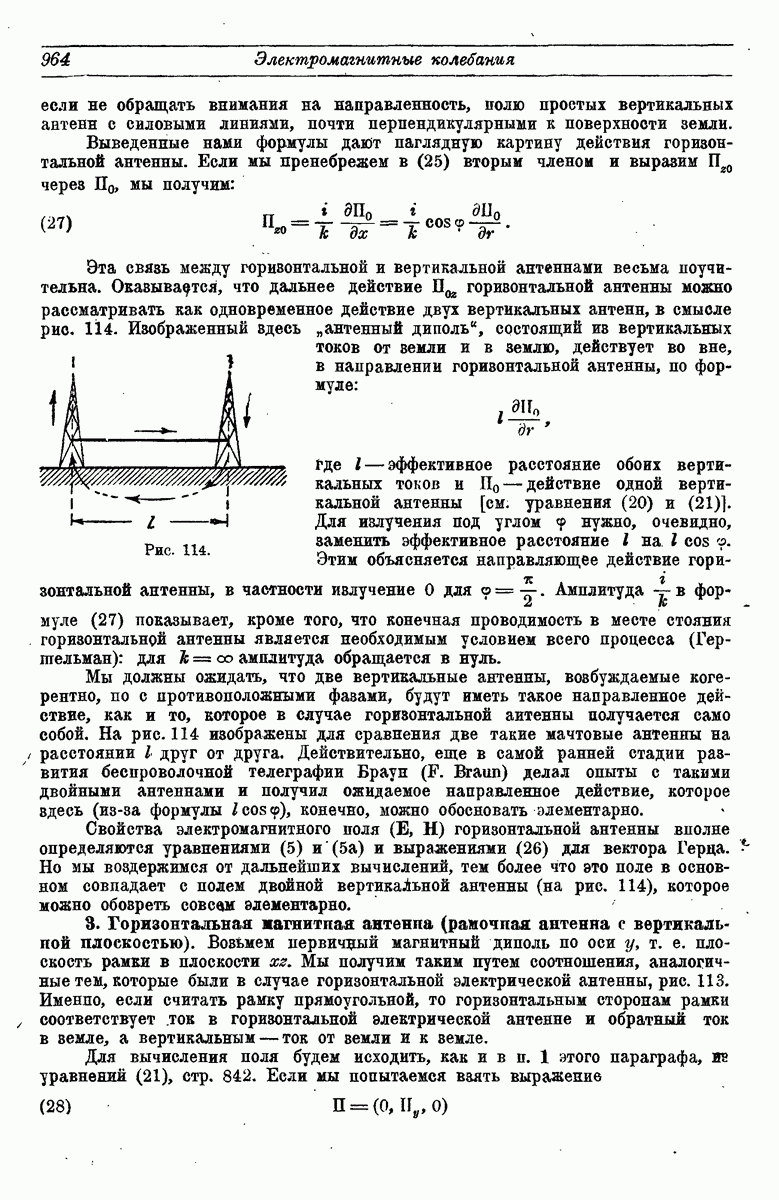
- 2. Горизонтальная электрическая антенна.
- 3. Горизонтальная магнитная антенна (рамочная антенна с вертикальной плоскостью).
- ПРИМЕЧАНИЕ
- § 3. Теорема взаимности в беспроволочной телеграфии
- 2. Две линейные электрические антенны.
- 3. Две магнитные антенны или одна электрическая и одна магнитная антенны.
- § 4. Беспроволочная телеграфия вокруг земли