| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. Линейный оператор, отображающий n-мерное пространство в m-мерное
1. Рассмотрим линейное преобразование
 (8)
(8)
коэффициенты
которого принадлежат числовому полю ![]() , и два векторных пространства над
этим полем:
, и два векторных пространства над
этим полем: ![]() -мерное
-мерное
![]() и
и ![]() -мерное
-мерное ![]() . Выберем в
. Выберем в ![]() некоторый базис
некоторый базис ![]() и в
и в ![]() некоторый базис
некоторый базис ![]() .
.
Тогда
преобразование (8) относит каждому вектору ![]() из
из ![]() некоторый вектор
некоторый вектор ![]() из
из ![]() , т. е. преобразование (8)
определяет некоторый оператор
, т. е. преобразование (8)
определяет некоторый оператор ![]() , относящий вектору
, относящий вектору ![]() вектор
вектор ![]() :
: ![]() . Нетрудно видеть,
что этот оператор
. Нетрудно видеть,
что этот оператор ![]() обладает свойством линейности,
которое мы сформулируем так:
обладает свойством линейности,
которое мы сформулируем так:
Определение 5.
Оператор ![]() ,
отображающий
,
отображающий ![]() в
в
![]() т. е.
относящий каждому вектору
т. е.
относящий каждому вектору ![]() из
из ![]() некоторый вектор
некоторый вектор ![]() из
из ![]() , называется линейным, если
для любых
, называется линейным, если
для любых ![]() ,
,
![]() из
из ![]() и
и ![]() из
из ![]()
![]() ,
, ![]() . (9)
. (9)
Таким образом,
преобразование (8) при заданных базисах в ![]() и
и ![]() определяет некоторый линейный
оператор, отображающий
определяет некоторый линейный
оператор, отображающий ![]() в
в ![]() .
.
Покажем теперь
обратное, т. е. что для произвольного линейного оператора ![]() , отображающего
, отображающего ![]() в
в ![]() , и произвольных
базисов
, и произвольных
базисов ![]() в
в
![]() и
и ![]() в
в ![]() существует такая прямоугольная
матрица с элементами из поля
существует такая прямоугольная
матрица с элементами из поля ![]()
 , (10)
, (10)
что составленное
при помощи этой матрицы линейное преобразование (1) выражает координаты
преобразованного вектора ![]() через координаты исходного вектора
через координаты исходного вектора ![]() .
.
Действительно,
применим оператор ![]() к базисному вектору
к базисному вектору ![]() и координаты
полученного вектора
и координаты
полученного вектора ![]() в базисе
в базисе ![]() обозначим через
обозначим через ![]()
![]() :
:
![]()
![]() . (11)
. (11)
Помножая обе
части равенства (11) на ![]() и суммируя в пределах от 1 до
и суммируя в пределах от 1 до ![]() получим:
получим:
 ,
,
откуда
 ,
,
где
![]()
![]() ,
,
что и требовалось установить.
Таким образом,
при заданных базисах в ![]() и
и ![]() каждому линейному оператору
каждому линейному оператору ![]() , отображающему
, отображающему ![]() в
в ![]() , отвечает
некоторая прямоугольная матрица (10) с размерами
, отвечает
некоторая прямоугольная матрица (10) с размерами![]() , наоборот, каждой такой матрице
отвечает некоторый линейный оператор, отображающий
, наоборот, каждой такой матрице
отвечает некоторый линейный оператор, отображающий ![]() в
в ![]() .
.
При этом в
матрице ![]() отвечающей
оператору
отвечающей
оператору ![]() ,
,
![]() -й
столбец состоит из последовательных координат вектора
-й
столбец состоит из последовательных координат вектора ![]() (
(![]() ).
).
Обозначим через ![]() и
и ![]() столбцы координат
векторов
столбцы координат
векторов ![]() и
и
![]() . Тогда
векторному равенству
. Тогда
векторному равенству
![]()
соответствует матричное равенство
![]() ,
,
которое является матричной записью преобразования (8).
Пример.
Рассмотрим
совокупность всех многочленов от ![]() степени
степени ![]() с коэффициентами из числового поля
с коэффициентами из числового поля ![]() . Эта совокупность
представляет собой некоторое
. Эта совокупность
представляет собой некоторое ![]() -мерное векторное пространство
-мерное векторное пространство ![]() (см. пример 4 на
стр. 66). Точно так же многочлены от
(см. пример 4 на
стр. 66). Точно так же многочлены от ![]() степени
степени ![]() с коэффициентами из
с коэффициентами из ![]() образуют
пространство
образуют
пространство ![]() .
.
Оператор
дифференцирования ![]() относит каждому многочлену из
относит каждому многочлену из ![]() некоторый многочлен
из
некоторый многочлен
из ![]() . Таким
образом, этот оператор отображает
. Таким
образом, этот оператор отображает ![]() в
в ![]() . Оператор дифференцирования
является линейным оператором, так как
. Оператор дифференцирования
является линейным оператором, так как
![]() ,
, ![]() .
.
В пространствах ![]() и
и ![]() выберем базисы
степеней
выберем базисы
степеней ![]() :
:
![]() и
и ![]() .
.
Пользуясь
формулой (11), построим прямоугольную матрицу размером ![]() , соответствующую оператору
дифференцирования
, соответствующую оператору
дифференцирования ![]() в этих базисах:
в этих базисах:
 .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие автора к первому изданию
- Предисловие автора ко второму изданию
- ЧАСТЬ I. ОСНОВЫ ТЕОРИИ
- Глава I. Матрицы и действия над ними
- § 1. Матрицы. Основные обозначения
- § 2. Сложение и умножение прямоугольных матриц
- § 3. Квадратные матрицы
- § 4. Ассоциированные матрицы. Миноры обратной матрицы
- § 5. Обращение прямоугольных матриц. Псевдообратная матрица
- Глава II. Алгоритм Гаусса и некоторые его применения
- § 1. Метод исключения Гаусса
- § 2. Механическая интерпретация алгоритма Гаусса
- § 3. Детерминантное тождество Сильвестра
- § 4. Разложение квадратной матрицы на треугольные множители
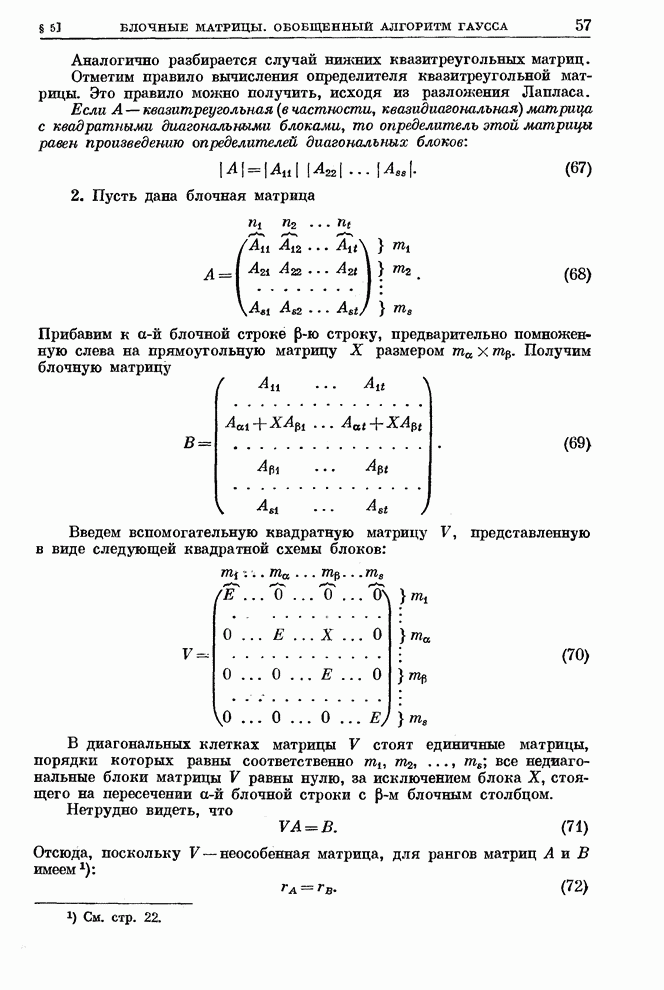
- § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса
- Глава III. Лииейиые операторы в n-мерном векторном пространстве
- § 1. Векторное пространство
- § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное
- § 3. Сложение и умножение линейных операторов
- § 4. Преобразование координат
- § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра
- § 6. Линейные операторы, отображающие n-мерное пространство само в себя
- § 7. Характеристические числа и собственные векторы линейного оператора
- § 8. Линейные операторы простой структуры
- Глава IV. Характеристический и минимальный многочлены матрицы
- § 1. Сложение и умножение матричных многочленов
- § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу
- § 3. Характеристический многочлен матрицы. Присоединенная матрица
- § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы
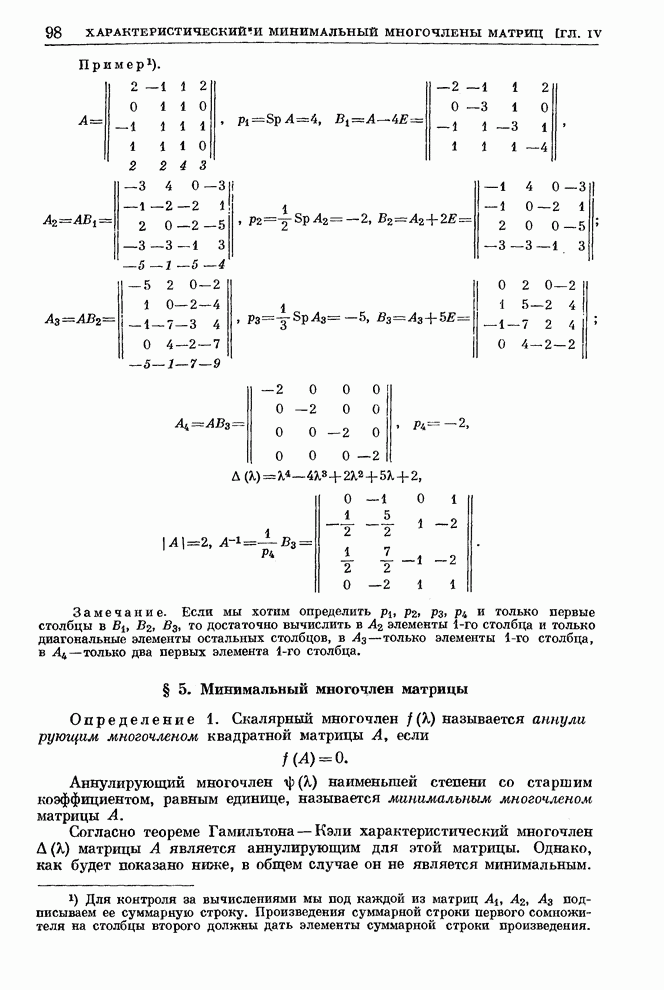
- § 5. Минимальный многочлен матрицы
- Глава V. Функции от матрицы
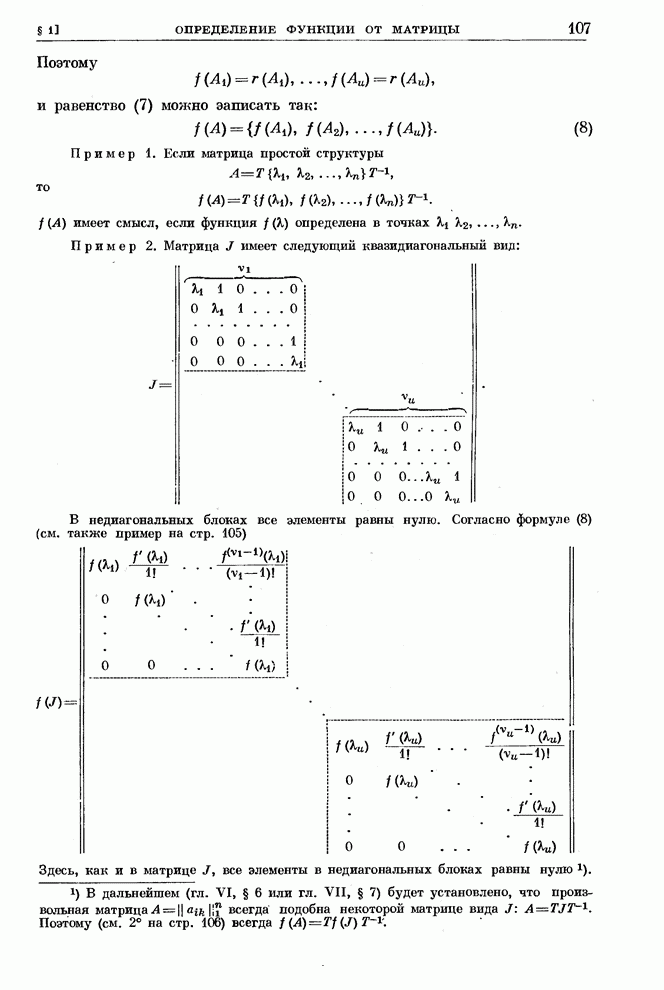
- § 1. Определение функции от матрицы
- § 2. Интерполяционный многочлен Лагранжа–Сильвестра
- § 3. Другие формы определения f(A). Компоненты матрицы A
- § 4. Представление функций от матриц рядами
- § 5. Некоторые свойства функций от матриц
- § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 7. Устойчивость движения в случае линейной системы
- Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей
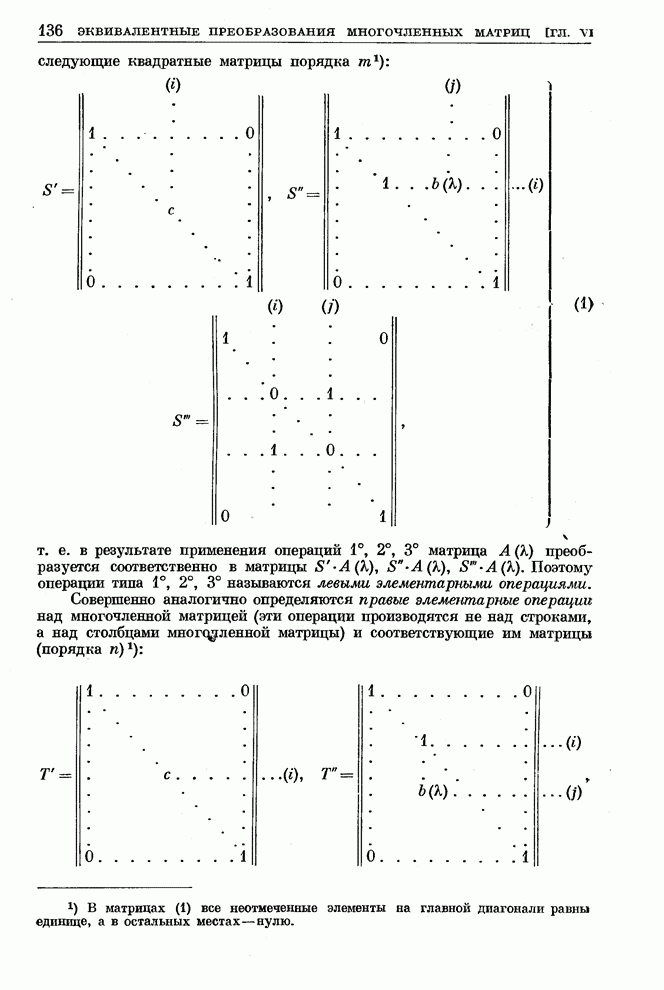
- § 1. Элементарные преобразования многочленной матрицы
- § 2. Канонический вид матрицы
- § 3. Инвариантные многочлены и элементарные делители многочленной матрицы
- § 4. Эквивалентность линейных двучленов
- § 5. Критерий подобия матриц
- § 6. Нормальные формы матрицы
- § 7. Элементарные делители матрицы f(A)
- § 8. Общий метод построения преобразующей матрицы
- § 9. Второй метод построения преобразующей матрицы
- Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей)
- § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора)
- § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами
- § 3. Сравнения. Надпространство
- § 4. Расщепление пространства на циклические инвариантные подпространства
- § 5. Нормальная форма матрицы
- § 6. Инвариантные многочлены. Элементарные делители
- § 7. Нормальная жорданова форма матрицы
- § 8. Метод акад. А. Н. Крылова преобразования векового уравнения
- Глава VIII. Матричные уравнения
- § 1. Уравнение AX=XB
- § 2. Частный случай: A=B. Перестановочные матрицы
- § 3. Уравнение AX-XB=C
- § 4. Скалярное уравнение f(X)=0
- § 5. Матричное многочленное уравнение
- § 6. Извлечение корня m-й степени из неособенной матрицы
- § 7. Извлечение корня m-й степени из особенной матрицы
- § 8. Логарифм матрицы
- Глава IX. Линейные операторы в унитарном пространстве
- § 1. Общие соображения
- § 2. Метризация пространства
- § 3. Критерий Грама линейной зависимости векторов
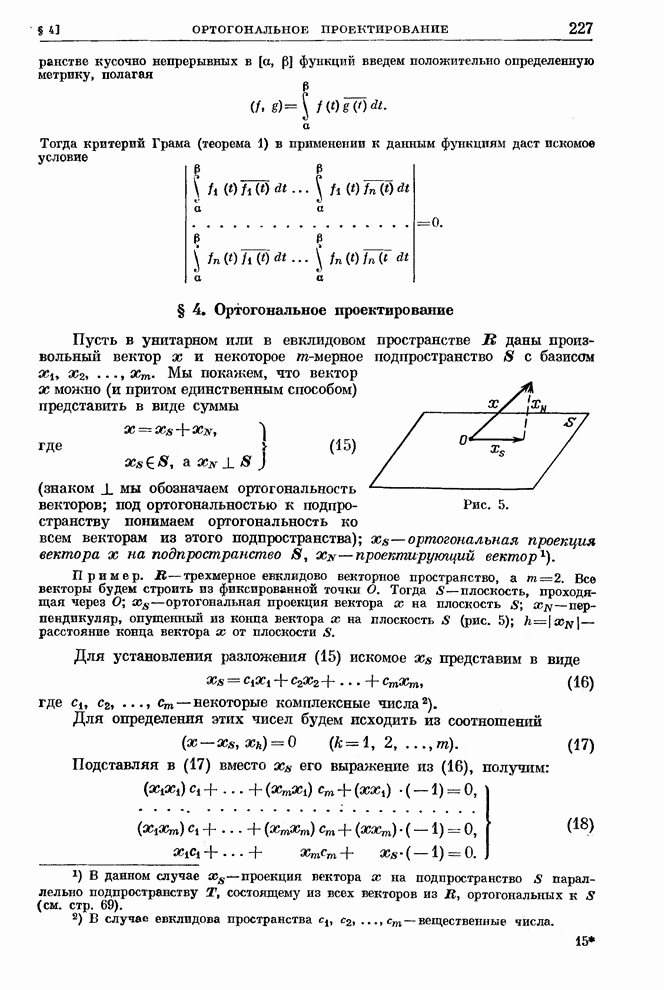
- § 4. Ортогональное проектирование
- § 5. Геометрический смысл определителя Грама и некоторые неравенства
- § 6. Ортогонализация ряда векторов
- § 7. Ортонормированный базис
- § 8. Сопряженный оператор
- § 9. Нормальные операторы в унитарном пространстве
- § 10. Спектр нормальных, эрмитовых, унитарных операторов
- § 11. Неотрицательные и положительно определенные эрмитовы операторы
- § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли
- § 13. Линейные операторы в евклидовом пространстве
- § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве
- § 15. Коммутирующие нормальные операторы
- § 16. Псевдообратный оператор
- Глава X. Квадратичные и эрмитовы формы
- § 1. Преобразование переменных в квадратичной форме
- § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции
- § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби
- § 4. Положительные квадратичные формы
- § 5. Приведение квадратичной формы к главным осям
- § 6. Пучок квадратичных форм
- § 7. Экстремальные свойства характеристических чисел регулярного пучка форм
- § 8. Малые колебания системы с n степенями свободы
- § 9. Эрмитовы формы
- § 10. Ганкелевы формы
- ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ
- Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы
- § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц
- § 2. Полярное разложение комплексной матрицы
- § 3. Нормальная форма комплексной симметрической матрицы
- § 4. Нормальная форма комплексной кососимметрической матрицы
- § 5. Нормальная форма комплексной ортогональной матрицы
- ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ
- § 1. Введение
- § 2. Регулярный пучок матриц
- § 3. Сингулярные пучки. Теорема о приведении
- § 4. Каноническая форма сингулярного пучка матриц
- § 5. Минимальные индексы пучка
- § 6. Сингулярные пучки квадратичных форм
- § 7. Приложения к дифференциальным уравнениям
- ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- § 1. Общие свойства
- § 2. Спектральные свойства неразложимых неотрицательных матриц
- § 3. Разложимые матрицы
- § 4. Нормальная форма разложимой матрицы
- § 5. Примитивные и импримитивные матрицы
- § 6. Стохастические матрицы
- § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний
- § 8. Вполне неотрицательные матрицы
- § 9. Осцилляционные матрицы
- Глава XIV. Различные критерии регулярности и локализации собственных значений
- § 1. Критерий регулярности Адамара и его обобщения
- § 2. Норма матрицы
- § 3. Распространение критерия Адамара на блочные матрицы
- § 4. Критерий регулярности Фидлера
- § 5. Круги Гершгорина и другие области локализации
- Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений
- § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия
- § 2. Преобразование Ляпунова
- § 3. Приводимые системы
- § 4. Каноническая форма приводимой системы. Теорема Еругина
- § 5. Матрицант
- § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра
- § 7. Дифференциальные системы в комплексной области. Общие свойства
- § 8. Мультипликативный интеграл в комплексной области
- § 9. Изолированная особая точка
- § 10. Регулярная особая точка
- § 11. Приводимые аналитические системы
- § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского
- ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ
- § 1. Введение
- § 2. Индексы Коши
- § 3. Алгоритм Рауса
- § 4. Особые случаи. Примеры
- § 5. Теорема Ляпунова
- § 6. Теорема Рауса-Гурвица
- § 7. Формула Орландо
- § 8. Особые случаи в теореме Рауса — Гурвица
- § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена
- § 10. Бесконечные ганкелевы матрицы конечного ранга
- § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя
- § 12. Второе доказательство теоремы Рауса—Гурвица
- § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара
- § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей
- § 15. Область устойчивости. Параметры Маркова
- § 16. Связь с проблемой моментов
- § 17. Связь между определителями Гурвица и определителями Маркова
- § 18. Теоремы Маркова и Чебышева
- § 19. Обобщенная задача Рауса-Гурвица
- ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ
- § 1. Мажорирующие последовательности
- § 2. Неравенства Неймана-Хорна
- § 3. Неравенства Вейля
- § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов
- § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов
- § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов
- ЛИТЕРАТУРА