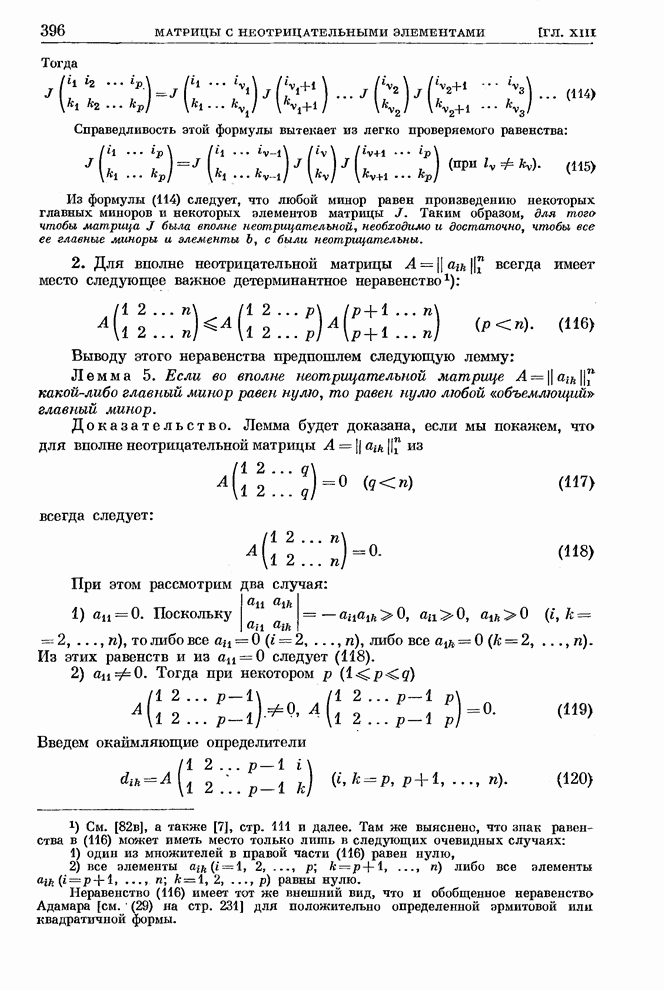| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Метод акад. А. Н. Крылова преобразования векового уравнения
1.
Если дана матрица ![]() , то ее характеристическое (вековое)
уравнение записывается в виде
, то ее характеристическое (вековое)
уравнение записывается в виде
 . (81)
. (81)
В
левой части этого уравнения стоит характеристический многочлен ![]() -й степени
-й степени ![]() . Для
непосредственного вычисления коэффициентов этого многочлена нужно раскрыть
характеристический определитель
. Для
непосредственного вычисления коэффициентов этого многочлена нужно раскрыть
характеристический определитель ![]() , а это связано при больших
, а это связано при больших ![]() с большим объемом
вычислительной работы, поскольку
с большим объемом
вычислительной работы, поскольку ![]() входит в диагональные элементы
определителя.
входит в диагональные элементы
определителя.
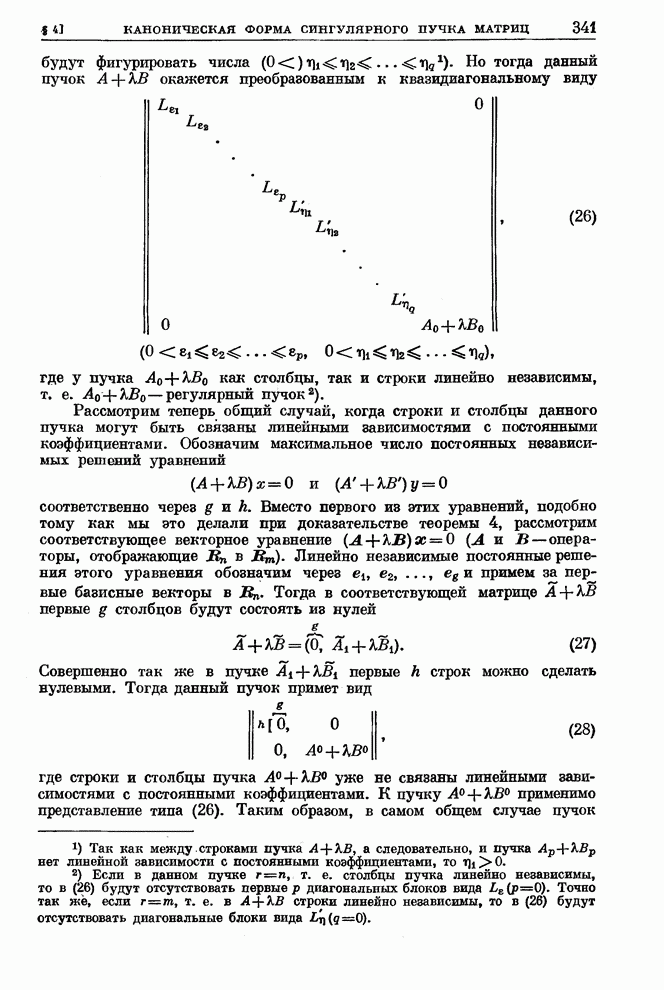
Академик
А. Н. Крылов в 1937 г. [103] предложил преобразование характеристического
определителя, в результате которого ![]() входит только в элементы одного
столбца (или строки). Преобразование Крылова существенно упрощает вычисление
коэффициентов характеристического уравнения.
входит только в элементы одного
столбца (или строки). Преобразование Крылова существенно упрощает вычисление
коэффициентов характеристического уравнения.
В этом параграфе мы дадим алгебраический вывод преобразованного характеристического уравнения, несколько отличающийся от вывода самого Крылова.
Введем
в рассмотрение ![]() -мерное
векторное пространство
-мерное
векторное пространство ![]() с базисом
с базисом ![]() и линейный оператор
и линейный оператор ![]() в
в ![]() , определяемый
данной матрицей
, определяемый
данной матрицей ![]() при
этом базисе. Выберем в
при
этом базисе. Выберем в ![]() произвольный вектор
произвольный вектор ![]() и составим ряд
векторов
и составим ряд
векторов
![]() . (82)
. (82)
Пусть
первые ![]() векторов
этого ряда
векторов
этого ряда ![]() линейно
независимы, а
линейно
независимы, а ![]() -й
вектор
-й
вектор ![]() есть
линейная комбинация этих
есть
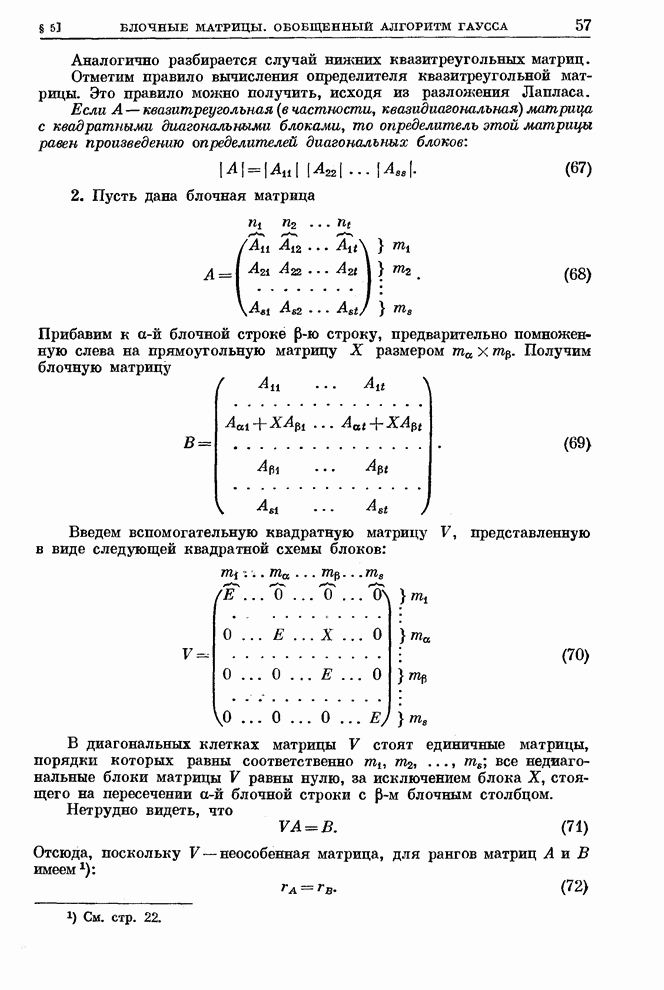
линейная комбинация этих ![]() векторов:
векторов:
![]() , (83)
, (83)
или
![]() , (84)
, (84)
где
![]() . (85)
. (85)
Все
дальнейшие векторы ряда (82) также линейно выражаются через первые ![]() векторов этого
ряда. Таким образом, в ряду (82) имеется
векторов этого
ряда. Таким образом, в ряду (82) имеется ![]() линейно независимых векторов, и это
максимальное число линейно независимых векторов ряда (82) может быть всегда
реализовано на первых
линейно независимых векторов, и это
максимальное число линейно независимых векторов ряда (82) может быть всегда
реализовано на первых ![]() векторах ряда.
векторах ряда.
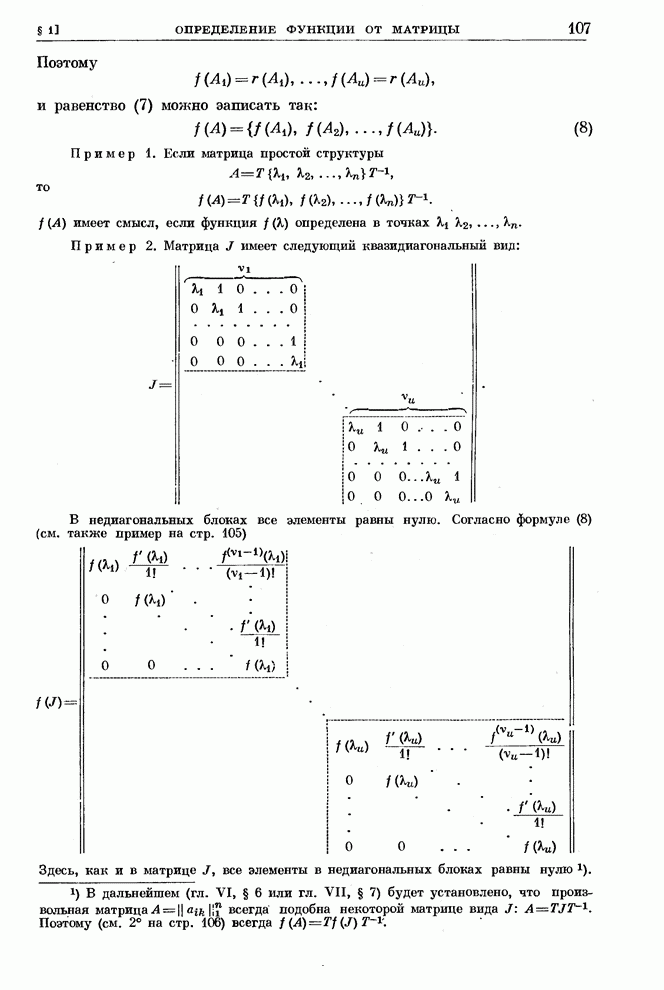
Многочлен
![]() является
минимальным (аннулирующим) многочленом вектора
является
минимальным (аннулирующим) многочленом вектора ![]() относительно оператора
относительно оператора ![]() (см. § 1). Метод
А. Н. Крылова есть метод эффективного определения минимального многочлена
(см. § 1). Метод
А. Н. Крылова есть метод эффективного определения минимального многочлена ![]() вектора
вектора ![]() .
.
Мы
рассмотрим раздельно два случая: регулярный случай, когда ![]() , и особый случай, когда
, и особый случай, когда ![]() .
.
Многочлен
![]() является
делителем минимального многочлена
является
делителем минимального многочлена ![]() всего пространства
всего пространства ![]() , а
, а ![]() в свою очередь
является делителем характеристического многочлена
в свою очередь
является делителем характеристического многочлена ![]() . Поэтому
. Поэтому ![]() всегда является делителем
всегда является делителем ![]() .
.
В
регулярном случае ![]() и
и ![]() имеют одну и ту же степень
имеют одну и ту же степень ![]() , и поскольку
старшие коэффициенты у них равны, то эти многочлены совпадают. Таким образом, в
регулярном случае
, и поскольку
старшие коэффициенты у них равны, то эти многочлены совпадают. Таким образом, в
регулярном случае
![]() ,
,
и
потому метод Крылова в регулярном случае есть метод вычисления коэффициентов
характеристического многочлена ![]() .
.
В
особом случае, как мы увидим ниже, метод Крылова не дает возможности определить
![]() и в этом
случае он определяет только многочлен
и в этом
случае он определяет только многочлен ![]() , являющийся делителем
, являющийся делителем ![]() .
.
При
изложении преобразования Крылова мы будем обозначать координаты вектора ![]() в заданном базисе
в заданном базисе ![]() через
через ![]() , а координаты вектора
, а координаты вектора
![]() через
через ![]()
![]() .
.
2.
Регулярный случай: ![]() . В этом случае векторы
. В этом случае векторы ![]() линейно
независимы, и равенства (83), (84), (85) принимают вид
линейно
независимы, и равенства (83), (84), (85) принимают вид
![]() (86)
(86)
или
![]() , (87)
, (87)
где
![]() . (88)
. (88)
Условие
лилейной независимости векторов ![]() может быть аналитически записано так
(см. гл. III, § 1):
может быть аналитически записано так
(см. гл. III, § 1):
 . (89)
. (89)
Рассмотрим
матрицу, составленную из координат векторов ![]() :
:
 . (90)
. (90)
В
регулярном случае ранг этой матрицы равен ![]() . Первые
. Первые ![]() строк этой матрицы линейно
независимы, а последняя,
строк этой матрицы линейно
независимы, а последняя, ![]() -я, строка есть линейная комбинация
предыдущих
-я, строка есть линейная комбинация
предыдущих ![]() .
.
Зависимость
между строками матрицы (90) получим, заменяя векторное равенство (86)
эквивалентной системой ![]() скалярных равенств
скалярных равенств
 (91)
(91)
Из
этой системы ![]() линейных
уравнений мы можем однозначно определить искомые коэффициенты
линейных
уравнений мы можем однозначно определить искомые коэффициенты ![]() и подставить
полученные значения в (88). Это исключение
и подставить
полученные значения в (88). Это исключение ![]() из (88) и (91) можно провести в
симметричной форме. Для этого перепишем (88) и (91) так:
из (88) и (91) можно провести в
симметричной форме. Для этого перепишем (88) и (91) так:

Поскольку
эта система из ![]() уравнений
с
уравнений
с ![]() неизвестными
неизвестными
![]() имеет
ненулевое решение
имеет
ненулевое решение ![]() , то определитель этой системы должен
равняться нулю:
, то определитель этой системы должен
равняться нулю:
 . (92)
. (92)
Отсюда
мы определяем ![]() ,
предварительно транспонируя определитель (92) относительно главной диагонали:
,
предварительно транспонируя определитель (92) относительно главной диагонали:
 , (93)
, (93)
где
постоянный множитель ![]() определяется формулой (89) и отличен
от нуля.
определяется формулой (89) и отличен
от нуля.
Тождество
(93) и представляет собой преобразование Крылова. В определителе Крылова,
стоящем в правой части этого тождества, ![]() входит только в элементы последнего
столбца; остальные же элементы этого определителя от
входит только в элементы последнего
столбца; остальные же элементы этого определителя от ![]() не зависят.
не зависят.
Замечание.
В регулярном случае все пространство ![]() является циклическим (относительно
оператора
является циклическим (относительно
оператора ![]() ).
Если в качестве базиса выбрать векторы
).
Если в качестве базиса выбрать векторы ![]() , то в этом базисе оператору
, то в этом базисе оператору ![]() соответствует
матрица
соответствует
матрица ![]() ,
имеющая естественную нормальную форму
,
имеющая естественную нормальную форму
 . (94)
. (94)
Переход
от основного базиса ![]() к базису
к базису ![]() осуществляется при помощи
неособенной преобразующей матрицы
осуществляется при помощи
неособенной преобразующей матрицы
 . (95)
. (95)
При этом
![]() . (96)
. (96)
3.
Особый случай: ![]() .
В этом случае векторы
.
В этом случае векторы ![]() линейно зависимы, и потому
линейно зависимы, и потому
 .
.
Равенство
(93) было выведено при условии ![]() . Но обе части этого равенства
представляют собой целые рациональные функции от
. Но обе части этого равенства
представляют собой целые рациональные функции от ![]() и параметров
и параметров ![]() . Поэтому «из соображений
непрерывности» следует, что равенство (93) имеет место и при
. Поэтому «из соображений
непрерывности» следует, что равенство (93) имеет место и при ![]() . Но тогда в
определителе Крылова (93) после его раскрытия все коэффициенты окажутся равными
нулю. Таким образом, в особом случае
. Но тогда в
определителе Крылова (93) после его раскрытия все коэффициенты окажутся равными
нулю. Таким образом, в особом случае ![]() формула (93) переходит в тривиальное
тождество
формула (93) переходит в тривиальное
тождество ![]() .
.
Рассмотрим
матрицу, составленную из координат векторов ![]()
 . (97)
. (97)
Эта
матрица имеет ранг ![]() и первые
и первые ![]() строк в ней линейно
независимы, последняя же
строк в ней линейно
независимы, последняя же ![]() -я строка есть линейная комбинация
первых
-я строка есть линейная комбинация
первых ![]() строк
с коэффициентами
строк
с коэффициентами ![]() [см. (83)]. Из
[см. (83)]. Из ![]() координат
координат ![]() мы сможем выбрать
такие
мы сможем выбрать
такие ![]() координат
координат
![]() , чтобы
определитель, составленный из этих координат векторов
, чтобы
определитель, составленный из этих координат векторов ![]() , был отличен от нуля:
, был отличен от нуля:
 . (98)
. (98)
Далее, из (83) вытекает:
 (99)
(99)
Из
этой системы уравнений однозначно определяются коэффициенты ![]() многочлена
многочлена ![]() (минимального многочлена
вектора
(минимального многочлена
вектора ![]() ).
Совершенно аналогично регулярному случаю (лишь с заменой
).
Совершенно аналогично регулярному случаю (лишь с заменой ![]() на
на ![]() и букв
и букв ![]() буквами
буквами ![]() ) мы сможем исключить
) мы сможем исключить ![]() из (85) и (99) и
получить следующую формулу для
из (85) и (99) и
получить следующую формулу для ![]() :
:
 . (100)
. (100)
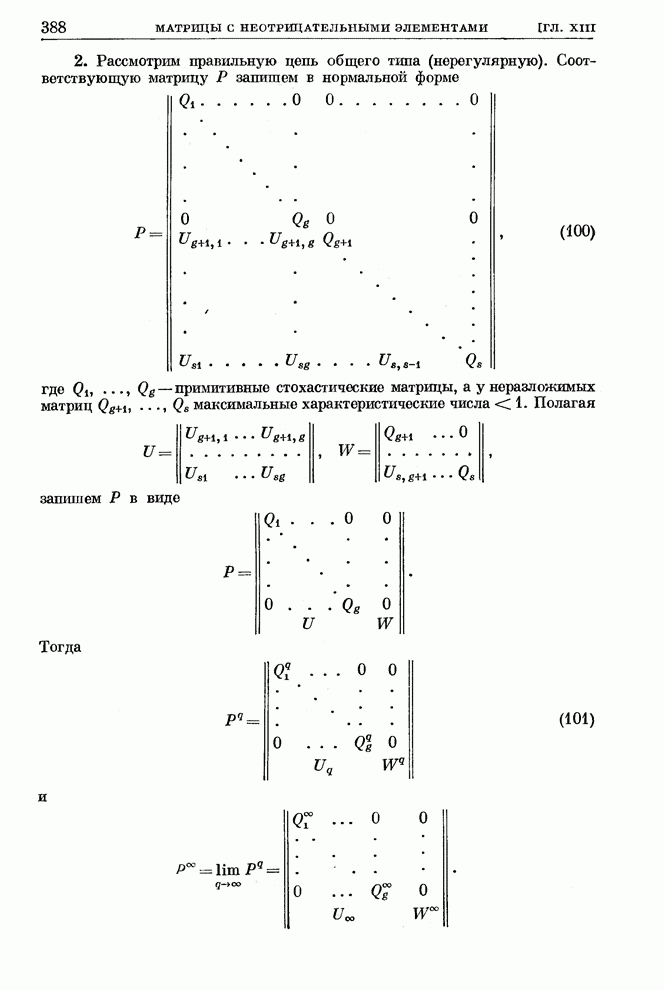
4.
Остановимся на выяснении вопроса, для каких матриц ![]() и при каком выборе исходного
вектора
и при каком выборе исходного
вектора ![]() или,
что то же, при каком выборе исходных параметров
или,
что то же, при каком выборе исходных параметров ![]() имеет место регулярный случай.
имеет место регулярный случай.
Мы уже видели, что в регулярном случае
![]() .
.
Совпадение
характеристического многочлена ![]() с минимальным многочленом
с минимальным многочленом ![]() означает, что у
матрицы
означает, что у
матрицы ![]() нет
двух элементарных делителей с одним и тем же характеристическим числом, т. е. все
элементарные делители попарно взаимно просты. В случае, когда
нет
двух элементарных делителей с одним и тем же характеристическим числом, т. е. все
элементарные делители попарно взаимно просты. В случае, когда ![]() – матрица простой
структуры, это требование равносильно условию, что характеристическое уравнение
матрицы
– матрица простой
структуры, это требование равносильно условию, что характеристическое уравнение
матрицы ![]() не
имеет кратных корней.
не
имеет кратных корней.
Совпадение
многочлена ![]() с
с
![]() означает,
что в качестве вектора
означает,
что в качестве вектора ![]() выбран вектор, порождающий (при
помощи оператора
выбран вектор, порождающий (при
помощи оператора ![]() )
все пространство
)
все пространство ![]() .
Такой вектор согласно теореме 2 § 2 всегда существует.
.
Такой вектор согласно теореме 2 § 2 всегда существует.
Если
же условие ![]() не
выполняется, то, как бы ни выбрать вектор
не
выполняется, то, как бы ни выбрать вектор ![]() , мы многочлена
, мы многочлена ![]() не получим, так как
полученный по методу Крылова многочлен
не получим, так как
полученный по методу Крылова многочлен ![]() является делителем
является делителем ![]() , который в
рассматриваемом случае не совпадает с многочленом
, который в
рассматриваемом случае не совпадает с многочленом ![]() , а является лишь его делителем. Варьируя
вектор
, а является лишь его делителем. Варьируя
вектор ![]() ,
мы можем в качестве
,
мы можем в качестве ![]() получить любой делитель
получить любой делитель ![]() .
.
Полученные выводы мы можем сформулировать в виде следующей теоремы:
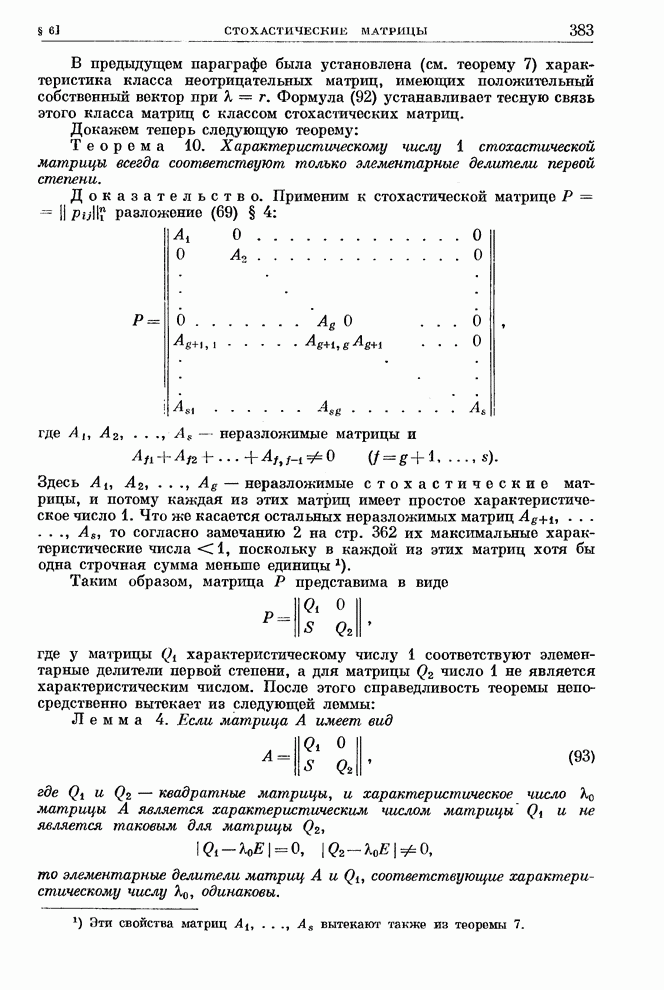
Теорема
14. Преобразование Крылова дает выражение для характеристического многочлена ![]() матрицы
матрицы ![]() в виде
определителя (93) в том и только в том случае, когда выполняются два условия:
в виде
определителя (93) в том и только в том случае, когда выполняются два условия:
1.
Элементарные делители матрицы ![]() попарно взаимно просты.
попарно взаимно просты.
2.
Исходные параметры ![]() являются координатами вектора
являются координатами вектора ![]() , порождающего (при
помощи оператора
, порождающего (при
помощи оператора ![]() ,
соответствующего матрице
,
соответствующего матрице ![]() ) все
) все ![]() -мерное пространство.
-мерное пространство.
В
общем же случае преобразование Крылова приводит к некоторому делителю ![]() характеристического
многочлена
характеристического
многочлена ![]() .
Этот делитель
.
Этот делитель ![]() является
минимальным многочленом для вектора
является
минимальным многочленом для вектора ![]() с координатами
с координатами ![]() (
(![]() – исходные параметры в
преобразовании Крылова).
– исходные параметры в
преобразовании Крылова).
5.
Покажем, как найти координаты собственного вектора ![]() для любого
характеристического числа
для любого
характеристического числа ![]() , которое является корнем многочлена
, которое является корнем многочлена ![]() , получающегося по
методу Крылова.
, получающегося по
методу Крылова.
Вектор
![]() будем
искать в виде
будем
искать в виде
![]() . (101)
. (101)
Подставляя
это выражение для ![]() в векторное равенство
в векторное равенство
![]()
и используя (101), мы получим:
 (102)
(102)
Отсюда,
между прочим, следует, что ![]() , так как равенство
, так как равенство ![]() в силу (102)
давало бы линейную зависимость между векторами
в силу (102)
давало бы линейную зависимость между векторами ![]() . В дальнейшем мы полагаем
. В дальнейшем мы полагаем ![]() . Тогда из (102)
получаем:
. Тогда из (102)
получаем:
 (103)
(103)
Первые
![]() из этих
равенств определяют нам последовательно величины
из этих
равенств определяют нам последовательно величины ![]() (координаты вектора
(координаты вектора ![]() в «новом» базисе
в «новом» базисе ![]() ); последнее же
равенство является следствием из предыдущих и из соотношения
); последнее же
равенство является следствием из предыдущих и из соотношения ![]() .
.
Координаты
![]() вектора
вектора ![]() в исходном базисе
могут быть найдены по следующим формулам, которые вытекают из (101):
в исходном базисе
могут быть найдены по следующим формулам, которые вытекают из (101):
 (104)
(104)
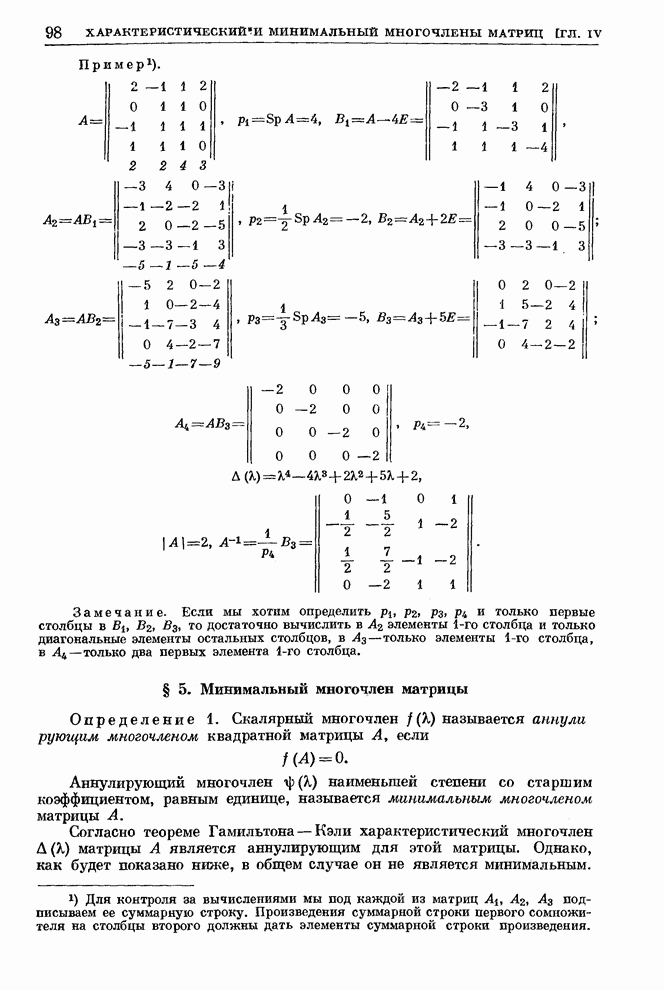
Пример 1.
Рекомендуем читателю следующую схему вычислений.
Под
данной матрицей ![]() выписываем
строку из координат вектора
выписываем
строку из координат вектора ![]() . Этими числами задаемся произвольно
(при одном лишь ограничении: по крайней мере одно из этих чисел отлично от
нуля). Под строкой
. Этими числами задаемся произвольно
(при одном лишь ограничении: по крайней мере одно из этих чисел отлично от
нуля). Под строкой ![]() пишем строку
пишем строку ![]() , т. е. координаты вектора
, т. е. координаты вектора ![]() . Числа
. Числа ![]() , получаются путем
последовательного умножения строки
, получаются путем
последовательного умножения строки ![]() на строки данной матрицы
на строки данной матрицы ![]() . Так, например,
. Так, например, ![]() ,
, ![]() и т. д. Под
строкой
и т. д. Под
строкой ![]() пишем
строку
пишем
строку ![]() и
т. д. Каждая из приписываемых строк, начиная со второй, определяется путем
последовательного умножения предыдущей строки па строки данной матрицы.
и
т. д. Каждая из приписываемых строк, начиная со второй, определяется путем
последовательного умножения предыдущей строки па строки данной матрицы.
Над строками данной матрицы выписываем контрольную суммарную строку
 .
.
В данном случае мы имеем регулярный случай, поскольку
 .
.
Определитель Крылова имеет вид
 .
.
Раскрывая
этот определитель и сокращая на ![]() , найдем:
, найдем:
![]() .
.
Обозначим
через ![]() собственный
вектор матрицы
собственный
вектор матрицы ![]() ,
соответствующий характеристическому числу
,
соответствующий характеристическому числу ![]() . Числа
. Числа ![]() найдем по формулам (103):
найдем по формулам (103):
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Контрольное
равенство ![]() ,
конечно, удовлетворяется.
,
конечно, удовлетворяется.
Полученные
числа ![]() располагаем
в вертикальном столбце параллельно столбцу векторов
располагаем
в вертикальном столбце параллельно столбцу векторов ![]() . Помножая столбец
. Помножая столбец ![]() на столбец
на столбец ![]() , мы получим первую
координату
, мы получим первую
координату ![]() вектора
вектора
![]() в
исходном базисе
в
исходном базисе ![]() ;
аналогично получаем
;
аналогично получаем ![]() . Находим координаты (после сокращения
на 4) вектора
. Находим координаты (после сокращения
на 4) вектора ![]() .
Аналогично определяем координаты
.
Аналогично определяем координаты ![]() собственного вектора
собственного вектора ![]() для
характеристического числа
для
характеристического числа ![]() .
.
Далее, согласно (94) и (95)
![]() ,
,
где
 ,
,
 .
.
Пример
2. Рассмотрим ту же матрицу ![]() , но в качестве исходных параметров
возьмем числа
, но в качестве исходных параметров
возьмем числа ![]() .
.
 .
.
Но в данном случае

и
![]() . Мы
имеем дело с особым случаем.
. Мы
имеем дело с особым случаем.
Беря
первые три координаты векторов ![]() , определитель Крылова записываем в
виде
, определитель Крылова записываем в
виде
 .
.
Раскрывая
этот определитель и сокращая на ![]() , получим:
, получим:
![]() .
.
Отсюда
находим три характеристических числа: ![]() ,
, ![]() ,
, ![]() . Четвертое характеристическое число
получим из условия, что сумма всех характеристических чисел равна следу
матрицы. Но
. Четвертое характеристическое число
получим из условия, что сумма всех характеристических чисел равна следу
матрицы. Но ![]() .
Поэтому
.
Поэтому ![]() .
.
Приведенные примеры показывают, что при применении метода Крылова, выписывая последовательно строки матрицы
 , (105)
, (105)
нужно
следить за рангом получаемой матрицы с тем, чтобы остановиться на первой [![]() -й сверху] строке,
которая является линейной комбинацией предыдущих. Определение ранга связано с
вычислением известных определителей. Кроме того, получив определитель Крылова в
виде (93) или (100), для раскрытия его по элементам последнего столбца следует вычислить
известное число определителей
-й сверху] строке,
которая является линейной комбинацией предыдущих. Определение ранга связано с
вычислением известных определителей. Кроме того, получив определитель Крылова в
виде (93) или (100), для раскрытия его по элементам последнего столбца следует вычислить
известное число определителей ![]() -го порядка [в регулярном случае
-го порядка [в регулярном случае ![]() -го порядка].
-го порядка].
Вместо
раскрытия определителя Крылова можно определить коэффициенты ![]() непосредственно из
системы уравнений (91) [или (99)], применяя к этой системе какой-либо
эффективный метод решения, например метод исключения. Этот метод можно
применить непосредственно к матрице
непосредственно из
системы уравнений (91) [или (99)], применяя к этой системе какой-либо
эффективный метод решения, например метод исключения. Этот метод можно
применить непосредственно к матрице
 , (106)
, (106)
пользуясь им параллельно с получением соответствующих строк по методу Крылова. Тогда мы своевременно обнаружим зависимую от предыдущих строку матрицы (105) без вычисления каких-либо определителей.
Поясним
это подробнее. В первой строке матрицы (106) выбираем какой-либо элемент ![]() и с его помощью
обращаем в нуль стоящий под ним элемент
и с его помощью
обращаем в нуль стоящий под ним элемент ![]() , вычитая из второй строки первую,
помноженную на
, вычитая из второй строки первую,
помноженную на ![]() .
Затем во второй строке выбираем какой-либо элемент
.
Затем во второй строке выбираем какой-либо элемент ![]() и с помощью элементов
и с помощью элементов ![]() и
и ![]() обращаем в нуль
элементы
обращаем в нуль
элементы ![]() и
и
![]() и т. д.
В результате такого преобразования в последнем столбце матрицы (106) степени
и т. д.
В результате такого преобразования в последнем столбце матрицы (106) степени ![]() заменятся
многочленами
заменятся
многочленами ![]() -й
степени
-й
степени ![]()
![]() .
.
Так
как при нашем преобразовании при любом ![]() ранг матрицы, образованной первыми
ранг матрицы, образованной первыми ![]() строками и первыми
строками и первыми
![]() столбцами
матрицы (106), не меняется, то
столбцами
матрицы (106), не меняется, то ![]() -я строка этой матрицы после
преобразования будем иметь вид
-я строка этой матрицы после
преобразования будем иметь вид
![]() .
.
Проведенное нами преобразование не изменяет величины определителя Крылова
 .
.
Поэтому
![]() , (107)
, (107)
т.
е. ![]() и
будем искомым многочленом
и
будем искомым многочленом ![]() .
.
Рекомендуем
следующее упрощение. Получив ![]() -ю преобразованную строку в матрице
(106)
-ю преобразованную строку в матрице
(106)
![]() , (108)
, (108)
следующую
![]() -ю строку
следует получать, умножая ряд
-ю строку
следует получать, умножая ряд ![]() (а не первоначальный ряд
(а не первоначальный ряд ![]() ) на строки данной
матрицы.
) на строки данной
матрицы.
Тогда
мы найдем ![]() -ю
строку в виде
-ю
строку в виде
![]()
и после вычитания предыдущих строк получим:
![]() .
.
Рекомендуемое
нами небольшое видоизменение метода Крылова (соединение его с методом
исключения) позволяет сразу получить интересующий нас многочлен ![]() [регулярном случае
[регулярном случае
![]() ] без
вычисления каких-либо определителей и решения вспомогательной системы
уравнений.
] без
вычисления каких-либо определителей и решения вспомогательной системы
уравнений.
Пример.

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие автора к первому изданию
- Предисловие автора ко второму изданию
- ЧАСТЬ I. ОСНОВЫ ТЕОРИИ
- Глава I. Матрицы и действия над ними
- § 1. Матрицы. Основные обозначения
- § 2. Сложение и умножение прямоугольных матриц
- § 3. Квадратные матрицы
- § 4. Ассоциированные матрицы. Миноры обратной матрицы
- § 5. Обращение прямоугольных матриц. Псевдообратная матрица
- Глава II. Алгоритм Гаусса и некоторые его применения
- § 1. Метод исключения Гаусса
- § 2. Механическая интерпретация алгоритма Гаусса
- § 3. Детерминантное тождество Сильвестра
- § 4. Разложение квадратной матрицы на треугольные множители
- § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса
- Глава III. Лииейиые операторы в n-мерном векторном пространстве
- § 1. Векторное пространство
- § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное
- § 3. Сложение и умножение линейных операторов
- § 4. Преобразование координат
- § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра
- § 6. Линейные операторы, отображающие n-мерное пространство само в себя
- § 7. Характеристические числа и собственные векторы линейного оператора
- § 8. Линейные операторы простой структуры
- Глава IV. Характеристический и минимальный многочлены матрицы
- § 1. Сложение и умножение матричных многочленов
- § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу
- § 3. Характеристический многочлен матрицы. Присоединенная матрица
- § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы
- § 5. Минимальный многочлен матрицы
- Глава V. Функции от матрицы
- § 1. Определение функции от матрицы
- § 2. Интерполяционный многочлен Лагранжа–Сильвестра
- § 3. Другие формы определения f(A). Компоненты матрицы A
- § 4. Представление функций от матриц рядами
- § 5. Некоторые свойства функций от матриц
- § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 7. Устойчивость движения в случае линейной системы
- Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей
- § 1. Элементарные преобразования многочленной матрицы
- § 2. Канонический вид матрицы
- § 3. Инвариантные многочлены и элементарные делители многочленной матрицы
- § 4. Эквивалентность линейных двучленов
- § 5. Критерий подобия матриц
- § 6. Нормальные формы матрицы
- § 7. Элементарные делители матрицы f(A)
- § 8. Общий метод построения преобразующей матрицы
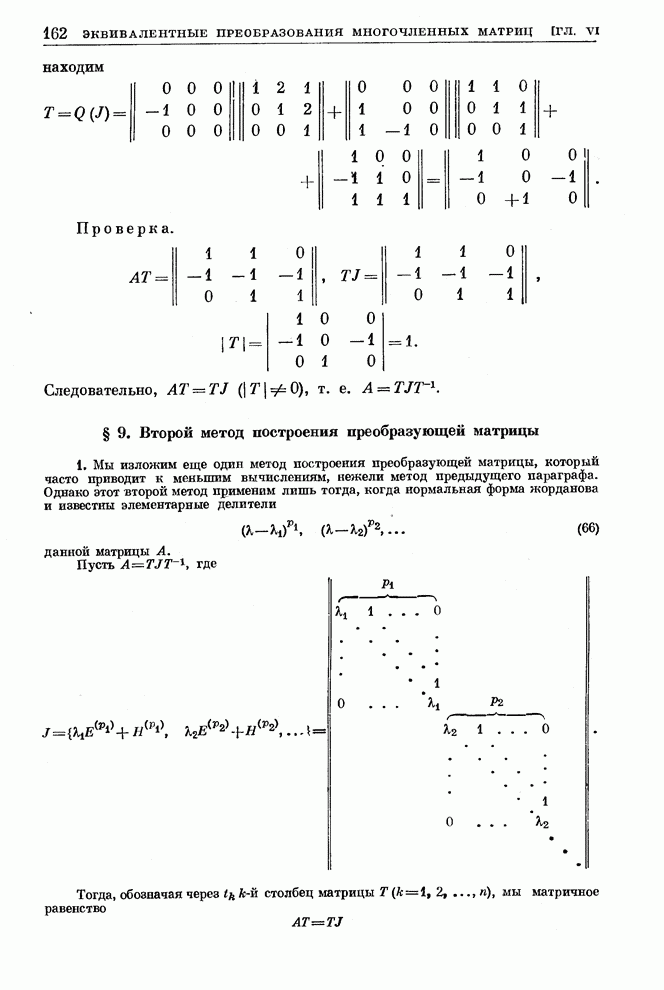
- § 9. Второй метод построения преобразующей матрицы
- Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей)
- § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора)
- § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами
- § 3. Сравнения. Надпространство
- § 4. Расщепление пространства на циклические инвариантные подпространства
- § 5. Нормальная форма матрицы
- § 6. Инвариантные многочлены. Элементарные делители
- § 7. Нормальная жорданова форма матрицы
- § 8. Метод акад. А. Н. Крылова преобразования векового уравнения
- Глава VIII. Матричные уравнения
- § 1. Уравнение AX=XB
- § 2. Частный случай: A=B. Перестановочные матрицы
- § 3. Уравнение AX-XB=C
- § 4. Скалярное уравнение f(X)=0
- § 5. Матричное многочленное уравнение
- § 6. Извлечение корня m-й степени из неособенной матрицы
- § 7. Извлечение корня m-й степени из особенной матрицы
- § 8. Логарифм матрицы
- Глава IX. Линейные операторы в унитарном пространстве
- § 1. Общие соображения
- § 2. Метризация пространства
- § 3. Критерий Грама линейной зависимости векторов
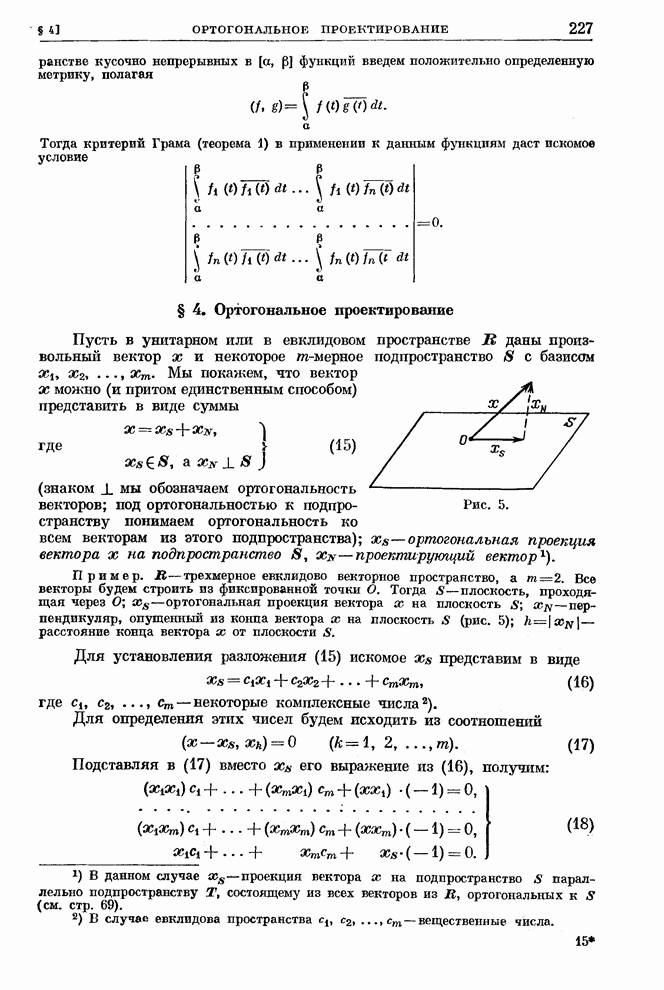
- § 4. Ортогональное проектирование
- § 5. Геометрический смысл определителя Грама и некоторые неравенства
- § 6. Ортогонализация ряда векторов
- § 7. Ортонормированный базис
- § 8. Сопряженный оператор
- § 9. Нормальные операторы в унитарном пространстве
- § 10. Спектр нормальных, эрмитовых, унитарных операторов
- § 11. Неотрицательные и положительно определенные эрмитовы операторы
- § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли
- § 13. Линейные операторы в евклидовом пространстве
- § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве
- § 15. Коммутирующие нормальные операторы
- § 16. Псевдообратный оператор
- Глава X. Квадратичные и эрмитовы формы
- § 1. Преобразование переменных в квадратичной форме
- § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции
- § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби
- § 4. Положительные квадратичные формы
- § 5. Приведение квадратичной формы к главным осям
- § 6. Пучок квадратичных форм
- § 7. Экстремальные свойства характеристических чисел регулярного пучка форм
- § 8. Малые колебания системы с n степенями свободы
- § 9. Эрмитовы формы
- § 10. Ганкелевы формы
- ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ
- Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы
- § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц
- § 2. Полярное разложение комплексной матрицы
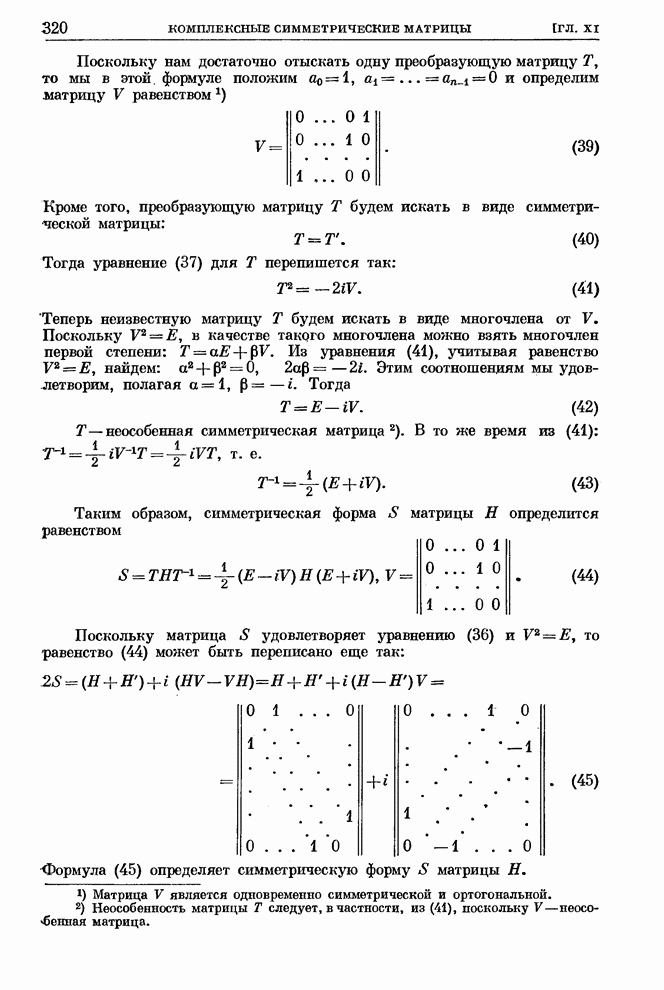
- § 3. Нормальная форма комплексной симметрической матрицы
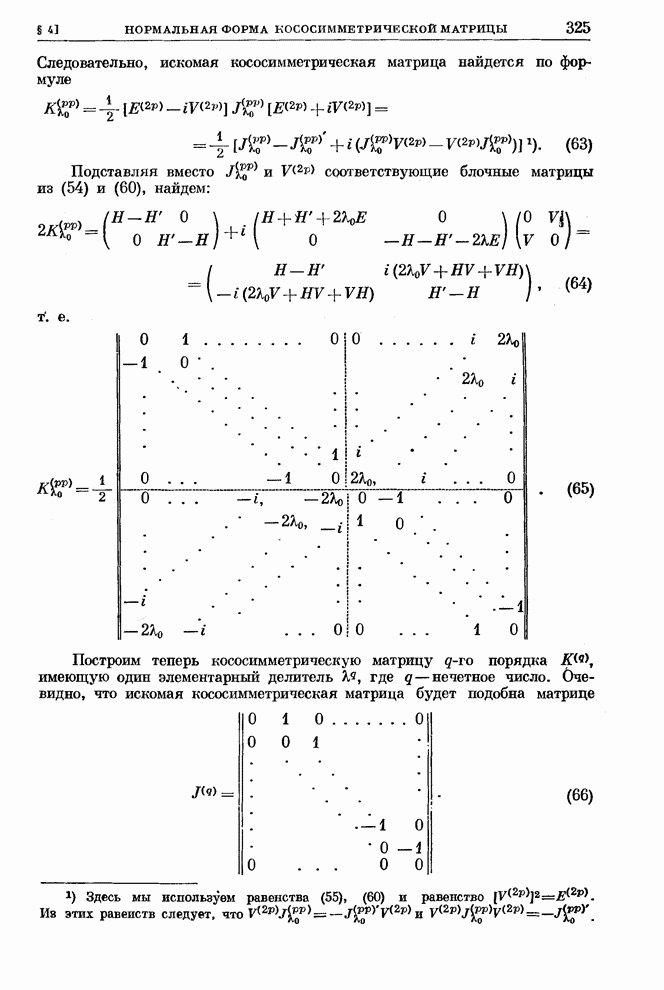
- § 4. Нормальная форма комплексной кососимметрической матрицы
- § 5. Нормальная форма комплексной ортогональной матрицы
- ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ
- § 1. Введение
- § 2. Регулярный пучок матриц
- § 3. Сингулярные пучки. Теорема о приведении
- § 4. Каноническая форма сингулярного пучка матриц
- § 5. Минимальные индексы пучка
- § 6. Сингулярные пучки квадратичных форм
- § 7. Приложения к дифференциальным уравнениям
- ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- § 1. Общие свойства
- § 2. Спектральные свойства неразложимых неотрицательных матриц
- § 3. Разложимые матрицы
- § 4. Нормальная форма разложимой матрицы
- § 5. Примитивные и импримитивные матрицы
- § 6. Стохастические матрицы
- § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний
- § 8. Вполне неотрицательные матрицы
- § 9. Осцилляционные матрицы
- Глава XIV. Различные критерии регулярности и локализации собственных значений
- § 1. Критерий регулярности Адамара и его обобщения
- § 2. Норма матрицы
- § 3. Распространение критерия Адамара на блочные матрицы
- § 4. Критерий регулярности Фидлера
- § 5. Круги Гершгорина и другие области локализации
- Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений
- § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия
- § 2. Преобразование Ляпунова
- § 3. Приводимые системы
- § 4. Каноническая форма приводимой системы. Теорема Еругина
- § 5. Матрицант
- § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра
- § 7. Дифференциальные системы в комплексной области. Общие свойства
- § 8. Мультипликативный интеграл в комплексной области
- § 9. Изолированная особая точка
- § 10. Регулярная особая точка
- § 11. Приводимые аналитические системы
- § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского
- ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ
- § 1. Введение
- § 2. Индексы Коши
- § 3. Алгоритм Рауса
- § 4. Особые случаи. Примеры
- § 5. Теорема Ляпунова
- § 6. Теорема Рауса-Гурвица
- § 7. Формула Орландо
- § 8. Особые случаи в теореме Рауса — Гурвица
- § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена
- § 10. Бесконечные ганкелевы матрицы конечного ранга
- § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя
- § 12. Второе доказательство теоремы Рауса—Гурвица
- § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара
- § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей
- § 15. Область устойчивости. Параметры Маркова
- § 16. Связь с проблемой моментов
- § 17. Связь между определителями Гурвица и определителями Маркова
- § 18. Теоремы Маркова и Чебышева
- § 19. Обобщенная задача Рауса-Гурвица
- ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ
- § 1. Мажорирующие последовательности
- § 2. Неравенства Неймана-Хорна
- § 3. Неравенства Вейля
- § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов
- § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов
- § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов
- ЛИТЕРАТУРА