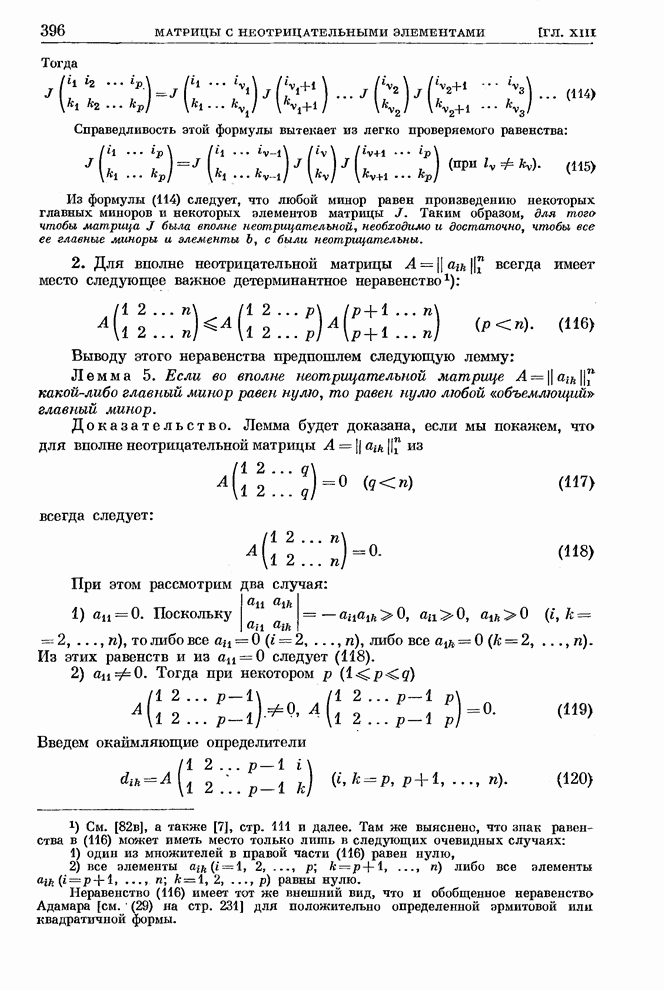| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
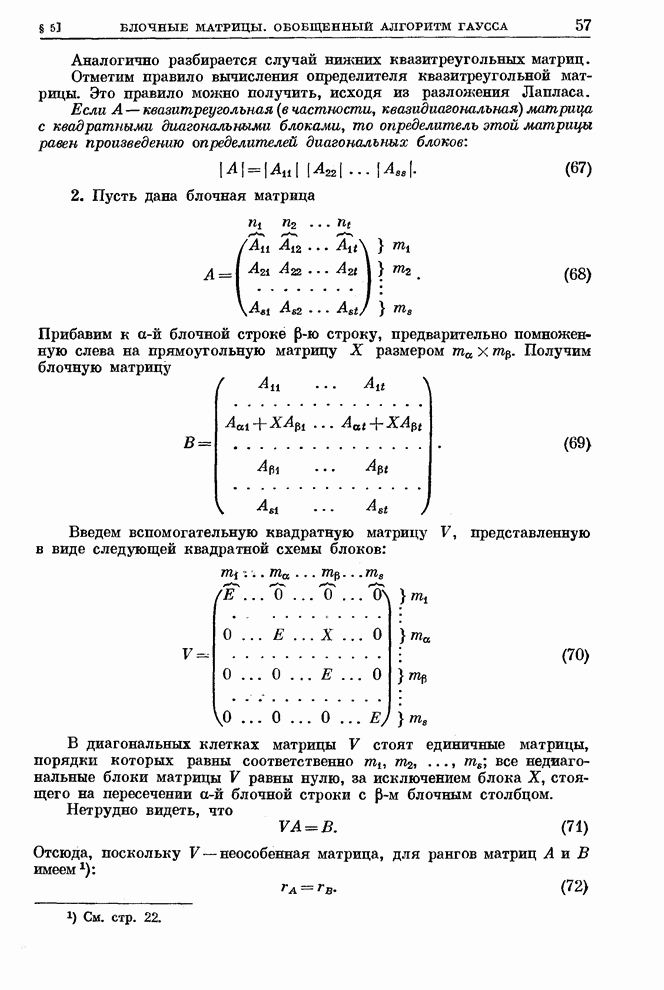
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
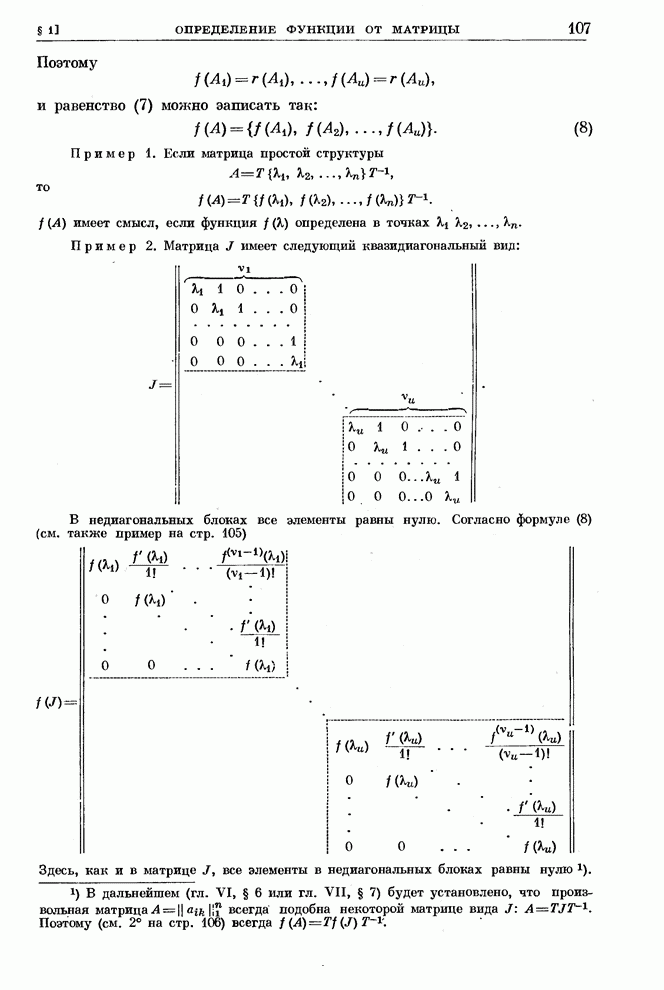
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
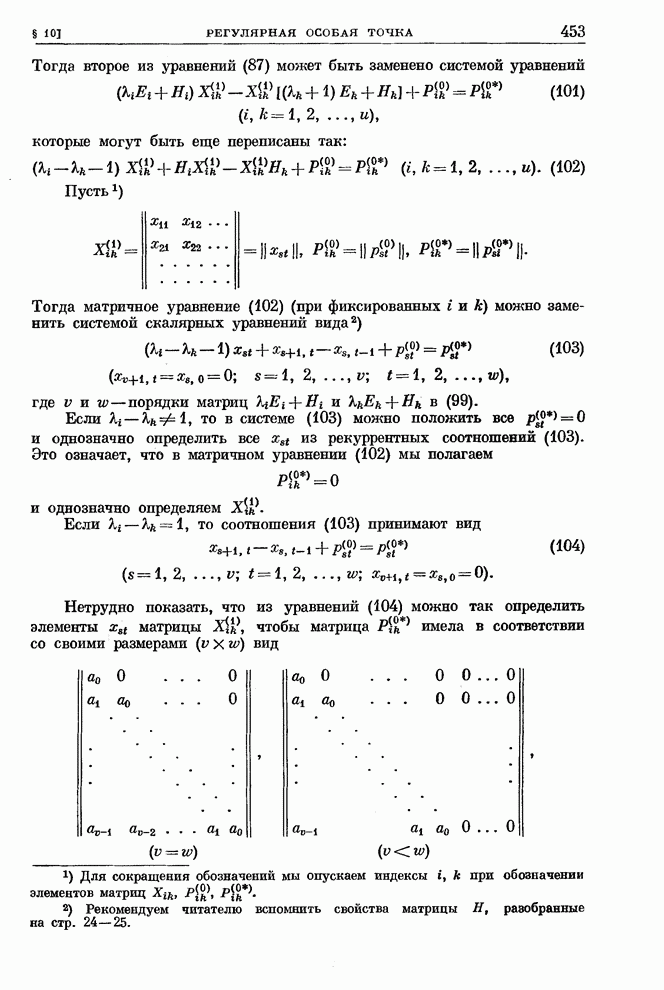
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
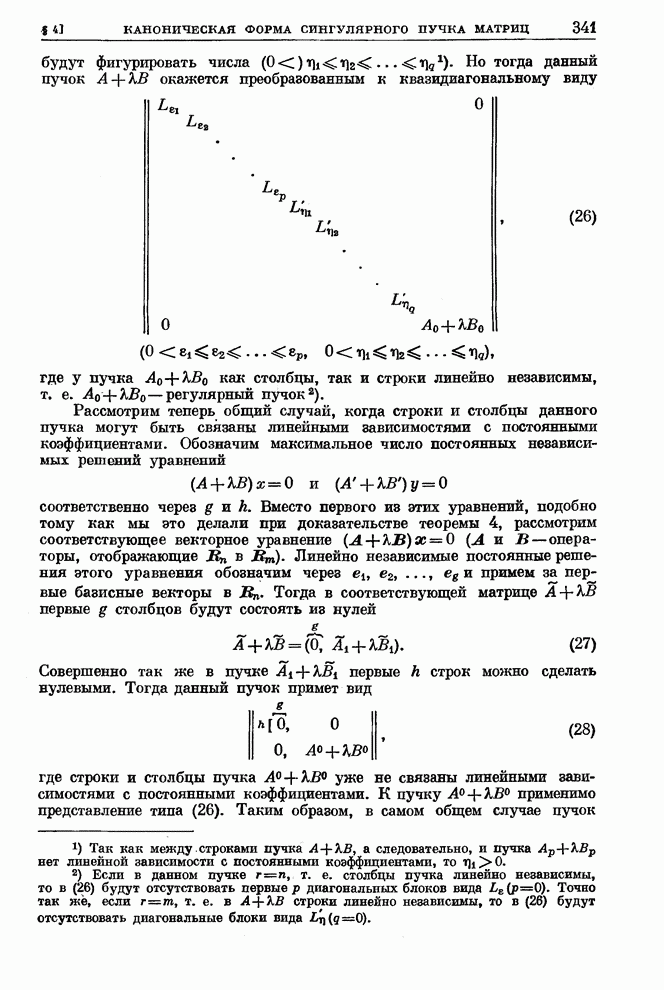
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
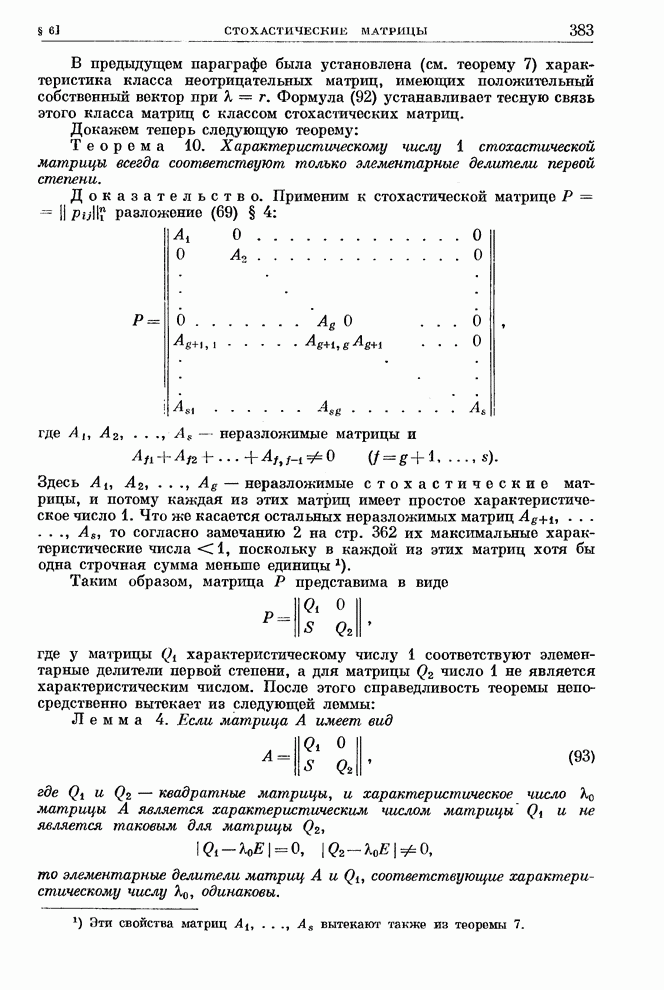
382
383
384
385
386
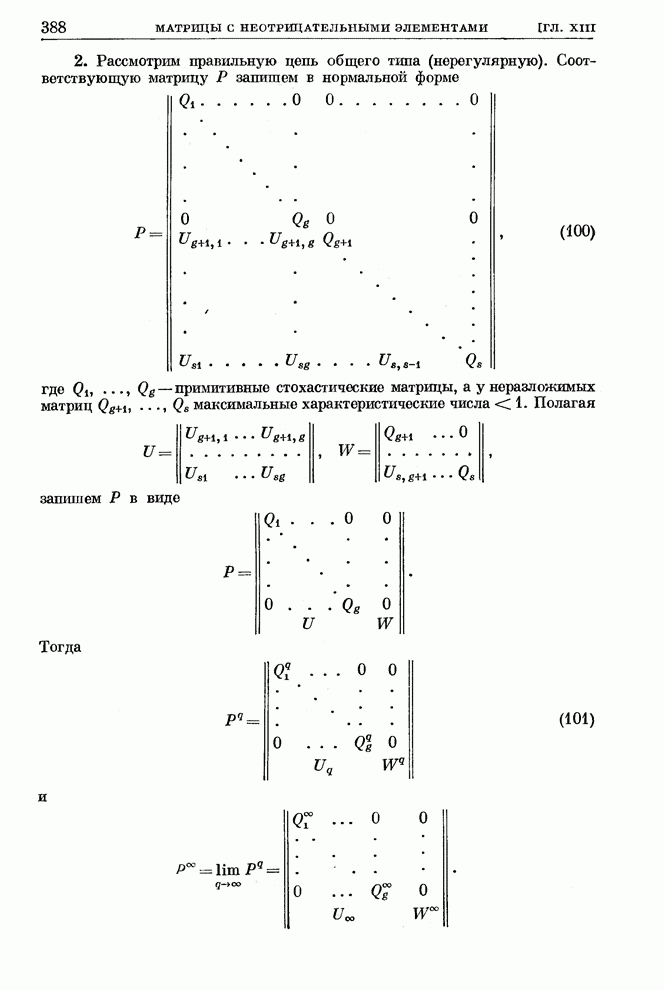
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8. Общий метод построения преобразующей матрицы
Во
многих вопросах теории матриц и их приложений достаточно знать только
нормальную форму, к которой приводится данная матрица ![]() преобразованием
подобия. Нормальная форма вполне определяется инвариантными многочленами
характеристической матрицы
преобразованием
подобия. Нормальная форма вполне определяется инвариантными многочленами
характеристической матрицы ![]() . Для нахождения
последних можно воспользоваться определяющими формулами [см. (10) на стр. 143]
или приведением характеристической матрицы
. Для нахождения
последних можно воспользоваться определяющими формулами [см. (10) на стр. 143]
или приведением характеристической матрицы ![]() при
помощи элементарных преобразований к канонической диагональной форме.
при
помощи элементарных преобразований к канонической диагональной форме.
В
некоторых же вопросах необходимо знать не только нормальную форму ![]() данной матрицы
данной матрицы ![]() , но и преобразующую неособенную
матрицу
, но и преобразующую неособенную
матрицу ![]() .
.
Непосредственный
способ определения матрицы ![]() состоит в
следующем.
состоит в
следующем.
Равенство
![]()
переписывается так:
![]() .
.
Это
матричное уравнение относительно ![]() равносильно
системе
равносильно
системе ![]() линейных однородных уравнений
относительно
линейных однородных уравнений
относительно ![]() неизвестных коэффициентов матрицы
неизвестных коэффициентов матрицы ![]() . Определение преобразующей матрицы
сводится к решению этой системы из
. Определение преобразующей матрицы
сводится к решению этой системы из ![]() уравнений. При
этом из множества решений необходимо выбрать такое решение, для которого
уравнений. При
этом из множества решений необходимо выбрать такое решение, для которого ![]() . Существование такого решения
обеспечено тем, что матрицы
. Существование такого решения
обеспечено тем, что матрицы ![]() и
и ![]() имеют одни и те же инвариантные
многочлены.
имеют одни и те же инвариантные
многочлены.
Заметим,
что в то время как нормальная форма определяется однозначно заданием данной
матрицы ![]() , для преобразующей матрицы
, для преобразующей матрицы ![]() мы всегда имеем бесчисленное
множество значений, охватываемых формулой
мы всегда имеем бесчисленное
множество значений, охватываемых формулой
![]() , (60)
, (60)
где
![]() – одна из преобразующих матриц, a
– одна из преобразующих матриц, a ![]() – произвольная матрица,
перестановочная с
– произвольная матрица,
перестановочная с ![]() .
.
Предложенный
выше способ определения преобразующей матрицы ![]() очень
прост по своей идее, но практически мало пригоден, так как связан с очень
большими вычислениями (так, уже при
очень
прост по своей идее, но практически мало пригоден, так как связан с очень
большими вычислениями (так, уже при ![]() он требует
решения системы из 16 линейных уравнений).
он требует
решения системы из 16 линейных уравнений).
Переходим
к изложению более эффективного метода построения преобразующей матрицы ![]() . Этот метод опирается на добавление
к теореме 7 (стр. 150). Согласно этому добавлению в качестве преобразующей
матрицы можно взять матрицу
. Этот метод опирается на добавление
к теореме 7 (стр. 150). Согласно этому добавлению в качестве преобразующей
матрицы можно взять матрицу
![]() , (61)
, (61)
коль скоро
![]() .
.
Последнее
равенство выражает собой эквивалентность характеристических матриц ![]() и
и ![]() .
Здесь
.
Здесь ![]() и
и ![]() –
многочленные матрицы с постоянными отличными от нуля определителями.
–
многочленные матрицы с постоянными отличными от нуля определителями.
Для
конкретного нахождения матрицы ![]() мы приводим к
канонической диагональной форме каждую из
мы приводим к
канонической диагональной форме каждую из ![]() -матриц
-матриц
![]() и
и ![]() при
помощи соответствующих элементарных преобразований:
при
помощи соответствующих элементарных преобразований:
![]() , (62)
, (62)
![]() , (63)
, (63)
где
![]() ,
, ![]() , (64)
, (64)
а
![]() ,
, ![]() –
элементарные матрицы, соответствующие элементарным операциям над столбцами
–
элементарные матрицы, соответствующие элементарным операциям над столбцами ![]() -матриц
-матриц ![]() и
и
![]() . Из (62), (63) и (64) следует:
. Из (62), (63) и (64) следует:
![]() ,
,
где
![]() . (65)
. (65)
Матрицу
![]() вычисляем, применив последовательно
к столбцам единичной матрицы
вычисляем, применив последовательно
к столбцам единичной матрицы ![]() элементарные
операции с матрицами
элементарные
операции с матрицами ![]() . После этого [согласно
формуле (61)] заменяем в
. После этого [согласно
формуле (61)] заменяем в ![]() аргумент
аргумент ![]() матрицей
матрицей ![]() .
.
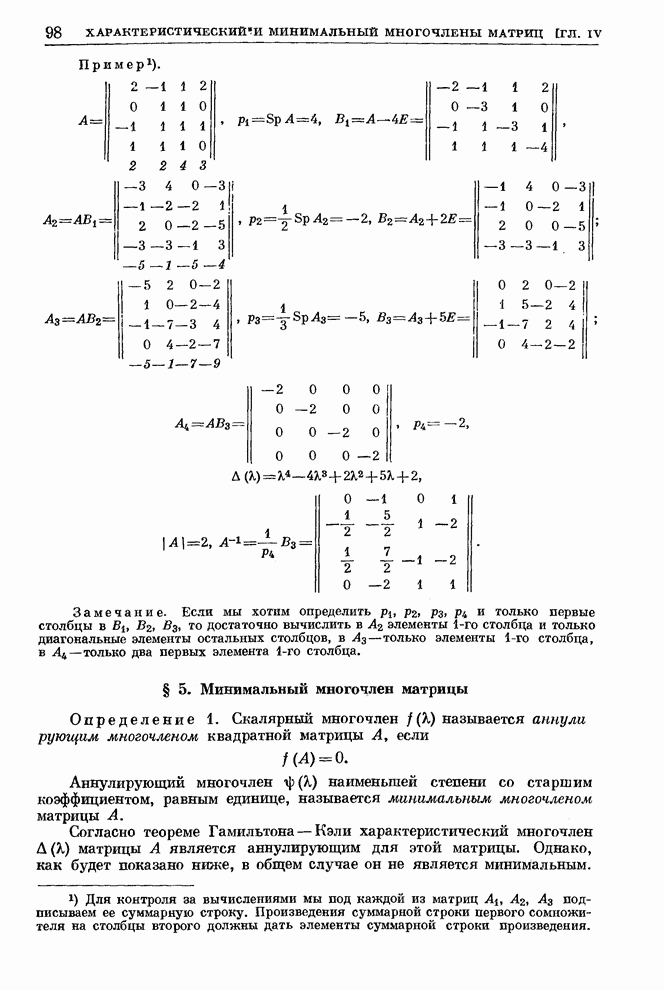
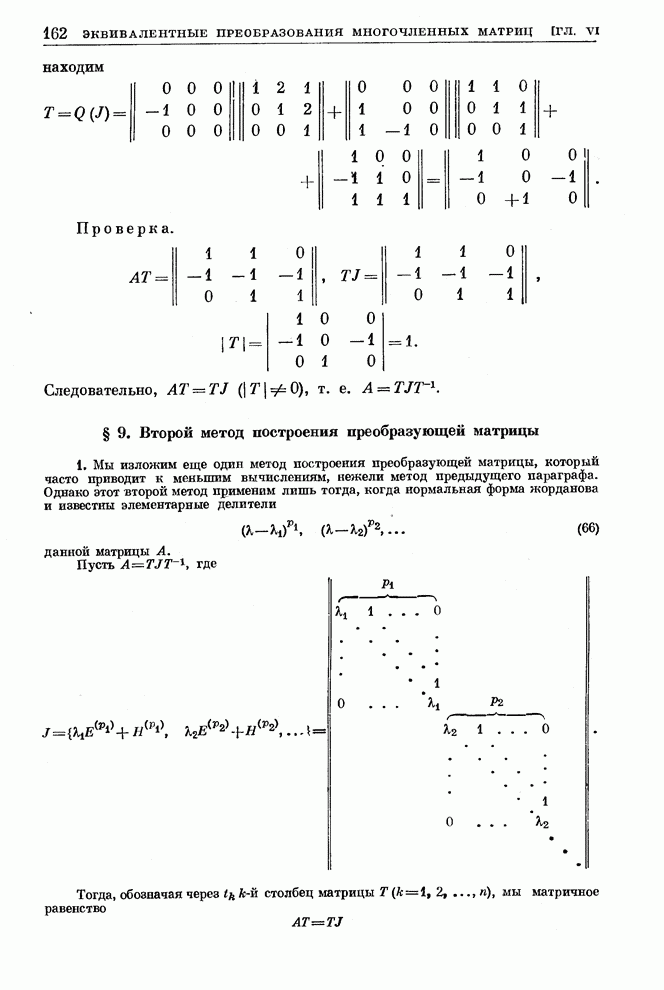
Пример.
 .
.
Введем символические обозначения для левых и правых элементарных операций и соответствующих матриц (см. стр. 136–137):

Читатель легко проверит, что характеристическая матрица

приводится к каноническому диагональному виду

с помощью следующих последовательно выполненных элементарных операций:
 (*)
(*)
Из
канонического диагонального вида матрицы ![]() усматриваем,
что матрица
усматриваем,
что матрица ![]() имеет только один элементарный
делитель
имеет только один элементарный
делитель ![]() . Поэтому соответствующей жордановой
формой будет матрица
. Поэтому соответствующей жордановой
формой будет матрица
 .
.
Нетрудно
видеть, что характеристическая матрица ![]() приводится
к тому же каноническому диагональному виду с помощью элементарных операций
приводится
к тому же каноническому диагональному виду с помощью элементарных операций
 (**)
(**)
Выбрасывая из (*) и (**) левые элементарные операции, обозначенные символом {...}, мы в соответствии с формулами (64), (65) получим
 Применим
к единичной матрице последовательно эти правые элементарные операции:
Применим
к единичной матрице последовательно эти правые элементарные операции:
 .
.
Таким образом,
 .
.
Замечая, что
 ,
,
находим
 .
.
Проверка.
 .
.
Следовательно,
![]()
![]() ,
т. е.
,
т. е. ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие автора к первому изданию
- Предисловие автора ко второму изданию
- ЧАСТЬ I. ОСНОВЫ ТЕОРИИ
- Глава I. Матрицы и действия над ними
- § 1. Матрицы. Основные обозначения
- § 2. Сложение и умножение прямоугольных матриц
- § 3. Квадратные матрицы
- § 4. Ассоциированные матрицы. Миноры обратной матрицы
- § 5. Обращение прямоугольных матриц. Псевдообратная матрица
- Глава II. Алгоритм Гаусса и некоторые его применения
- § 1. Метод исключения Гаусса
- § 2. Механическая интерпретация алгоритма Гаусса
- § 3. Детерминантное тождество Сильвестра
- § 4. Разложение квадратной матрицы на треугольные множители
- § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса
- Глава III. Лииейиые операторы в n-мерном векторном пространстве
- § 1. Векторное пространство
- § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное
- § 3. Сложение и умножение линейных операторов
- § 4. Преобразование координат
- § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра
- § 6. Линейные операторы, отображающие n-мерное пространство само в себя
- § 7. Характеристические числа и собственные векторы линейного оператора
- § 8. Линейные операторы простой структуры
- Глава IV. Характеристический и минимальный многочлены матрицы
- § 1. Сложение и умножение матричных многочленов
- § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу
- § 3. Характеристический многочлен матрицы. Присоединенная матрица
- § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы
- § 5. Минимальный многочлен матрицы
- Глава V. Функции от матрицы
- § 1. Определение функции от матрицы
- § 2. Интерполяционный многочлен Лагранжа–Сильвестра
- § 3. Другие формы определения f(A). Компоненты матрицы A
- § 4. Представление функций от матриц рядами
- § 5. Некоторые свойства функций от матриц
- § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами
- § 7. Устойчивость движения в случае линейной системы
- Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей
- § 1. Элементарные преобразования многочленной матрицы
- § 2. Канонический вид матрицы
- § 3. Инвариантные многочлены и элементарные делители многочленной матрицы
- § 4. Эквивалентность линейных двучленов
- § 5. Критерий подобия матриц
- § 6. Нормальные формы матрицы
- § 7. Элементарные делители матрицы f(A)
- § 8. Общий метод построения преобразующей матрицы
- § 9. Второй метод построения преобразующей матрицы
- Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей)
- § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора)
- § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами
- § 3. Сравнения. Надпространство
- § 4. Расщепление пространства на циклические инвариантные подпространства
- § 5. Нормальная форма матрицы
- § 6. Инвариантные многочлены. Элементарные делители
- § 7. Нормальная жорданова форма матрицы
- § 8. Метод акад. А. Н. Крылова преобразования векового уравнения
- Глава VIII. Матричные уравнения
- § 1. Уравнение AX=XB
- § 2. Частный случай: A=B. Перестановочные матрицы
- § 3. Уравнение AX-XB=C
- § 4. Скалярное уравнение f(X)=0
- § 5. Матричное многочленное уравнение
- § 6. Извлечение корня m-й степени из неособенной матрицы
- § 7. Извлечение корня m-й степени из особенной матрицы
- § 8. Логарифм матрицы
- Глава IX. Линейные операторы в унитарном пространстве
- § 1. Общие соображения
- § 2. Метризация пространства
- § 3. Критерий Грама линейной зависимости векторов
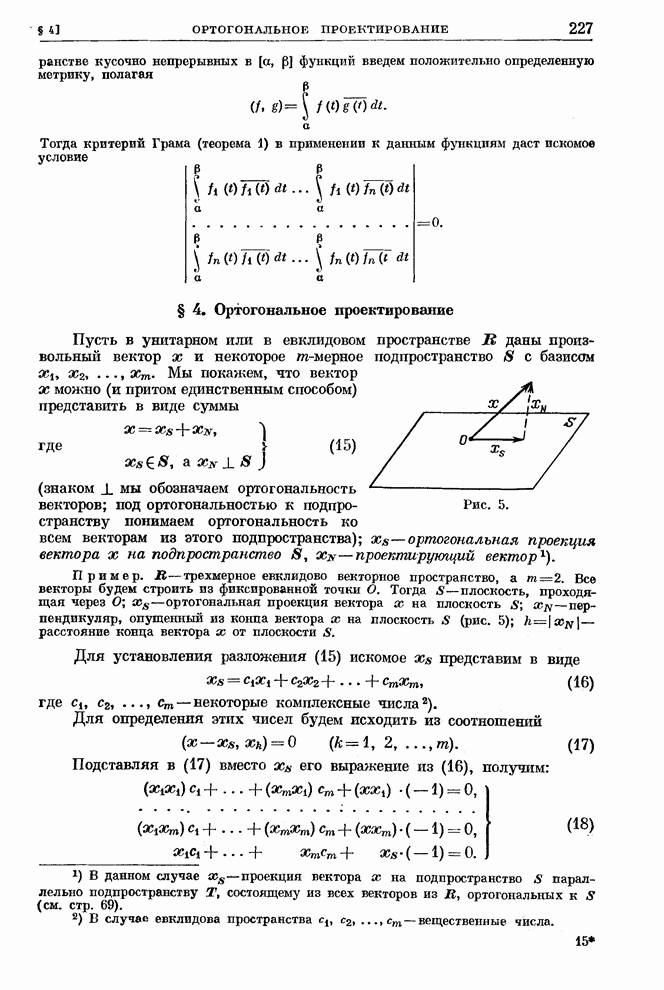
- § 4. Ортогональное проектирование
- § 5. Геометрический смысл определителя Грама и некоторые неравенства
- § 6. Ортогонализация ряда векторов
- § 7. Ортонормированный базис
- § 8. Сопряженный оператор
- § 9. Нормальные операторы в унитарном пространстве
- § 10. Спектр нормальных, эрмитовых, унитарных операторов
- § 11. Неотрицательные и положительно определенные эрмитовы операторы
- § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли
- § 13. Линейные операторы в евклидовом пространстве
- § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве
- § 15. Коммутирующие нормальные операторы
- § 16. Псевдообратный оператор
- Глава X. Квадратичные и эрмитовы формы
- § 1. Преобразование переменных в квадратичной форме
- § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции
- § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби
- § 4. Положительные квадратичные формы
- § 5. Приведение квадратичной формы к главным осям
- § 6. Пучок квадратичных форм
- § 7. Экстремальные свойства характеристических чисел регулярного пучка форм
- § 8. Малые колебания системы с n степенями свободы
- § 9. Эрмитовы формы
- § 10. Ганкелевы формы
- ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ
- Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы
- § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц
- § 2. Полярное разложение комплексной матрицы
- § 3. Нормальная форма комплексной симметрической матрицы
- § 4. Нормальная форма комплексной кососимметрической матрицы
- § 5. Нормальная форма комплексной ортогональной матрицы
- ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ
- § 1. Введение
- § 2. Регулярный пучок матриц
- § 3. Сингулярные пучки. Теорема о приведении
- § 4. Каноническая форма сингулярного пучка матриц
- § 5. Минимальные индексы пучка
- § 6. Сингулярные пучки квадратичных форм
- § 7. Приложения к дифференциальным уравнениям
- ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- § 1. Общие свойства
- § 2. Спектральные свойства неразложимых неотрицательных матриц
- § 3. Разложимые матрицы
- § 4. Нормальная форма разложимой матрицы
- § 5. Примитивные и импримитивные матрицы
- § 6. Стохастические матрицы
- § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний
- § 8. Вполне неотрицательные матрицы
- § 9. Осцилляционные матрицы
- Глава XIV. Различные критерии регулярности и локализации собственных значений
- § 1. Критерий регулярности Адамара и его обобщения
- § 2. Норма матрицы
- § 3. Распространение критерия Адамара на блочные матрицы
- § 4. Критерий регулярности Фидлера
- § 5. Круги Гершгорина и другие области локализации
- Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений
- § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия
- § 2. Преобразование Ляпунова
- § 3. Приводимые системы
- § 4. Каноническая форма приводимой системы. Теорема Еругина
- § 5. Матрицант
- § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра
- § 7. Дифференциальные системы в комплексной области. Общие свойства
- § 8. Мультипликативный интеграл в комплексной области
- § 9. Изолированная особая точка
- § 10. Регулярная особая точка
- § 11. Приводимые аналитические системы
- § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского
- ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ
- § 1. Введение
- § 2. Индексы Коши
- § 3. Алгоритм Рауса
- § 4. Особые случаи. Примеры
- § 5. Теорема Ляпунова
- § 6. Теорема Рауса-Гурвица
- § 7. Формула Орландо
- § 8. Особые случаи в теореме Рауса — Гурвица
- § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена
- § 10. Бесконечные ганкелевы матрицы конечного ранга
- § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя
- § 12. Второе доказательство теоремы Рауса—Гурвица
- § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара
- § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей
- § 15. Область устойчивости. Параметры Маркова
- § 16. Связь с проблемой моментов
- § 17. Связь между определителями Гурвица и определителями Маркова
- § 18. Теоремы Маркова и Чебышева
- § 19. Обобщенная задача Рауса-Гурвица
- ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ
- § 1. Мажорирующие последовательности
- § 2. Неравенства Неймана-Хорна
- § 3. Неравенства Вейля
- § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов
- § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов
- § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов
- ЛИТЕРАТУРА