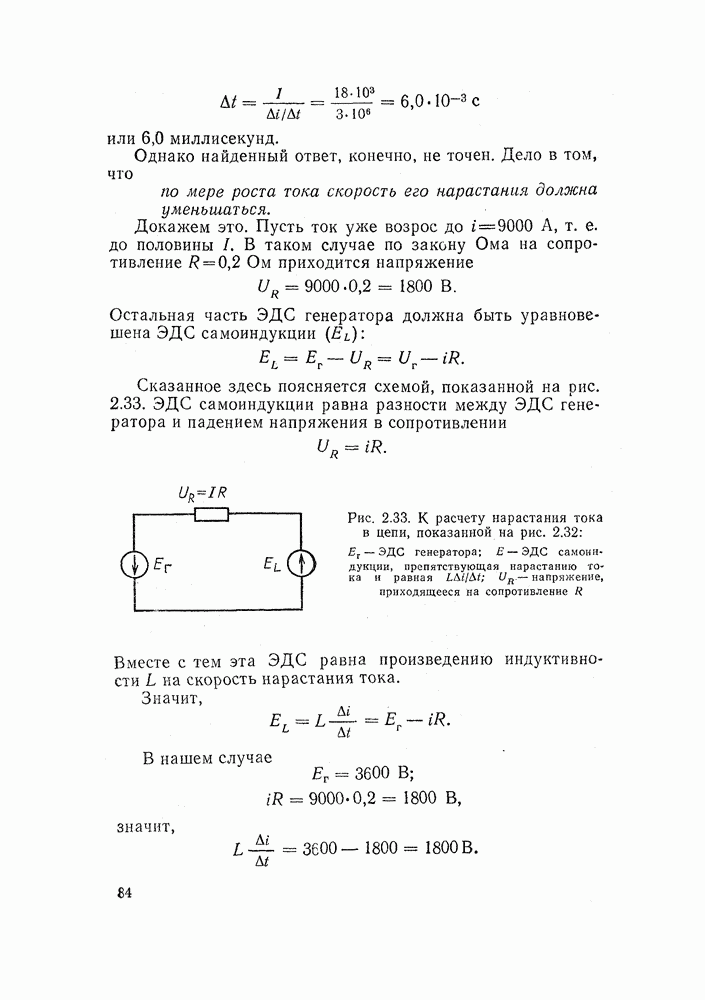
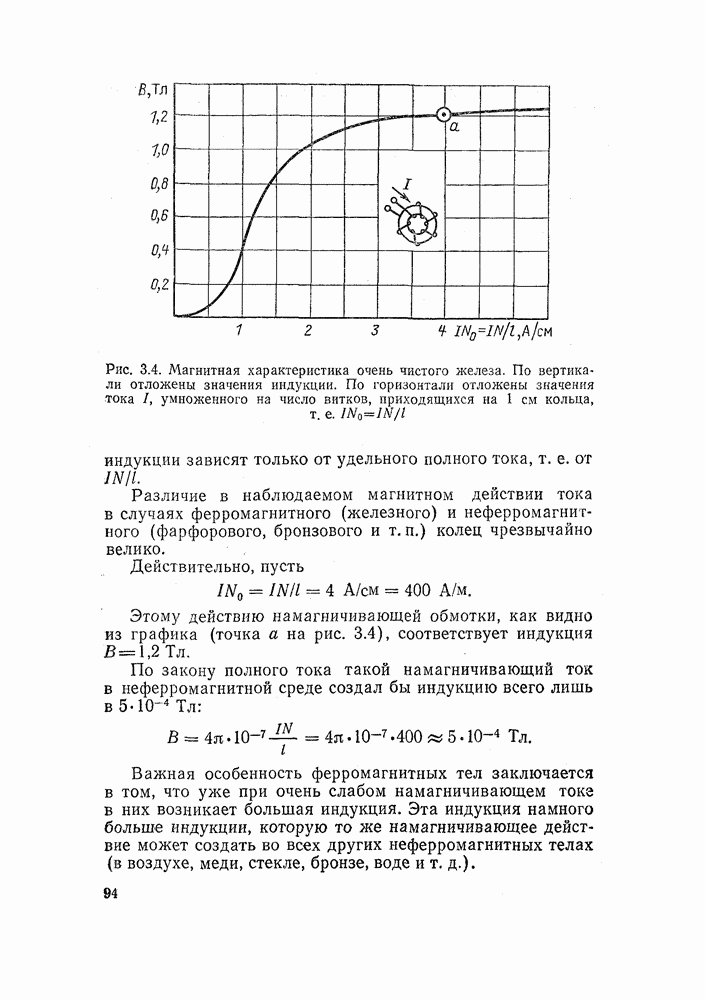
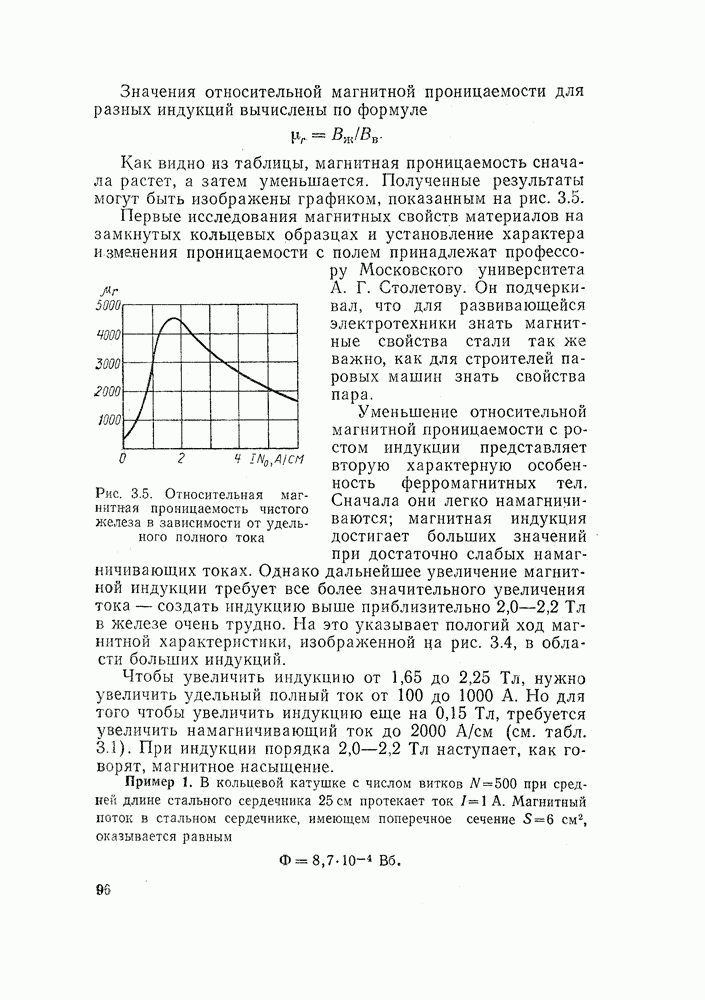
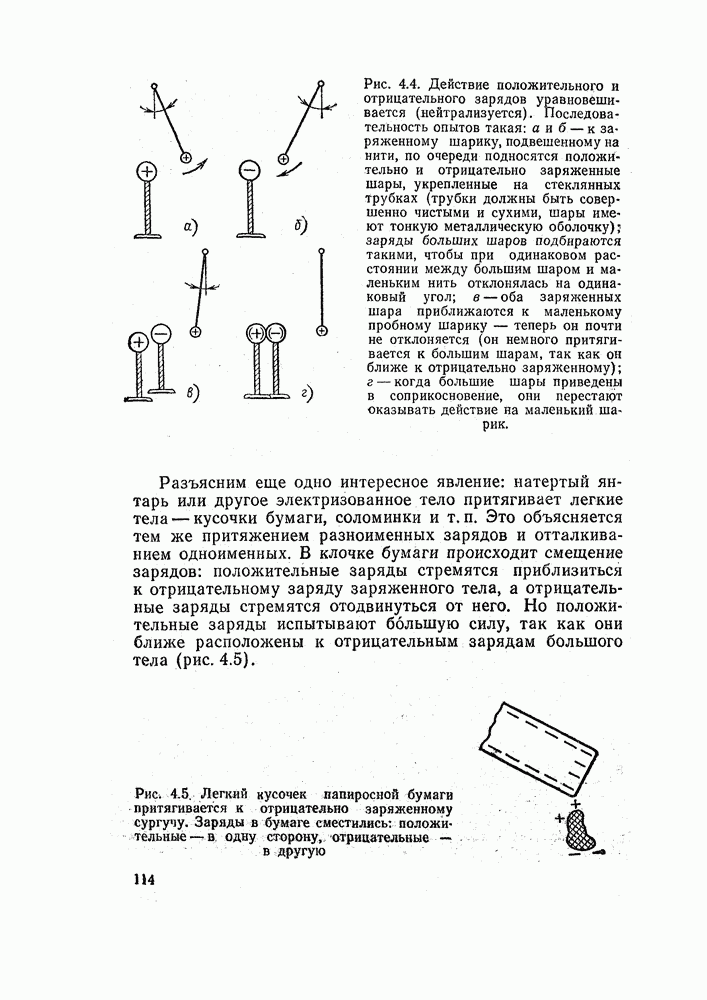
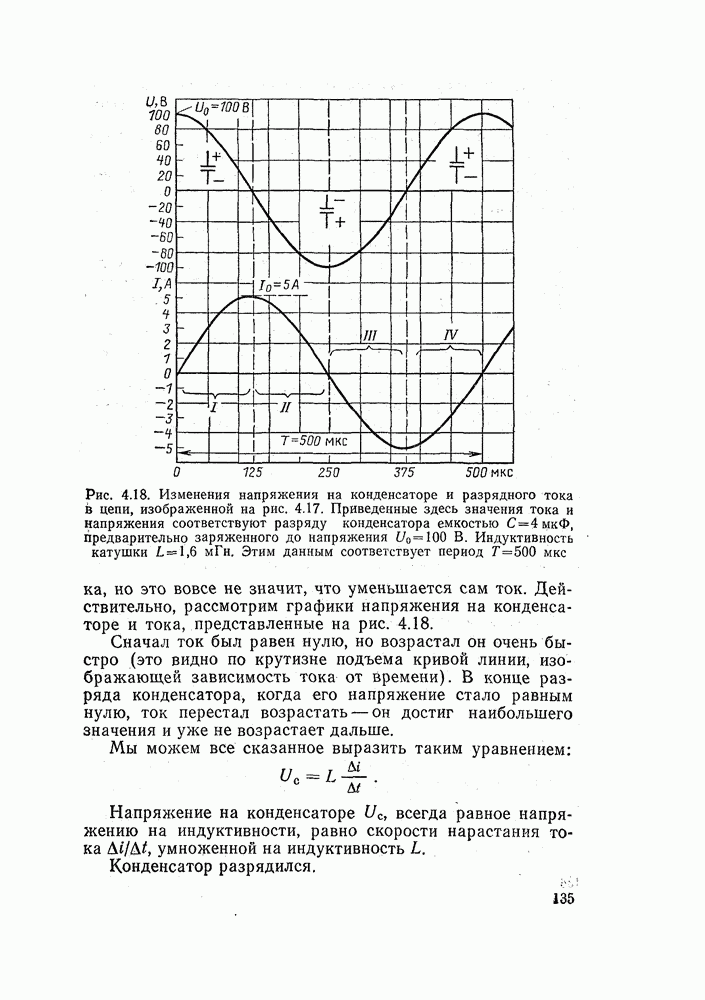
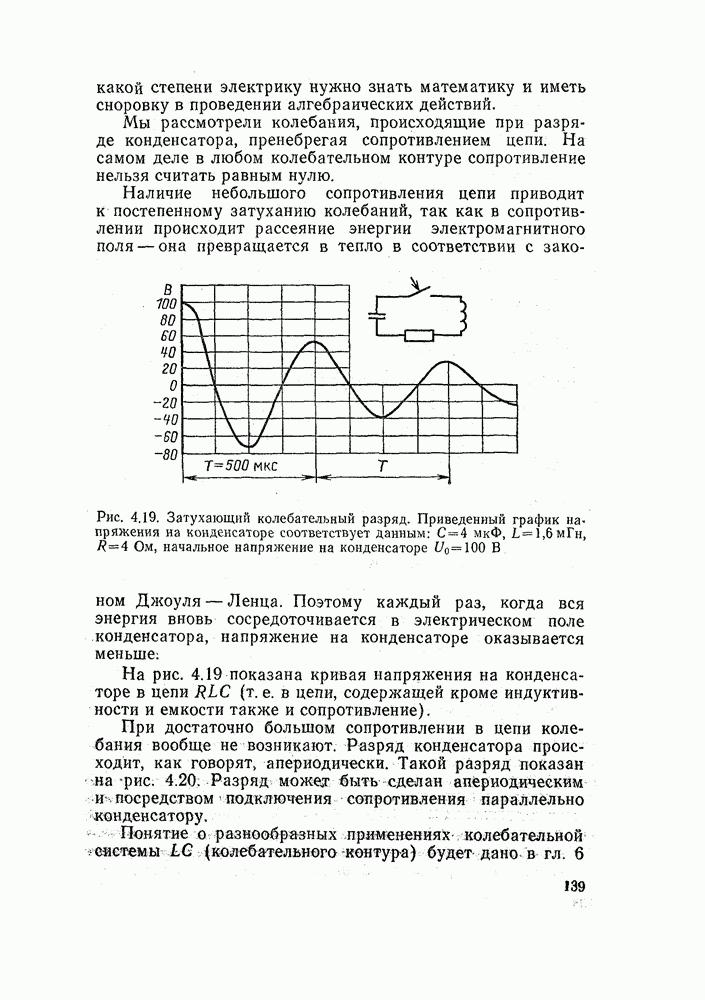
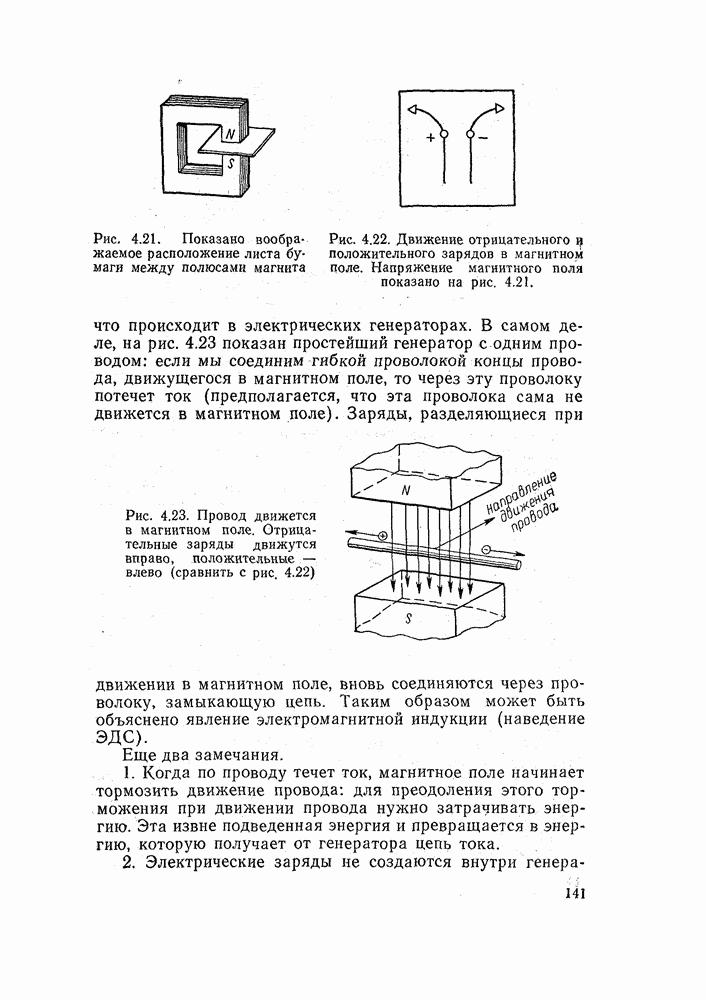
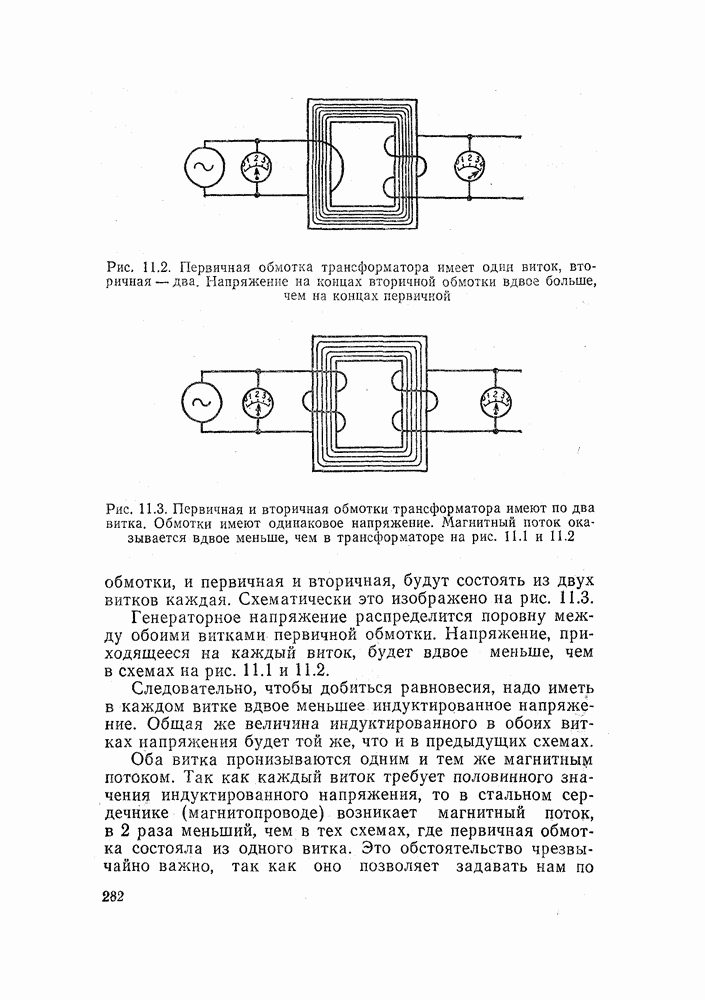
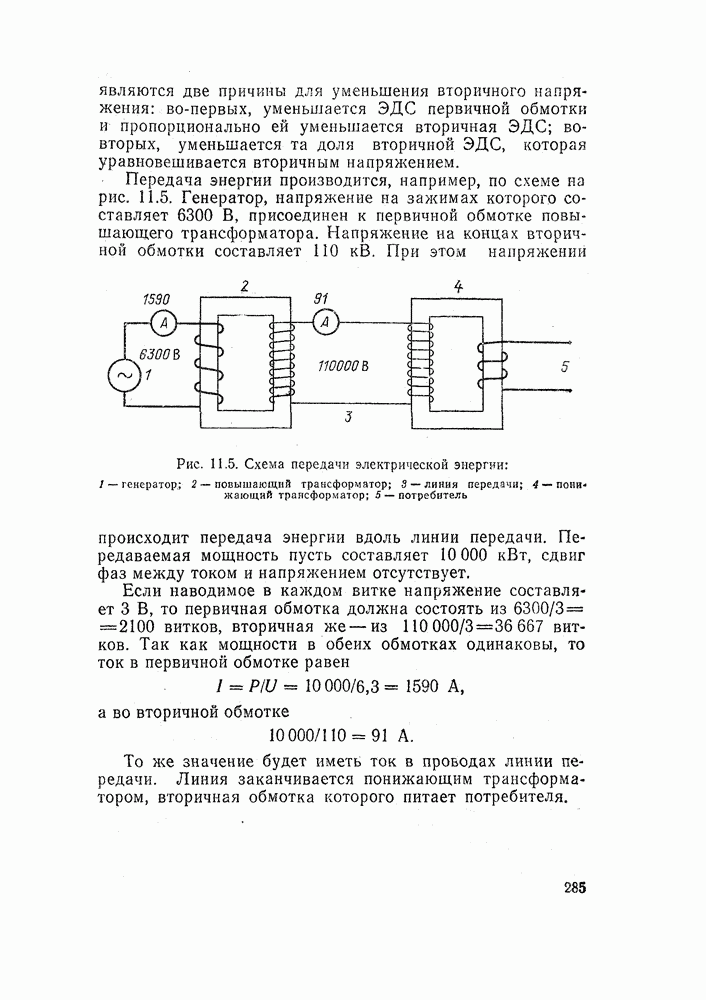
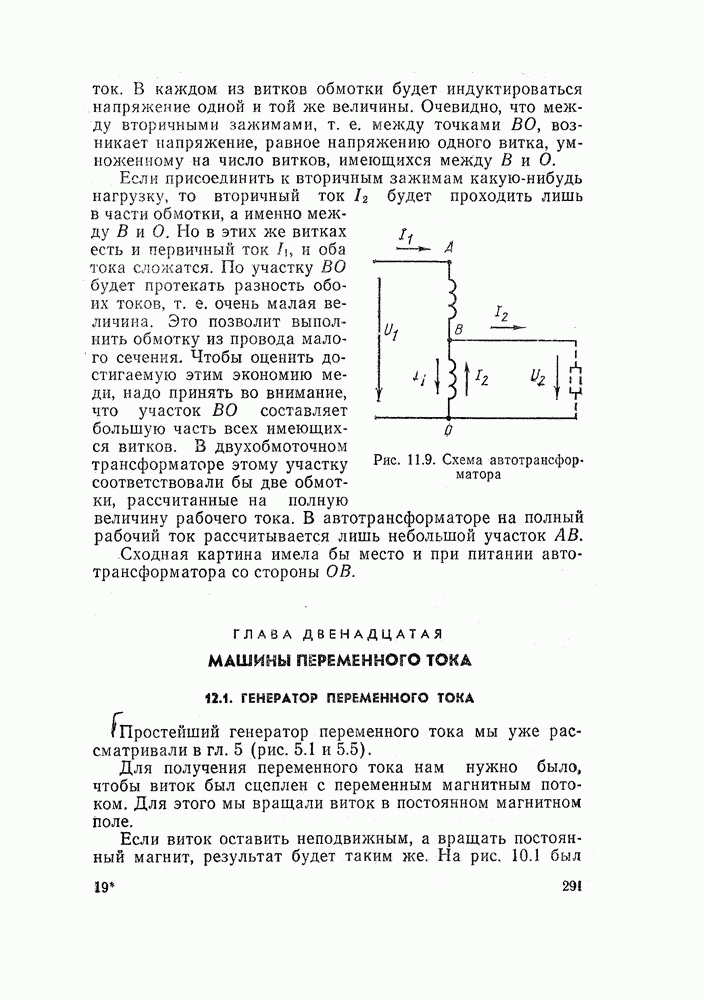
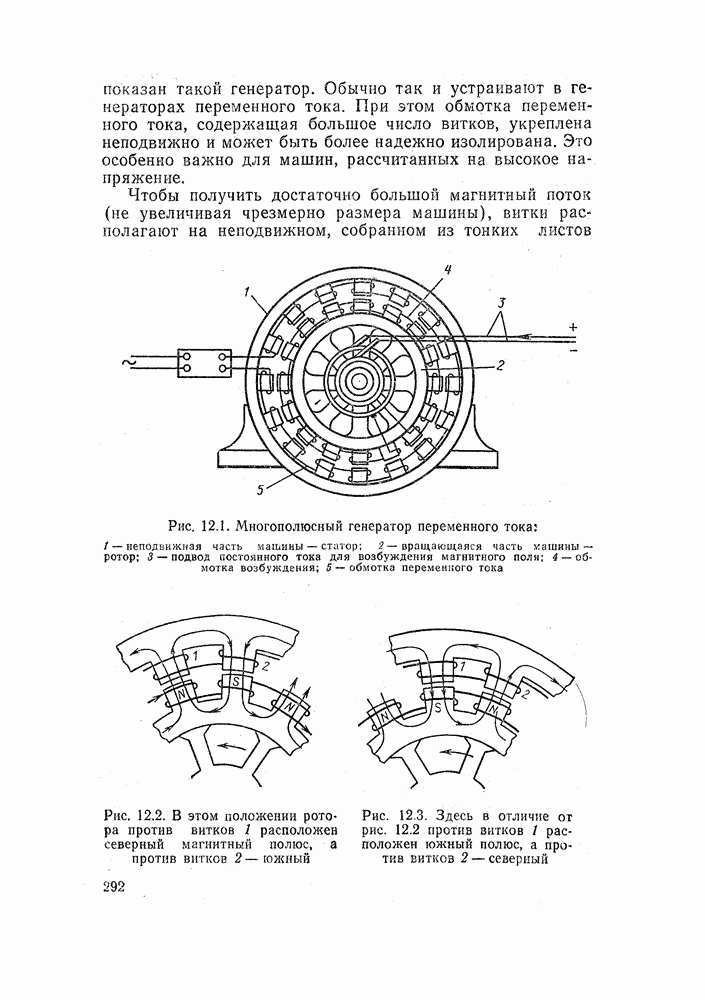
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ
До сих пор мы рисовали электрические схемы управления и описывали их словами. Теперь нам нужно научиться записывать структуру схем в виде математических формул. Для этого в электротехнике используют математический аппарат алгебры логики. В этой алгебре только две переменные величины: 0 и 1. Сами числа 0 и 1 особого значения не имеют. Мы используем 1 для обозначения того факта, что некоторые события (например, замыкание контактов) произошло.
Отсутствие этого события (или размыкание контактов) обозначим 0. Можно было бы использовать для этого другие цифры или буквенные обозначения.
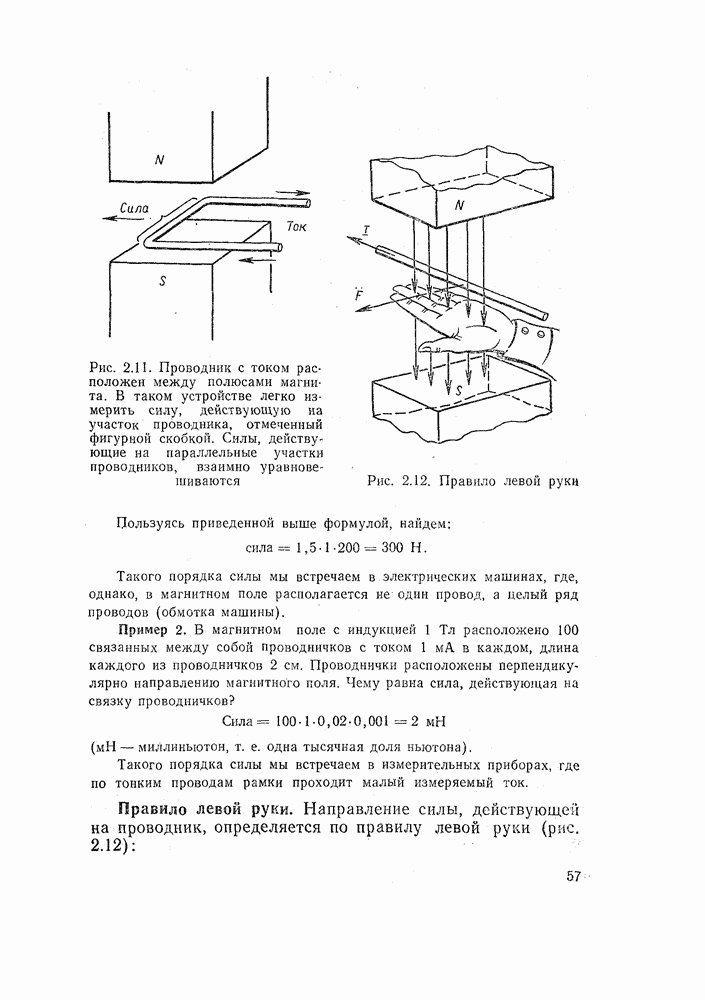
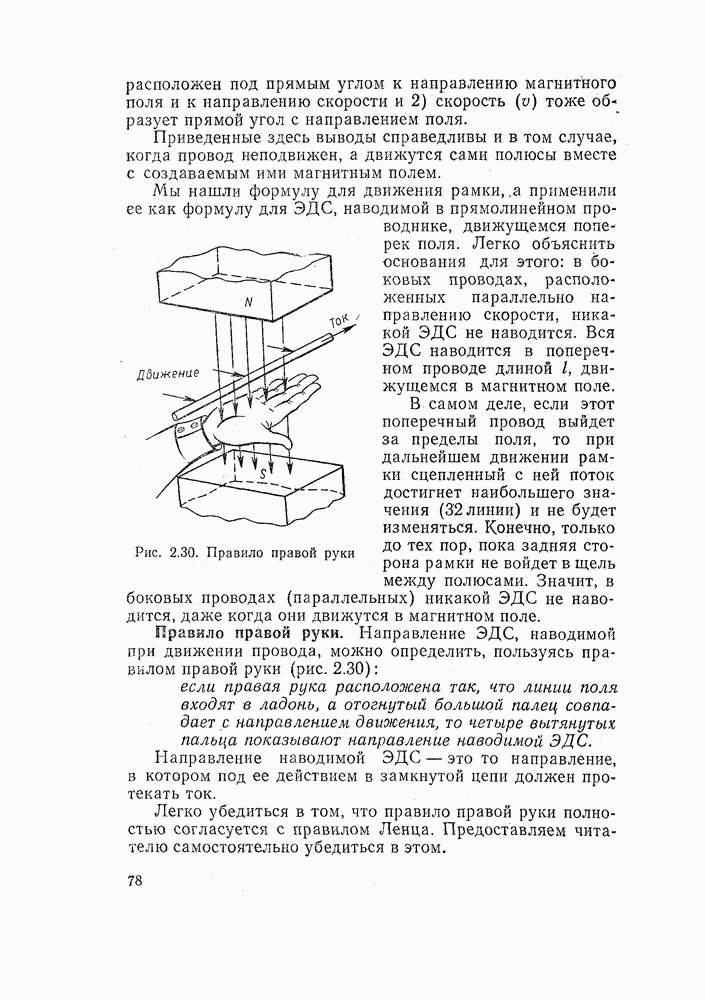
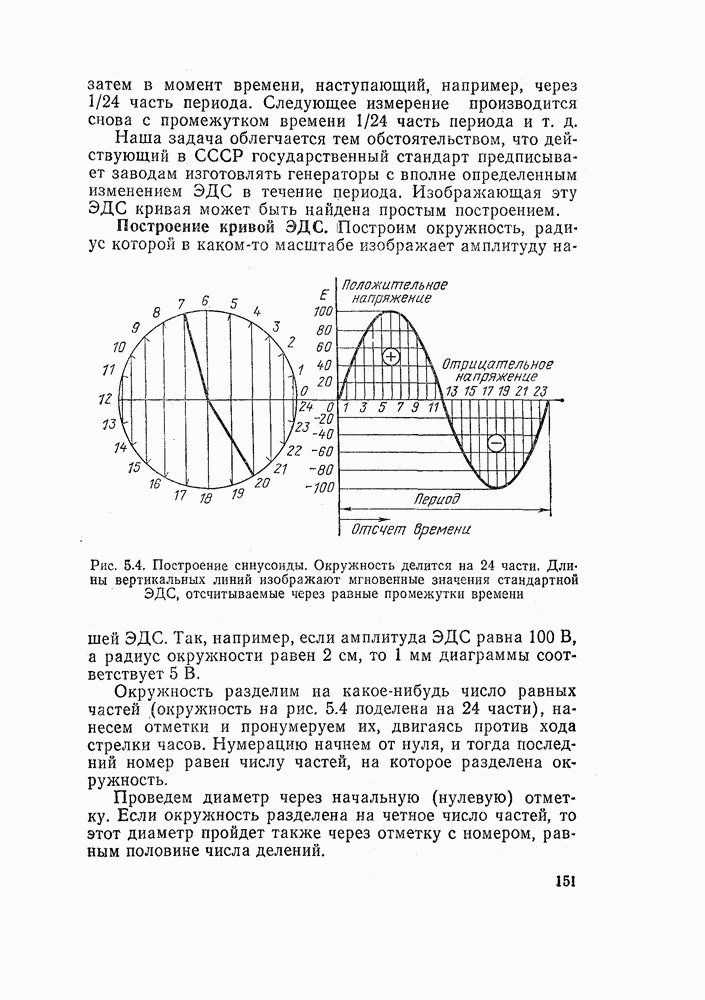
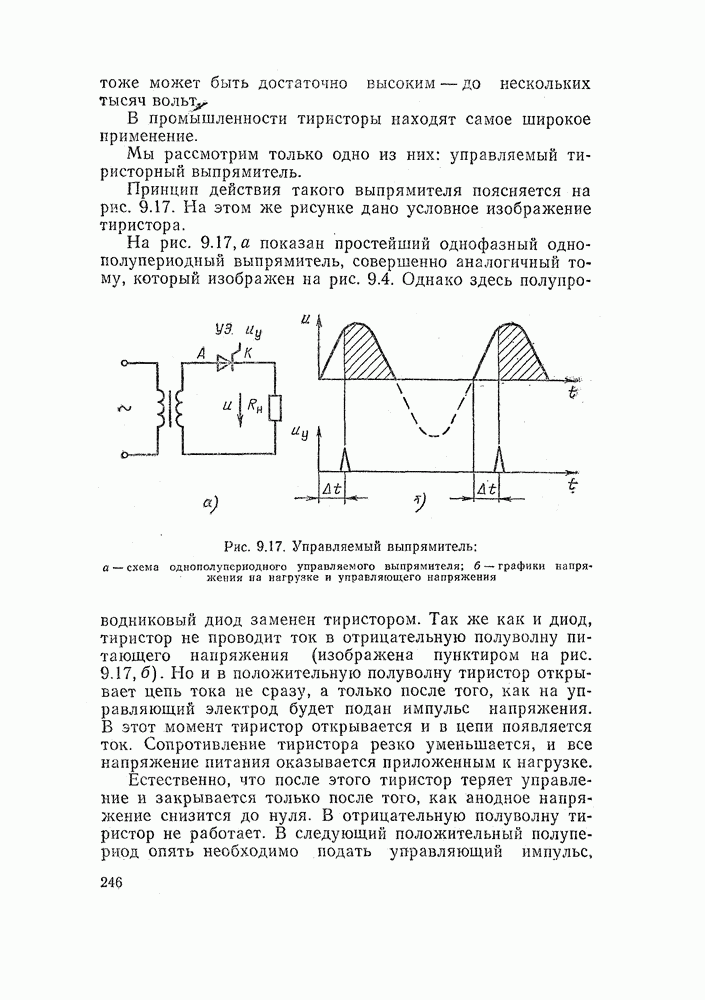
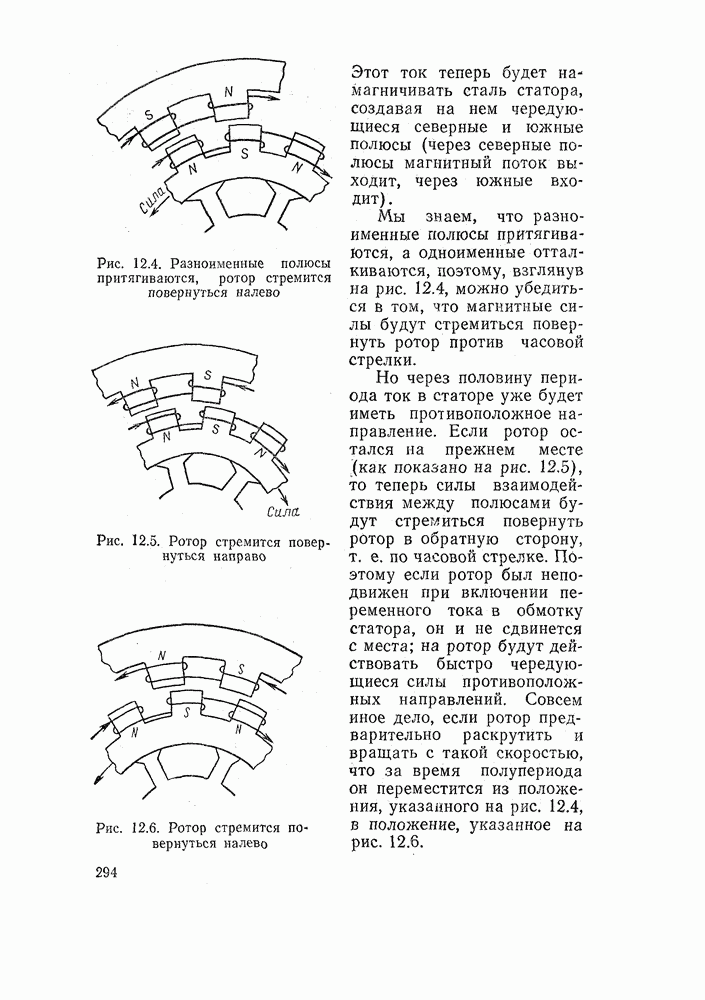
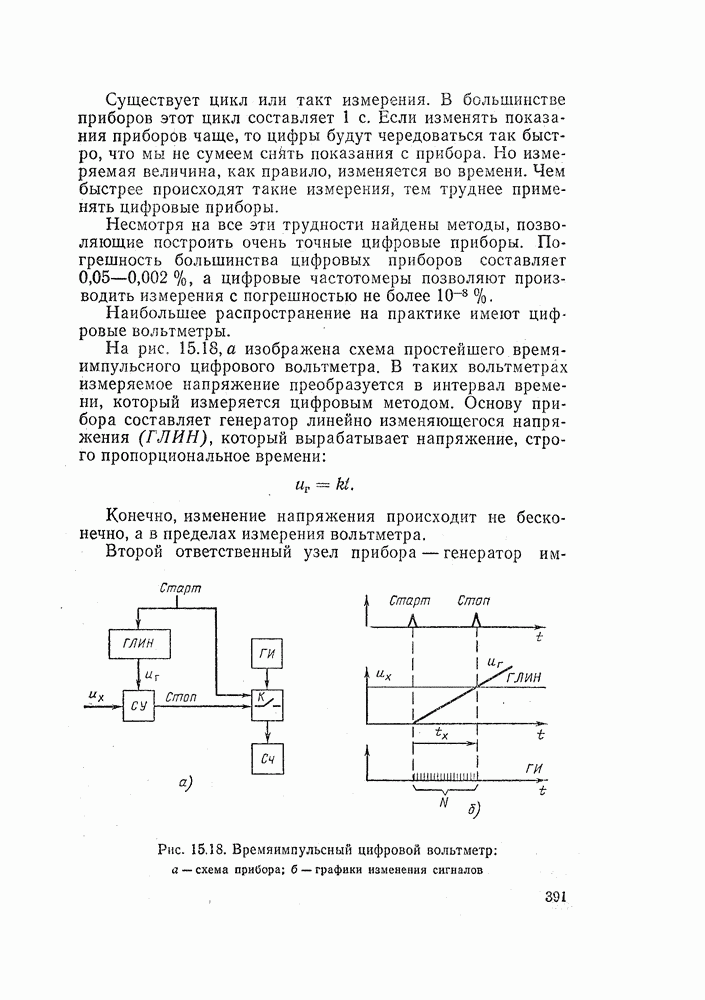
Рассмотрим для примера простейшую схему, состоящую из кнопки SB и реле К (рис. 14.15, а). Из схемы ясно, что если мы нажмем кнопку, контакты замкнутся и реле сработает.
При математическом описании использовать электротехнические буквенные обозначения не очень удобно. Принято обозначать математические переменные х, у....

Рис. 14.15. Простейшие логические функции: а — повторитель; б — инвертор, функция НЕ
Пусть кнопка будет аппарат х, а реле—аппарат у. В этом есть определенный смысл. Математики буквой х обозначают независимую переменную, а у — ее функцию. Но в нашей схеме положение кнопки независимо, мы можем по своему желанию нажать ее в любой момент времени. Совсем иное дело реле. Его состояние зависит от положения кнопки: если кнопка нажата — реле сработает, если отпустить кнопку — реле отключится. Следовательно, можно реле обозначить буквой у и состояние реле считать зависимой переменной.
Теперь мы можем описать нашу схему математически так:

Посмотрев на эту формулу, инженер-электрик скажет, что это «повторитель»: состояние аппарата у повторяет состояние аппарата х.
Переменная х может иметь только два значения: кнопка может быть нажата или нет. Мы уже говорили, что математики обозначают одно значение 0, а другое 1.
Логические нуль и единица отличаются от алгебраических. Они не служат для количественной оценки каких-либо величин, а только указывают на наличие или отсутствие каких-либо явлений.
Условимся, что если кнопка не нажата и ее контакты разомкнуты, х=0.
Замкнутым контактам соответствует значение х=1.
Такие же два значения может иметь и переменная у. Если реле сработало, у = 1, если отключилось, у=0.
Никаких других значений переменные х и у принимать не могут.
Связь между переменными х и у часто записывают в виде таблицы;

На рис. 14.15, б изображена простейшая схема, на которой реле К включено последовательно с размыкающим контактом кнопки SB. Здесь мы также введем независимую переменную х (состояние кнопки) и ее функцию у (состояние реле). Эта схема работает иначе, чем предыдущая. Когда кнопка нажата, реле отключается, если кнопку отпустить, то реле срабатывает.
Математики записывают это так:

Черта над переменной х означает, что состояние элемента у противоположно (инверсно) состоянию элемента х. Такую логическую функцию называют инверсией, или функцией НЕ, а соответствующую электрическую схему — инвертором. Действительно, реле срабатывает, когда кнопка НЕ нажата.
Теперь мы можем составить табличку значений переменных х и у для инвертора:

Из приведенных примеров можно уяснить очень полезное правило логического обозначения контактов. Если замыкающий контакт аппарата мы обозначаем какой-либо буквой (например, х), то размыкающий контакт нужно обозначить той же буквой с чертой сверху (т. е. так: х) и считать, что эти контакты взаимно инверсны (т. е. противоположны).
Разомкнутое состояние контактов мы обозначили О, а замкнутое — 1.
Поэтому в нормальном состоянии любого аппарата 
При срабатывании состояние контактов меняется на противоположное.
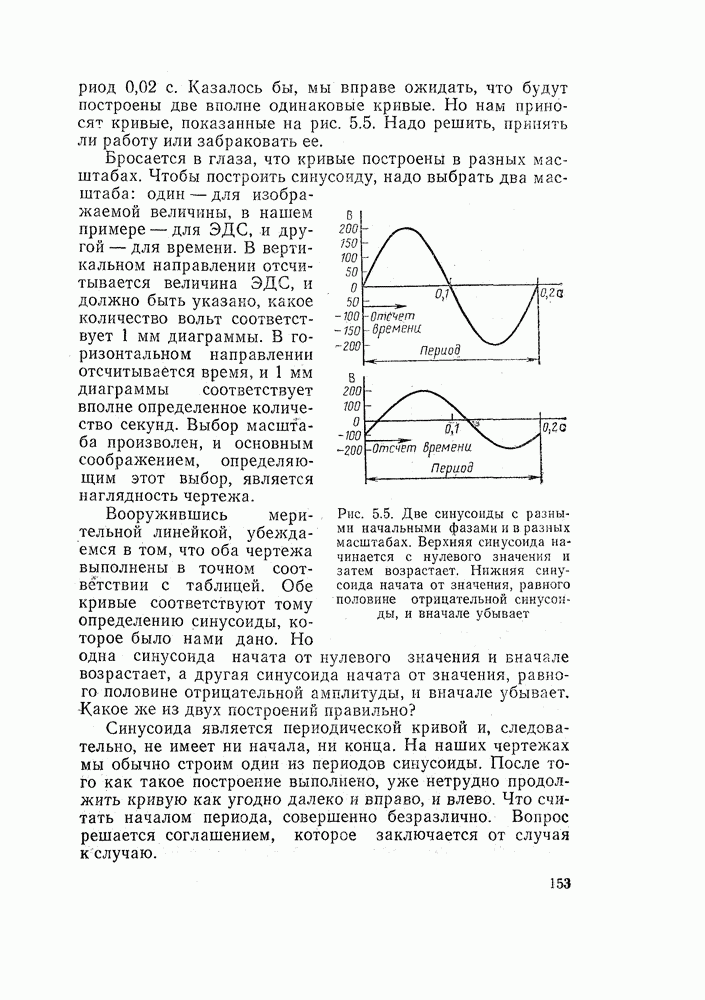
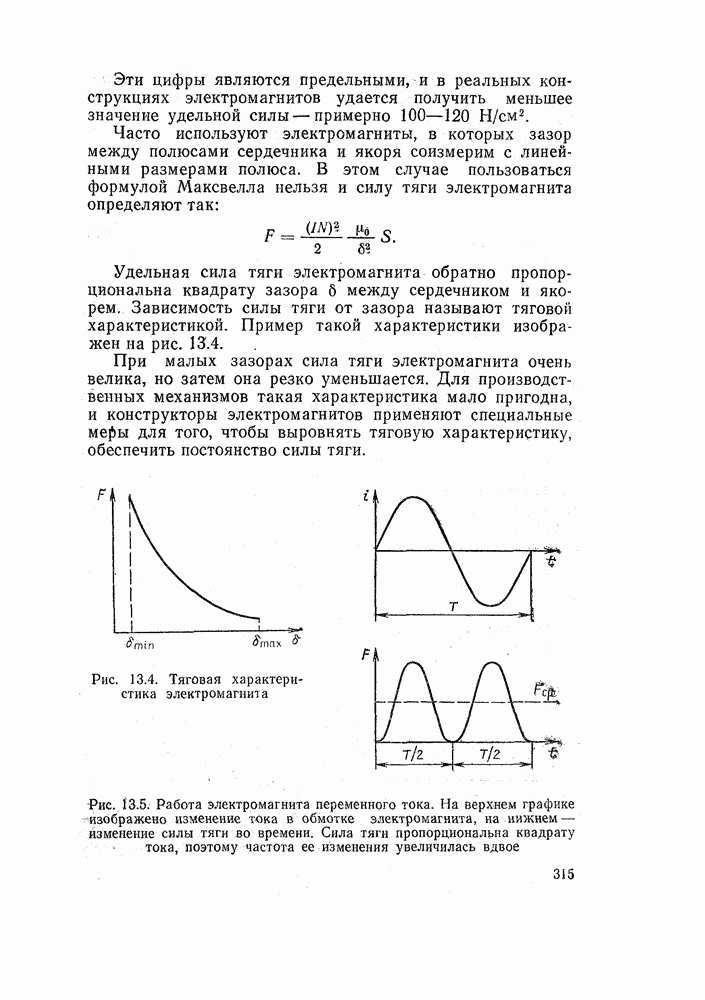
Рассмотрим теперь более сложную схему, когда катушка реле К управляется двумя замыкающими контактами, включенными последовательно, которые мы обозначим  (рис. 14.16, а). Совершенно очевидно, что состояние реле зависит и от состояния контакта
(рис. 14.16, а). Совершенно очевидно, что состояние реле зависит и от состояния контакта  и от состояния контакта
и от состояния контакта 
Если, как и прежде, обозначить состояние реле буквой у, то переменная у будет функцией двух независимых переменных  . Остается определить, какая это функция. Проследим за работой реле. Реле срабатывает, когда одновременно замкнуты контакты
. Остается определить, какая это функция. Проследим за работой реле. Реле срабатывает, когда одновременно замкнуты контакты  . Если замкнут только один контакт
. Если замкнут только один контакт  или
или  или оба они разомкнуты, реле отключено.
или оба они разомкнуты, реле отключено.

Рис. 14.16. Логические функции двух переменных: а — функция И; б — функция ИЛИ
Запишем эти рассуждения в виде таблицы. В каждой строке запишем состояние контактов  и реле у. Всего в таблице будет четыре строки — по числу возможных комбинаций состояния контактов
и реле у. Всего в таблице будет четыре строки — по числу возможных комбинаций состояния контактов  :
:

Связь между переменными, соответствующую этой таблице, называют логическим умножением:

Если в каждой строке перемножить две первые цифры, то получим цифру, стоящую в третьем столбце, т. е. переменную у.
Логическое умножение часто называют функцией И. Реле срабатывает, когда замкнуты контакт  И контакт
И контакт  Говорят также, что логическое умножение осуществляется схемой совпадения. Реле срабатывает, когда совпадают замыкания контактов
Говорят также, что логическое умножение осуществляется схемой совпадения. Реле срабатывает, когда совпадают замыкания контактов  .
.
Теперь обратите внимание на рис. 14.16, б. Здесь в цепи реле К Вы также видите два управляющих контакта  . Однако теперь они включены параллельно и работа схемы совершенно иная. Реле срабатывает, если включен любой из контактов или оба вместе. Реле отключено только тогда, когда оба контакта разомкнуты.
. Однако теперь они включены параллельно и работа схемы совершенно иная. Реле срабатывает, если включен любой из контактов или оба вместе. Реле отключено только тогда, когда оба контакта разомкнуты.
Составим таблицу состояний реле:

Логическую функцию двух переменных, соответствующую этой таблице, называют логическим сложением (логической суммой):

Проверим:

Всюду сложение правильное, кроме третьей строки. Почему 1+1=1, а не 1+1=2, как должно быть?
Вспомним, что здесь речь идет о том, есть или нет срабатывание реле. Если цепь реле включена дважды, то оно все равно срабатывает один раз, а срабатывание реле — это логическая единица. Поэтому и считается, вопреки математике, что сумма двух единиц есть единица.
Логическую сумму называют еще функцией ИЛИ, Реле срабатывает, если замкнут контакт  ИЛИ контакт х.
ИЛИ контакт х.
Ограничимся этими простейшими логическими функциями и попытаемся использовать их для описания электрических схем управления на нескольких примерах.
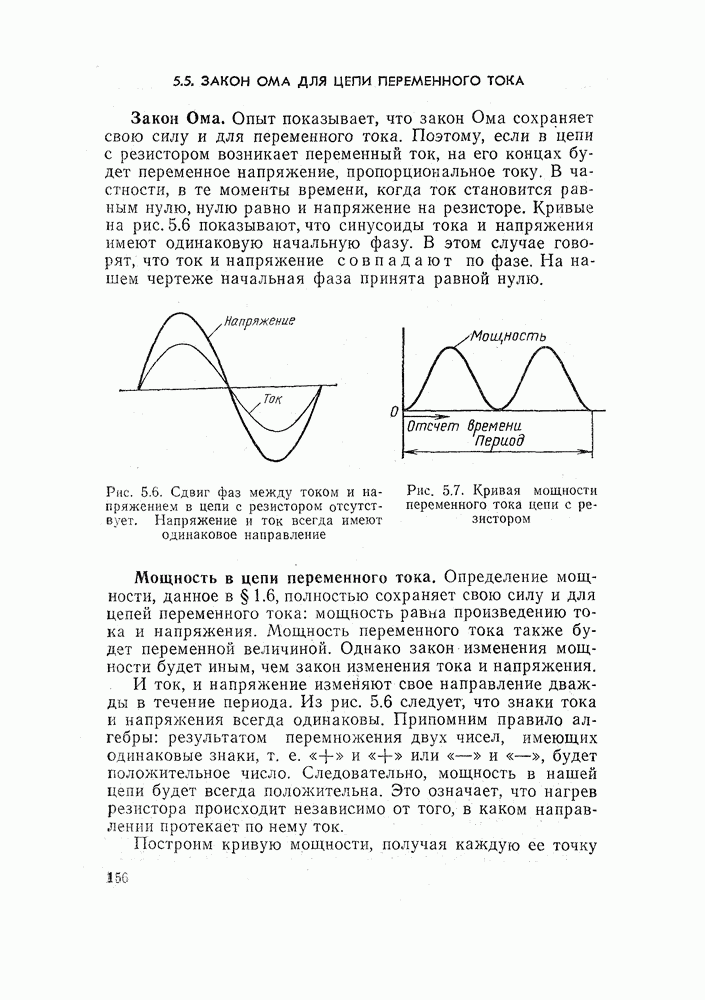
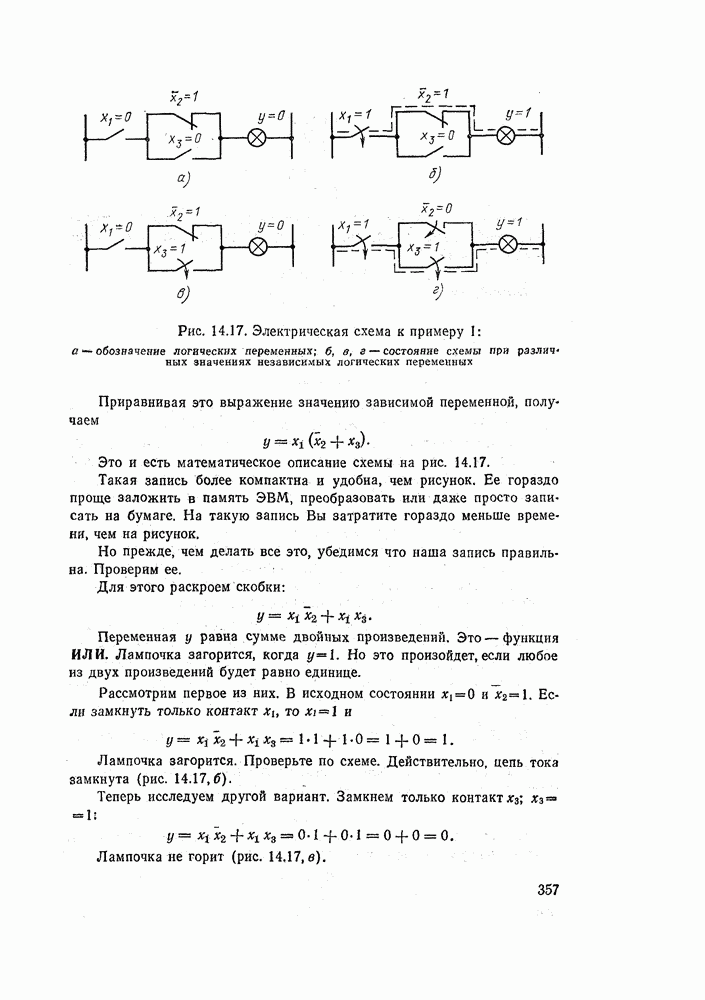
Пример 1. Составить логическую функцию для схемы управления, изображенной на рис. 14.17, а. В цепи электрической лампочки включены три управляющих контакта. Контакты  включены параллель: но, а контакт — к ним последовательно. Из схемы видно, что контакты
включены параллель: но, а контакт — к ним последовательно. Из схемы видно, что контакты  — замыкающие, а контакт
— замыкающие, а контакт  — размыкающий. Поэтому мы и ставим черту сверху буквы
— размыкающий. Поэтому мы и ставим черту сверху буквы 
Перейдем теперь к составлению формулы, описывающей работу схемы.
Мы знаем, что параллельное соединение контактов соответствует логическому сложению. Следовательно, нужно сложить

Последовательное соединение описывается логическим умножением. Поэтому нашу сумму нужно умножить на переменную 


Рис. 14.17. Электрическая схема к примеру 1: а — обозначение логических переменных; б, в, г — состояние схемы при различных значениях независимых логических переменных
Приравнивая это выражение значению зависимой переменной, получаем

Это и есть математическое описание схемы на рис. 14.17.
Такая запись более компактна и удобна, чем рисунок. Ее гораздо проще заложить в память ЭВМ, преобразовать или даже просто записать на бумаге. На такую запись Вы затратите гораздо меньше временя, чем на рисунок.
Но прежде, чем делать все это, убедимся что наша запись правильна. Проверим ее.
Для этого раскроем скобки:

Переменная у равна сумме двойных произведений. Это — функция ИЛИ. Лампочка загорится, когда  Но это произойдет, если любое из двух произведений будет равно единице.
Но это произойдет, если любое из двух произведений будет равно единице.
Рассмотрим первое из них. В исходном состоянии  Если замкнуть только контакт
Если замкнуть только контакт  то
то  и
и

Лампочка загорится. Проверьте по схеме. Действительно, цепь тока замкнута (рис. 14.17,6).
Теперь исследуем другой вариант. Замкнем только контакт 

Лампочка не горит (рис. 14,17, в).
Наконец, замкнем контакты  и разомкнем контакт
и разомкнем контакт  Получим
Получим 

Лампочка горит, что подтверждает схема на рис. 14.17, г.
Этот пример наглядно показывает преимущества математической записи схем управления. Разбирая сложную схему, очень легко сделать ошибку. Математическая формула всегда дает совершенно точный ответ. Кроме того, на помощь может прийти ЭВМ.
Пример 2. Составим теперь математическое описание электрической схемы на рис. 14.18, а. Это — лестничное включение лампочки, которое мы разбирали в § 14.1. Только теперь мы изобразили контакты несколько иначе и обозначили их в виде логических переменных.
Рассуждая совершенно аналогично, можно записать

Предоставим Вам самим разобраться в этой формуле и убедиться, что она полностью совпадает со словесным описанием, которым мы пользовались в § 14.1.

Рис. 14.18. Электрические схемы к примерам 2 и 3: а — лестничная схема; б — схема нереверсивного магнитного пускателя; в — схема реверсивного пускателя
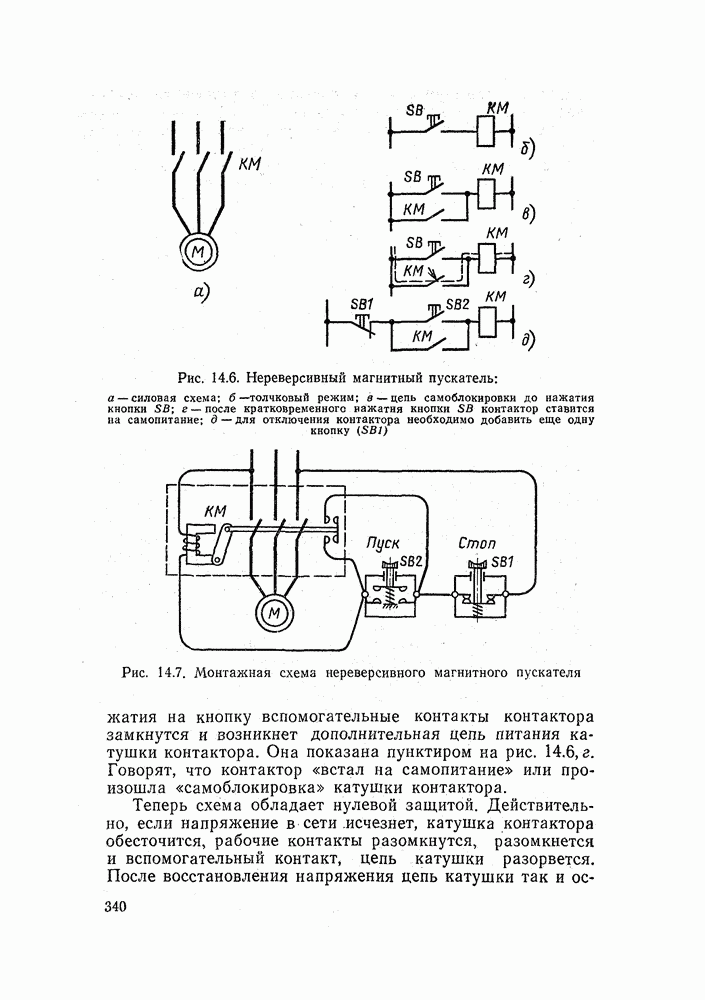
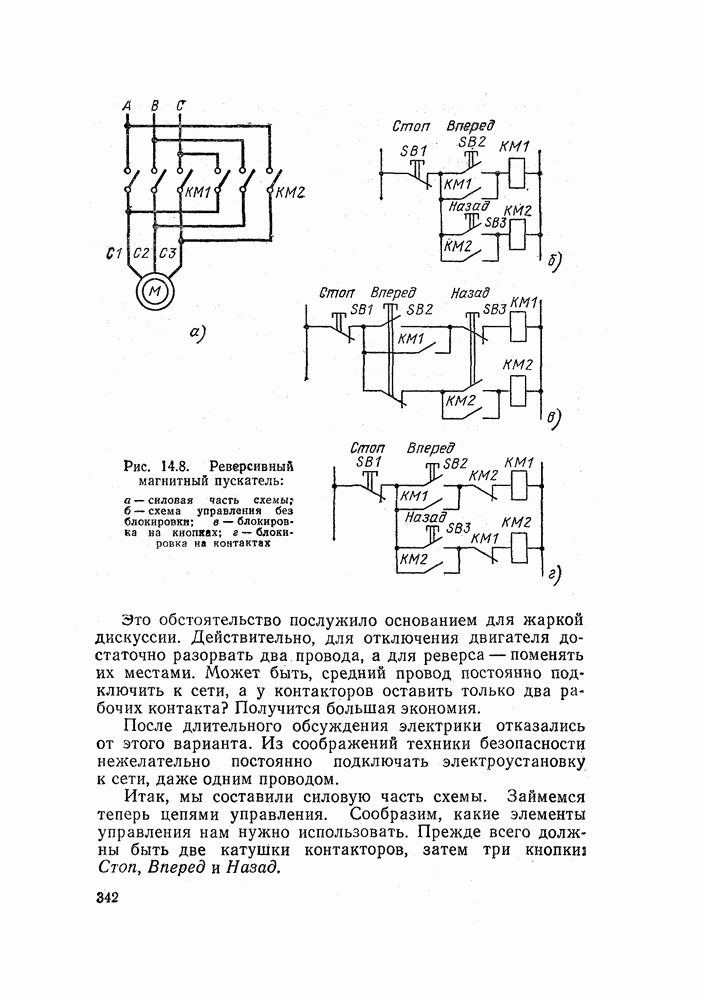
Пример 3. Составим математическое описание нереверсивного и реверсивного магнитных пускателей (рис. 14.18, б и 14.18, в).
Начнем с более простого, нереверсивного магнитного пускателя, работу которого мы рассмотрели в § 14.3. На рис. 14.18, б представлена его схема с обозначением логических переменных.
Пользуясь правилами логического умножения и сложения, можно написать

Здесь все понятно, но вызывает удивление, что зависимая переменная у попала и в левую, и в правую часть формулы. Сверившись со схемой, видим, что формула написана совершенно правильно.
В чем же дело? Вспомним, что после нажатия кнопки  контактор срабатывает и ставит себя на самопитание. После этого кнопку можно отпустить. Схема обладает памятью или представляет элемент памяти.
контактор срабатывает и ставит себя на самопитание. После этого кнопку можно отпустить. Схема обладает памятью или представляет элемент памяти.
Раскроем скобки:

Пусть в начальном состоянии

Нажмем кнопку  будем считать, что это — первый такт работы схемы:
будем считать, что это — первый такт работы схемы:

Здесь мы знаком ? обозначили состояние вспомогательных контактов контактора. Пока нажата кнопка  их состояние не оказывает влияния на работу схемы. Они включены параллельно кнопке.
их состояние не оказывает влияния на работу схемы. Они включены параллельно кнопке.
На втором такте отпустим кнопку 

Теперь уже схема встала на самопитание. Вспомогательный контакт включен  и для того чтобы отключить контактор, достаточно нажать кнопку
и для того чтобы отключить контактор, достаточно нажать кнопку  Из формулы видно, что кнопка
Из формулы видно, что кнопка  отключает схему при любом состоянии кнопки
отключает схему при любом состоянии кнопки  Говорят, что схема обладает приоритетом (первенством) на отключение.
Говорят, что схема обладает приоритетом (первенством) на отключение.
Итак, наша схема работает в два этапа — такта, которые должны быть разделены во времени и выполняться в определенной последовательности. Сначала нажимается кнопка  потом контактор ставится на самопитание, но не наоборот.
потом контактор ставится на самопитание, но не наоборот.
Таким образом, эта схема отличается от схем, которые мы рассмотрели в примерах 1 и 2. Там работа схемы зависела только от комбинации включения и выключения контактов. Такие схемы так и называют — «комбинационные».
В схемах примера 3 имеет значение еще и последовательность включения контактов.
Но вернемся к описанию магнитных пускателей. Теперь на очереди реверсивный магнитный пускатель (рис. 14.18, в).
Реверсивный пускатель состоит из двух нереверсивных с наложением дополнительных блокировок.
В нем два исполнительных элемента, дна контактора — 
Следовательно, работа этой схемы описывается двумя логическими уравнениями

Проанализируйте эти уравнения самостоятельно и сопоставьте с работой схемы по описанию в § 14.3.
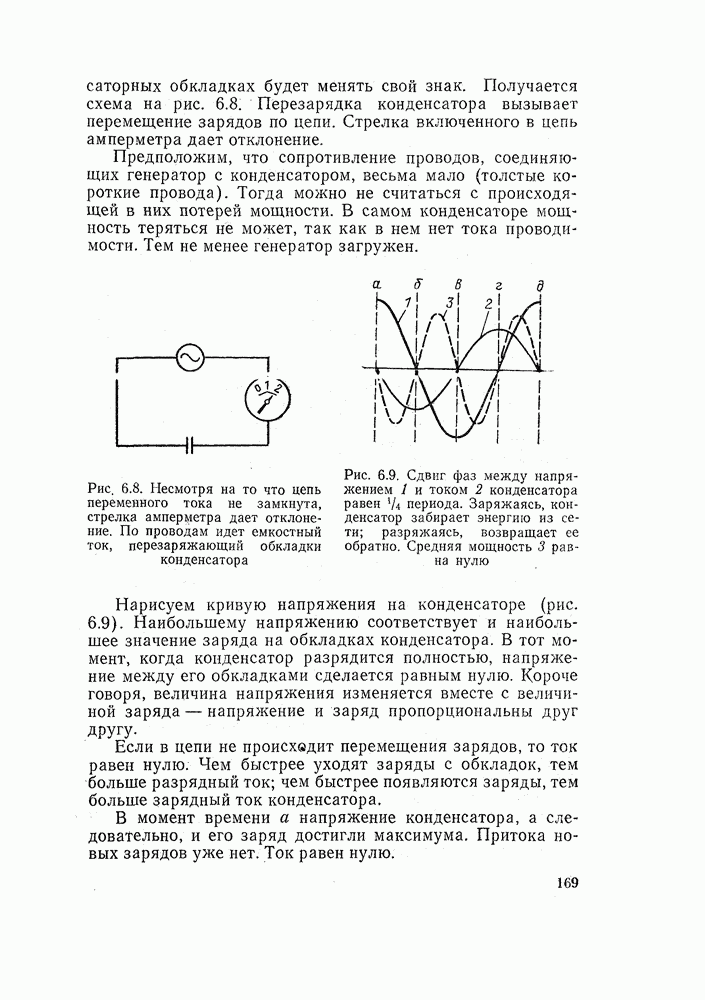
Пример 4. Решим теперь обратную задачу. Составим электрическую схему по ее математическому описанию. Пусть нам задана формула

По ее внешнему виду очень легко составить электрическую схему. Прежде всего здесь: должен быть исполнительный элемент — это реле или контактор у. У него имеются вспомогательные замыкающие контакты, обозначение которых есть в правой части формулы. Далее нам нужны замыкающий контакт  и размыкающий контакт
и размыкающий контакт 
Контакты  и у включены последовательно, а контакт
и у включены последовательно, а контакт  — к ним параллельно. Это следует из правил логической суммы и произведения. Полученная схема представлена на рис. 14.19. Ее особенность в том, что контакт
— к ним параллельно. Это следует из правил логической суммы и произведения. Полученная схема представлена на рис. 14.19. Ее особенность в том, что контакт  может включить схему при любом состоянии контакта
может включить схему при любом состоянии контакта  Это схема с приоритетом на включение.
Это схема с приоритетом на включение.
В начале этой главы Вы вйдели, как трудно составлять даже очень простые электрические схемы. А если схема сложная — такая, что ее изображение умещается только на многих листах ватманской бумаги? Тогда неизбежны ошибки, долгие исправления.
Математическое описание позволяет автоматизировать процесс составления электрической схемы. Оперируя с математическими формулами, ЭВМ составит схему по Вашему заданию, а затем, если нужно, «нарисует» ее.

Рис. 14.19. Электрическая схема к примеру 4
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ
- 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА
- 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА
- 1.6. МОЩНОСТЬ
- 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА
- 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ
- 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ
- 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ
- 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА
- 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ
- 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА
- 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ
- 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ
- 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ
- 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ
- 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ
- 1.20. ЗАКОНЫ КИРХГОФА
- ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ
- 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ
- 2.4. МАГНИТНАЯ ИНДУКЦИЯ
- 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ
- 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ
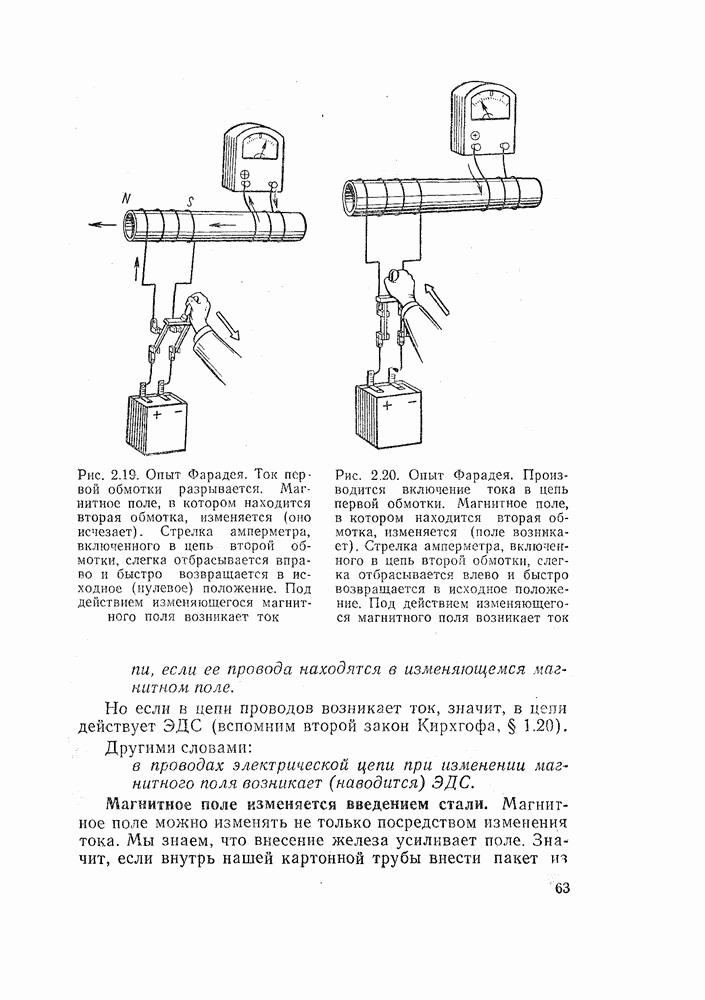
- 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ
- 2.9. ПРАВИЛО ЛЕНЦА
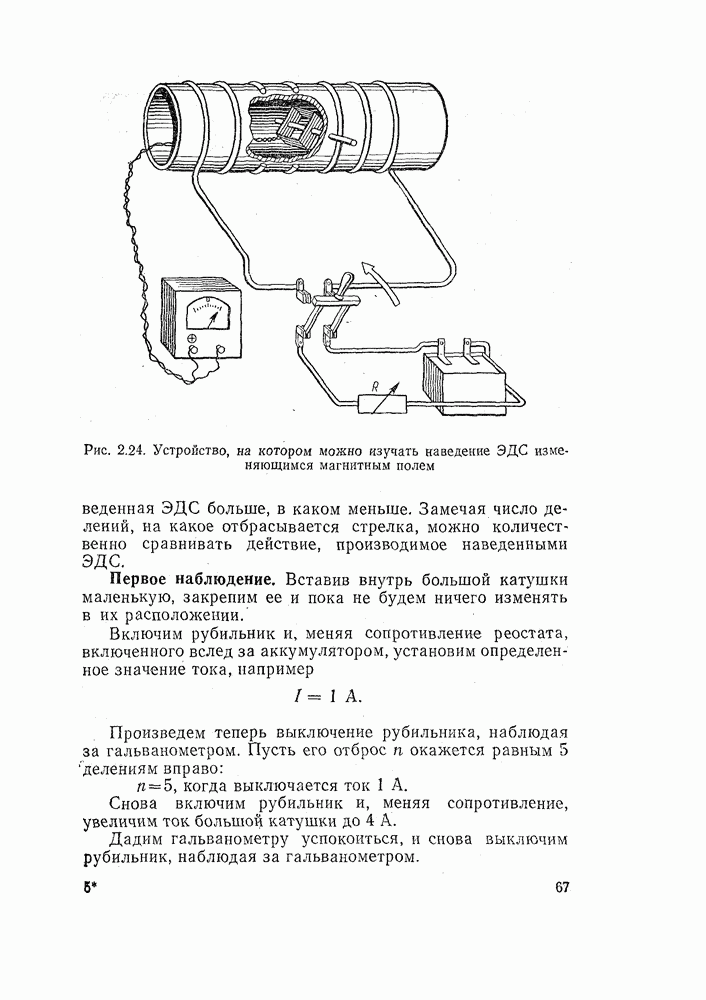
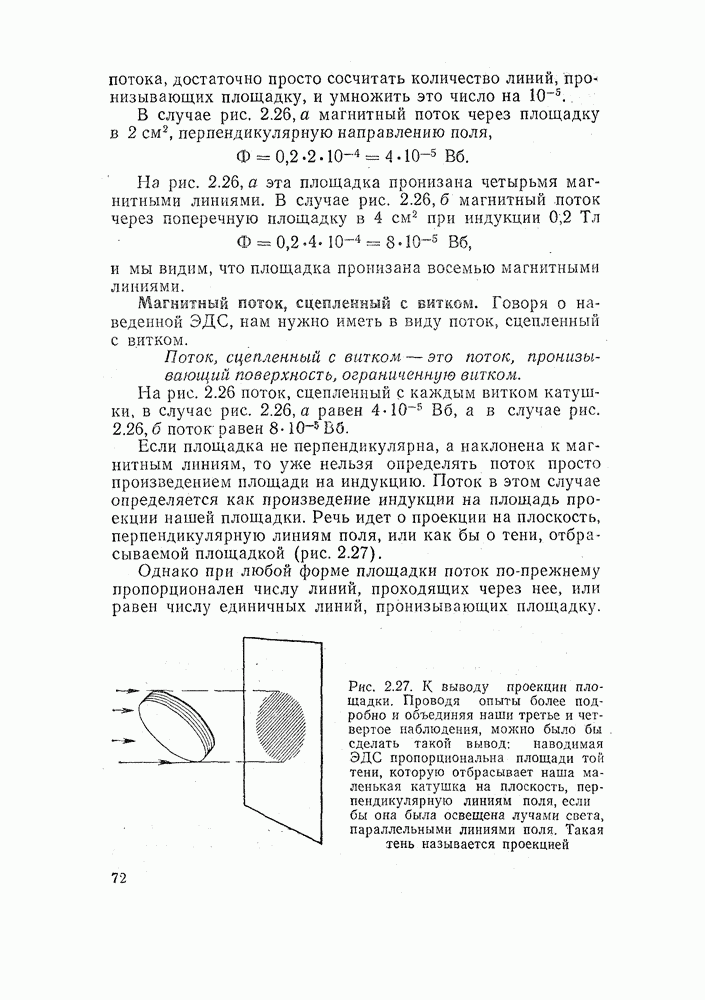
- 2.10. МАГНИТНЫЙ ПОТОК
- 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
- 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ
- 2.13. ВЗАИМНАЯ ИНДУКДИЯ
- 2.14. САМОИНДУКЦИЯ
- 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ
- 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА
- 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА
- 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
- 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ
- 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ
- 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ
- 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ
- 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ
- 3.9. НАМАГНИЧЕННОСТЬ
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ
- 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА)
- 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ)
- 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
- 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ
- ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК
- 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК?
- 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 5.4. СИНУСОИДА
- 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ
- 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ
- 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ
- 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
- 6.7. РЕЗОНАНС ТОКОВ
- 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ
- ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК
- 7.1. ТРЕХФАЗНАЯ СИСТЕМА
- 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ
- 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС
- 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ
- 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА
- 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ
- ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ
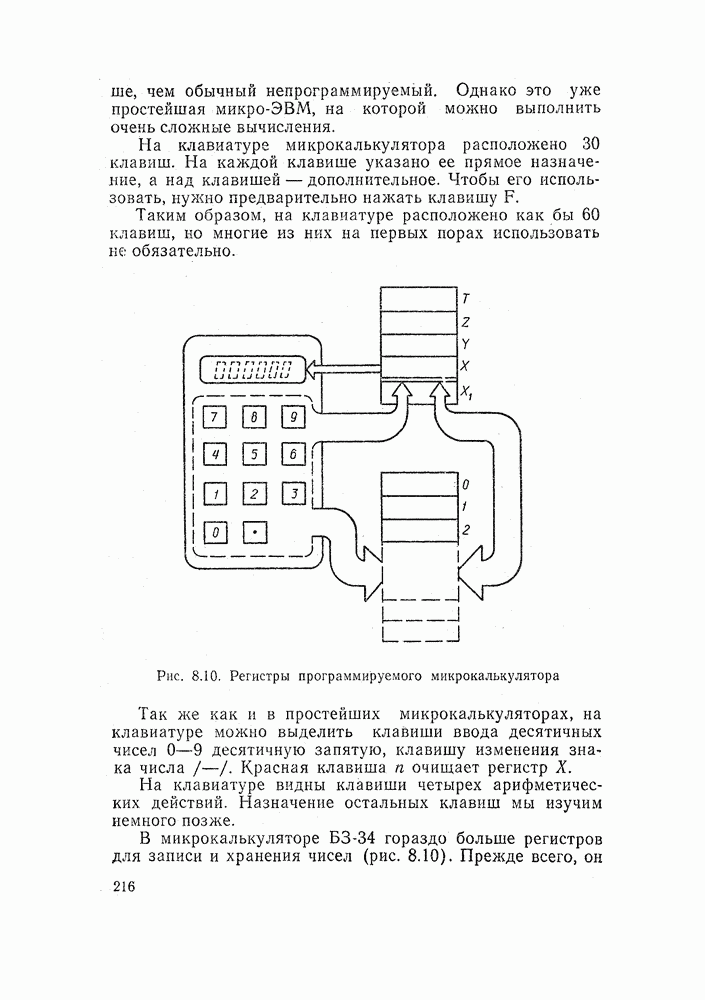
- 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР
- 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ
- 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
- 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ
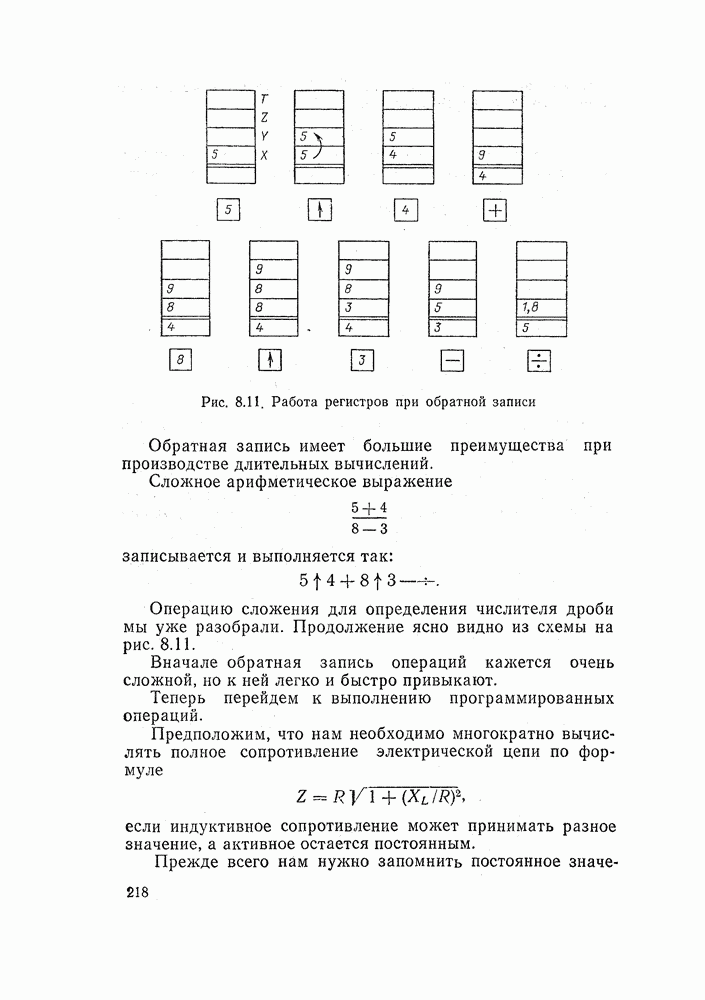
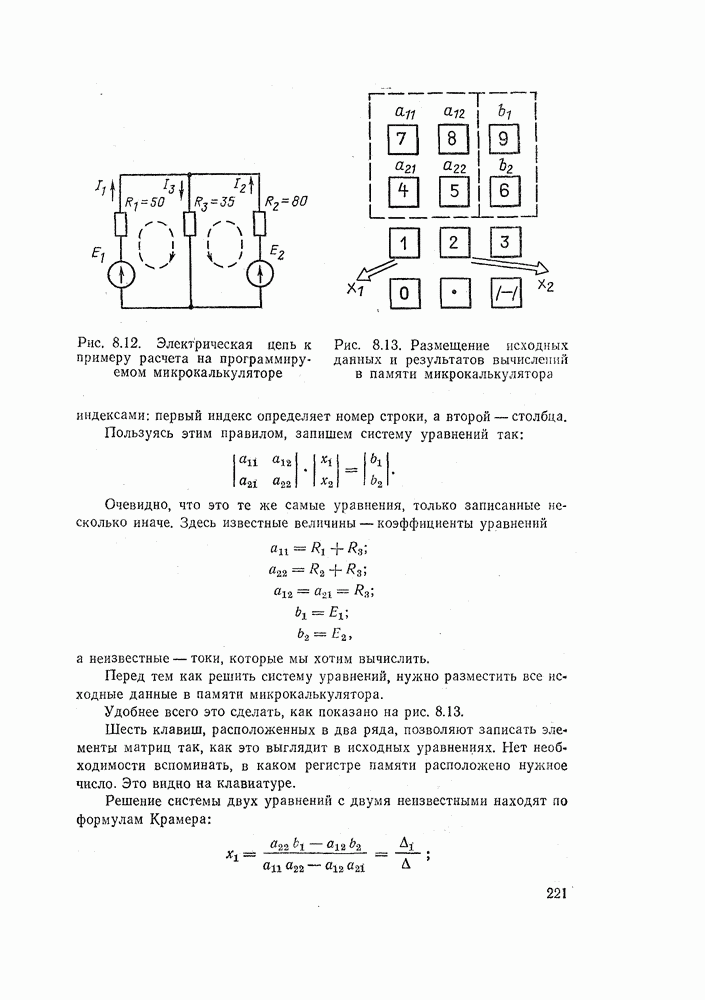
- 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ
- ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
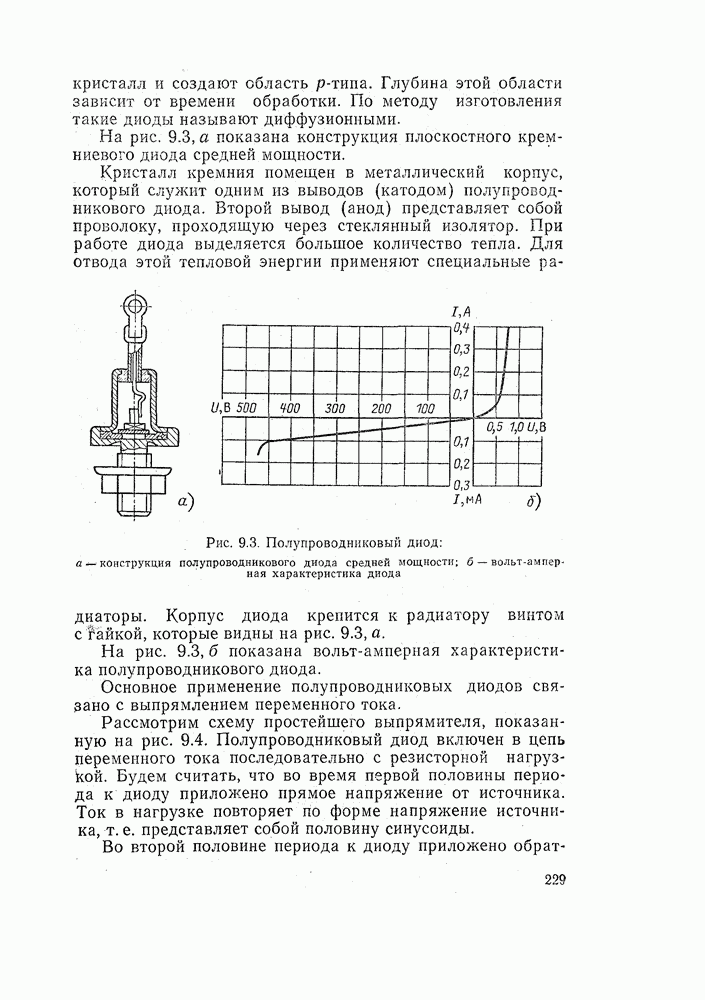
- 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ
- 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ
- 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
- 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ
- 9.7. КЛЮЧИ
- 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ
- 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА
- 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН
- 10.2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА
- 10.3. КОЛЛЕКТОР
- 10.4. ЯКОРНЫЕ ОБМОТКИ
- 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА
- 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН
- 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ
- 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ
- ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ
- 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- 11.2. РАБОТА ТРАНСФОРМАТОРА
- 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА
- 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ
- 11.1. АВТОТРАНСФОРМАТОРЫ
- ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА
- 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.4. РАБОТА СИНХРОННЫХ МАШИН
- 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ
- 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
- 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ
- 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН
- ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ
- 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ
- 13.3. ЭЛЕКТРОМАГНИТЫ
- 13.4. КОНТАКТОРЫ
- 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
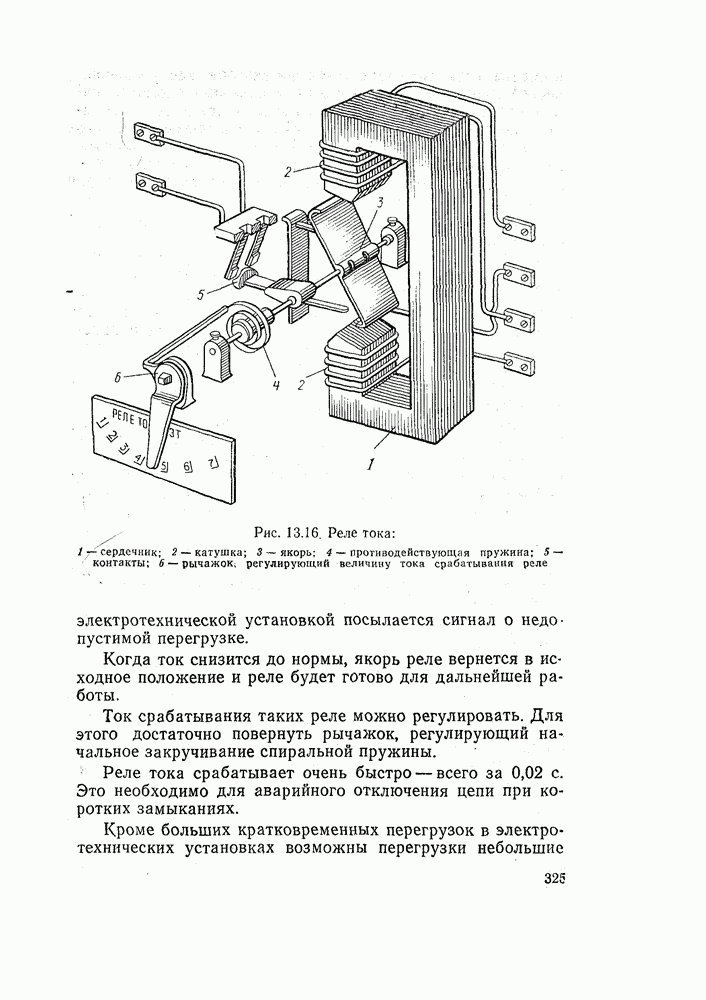
- 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ
- 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ
- 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ
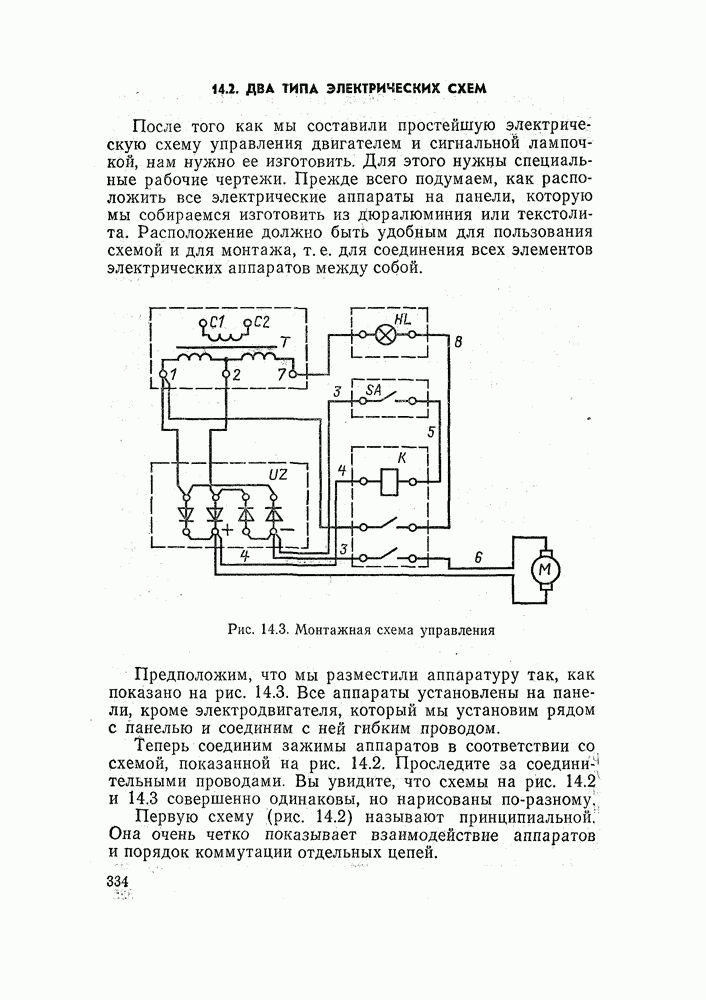
- 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ
- 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ
- 14.4. СХЕМЫ ТОРМОЖЕНИЯ
- 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ
- 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ
- 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА
- 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ
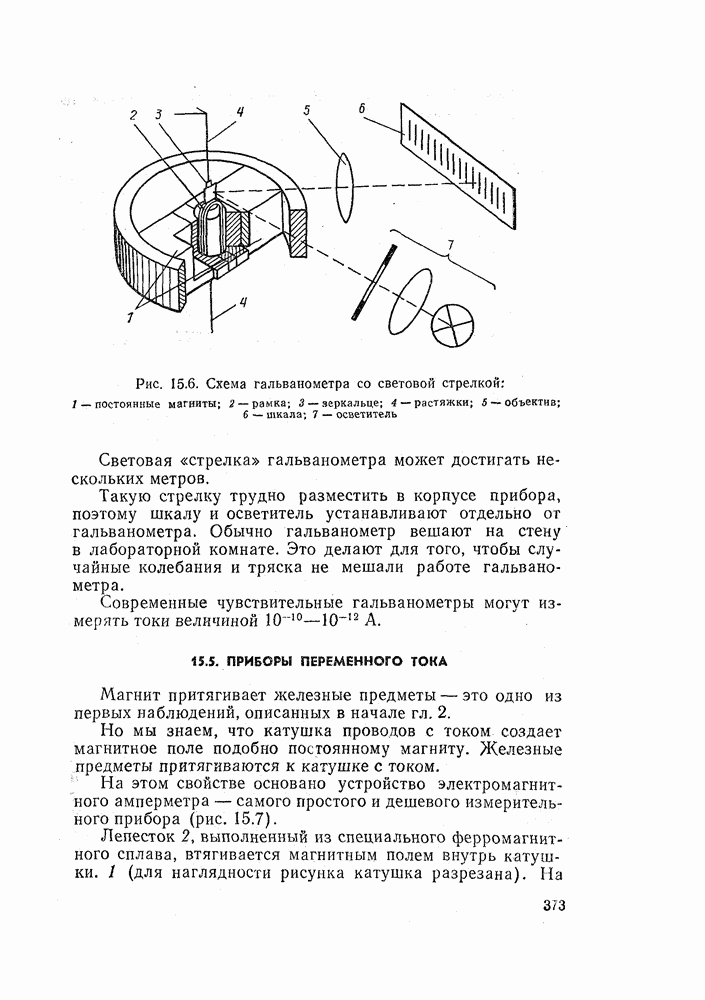
- 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ
- 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА
- 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
- 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА
- 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА
- 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ
- 15.10. ЦИФРОВЫЕ ПРИБОРЫ
- 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ