| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ
При решении ряда задач, как это видно из только что приведенных примеров, очень большую роль ищает величина

Этой величиной пользуются для многих расчетов и при целом ряде теоретических выводов. Эту величину называют напряженностью магнитного поля и обозначают буквой Н («аш» или «ха»):

Множитель  выбран так, чтобы при подстановке в формулу значений индукции, выраженных в теслах, левая часть давала значения напряженности поля, выраженные в амперах на метр (А/м).
выбран так, чтобы при подстановке в формулу значений индукции, выраженных в теслах, левая часть давала значения напряженности поля, выраженные в амперах на метр (А/м).
Вспомнив определение магнитной проницаемости, легко увидеть, что в случае кольцевой катушки со сплошным сердечником

Заметим сразу же, что наша вторая формула справедлива только для замкнутых сердечников, имеющих форму кольца, охватывающего все витки катушки, да еще обязательно кольца с неизменным сечением и с одинаковыми свойствами по всей длине!
Напротив, первая формула для определения напряженности поля справедлива всегда.
Ранее нами была получена формула

Введя обозначения

и

(ведь в воздухе  ), мы перепишем ее в виде
), мы перепишем ее в виде

Полезно также разобрать и примеры предыдущего параграфа. Так, в примере 1, рассматривая сердечник с воздушным зазором, мы нашли, что полный ток IN = 665 А соответствует индукции 1,2 Тл при относительной проницаемости стали 
Вынув стальной сердечник, мы получим при том же токе напряженность поля

Ей соответствует магнитная индукция, равная всего лишь

Обратившись еще раз к примеру 2 предыдущего параграфа, мы увидим, что в случае сплошного сердечника индукция в  создавалась полным током
создавалась полным током  . Такой же полный ток после удаления сердечника создает в воздухе индукцию
. Такой же полный ток после удаления сердечника создает в воздухе индукцию

Пользуясь понятием напряженности поля, можно записать закон полного тока в такой форме:

или

Здесь предполагается, что Н выражено в  .
.
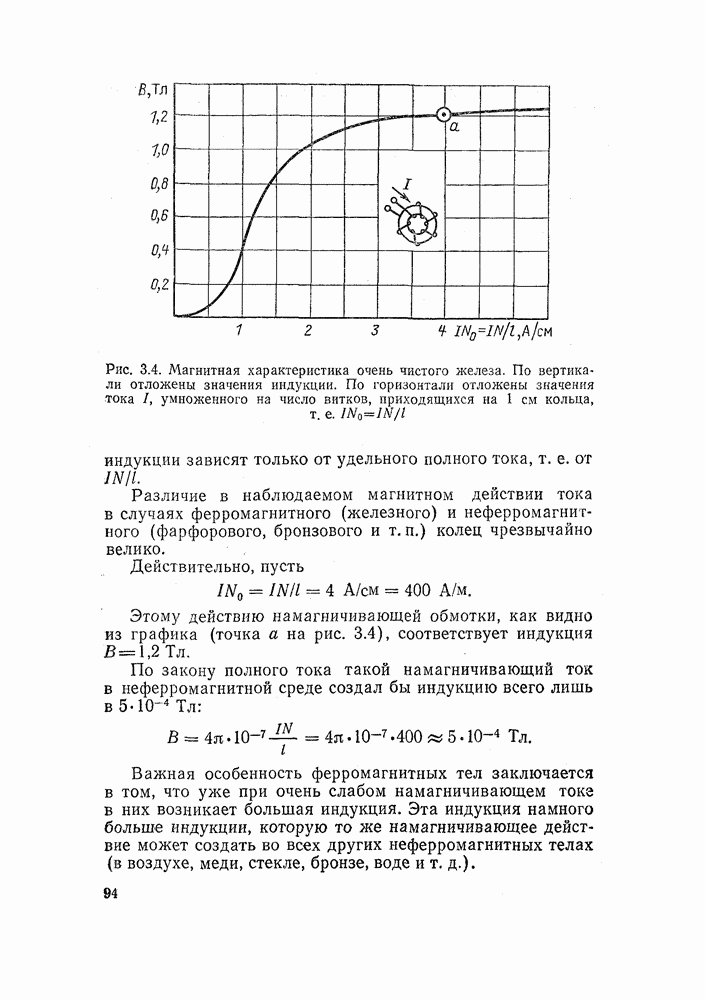
Заметим, что величина, называвшаяся выше удельным полным током  и откладывавшаяся по горизонтальной оси магнитных характеристик (рис. 3.4-3.6), оказывается не чем иным, как напряженностью магнитного поля, выраженной в А/см.
и откладывавшаяся по горизонтальной оси магнитных характеристик (рис. 3.4-3.6), оказывается не чем иным, как напряженностью магнитного поля, выраженной в А/см.
В заключение заметим еще следующее: формула  может применяться и к сердечнику, имеющему форму, отличную от кольца, так как при большой проницаемости стали магнитный поток в основном следует за формой сердечника.
может применяться и к сердечнику, имеющему форму, отличную от кольца, так как при большой проницаемости стали магнитный поток в основном следует за формой сердечника.
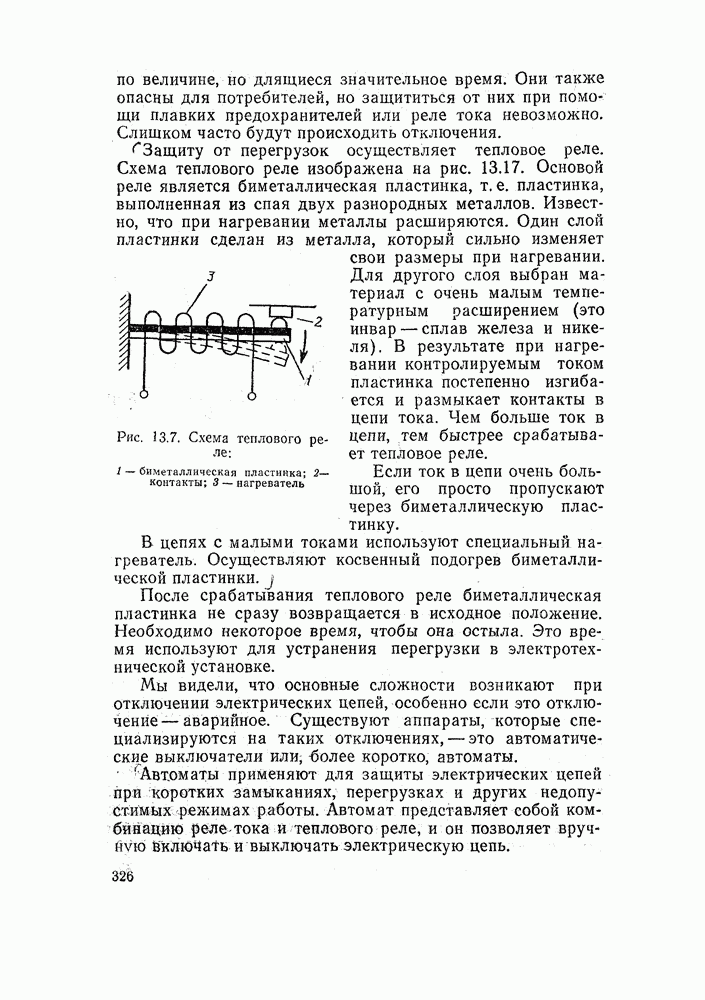
Пример. В прямоугольном стальном сердечнике из стали высокой проницаемости (рис. 3.6), изображенном на рис. 3.9, требуется создать индукцию 1,4 Тл. В сердечнике содержатся два воздушных зазора общей длиной 0,02 см. Размеры сердечника указаны на рис. 3.9.
Спрашивается, какой полный ток должен создаваться в катушках, надетых на сердечнике?

Рис. 3.9. Прямоугольный сердечник с воздушным зазором

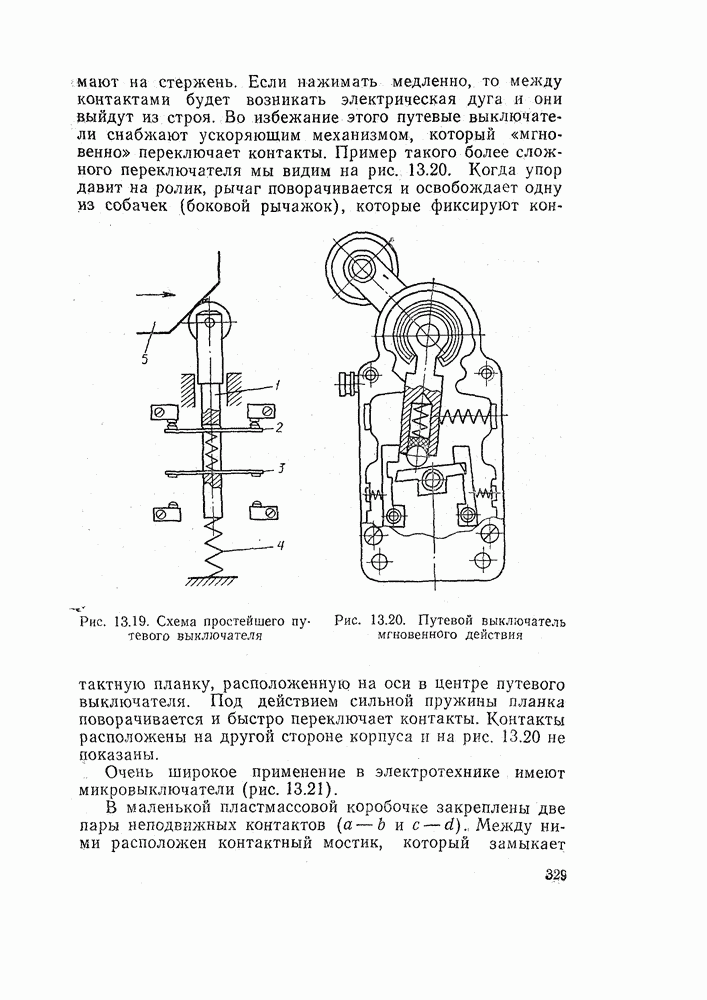
Рис. 3.10. Разветвленная магнитная цепь с двумя намагничивающими катушками
Решение. Найдя по графику на рис. 3.6 соответствующее 1,4 Тл значение напряженности магнитного поля в сердечнике

и по формуле

— значение напряженности магнитного поля в воздушном зазоре, получаем для полного тока величину

Этот пример еще раз показывает, какую роль играют даже очень малые зазоры.
Приведенные примеры являются простейшими расчетами магнитной цепи, т. е. цепи магнитного потока.
При более сложной форме сердечника поток может разветвляться (рис. 3.10). Кроме того, в таких случаях при вычислении для разных замкнутых контуров в правой части нашей основной расчетной формулы (закон полного тока) могут оказаться разные значения полного тока.
Расчет очень осложняется. Однако и для такой более сложной цепи остается справедливым наш закон полного тока.
Добавочным уравнением для расчета сложных магнитных цепей является условие непрерывности магнитного потока: магнитный поток, приходящий к какому-нибудь узлу, где он разветвляется, равен сумме отходящих потоков. В случае, изображенном на рис. 3.10, это значит, что

Этот закон напоминает первое правило (первый закон) Кирхгофа для электрической цепи. Нетрудно усмотреть аналогию со вторым правилом Кирхгофа в законе полного тока

На основании этой аналогии часто полный ток и называют магнитодвижущей силой (МДС).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ
- 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА
- 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА
- 1.6. МОЩНОСТЬ
- 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА
- 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ
- 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ
- 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ
- 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА
- 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ
- 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА
- 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ
- 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ
- 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ
- 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ
- 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ
- 1.20. ЗАКОНЫ КИРХГОФА
- ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ
- 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ
- 2.4. МАГНИТНАЯ ИНДУКЦИЯ
- 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ
- 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ
- 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ
- 2.9. ПРАВИЛО ЛЕНЦА
- 2.10. МАГНИТНЫЙ ПОТОК
- 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
- 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ
- 2.13. ВЗАИМНАЯ ИНДУКДИЯ
- 2.14. САМОИНДУКЦИЯ
- 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ
- 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА
- 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА
- 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
- 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ
- 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ
- 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ
- 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ
- 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ
- 3.9. НАМАГНИЧЕННОСТЬ
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ
- 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА)
- 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ)
- 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
- 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ
- ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК
- 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК?
- 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 5.4. СИНУСОИДА
- 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ
- 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ
- 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ
- 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
- 6.7. РЕЗОНАНС ТОКОВ
- 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ
- ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК
- 7.1. ТРЕХФАЗНАЯ СИСТЕМА
- 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ
- 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС
- 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ
- 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА
- 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ
- ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ
- 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР
- 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ
- 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
- 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ
- 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ
- ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ
- 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ
- 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
- 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
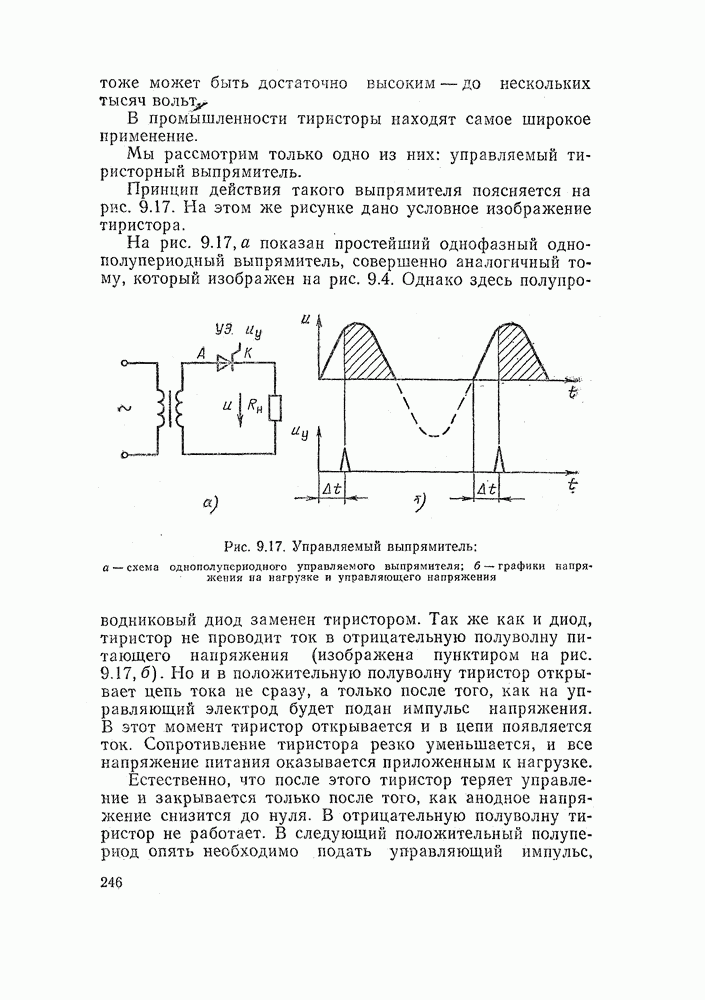
- 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ
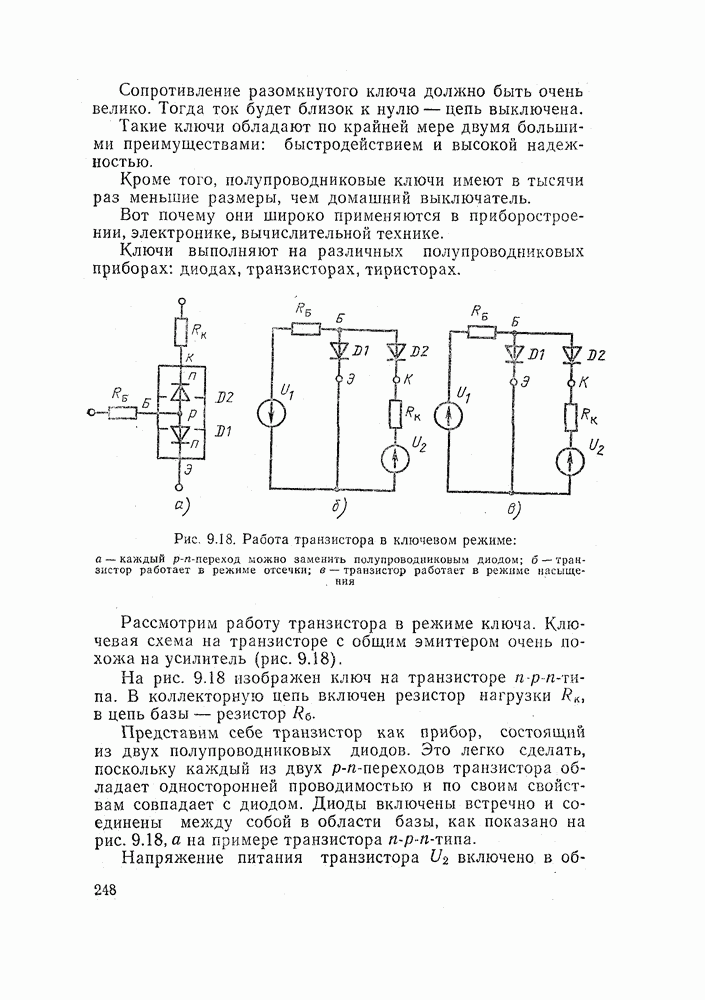
- 9.7. КЛЮЧИ
- 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ
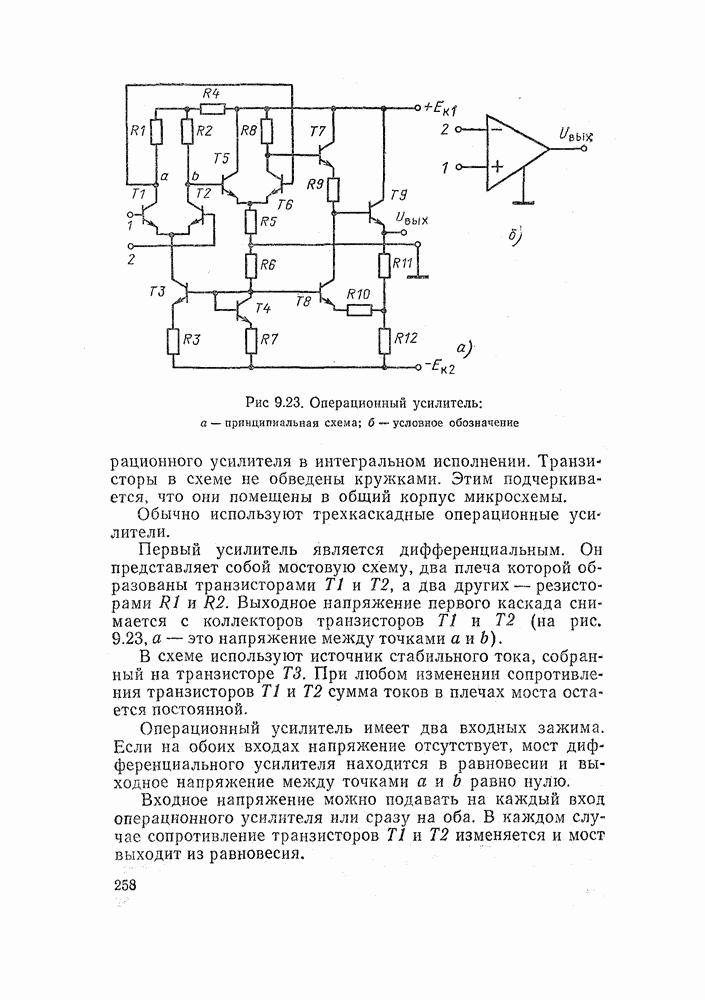
- 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА
- 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН
- 10.2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА
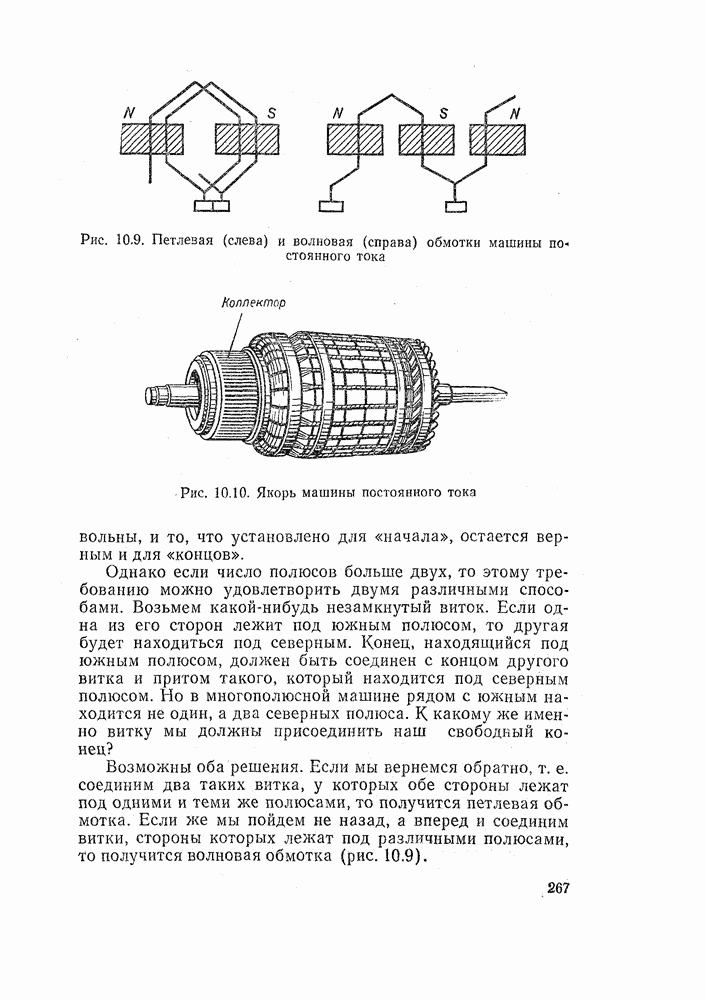
- 10.3. КОЛЛЕКТОР
- 10.4. ЯКОРНЫЕ ОБМОТКИ
- 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА
- 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН
- 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ
- 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ
- ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ
- 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- 11.2. РАБОТА ТРАНСФОРМАТОРА
- 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА
- 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ
- 11.1. АВТОТРАНСФОРМАТОРЫ
- ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА
- 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.4. РАБОТА СИНХРОННЫХ МАШИН
- 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ
- 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
- 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ
- 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН
- ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ
- 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ
- 13.3. ЭЛЕКТРОМАГНИТЫ
- 13.4. КОНТАКТОРЫ
- 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ
- 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ
- 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ
- 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ
- 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ
- 14.4. СХЕМЫ ТОРМОЖЕНИЯ
- 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ
- 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ
- 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА
- 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ
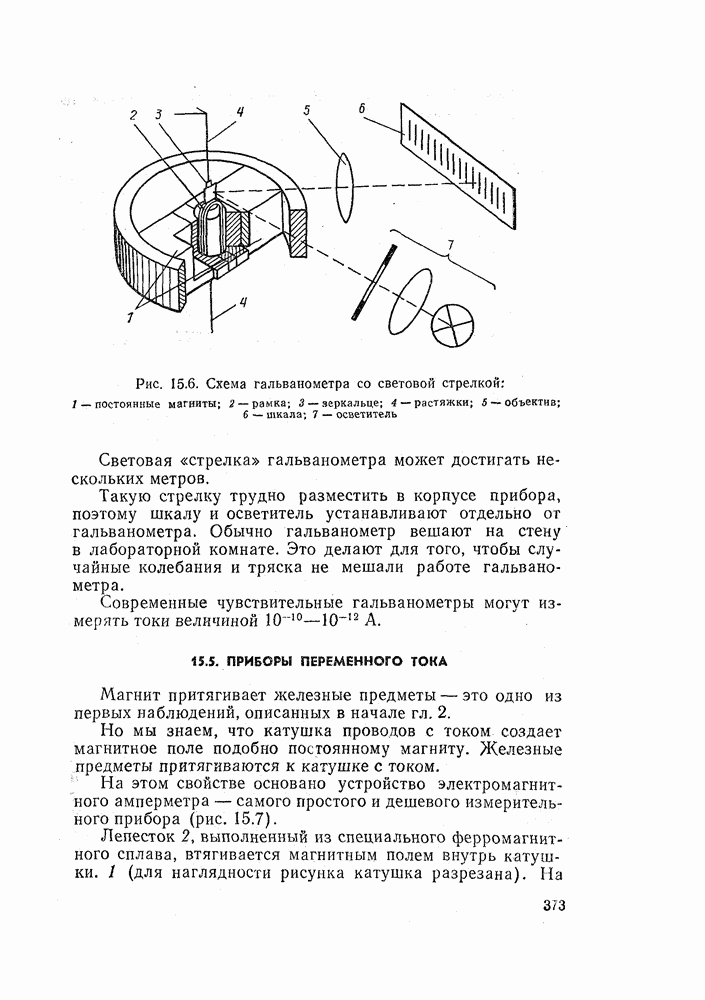
- 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ
- 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА
- 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
- 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА
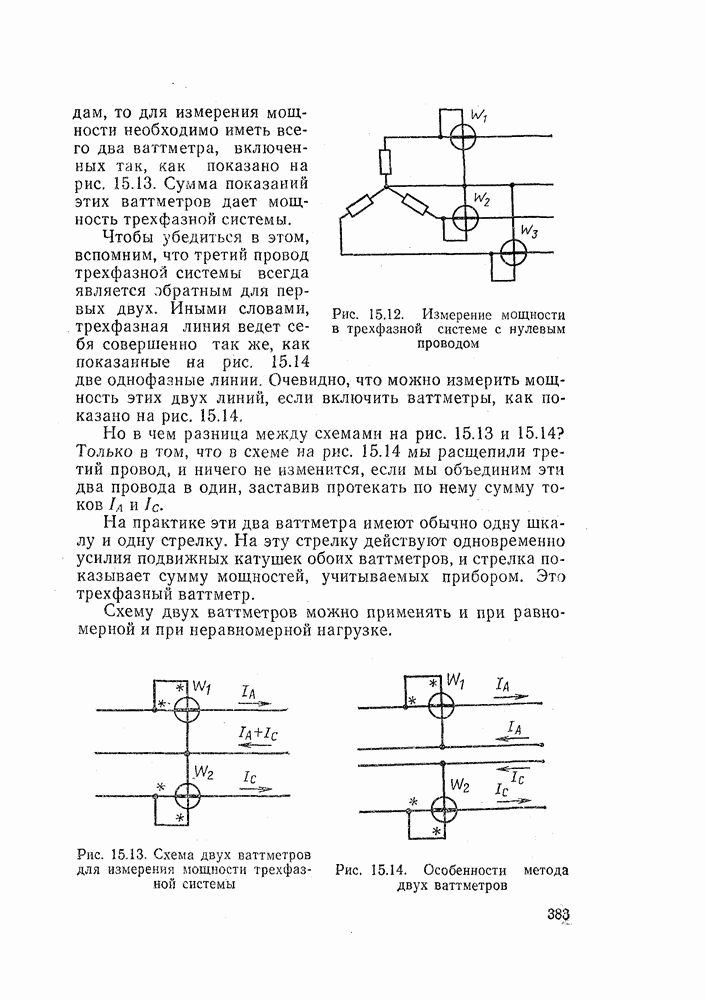
- 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА
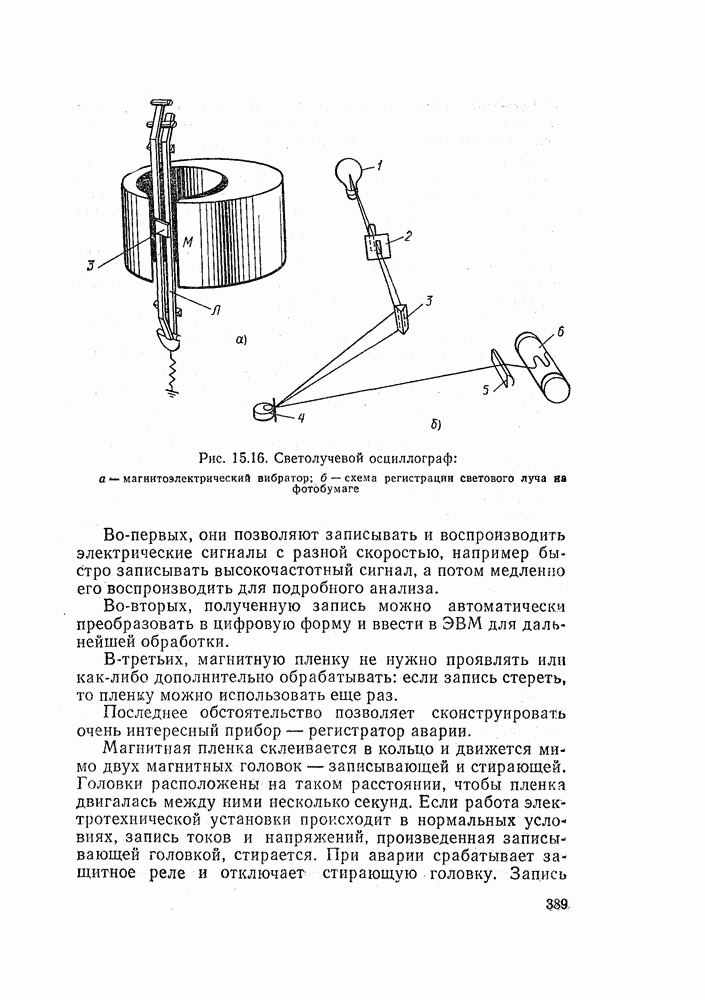
- 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ
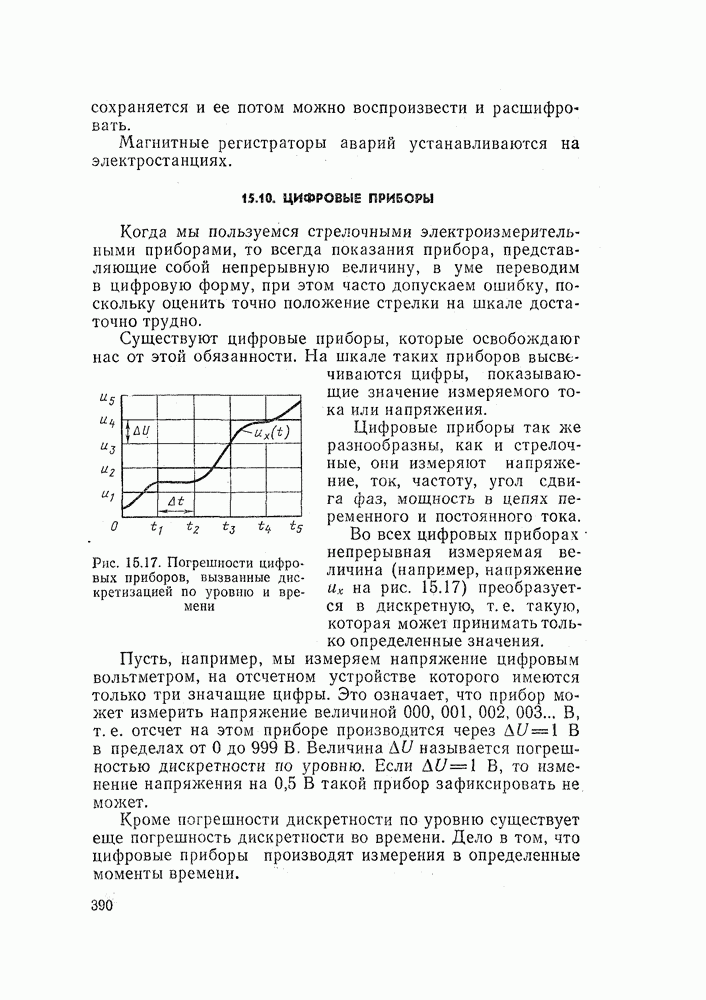
- 15.10. ЦИФРОВЫЕ ПРИБОРЫ
- 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ