| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ
Микрокалькуляторы значительно ускоряют и упрощают расчеты режимов работы электротехнических цепей и различных устройств. Точность вычислений при этом повышается во много раз.
Однако для того, чтобы правильно использовать возможности микрокалькулятора, необходимо выполнять определенные правила. Необходимо продумать и даже написать на бумаге порядок вычислений на микрокалькуляторе. В математике правила, по которым производят вычисления, называют алгоритмом.
Алгоритм вычислений должен быть рациональным. Что под этим понимать?
Существует такое правило: вычисление следует производить без записи промежуточных результатов и при этом как можно меньше нажимать на клавиши.
Если строго следовать этому правилу, то вычисления станут точными и быстрыми. Умение пользоваться микрокалькулятором приходит не сразу.
Постепенно Вы овладеете техникой быстрого счета, узнаете «маленькие хитрости», позволяющие упростить вычисления.
Но для этого очень важно знать и все время помнить, как работает микрокалькулятор, что происходит с числами, когда Вы нажимаете на клавиши.
В каждой области техники существуют свои специальные методы и приемы вычислений. Есть они и в электротехнике.
Некоторые из них мы покажем на примерах.
Пример 1. Рассмотрим простейший пример вычисления эквивалентного сопротивления при параллельном соединении двух резисторов с сопротивлениями  Ом и
Ом и  Ом.
Ом.
Эквивалентная проводимость такой цепи вручную вычисляется в четыре этапа:

На каждом этапе расчета необходимо выполнить вычисление и записать результат, чтобы использовать его в дальнейших вычислениях.
Если соединить все этапы расчета в одну формулу, то она будет выглядеть так;

С помощью простейшего микрокалькулятора расчет выполняется так:

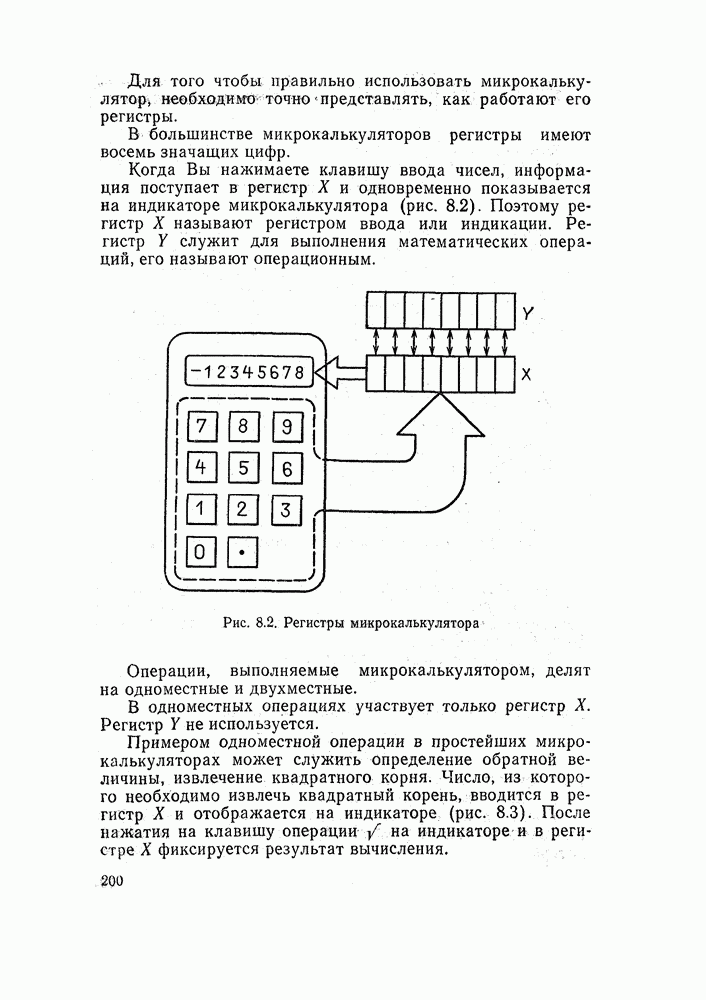
Напомним, что содержимое регистра X выводится на индикатор.
Записывать результат приходится дважды: один раз, чтобы запомнить величину  второй — эквивалентную проводимость
второй — эквивалентную проводимость 
Очень часто исходную формулу можно преобразовать так, чтобы количество промежуточных записей уменьшить или вовсе исключить.
В нашем случае эквивалентную проводимость можно представить в таком виде:

Формула кажется более сложной, однако при вычислении на микрокалькуляторе она имеет преимущества:

Действительно, промежуточная запись результатов нам не понадобилась, но второе сопротивление  пришлось вводить дважды. Чтобы найти эквивалентное; сопротивление, нужно значение
пришлось вводить дважды. Чтобы найти эквивалентное; сопротивление, нужно значение  записать, а затем найти обратную величину, набрав на калькуляторе
записать, а затем найти обратную величину, набрав на калькуляторе

Исключить промежуточную запись можно при помощи клавиши при нажатии которой содержание регистров X и У обменивается. Алгоритм вычисления на шагах 1—12 остается прежним, а окончание изменяется:

Операция  меняет местами делимое и делитель перед выполнением операции деления, и поэтому в конечном результате мы получим уже не проводимость, а сопротивление.
меняет местами делимое и делитель перед выполнением операции деления, и поэтому в конечном результате мы получим уже не проводимость, а сопротивление.
Если на калькуляторе имеется специальная клавиша  то электротехнические расчеты параллельного соединения значительно упрощаются. Тогда можно использовать (короткий) алгоритм
то электротехнические расчеты параллельного соединения значительно упрощаются. Тогда можно использовать (короткий) алгоритм

Операция обращения числа одноместная. Информация при этом обрабатывается в регистре X, а регистр У используется в качестве памяти.
Этот алгоритм можно использовать при определении эквивалентного сопротивления трех, четырех и вообще любого числа резисторов, включенных параллельно. Так, для трех резисторов 
Ом на клавиатуре микрокалькулятора нужно набрать

На индикаторе прочитаем 2 (Ом).
Пример 2. Определить эквивалентную проводимость электрической цепи, содержащей три резистора, включенных параллельно.
Сопротивления резисторов:  .
.
Формулу эквивалентной проводимости цепи удобно преобразовать так:

На клавиатуре микрокалькулятора нужно набрать

Ответ на индикаторе — 0,5 будет соответствовать эквивалентной проводимости цепи.
Если микрокалькулятор имеет клавишу обратного значения, то алгоритм выглядит особенно просто:

Этот алгоритм можно использовать при определении эквивалентной проводимости и сопротивления (в этом случае добавляется еще одна операция 1/х) четырех, пяти и вообще любого числа резисторов, включенных параллельно.

Рис. 8.6. Схема смешанного соединения трех резисторов (к примеру 3)
В электротехнических расчетах часто используются дробные выражении. При вычислении значения дроби всегда сначала следует вычислить знаменатель, а затем уже числитель. Тогда можно сразу же разделить его на знаменатель дроби и получить окончательное значение.
Пример 3. Найти эквивалентное сопротивление электрической схемы, изображенной на рис. 8.5. Значение сопротивлений:  .
.
Эквивалентная проводимость электрической цепи

Эквивалентное сопротивление найдем как обратную величину:

Один из возможных алгоритмов вычисления выглядит так:

Промежуточный результат (знаменатель дроби), полученный на 6-м щаге, следует записать и снова ввести на шаге 15.
В электротехнических расчетах цепей переменного тока часто вычисляют среднеквадратическое значение двух величин.
Так, например, полное сопротивление электрической цепи, состоящей из резистора и катушки индуктивности, равно

Прямой алгоритм вычисления, которым часто пользуются, очень далек от совершенства:
1. Определить  записать.
записать.
2. Определить  , записать.
, записать.
3. Сложить эти две величины.
4. Извлечь из суммы квадратный корень.
Две промежуточные записи и последующий ввод полученных значений усложняют вычисления. Удобнее перестроить формулу:

В этом случае промежуточная запись совсем исключается.
Пример 4. Найти полное соппотилпрнир прим 

Алгоритм вычислений:

На индикаторе прочтете 10 (Ом).
Действительно,

Этот алгоритм предполагает, что калькулятор имеет клавишу извлечения квадратного корня.
Если на Вашем калькуляторе такой клавиши нет, ситуация усложняется, но не становится безнадежной. Корень можно найти приближенно. Если  то
то

Наберите на клавиатуре микрокалькулятора 
На индикаторе появится число 10,06464, которое отличается от истинного значения  Ом. Относительная погрешность вычисления равна
Ом. Относительная погрешность вычисления равна

В том случае, когда в электрической цели реактивное сопротивление больше активного  также можно пользоваться приближенной формулой, но записать ее нужно иначе:
также можно пользоваться приближенной формулой, но записать ее нужно иначе:

Во всех случаях такие приближенные формулы дают погрешность не более 4 %.
Для очень точных вычислений полное сопротивление электрической цепи можно определить итерационным методом. Предположим опять, что  тогда
тогда

Здесь отношение  обозначено одной буквой а.
обозначено одной буквой а.
Приближенное значение квадратного корня (обозначим его  ) определяется так:
) определяется так:

Если требуется более точное приближение корня, то можно последовательно найти

Этот метод называют алгоритмом Герона. Покажем его применение на данных примера 4.
Найдем первое приближение:

Погрешность достаточно велика — 13,3 %
Теперь найдем второе приближение:

Погрешность значительно уменьшилась. Теперь она равна 0,78 % Подобная точность обычно вполне достаточна. Однако продолжим наши вычисления еще на один шаг:

Погрешность вычисления стала ничтожной — 0,003 %.
Легко заметить, что точность определения полного сопротивления цепи по приближенным формулам зависит от соотношения между активным и реактивным сопротивлениями. Если это соотношение превышает 10 раз, то полное сопротивление можно считать равным большему из них.
Пусть, например, 
Найдем полное сопротивление:

Если приравнять  Ом, то ошибка составит примерно 0,5 %.
Ом, то ошибка составит примерно 0,5 %.
При расчете электрических цепей переменного тока весьма просто определяются тригонометрические функции угла сдвига фазы между током и напряжением в цепи: 
Эти функции выражаются простыми алгебраическими формулами через параметры электрической цепи. Чаще всего определяют  — коэффициент мощности цепи.
— коэффициент мощности цепи.
Для того чтобы узнать угол сдвига фаз, необходимо найти обратную тригонометрическую функцию (агсфункцию). Так, например, если известно значение  то нужно найти функцию
то нужно найти функцию

Многие инженерные микрокалькуляторы имеют специальные клавиши для определения обратных тригонометрических функций. Но у простейших микрокалькуляторов таких клавиш нет. Приходится тогда идти на «математические хитрости».
Функция  может быть представлена суммой бесконечного числа слагаемых. В математике такая сумма называется рядом
может быть представлена суммой бесконечного числа слагаемых. В математике такая сумма называется рядом

Для приближенных значений ряд необходимо ограничить конечным числом членов, оборвать.
Пусть например, мы решили ограничиться двумя членами — теми, которые мы только что написали:

Но в таком виде производить вычисления на микрокалькуляторе неудобно, потому что нужно возводить число а в высокую степень и обязательно запоминать промежуточный результат. Постараемся избежать этого и перепишем формулу:

В такой формуле производить вычисления гораздо удобнее.
Точность вычисления по приближенной формуле зависит от величины  Чем меньше
Чем меньше  тем точнее вычисление угла
тем точнее вычисление угла  При
При  погрешность не превышает 5 %.
погрешность не превышает 5 %.
Если  необходимость вычислить обратную величину
необходимость вычислить обратную величину  а полученный угол вычесть из 90°.
а полученный угол вычесть из 90°.

Рис. 8.6. Электрическая цепь (к примеру 5)
Пример 5. Найти угол сдвига фаз между током и напряжением в электрической цепи, изображенной на рис. 8.6.
Из треугольника сопротивлений ясно, что

Обозначим эту величину  . Ее квадрат равен
. Ее квадрат равен 
Вычисление угла  на микрокалькуляторе можно выполнить по следующему алгоритму:
на микрокалькуляторе можно выполнить по следующему алгоритму:

На индикаторе микрокалькулятора прочтем число 0,3786666 = 0,3787. Более точное значение угла  . Поэтому погрешность составляет при таком вычислении менее
. Поэтому погрешность составляет при таком вычислении менее 
При вычислении по приближенной формуле результат получен в радианах. Если необходимо выразить угол сдвига фаз в градусах, не обходимо воспользоваться формулой перевода

В этом случае алгоритм вычисления должен быть

В результате на индикаторе появится число — угол сдвига фаз

Во многих микрокалькуляторах есть специальная клавиша вызова числа  , тогда набирать 3,14 на клавиатуре не нужно.
, тогда набирать 3,14 на клавиатуре не нужно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ
- 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА
- 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА
- 1.6. МОЩНОСТЬ
- 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА
- 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ
- 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ
- 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ
- 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА
- 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ
- 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА
- 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ
- 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ
- 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ
- 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ
- 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ
- 1.20. ЗАКОНЫ КИРХГОФА
- ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ
- 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ
- 2.4. МАГНИТНАЯ ИНДУКЦИЯ
- 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ
- 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ
- 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ
- 2.9. ПРАВИЛО ЛЕНЦА
- 2.10. МАГНИТНЫЙ ПОТОК
- 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
- 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ
- 2.13. ВЗАИМНАЯ ИНДУКДИЯ
- 2.14. САМОИНДУКЦИЯ
- 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ
- 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА
- 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА
- 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
- 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ
- 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ
- 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ
- 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ
- 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ
- 3.9. НАМАГНИЧЕННОСТЬ
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ
- 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА)
- 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ)
- 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
- 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ
- ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК
- 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК?
- 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 5.4. СИНУСОИДА
- 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ
- 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ
- 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ
- 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
- 6.7. РЕЗОНАНС ТОКОВ
- 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ
- ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК
- 7.1. ТРЕХФАЗНАЯ СИСТЕМА
- 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ
- 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС
- 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ
- 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА
- 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ
- ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ
- 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР
- 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ
- 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
- 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ
- 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ
- ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ
- 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ
- 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
- 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ
- 9.7. КЛЮЧИ
- 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ
- 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА
- 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН
- 10.2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА
- 10.3. КОЛЛЕКТОР
- 10.4. ЯКОРНЫЕ ОБМОТКИ
- 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА
- 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН
- 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ
- 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ
- ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ
- 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- 11.2. РАБОТА ТРАНСФОРМАТОРА
- 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА
- 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ
- 11.1. АВТОТРАНСФОРМАТОРЫ
- ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА
- 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.4. РАБОТА СИНХРОННЫХ МАШИН
- 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ
- 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
- 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ
- 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН
- ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ
- 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ
- 13.3. ЭЛЕКТРОМАГНИТЫ
- 13.4. КОНТАКТОРЫ
- 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
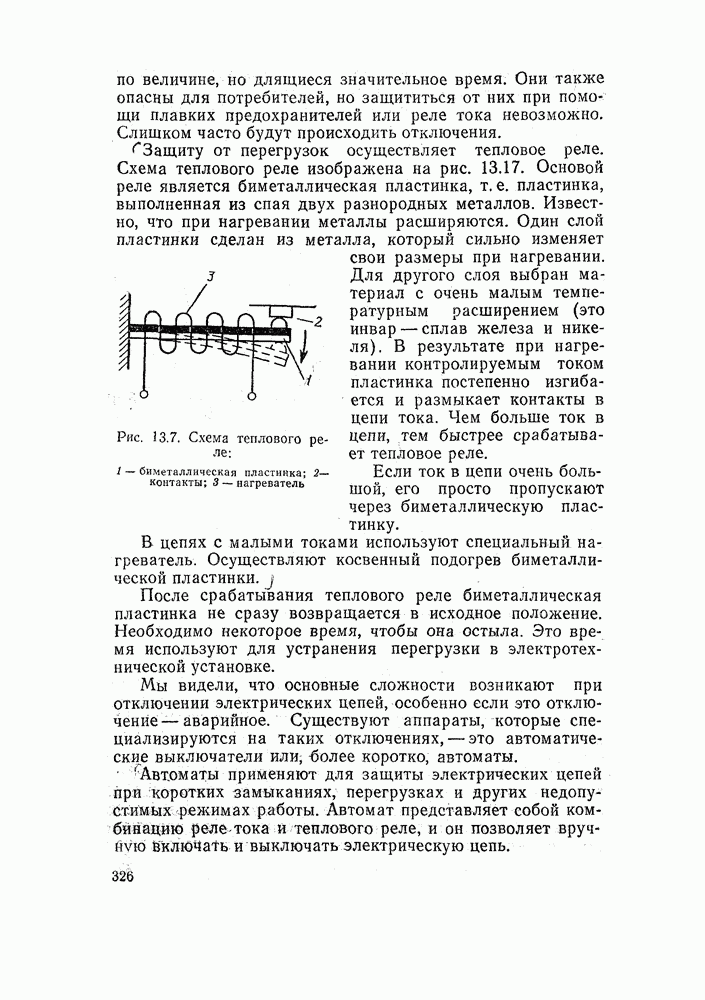
- 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ
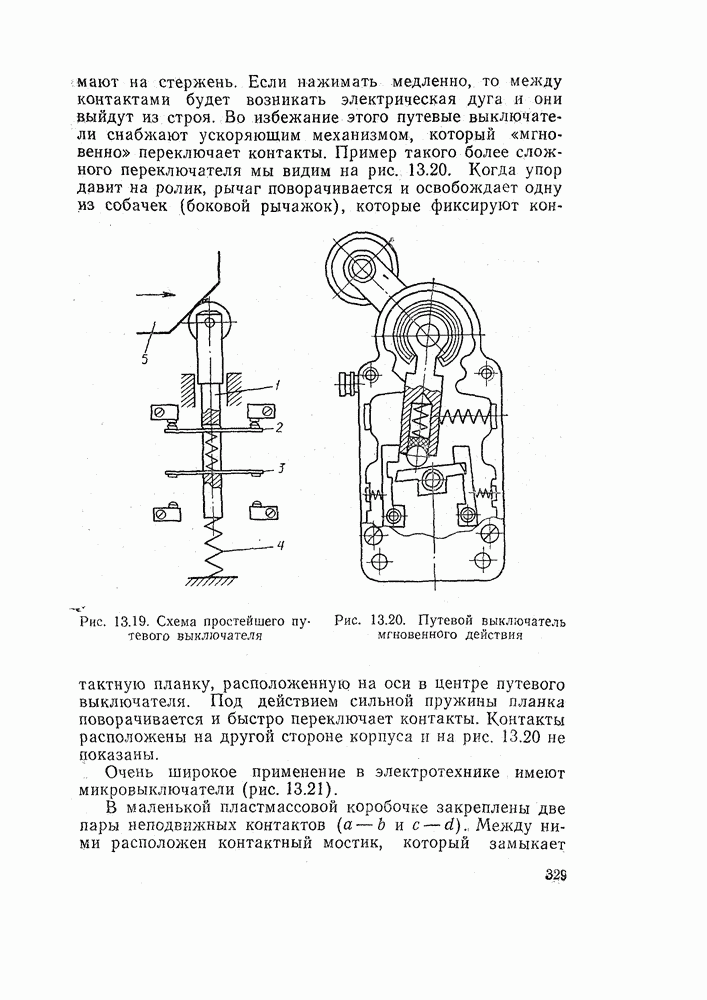
- 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ
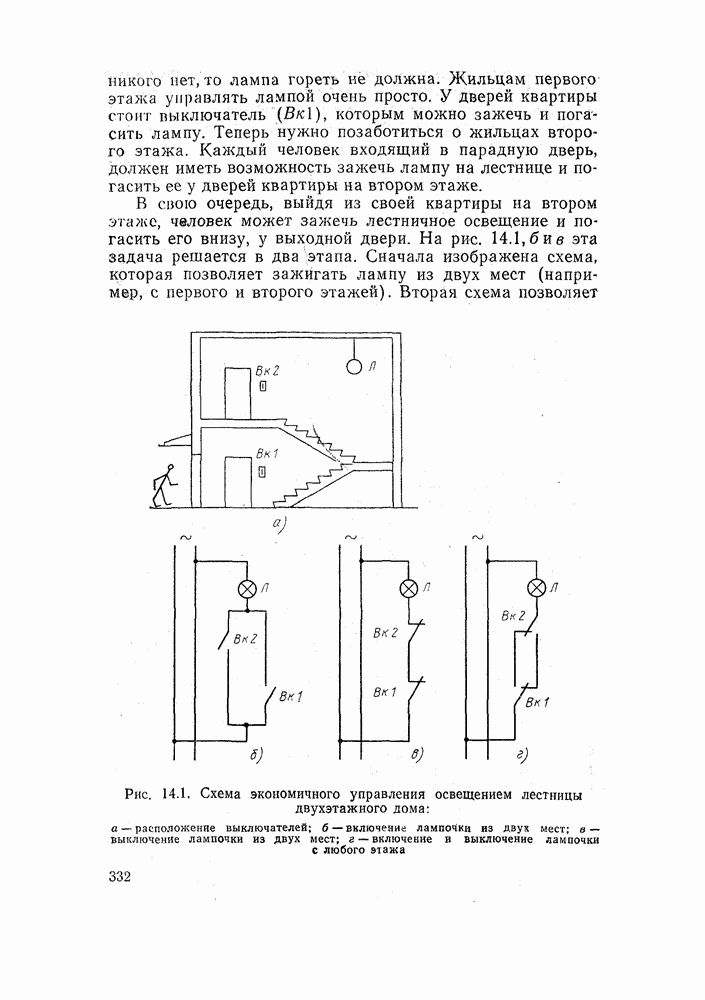
- 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ
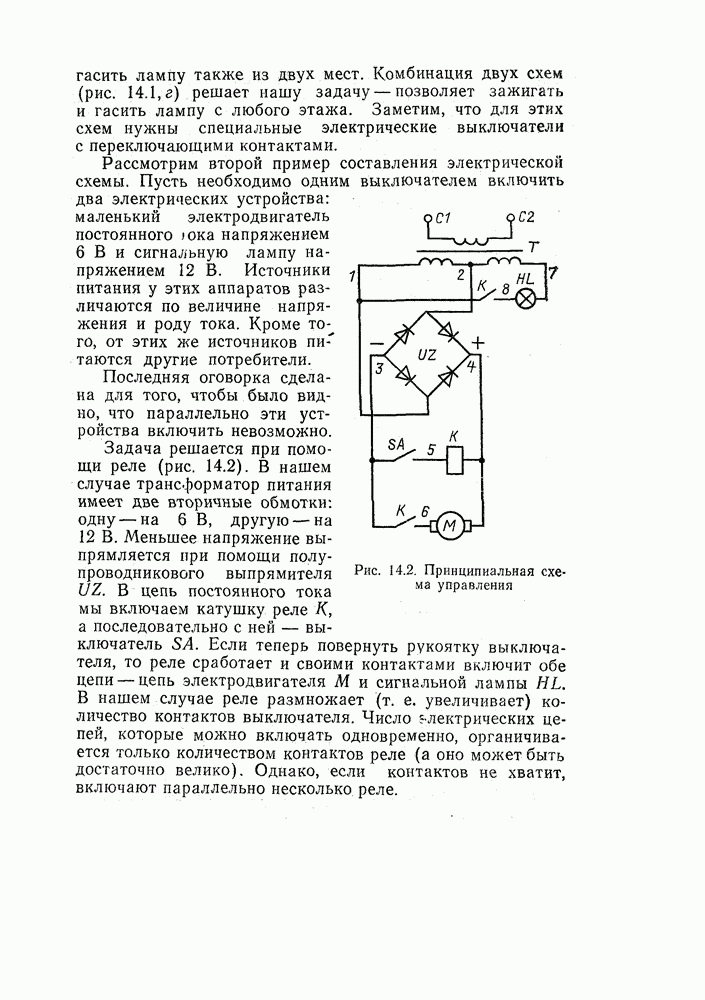
- 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ
- 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ
- 14.4. СХЕМЫ ТОРМОЖЕНИЯ
- 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ
- 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ
- 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА
- 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ
- 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ
- 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА
- 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
- 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА
- 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА
- 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ
- 15.10. ЦИФРОВЫЕ ПРИБОРЫ
- 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ