| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
Большинство микрокалькуляторов производят вычио ления и индикацию результатов с восьмиразрядными числами. Для большинства технических вычислений этого вполне достаточно.
Более того, известно, что излишние значащие цифры в ответе или промежуточном результате приносят большой вред. Они не только снижают скорость вычислений (особенно когда при расчетах на микрокалькуляторах приходится записывать промежуточный результат), но и приводят к серьезным техническим недоразумениям.
Разберем простой пример. Пусть резистор с сопротивлением  Ом включен на напряжение
Ом включен на напряжение  . По закону Ома определим ток в цепи:
. По закону Ома определим ток в цепи:

Воспользуемся микрокалькулятором:

Такое число будет высвечиваться на индикаторе микрокалькулятора после операции деления. Интуитивно чувствуется некоторое противоречие. Исходные числа имеют два десятичных знака, а результат — восемь.
Постараемся разобраться в этом подробнее. Абсолютно точное значение напряжения и сопротивления в электрической цепи определить невозможно. Поэтому исходные данные, участвующие в расчете, являются приближенными числами.
В записи приближенных чисел верны все знаки, кроме последнего, который может отличаться на единицу.
Таким образом, когда пишут  Ом, то в действительности сопротивление цепи лежит в промежутке между
Ом, то в действительности сопротивление цепи лежит в промежутке между

Математически это записывается так:

Можно считать, что абсолютная погрешность А (дельта) приближенного числа 4,64 не превосходит

Если бы мы хотели подчеркнуть, что сопротивление цепи составляет именно 4,64 Ом, следовало бы написать  Тогда стало бы ясно, что измерение сопротивления производилось с четырьмя значащими цифрами, при этом гарантируется, что вторая цифра после запятой — 4, а сомнение может коснуться только последнего нуля. Абсолютная погрешность уменьшится до величины
Тогда стало бы ясно, что измерение сопротивления производилось с четырьмя значащими цифрами, при этом гарантируется, что вторая цифра после запятой — 4, а сомнение может коснуться только последнего нуля. Абсолютная погрешность уменьшится до величины

Несмотря на сомнение в последнем знаке, говорят, что число 4,64 записано с тремя, а число 4 640 — с четырьмя верными знаками.
Количество верных знаков числа (исключая передние нули) определяет относительную погрешность приближенного числа.
Если число верных знаков  , то наибольшая (предельная) относительная погрешность не превосходит
, то наибольшая (предельная) относительная погрешность не превосходит  Эта простейшая оценка достаточно грубая, и в курсах приближенных вычислений даются более точные методы определения относительной погрешности, но мы ограничимся этим простейшим методом.
Эта простейшая оценка достаточно грубая, и в курсах приближенных вычислений даются более точные методы определения относительной погрешности, но мы ограничимся этим простейшим методом.
Таким образом, можно сказать, что три сопротивления  определены с одинаковой относительной погрешностью, равной
определены с одинаковой относительной погрешностью, равной  или 0,1 %, хотя абсолютная погрешность всех этих приближенных чисел разная:
или 0,1 %, хотя абсолютная погрешность всех этих приближенных чисел разная:
 .
.
Таким образом, простейшие оценки точности приближенного числа можно сделать по форме его записи.
Количество верных знаков приближенного числа определяет его относительную погрешность, а число десятичных знаков — абсолютную.
Вернемся теперь к нашему примеру вычисления тока в цепи, где напряжение и сопротивление определены с тремя верными цифрами.
В теории приближенных вычислений доказывается, что при делении двух чисел относительные погрешности суммируются, а число верных знаков частного должно быть равно наименьшему количеству верных знаков чисел, участвующих в делении.
Поскольку напряжение и сопротивление определены с тремя верными знаками, ток в цепи можно определить тоже только с тремя верными знаками.
Таким образом,

Результат, полученный на индикаторе, следует округлить и оставить только три значащие цифры. Принимать во внимание все остальные цифры бессмысленно, поскольку они не являются достоверными.
Мы начали разговор о точности вычислений с операции деления. Теперь рассмотрим другие арифметические действия.
При умножении двух приближенных чисел действует такое же правило, как и при делении.
Пусть в электрической цепи заданы ток  и сопротивление
и сопротивление  .
.
Необходимо найти величину напряжения 
Умножая на микрокалькуляторе, получаем

Однако записать такой результат было бы неверно. В действительности наша запись исходных данных означает, что ток и сопротивление в цепи заключены в таких пределах:

Если взять минимальное значение тока и сопротивления, то получим

Максимальные значения тока и сопротивления дают такое напряжение:

Из сравнения этих двух значений видно, что ручаться можно только за два первых знака и значение напряжения в цепи следует округлить до значения

Следует отметить, что запись

была бы не совсем точной, поскольку здесь не два, а три верных знака.
Рассмотрим теперь, как производится арифметическое сложение в электрических расчетах.
Предположим, что в электрической цепи (рис. 8.7) измерены три напряжения на последовательно соединенных резисторах:  . Требуется определить напряжение в цепи
. Требуется определить напряжение в цепи

Складывая на микрокалькуляторе, получаем

Такой ответ нельзя считать правильным.

Рис. 8.7. Электрическая цепь к примеру суммирования трех напряжений
При суммировании абсолютные погрешности приближенных чисел складываются, поэтому существует такое правило:
при сложении приближенных чисел в сумме оставляют столько десятичных знаков, сколько их имеется в слагаемом с наибольшей абсолютной погрешностью.
В нашем примере следует отбросить лишние знаки и считать, что общее напряжение в сети равно

При вычитании приближенных чисел абсолютные погрешности также складываются, но, как правило, относительная точность вычисления при этом значительно ухудшается. Это особенно опасно при вычитании близких чисел, когда результат получается значительно меньшим, чем каждое из них.
Пример. В электрической цепи (рис. 8.8) заданы токи —25,12 А и  . Определить ток
. Определить ток 
По первому закону Кирхгофа ток  равен разности токов:
равен разности токов:

Исходные токи заданы с абсолютной погрешностью, не превышающей единицы последнего разряда, т. е.  , и относительной погрешностью
, и относительной погрешностью 
Если считать, что в разности абсолютные погрешности складываются, то получим

и огромную относительную погрешность

Наш результат весьма недостоверен.

Рис. 8.8. При определении тока  в этой цепи приходится находить разность двух близких чисел
в этой цепи приходится находить разность двух близких чисел
С практической точки зрения это означает, что правильнее было бы непосредственно измерить ток  чем определять его методом вычисления разности токов
чем определять его методом вычисления разности токов  и
и 
Иногда в процессе вычислений удается преобразовать исходную формулу так, что можно избежать вычитания близких чисел.
Из приведенных примеров видно, что увлекаться выписыванием лишних знаков с индикатора микрокалькулятора не следует. Простые правила показывают, сколько знаков нужно оставить в конечном результате. Для промежуточных вычислений рекомендуется число верных знаков увеличивать на одну (в крайнем случае на две) цифры. В конечном ответе эту цифру отбрасывают.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ
- 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА
- 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА
- 1.6. МОЩНОСТЬ
- 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА
- 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ
- 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ
- 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ
- 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА
- 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ
- 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА
- 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ
- 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ
- 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ
- 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ
- 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ
- 1.20. ЗАКОНЫ КИРХГОФА
- ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ
- 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ
- 2.4. МАГНИТНАЯ ИНДУКЦИЯ
- 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ
- 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ
- 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ
- 2.9. ПРАВИЛО ЛЕНЦА
- 2.10. МАГНИТНЫЙ ПОТОК
- 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
- 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ
- 2.13. ВЗАИМНАЯ ИНДУКДИЯ
- 2.14. САМОИНДУКЦИЯ
- 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ
- 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА
- 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА
- 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
- 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ
- 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ
- 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ
- 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ
- 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ
- 3.9. НАМАГНИЧЕННОСТЬ
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ
- 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА)
- 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ)
- 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
- 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ
- ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК
- 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК?
- 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
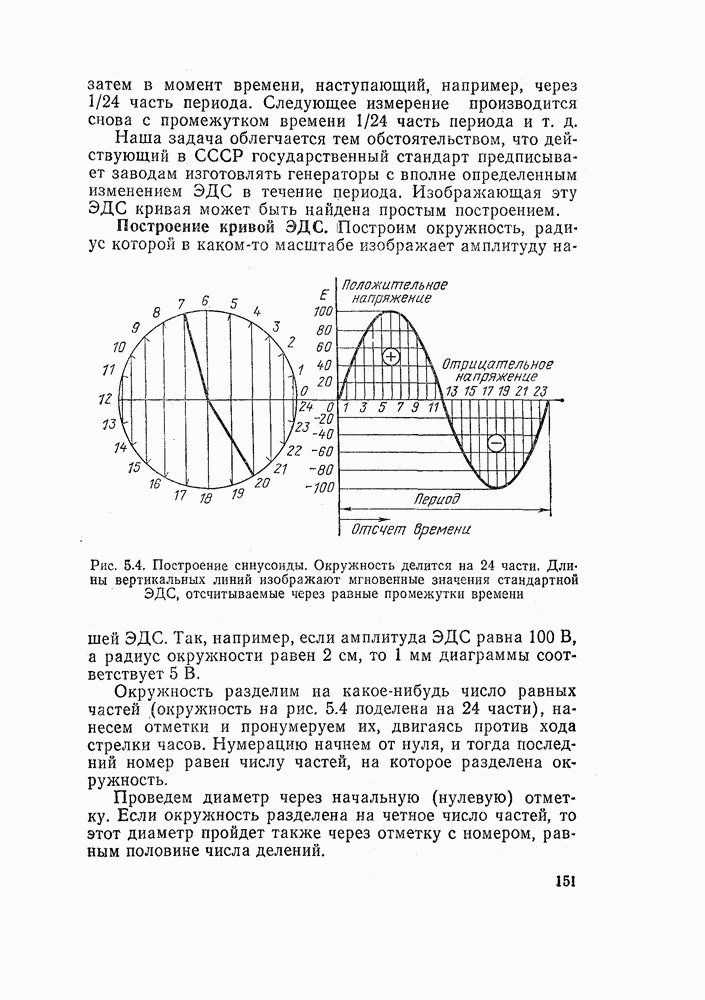
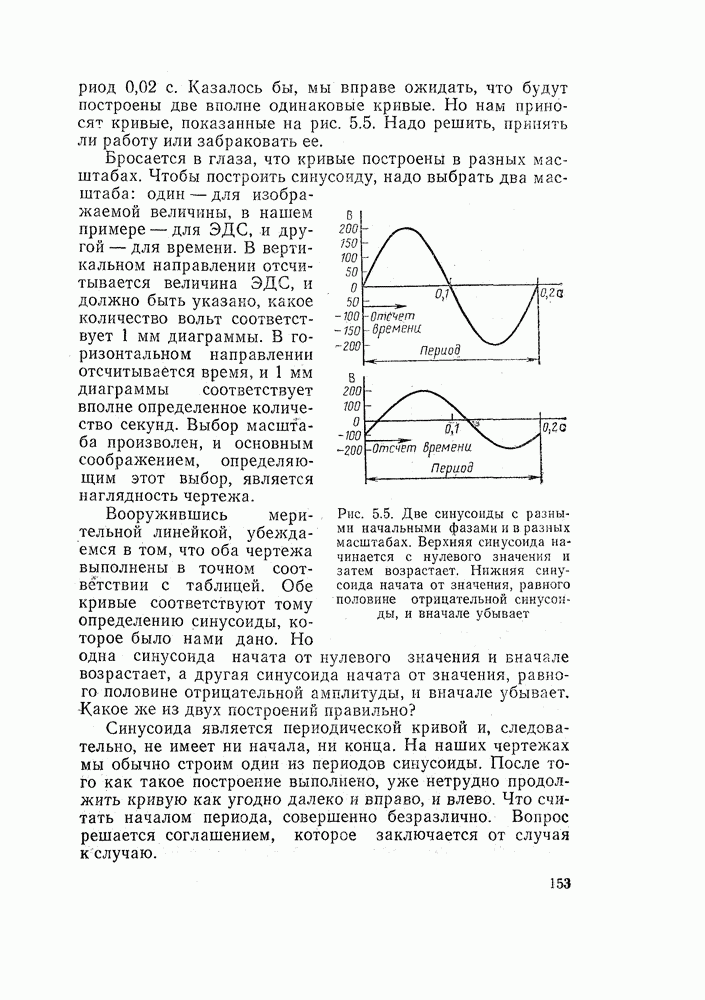
- 5.4. СИНУСОИДА
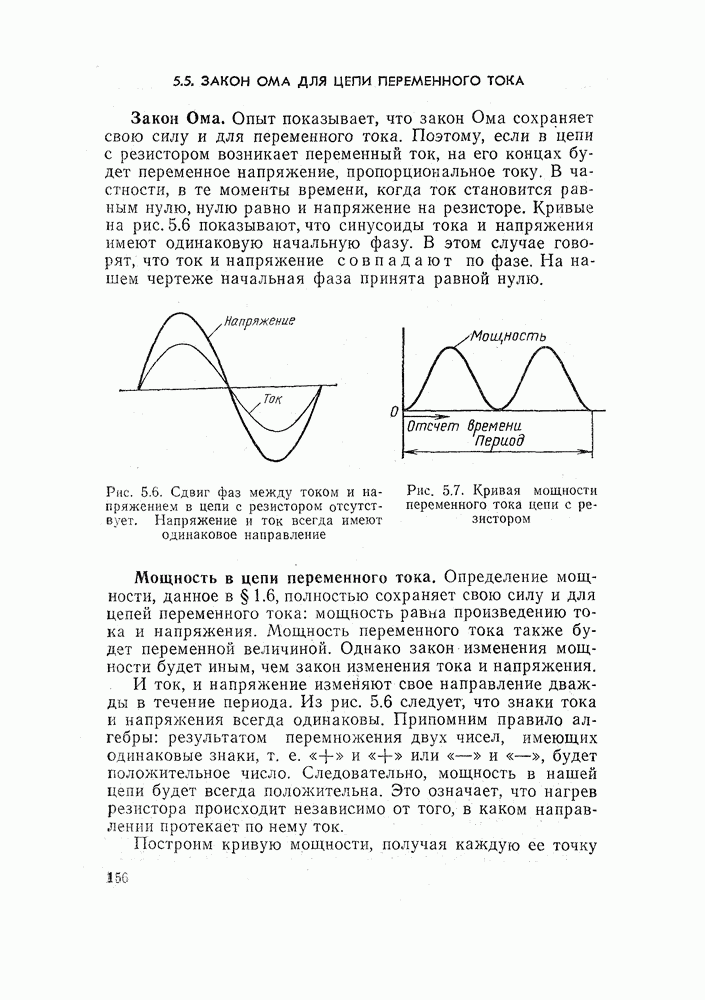
- 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ
- 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ
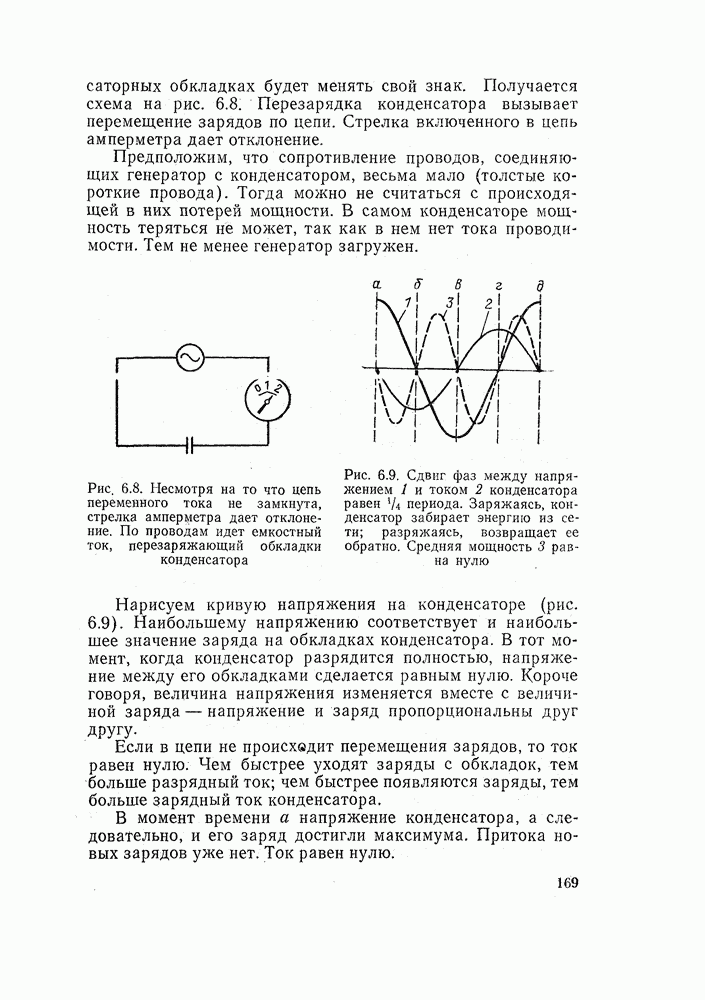
- 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ
- 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
- 6.7. РЕЗОНАНС ТОКОВ
- 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ
- ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК
- 7.1. ТРЕХФАЗНАЯ СИСТЕМА
- 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ
- 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС
- 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ
- 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА
- 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ
- ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ
- 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР
- 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ
- 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
- 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ
- 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ
- ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ
- 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ
- 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
- 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ
- 9.7. КЛЮЧИ
- 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ
- 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА
- 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН
- 10.2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА
- 10.3. КОЛЛЕКТОР
- 10.4. ЯКОРНЫЕ ОБМОТКИ
- 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА
- 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН
- 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ
- 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ
- ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ
- 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- 11.2. РАБОТА ТРАНСФОРМАТОРА
- 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА
- 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ
- 11.1. АВТОТРАНСФОРМАТОРЫ
- ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА
- 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.4. РАБОТА СИНХРОННЫХ МАШИН
- 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ
- 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
- 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ
- 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН
- ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ
- 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ
- 13.3. ЭЛЕКТРОМАГНИТЫ
- 13.4. КОНТАКТОРЫ
- 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
- 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ
- 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ
- 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ
- 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ
- 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ
- 14.4. СХЕМЫ ТОРМОЖЕНИЯ
- 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ
- 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ
- 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА
- 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ
- 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ
- 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА
- 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
- 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА
- 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА
- 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ
- 15.10. ЦИФРОВЫЕ ПРИБОРЫ
- 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ