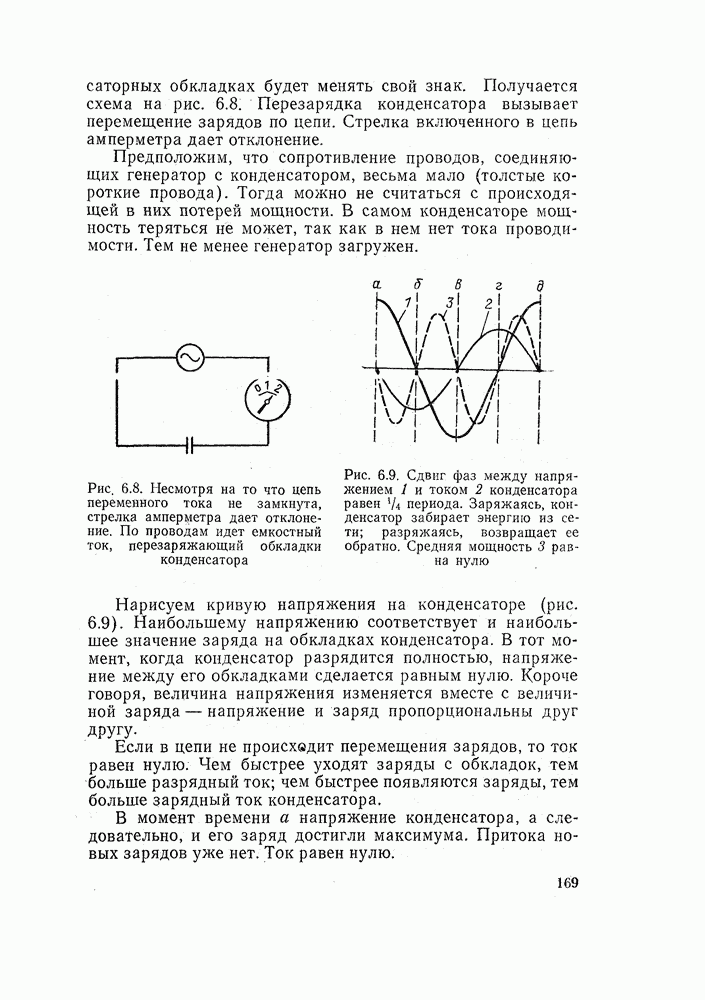
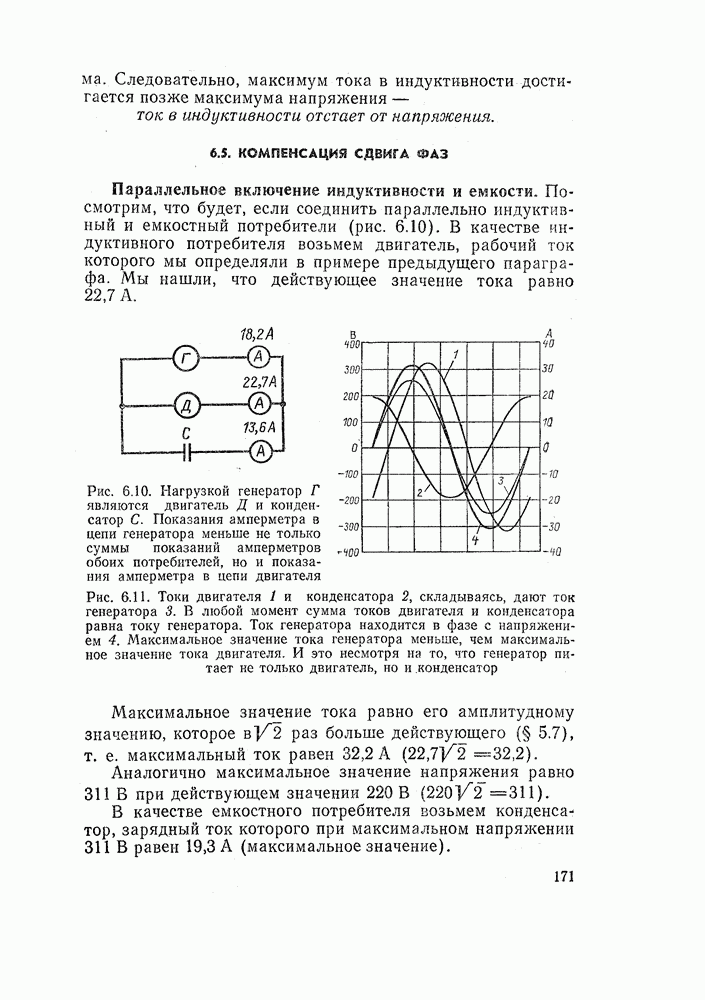
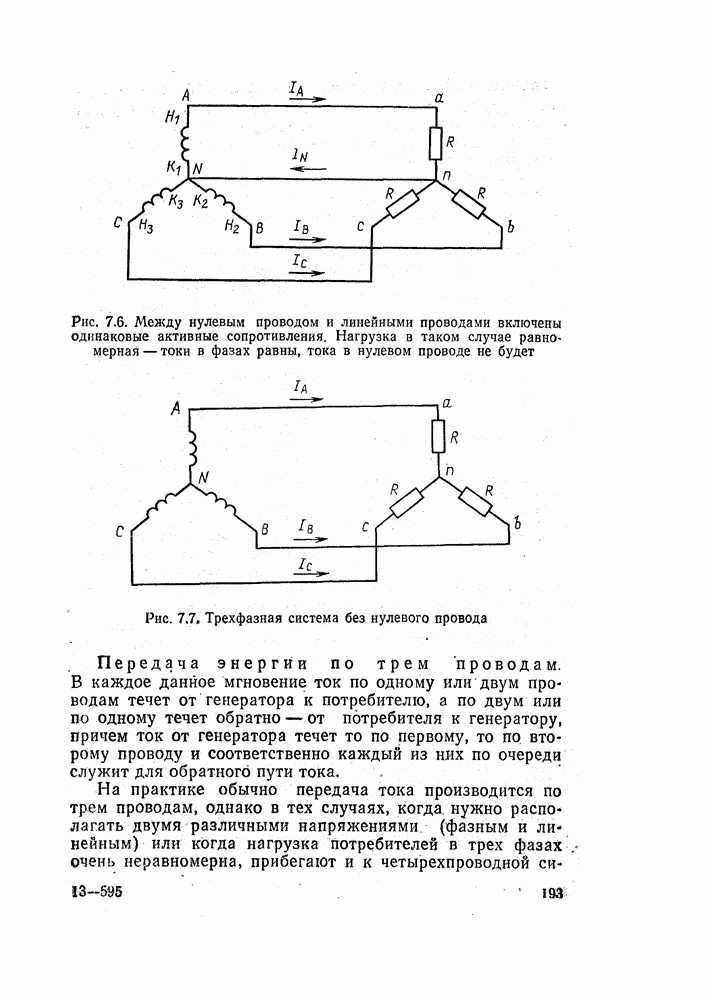
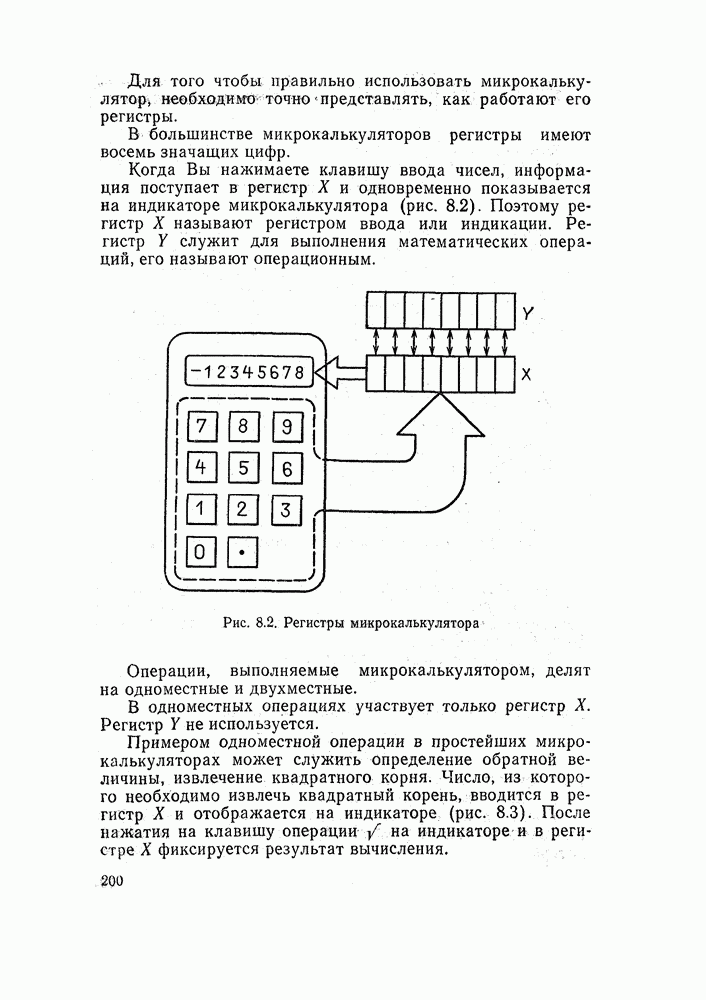
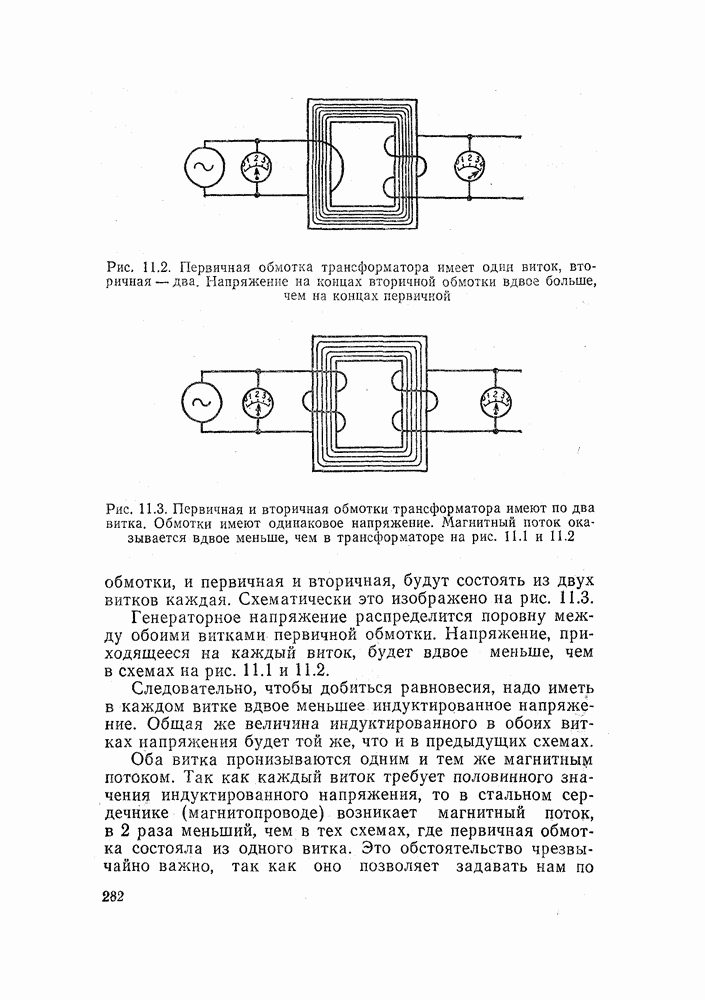
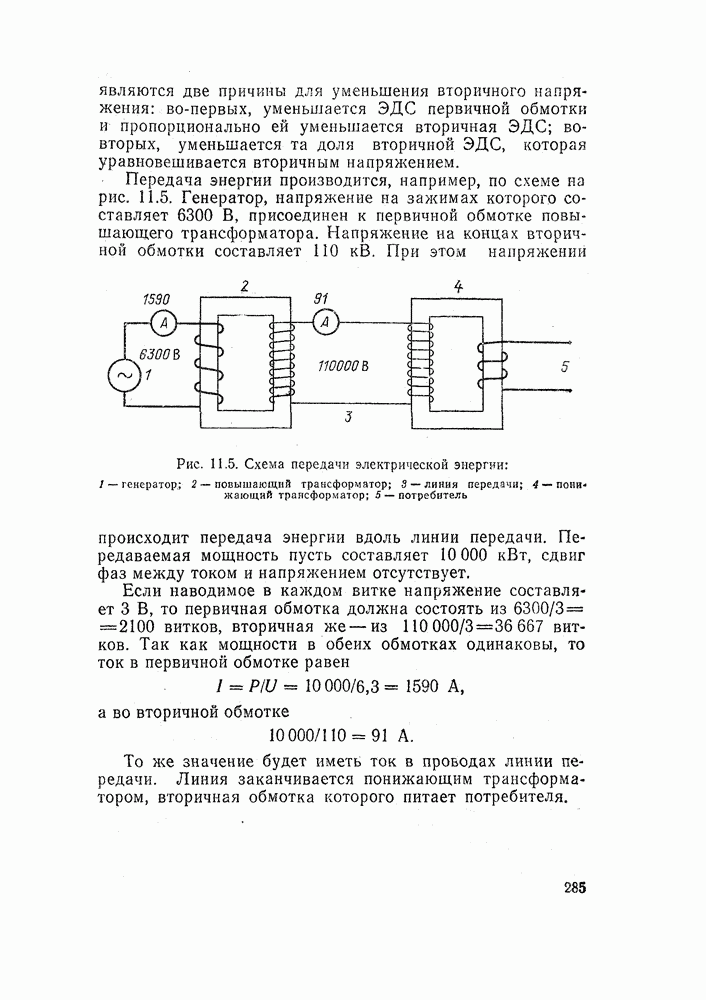
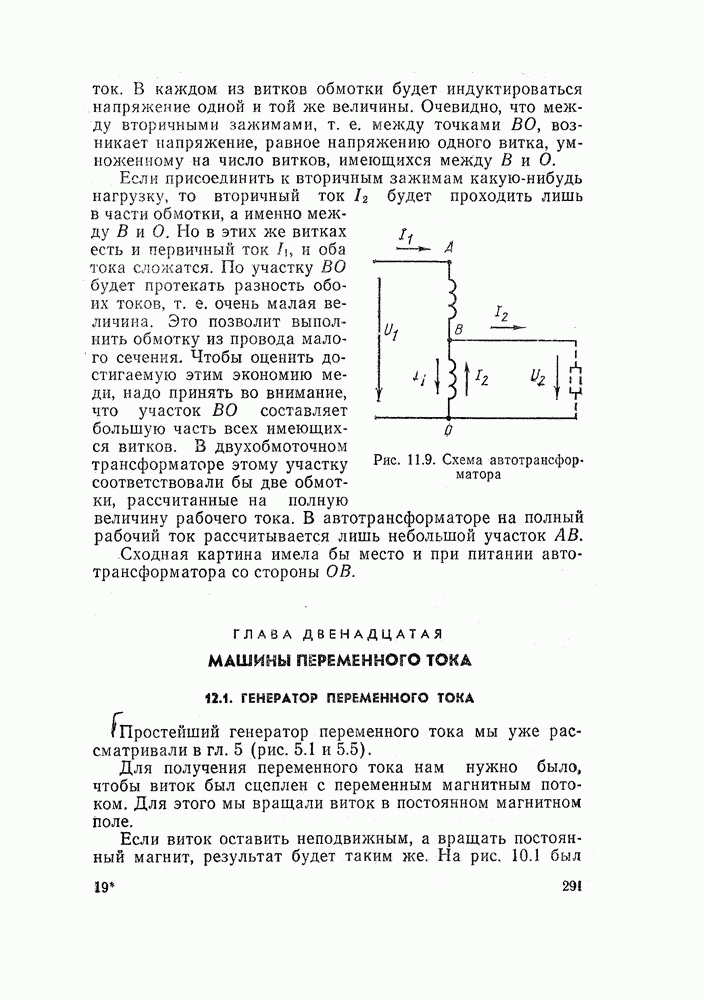
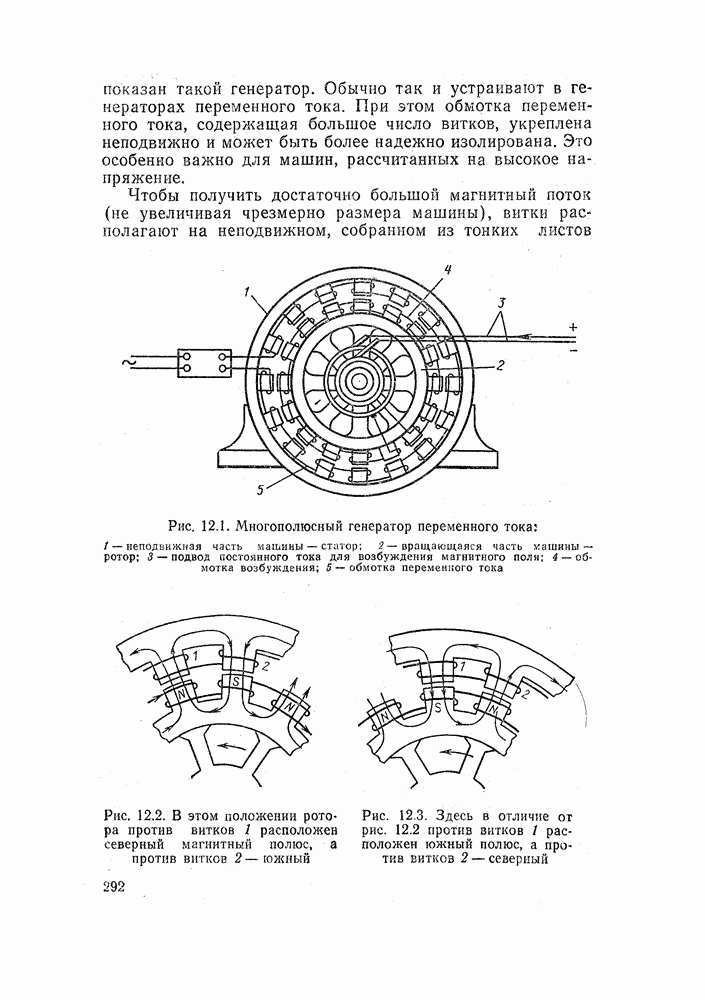
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.4. СИНУСОИДА
Чтобы получить исчерпывающее представление о повторяющемся каждый период или, как говорят, периодическом явлении, достаточно изучить его в промежутке времени, равном одному периоду. Так, например, зная, как изменяется продолжительность дня в течение какого-нибудь одного года, можно указать, чему равна продолжительность любого дня в любом году. Этой цели служат раз навсегда составленные таблицы, приводимые в календарях.
Подобные таблицы можно составить для периодических токов и ЭДС. Период разбивается на несколько частей, например на 24. Замеряется значение тока в начале периода, затем в момент времени, наступающий, например, через 1/24 часть периода.
Следующее измерение производится снова с промежутком времени 1/24 часть периода и т. д.
Наша задача облегчается тем обстоятельством, что действующий в СССР государственный стандарт предписывает заводам изготовлять генераторы с вполне определенным изменением ЭДС в течение периода. Изображающая эту ЭДС кривая может быть найдена простым построением.
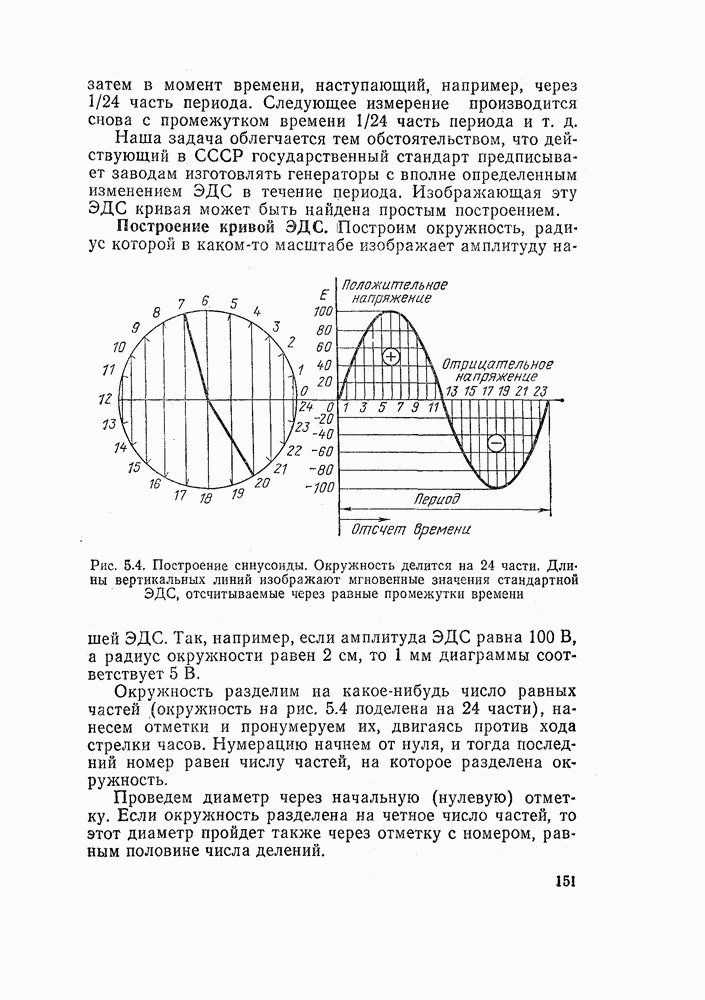
Построение кривой ЭДС. Построим окружность, радиус которой в каком-то масштабе изображает амплитуду нашей ЭДС.

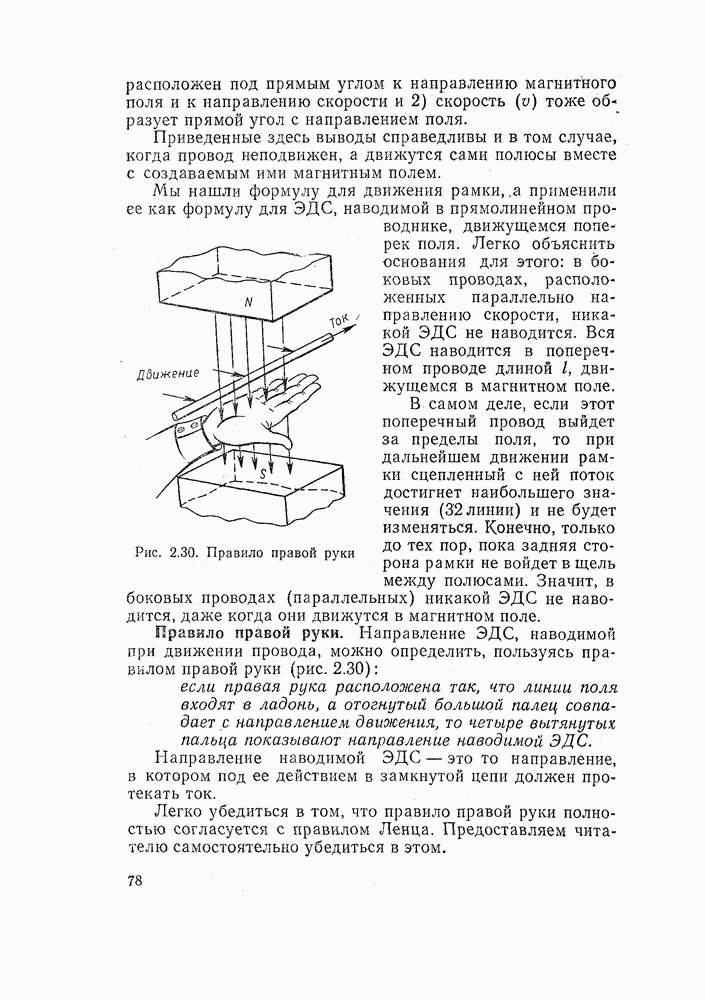
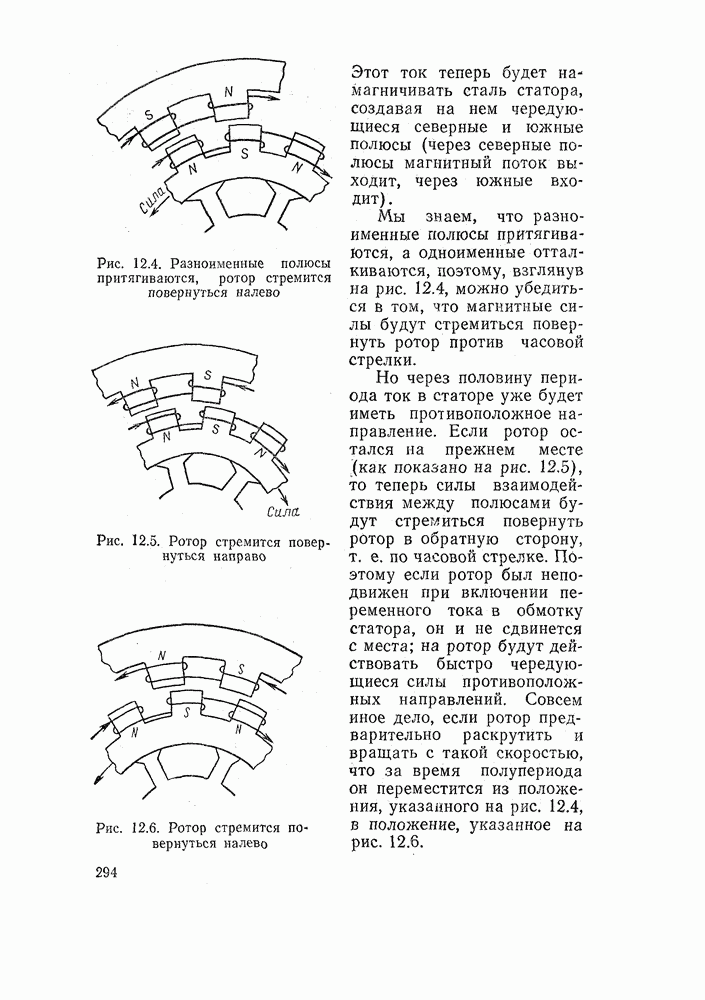
Рис. 5.4. Построение синусоиды. Окружность делится на 24 части. Длины вертикальных линий изображают мгновенные значения стандартной ЭДС, отсчитываемые через равные промежутки времени
Так, например, если амплитуда ЭДС равна 100 В, а радиус окружности равен 2 см, то 1 мм диаграммы соответствует 5 В.
Окружность разделим на какое-нибудь число равных частей (окружность на рис. 5.4 поделена на 24 части), нанесем отметки и пронумеруем их, двигаясь против хода стрелки часов. Нумерацию начнем от нуля, и тогда последний номер равен числу частей, на которое разделена окружность.
Проведем диаметр через начальную (нулевую) отметку. Если окружность разделена на четное число частей, то этот диаметр пройдет также через отметку с номером, равным половине числа делений.
На этот диаметр опускаем вертикальные линии перпендикуляры из каждой отметки. Исключение составят отметки, лежащие на диаметре. Мы скажем, что длина принадлежащих им вертикалей равна нулю.
Длины вертикалей изображают мгновенные значения ЭДС, отсчитываемые через равномерные промежутки времени. Если вертикаль расположена над диаметром, то величина ЭДС будет положительной. Вертикали, находящиеся под диаметром, соответствуют отрицательным значениям ЭДС. Длины вертикалей указаны в таблице. Знак для отметок, находящихся в левом столбце, — положительный, а в правом — отрицательный.

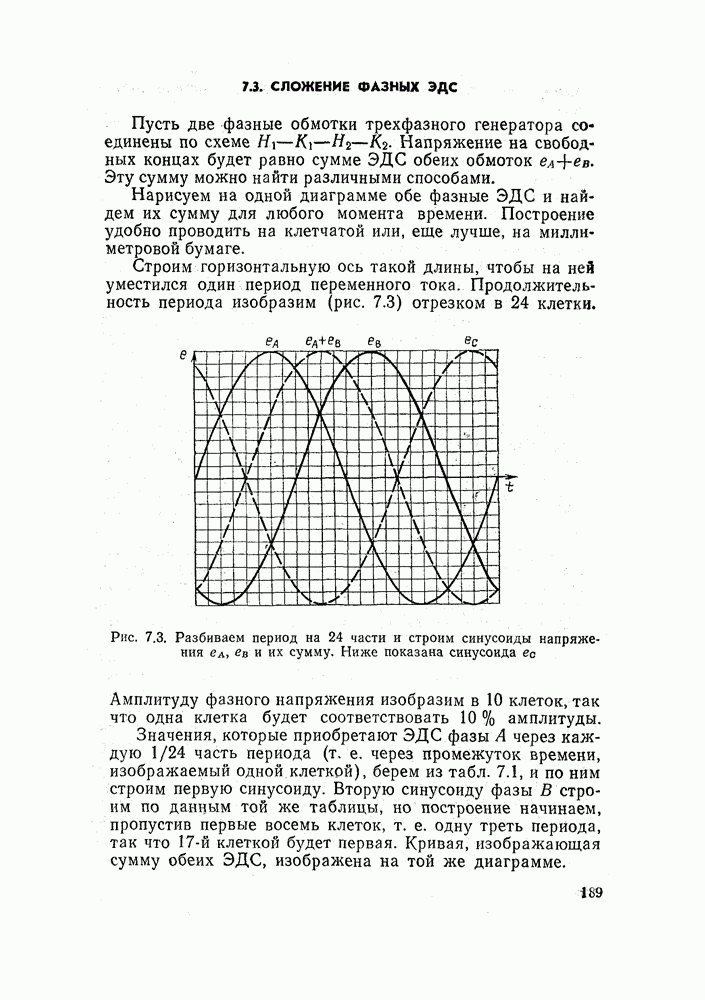
Выполним еще одно построение. Построим прямолинейный отрезок, длина которого будет изображать продолжительность периода. Разделим этот отрезок на такое же число равных частей, на которое мы делили окружность. В нашем примере каждому из делений будет соответствовать 1/24 часть периода. К этой прямой пристраиваем вертикали, беря их длину из таблицы или перенося их с диаграммы на рис. 5.4. При этом соблюдаем такое правило: положительные вертикали откладываем вверх, отрицательные вниз. Свободные концы вертикальных линий соединяем плавной линией (рис. 5.4). Полученная кривая называется синусоидой. Она играет исключительно важную роль в электротехнике.
Синусоида изображает последовательные значения, принимаемые стандартной ЭДС. По тому же закону изменяются и токи в цепях, где действует синусоидальная ЭДС.
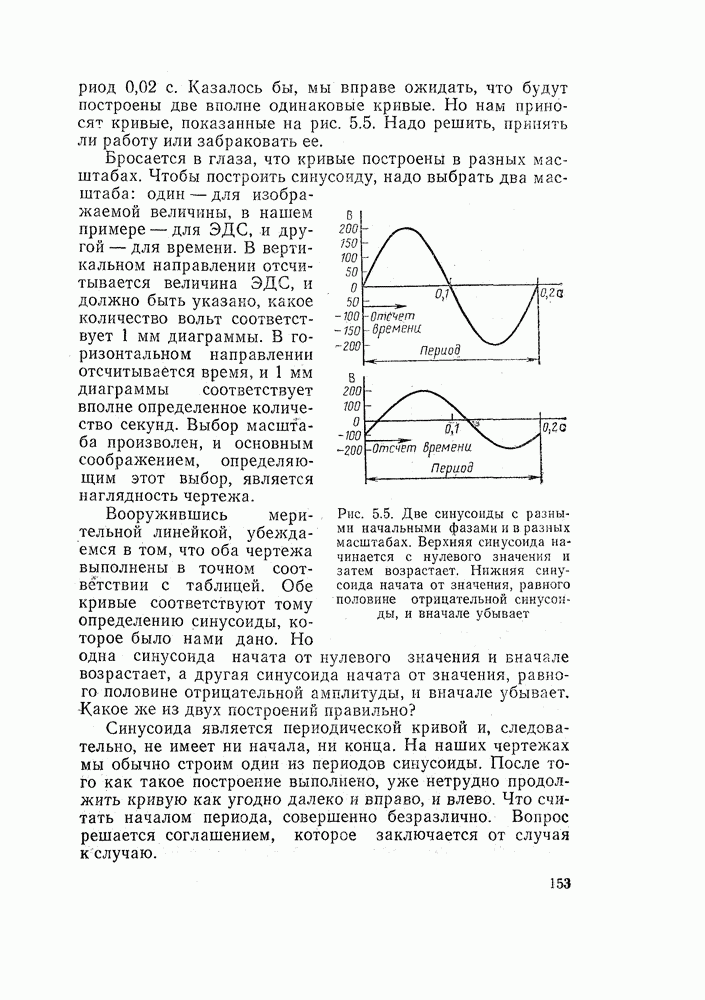
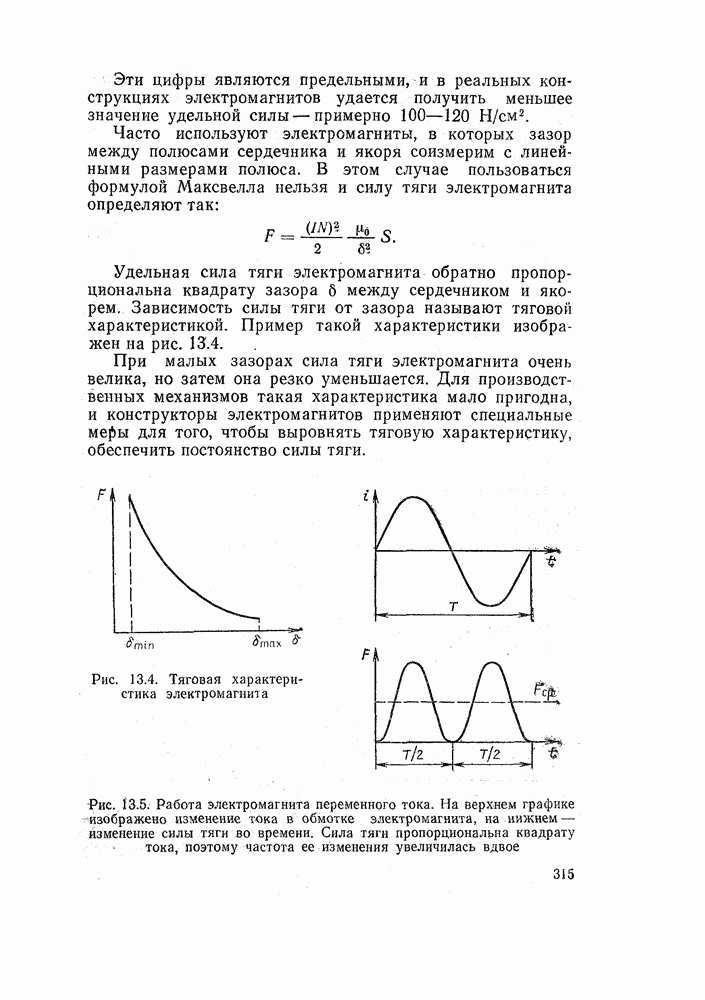
Две синусоиды с разными начальными фазами. Двое получили от нас одинаковое задание: построить кривую синусоидальной ЭДС, амплитуда которой равна 200 В, а период 0,02 с.
Казалось бы, мы вправе ожидать, что будут построены две вполне одинаковые кривые. Но нам приносят кривые, показанные на рис. 5.5. Надо решить, принять ли работу или забраковать ее.
Бросается в глаза, что кривые построены в разных масштабах. Чтобы построить синусоиду, надо выбрать два масштаба: один — для изображаемой величины, в нашем примере — для ЭДС, и другой — для времени. В вертикальном направлении отсчитывается величина ЭДС, и должно быть указано, какое количество вольт соответствует 1 мм диаграммы. В горизонтальном направлении отсчитывается время, и 1 мм диаграммы соответствует вполне определенное количество секунд. Выбор масштаба произволен, и основным соображением, определяющим этот выбор, является наглядность чертежа.

Рис. 5.5. Две синусоиды с разными начальными фазами и в разных масштабах. Верхняя синусоида начинается с нулевого значения и затем возрастает. Нижняя синусоида начата от значения, равного половине отрицательной синусоиды, и вначале убывает
Вооружившись мерительной линейкой, убеждаемся в том, что оба чертежа выполнены в точном соответствии с таблицей. Обе кривые соответствуют тому определению синусоиды, которое было нами дано. Но одна синусоида начата от нулевого значения и вначале возрастает, а другая синусоида начата от значения, равного половине отрицательной амплитуды, и вначале убывает. Какое же из двух построений правильно?
Синусоида является периодической кривой и, следовательно, не имеет ни начала, ни конца. На наших чертежах мы обычно строим один из периодов синусоиды. После того как такое построение выполнено, уже нетрудно продолжить кривую как угодно далеко и вправо, и влево. Что считать началом периода, совершенно безразлично. Вопрос решается соглашением, которое заключается от случая к случаю.
Подытоживая наши рассуждения, мы можем сделать заключение, что обе кривые на рис. 5.5 построены в точном соответствии с заданием.
Синусоида характеризуется тремя величинами. Чтобы полностью описать периодическое явление, протекающее по синусоидальному закону, мы должны указать амплитуду, период и то значение синусоиды, которое мы хотим считать ее началом. На последнем признаке синусоиды надо остановиться подробнее.
Допустим, мы хотим считать началом периода тот момент, когда синусоида принимает значение, равное одной трети своей амплитуды. Такое определение было бы недостаточным указанное значение наступает четырежды на протяжении одного периода. Удобнее пользоваться понятием начальной фазы. Для этого надо вернуться к рис. 5.4.
Соединим какую-нибудь из отметок, сделанных нами на окружности, с ее центром. На рис. 5.4 такое построение выполнено для отметок 7 и 20. Радиус, принадлежащий отметке 0, назовем начальным. Полуокружности соответствует угол 180°. Так как полуокружность разделена на 12 частей, то при переходе от отметки к отметке угол изменяется на 15°. Поэтому мы припишем отметке 7 угол, равный  . Отметке 20 можно приписать угол
. Отметке 20 можно приписать угол  и это будет совершенно правильно. Однако удобнее не вводить в расчет углов, больших 180°. Мы припишем отметке 20 отрицательный угол, равный
и это будет совершенно правильно. Однако удобнее не вводить в расчет углов, больших 180°. Мы припишем отметке 20 отрицательный угол, равный  Полезно запомнить, что углы, отсчитываемые в направлении хода часовой стрелки, считаются отрицательными.
Полезно запомнить, что углы, отсчитываемые в направлении хода часовой стрелки, считаются отрицательными.
Итак, для исчерпывающего определения синусоиды достаточно указать ее амплитуду, период и начальную фазу. Рекомендуем читателю самостоятельно построить две-три синусоиды с разными начальными фазами.
Необходимость определения начальной фазы. Необходимость определения начальной фазы легко вытекает из следующего простого примера.
Представьте себе два последовательно включенных генератора, частоты и амплитуды ЭДС которых одинаковы. Спрашивается: можно ли заранее определить, какое суммарное напряжение будет в каждый момент времени?
Очевидно, что нельзя.
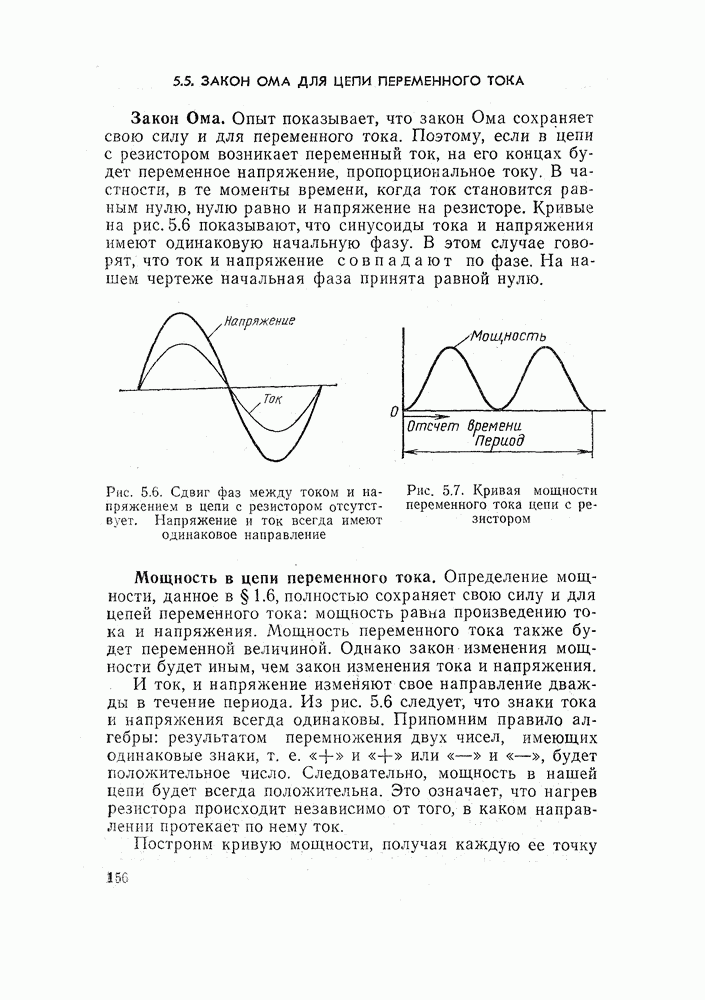
Согласное включение двух генераторов. Если генераторы имеют одинаковую начальную фазу, то кривые напряжения (синусоиды в данном случае) для каждого генератора, изображенные на одном и том же чертеже и в одинаковом масштабе, совпадут.
Следовательно, общее (суммарное) напряжение обоих генераторов будет всегда вдвое больше напряжения каждого генератора в отдельности.
Обычно такое включение генераторов называют согласным.
Встречное включение двух генераторов. Предположим, что один генератор имеет начальную фазу, равную нулю, а другой — равную 180°, т. е. величина напряжения первого генератора в любой момент времени имеет то же значение, что и величина напряжения второго генератора, однако знаки напряжений («+» или «-») не будут совпадать.
В момент времени, когда - напряжение первого генератора положительно, напряжение второго генератора отрицательно, и наоборот.
Учитывая, что напряжения складываются алгебраически, приходим к выводу, что результирующее напряжение в каждый момент времени равно нулю,
Заметим, что если фазы генераторов отличаются на 180°, то иногда говорят, что генераторы работают в противофазе или соединены встречно.
Читателю предлагается самому построить результирующую кривую напряжения генераторов, имеющих одинаковые частоту и амплитуду, а начальные фазы равными соответственно:

Сдвиг фазы. Очевидно, что две синусоиды, имеющие разные начальные фазы, как бы сдвинуты одна относительно другой по горизонтали. Поэтому разность начальных фаз двух синусоид и называют обычно сдвигом фазы.
Сложение двух синусоид дает опять синусоиду. Непосредственным построением суммарных кривых для любых двух синусоид, в том числе и с разными амплитудами, можно убедиться, что полученная кривая имеет опять-таки форму синусоиды, у которой может оказаться измененной начальная фаза или амплитуда, или то и другое вместе.
Таким образом,
сумма двух синусоид также является синусоидой.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ
- 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА
- 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА
- 1.6. МОЩНОСТЬ
- 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА
- 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ
- 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ
- 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ
- 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА
- 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ
- 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА
- 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ
- 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ
- 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ
- 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ
- 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ
- 1.20. ЗАКОНЫ КИРХГОФА
- ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ
- 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ
- 2.4. МАГНИТНАЯ ИНДУКЦИЯ
- 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ
- 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ
- 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ
- 2.9. ПРАВИЛО ЛЕНЦА
- 2.10. МАГНИТНЫЙ ПОТОК
- 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
- 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ
- 2.13. ВЗАИМНАЯ ИНДУКДИЯ
- 2.14. САМОИНДУКЦИЯ
- 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ
- 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА
- 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА
- 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
- 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ
- 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ
- 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ
- 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ
- 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ
- 3.9. НАМАГНИЧЕННОСТЬ
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ
- 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА)
- 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ)
- 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
- 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ
- ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК
- 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК?
- 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 5.4. СИНУСОИДА
- 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ
- 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ
- 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ
- 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
- 6.7. РЕЗОНАНС ТОКОВ
- 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ
- ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК
- 7.1. ТРЕХФАЗНАЯ СИСТЕМА
- 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ
- 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС
- 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ
- 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА
- 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ
- ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ
- 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР
- 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ
- 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
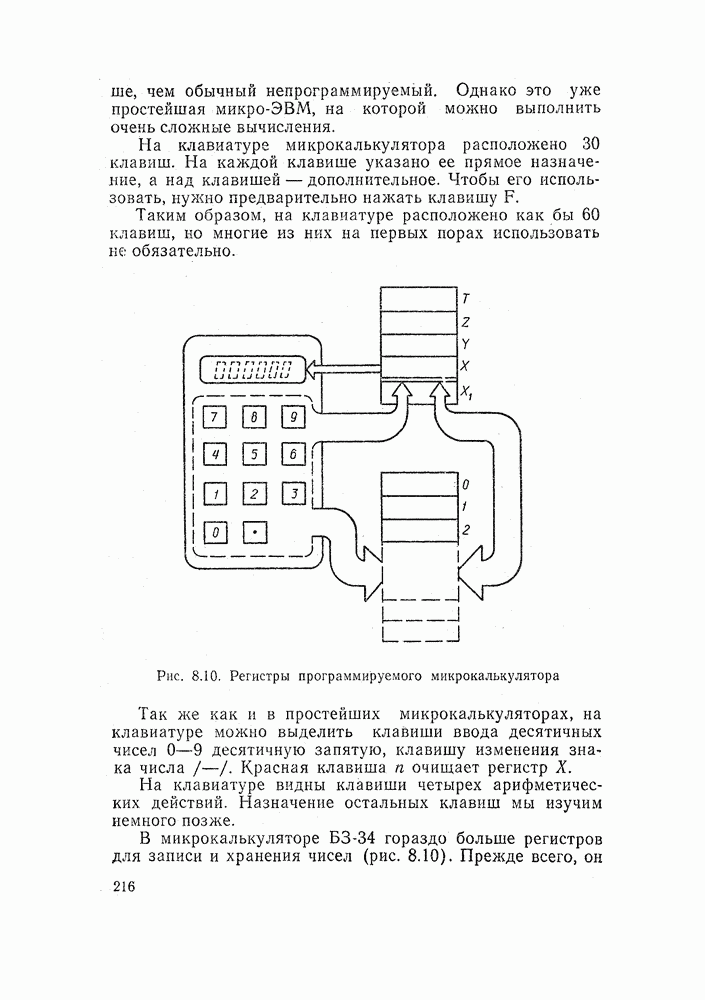
- 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ
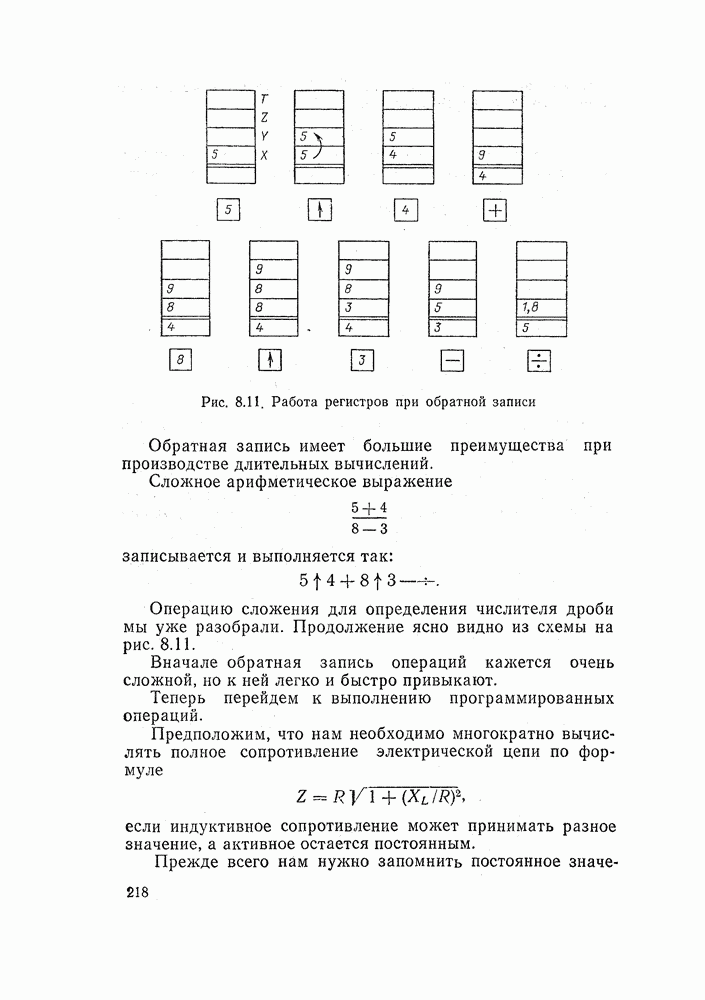
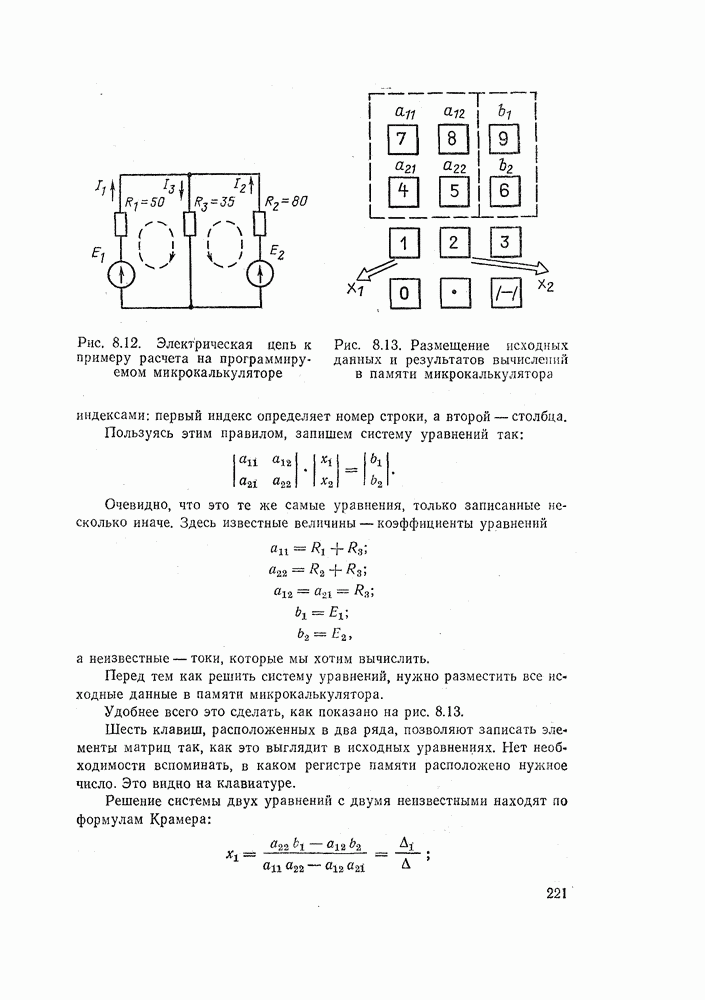
- 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ
- ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
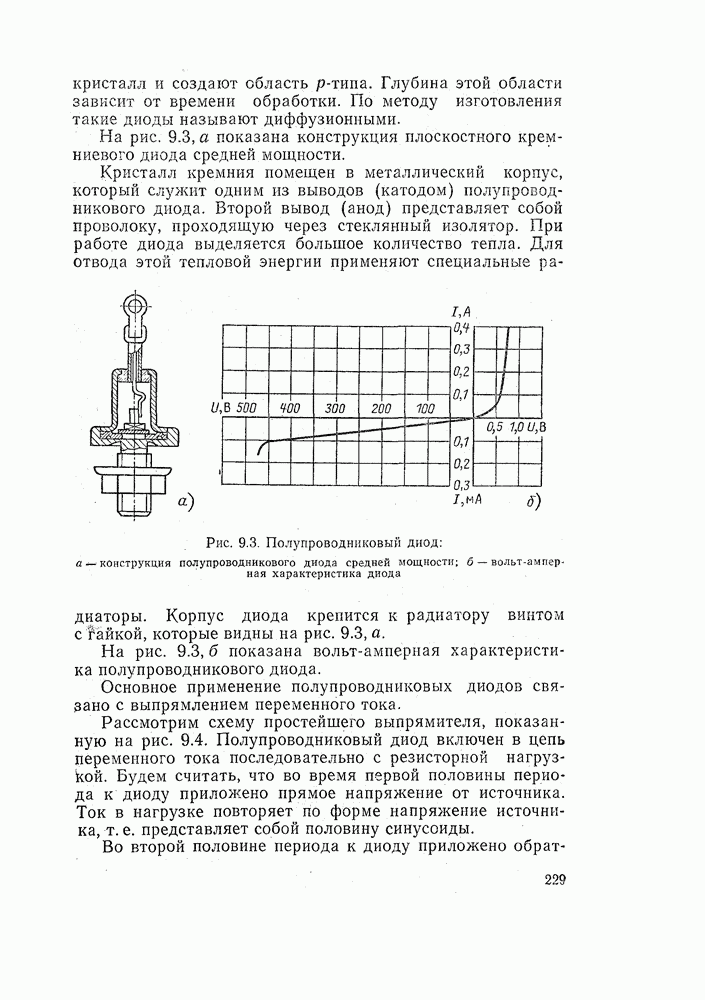
- 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ
- 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ
- 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
- 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ
- 9.7. КЛЮЧИ
- 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ
- 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА
- 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН
- 10.2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА
- 10.3. КОЛЛЕКТОР
- 10.4. ЯКОРНЫЕ ОБМОТКИ
- 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА
- 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН
- 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ
- 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ
- ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ
- 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- 11.2. РАБОТА ТРАНСФОРМАТОРА
- 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА
- 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ
- 11.1. АВТОТРАНСФОРМАТОРЫ
- ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА
- 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.4. РАБОТА СИНХРОННЫХ МАШИН
- 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ
- 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
- 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ
- 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН
- ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ
- 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ
- 13.3. ЭЛЕКТРОМАГНИТЫ
- 13.4. КОНТАКТОРЫ
- 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
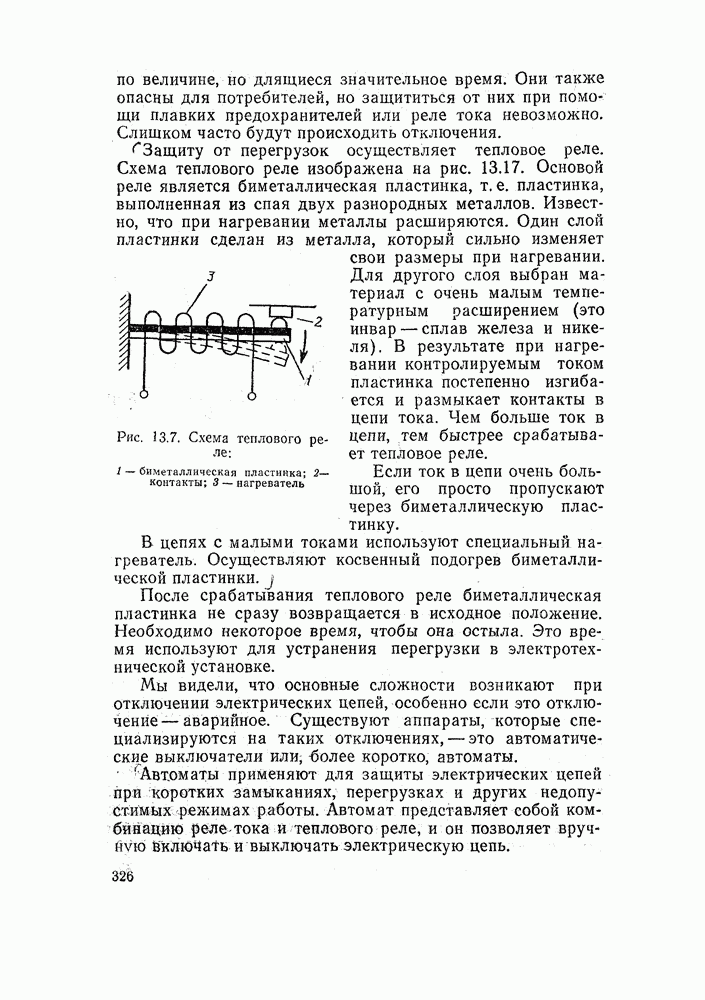
- 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ
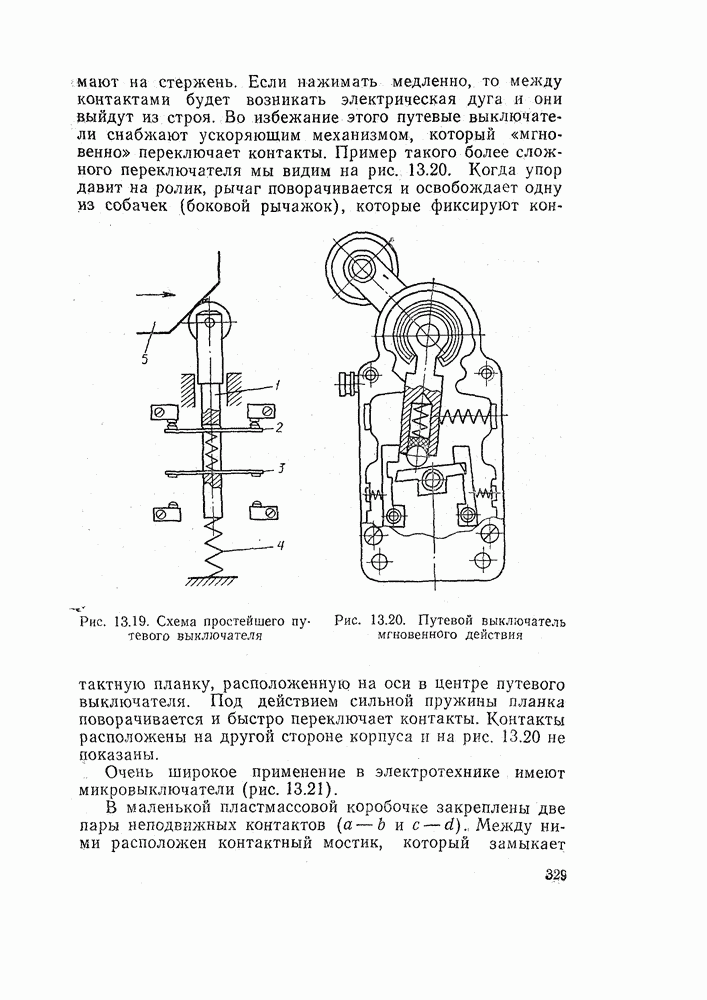
- 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ
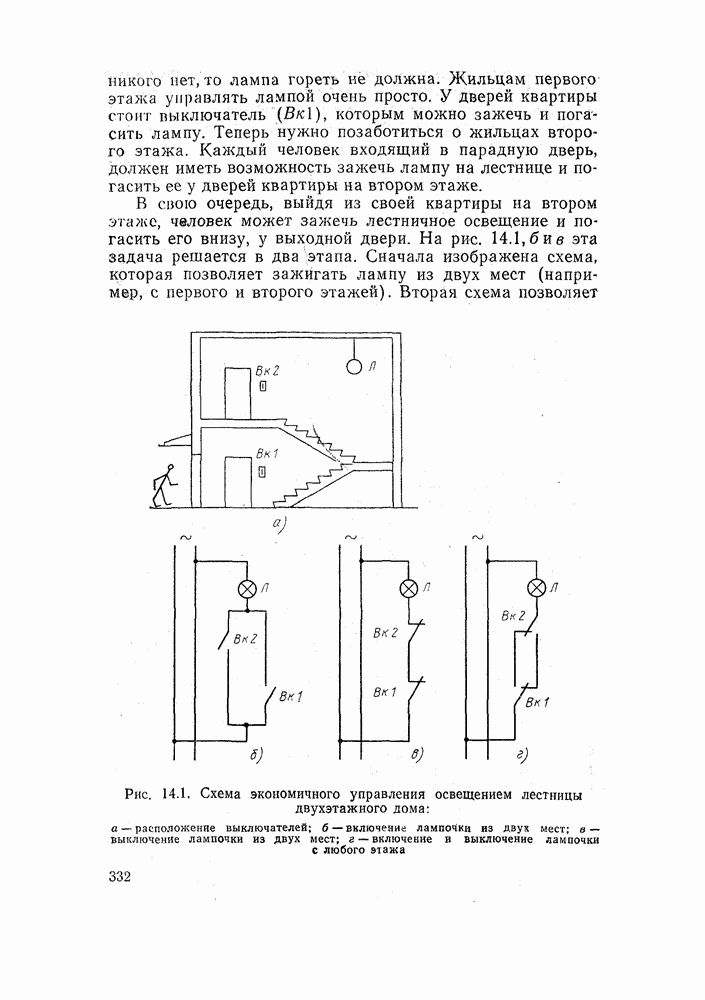
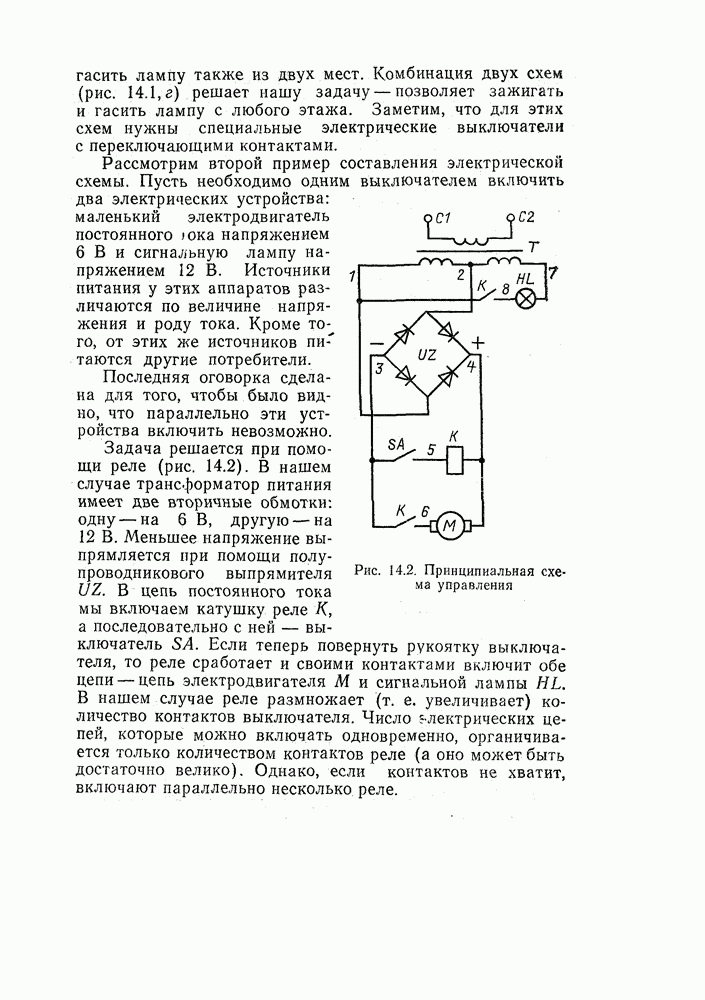
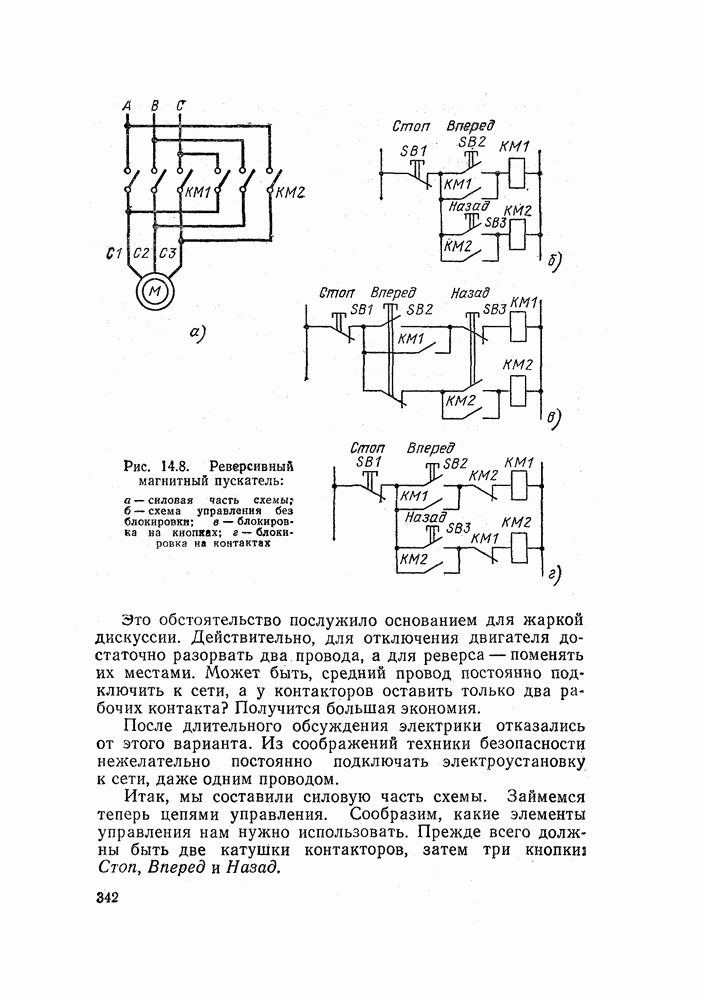
- 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ
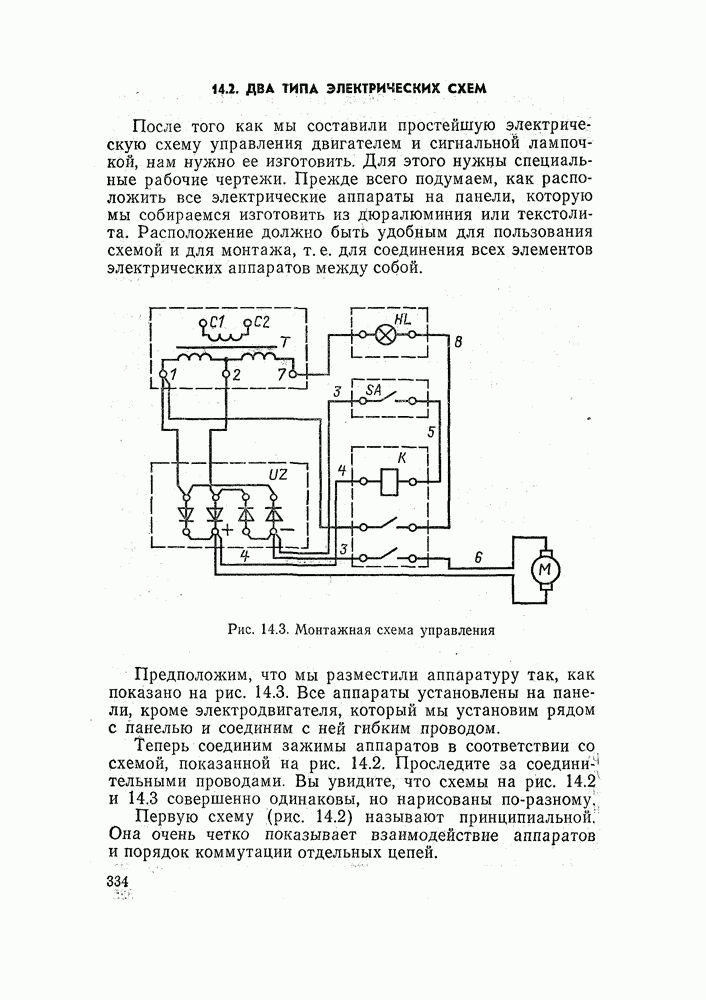
- 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ
- 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ
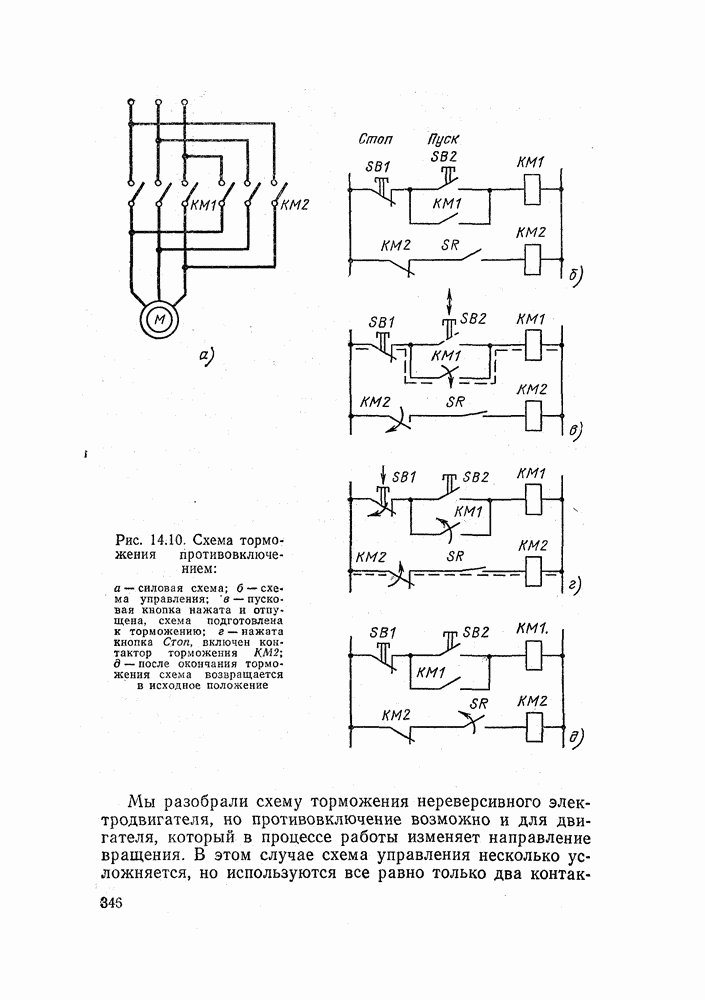
- 14.4. СХЕМЫ ТОРМОЖЕНИЯ
- 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
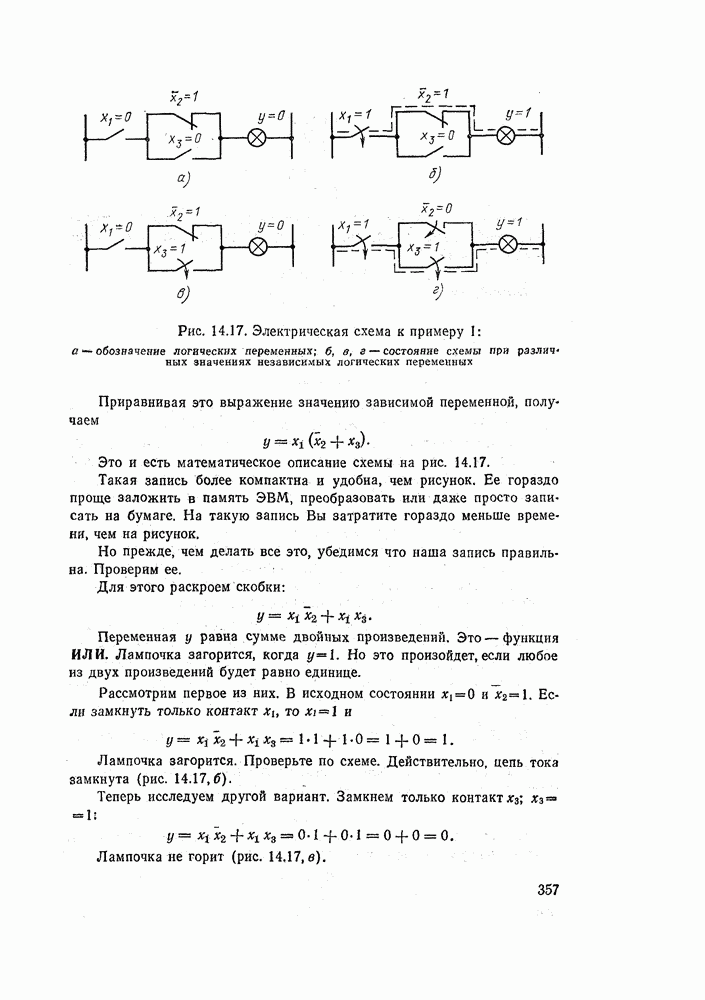
- 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ
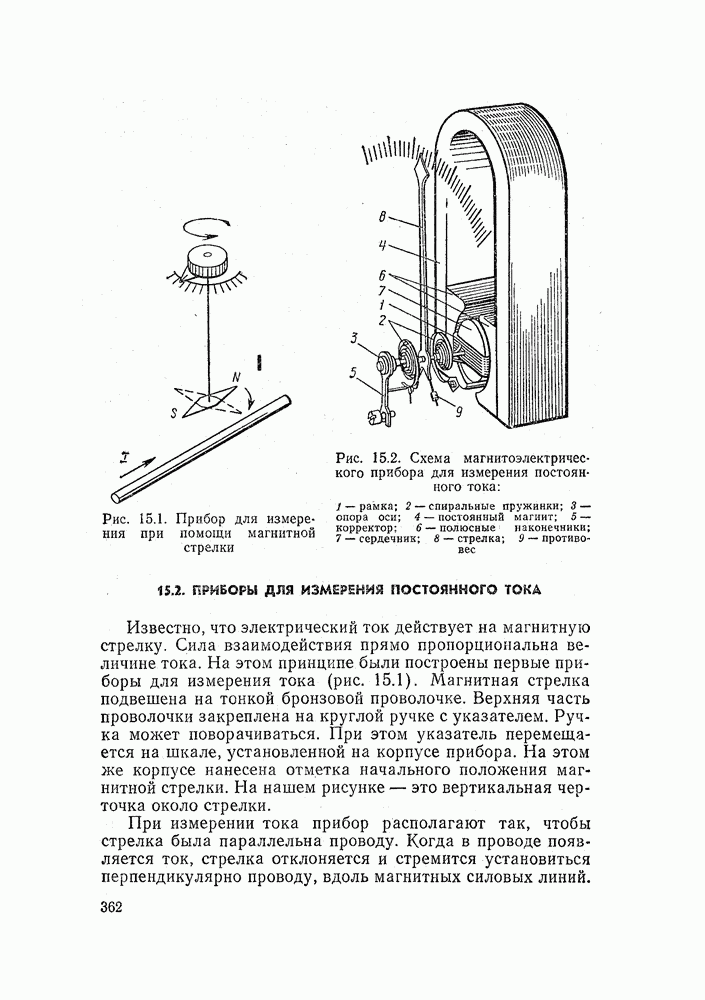
- 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ
- 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА
- 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ
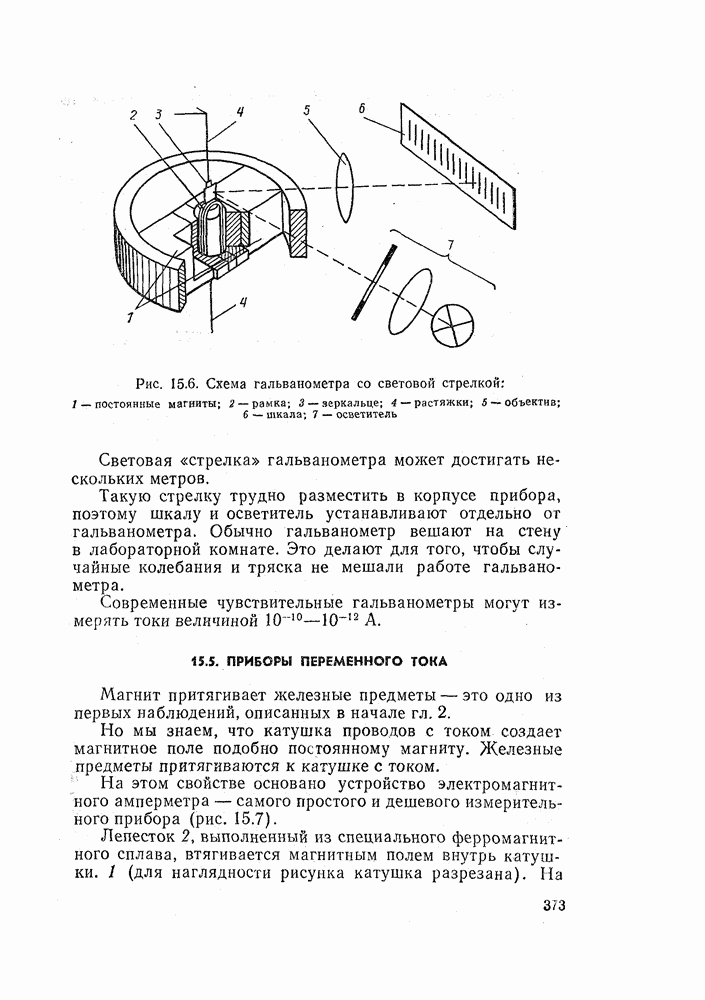
- 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ
- 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА
- 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
- 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА
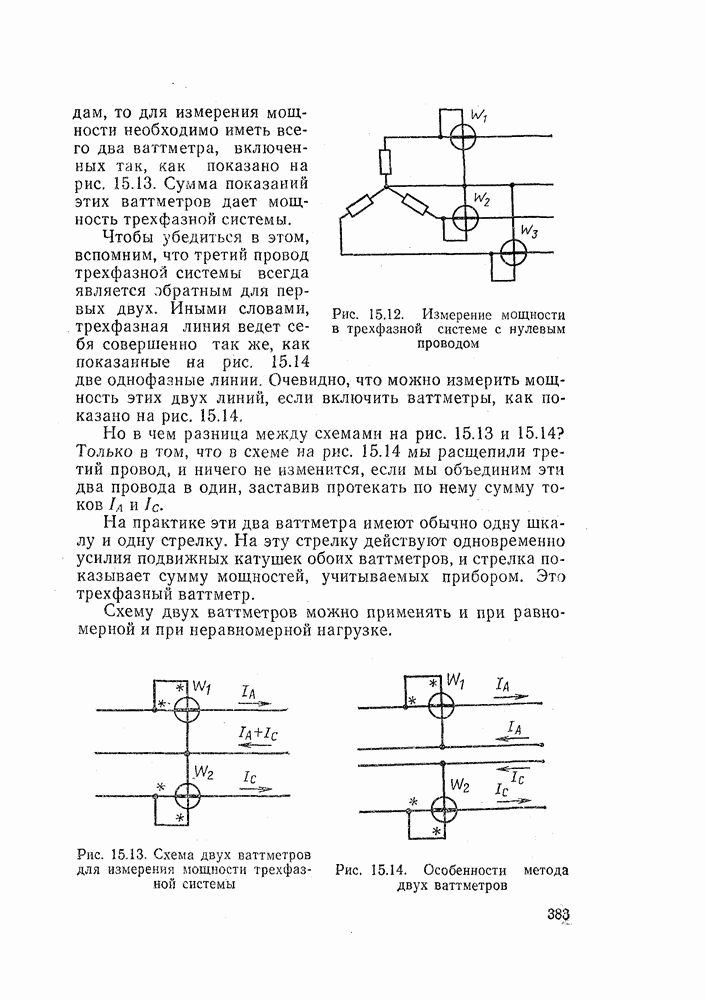
- 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА
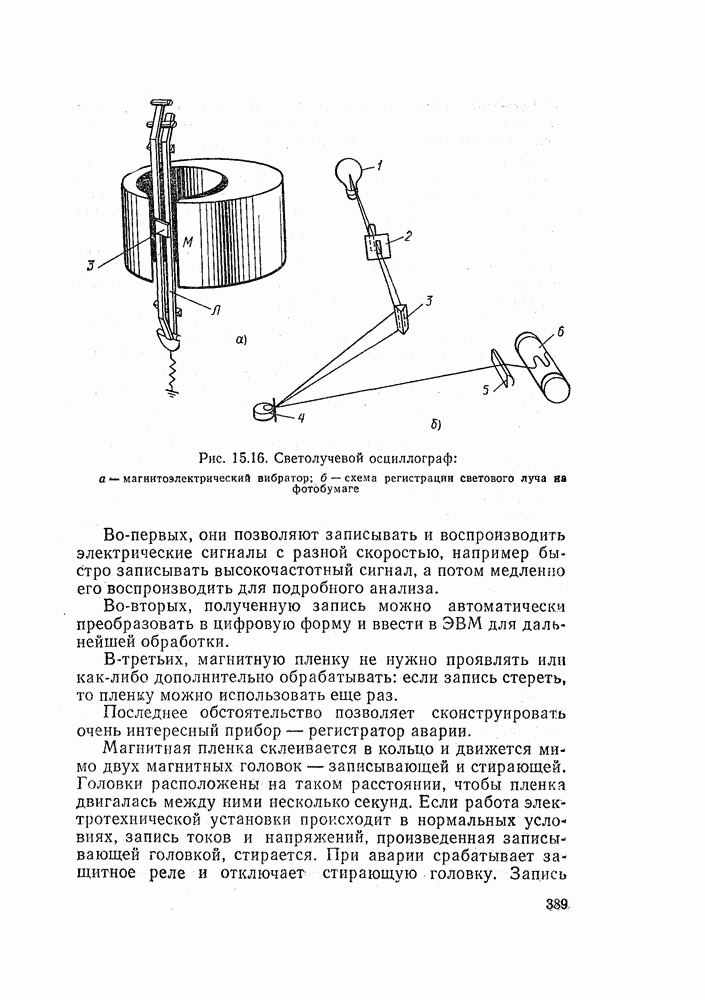
- 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ
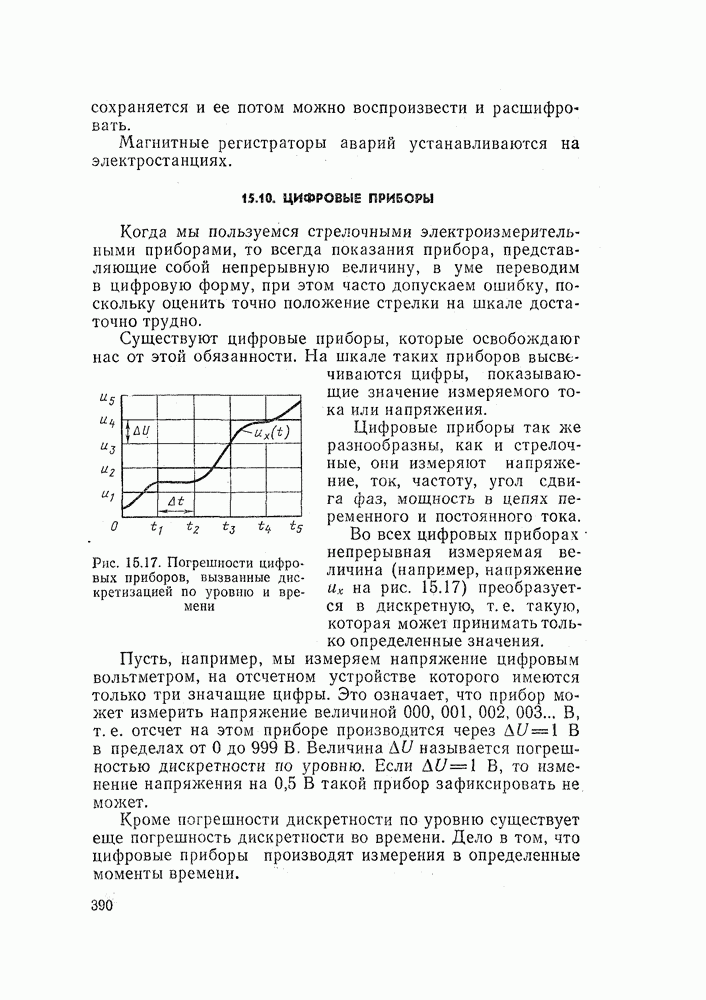
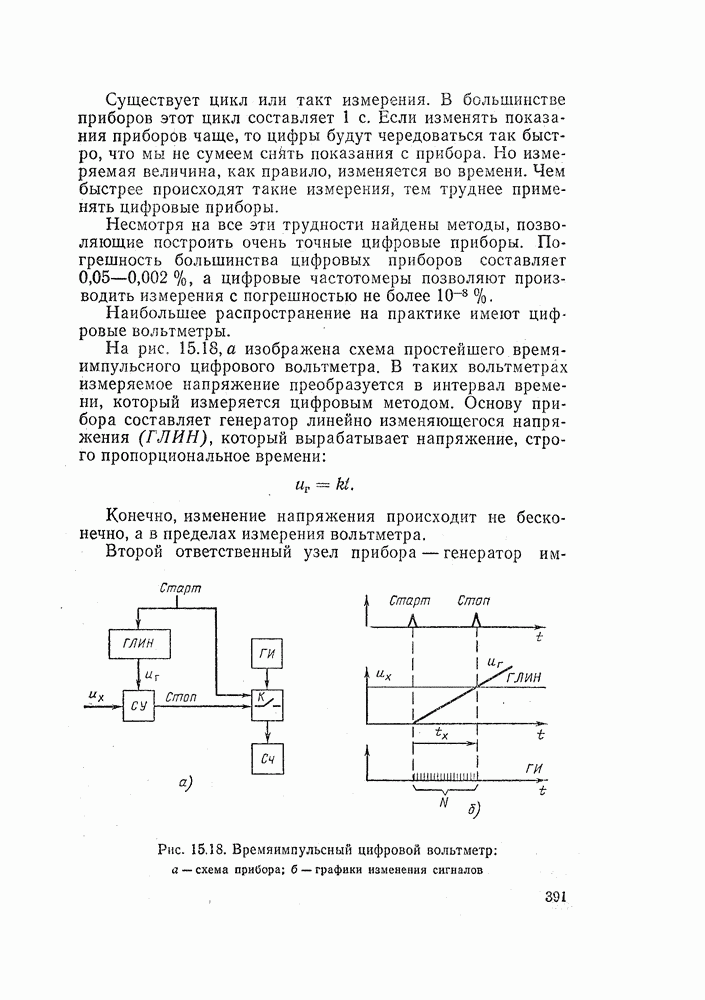
- 15.10. ЦИФРОВЫЕ ПРИБОРЫ
- 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ