| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ
Пусть две ветви электрической цепи включены параллельно, как показано на рис. 1.21. Ток в каждой из них можно найти по закону Ома, если известны их сопротивления и напряжение, к которому они подключены. Что касается общего тока, т. е. тока  неразветвленном участке цепи, то он равен сумме токов.
неразветвленном участке цепи, то он равен сумме токов.
Значит, общий ток можно вычислить так:

Обращаем внимание на то, что напряжение U для обеих ветвей (при параллельном соединении) одинаково.
Подобным же способом можно вычислить общий ток и в том случае, когда имеется не две, а три или большее число параллельных ветвей.

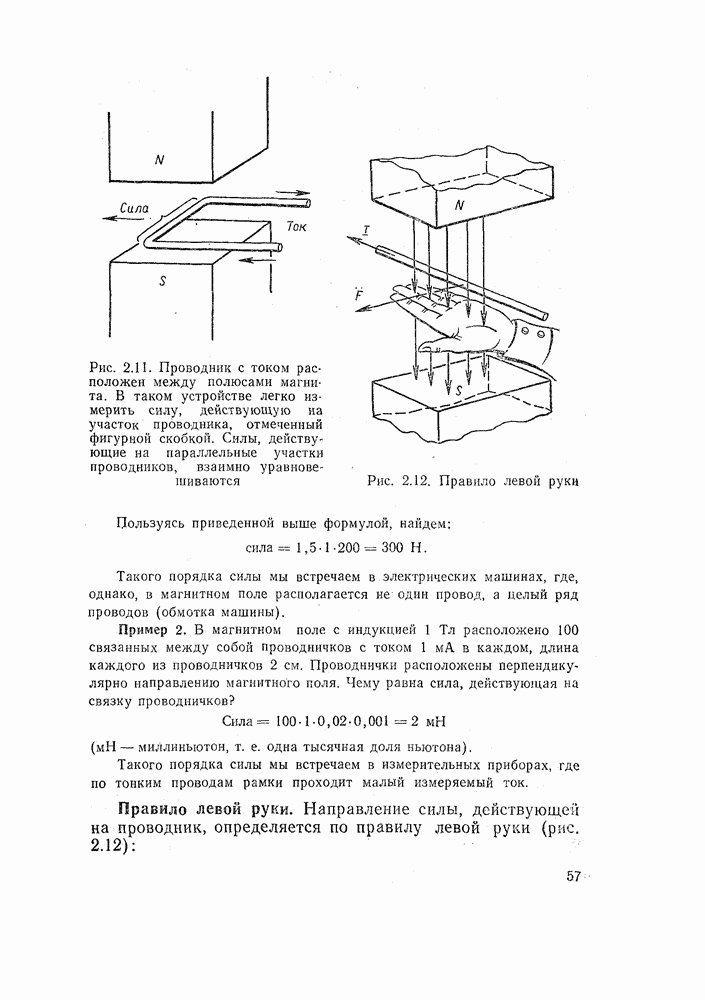
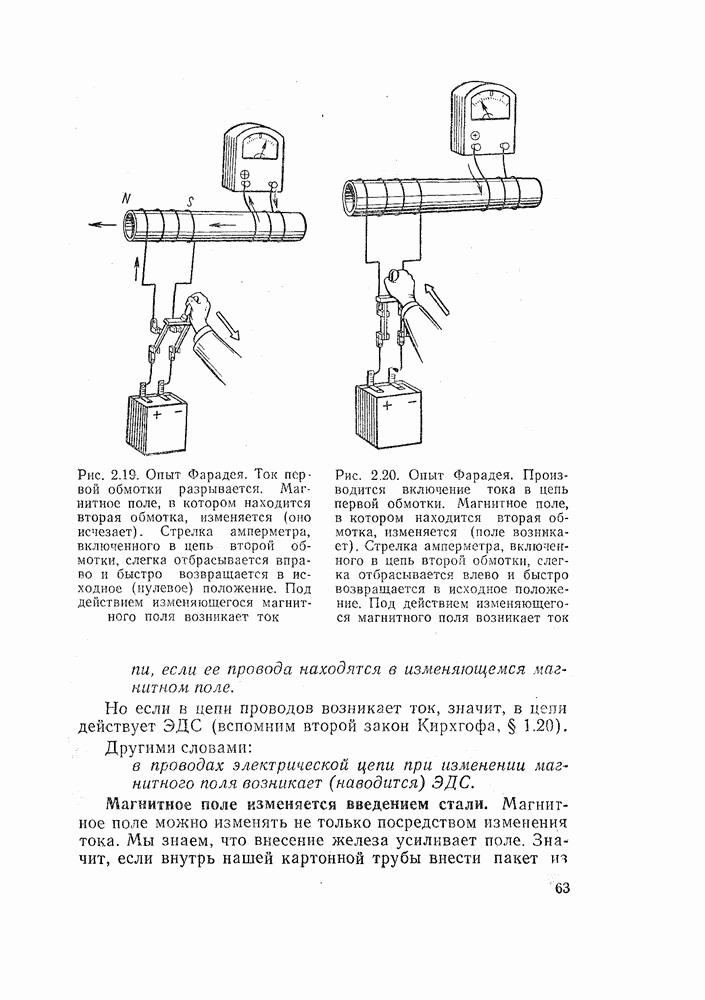
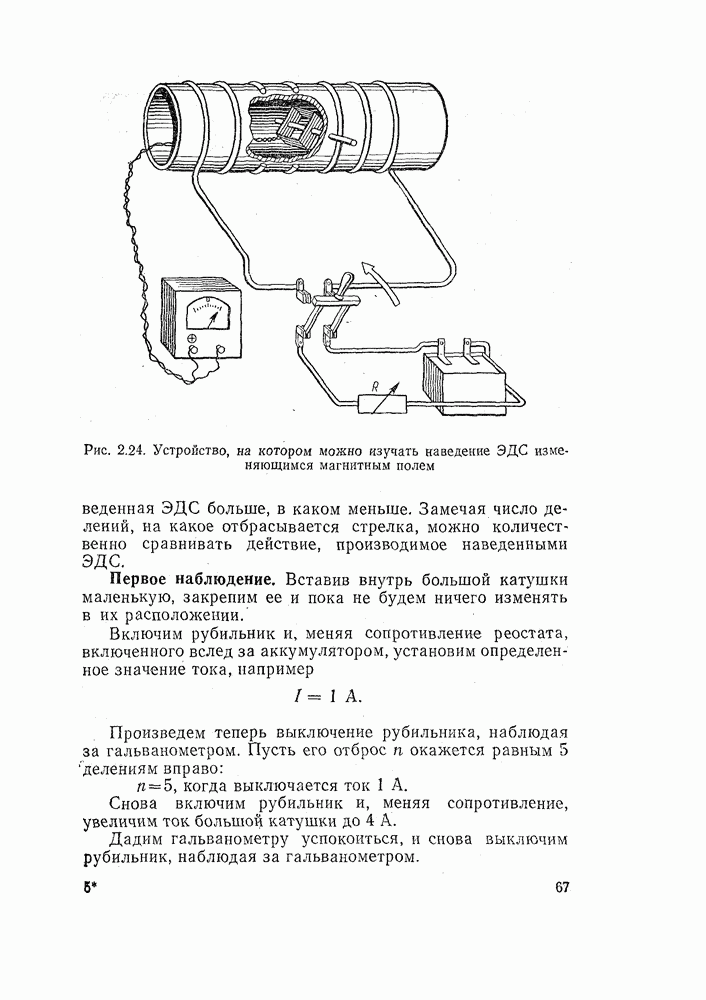
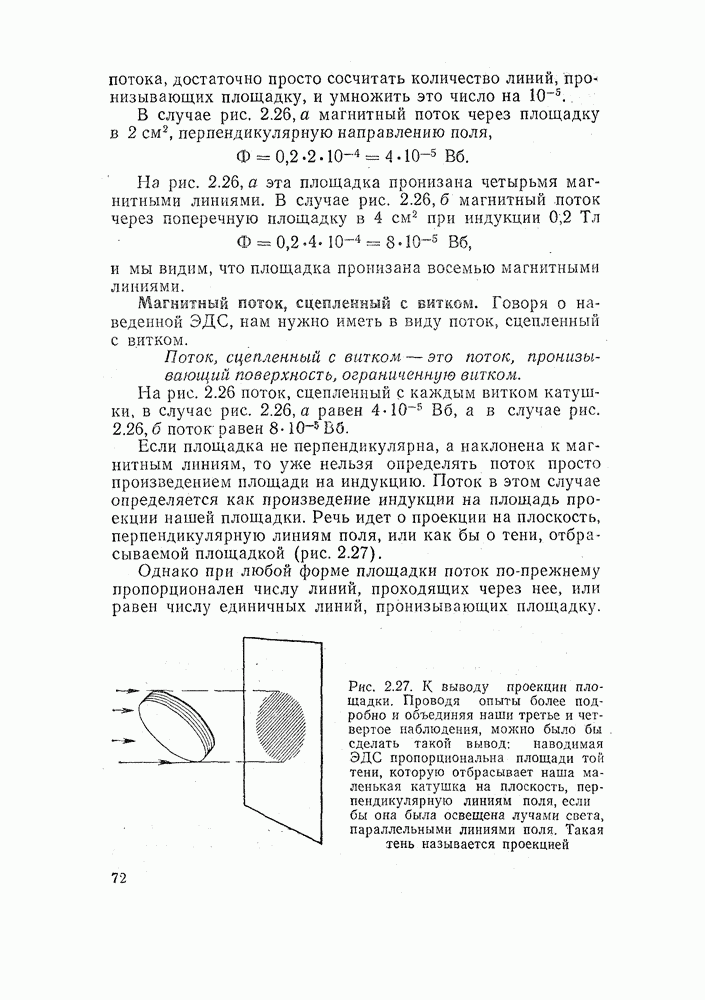
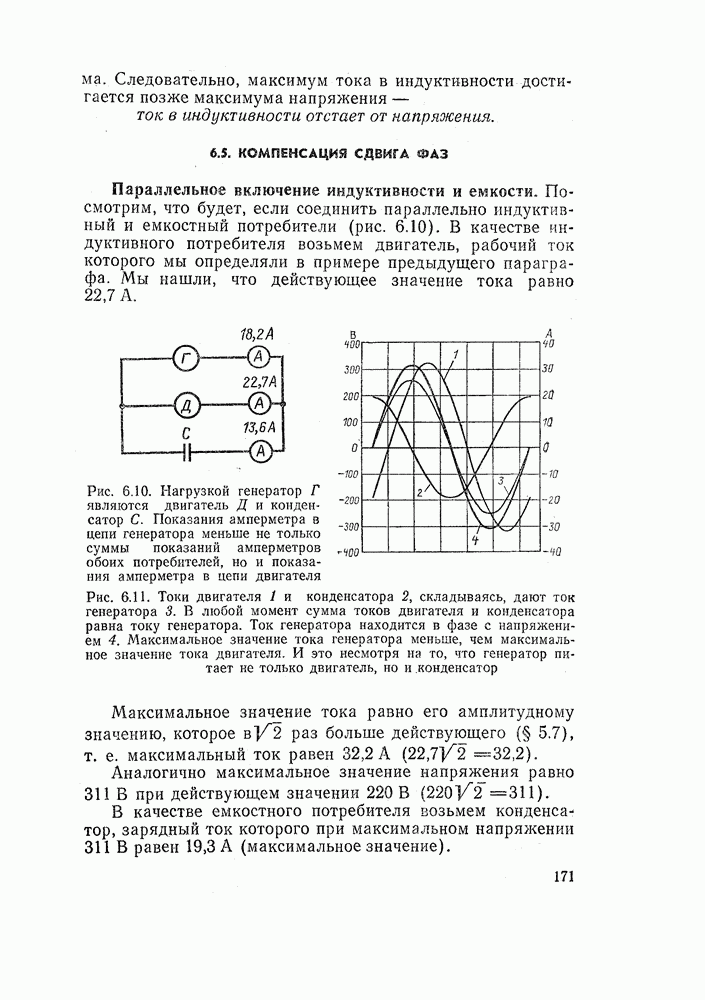
Рис. 1.21. Два параллельно включенных резистора. В неразветвленном участке цепи ток равен сумме токов в параллельных ветвях
Пример 1. Две параллельные ветви с сопротивлениями  Ом и
Ом и  Ом подсоединены к напряжению 300 В. Найти общий ток (ток в неразветвленной части цепи).
Ом подсоединены к напряжению 300 В. Найти общий ток (ток в неразветвленной части цепи).
Решеви е. Общий ток

В тех случаях, когда имеется несколько параллельных ветвей и когда нужно найти общий ток, удобно пользоваться понятием проводимости.
Проводимостью называют величину, обратную сопротивлению:

Проводимость обычно обозначается латинской буквой G:

Единицей проводимости служит единица, обратная ему; ее обозначают  Есть и специальная единица проводимости сименс (См).
Есть и специальная единица проводимости сименс (См).
Если сопротивление какого-нибудь участка цепи равно 100 Ом, то его проводимость равна  если сопротивление равно 1/2 Ом, то проводимость равна
если сопротивление равно 1/2 Ом, то проводимость равна

Из сказанного видно, что вместо деления напряжения на сопротивление можно умножить его на проводимость. Поэтому

В случае двух параллельных ветвей мы можем теперь так выразить общий ток:

Но тот же результат мы получим, если умножим напряжение (одинаковое для обеих ветвей) на сумму проводимостей:

Все сказанное о двух ветвях относится и к случаю большего числа параллельных ветвей: общий ток равен приложенному напряжению, умноженному на сумму проводимостей всех параллельных ветвей.
Отсюда мы заключаем, что общая проводимость ряда параллельных ветвей равна сумме проводимостей этих ветвей.
Замена параллельных ветвей одной с эквивалентным сопротивлением. Если мы захотим все параллельные ветви заменить одной ветвью с таким сопротивлением, чтобы ток в неразветвленной части цепи не изменился, нам нужно это сопротивление сделать равным единице, деленной на сумму проводимостей всех параллельных ветвей.
Это сопротивление называется сопротивлением, эквивалентным сопротивлению параллельных ветвей.
В случае параллельного соединения

Пример 2. Решим, пользуясь понятием проводимости, задачу, поставленную в предыдущем примере. Две параллельные ветви с сопротивлевиями  Ом присоединены к напряжению 300 В.
Ом присоединены к напряжению 300 В.
Найти общий ток.
Решение. Вычисляем проводимости:
проводимость первой ветви

проводимость второй

общая проводимость

Общий ток равен напряжению, умноженному на сумму проводимостей:

Пример 3. К напряжению 240 В параллельно включены две ветви с сопротивлением  Ом и
Ом и  Ом. Найти эквивалентное сопротивление и вычислить общий ток.
Ом. Найти эквивалентное сопротивление и вычислить общий ток.
Эквивалентное сопротивление

Общий ток равен напряжению, деленному на эквивалентное сопротивление:

Ответ нами найден. Проверим его следующим образом:
ток в первой ветви

ток во второй ветви

Их сумма действительно равна найденному выше общему току:

Общее эквивалентное сопротивление ряда параллельных ветвей всегда должно быть меньше сопротивления каждой из этих ветвей. Действительно, ведь подключая новую ветвь, мы создаем новый путь току, увеличиваем проводимость, а сопротивление и проводимость — это величины взаимно обратные.
Отметим два важных частных случая. Если параллельно соединены несколько ветвей с одинаковыми сопротивлениями, то эквивалентное сопротивление такой цепи можно найти, разделив сопротивление одной ветви на число ветвей.
Так, например, при параллельном соединении восьми ламп по 100 Ом сопротивление, эквивалентное сопротивлению восьми ламп, равно

Общее сопротивление двух параллельных ветвей. Если параллельно соединены две (но не больше) ветви с различными сопротивлениями, то эквивалентное им сопротивление (общее сопротивление) равно произведению этих двух сопротивлений, деленному на их сумму:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ
- 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА
- 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
- 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА
- 1.6. МОЩНОСТЬ
- 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА
- 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ
- 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ
- 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ
- 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА
- 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ
- 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА
- 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ
- 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ
- 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ
- 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ
- 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ
- 1.20. ЗАКОНЫ КИРХГОФА
- ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ
- 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА
- 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ
- 2.4. МАГНИТНАЯ ИНДУКЦИЯ
- 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ
- 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ
- 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ
- 2.9. ПРАВИЛО ЛЕНЦА
- 2.10. МАГНИТНЫЙ ПОТОК
- 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
- 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ
- 2.13. ВЗАИМНАЯ ИНДУКДИЯ
- 2.14. САМОИНДУКЦИЯ
- 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ
- 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА
- 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА
- 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ
- 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ
- 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ
- 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ
- 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ
- 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ
- 3.9. НАМАГНИЧЕННОСТЬ
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ
- 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА)
- 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ)
- 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
- 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ
- ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК
- 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК?
- 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
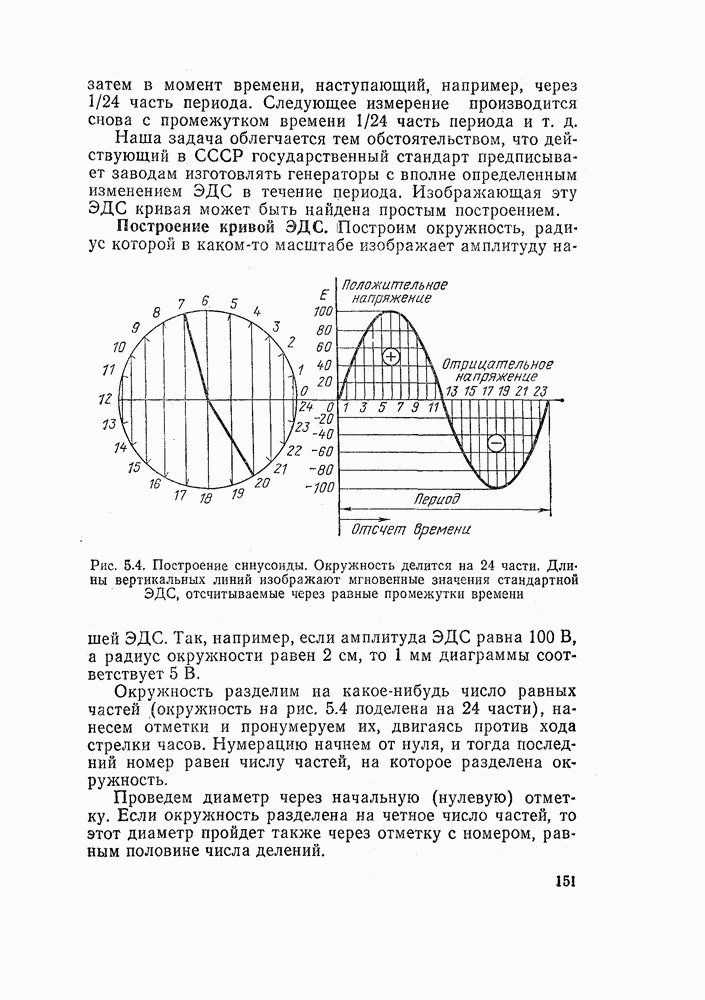
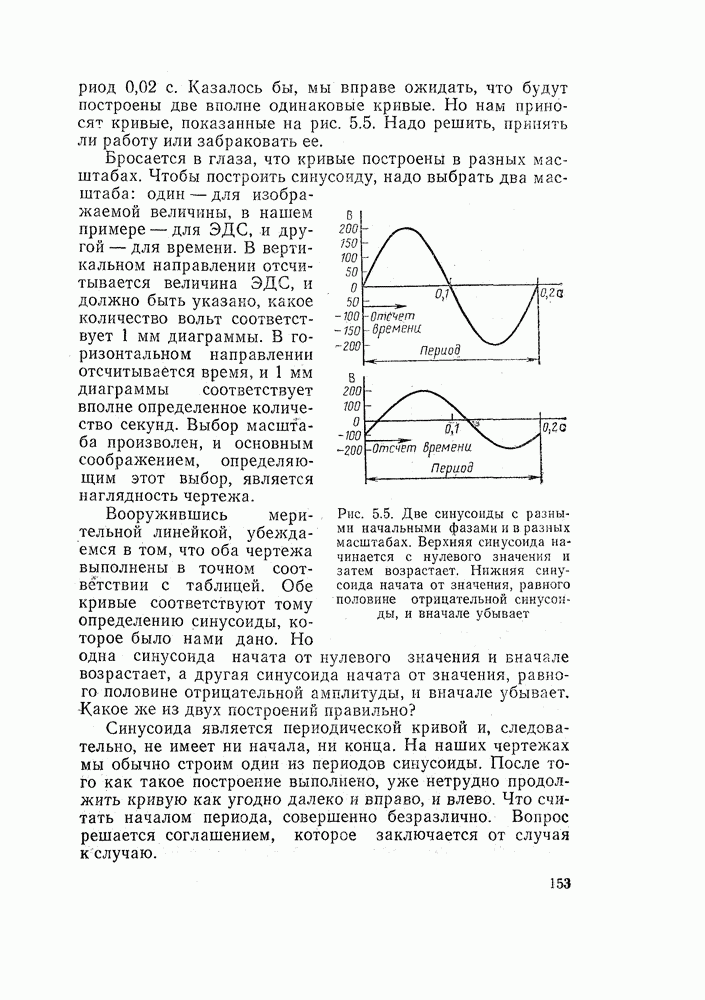
- 5.4. СИНУСОИДА
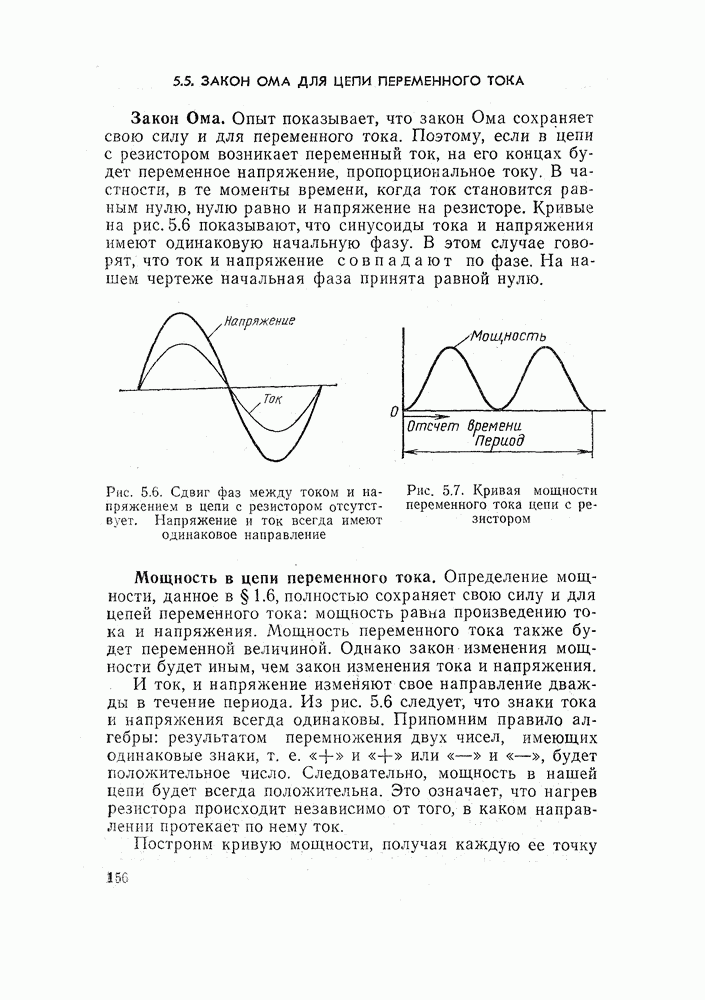
- 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА
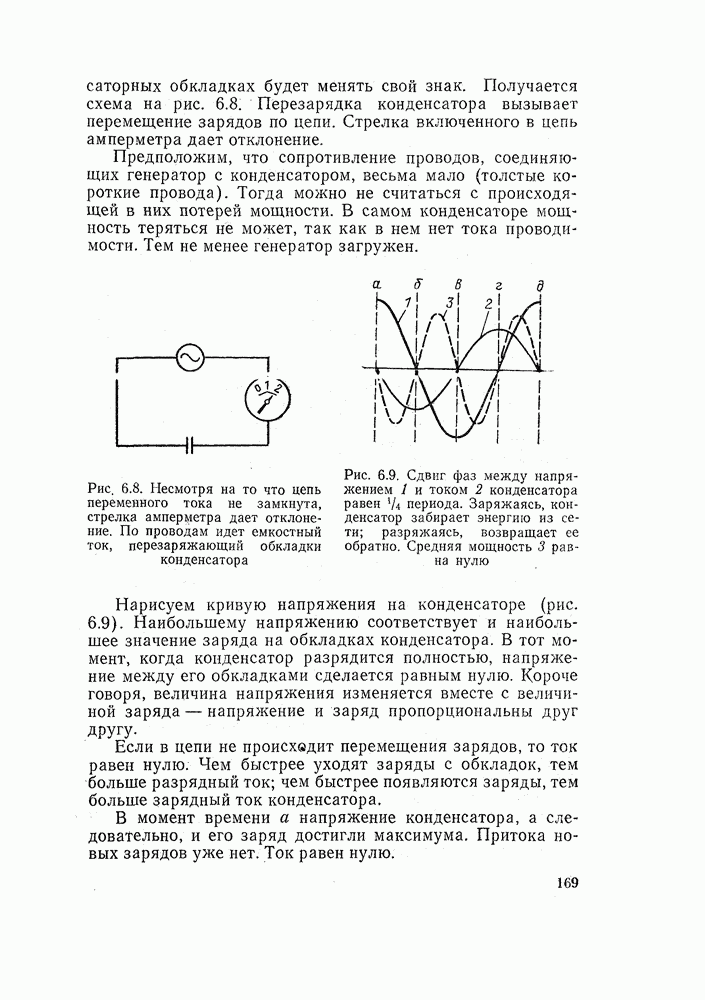
- ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ
- 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ
- 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ
- 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
- 6.7. РЕЗОНАНС ТОКОВ
- 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ
- ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК
- 7.1. ТРЕХФАЗНАЯ СИСТЕМА
- 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ
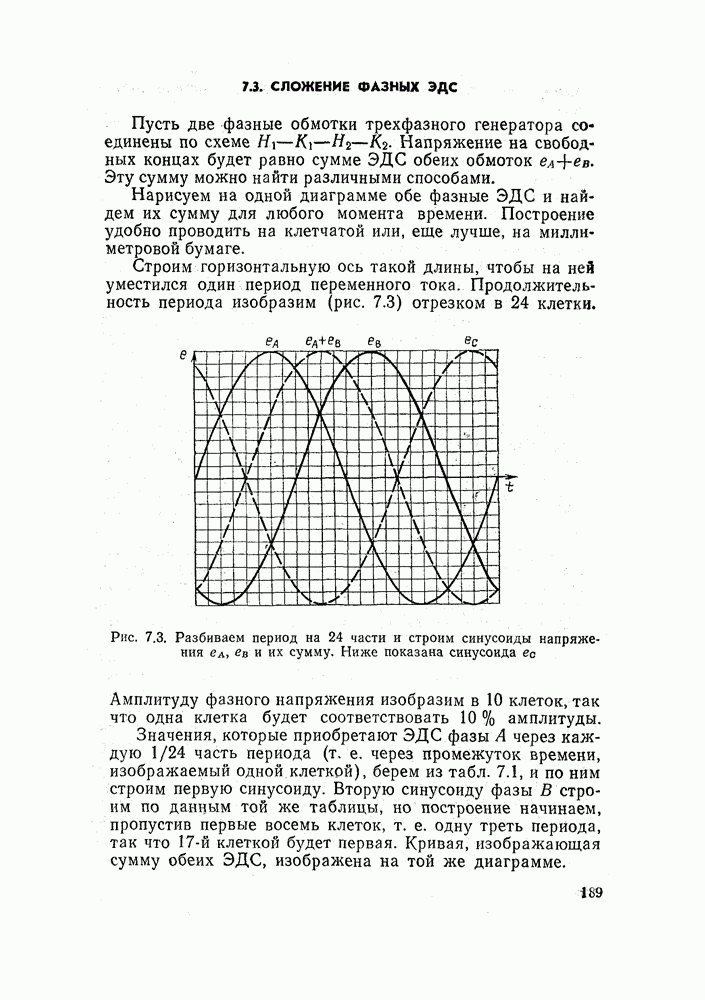
- 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС
- 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ
- 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА
- 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ
- ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ
- 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР
- 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ
- 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ
- 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ
- 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ
- ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ
- 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ
- 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
- 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ
- 9.7. КЛЮЧИ
- 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ
- 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА
- 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН
- 10.2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА
- 10.3. КОЛЛЕКТОР
- 10.4. ЯКОРНЫЕ ОБМОТКИ
- 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА
- 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН
- 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ
- 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ
- ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ
- 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- 11.2. РАБОТА ТРАНСФОРМАТОРА
- 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА
- 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ
- 11.1. АВТОТРАНСФОРМАТОРЫ
- ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
- 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА
- 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА
- 12.4. РАБОТА СИНХРОННЫХ МАШИН
- 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ
- 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
- 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ
- 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН
- ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ
- 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ
- 13.3. ЭЛЕКТРОМАГНИТЫ
- 13.4. КОНТАКТОРЫ
- 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ
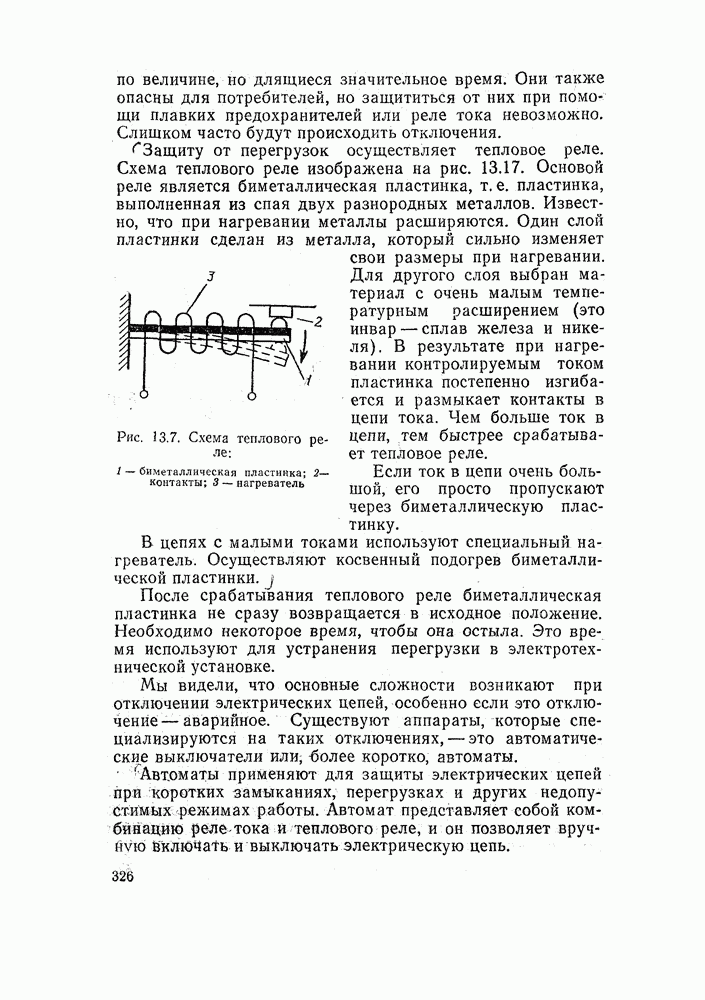
- 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ
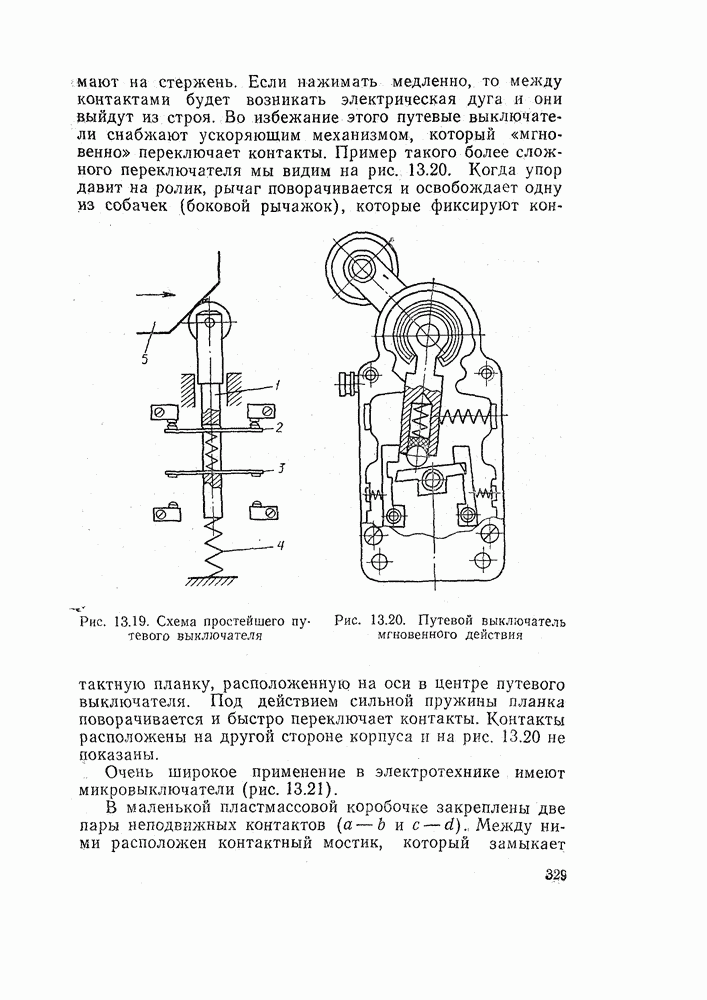
- 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ
- ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ
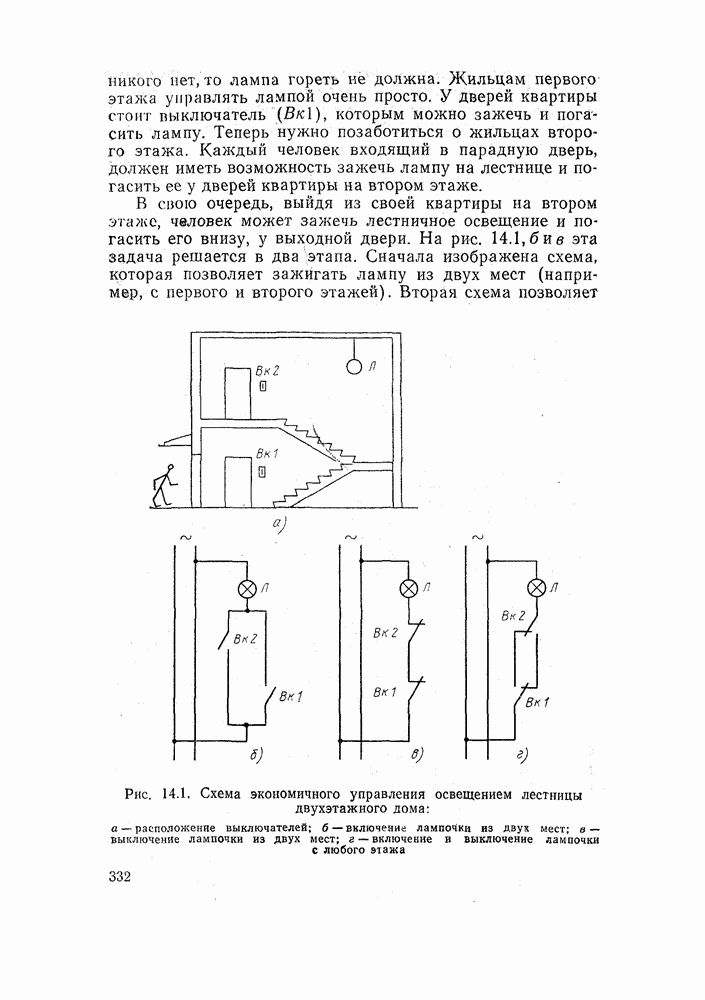
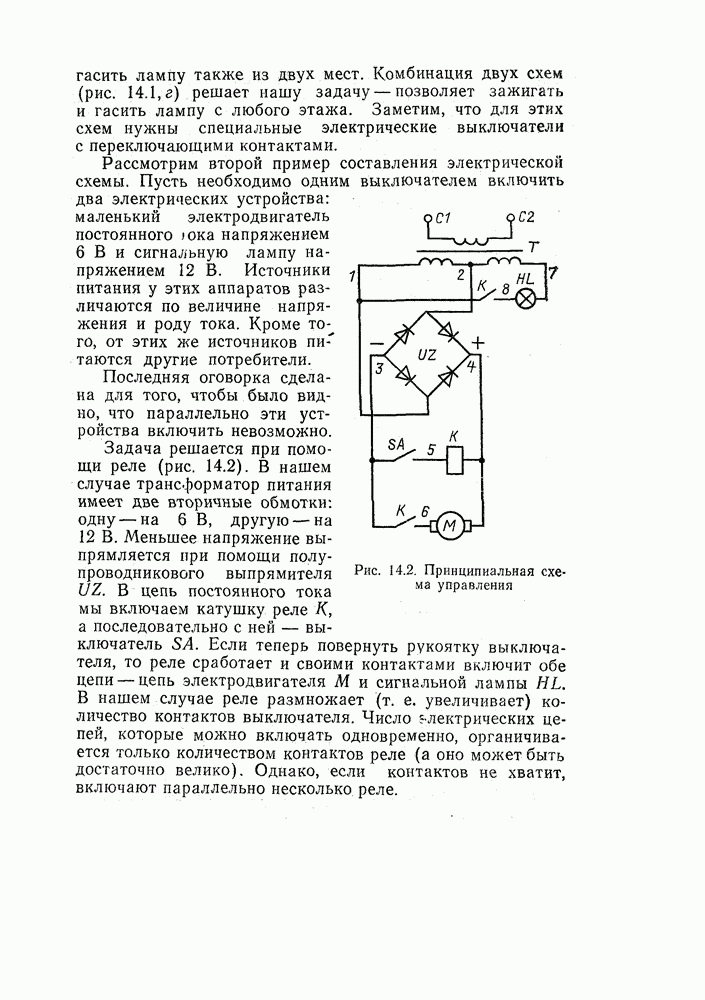
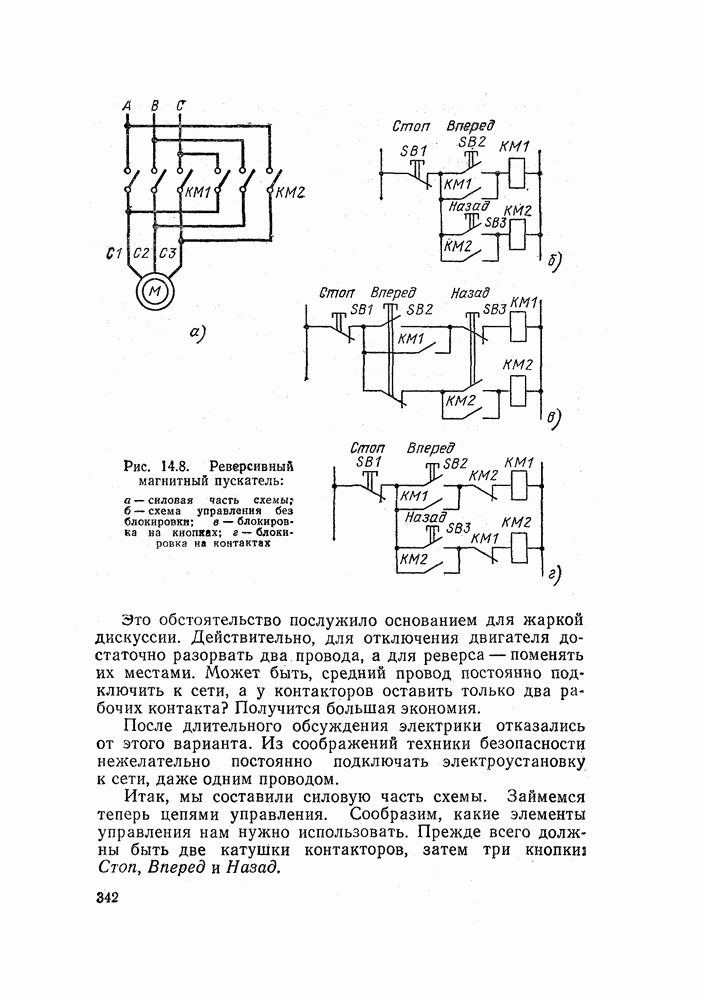
- 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ
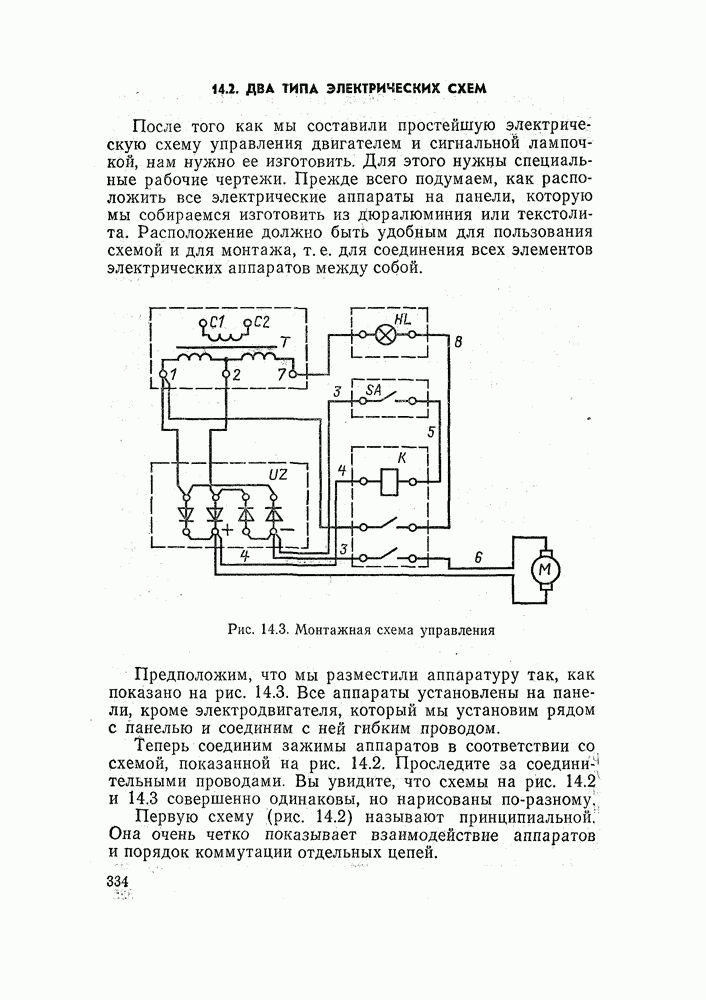
- 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ
- 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ
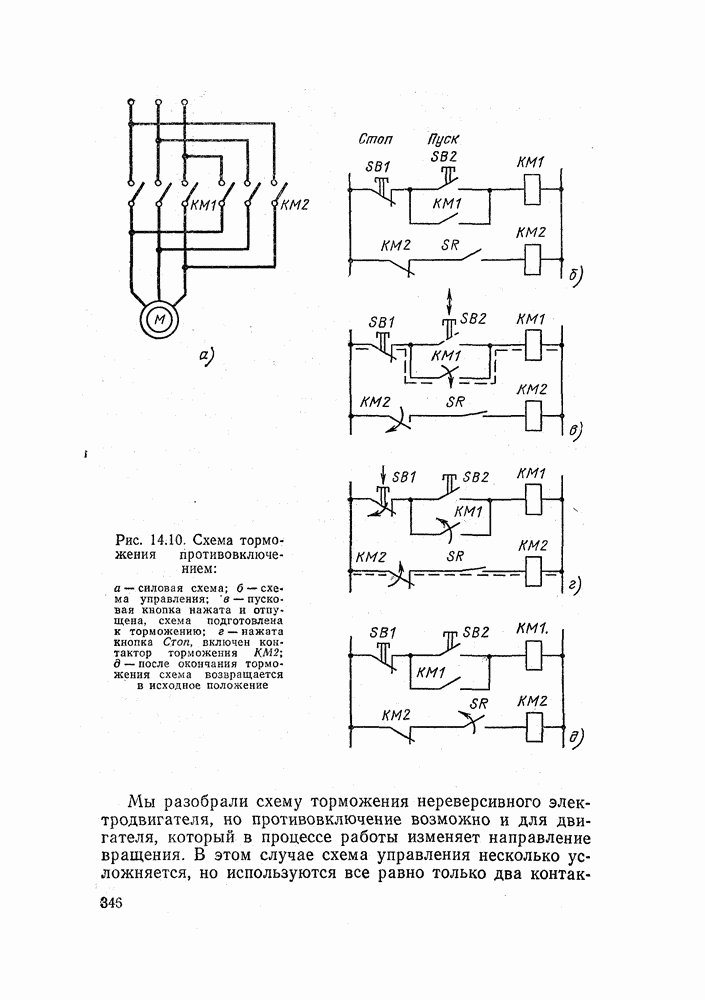
- 14.4. СХЕМЫ ТОРМОЖЕНИЯ
- 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
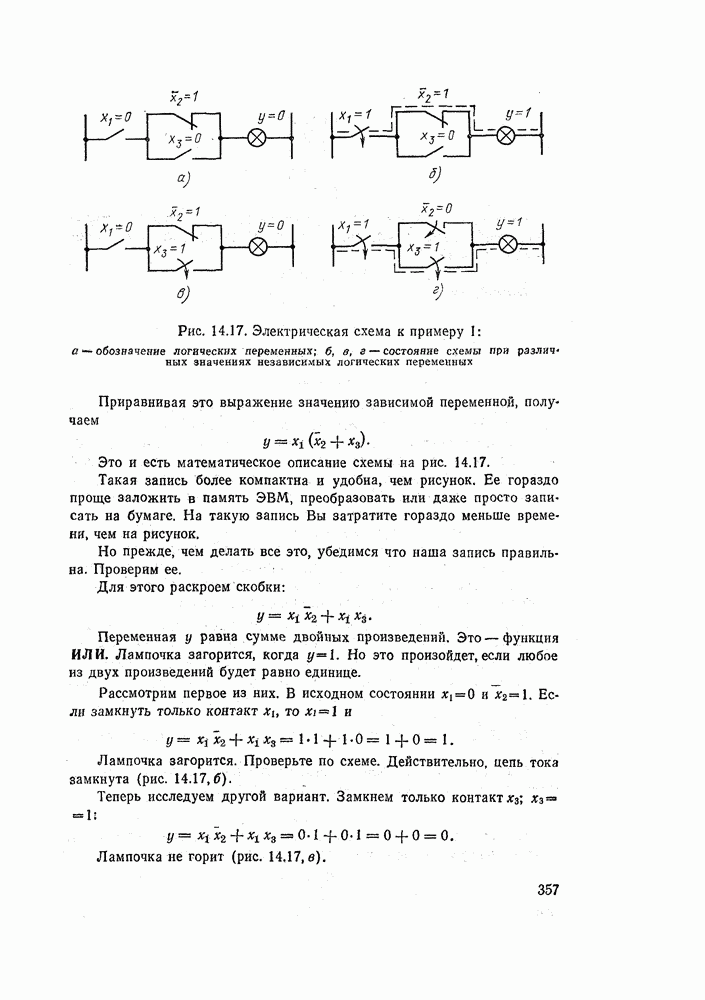
- 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ
- ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ
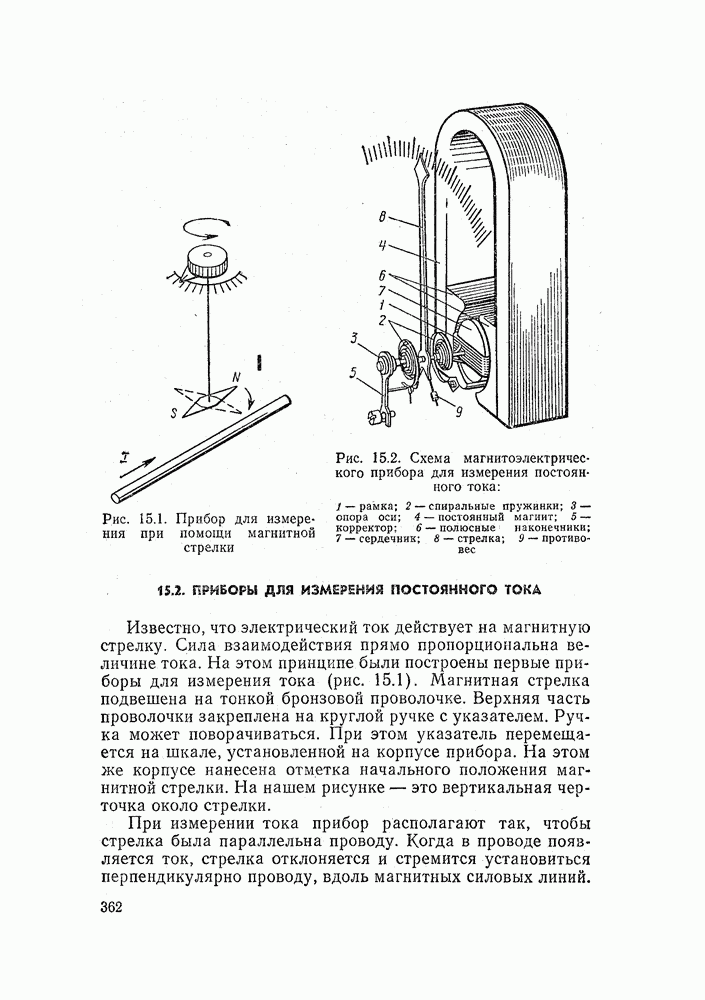
- 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ
- 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА
- 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ
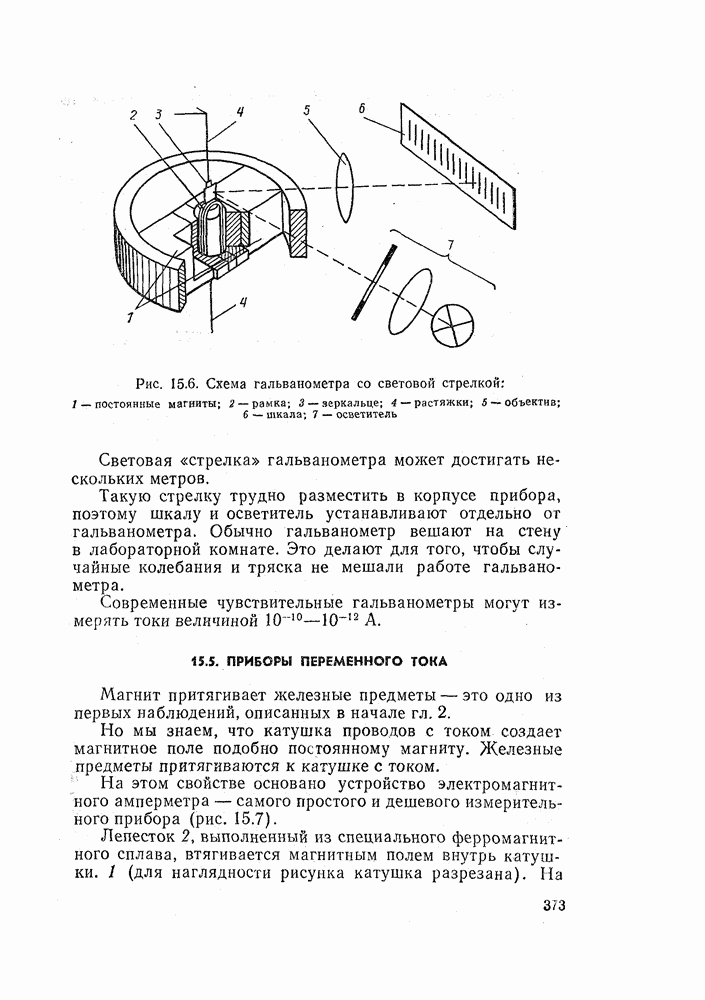
- 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ
- 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА
- 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
- 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА
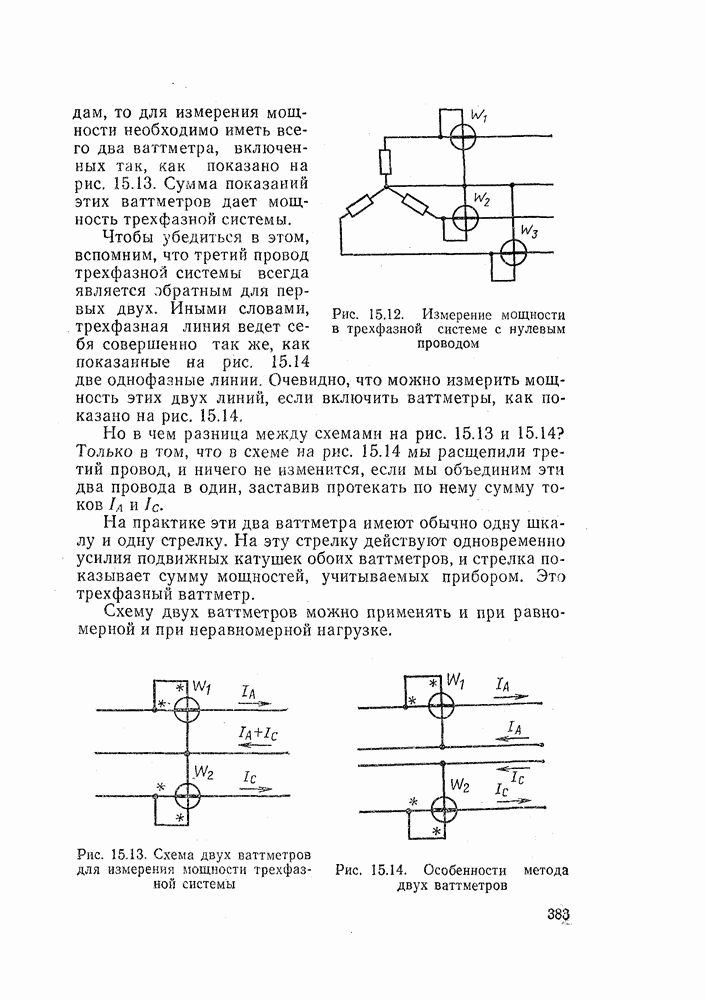
- 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА
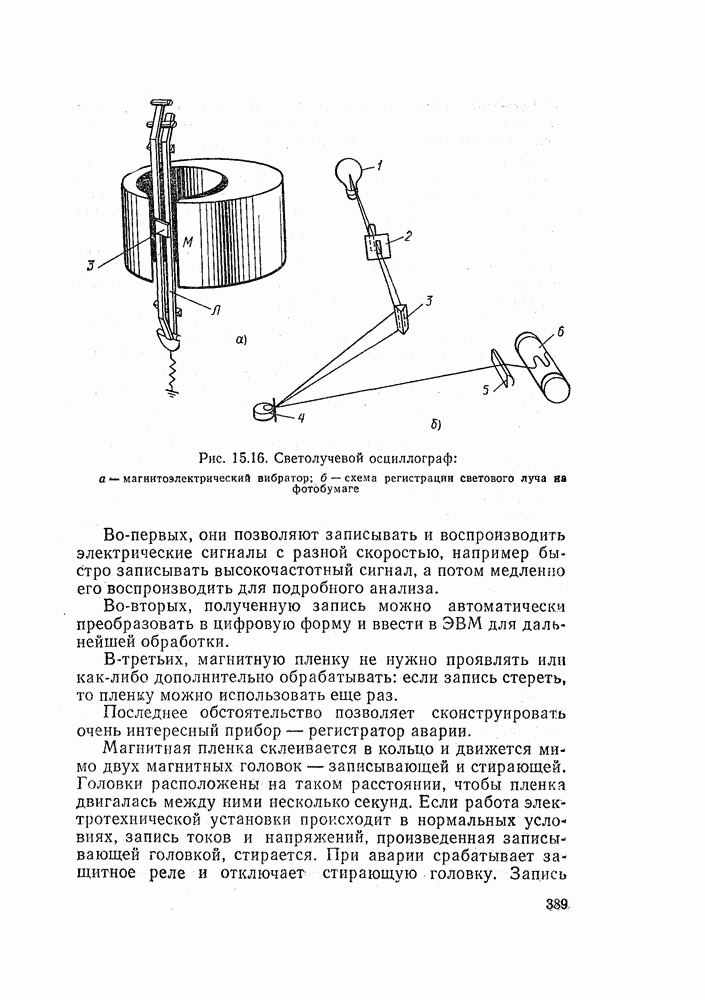
- 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ
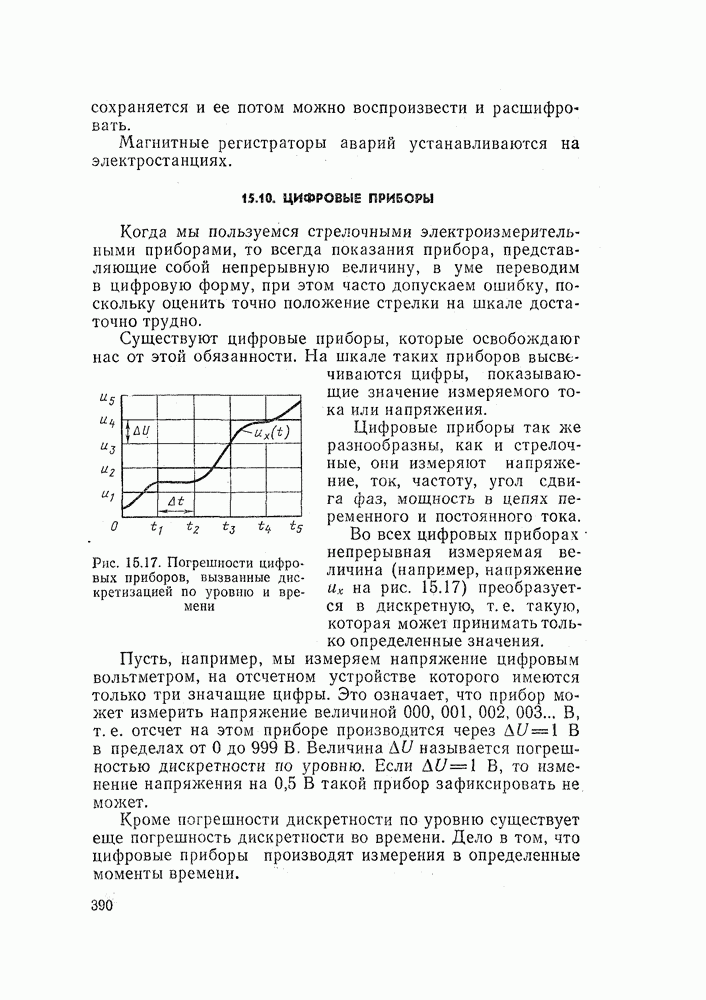
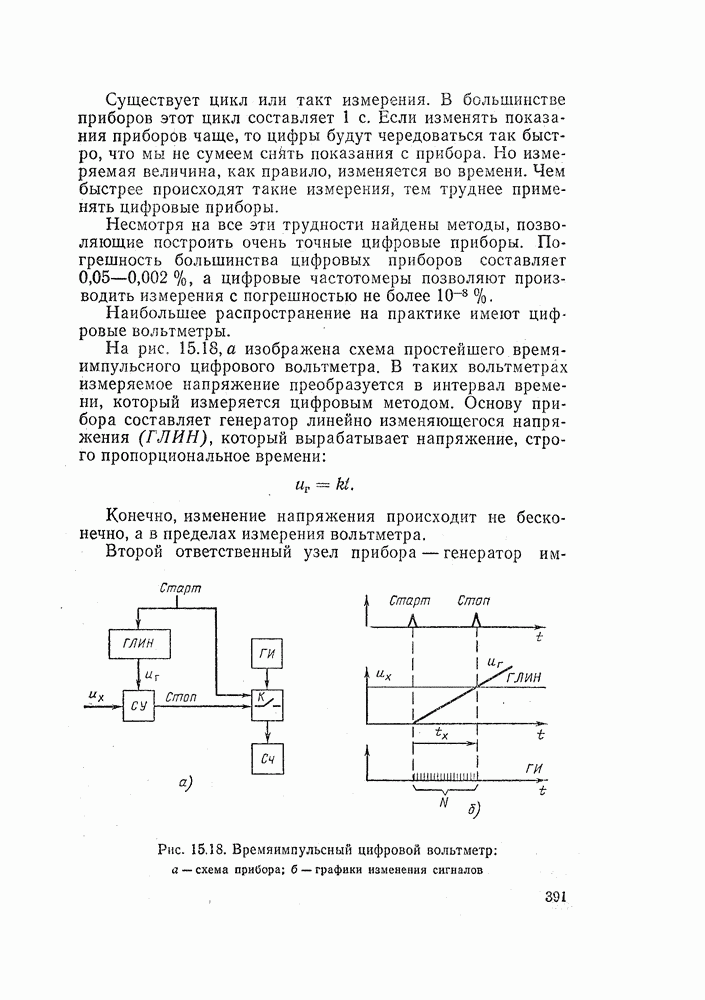
- 15.10. ЦИФРОВЫЕ ПРИБОРЫ
- 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ