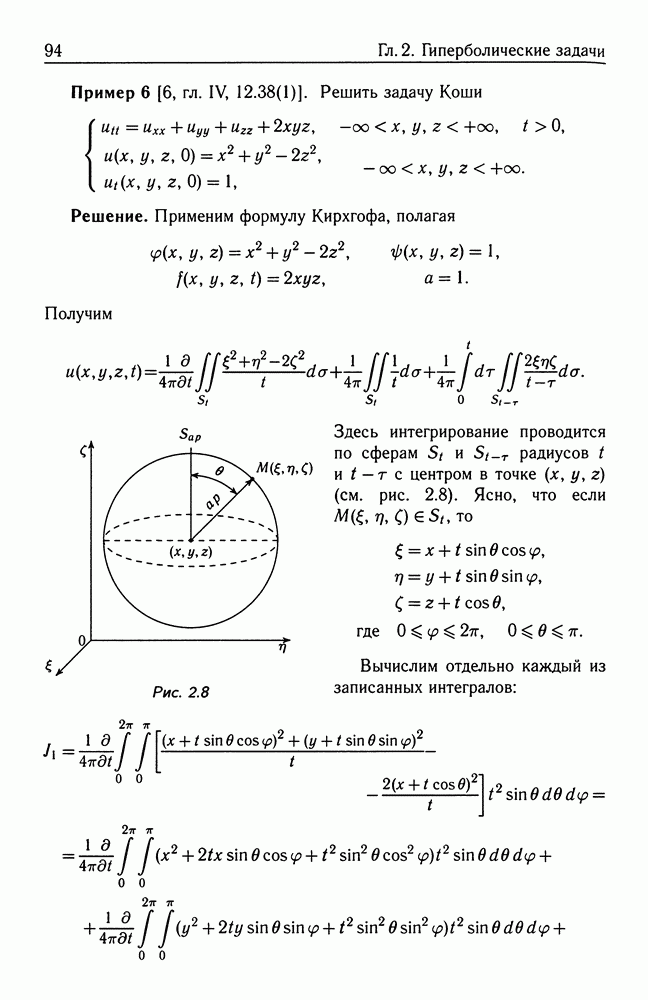
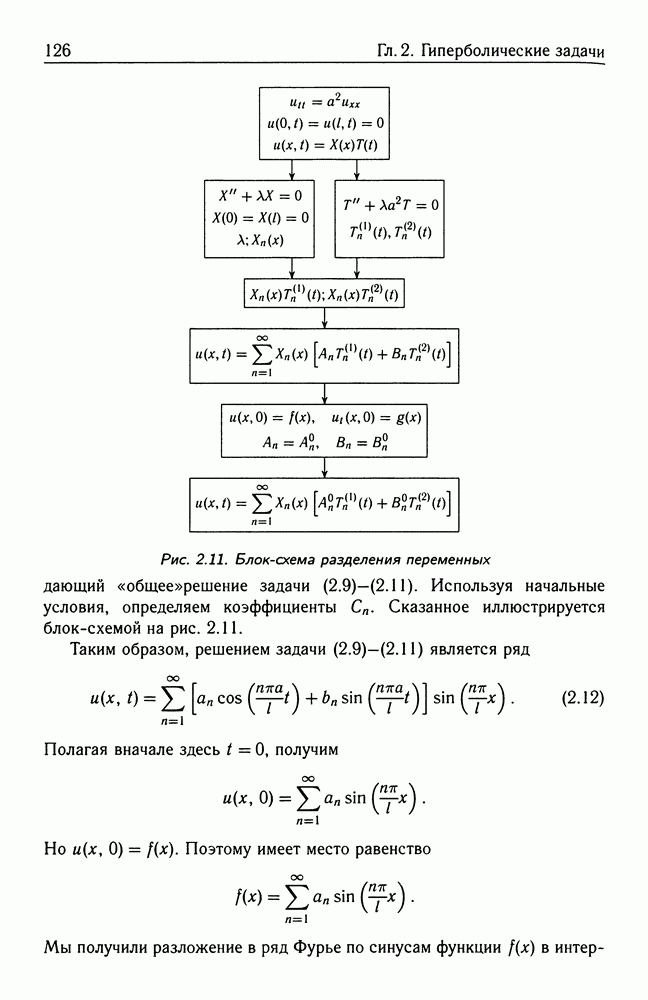
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
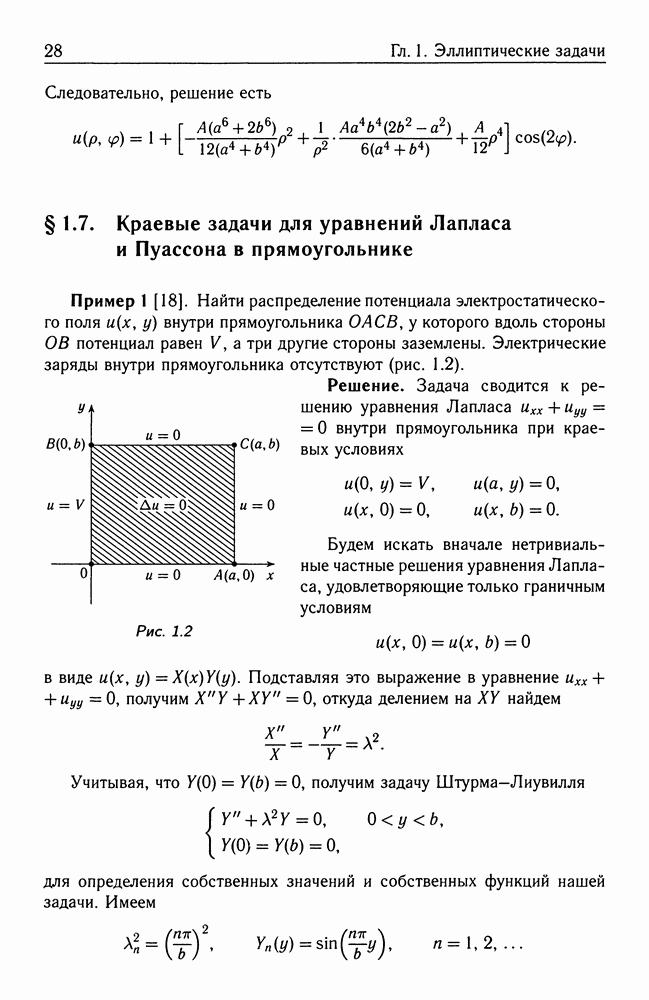
§ 1.16. Метод функций Грина
Определение функции Грина. Будем рассматривать краевые задачи

Считаем функцию  непрерывной вместе с первыми частными производными в замкнутой области
непрерывной вместе с первыми частными производными в замкнутой области  ограниченной достаточно гладкой поверхностью
ограниченной достаточно гладкой поверхностью  и имеющей вторые частные производные в
и имеющей вторые частные производные в  интегрируемые в этой области
интегрируемые в этой области  Здесь
Здесь  единичная внешняя нормаль к поверхности
единичная внешняя нормаль к поверхности  вещественные числа такие, что
вещественные числа такие, что 
Метод функций Грина решения таких задач состоит в следующем. Сначала решаем вспомогательную задачу [1]

где  функция, которую можно формально определить при помощи соотношений
функция, которую можно формально определить при помощи соотношений

 (обозначение
(обозначение  ясно). Основным свойством
ясно). Основным свойством  -функции является равенство
-функции является равенство

где  произвольная непрерывная функция точки
произвольная непрерывная функция точки 
Определение. Решение задачи (1.51) называется функцией Грина задачи (1.50).
Будем требовать, чтобы функция Грина  была непрерывной (вместе с частными производными первого порядка) всюду в замкнутой области
была непрерывной (вместе с частными производными первого порядка) всюду в замкнутой области  кроме точки
кроме точки  в которой функция
в которой функция  может иметь особенность.
может иметь особенность.
Если функция Грина найдена, то с ее помощью легко найти решение исходной задачи (1.50). Для этого воспользуемся второй формулой Грина

Эта формула легко получается из формулы Гаусса-Остроградского

(а — векторное поле;  скалярное произведение векторов
скалярное произведение векторов  ), если положить последовательно
), если положить последовательно  и вычесть результаты. Действительно, имеем два равенства
и вычесть результаты. Действительно, имеем два равенства

Учитывая, что  и
и  из равенств (1.53) и (1.54) вычитанием получим вторую формулу Грина.
из равенств (1.53) и (1.54) вычитанием получим вторую формулу Грина.
Положим теперь в формуле Грина  Тогда, учитывая, что
Тогда, учитывая, что  получим
получим

Но по основному свойству  -функции
-функции

Поэтому предыдущее равенство дает

Из этой формулы получаем:
а) решение задачи Дирихле при

в виде

б) решение задачи Неймана при

в виде

Замечание 1. Физическая интерпретация интеграла

состоит в том, что правая часть уравнения рассматривается как некоторое входное воздействие на систему и разлагается в непрерывную совокупность источников, распределенных на области  Затем находится отклик системы на каждый такой источник и все отклики суммируются.
Затем находится отклик системы на каждый такой источник и все отклики суммируются.
Построение функции Грина. Одним из методов построения функции Грина является метод отражений. Например, функция Грина задачи Дирихле для уравнения Пуассона в случае полупространства  имеют вид
имеют вид

где  расстояние между точками
расстояние между точками  точка, лежащая в верхнем полупространстве
точка, лежащая в верхнем полупространстве  точка, симметричная точке
точка, симметричная точке  относительно плоскости
относительно плоскости  произвольная точка полупространства
произвольная точка полупространства 
С физической точки зрения функцию Грина можно интерпретировать как потенциал поля, созданного точечными зарядами, помещенными в точку  (над заземленной проводящей плоскостью
(над заземленной проводящей плоскостью  и точку
и точку  (рис. 1.11).
(рис. 1.11).

Рис. 1.11. Потенциал в точке  равен
равен  — заземленная проводящая плоскость)
— заземленная проводящая плоскость)

Рис. 1.12. Потенциал в точке  равен
равен 
Заметим, что в случае полуплоскости  функция Грина примет вид (рис. 1.12)
функция Грина примет вид (рис. 1.12)

Примеры решения задач с помощью функции Грина. Пусть требуется решить задачу Дирихле для уравнения Лапласа в полуплоскости

Тогда решение этой задачи есть

(мы положили  где
где

Вычислив  получим
получим

Пример 1 [3, № 244]. Найти гармоническую в полуплоскости  функцию
функцию  если известно, что
если известно, что

Решение. Требуется вычислить интеграл

По-видимому, проще всего это сделать, если воспользоваться теорией вычетов, а именно следующей формулой:

Поскольку

выполнено равенство

Итак, искомое решение задачи есть

Замечание 2. Решение рассмотренной задачи Дирихле

можно получить, не прибегая к функции Грина.
В самом деле, используя тот факт, что функция  является решением уравнения Лапласа в верхней полуплоскости
является решением уравнения Лапласа в верхней полуплоскости  можно написать
можно написать

Дифференцируя это равенство по переменной  будем иметь
будем иметь

Таким образом, функция  является гармонической в верхней полуплоскости. В нашем случае с учетом граничного условия решением задачи Дирихле является функция
является гармонической в верхней полуплоскости. В нашем случае с учетом граничного условия решением задачи Дирихле является функция

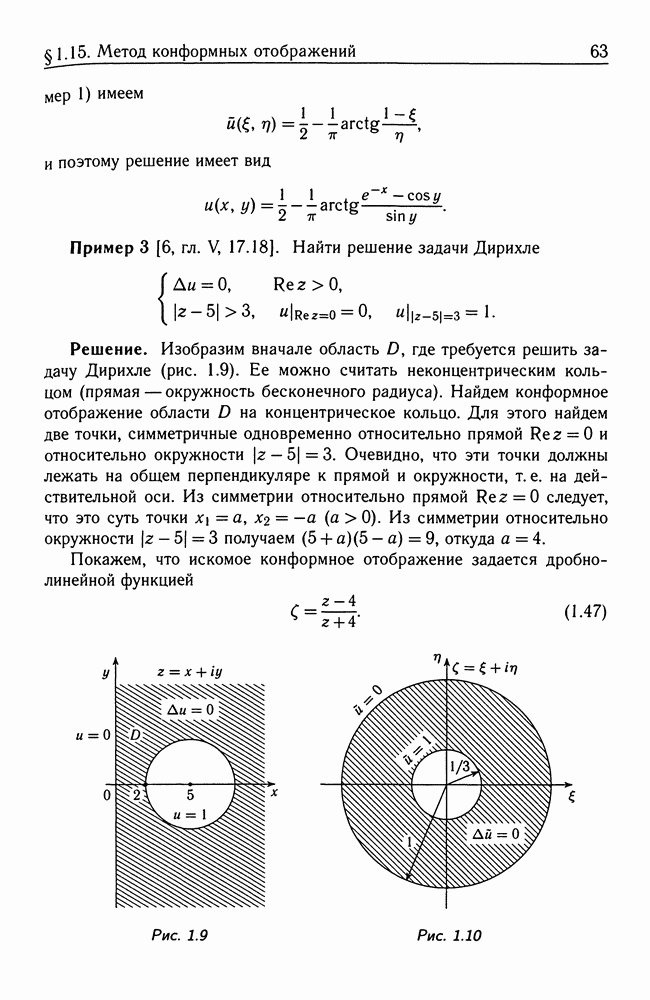
Пример 2 [6, гл. V, 17.4(2)]. Найти решение задачи Дирихле

Решение. Известно, что искомая гармоническая функция находится по формуле

Для вычисления интеграла произведем замену  якобианом, равным единице. Получим
якобианом, равным единице. Получим

ибо все остальные три интеграла равны нулю в силу нечетности соответствующей подынтегральной функции.
Теперь вычислим интеграл:

так как другой интеграл равен нулю.
Сделаем замену независимых переменных

что соответствует повороту плоскости на угол 45° против часовой стрелки. Тогда будем иметь

Но  с помощью подстановки
с помощью подстановки  преобразуется к виду
преобразуется к виду

Значит, интеграл

по теореме Коши о вычетах равен

Итак, решение есть 
Замечание 3. Так как  где
где  то формулу Пуассона (1.55) можно записать в виде
то формулу Пуассона (1.55) можно записать в виде

Рассмотрим теперь задачу Дирихле для уравнения Лапласа в полуплоскости  (т. е. при
(т. е. при 

где рациональная функция  действительна, не имеет полюсов на действительной оси и
действительна, не имеет полюсов на действительной оси и  при
при  Решением указанной задачи Дирихле в силу (1.56) является функция
Решением указанной задачи Дирихле в силу (1.56) является функция

Этот интеграл можно вычислить с помощью вычетов по теореме Коши

где вычеты берутся по всем полюсам функции  лежащим в нижней полуплоскости
лежащим в нижней полуплоскости 
Пример 3. Решить задачу Дирихле

Решение. По формуле (1.57) получим

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава 1. Эллиптические задачи
- § 1.1. Задача Дирихле в кольце для уравнения Лапласа
- § 1.2. Примеры задач Дирихле в кольце
- § 1.3. Внутренняя и внешняя задачи Дирихле
- § 1.4. Интеграл Пуассона для круга. Запись в комплексной форме. Решение задачи Дирихле, когда граничное условие есть рациональная функция …
- § 1.5. Внутренняя и внешняя задачи Неймана для круга
- § 1.6. Краевые задачи для уравнения Пуассона в кольце и круге
- § 1.7. Краевые задачи для уравнений Лапласа и Пуассона в прямоугольнике
- § 1.8. Краевые задачи для уравнения Лапласа и Пуассона в ограниченном цилиндре
- § 1.9. Краевые задачи для уравнения Лапласа и Пуассона в шаре
- § 1.10. Краевые задачи для уравнения Гельмгольца
- § 1.11. Краевая задача для уравнения Гельмгольца в цилиндре
- § 1.12. Краевые задачи для уравнения Гельмгольца в круге
- § 1.13. Краевые задачи для уравнения Гельмгольца в шаре
- § 1.14. Направленные электромагнитные волны
- § 1.15. Метод конформных отображений (решение краевых задач на плоскости)
- § 1.16. Метод функций Грина
- § 1.17. Другие методы
- Глава 2. Гиперболические задачи
- § 2.1. Метод бегущих волн
- § 2.2. Метод подбора частных решений
- § 2.3. Метод интегрального преобразования Фурье
- § 2.4. Метод интегрального преобразования Лапласа
- § 2.5. Метод интегрального преобразования Ханкеля
- § 2.6. Метод стоячих волн. Колебания ограниченной струны
- § 2.7. Некоторые примеры смешанных задач для уравнения колебаний струны
- § 2.8. Метод Фурье. Колебания прямоугольной мембраны
- § 2.9. Метод Фурье. Колебания круглой мембраны
- § 2.10. Метод Фурье. Колебания балки
- § 2.11. Метод возмущений
- Глава 3. Параболические задачи
- § 3.1. Метод интегрального преобразования Фурье
- § 3.2. Метод интегрального преобразования Лапласа
- § 3.3. Метод Фурье (метод разделения переменных)
- § 3.4. Модификация метода разделения переменных для решения задачи Коши