| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Взаимная корреляция, автокорреляция и свертка
Если  и
и  являются соответственно Т-периодическими продолжениями сигналов
являются соответственно Т-периодическими продолжениями сигналов  и
и  то их взаимная корреляционная функция определяется как
то их взаимная корреляционная функция определяется как
 (2.5.1)
(2.5.1)
где  — временной сдвиг, непрерывно изменяющийся в интервале
— временной сдвиг, непрерывно изменяющийся в интервале  независимо от t. В общей теории гармонического анализа взаимокорреляционная функция
независимо от t. В общей теории гармонического анализа взаимокорреляционная функция  представляет значительный интерес.
представляет значительный интерес.
Прежде чем продолжить изложение, имеет смысл рассмотреть простой пример, который позволит графически проиллюстрировать смысл выражения (2.5.1). Допустим
 (2.5.2)
(2.5.2)
и
 (2.5.3)
(2.5.3)
Тогда соответствующие  и
и  имеют вид, показанный на рис. 2.6.
имеют вид, показанный на рис. 2.6.

Рис. 2.6. Периодическое продолжение сигналов  и
и 
Из выражения (2.5.1) следует, что  является также периодической функцией. Поэтому ее достаточно вычислить в
является также периодической функцией. Поэтому ее достаточно вычислить в  одного периода. Теперь рассмотрим произведение
одного периода. Теперь рассмотрим произведение  и
и  , где
, где  перемещается относительно
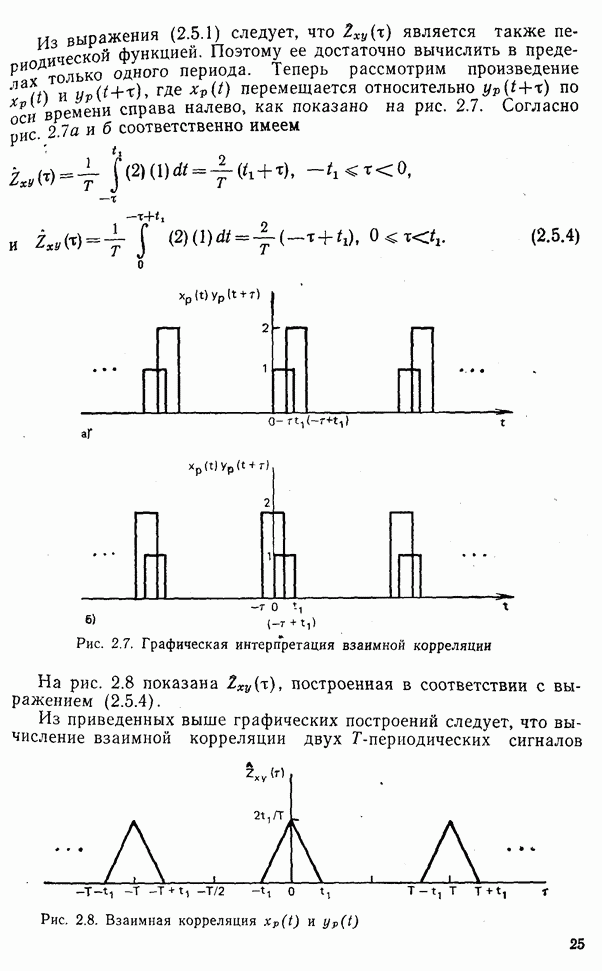
перемещается относительно  по времени справа налево, как показано на рис. 2.7. Согласно рис. 2.7а и б соответственно имеем
по времени справа налево, как показано на рис. 2.7. Согласно рис. 2.7а и б соответственно имеем

и  (2.5.4)
(2.5.4)

Рис. 2.7. Графическая интерпретация взаимной корреляции
На рис. 2.8 показана  построенная в соответствии с выражением (2.5.4).
построенная в соответствии с выражением (2.5.4).
Из приведенных выше графических построений следует, что вычисление взаимной корреляции двух Т-периодических сигналов сводится к сдвигу одного сигнала относительно другого и соответственно усреднению их произведения за один период.

Рис. 2.8. Взаимная корреляция  и
и 
Теорема корреляции. Если  и
и  являются коэффициентами разложения в ряд Фурье соответственно сигналов
являются коэффициентами разложения в ряд Фурье соответственно сигналов  и
и  , то
, то
 (2.5.5)
(2.5.5)
где  коэффициент разложения
коэффициент разложения  в ряд Фурье, а
в ряд Фурье, а  — величина комплексно-сопряженная с
— величина комплексно-сопряженная с  .
.
Доказательство достаточно простое. Согласно выражению (2.1.13) получаем
 (2.5.6)
(2.5.6)
 (2.5.7)
(2.5.7)
и  (2.5.8)
(2.5.8)
где
 (2.5.9)
(2.5.9)
 (2.5.10)
(2.5.10)
и  (2.5.11)
(2.5.11)
Подставляя (2.5.7) в (2.5.1), получаем
 (2.5.12)
(2.5.12)
Согласно (2.5.9) выражение, заключенное в квадратные скобки в (2.5.12), представляет собой  . Таким образом, выражение (2.5.12) можно записать как
. Таким образом, выражение (2.5.12) можно записать как
 (2.5.13)
(2.5.13)
Сравнивая между собой  и (2.5.8), получаем
и (2.5.8), получаем
жение (2.5.5), а именно  и
и  . Если в выражение (2.5.1) вместо
. Если в выражение (2.5.1) вместо  подставить функцию
подставить функцию  , то получим
, то получим
 (2.5.14)
(2.5.14)
где  по определению представляет собой автокорреляционную функцию. Обозначив в выражении (2.5.5)
по определению представляет собой автокорреляционную функцию. Обозначив в выражении (2.5.5)  и
и  как
как  получаем
получаем
 (2.5.15)
(2.5.15)
Из выражений (2.5.14) и (2.5.15) следует, что выражение (2.5.8) можно записать в следующем виде:
 (2.5.16)
(2.5.16)
При  имеем
имеем

или
 (2.5.17)
(2.5.17)
Нетрудно заметить, что формула (2.5.17) выражает теорему Парсеваля, доказательство которой было приведено выше [см. выражение (2.1.15)].
Свертка. Если  и
и  представляют собой Т-периодические продолжения соответственно двух сигналов
представляют собой Т-периодические продолжения соответственно двух сигналов  и
и  то свертка функций определяется следующим образом:
то свертка функций определяется следующим образом:
 (2.5.18)
(2.5.18)
Отметим сходство функций  и
и  соответственно в выражениях (2.5.1) и (2.5.18). Как и в случае функции взаимной корреляции, легко дать графическую интерпретацию выражения (2.5.18). Допустим, что
соответственно в выражениях (2.5.1) и (2.5.18). Как и в случае функции взаимной корреляции, легко дать графическую интерпретацию выражения (2.5.18). Допустим, что  и
и  заданы соответственно выражениями (2.5.2) и (2.5.3). Тогда соответствующие им функции
заданы соответственно выражениями (2.5.2) и (2.5.3). Тогда соответствующие им функции  и
и  показаны на рис. 2.9. Необходимо отметить, что
показаны на рис. 2.9. Необходимо отметить, что  представляет собой зеркальное отображение
представляет собой зеркальное отображение  . Так
. Так  в выражении (2.5.18) является периодической функцией, то ее достаточно вычислить только в пределах одного периода.
в выражении (2.5.18) является периодической функцией, то ее достаточно вычислить только в пределах одного периода.

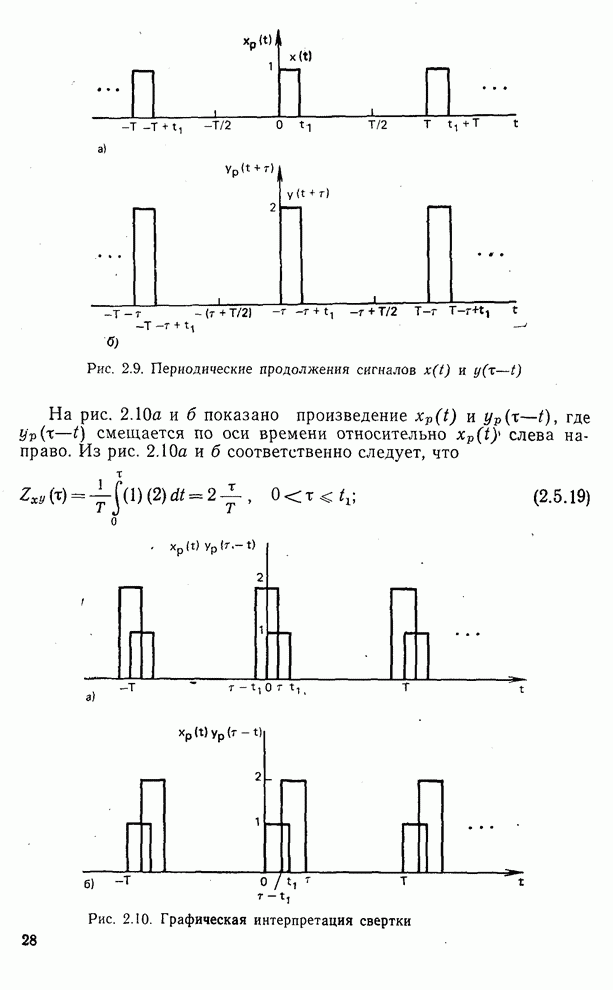
Рис. 2.9. Периодические продолжения сигналов  и
и 
На рис. 2.10а и б показано произведение  и
и  -t), где
-t), где  смещается по оси времени относительно
смещается по оси времени относительно  слева направо. Из рис. 2.10а и б соответственно следует, что
слева направо. Из рис. 2.10а и б соответственно следует, что
 (2.5.19)
(2.5.19)

Рис. 2.10. Графическая интерпретация свертки
и
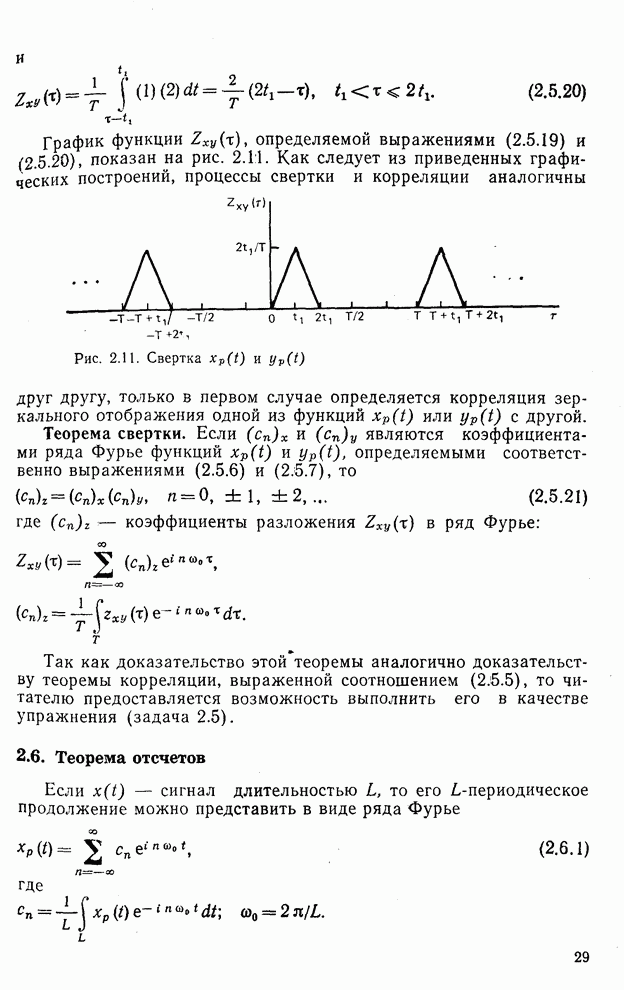
 (2.5.20)
(2.5.20)
График функции  определяемой выражениями (2.5.19) и (2.5.20) показан на рис. 2.11. Как следует из приведенных графических построений, процессы свертки и корреляции аналогичны друг другу, только в первом случае определяется корреляция зеркального отображения одной из функций
определяемой выражениями (2.5.19) и (2.5.20) показан на рис. 2.11. Как следует из приведенных графических построений, процессы свертки и корреляции аналогичны друг другу, только в первом случае определяется корреляция зеркального отображения одной из функций  или
или  с другой.
с другой.

Рис. 2.11. Свертка  и
и 
Теорема свертки. Если  и
и  являются коэффициентами ряда Фурье функций
являются коэффициентами ряда Фурье функций  и
и  определяемыми соответственно выражениями (2.5.6) и (2.5.7), то
определяемыми соответственно выражениями (2.5.6) и (2.5.7), то
 (2.5.21)
(2.5.21)
где  — коэффициенты разложения
— коэффициенты разложения  в ряд Фурье:
в ряд Фурье:

Так как доказательство этой теоремы аналогично доказательству теоремы корреляции, выраженной соотношением (2.5.5), то читателю предоставляется возможность выполнить его в качестве упражнения (задача 2.5).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
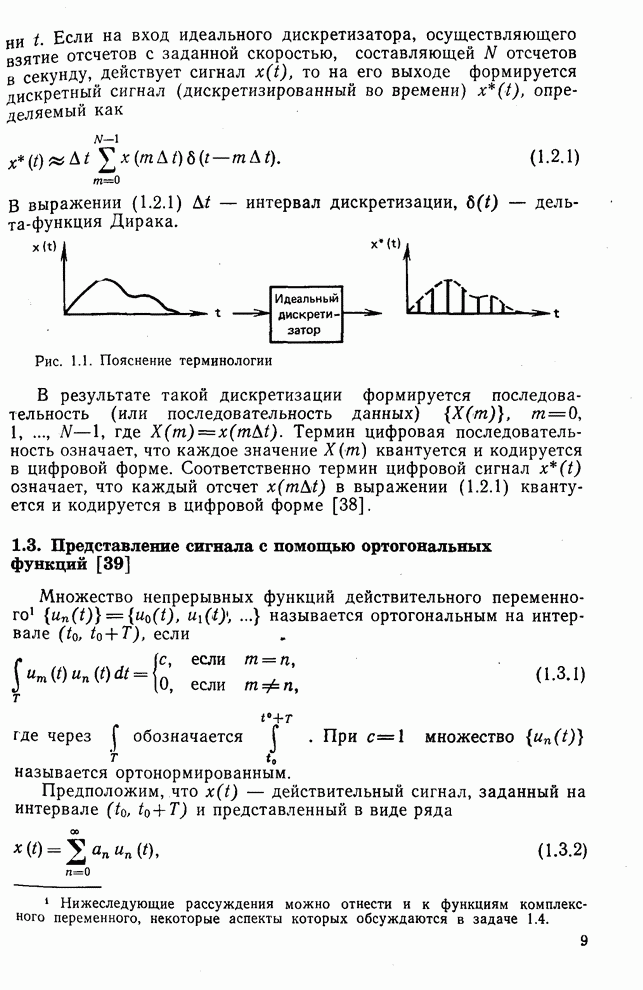
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
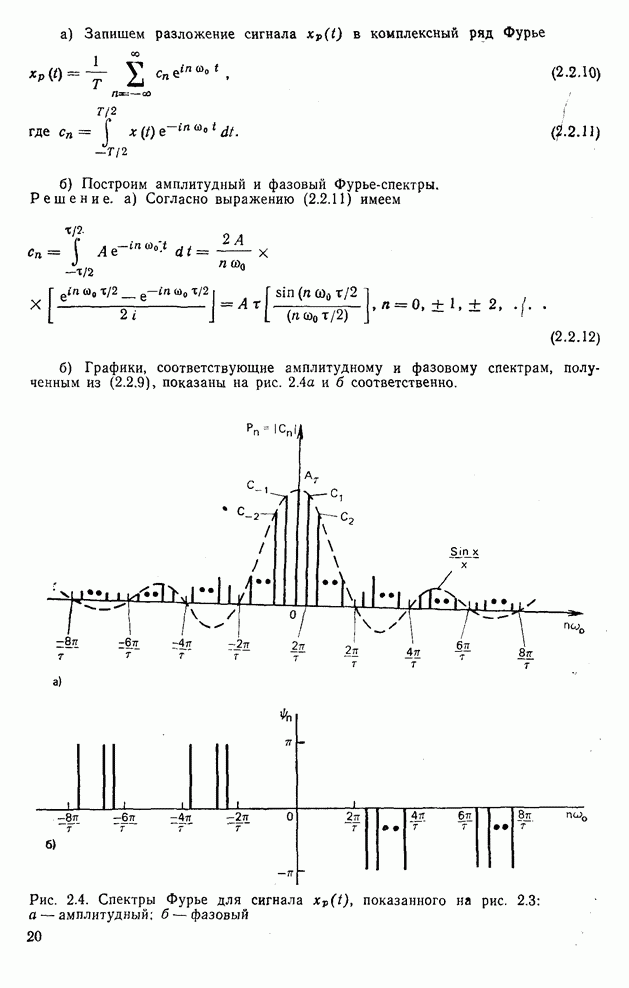
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
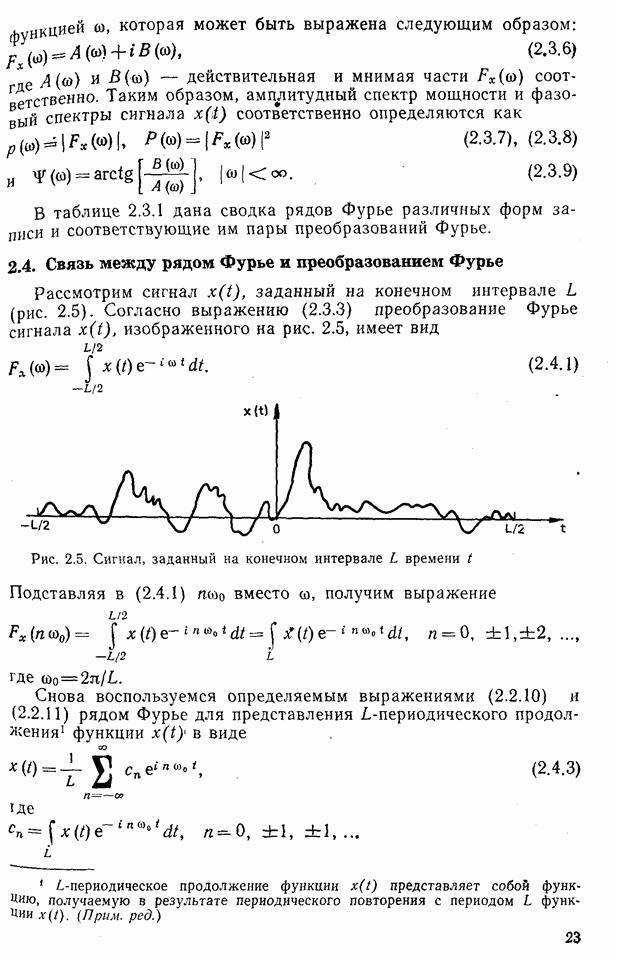
- 2.4. Связь между рядом Фурье и преобразованием Фурье
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
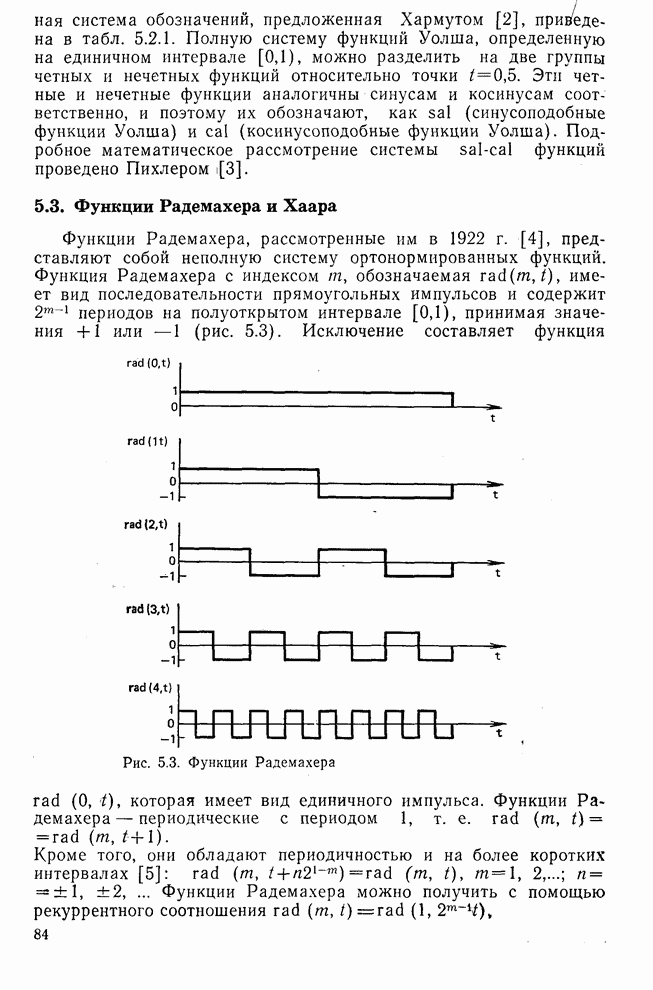
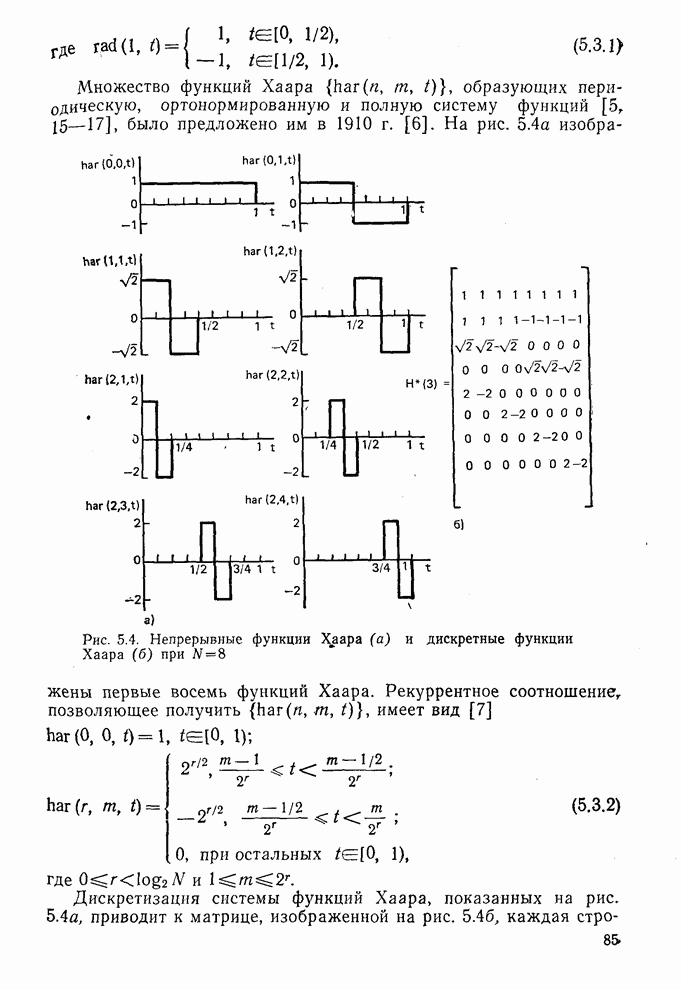
- 5.3. Функции Радемахера и Хаара
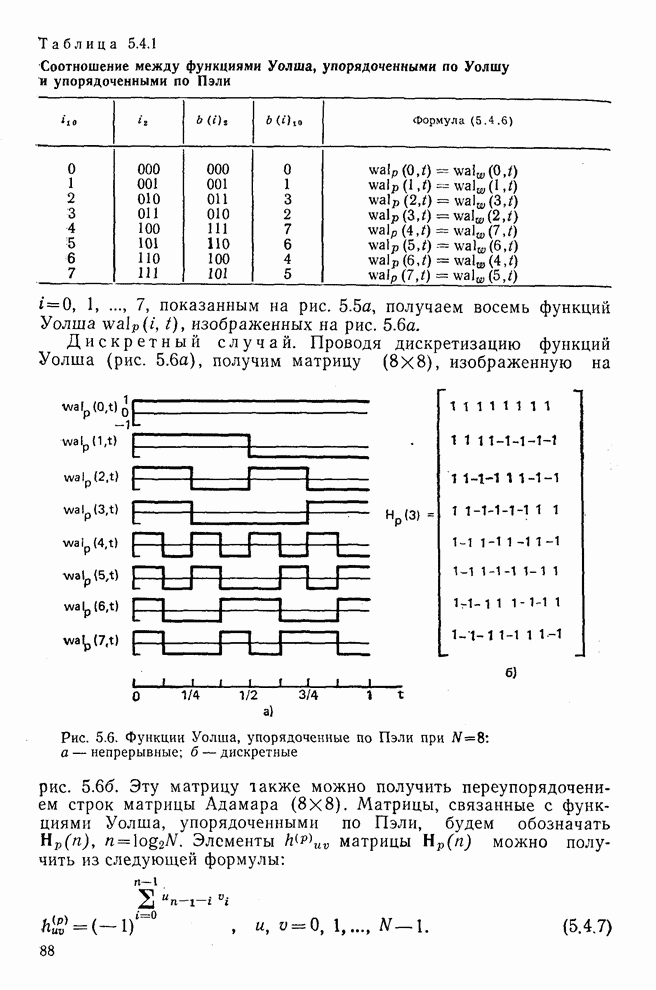
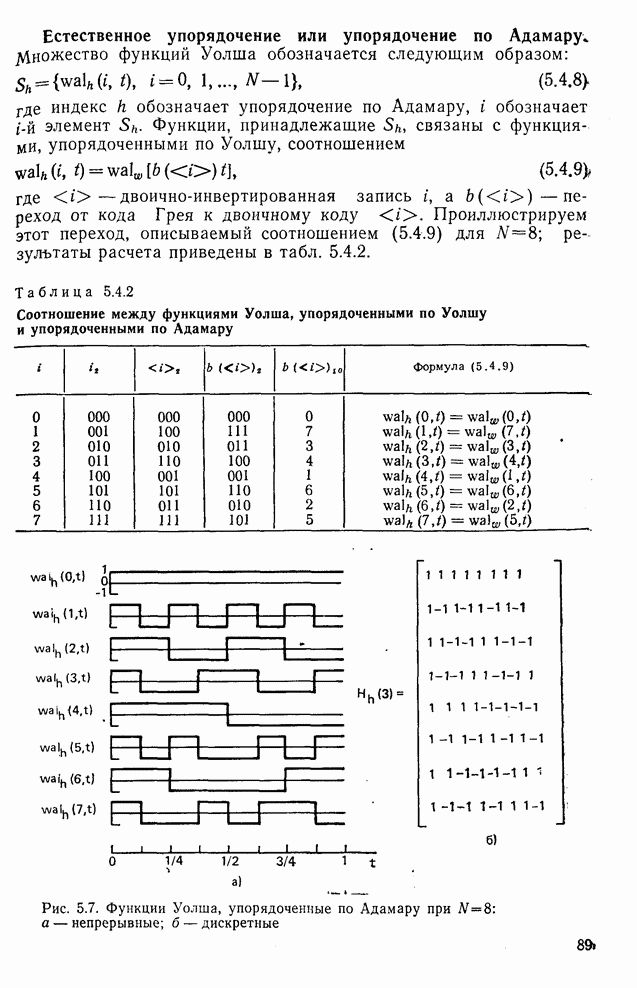
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
- 10.6. Метод отображения по методу наименьших квадратов
- 10.7. Расширенное пространство признаков
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ