| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
С поверхностными и внутренними повреждениями диэлектрика (чаще всего повреждения возникают в оптических стеклах, нелинейных кристаллах или активных элементах лазеров) исследователи столкнулись после создания в 1962 г. лазеров, работающих в режиме гигантских импульсов. Позднее это явление получило новые объяснения в работах Любимова и др. [1], Криспа и др. [2] и Бломбергена с сотрудниками [3—61. Авторы работы [1] исследовали разрушение отражающей грани в стеклянной призме. В результате полного внутреннего отражения света напряженность электрического поля возрастает до значения  при состоянии поляризации
при состоянии поляризации  или до значения
или до значения  при состоянии поляризации
при состоянии поляризации  (рис. 29.1). Эти идеи были развиты в работах [2]. Их авторы полагают, что френелевское отражение от граничных поверхностей диэлектрика приводит к ослаблению электрического поля на входе в образец и его усилению на выходе. С учетом изменения фазы при отражении это явление проиллюстрировано на рис. 29.2. Простые выкладки с помощью формул Френеля дают
(рис. 29.1). Эти идеи были развиты в работах [2]. Их авторы полагают, что френелевское отражение от граничных поверхностей диэлектрика приводит к ослаблению электрического поля на входе в образец и его усилению на выходе. С учетом изменения фазы при отражении это явление проиллюстрировано на рис. 29.2. Простые выкладки с помощью формул Френеля дают

Для типичного стекла  Это дает
Это дает


Рис. 29.1. Распространение светового пучка и направления вектора Е при полном внутреннем отражении в призме.

Рис. 29.2. Изменения амплитуды и фазы электрического поля на границах прозрачного диэлектрика.
Следовательно,

Крисп с сотрудниками исследовали повреждения на входных и выходных поверхностях стекла и обнаружили, что асимметрия пороговых значений интенсивности при поверхностных повреждениях целиком обусловлена интерференцией падающего и отраженного пучков, т. е. описывается простой моделью френелевского отражения. Экспериментальные данные хорошо согласуются с результатами расчетов по формулам Френеля. Увеличение электрического поля на выходе из диэлектрика приводит к уменьшению порога пробоя по сравнению с входной поверхностью. Действительно, в эксперименте сначала наблюдаются искра и возникновение плазмы на выходной поверхности и лишь после некоторого увеличения мощности пучка — также на входной поверхности.
Однако объяснение асимметрии только френелевским отражением не вполне обосновано и не согласуется с некоторыми экспериментальными фактами. Часто наблюдается повреждение стеклянных кювет с внутренней стороны, т. е. на границе стекло — жидкость,

Рис. 29.3. Пробой на внутренней и наружной поверхностях стекла под действием пучка рубинового лазера. Пучок распространяется слева направо. Сначала возникает пробои на внутренней поверхности и лишь после увеличения мощности лазера — также на наружной (отдел квантовой электроники Института физики Университета им. Адама Мицкевича в Познани).

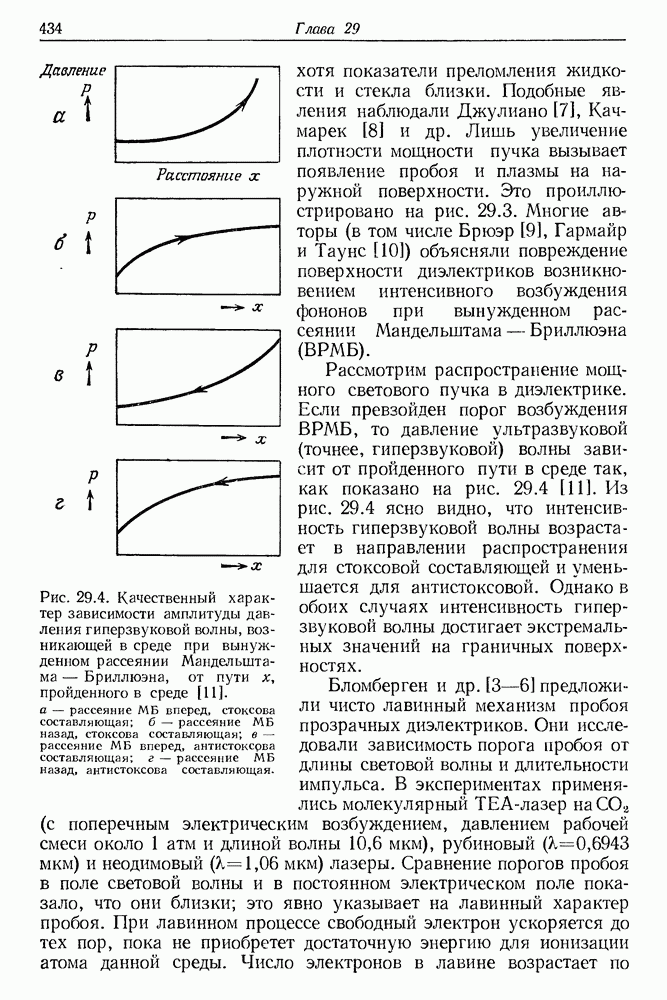
Рис. 29.4. Качественный характер зависимости амплитуды давления гиперзвуковой волны, возникающей в среде при вынужденном рассеянии Мандельштама — Бриллюэна, от пути х, пройденного в среде [11]. а — рассеяние МБ вперед, стоксова составляющая; б - рассеяние МБ назад, стоксова составляющая; в — рассеяние МБ вперед, антистоксова составляющая; г - рассеяние МБ назад, антистоксова составляющая.
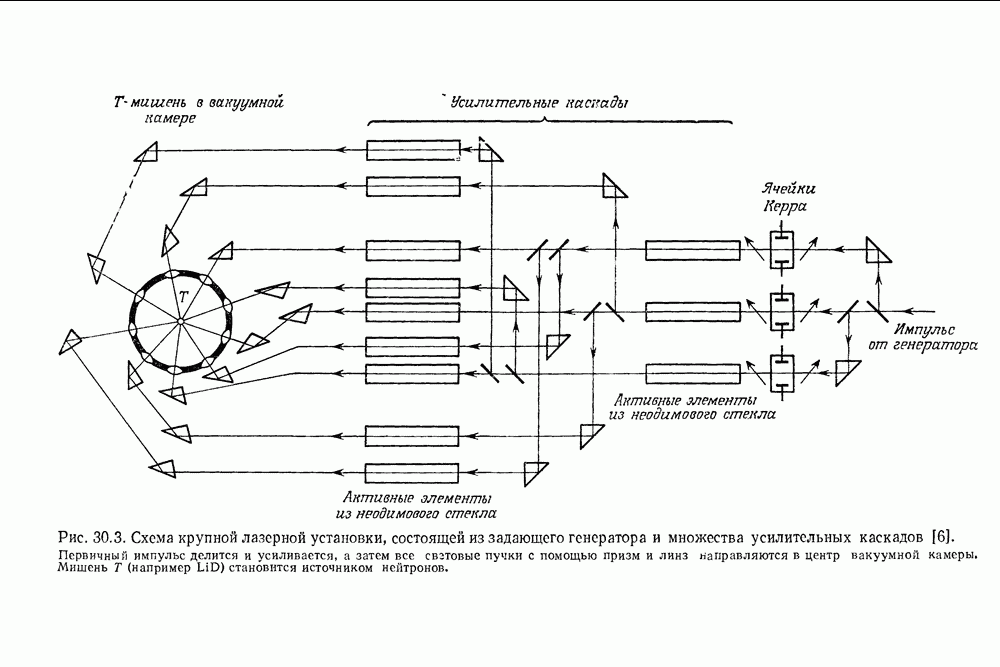
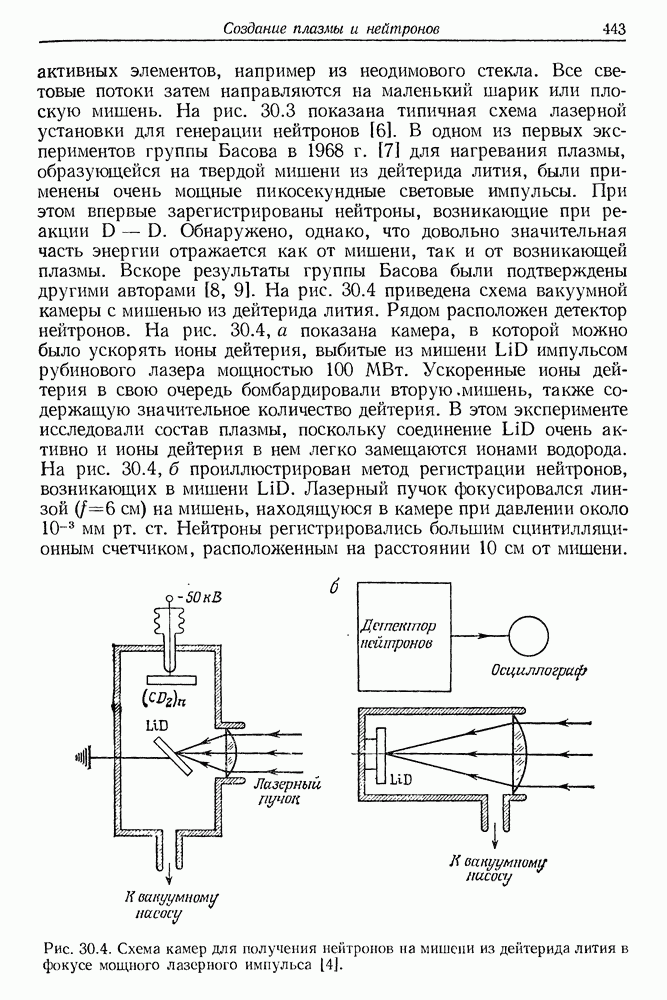
хотя показатели преломления жидкости и стекла близки. Подобные явления наблюдали Джулиано [7], Качмарек [8] и др. Лишь увеличение плотности мощности пучка вызывает появление пробоя и плазмы на наружной поверхности. Это проиллюстрировано на рис. 29.3. Многие авторы (в том числе Брюэр [9], Гармайр и Таунс [10]) объясняли повреждение поверхности диэлектриков возникновением интенсивного возбуждения фононов при вынужденном рассеянии Мандельштама — Бриллюэна (ВРМБ).
Рассмотрим распространение мощного светового пучка в диэлектрике. Если превзойден порог возбуждения ВРМБ, то давление ультразвуковой (точнее, гиперзвуковой) волны зависит от пройденного пути в среде так, как показано на рис. 29.4 [11]. Из рис. 29.4 ясно видно, что интенсивность гиперзвуковой волны возрастает в направлении распространения для стоксовой составляющей и уменьшается для антистоксовой. Однако в обоих случаях интенсивность гиперзвуковой волны достигает экстремальных значений на граничных поверхностях.
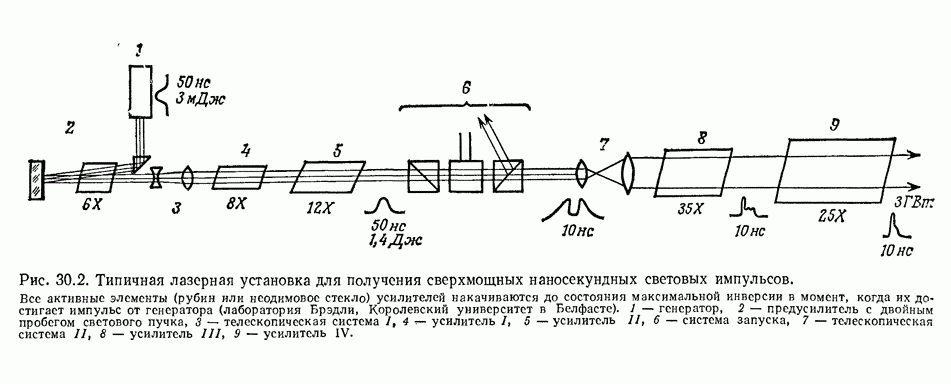
Бломберген и др. [3—6] предложили чисто лавинный механизм пробоя прозрачных диэлектриков. Они исследовали зависимость порога пробоя от длины световой волны и длительности импульса. В экспериментах применялись молекулярный ТЕА-лазер  (с поперечным электрическим возбуждением, давлением рабочей смеси около 1 атм и длиной волны 10,6 мкм), рубиновый (
(с поперечным электрическим возбуждением, давлением рабочей смеси около 1 атм и длиной волны 10,6 мкм), рубиновый ( мкм) и неодимовый (
мкм) и неодимовый ( мкм) лазеры. Сравнение порогов пробоя в поле световой волны и в постоянном электрическом поле показало, что они близки; это явно указывает на лавинный характер пробоя. При лавинном процессе свободный электрон ускоряется до тех пор, пока не приобретет достаточную энергию для ионизации атома данной среды. Число электронов в лавине возрастает по
мкм) лазеры. Сравнение порогов пробоя в поле световой волны и в постоянном электрическом поле показало, что они близки; это явно указывает на лавинный характер пробоя. При лавинном процессе свободный электрон ускоряется до тех пор, пока не приобретет достаточную энергию для ионизации атома данной среды. Число электронов в лавине возрастает по
закону

где  — коэффициент ионизации для одного электрона в единицу времени,
— коэффициент ионизации для одного электрона в единицу времени,  — число Ьервичных электронов. Увеличение числа электронов зависит от пути, проходимого электроном между электродами (при разряде постоянного тока). Если скорость дрейфа электронов равна
— число Ьервичных электронов. Увеличение числа электронов зависит от пути, проходимого электроном между электродами (при разряде постоянного тока). Если скорость дрейфа электронов равна  а расстояние между электродами х, то
а расстояние между электродами х, то

При этом экспоненциальный множитель в формуле (29.4) принимает вид

где
Зависимость порога пробоя от толщины образца позволяет определить коэффициент ионизации. Действительно,

Пробой наступает, когда  достигает значения порядка
достигает значения порядка  При этом
При этом  равно
равно  . Следовательно,
. Следовательно,

где  — длительность лазерного импульса. Здесь принято, что поле световой волны квазистационарно. Для кристалла NaCl коэффициенты
— длительность лазерного импульса. Здесь принято, что поле световой волны квазистационарно. Для кристалла NaCl коэффициенты  приближенно равны:
приближенно равны:

Скорость нарастания энергии электрона в классическом приближении описывается формулой

 — время между соударениями. Как прирост энергии электрона, так и эффективность ионизации зависят от произведения сот. Для молекулярного лазера
— время между соударениями. Как прирост энергии электрона, так и эффективность ионизации зависят от произведения сот. Для молекулярного лазера  для «горячих» электронов порядка
для «горячих» электронов порядка  ; следовательно,
; следовательно,  Поэтому поле световой волны можно считать квазистационарным. Согласно Бломбергену, поле напряженностью
Поэтому поле световой волны можно считать квазистационарным. Согласно Бломбергену, поле напряженностью  является пороговым для различных типов пробоя в веществе.
является пороговым для различных типов пробоя в веществе.
Для кристалла NaCl пробивные напряженности поля имели следующие значения:


Бломберген с сотрудниками использовали в своих экспериментах одномодовые лазерные пучки. Фокусировка пучков производилась безаберрационными линзами. Таким образом, диаметр светового пятна в фокусе определялся лишь дифракционной расходимостью. Он составлял около 100 мкм для молекулярного лазера  и 10—20 мкм для рубинового или неодимового лазеров.
и 10—20 мкм для рубинового или неодимового лазеров.
Если благодаря самофокусировке диаметр светового канала в диэлектрике уменьшается до нескольких десятков микрон или даже до нескольких микрон, то в центральной части канала часто возникают ионизация или пробой. Например, при диаметре светового канала, равном 5 мкм, диаметр нити дефектов в диэлектрике составляет лишь 1 мкм. В ионизованной области показатель преломления выражается следующей формулой [31:

где  — начальный (линейный) показатель преломления,
— начальный (линейный) показатель преломления,  — эффективная масса носителей тока. Действительная часть показателя преломления отрицательна, а мнимая часть описывает поглощение энергии световой волны. Плазма стабилизирует световой канал, возникший в результате самофокусировки. Диаметр наблюдаемых световых каналов не зависит от рода материала и составляет от 3 до 15 мкм. Если принять, что пробой целиком обусловлен лавинными процессами, то возникающая при этом плазма, хотя она вначале невидима и не дает эффектов, типичных для искры, может привести к самофокусировке благодаря своим ярко выраженным нелинейным свойствам.
— эффективная масса носителей тока. Действительная часть показателя преломления отрицательна, а мнимая часть описывает поглощение энергии световой волны. Плазма стабилизирует световой канал, возникший в результате самофокусировки. Диаметр наблюдаемых световых каналов не зависит от рода материала и составляет от 3 до 15 мкм. Если принять, что пробой целиком обусловлен лавинными процессами, то возникающая при этом плазма, хотя она вначале невидима и не дает эффектов, типичных для искры, может привести к самофокусировке благодаря своим ярко выраженным нелинейным свойствам.
Уменьшение пороговой пробивной напряженности поля на поверхности диэлектрика по сравнению с порогом пробоя внутри того же образца Бломберген [3] объясняет локальным усилением поля на дефектах поверхности. На рис. 29.5 изображены три типа дефектов: в форме сферической  или цилиндрической
или цилиндрической  раковины и в форме
раковины и в форме  -образного кратера
-образного кратера  В общем случае электрическое поле в полости равно
В общем случае электрическое поле в полости равно

где  — коэффициент деполяризации, зависящий от формы полости. Для сферы
— коэффициент деполяризации, зависящий от формы полости. Для сферы  поэтому поле в области А равно
поэтому поле в области А равно


Рис. 29.5. Виды дефектов на поверхности диэлектрика, существенно изменяющих напряженность локального электрического поля. Типичные размеры дефектов:  мкм,
мкм,  мкм, мкм [3].
мкм, мкм [3].
Если  то Для цилиндрической полости
то Для цилиндрической полости  откуда
откуда

При  получаем
получаем 
Наконец, для  -образного кратера
-образного кратера

При —1 получаем 
Для кристалла  мкм). В этом случае усиление поля максимально.
мкм). В этом случае усиление поля максимально.
Действительно, экспериментально обнаружена зависимость порога пробоя от качества поверхности диэлектрика. Отношения порогов пробоя на поверхности и внутри образца составляли: около 1,21 (для шаровидных дефектов), от 1,35 до 1,39 (для цилиндрических дефектов) и от 2,2 до 2,35 (для  -образных кратеров).
-образных кратеров).
Если поверхность образца была очищена ионной бомбардировкой, то в пределах ошибок измерений разница между порогами пробоя на поверхности и внутри прозрачного диэлектрика отсутствовала. Пробивные напряженности в абсолютных единицах для ряда материалов равны:
плавленый кварц  В/см,
В/см,
сапфир  В/см,
В/см,
оптическое стекло типа  В/см.
В/см.
Эти значения относятся к пробою внутри материала пучком молекулярного лазера  мкм).
мкм).
Следует также отметить тот факт, что применение очень коротких (пикосекундных) световых импульсов и осуществление пробоя в канале диаметром в несколько микрон в значительной степени исключают влияние дефектов и загрязнений на величину порогового пробивного поля. Подробное обсуждение вопросов пробоя конденсированных сред лазерными пучками читатели могут найти в работе Гласса и Гутера [12].
Вопросы пробоя лазерными пучками до сих пор не утратили своего значения. В отделе квантовой электроники Института
физики Университета им. Адама Мицкевича подобные работы были начаты давно, а в последние годы теоретические и экспериментальные исследования пробоя возобновлены. Например, теоретические работы, которые на начальном этапе были посвящены пробою в разреженных средах, выявили сильную зависимость порога пробоя (при многофотонной ионизации) от состояния поляризации света. Нельзя согласиться с утверждением, что пробой целиком определяется лавинными процессами, хотя не исключено, что в некоторых условиях эти процессы играют преобладающую роль. В частности, не решена проблема возникновения первых электронов, инициирующих лавинный процесс. Не полностью выяснены причины низкого порога пробоя на поверхности тела, хотя отчасти это можно объяснить с помощью модели френелевского отражения или гипотезы Бломбергена, которые включают как случаи усиления, так и ослабления электрического поля световой волны на поверхности. Экспериментальное изучение эффектов пробоя весьма осложняется трудностью получения чистых поверхностей и материалов. Так, в обычных условиях при выплавке стекла или выращивании кристаллов в образец вносятся загрязнения, которые снижают порог пробоя. Это подтверждено многими экспериментами. Вначале казалось, что проблема чистоты образца не будет играть столь существенной роли, как в глучае пробоя в постоянных полях. Это привело к относительно большим расхождениям в литературных данных о порогах пробоя газов и конденсированных сред.
Таким образом, проблема пробоя материалов лазерным пучком требует дальнейших исследований, как теоретических, так и экспериментальных.
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
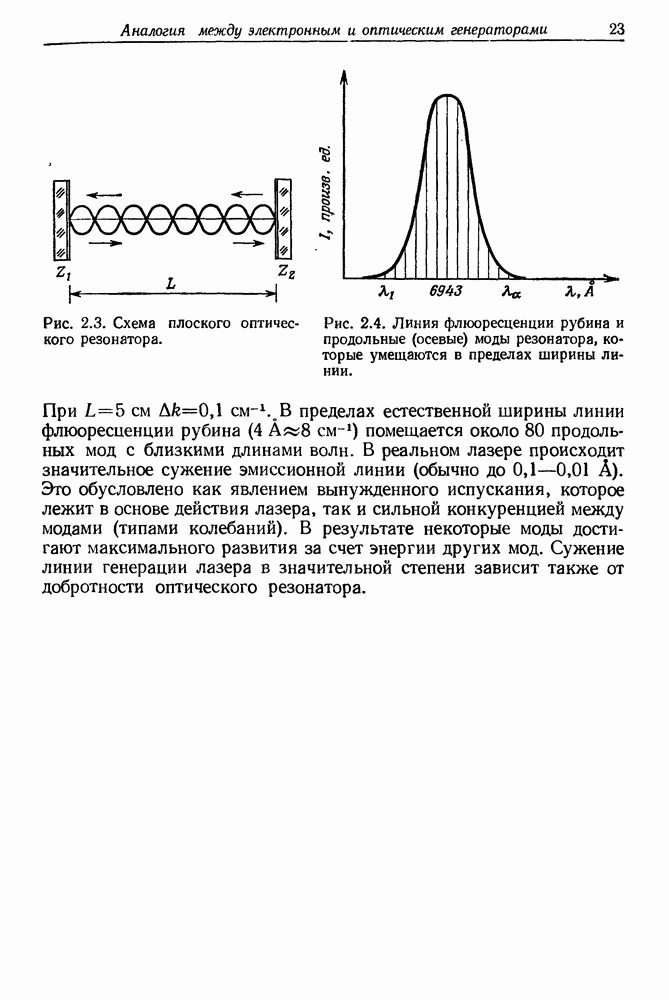
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
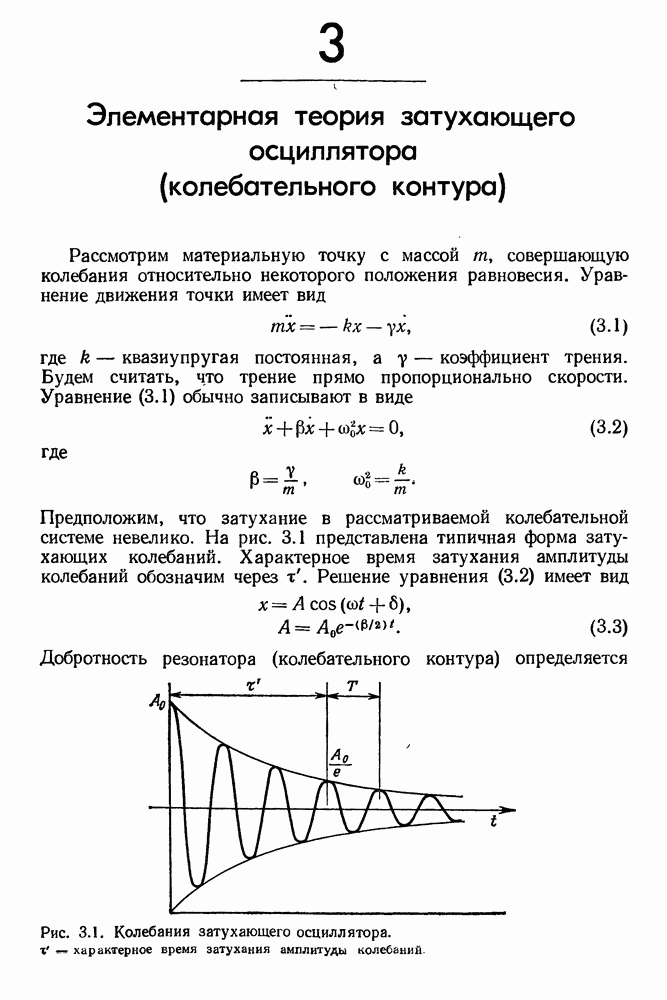
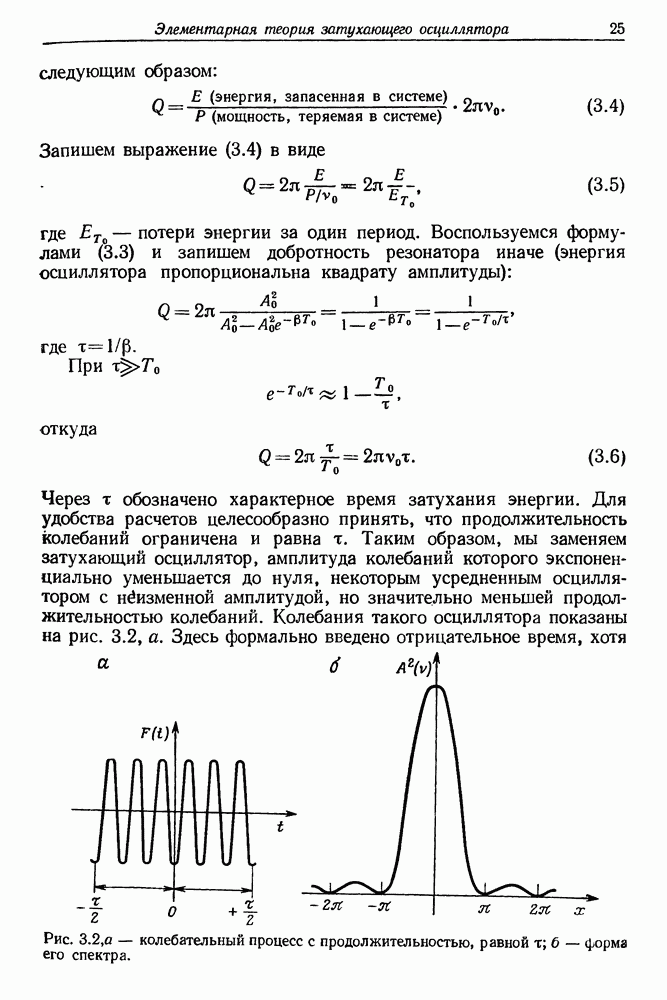
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
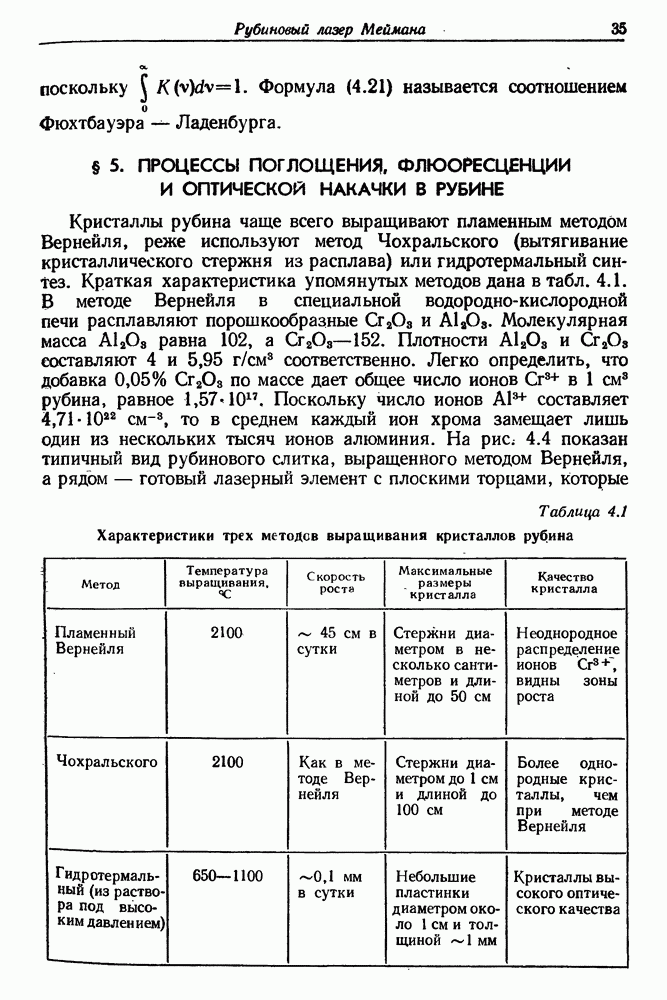
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
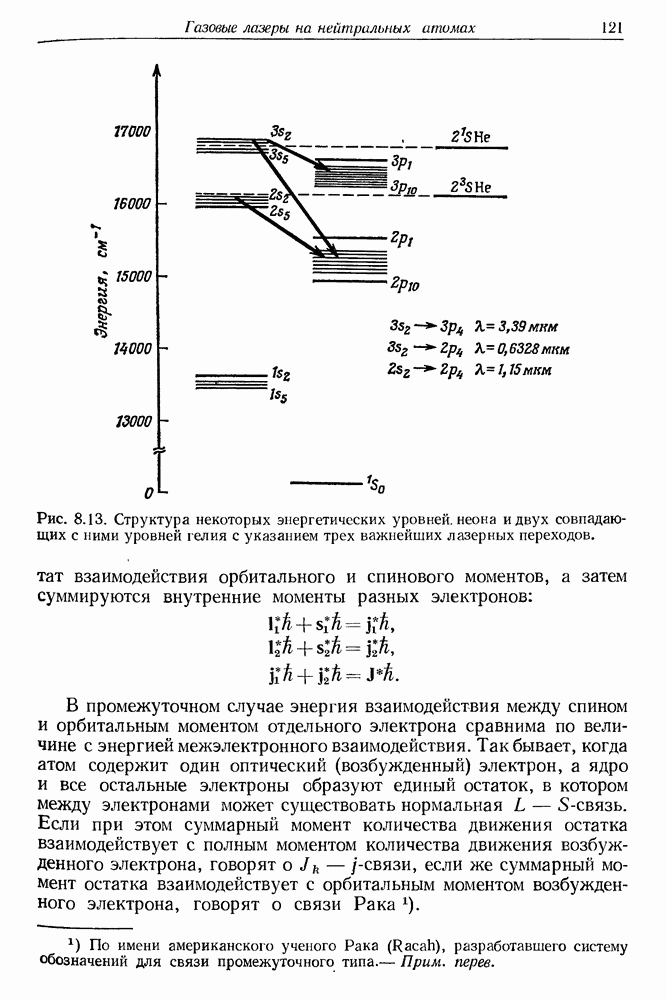
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
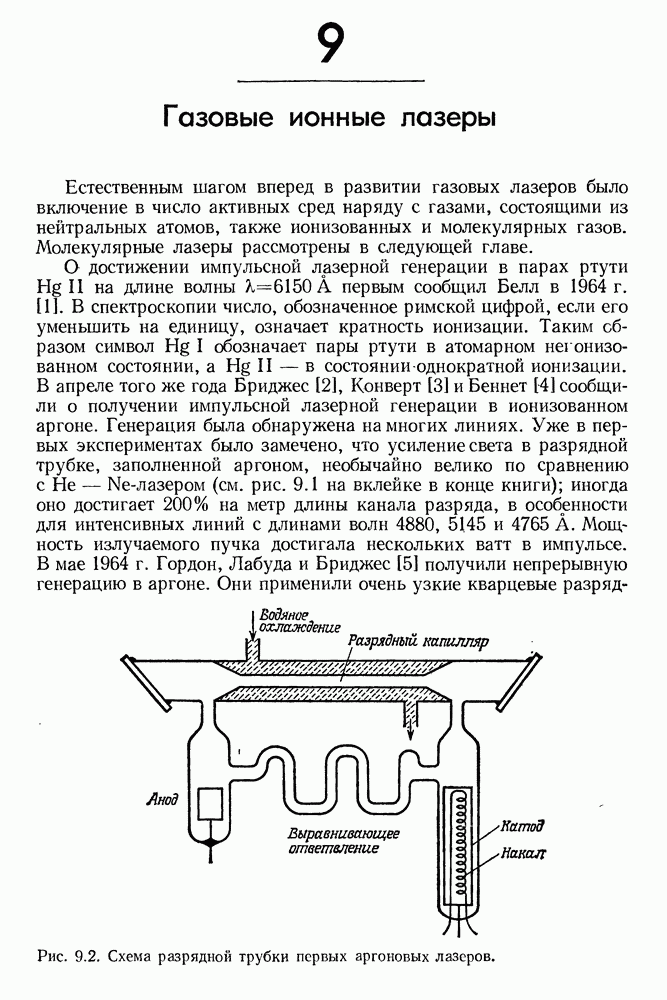
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
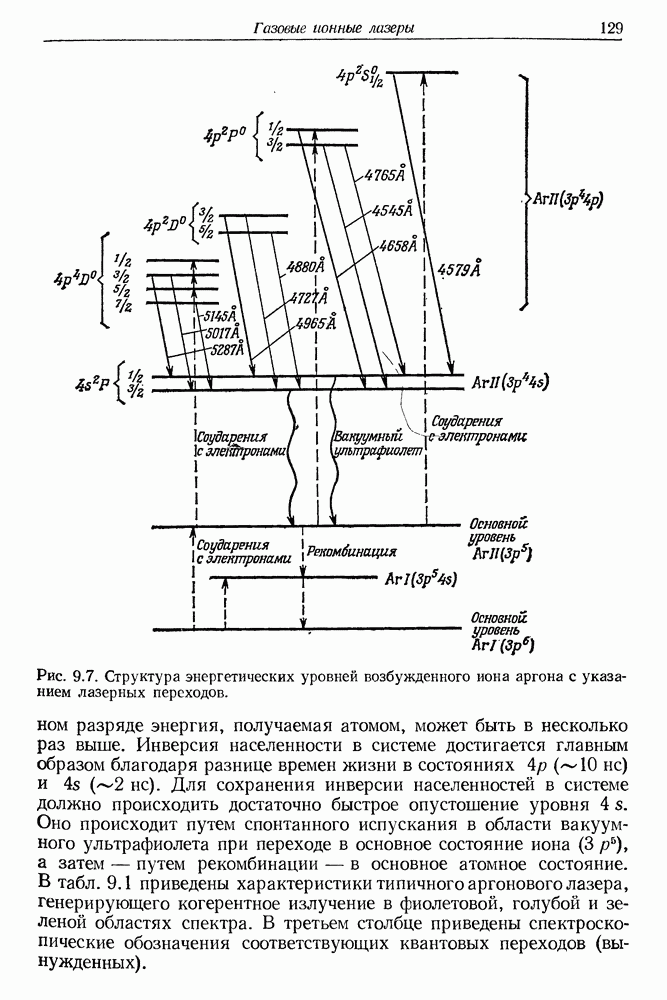
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
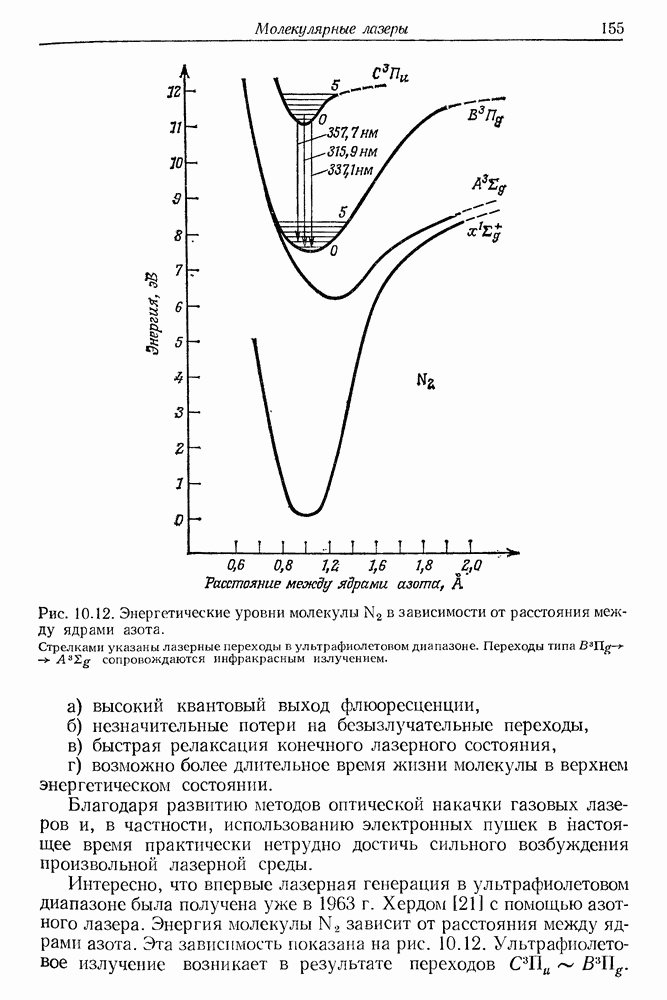
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
- б. Вращающаяся призма
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
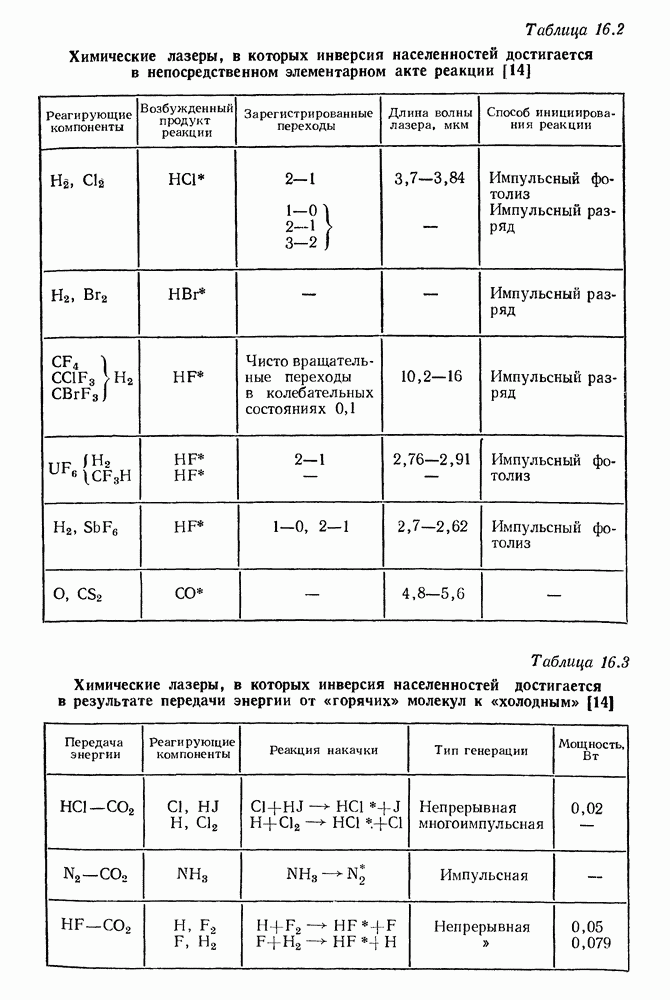
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
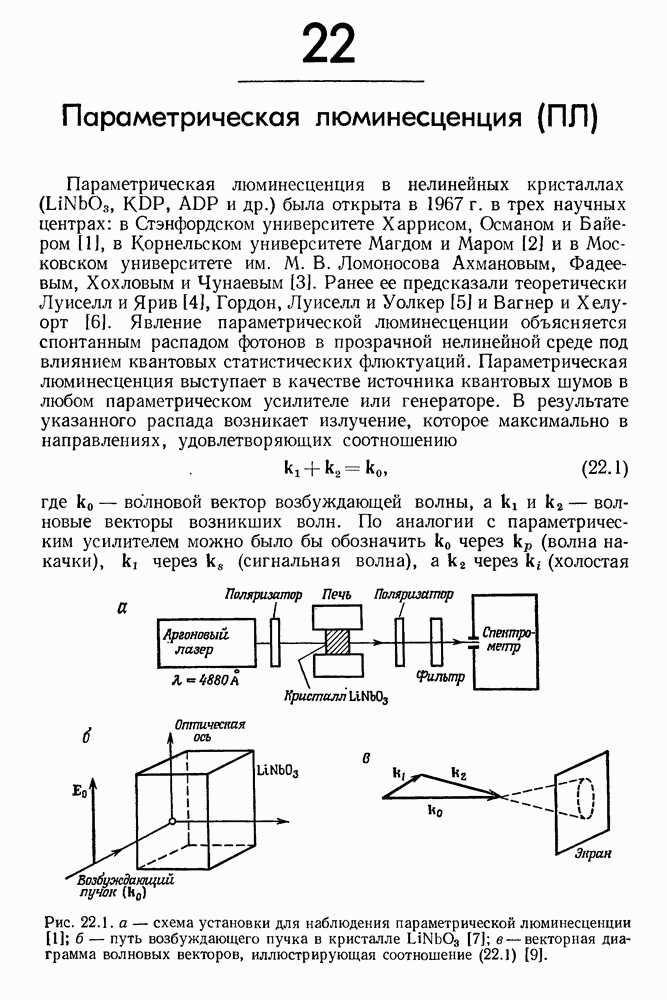
- 22. Параметрическая люминесценция (ПЛ)
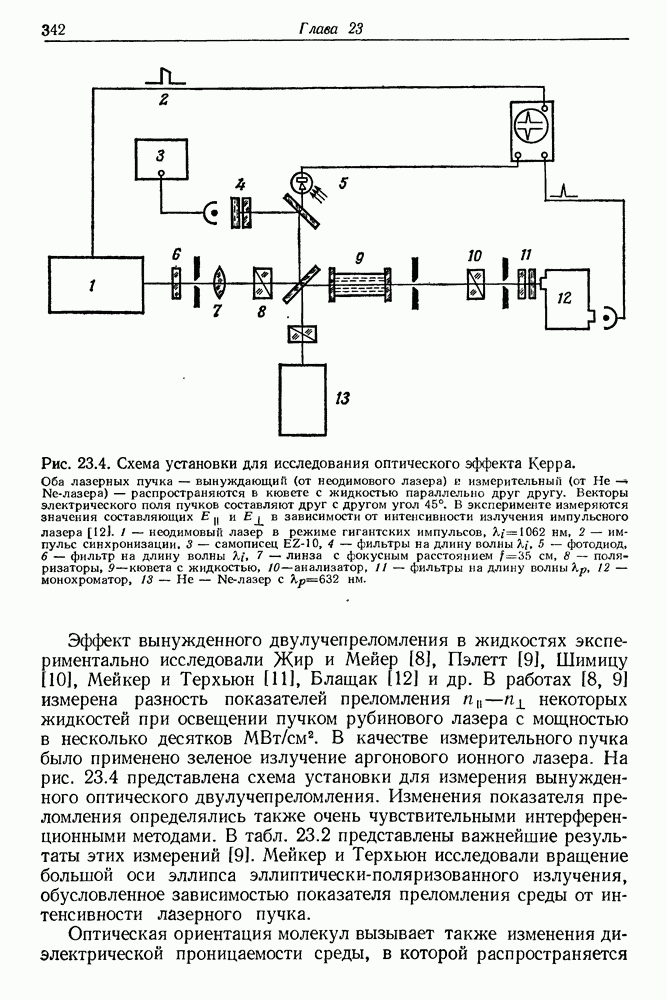
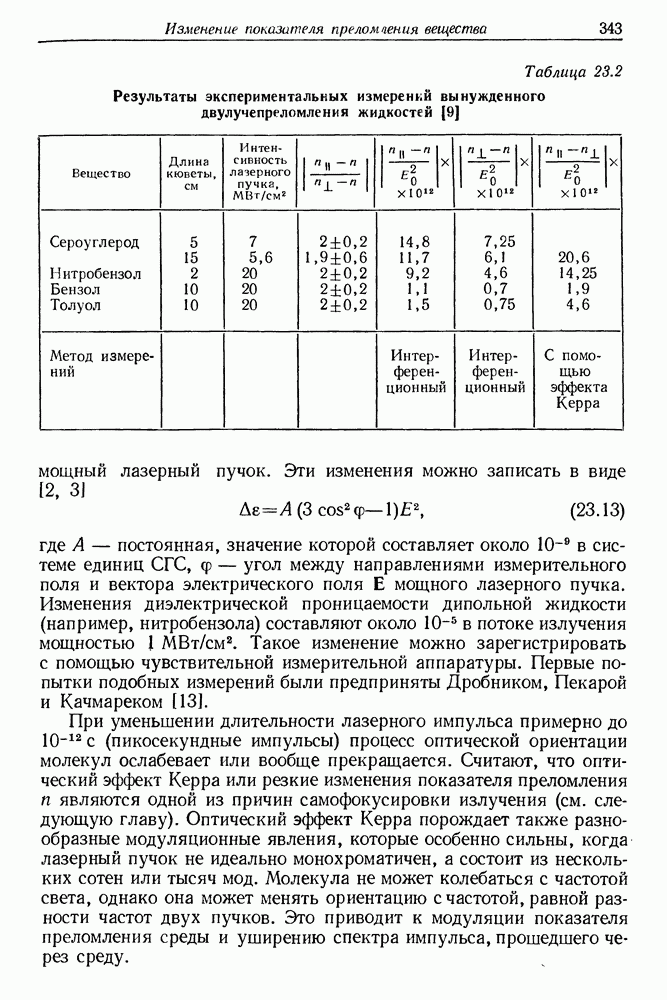
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
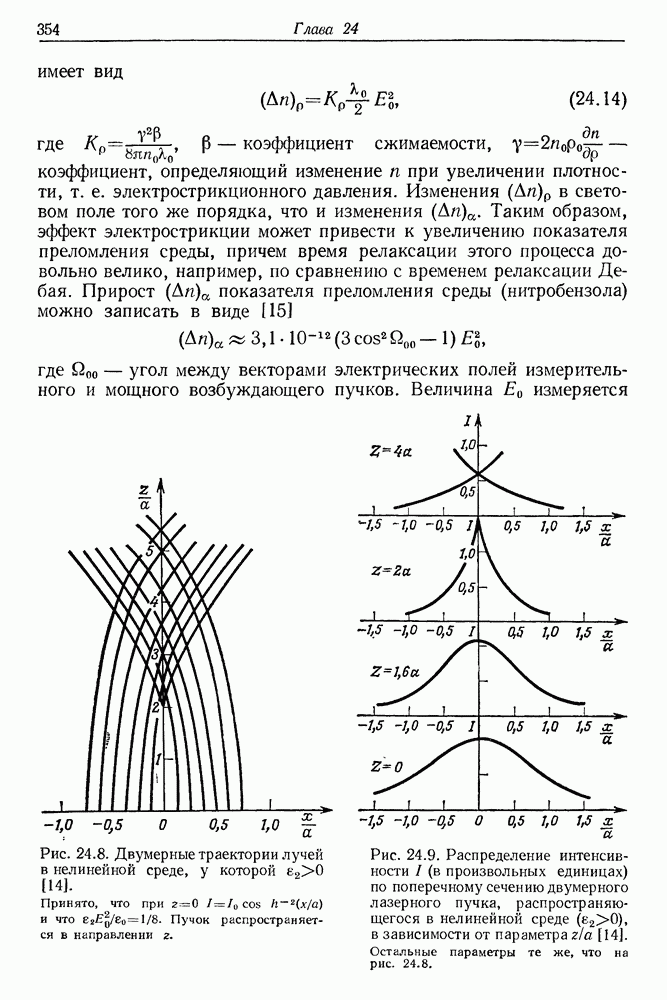
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
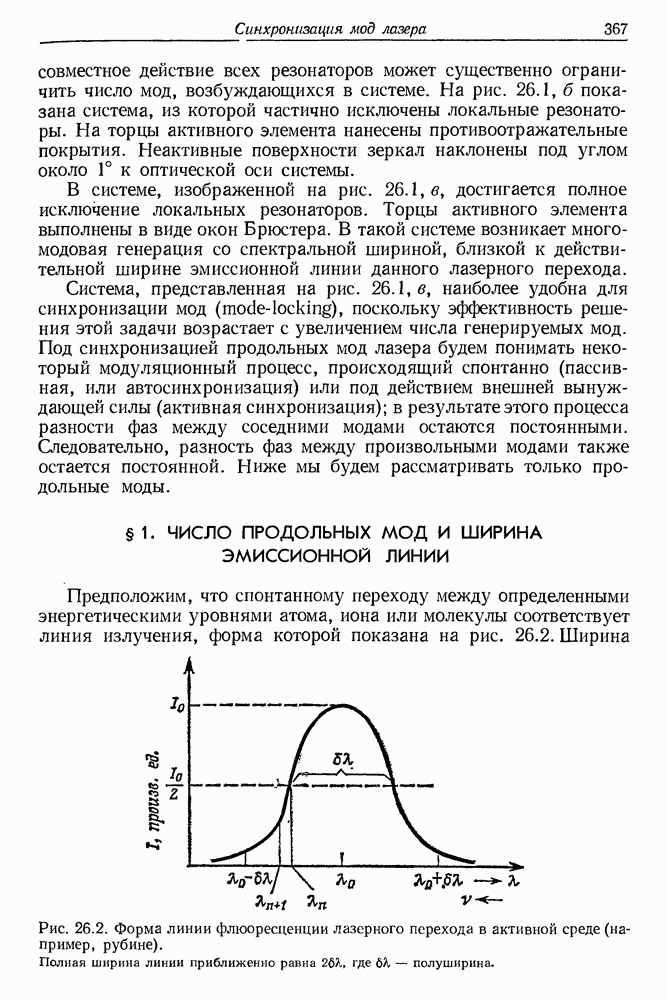
- 26. Синхронизация мод лазера
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
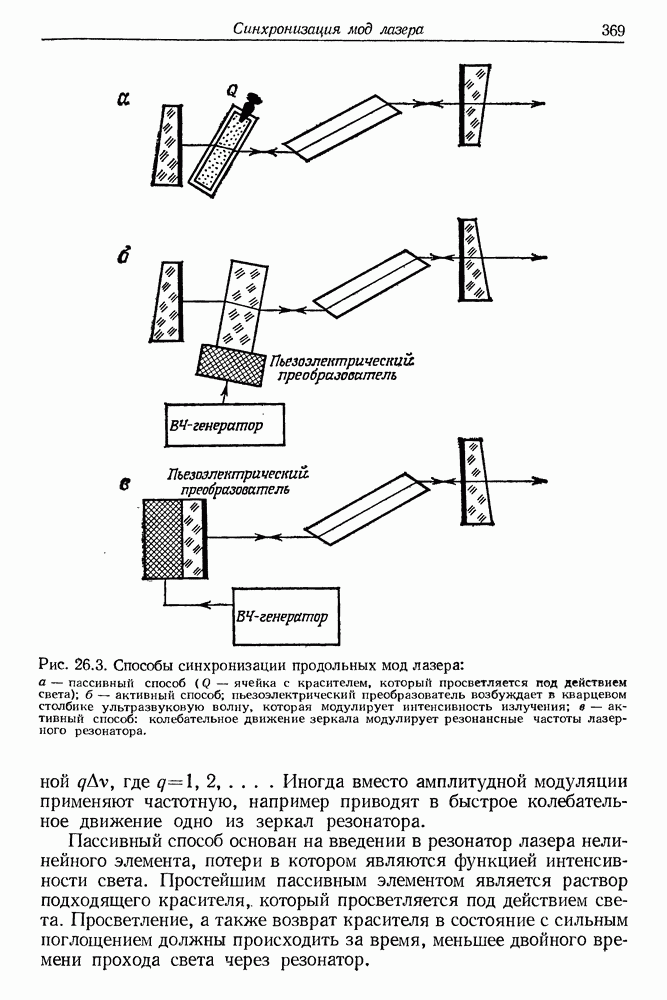
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
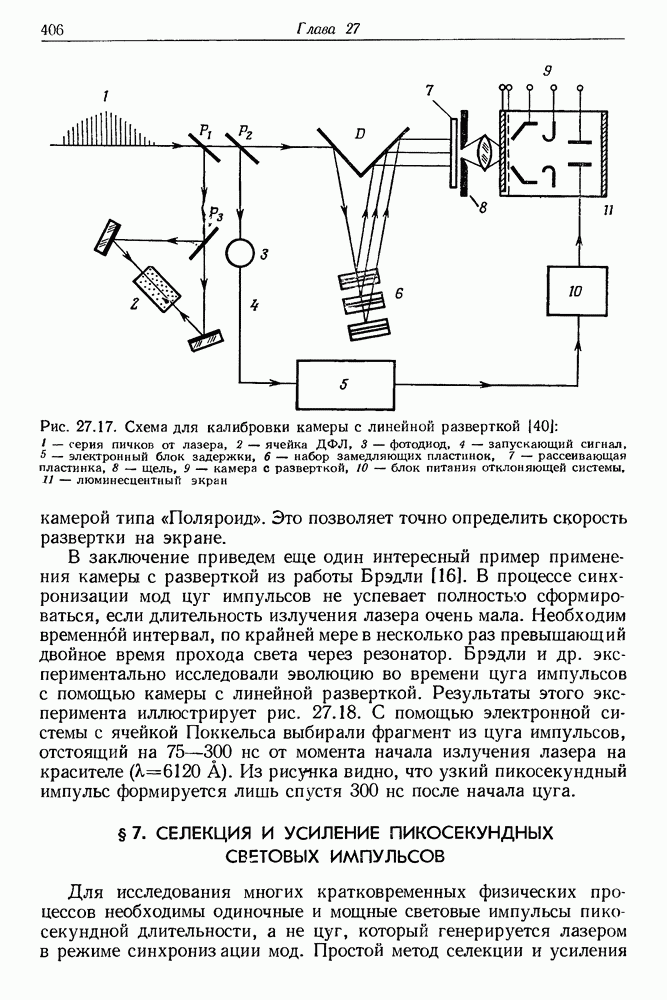
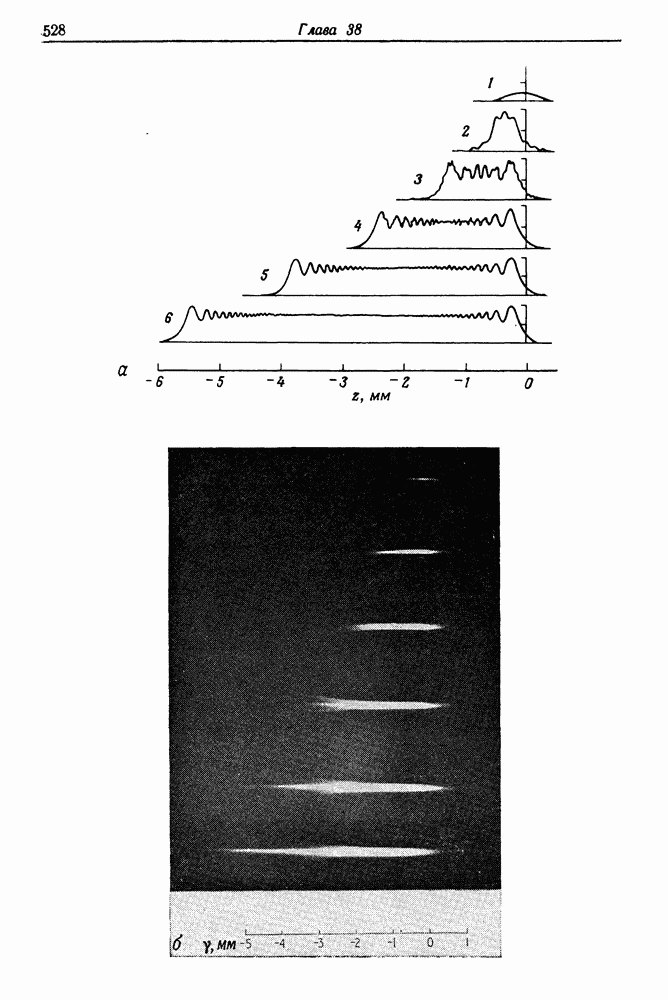
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
- в. Примеры использования камеры с разверткой
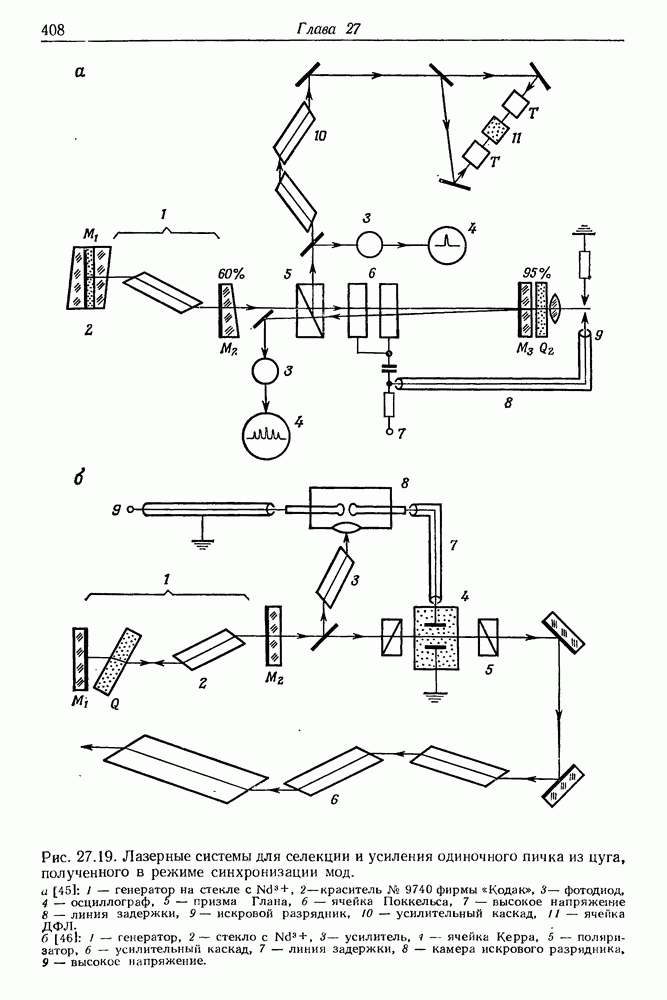
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
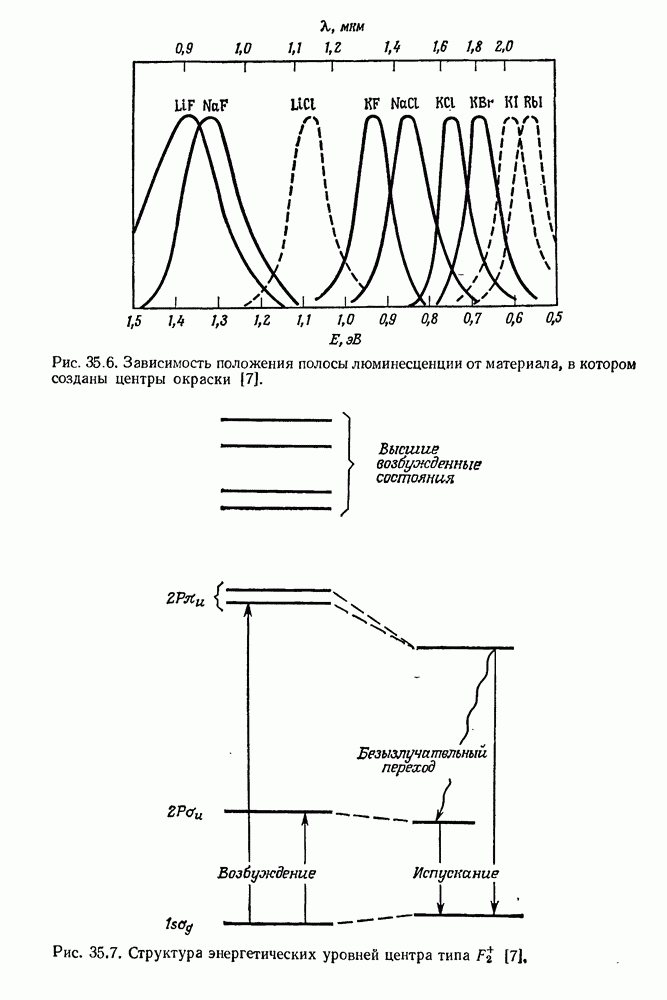
- 35. Лазеры на центрах окраски
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
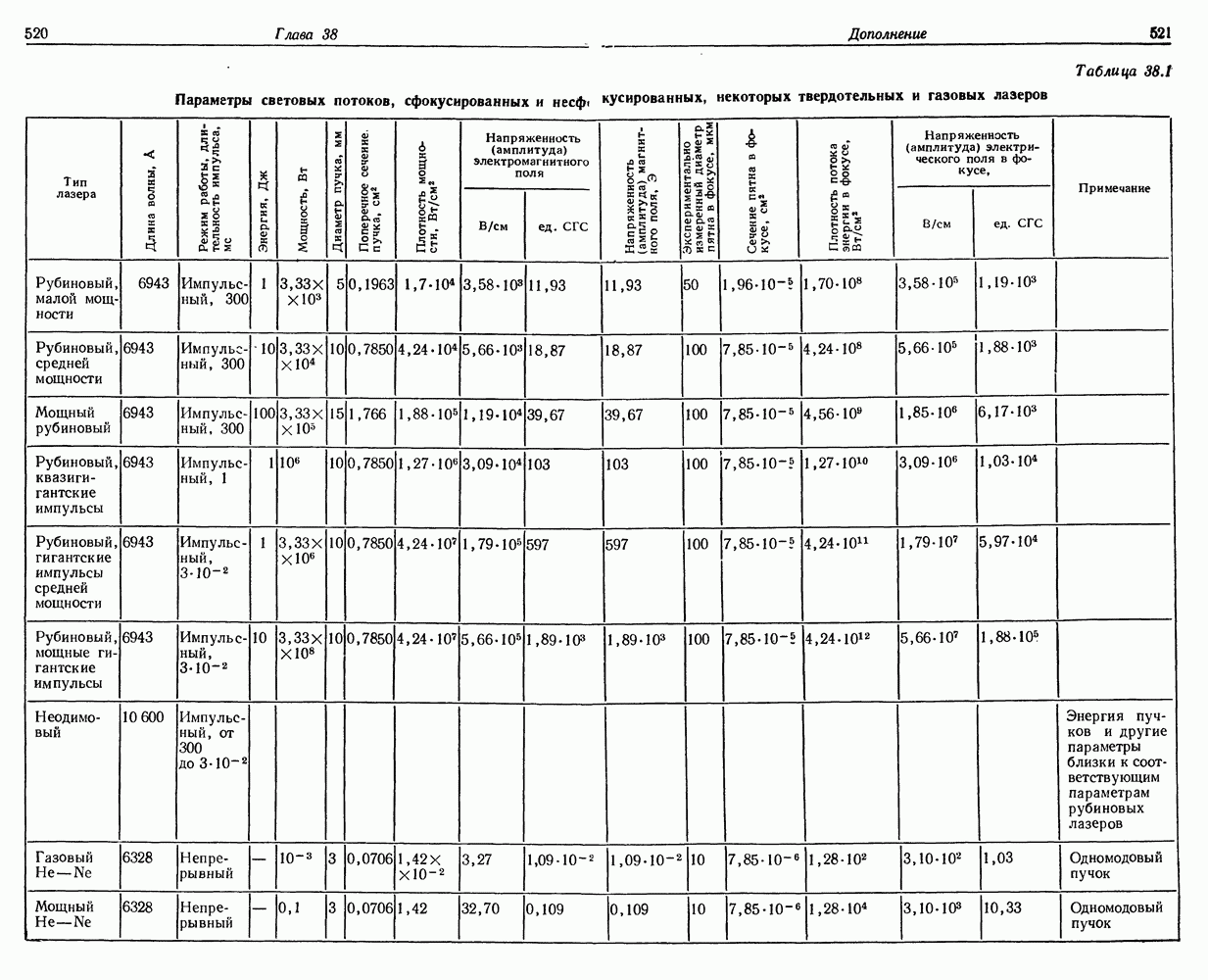
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
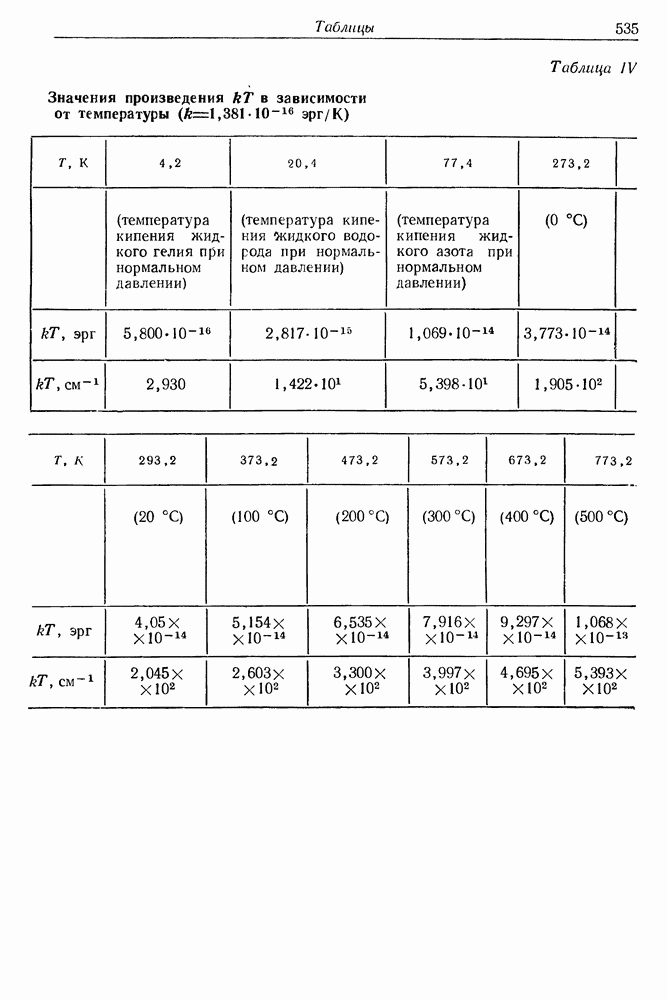
- Таблицы