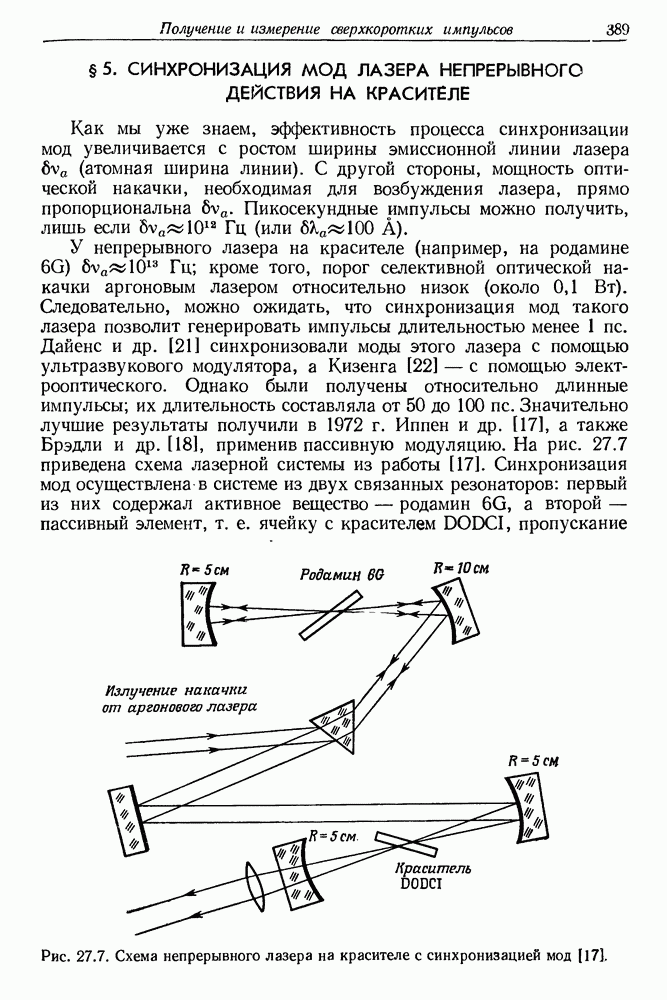
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
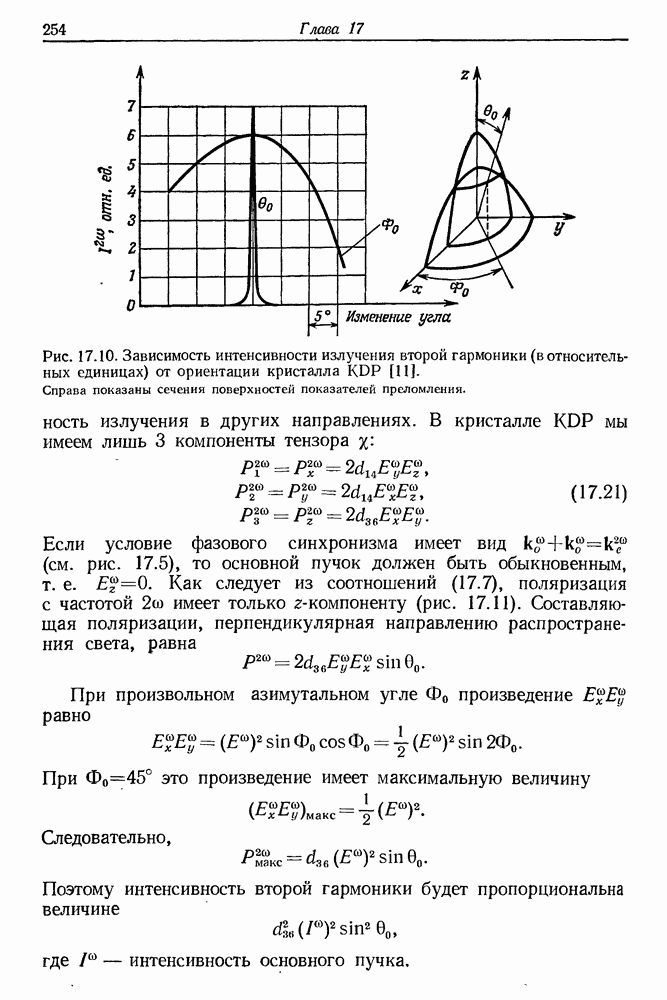
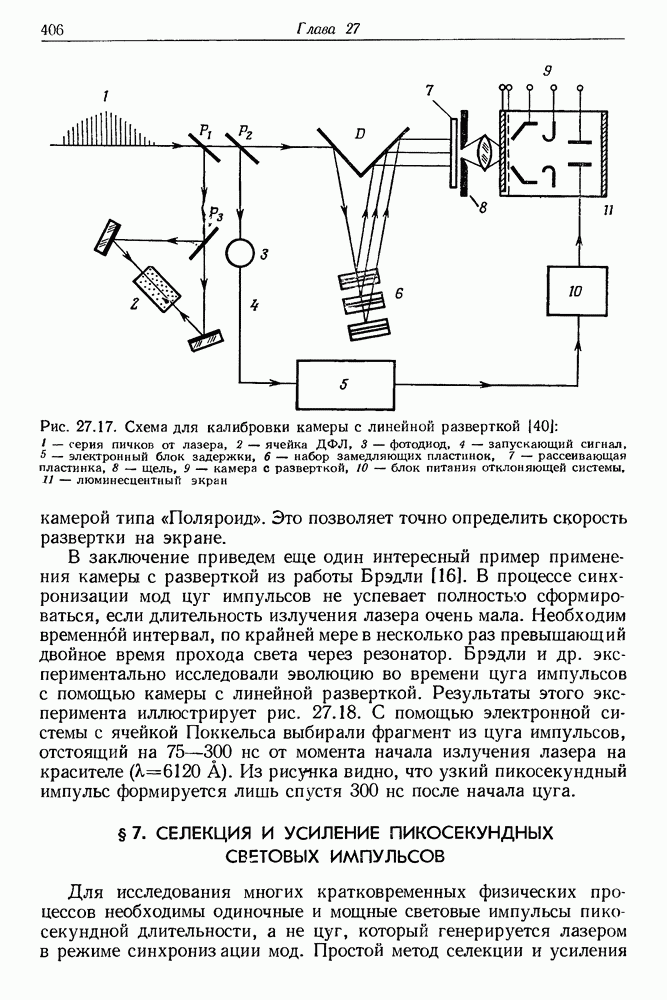
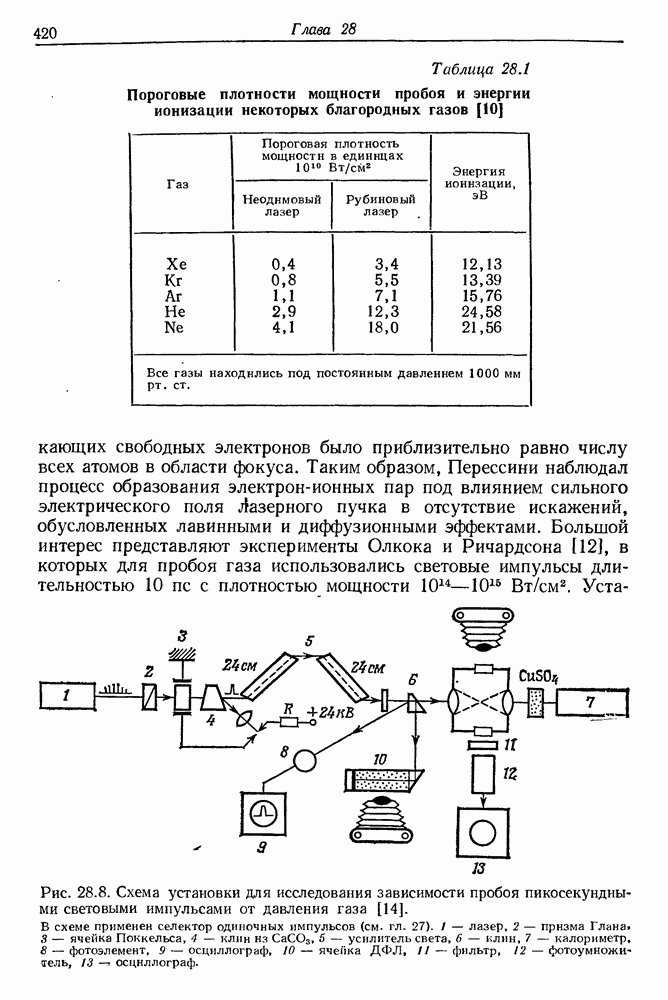
33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
Среди многочисленных физических и физико-химических применений сверхкоротких импульсов света особый интерес представляет нано- и пикосекундная спектроскопия испускания и поглощения. В этой области спектроскопии чаще всего применяют комбинацию коротких монохроматических импульсов или одного монохроматического импульса и континуума, который относительно легко получить, например методом фазовой самомодуляции.
§ 1. СПЕКТРАЛЬНОЕ УШИРЕНИЕ ЛАЗЕРНОГО ПУЧКА
Рассмотрим сначала спектральное уширение коротких световых импульсов при распространении в нелинейных средах. Это уширение было обнаружено уже в 1963 — 1967 гг. в экспериментах Стойчева [11, Джонса и Стойчева [2], Бломбергена и Лаллеманда [31, Шимицу [4], Гармайр, Чиао и Таунса [5], Брюэра и Лифшица [63 и др.
В известном эксперименте группы Таунса 1964 г. был сфотографирован сужающийся световой канал лазерного пучка в жидкости и установлено, что самофокусировка приводит к расфазировке в отдельных точках поперечного сечения пучка на выходе. Свет, захваченный в канале, увеличивает показатель преломления среды и поэтому распространяется медленнее, чем в невозмущенной части среды. По измеренной разности фаз на выходе из кюветы с жидкостью определили изменения показателя преломления. Они составили  . Брюэр и Лифшиц [6] получили еще большие изменения показателя преломления:
. Брюэр и Лифшиц [6] получили еще большие изменения показателя преломления:  Оказалось, что относительные изменения показателя преломления в каналах диаметром в несколько микрон, образующихся при самофокусировке, могут достигать даже 10%. Столь значительные изменения показателя преломления приводят к расфазировке световых лучей. Отметим, что эта расфазировка является функцией квадрата напряженности электрического поля световой волны.
Оказалось, что относительные изменения показателя преломления в каналах диаметром в несколько микрон, образующихся при самофокусировке, могут достигать даже 10%. Столь значительные изменения показателя преломления приводят к расфазировке световых лучей. Отметим, что эта расфазировка является функцией квадрата напряженности электрического поля световой волны.
Бломберген и Лаллеманд [3] показали, что в активных с точки зрения комбинационного рассеяния жидкостях, состоящих из анизотропно-поляризуемых молекул, могут появляться боковые полосы в результате возникновения связи между различными модами лазерного пучка. Некоторую роль в спектральном уширении играет
также вынужденное рассеяние в крыле линии Рэлея (см. гл. 21). Рассмотрим ансамбль молекул, обладающих осевой симметрией [3]. Пусть в лазерном пучке присутствуют две моды с частотами  причем
причем  Соответствующие напряженности электрического поля обозначим через
Соответствующие напряженности электрического поля обозначим через  и
и  Допустим также, что пучки линейно-поляризованы в одной и той же плоскости. Молекула может реагировать на ориентирующий момент, который зависит от разности частот
Допустим также, что пучки линейно-поляризованы в одной и той же плоскости. Молекула может реагировать на ориентирующий момент, который зависит от разности частот  Вероятность того, что ось молекулы окажется внутри телесного угла
Вероятность того, что ось молекулы окажется внутри телесного угла  составляющего угол
составляющего угол  с направлением поля, равна
с направлением поля, равна

где  и — главные оптические поляризуемости молекулы.
и — главные оптические поляризуемости молекулы.
Явление оптической ориентации молекул рассмотрено подробнее в гл. 23 (оптический эффект Керра). Член, зависящий от времени, изменяется с частотой  Характерное время
Характерное время  называемое временем релаксации анизотропии, равно
называемое временем релаксации анизотропии, равно

Здесь а — радиус молекулы,  — коэффициент вязкости. Анизотропный член в выражении (33.1) приводит к зависимости показателя преломления жидкости от интенсивности света, причем эта зависимость промодулирована частотой
— коэффициент вязкости. Анизотропный член в выражении (33.1) приводит к зависимости показателя преломления жидкости от интенсивности света, причем эта зависимость промодулирована частотой  Рассмотрим третий линейно-поляризованный пучок, частота которого
Рассмотрим третий линейно-поляризованный пучок, частота которого  достаточно сильно отличается от
достаточно сильно отличается от  Изменение показателя преломления равно
Изменение показателя преломления равно

где  показатель преломления,
показатель преломления,  — коэффициент, который зависит от значения локального поля (поправка на локальное поле). Модулирующий член дает боковые полосы, удаленные от на
— коэффициент, который зависит от значения локального поля (поправка на локальное поле). Модулирующий член дает боковые полосы, удаленные от на  Если разность
Если разность  невелика, пространственной дисперсией можно пренебречь.
невелика, пространственной дисперсией можно пренебречь.
Бломберген и Лаллеманд показали экспериментально, что свет действительно промодулирован частотой  Лазерный пучок с двумя продольными модами, отстоящими друг от друга на
Лазерный пучок с двумя продольными модами, отстоящими друг от друга на
 фокусировали в циклогексан с добавкой
фокусировали в циклогексан с добавкой  Добавка в кювету
Добавка в кювету  приводила к широкой модуляции частоты стоксовой линии комбинационного рассеяния
приводила к широкой модуляции частоты стоксовой линии комбинационного рассеяния  в полосе около 140 А. Остальные стоксовы линии были также промодулированы по частоте. Теоретические и экспериментальные исследования Бломбергена и Лаллеманда показывают, что эффект спектрального уширения линии лазера обусловлен, в частности, возбуждением линий комбинационного рассеяния и их модуляцией благодаря существованию различных мод лазера. Модуляция эта происходит в нелинейной среде.
в полосе около 140 А. Остальные стоксовы линии были также промодулированы по частоте. Теоретические и экспериментальные исследования Бломбергена и Лаллеманда показывают, что эффект спектрального уширения линии лазера обусловлен, в частности, возбуждением линий комбинационного рассеяния и их модуляцией благодаря существованию различных мод лазера. Модуляция эта происходит в нелинейной среде.
В то же время Шимицу [4] считает, что спектральное уширение объясняется прежде всего фазовой самомодуляцией. Зависимость показателя преломления среды от  вносит значительные, возмущения в распространение лазерного излучения. Теоретически этот эффект подробнее исследовали Де Мартини и др. [7] и Луговой и Прохоров [8]. Рассмотрим основные результаты работ [7, 8]. В нелинейной среде сверхкороткий импульс (особенно пикосекундный) подвергается сжатию. Средняя часть импульса, где интенсивность максимальна, распространяется медленнее, чем его задний фронт. Предположим, что импульс входит в нелинейную среду в точке
вносит значительные, возмущения в распространение лазерного излучения. Теоретически этот эффект подробнее исследовали Де Мартини и др. [7] и Луговой и Прохоров [8]. Рассмотрим основные результаты работ [7, 8]. В нелинейной среде сверхкороткий импульс (особенно пикосекундный) подвергается сжатию. Средняя часть импульса, где интенсивность максимальна, распространяется медленнее, чем его задний фронт. Предположим, что импульс входит в нелинейную среду в точке  а его форму можно аппроксимировать выражением
а его форму можно аппроксимировать выражением

где  радиус пучка,
радиус пучка,  — поперечная координата, отсчитываемая от его оси.
— поперечная координата, отсчитываемая от его оси.
Примем также, что зависимость мощности импульса от времени имеет вид

где  — ширина импульса на полувысоте. Положим
— ширина импульса на полувысоте. Положим

где  линейный показатель преломления (измеряемый с помощью слабого светового сигнала). Опуская выкладки, которые читатель найдет в работе Лугового и Прохорова, приведем выражение для изменения частоты лазерного пучка:
линейный показатель преломления (измеряемый с помощью слабого светового сигнала). Опуская выкладки, которые читатель найдет в работе Лугового и Прохорова, приведем выражение для изменения частоты лазерного пучка:

Функция  является нечетной относительно точки
является нечетной относительно точки  и изменяется в пределах
и изменяется в пределах


Рис. 33.1. График функции  и спектральное распределение интенсивности лазерного импульса в нелинейной среде
и спектральное распределение интенсивности лазерного импульса в нелинейной среде 
На рис. 33.1 показан график функции  и соответствующее спектральное распределение интенсивности лазерного импульса. Спектральное распределение интенсивности на оси пучка имеет вид (черта над Е означает нестационарность этой величины)
и соответствующее спектральное распределение интенсивности лазерного импульса. Спектральное распределение интенсивности на оси пучка имеет вид (черта над Е означает нестационарность этой величины)

где  представляет собой фурье-образ
представляет собой фурье-образ

Если  то пределы интегрирования равны Ашмакс и Дсомин или
то пределы интегрирования равны Ашмакс и Дсомин или

В то же время

Подобное выражение получено Де Мартини и др. [7], Шимизу [4] и Дженком и Ландауэром [9]. Формулу (33.9) можно преобразовать к виду

где  скорость в линейной среде (для слабых световых сигналов). Относительные изменения частоты могут быть достаточно велики. В качестве иллюстрации используем следующие значения:
скорость в линейной среде (для слабых световых сигналов). Относительные изменения частоты могут быть достаточно велики. В качестве иллюстрации используем следующие значения:

Тогда


Рис. 33.2. Фрагмент спектрального уширения серии пикосекундных импульсов лазера на неодимовом стекле в образце из оптического стекла  до 760 нм). (Отдел квантовой электроники Института физики Университета им. Адама Мицкевича.)
до 760 нм). (Отдел квантовой электроники Института физики Университета им. Адама Мицкевича.)
Для сравнения напомним, что спектральная ширина видимого диапазона, отнесенная к средней частоте диапазона, равна

На рис. 33.2 показан фрагмент спектрального уширения в диапазоне длин волн от 480 до 760 нм, полученный с помощью серии мощных пикосекундных импульсов лазера на неодимовом стекле в образце из стекла  Сбоку видна узкая реперная линия гелий-неонового лазера
Сбоку видна узкая реперная линия гелий-неонового лазера  .
.
Таким образом, фазовая самомодуляция сверхкоротких световых импульсов в нелинейной среде может быть очень сильной. Одним из условий обеспечения столь широкого спектра импульса является относительное изменение показателя преломления примерно на  Такие значительные изменения
Такие значительные изменения  могут происходить при самофокусировке света или вследствие образования плазмы в веществе [10].
могут происходить при самофокусировке света или вследствие образования плазмы в веществе [10].

Рис. 33.3. Спектр импульса рубинового лазера, сфотографированный после прохождения импульса через рубиновый элемент усилителя длиной 25 см [11].  — радиальная координата. Диаметр пучка составлял 1 мм.
— радиальная координата. Диаметр пучка составлял 1 мм.
Фазовая самомодуляция может иметь место также в усиливающей среде. Флек и Карман [11] показали экспериментально, что мощные импульсы рубинового лазера при дальнейшем усилении в рубине испытывают частотную модуляцию. Этот эффект обусловлен нелинейной зависимостью показателя преломления  от напряженности электрического поля световой волны:
от напряженности электрического поля световой волны:  Значение коэффициента
Значение коэффициента  в рубине невелико:
в рубине невелико:  Снимок, полученный Флеком и Карманом [11] (рис. 33.3), демонстрирует эффект сильной фазовой самомодуляции импульса с начальной длительностью
Снимок, полученный Флеком и Карманом [11] (рис. 33.3), демонстрирует эффект сильной фазовой самомодуляции импульса с начальной длительностью  Благодаря сжатию импульса в усиливающей среде его длительность уменьшилась до
Благодаря сжатию импульса в усиливающей среде его длительность уменьшилась до  Начальная энергия импульса составляла
Начальная энергия импульса составляла  конечная
конечная  коэффициент усиления был равен примерно 7.
коэффициент усиления был равен примерно 7.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
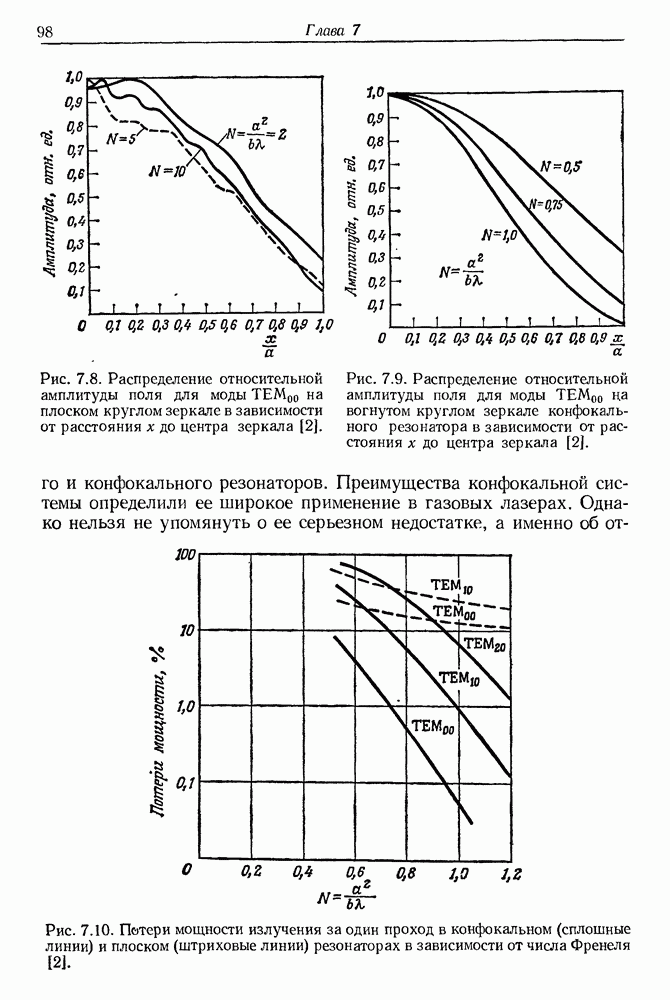
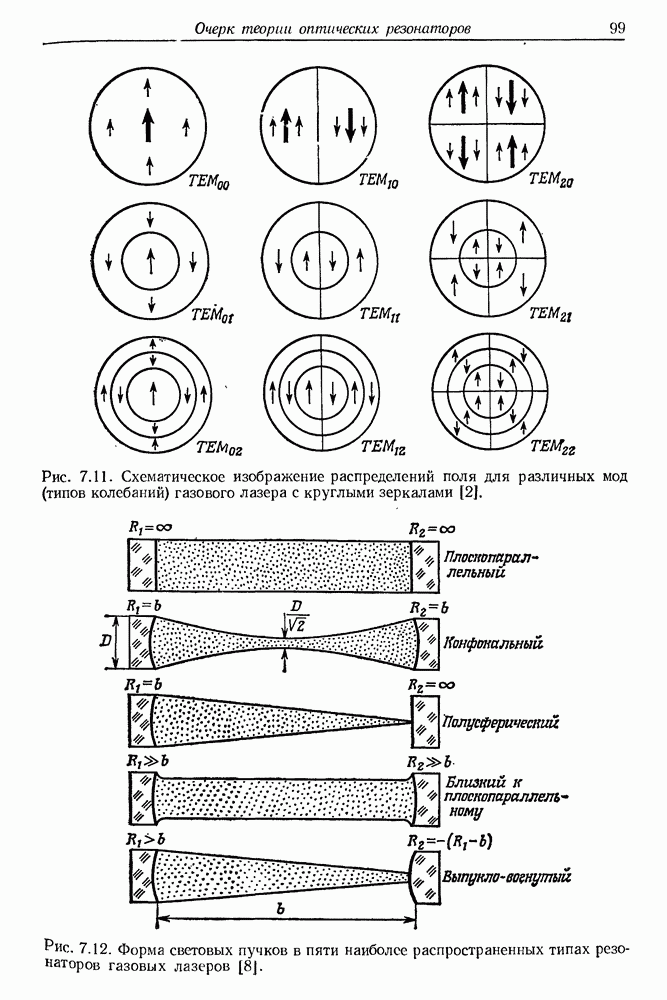
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
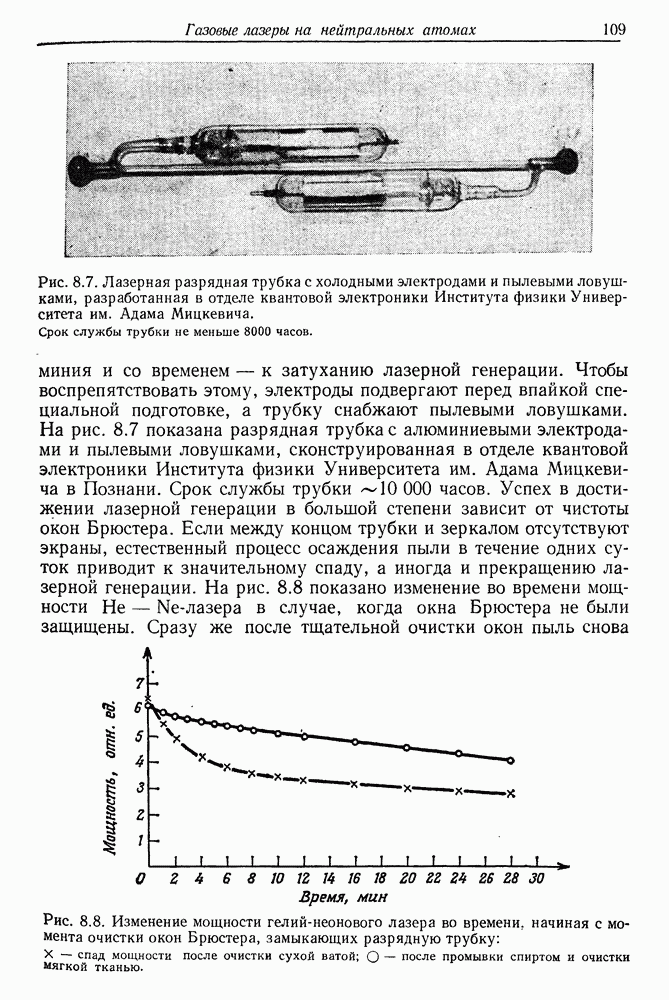
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
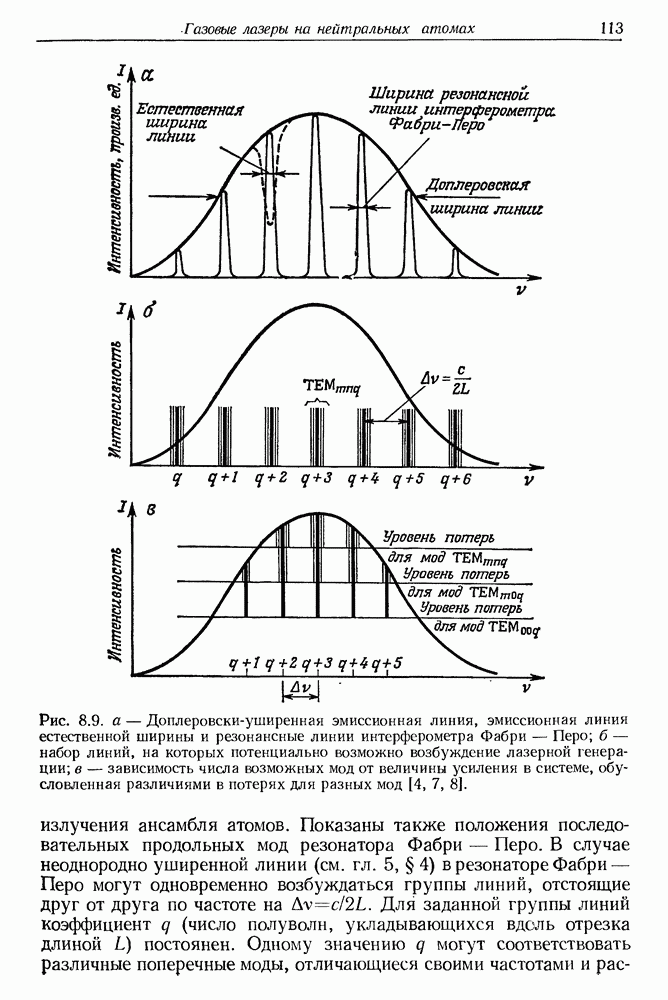
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
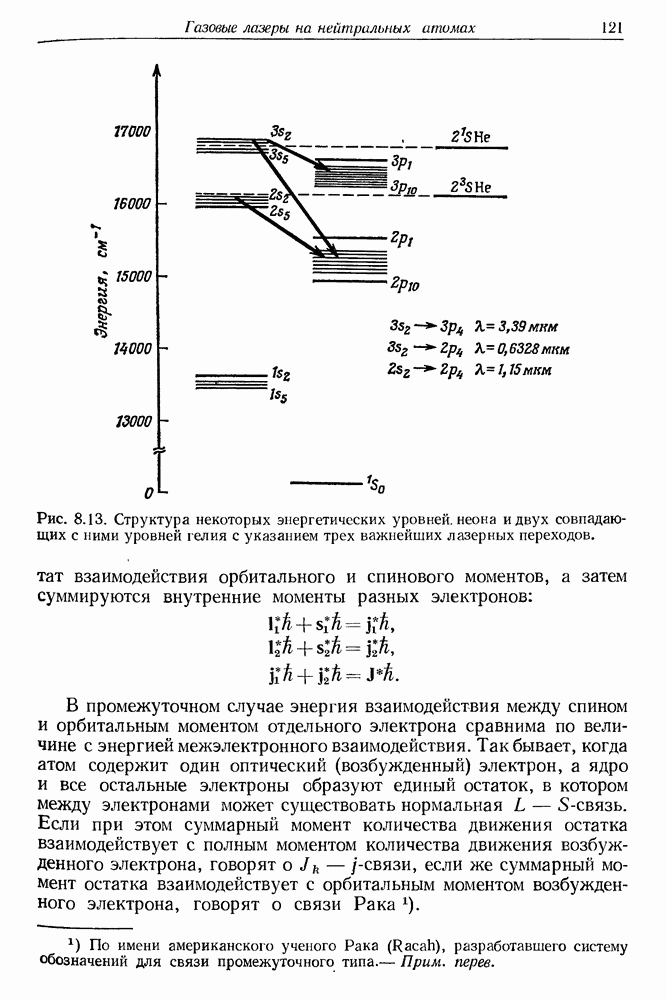
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
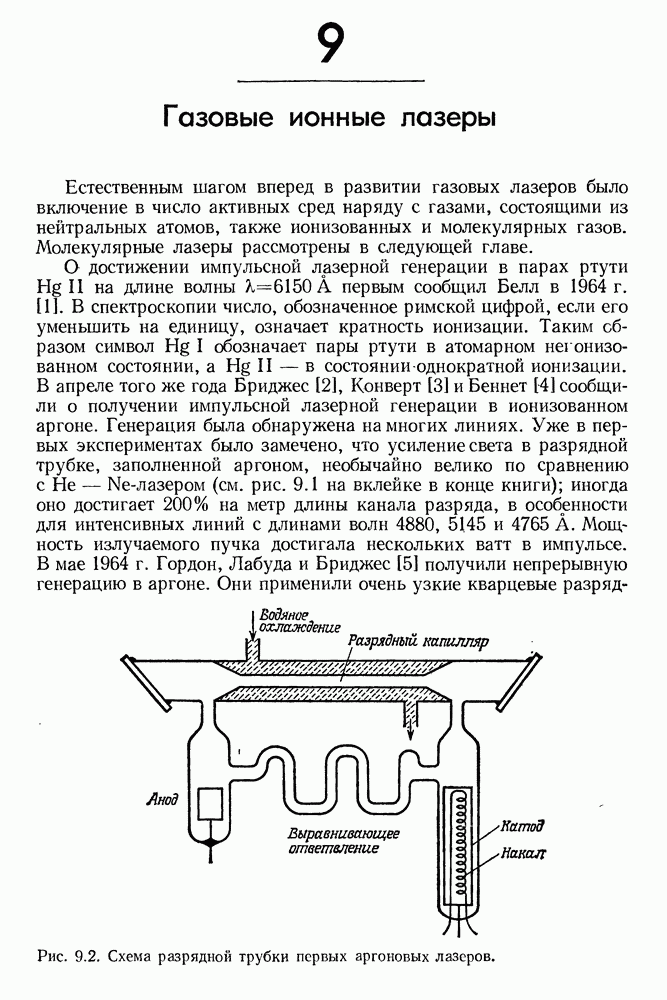
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
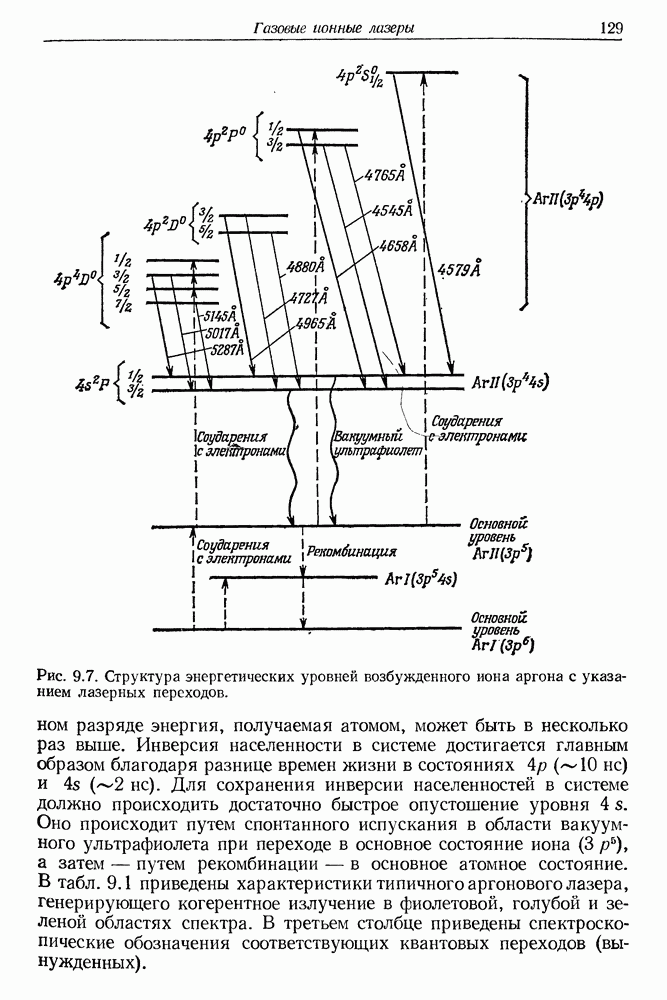
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
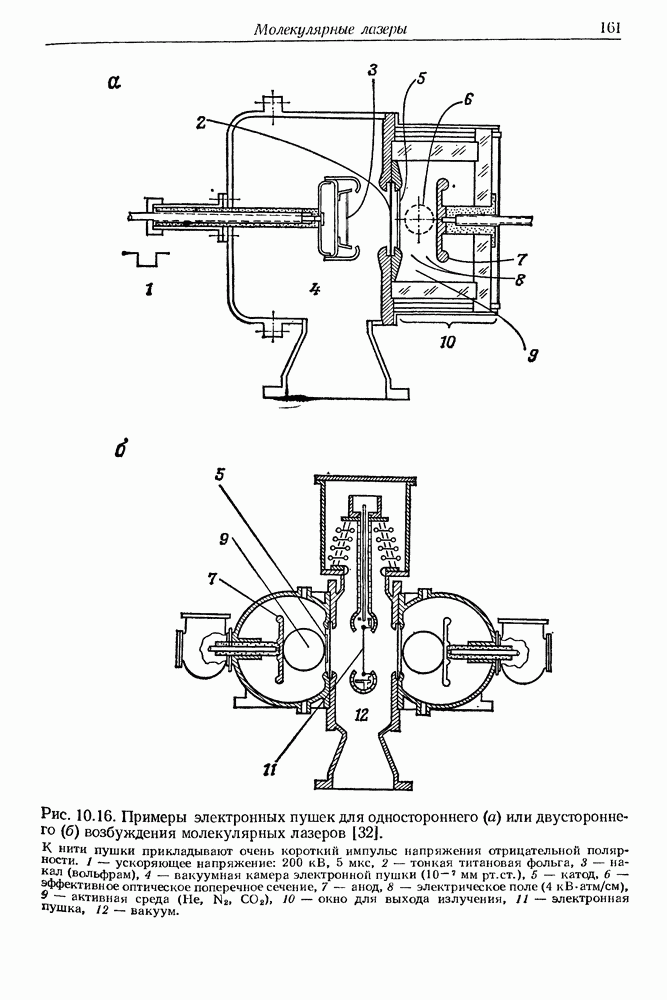
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
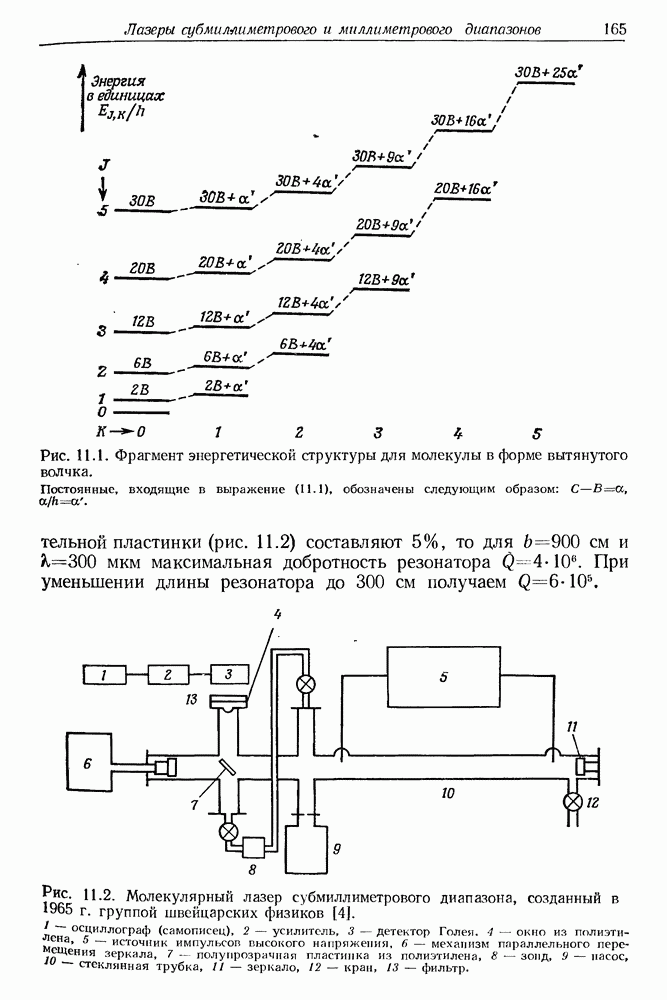
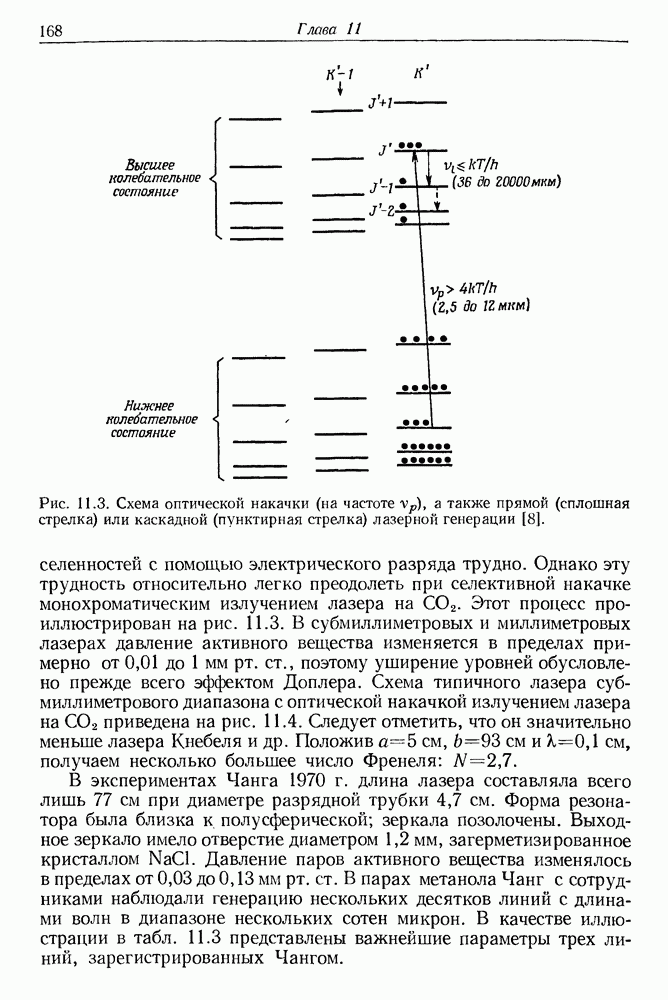
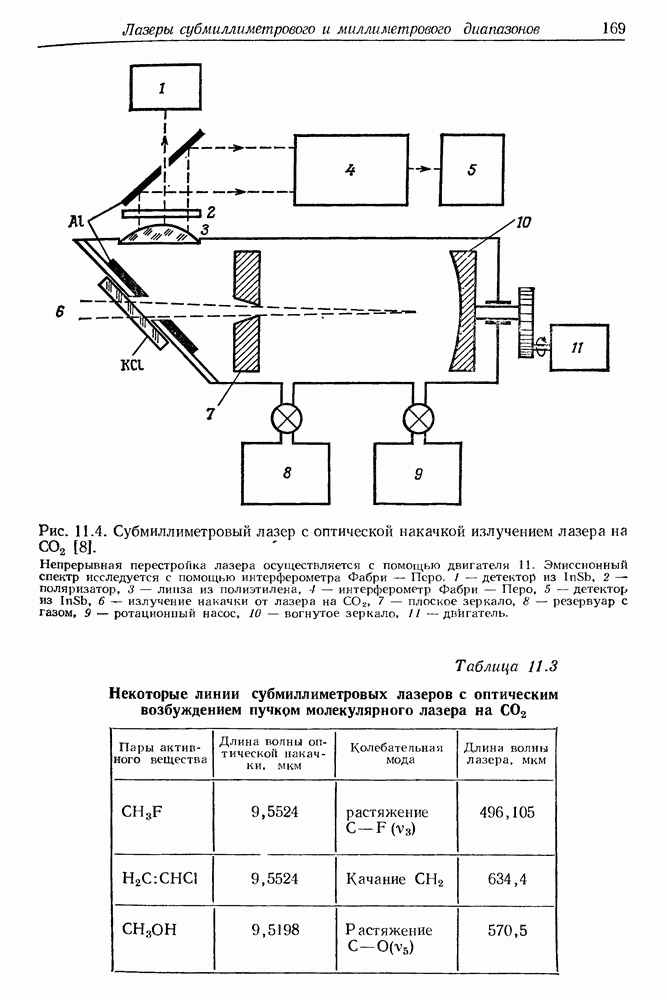
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
- б. Вращающаяся призма
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
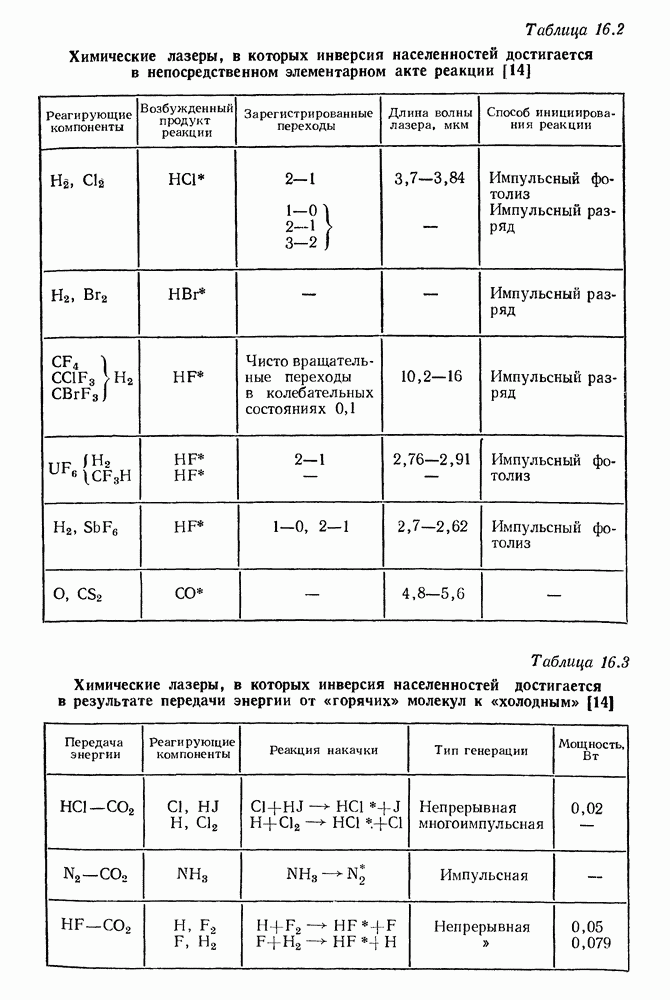
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
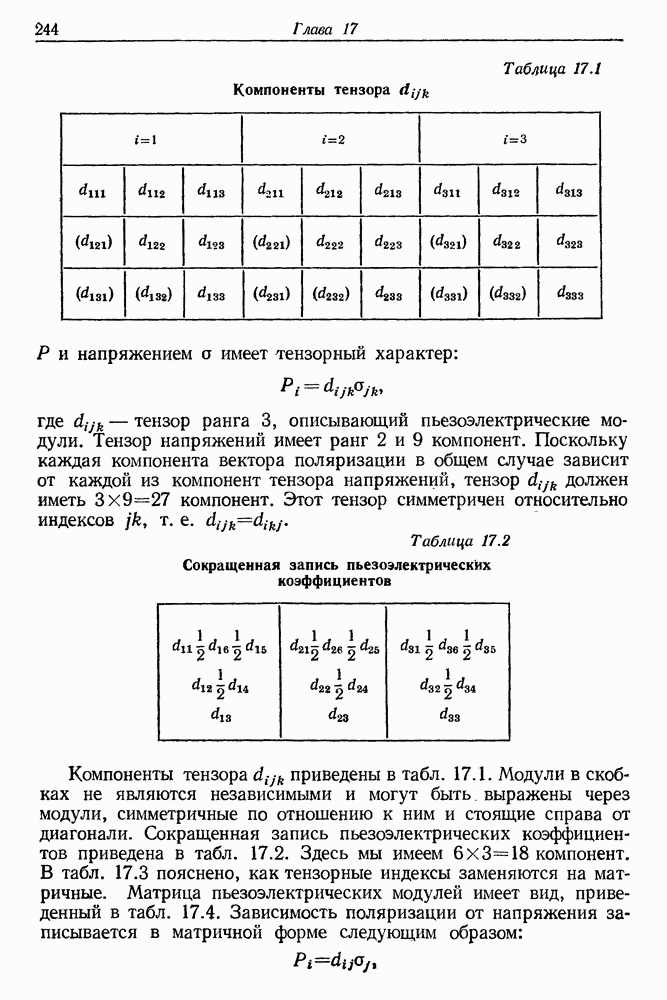
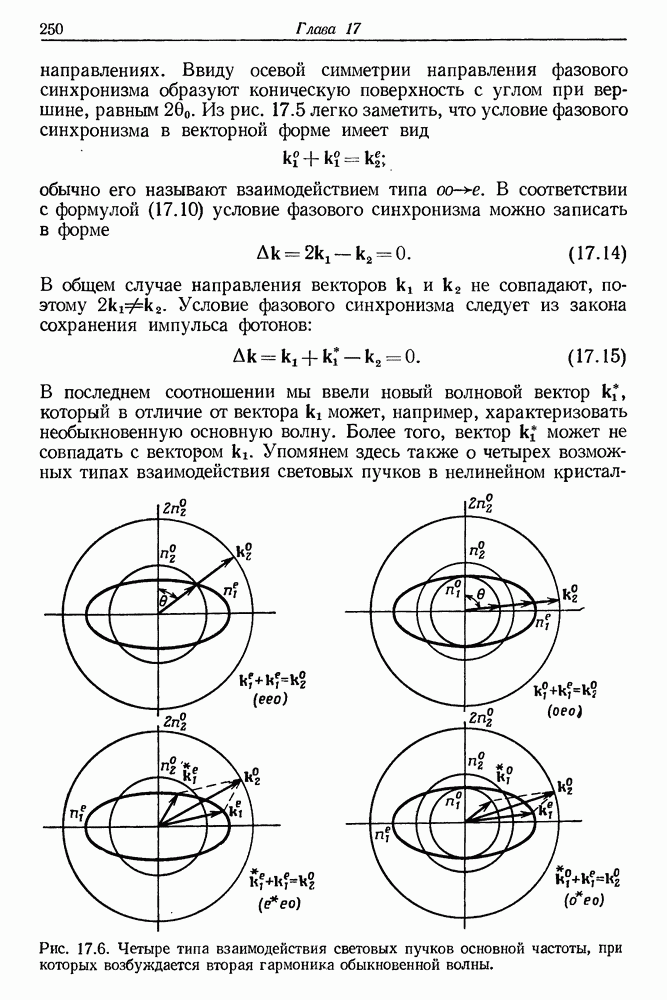
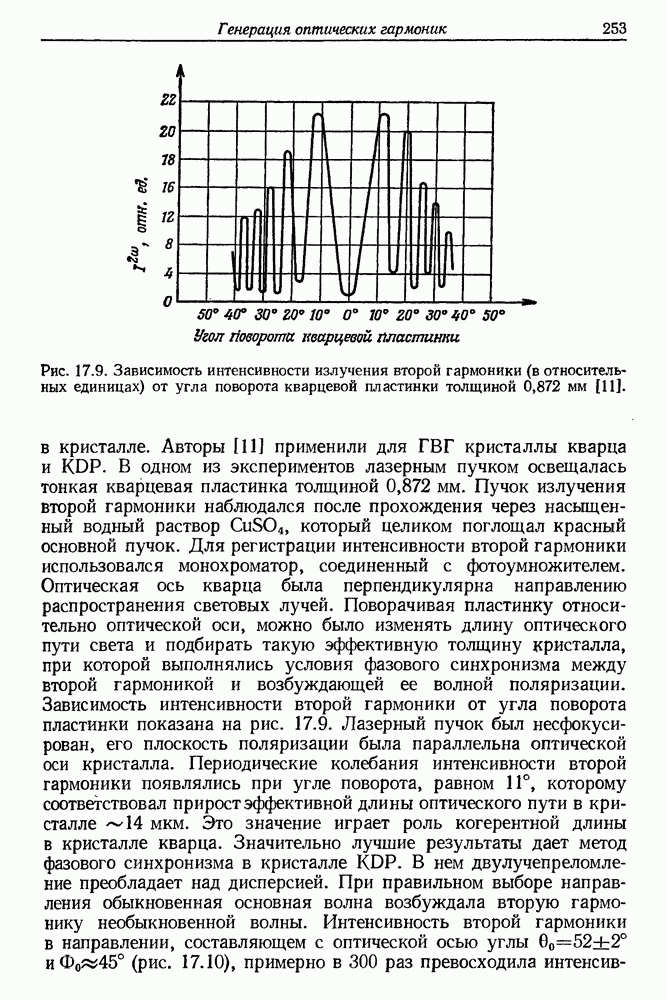
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
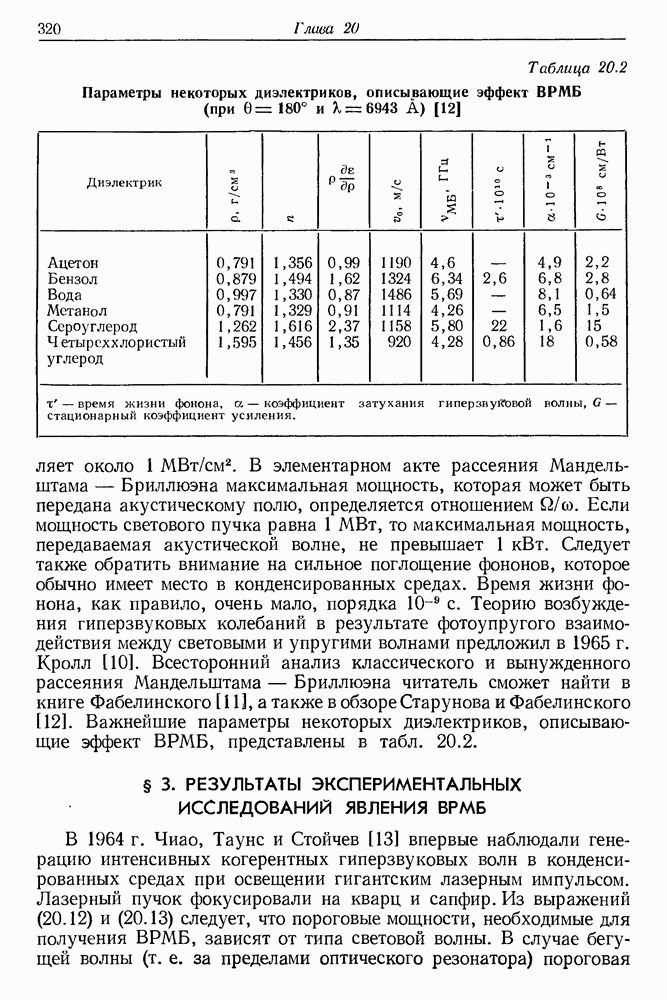
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
- 22. Параметрическая люминесценция (ПЛ)
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
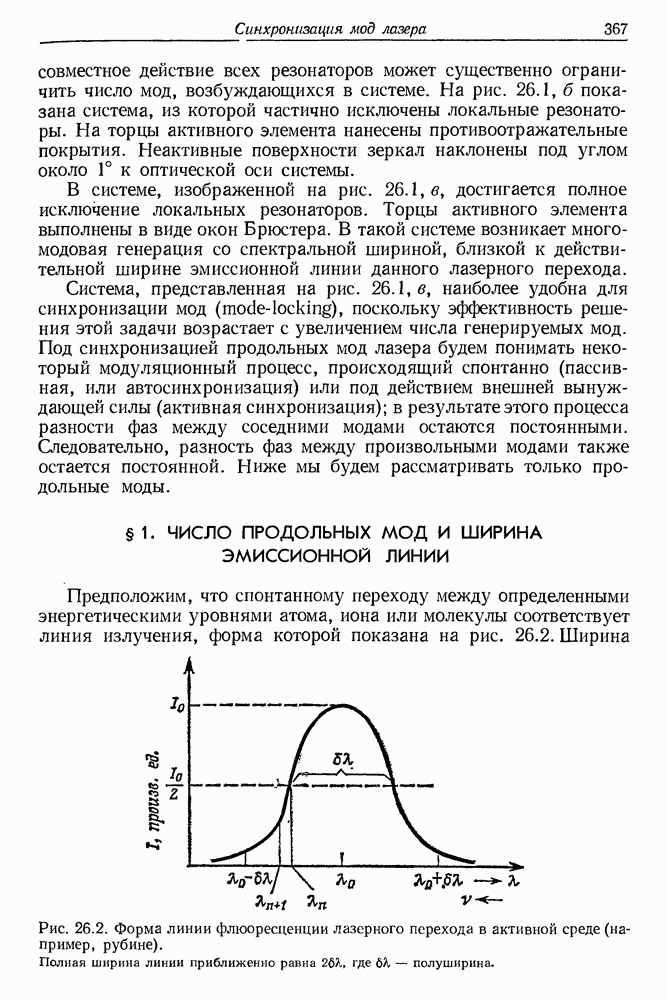
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
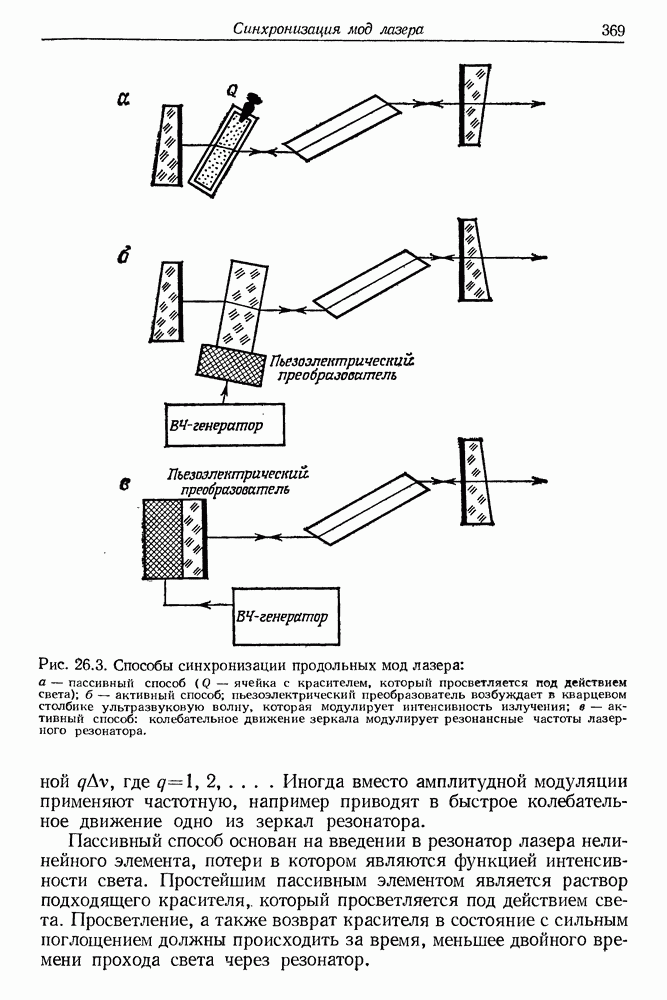
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
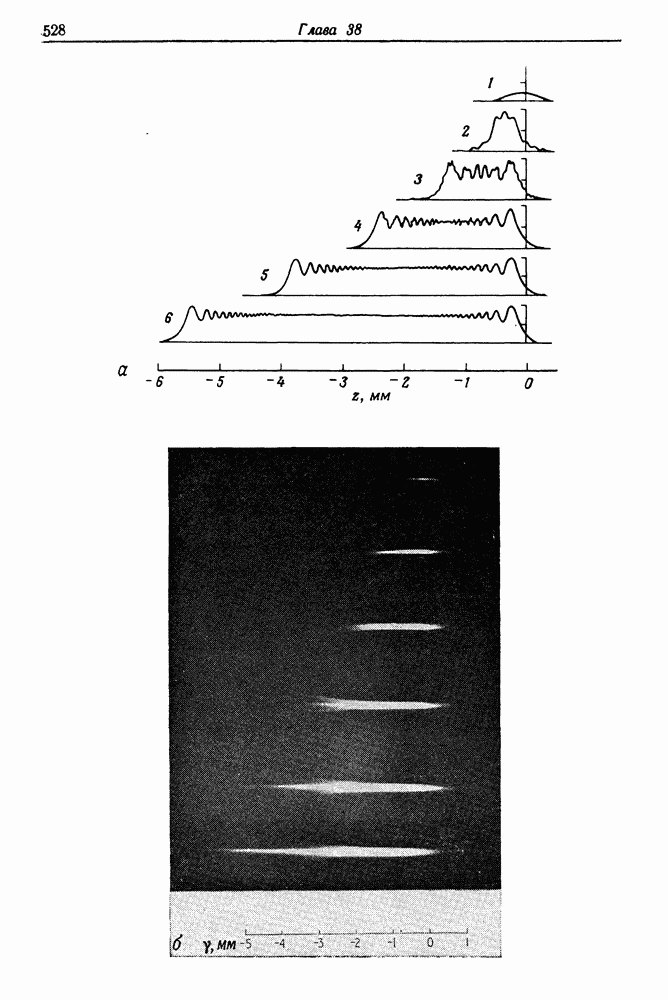
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
- в. Примеры использования камеры с разверткой
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
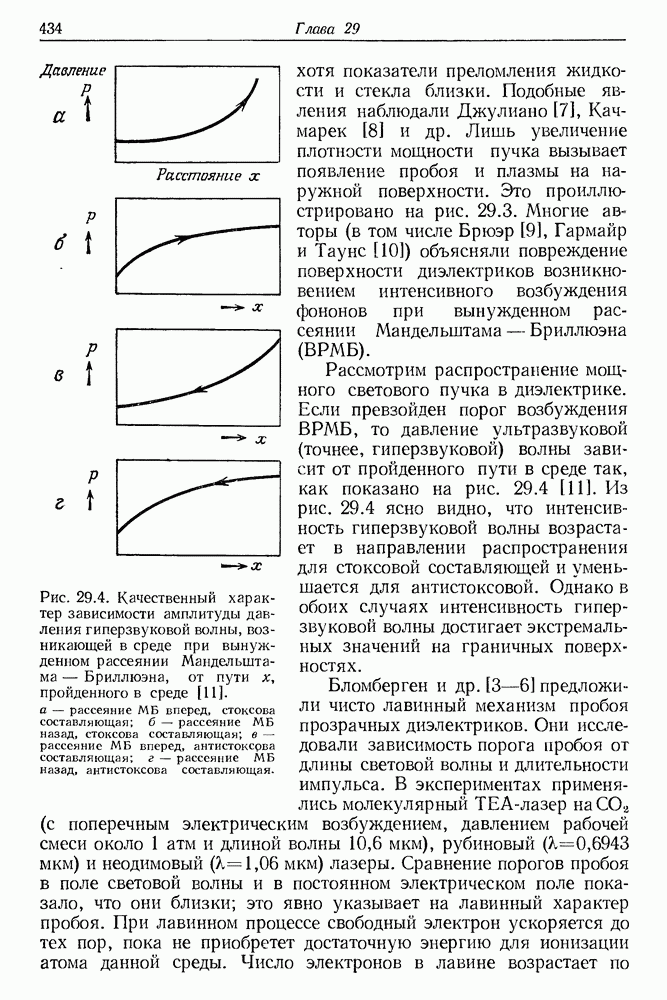
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
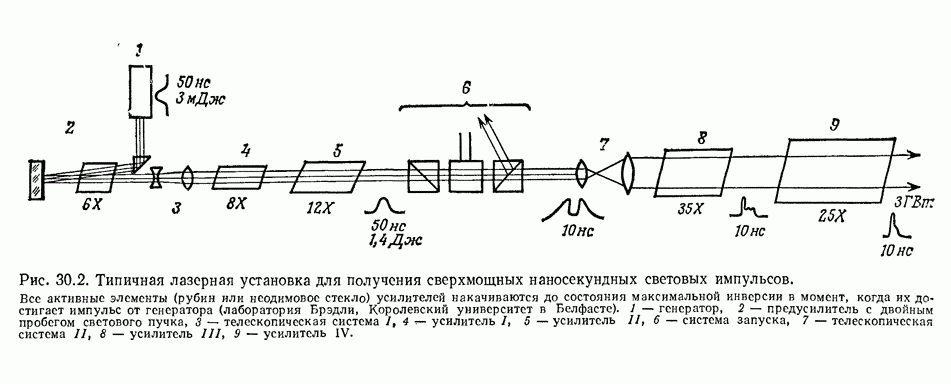
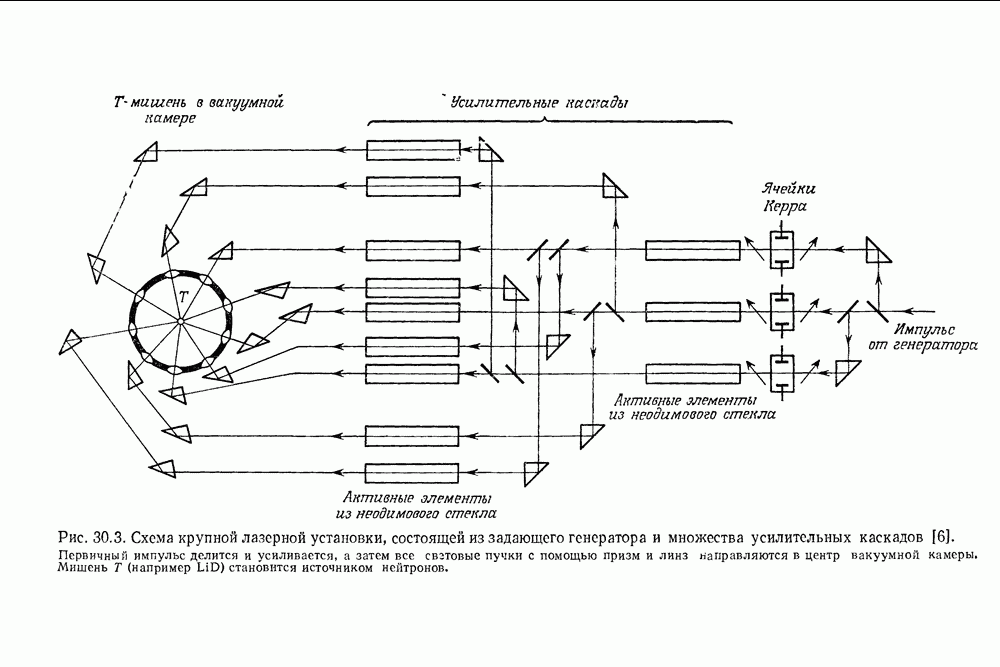
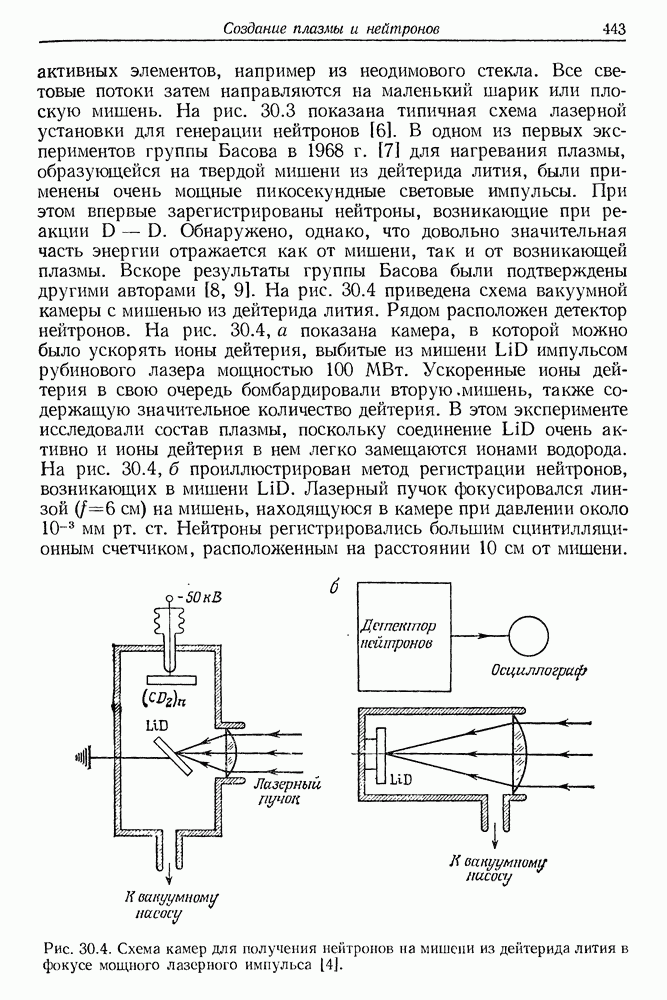
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
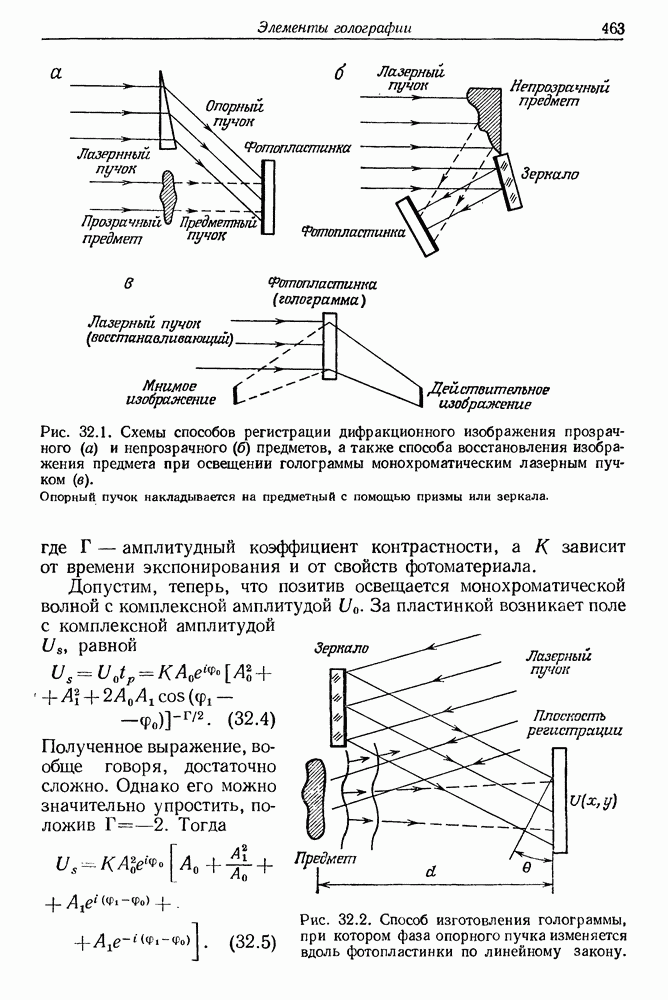
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
- 35. Лазеры на центрах окраски
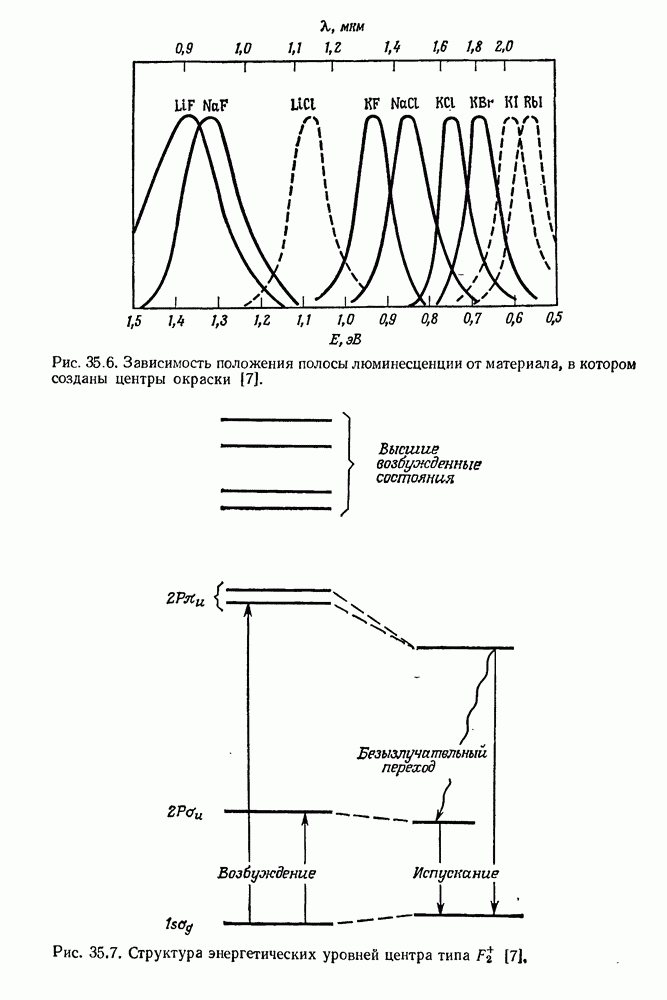
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
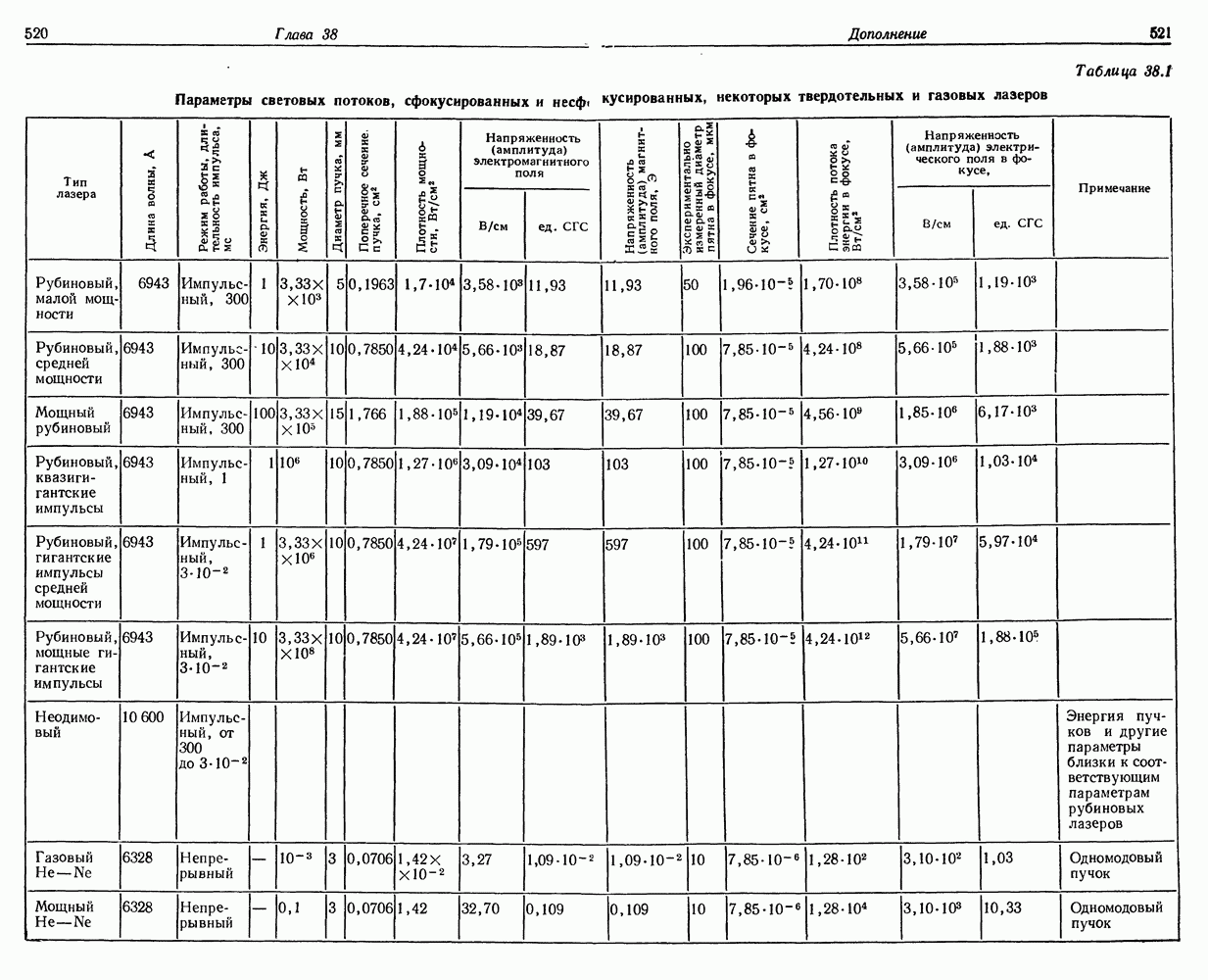
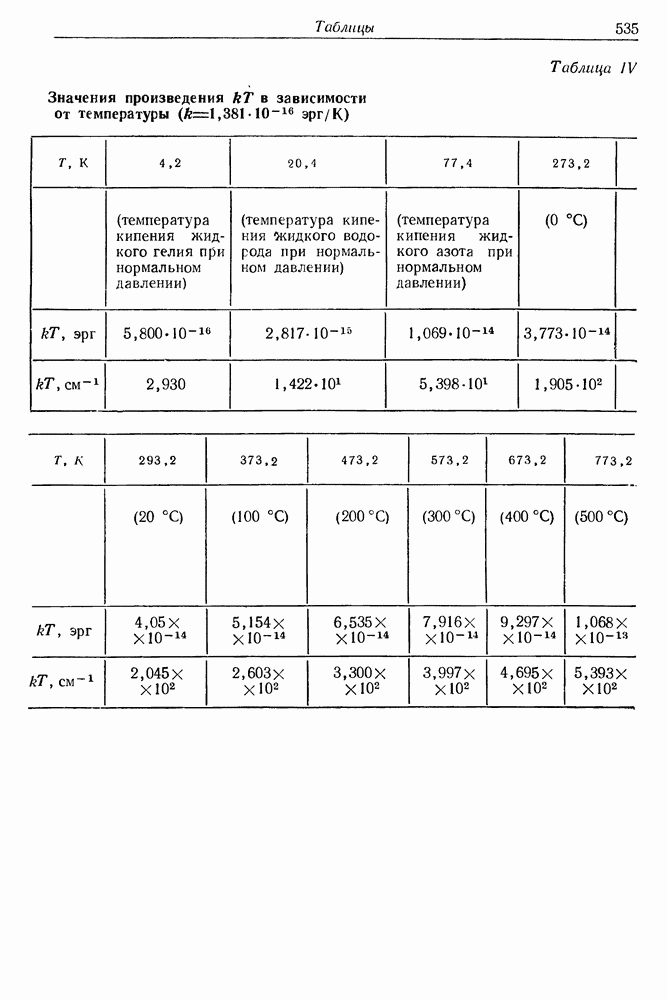
- Таблицы