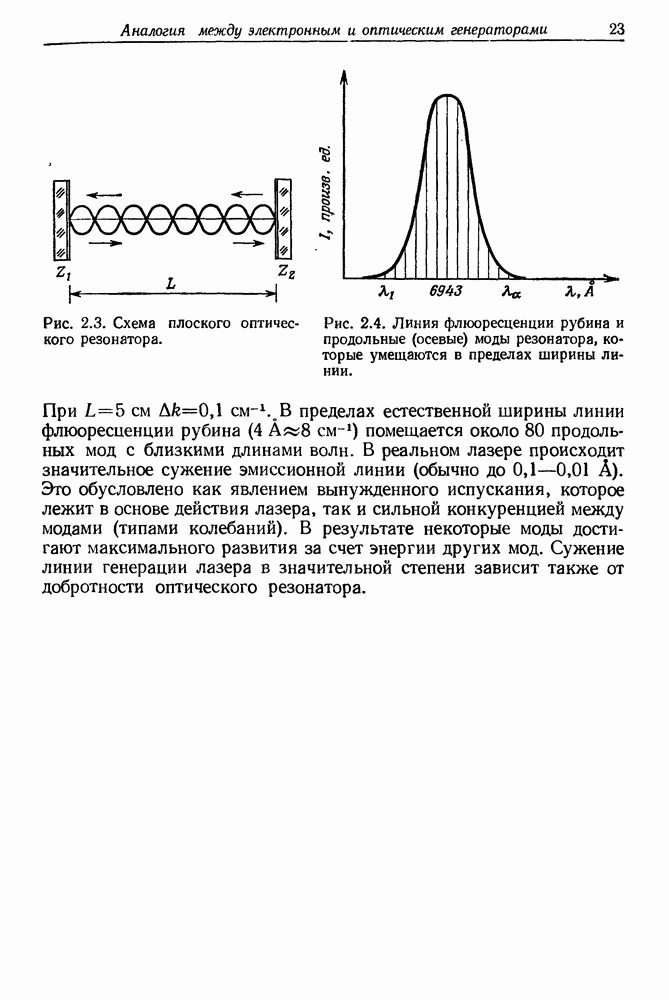
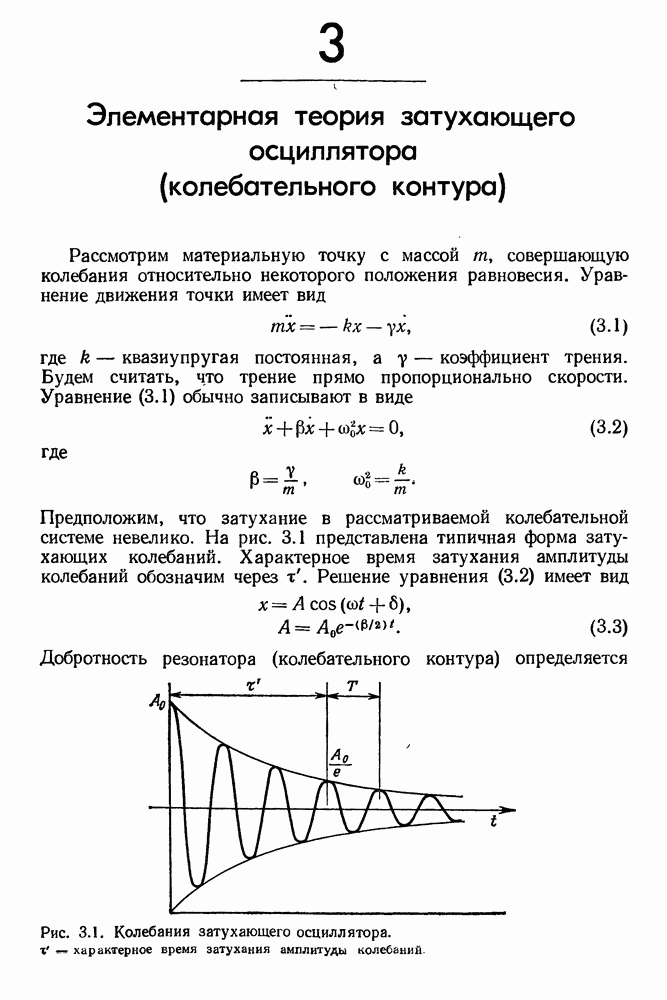
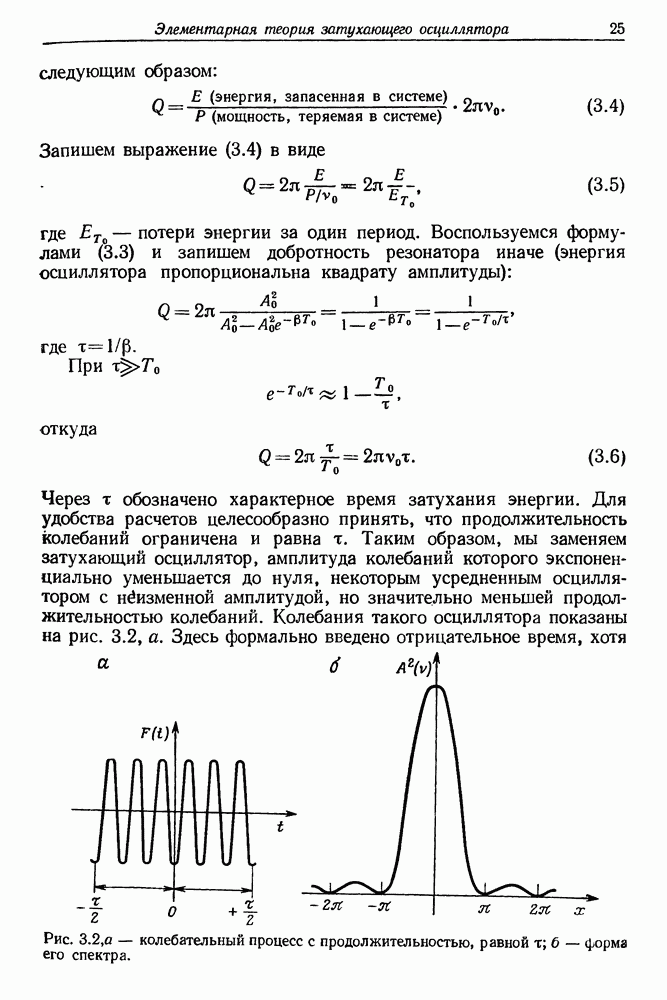
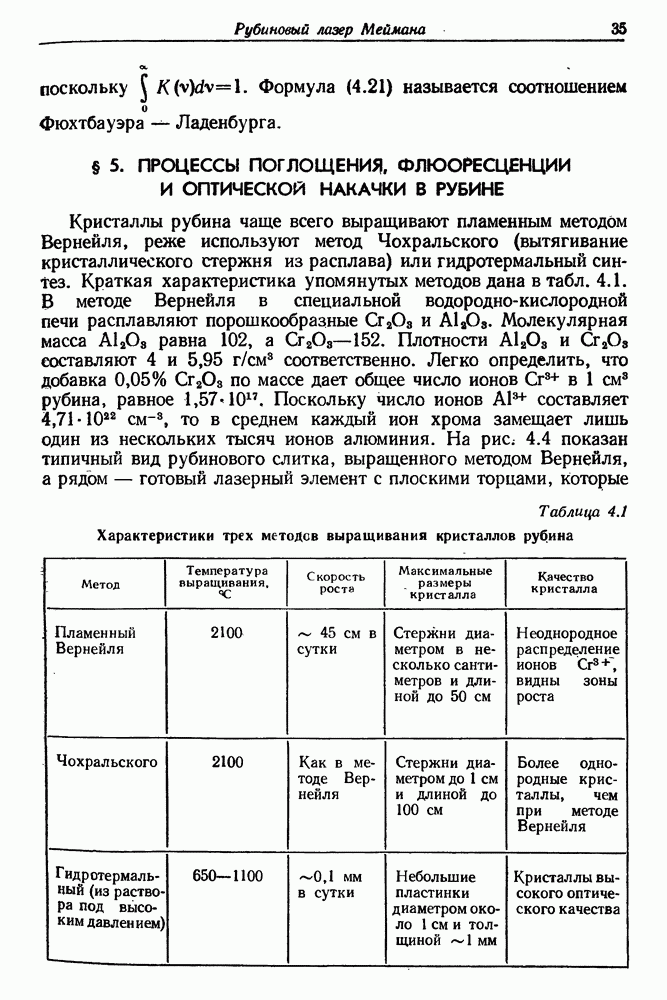
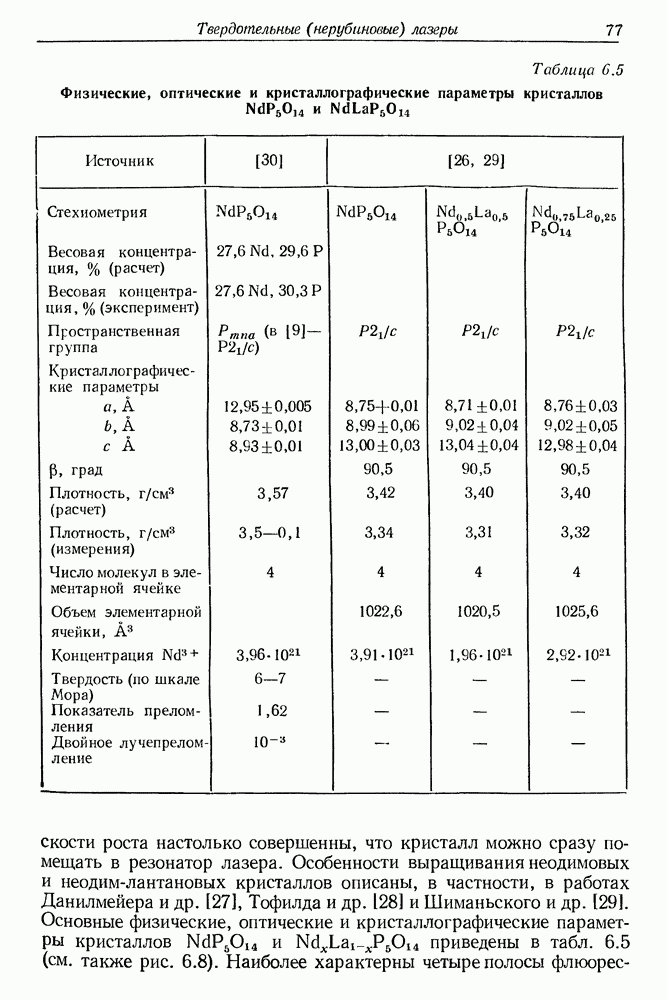
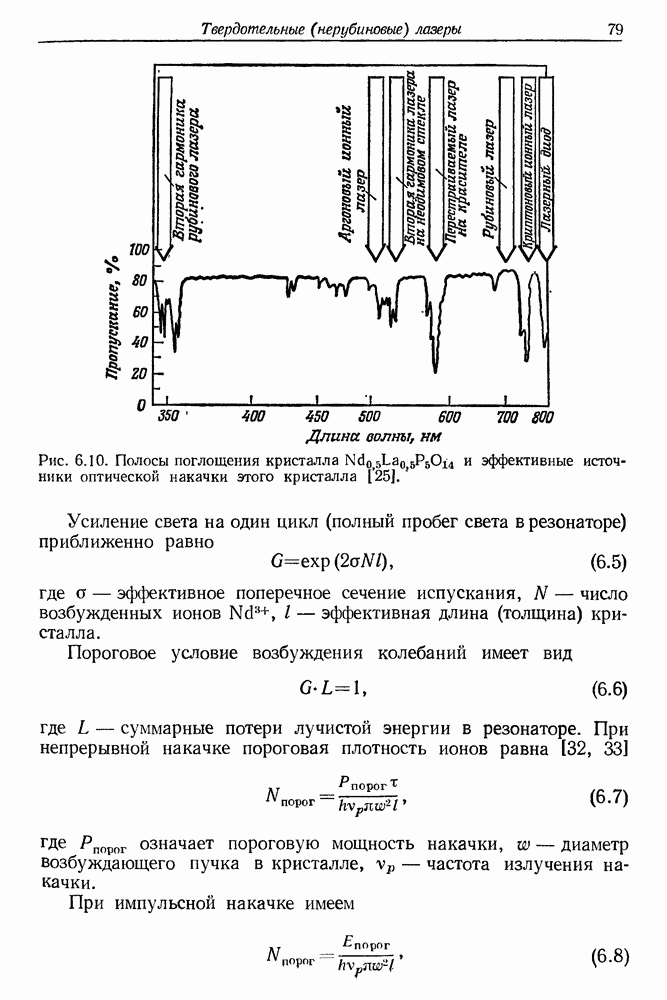
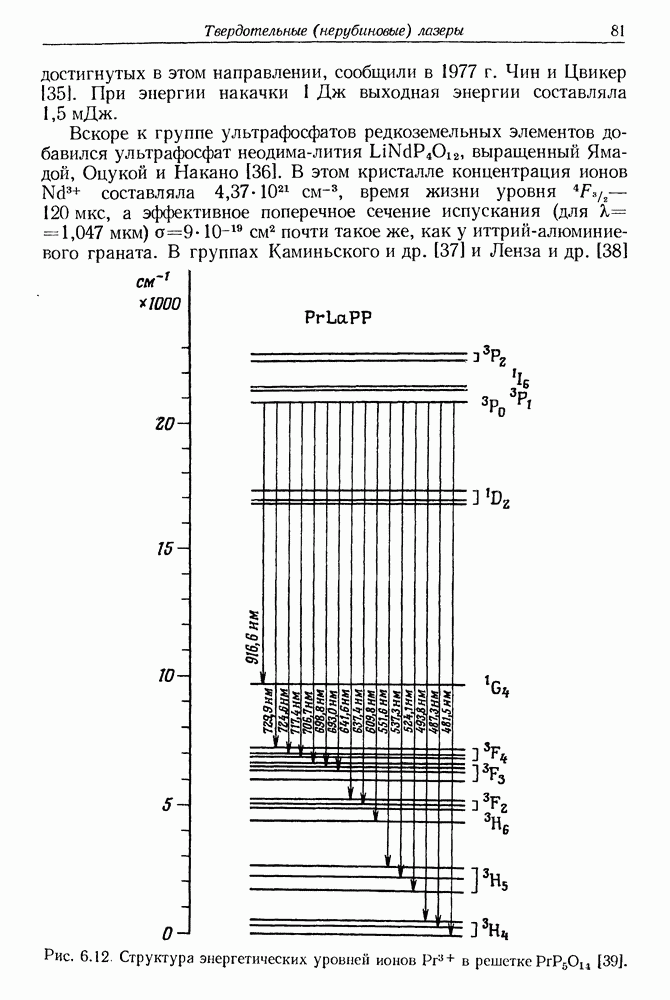
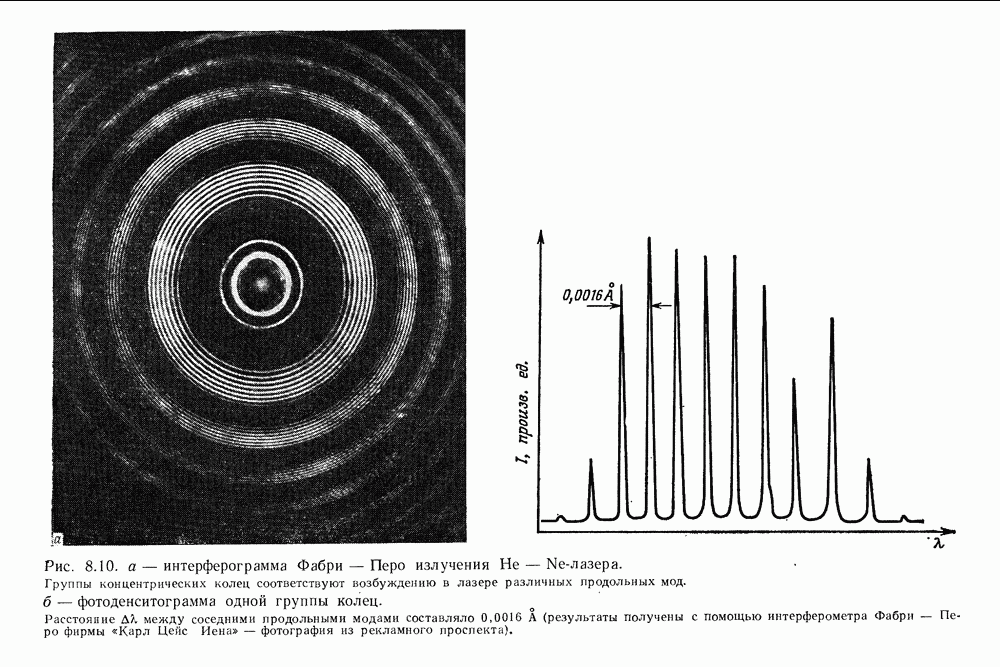
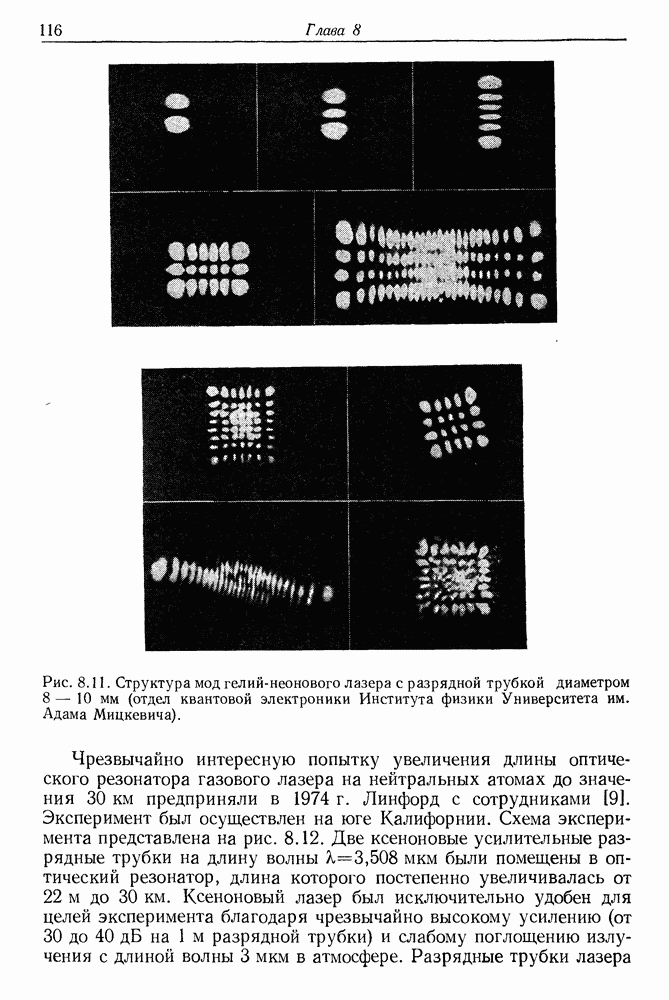
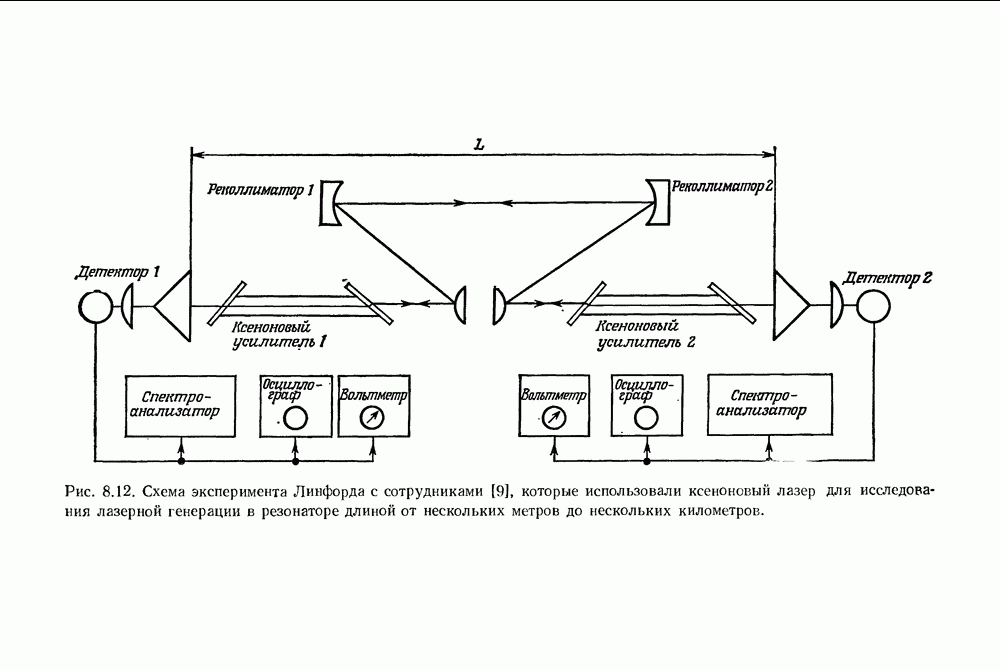
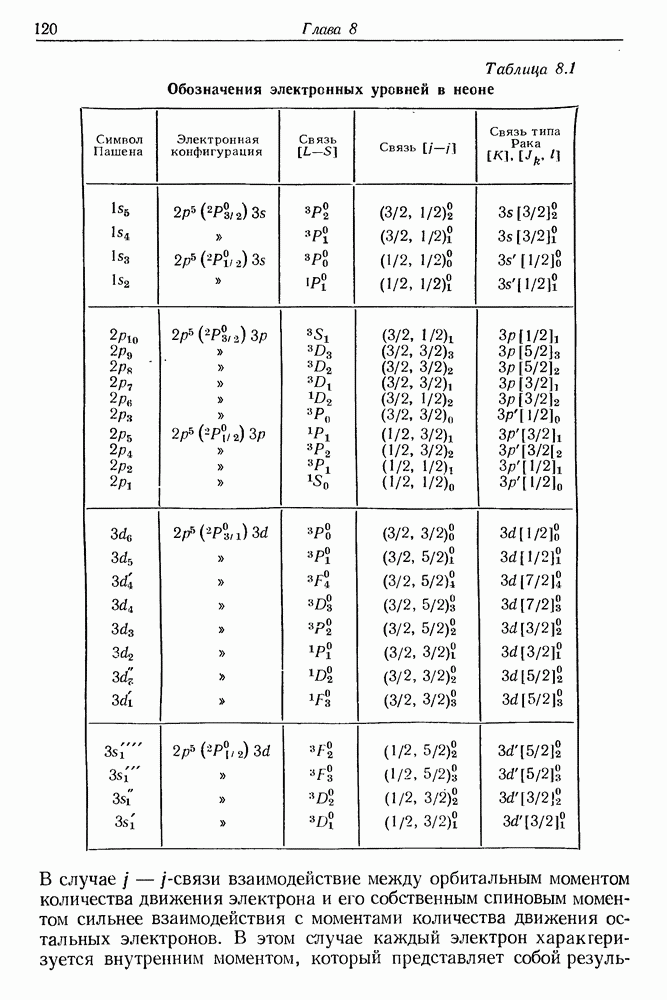
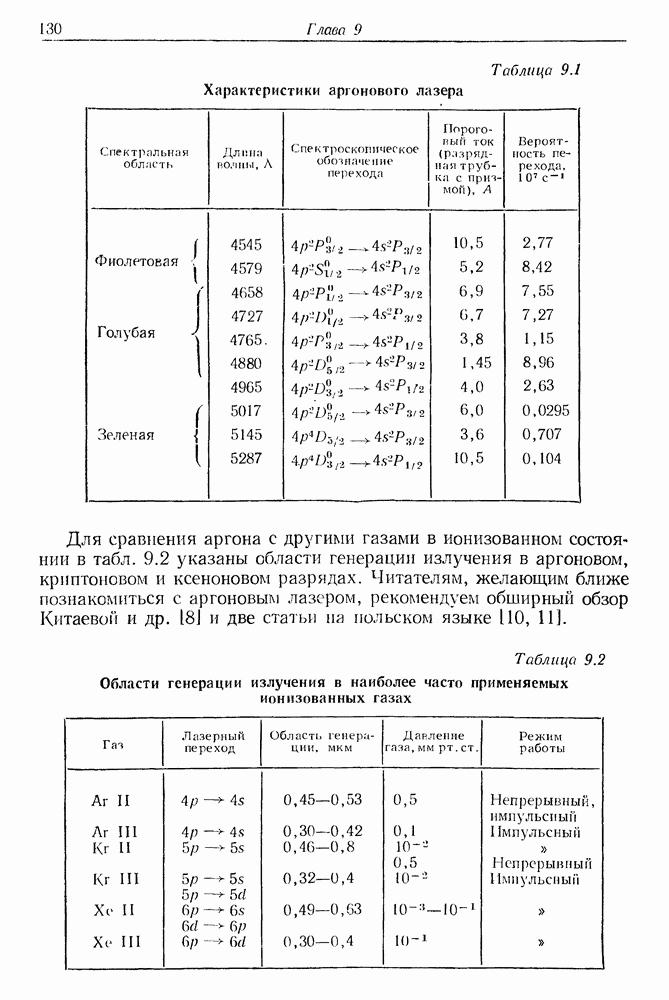
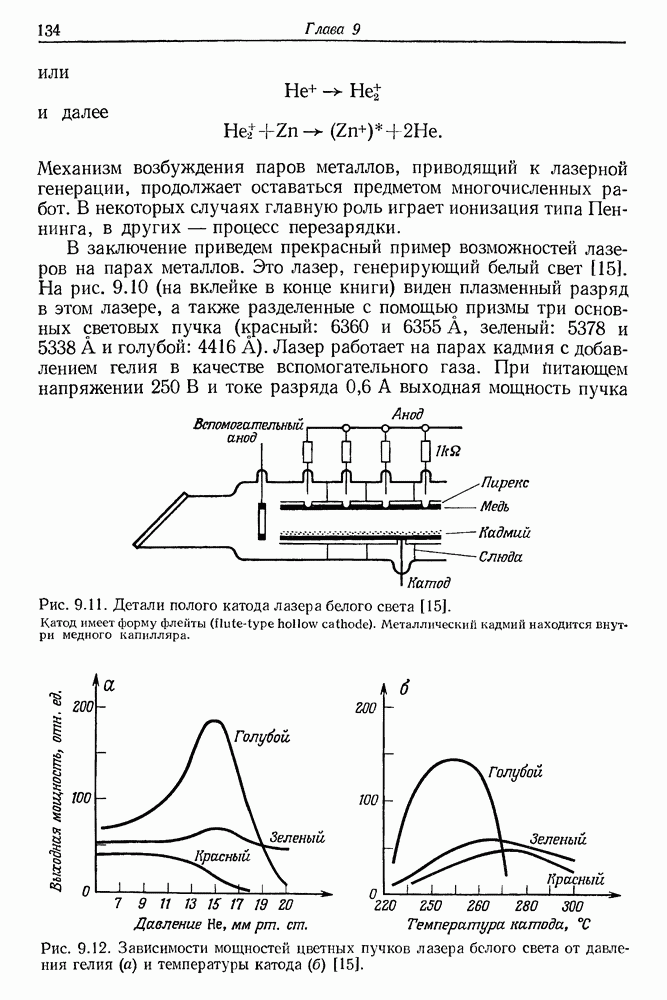
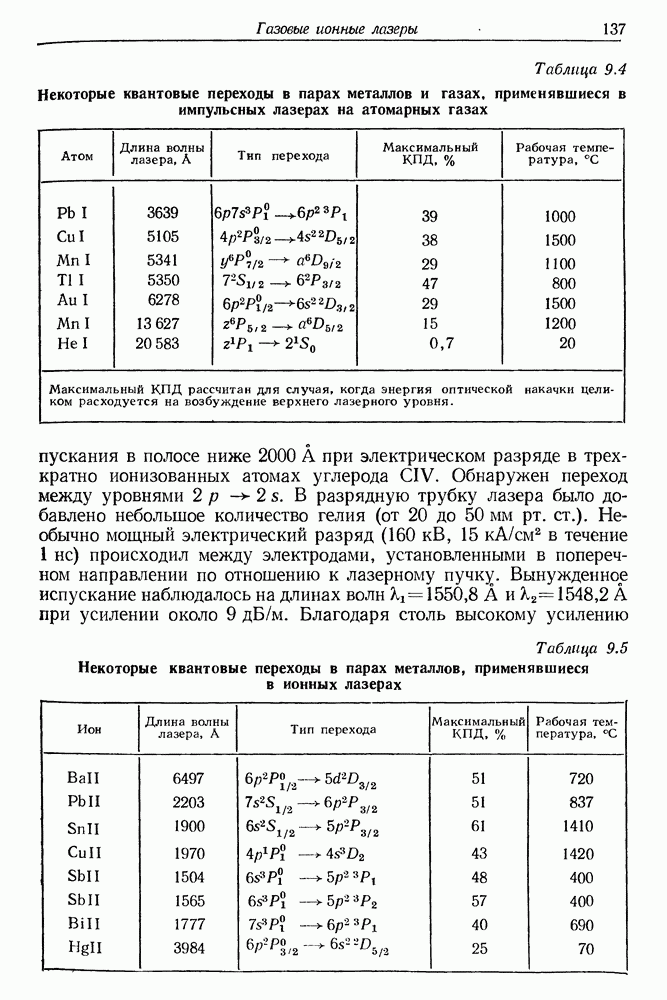
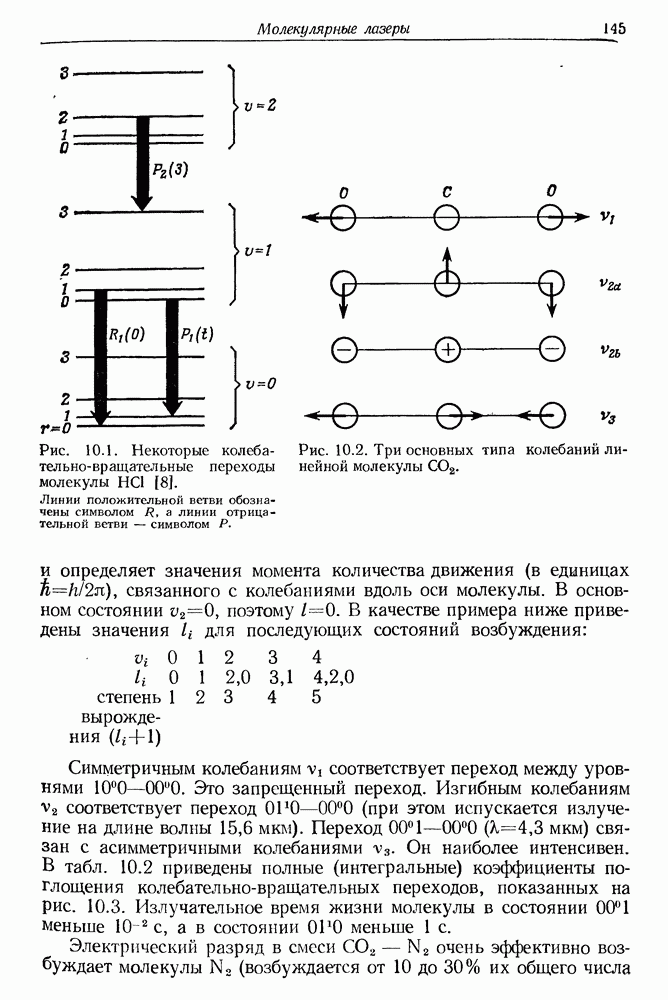
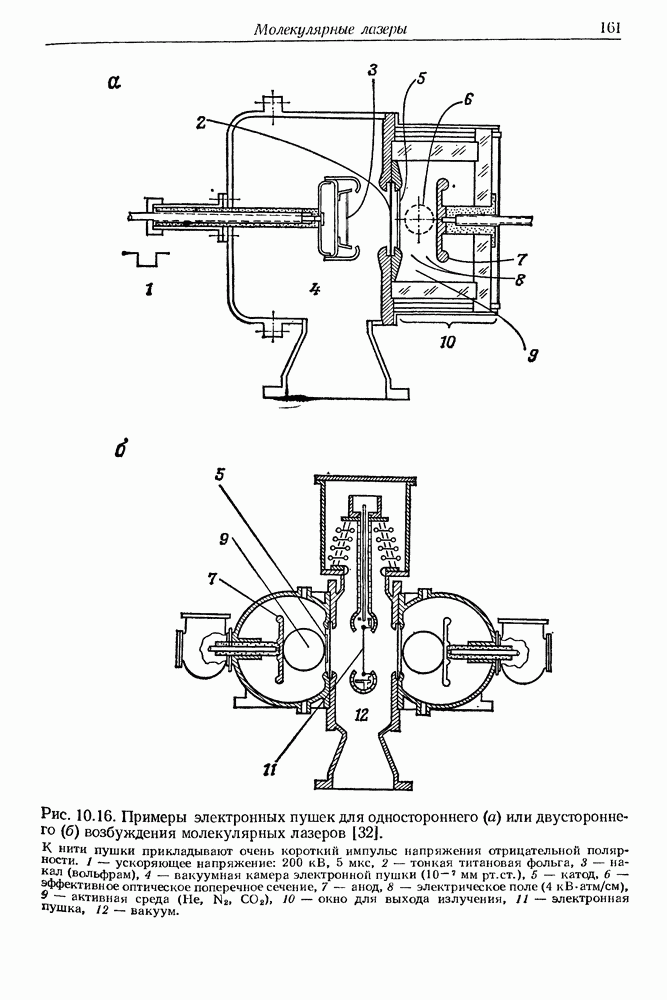
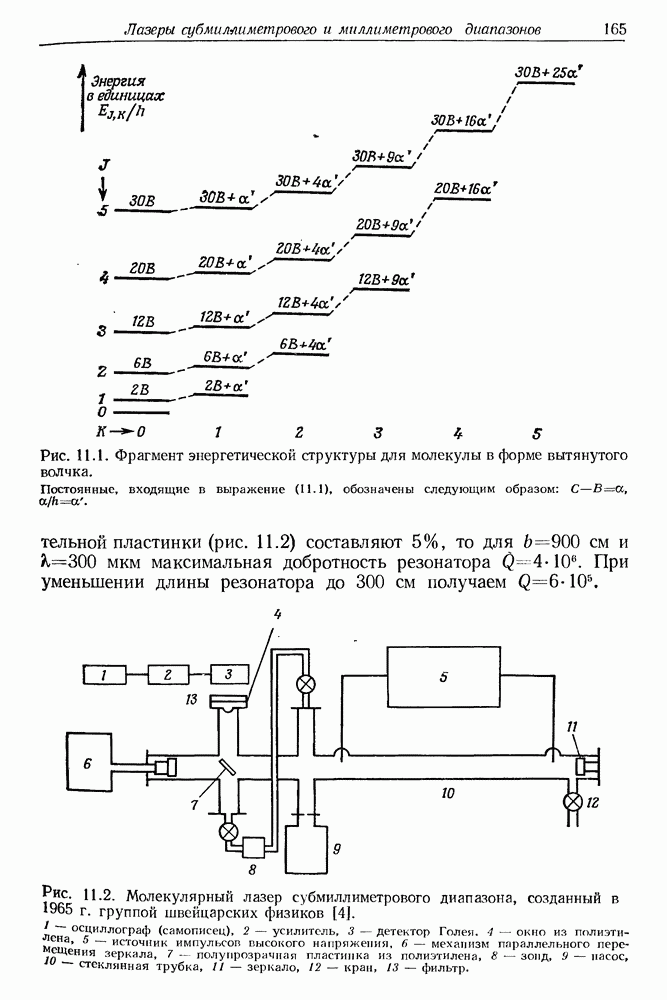
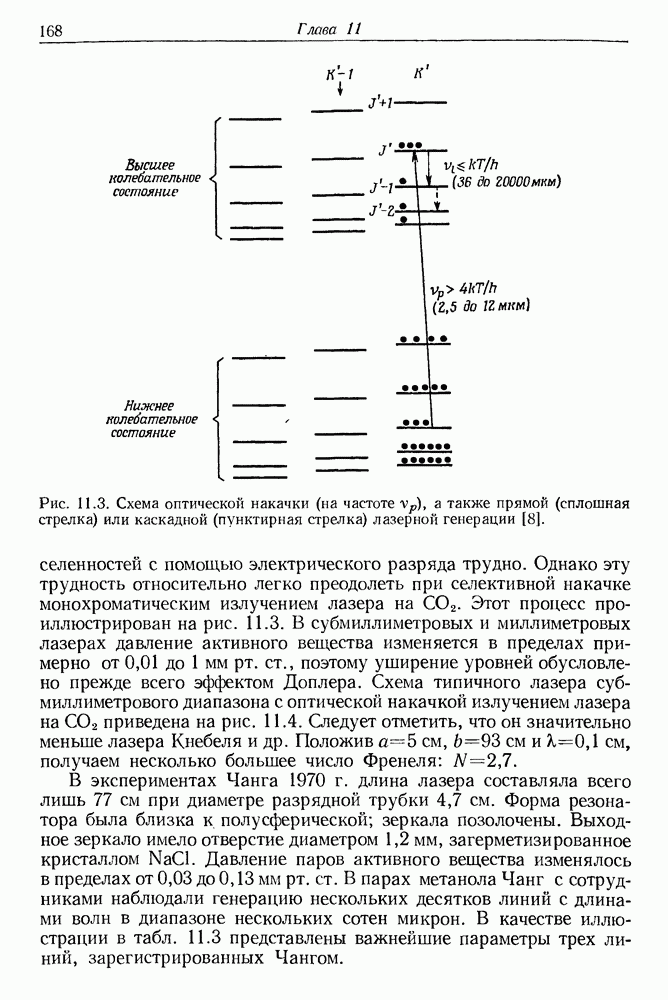
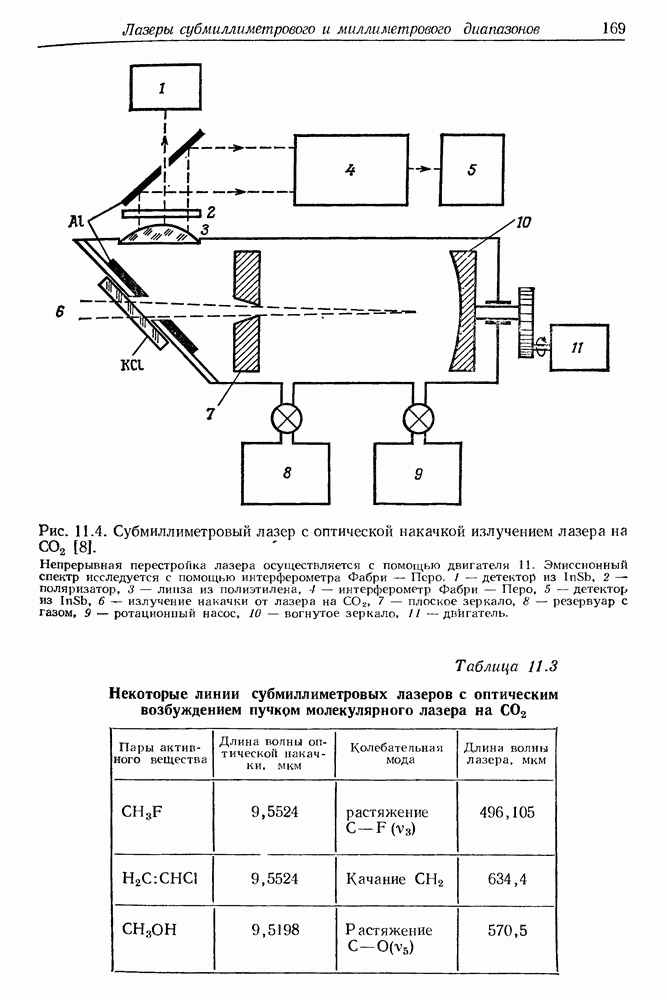
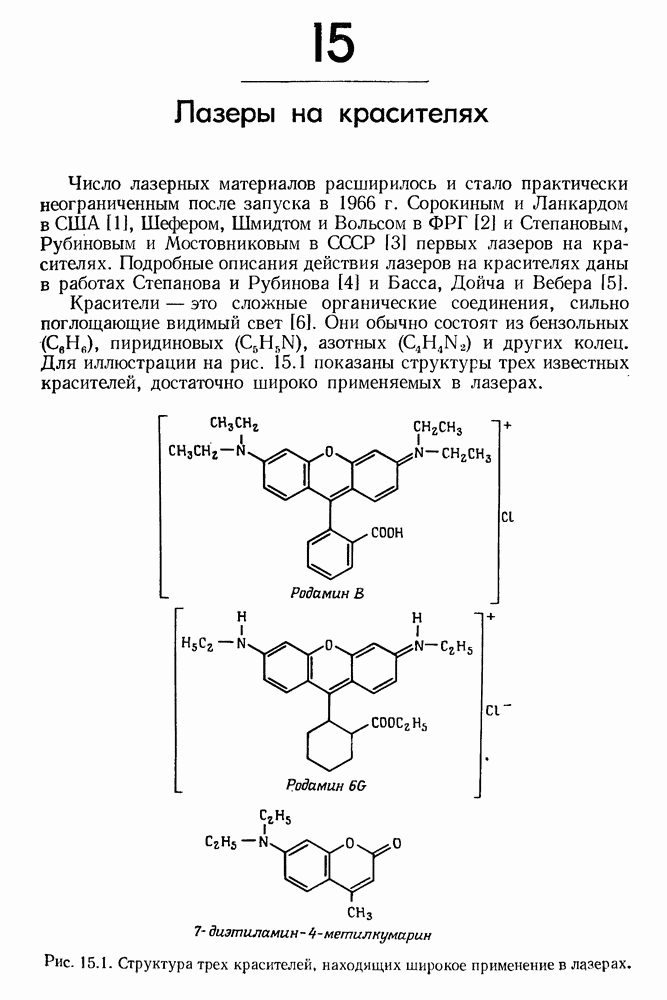
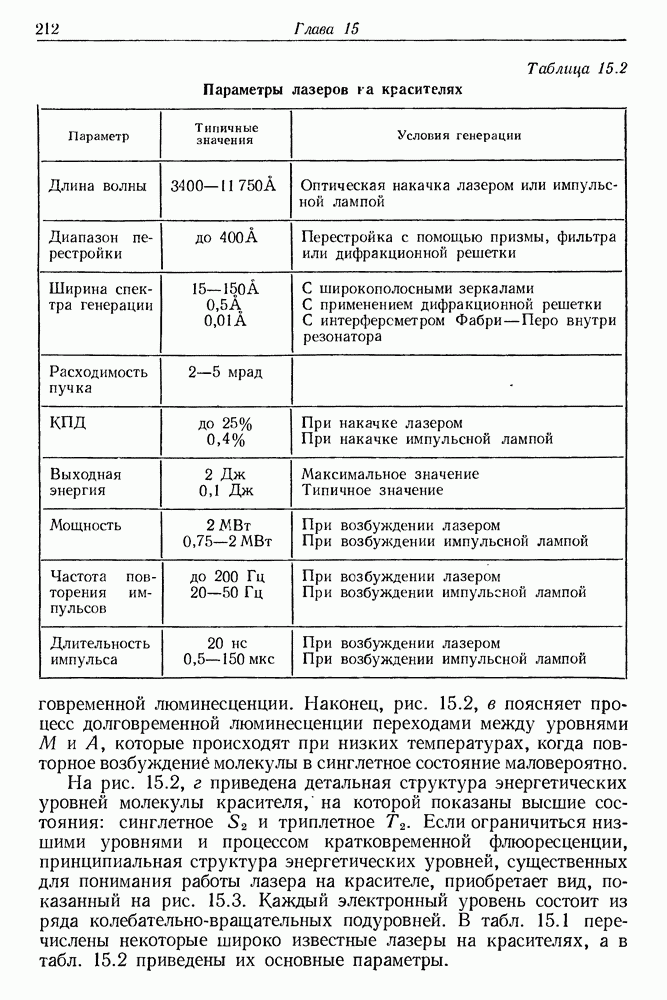
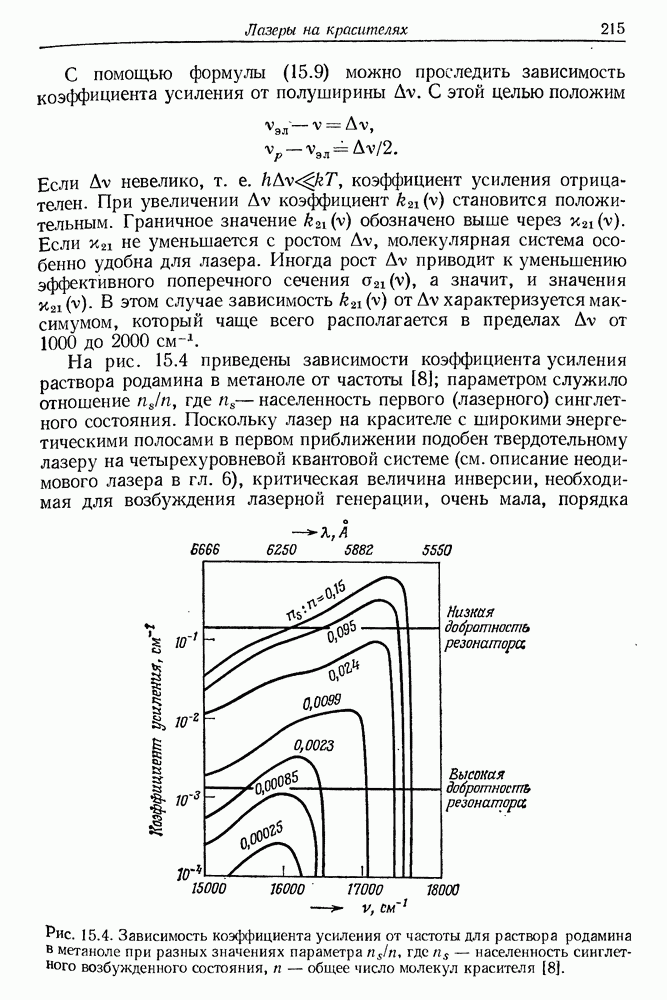
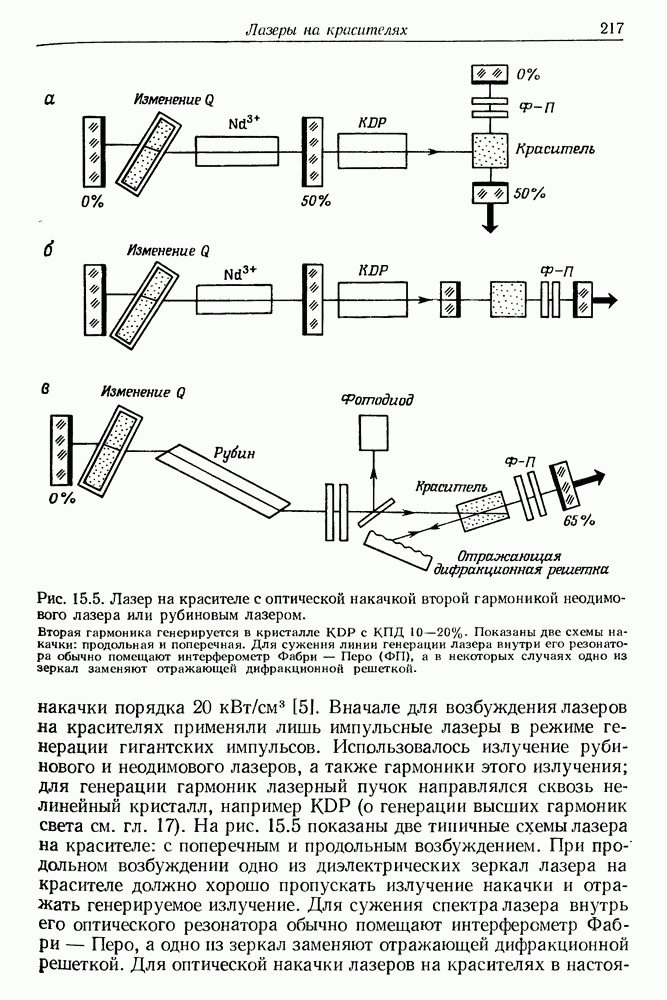
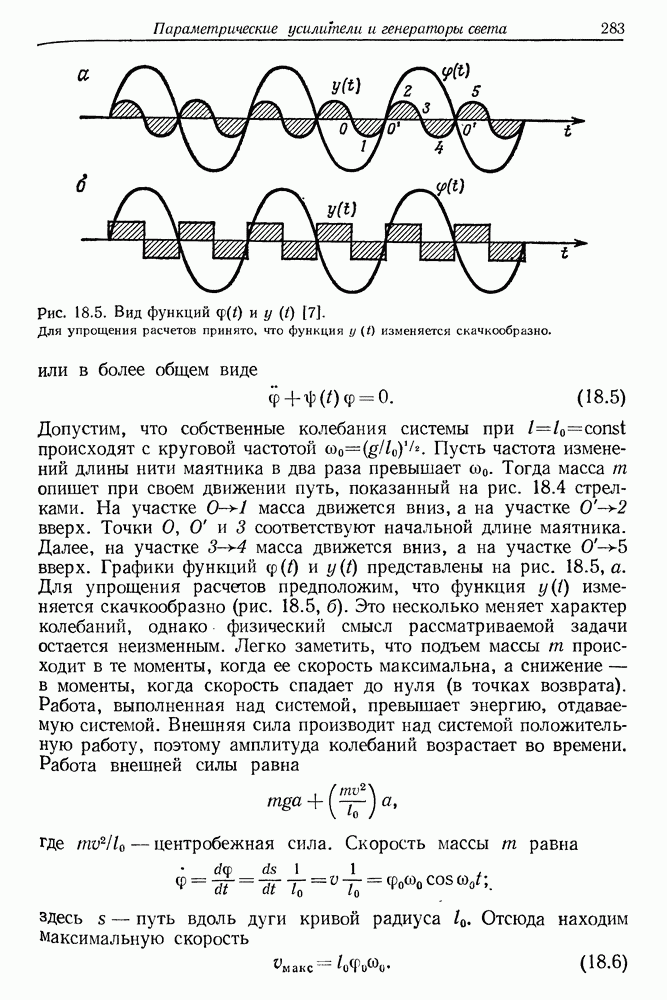
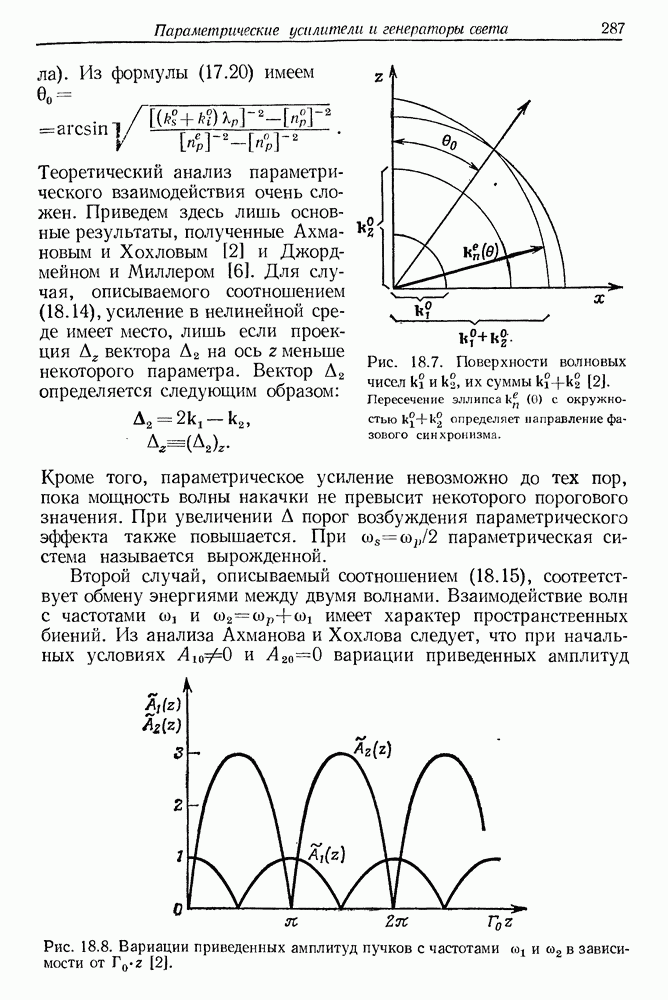
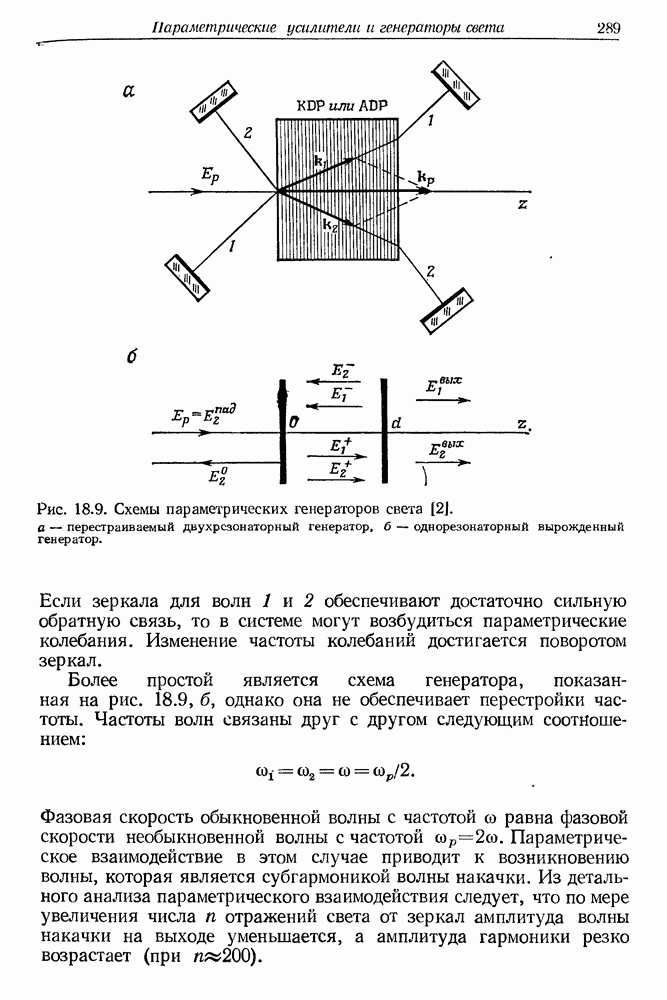
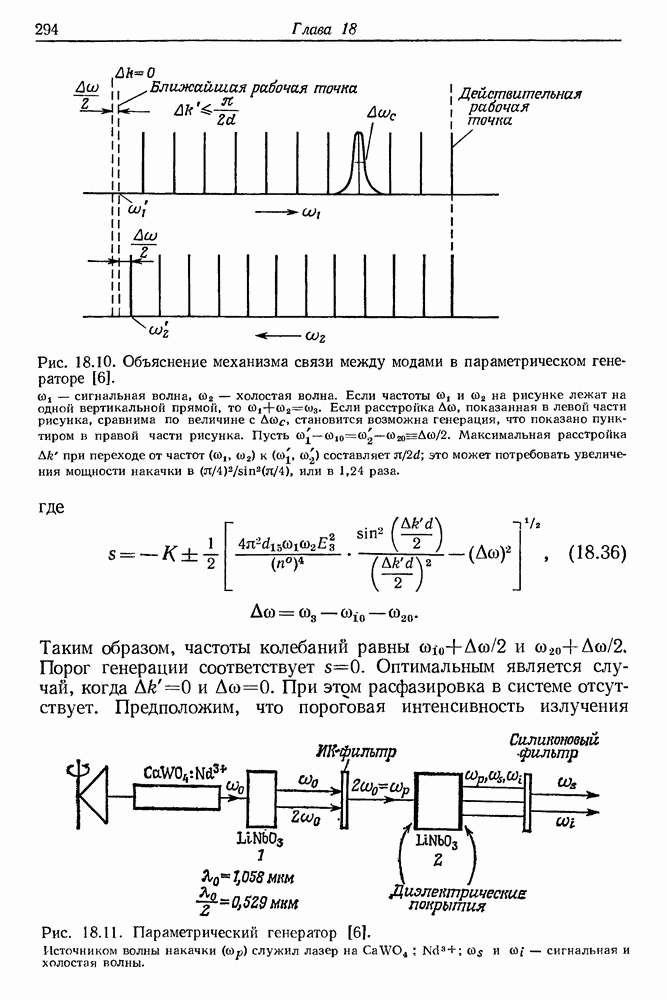
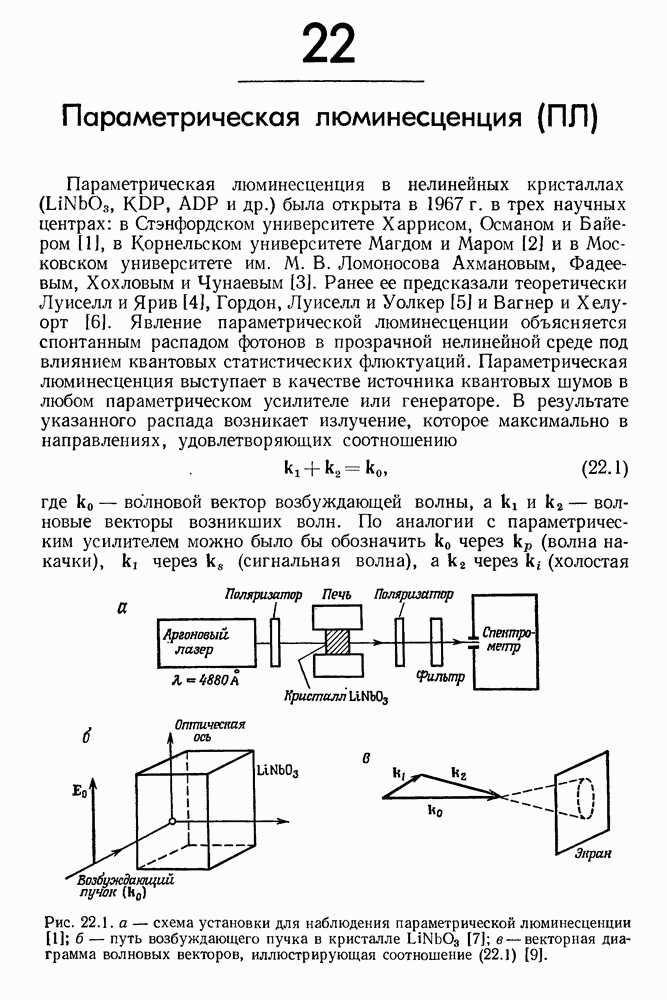
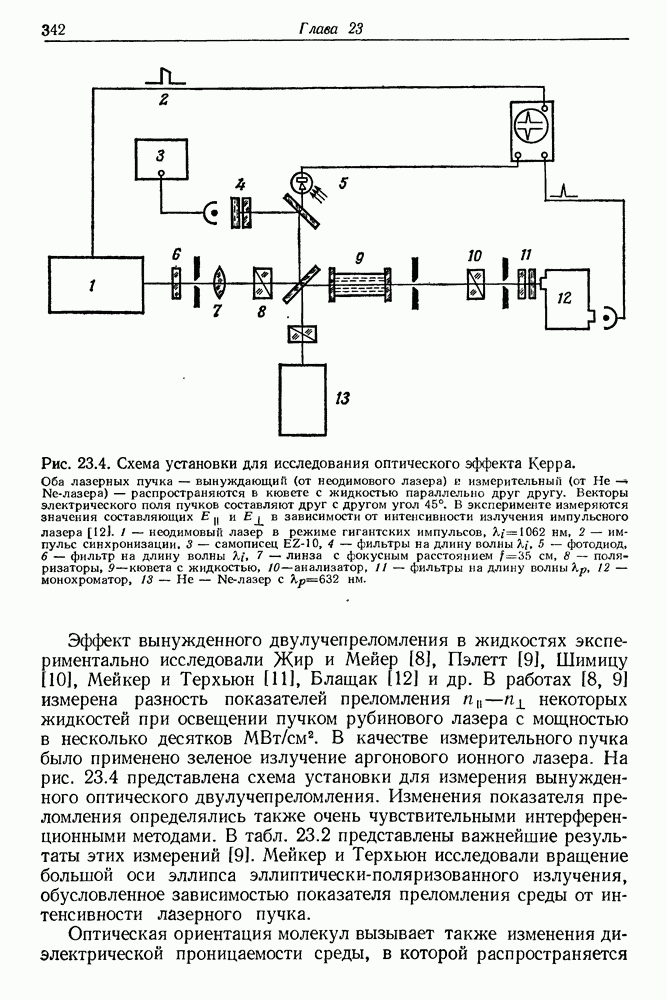
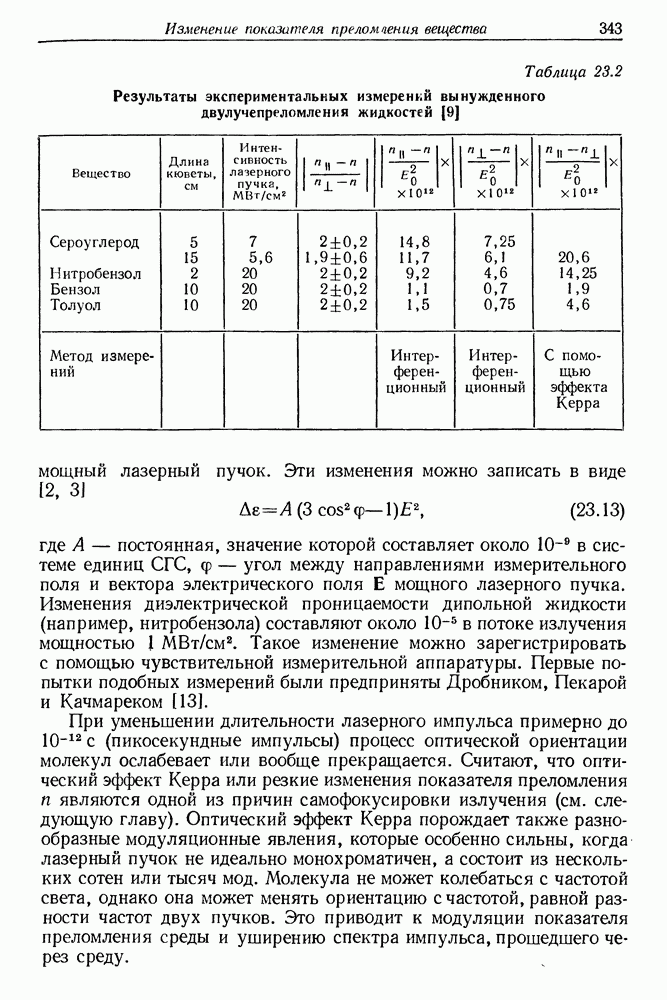
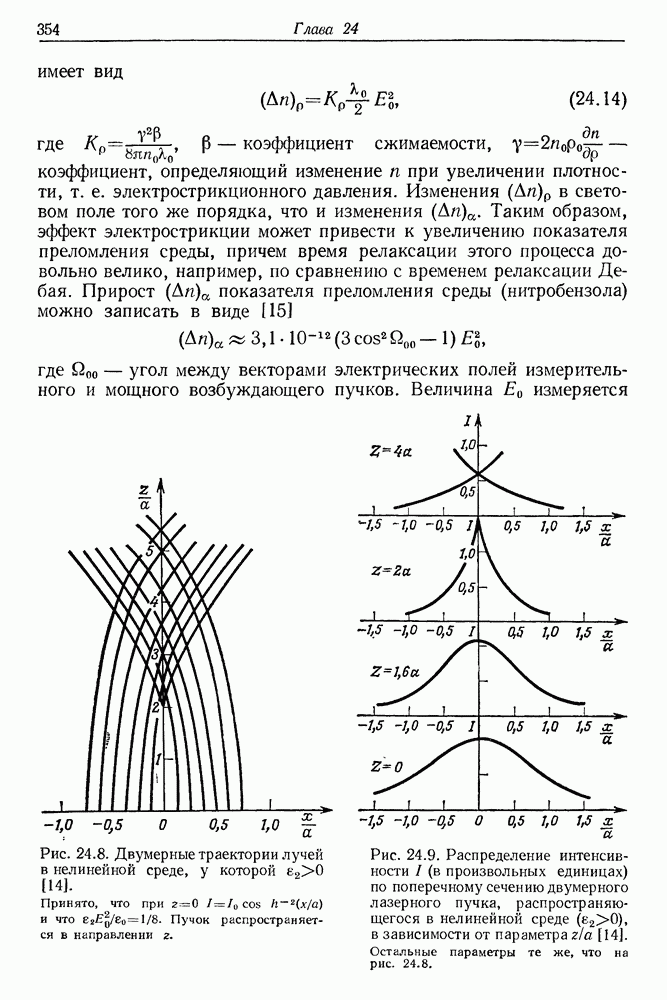
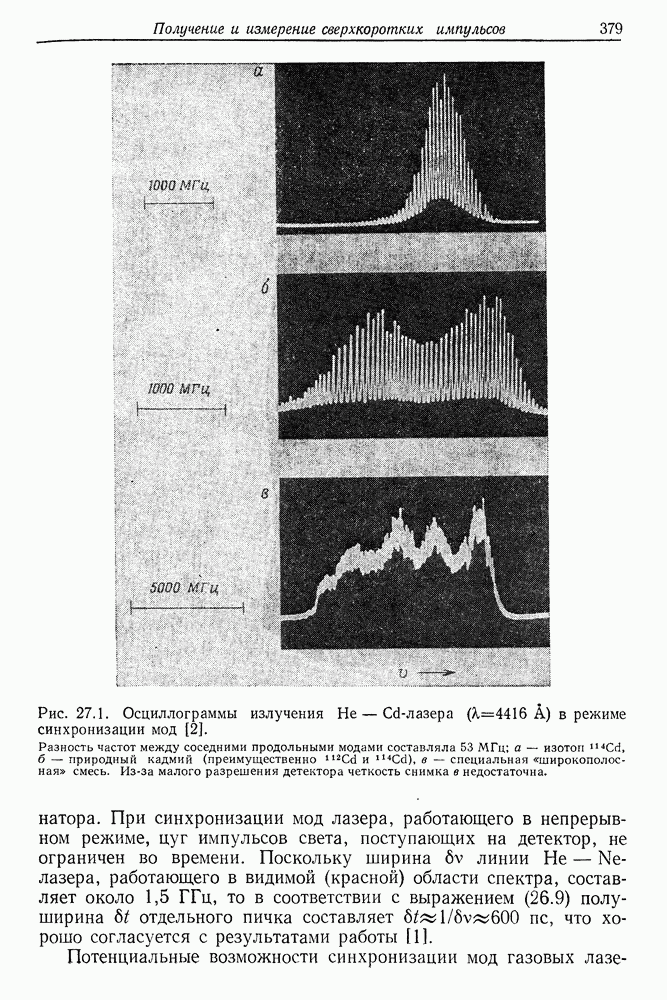
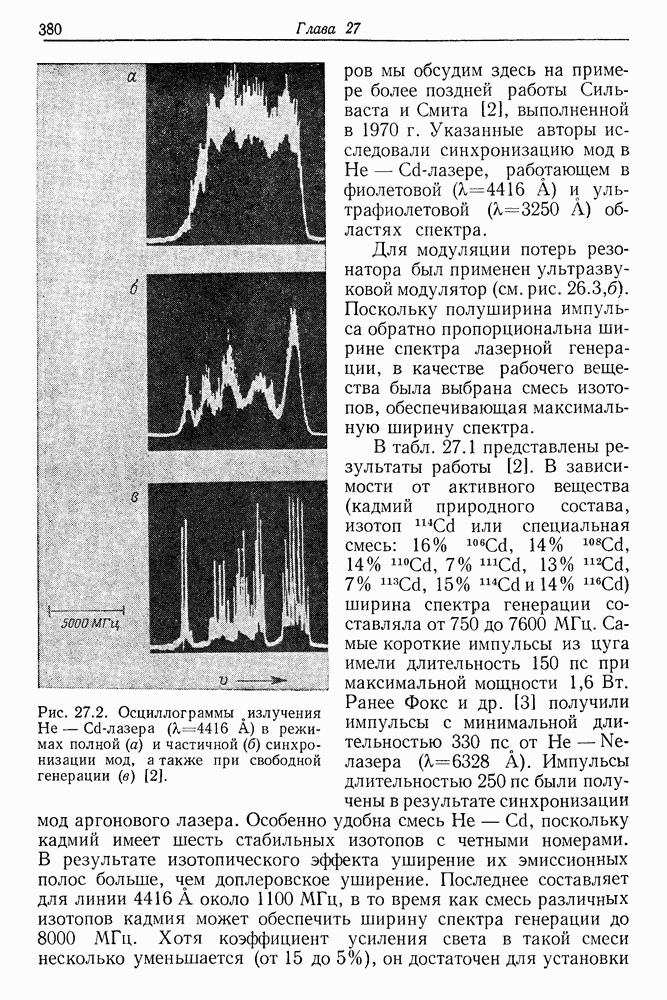
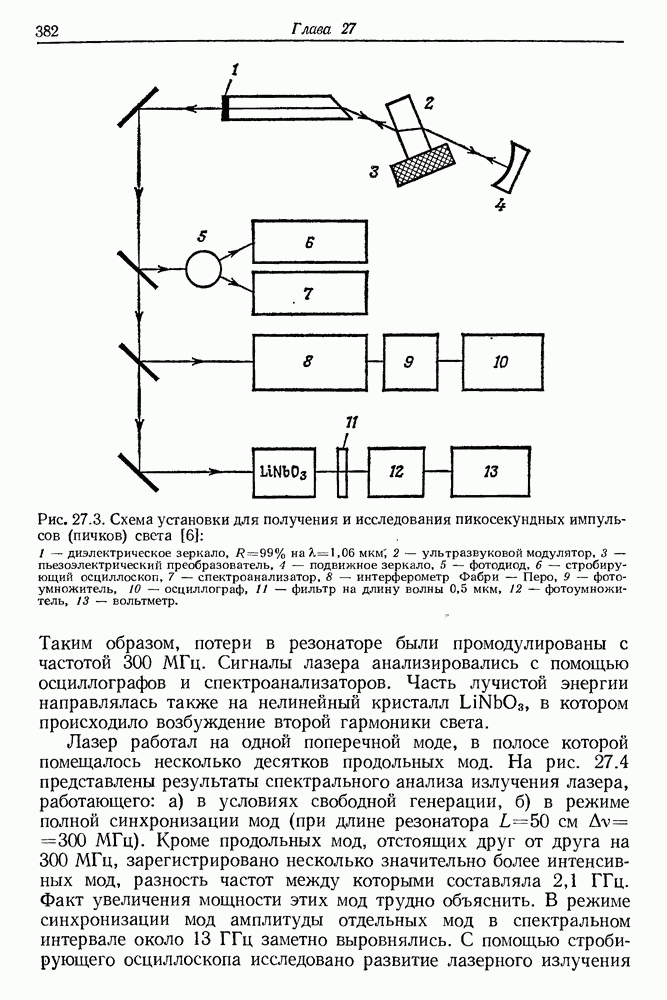
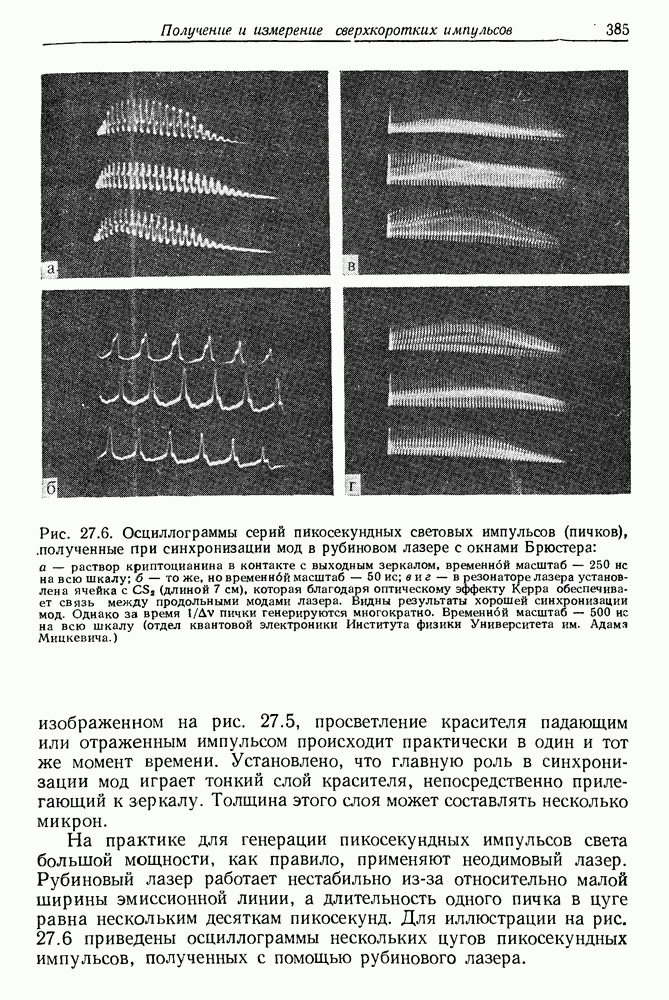
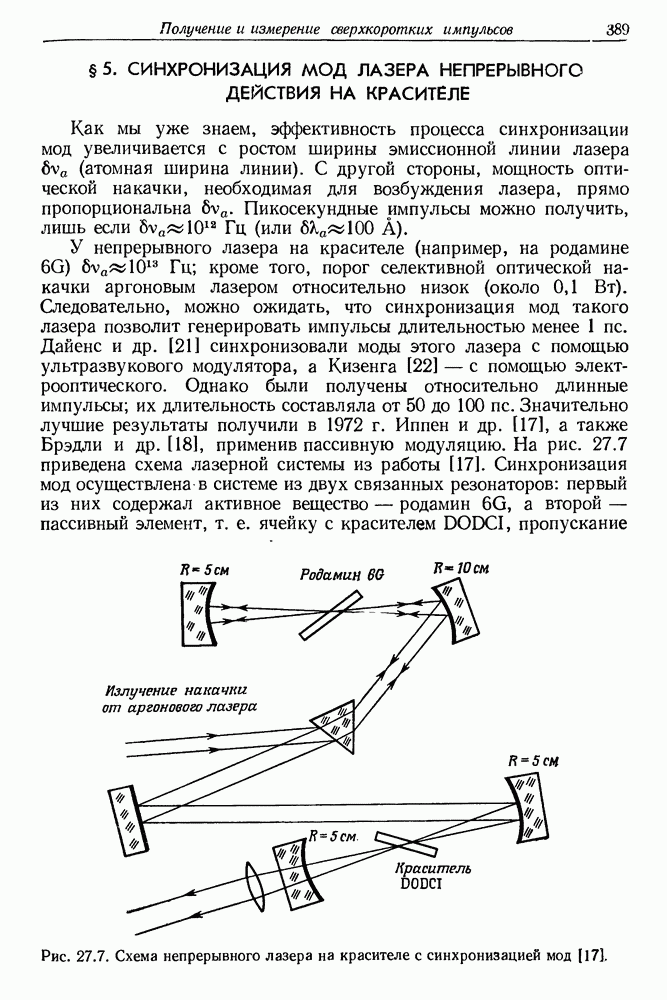
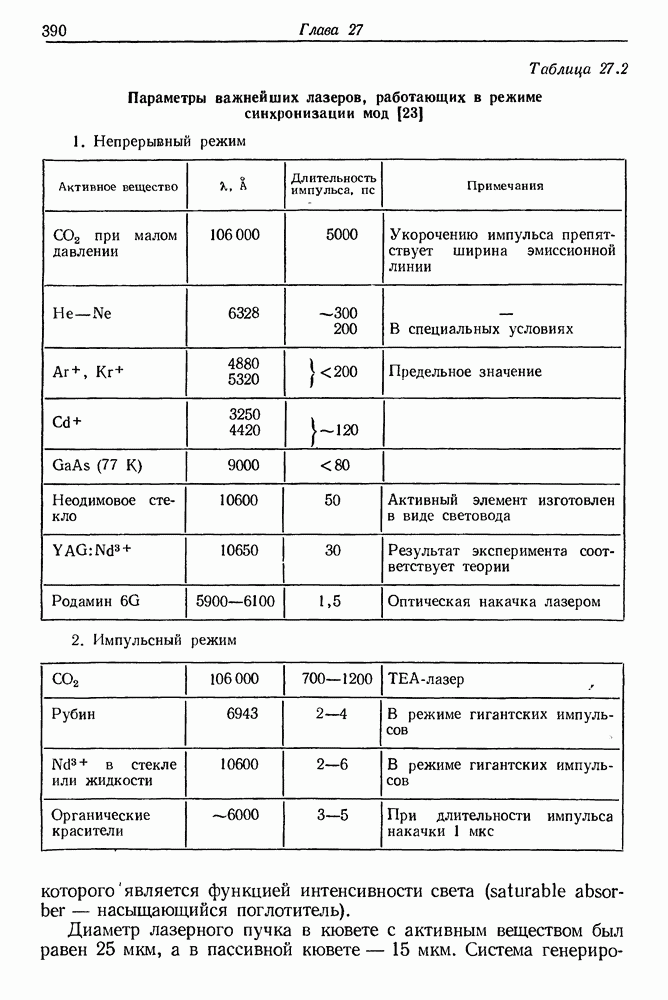
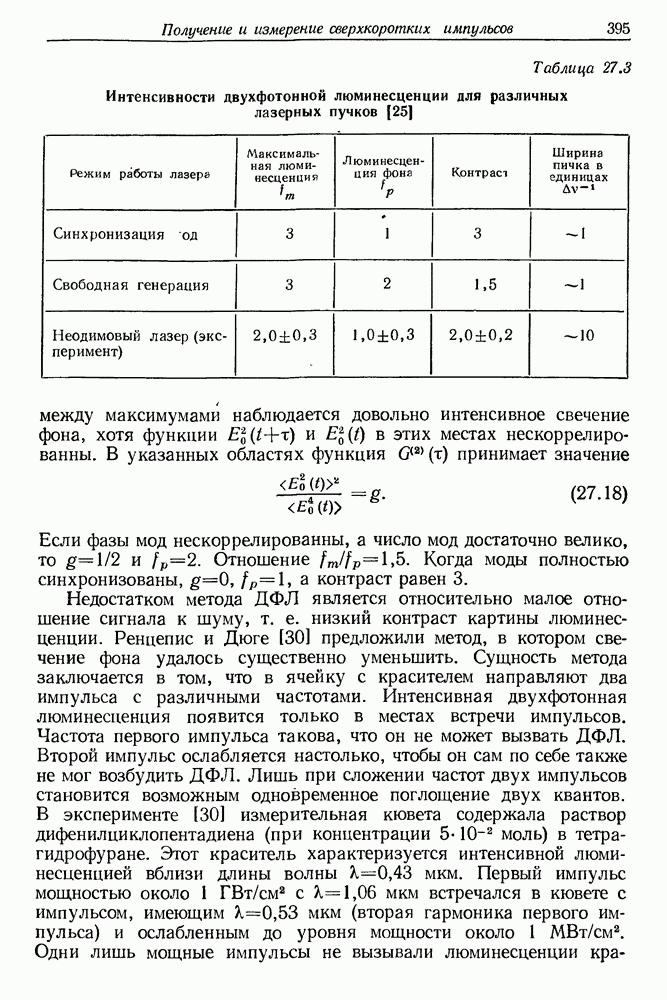
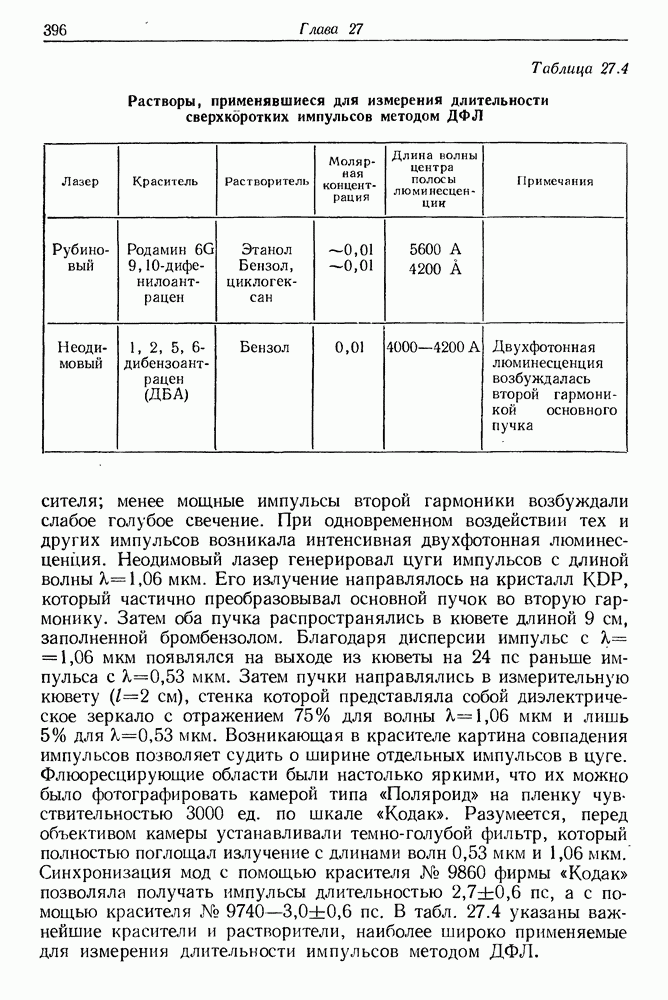
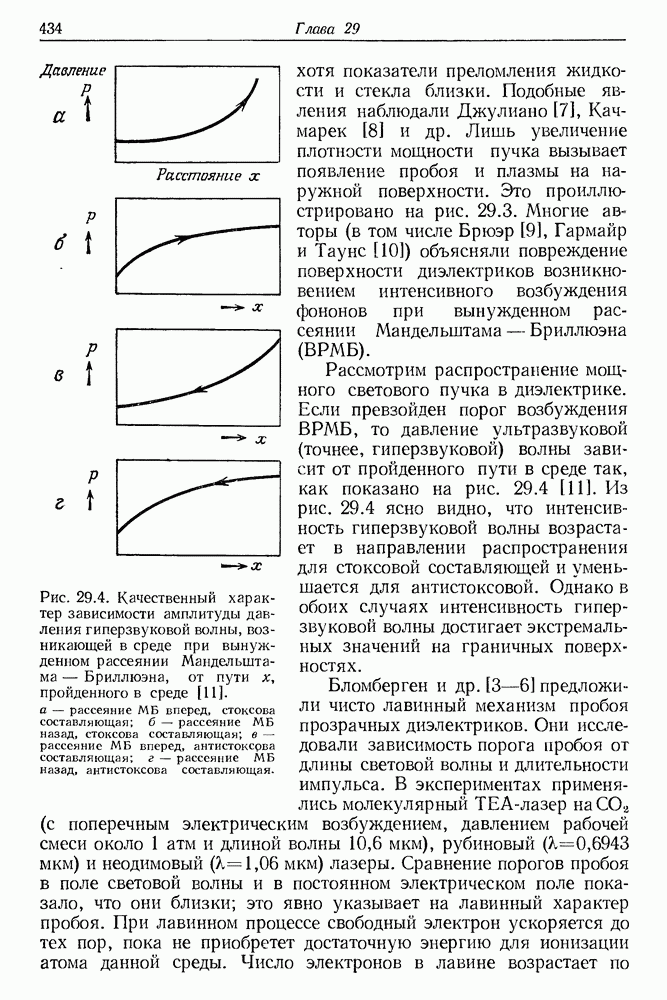
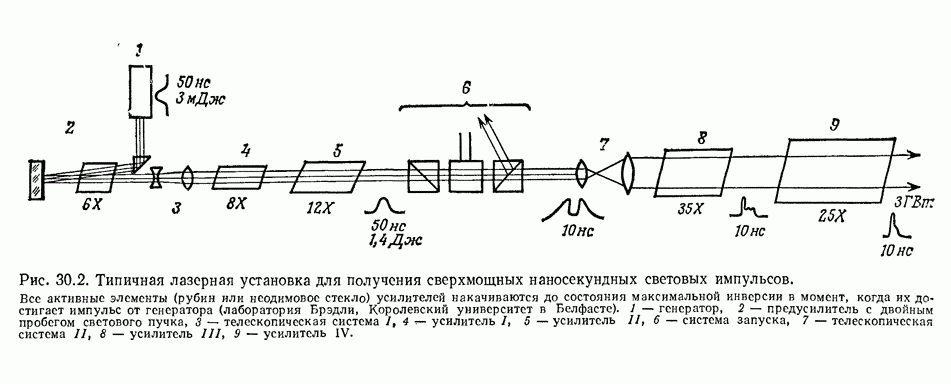
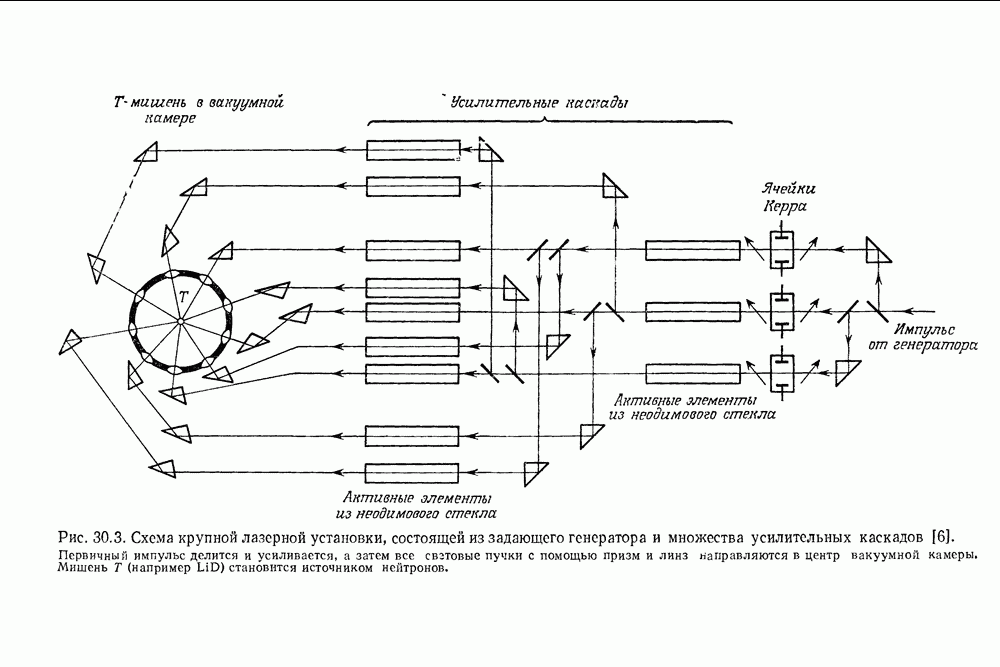
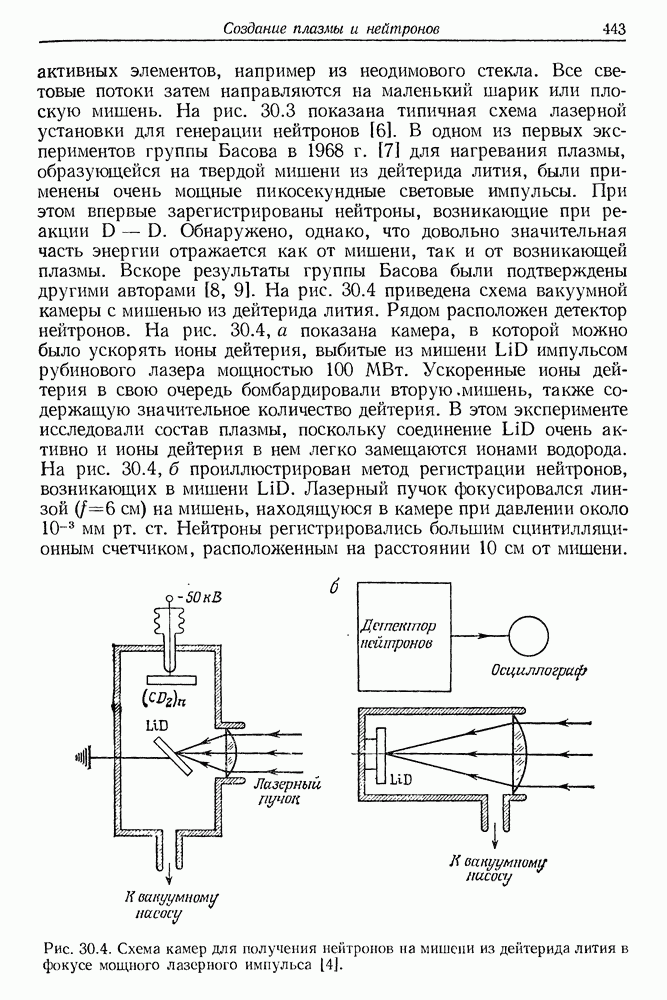
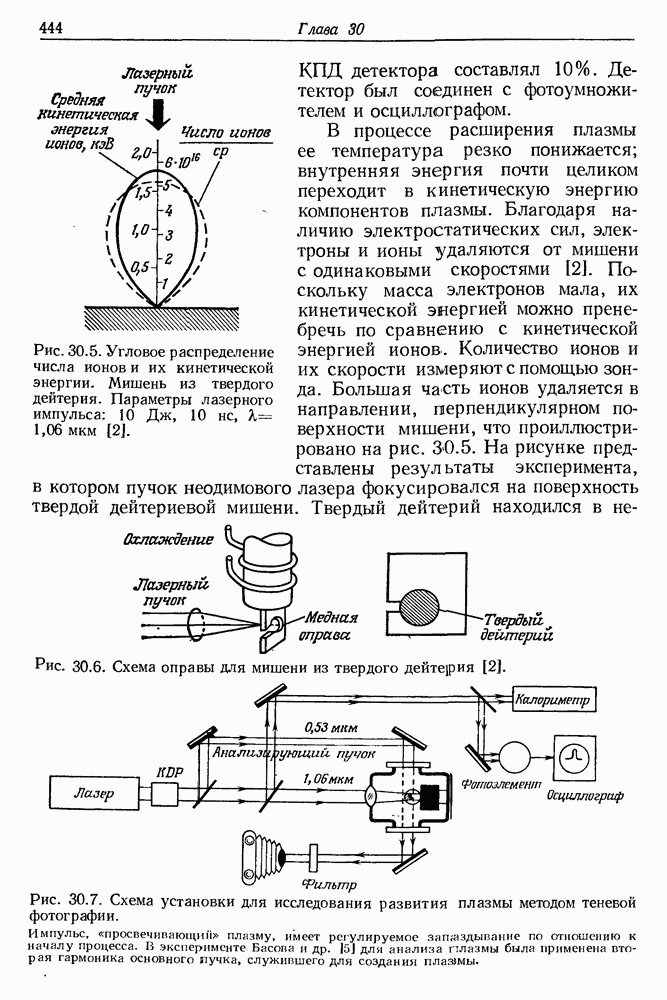
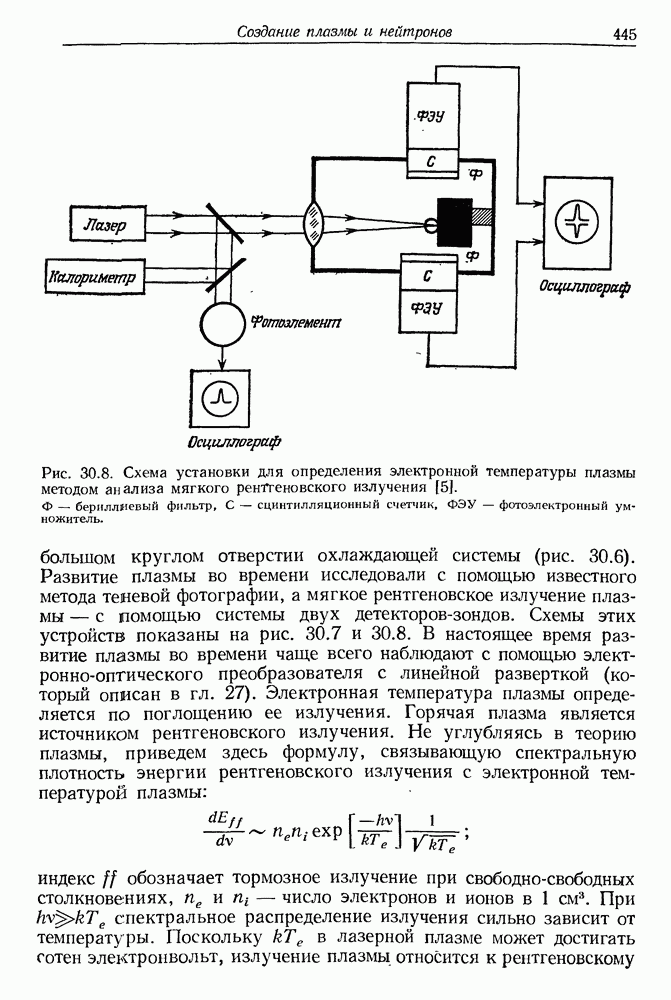
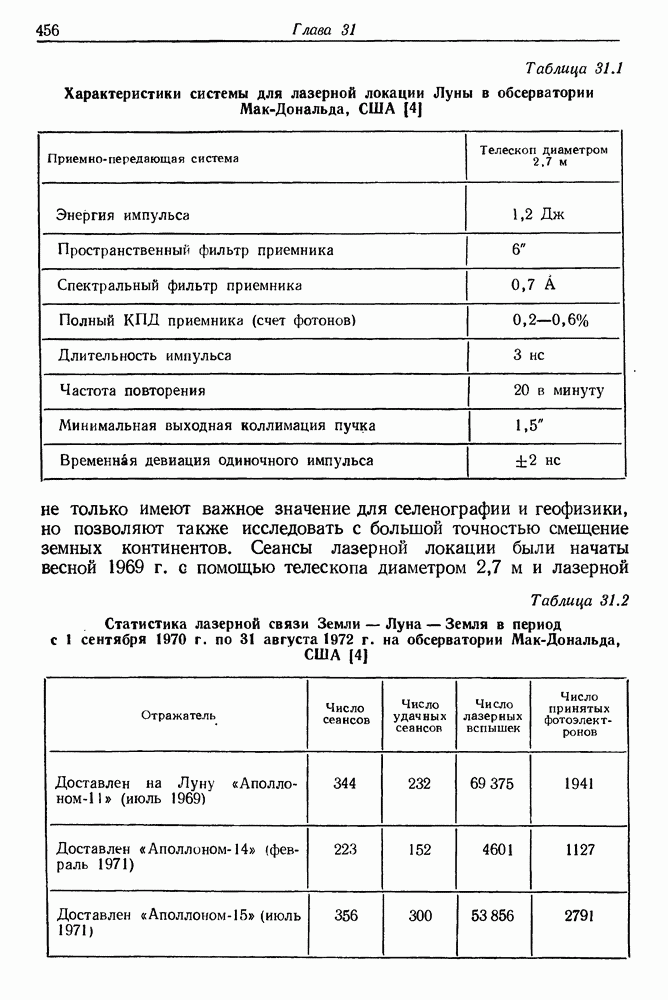
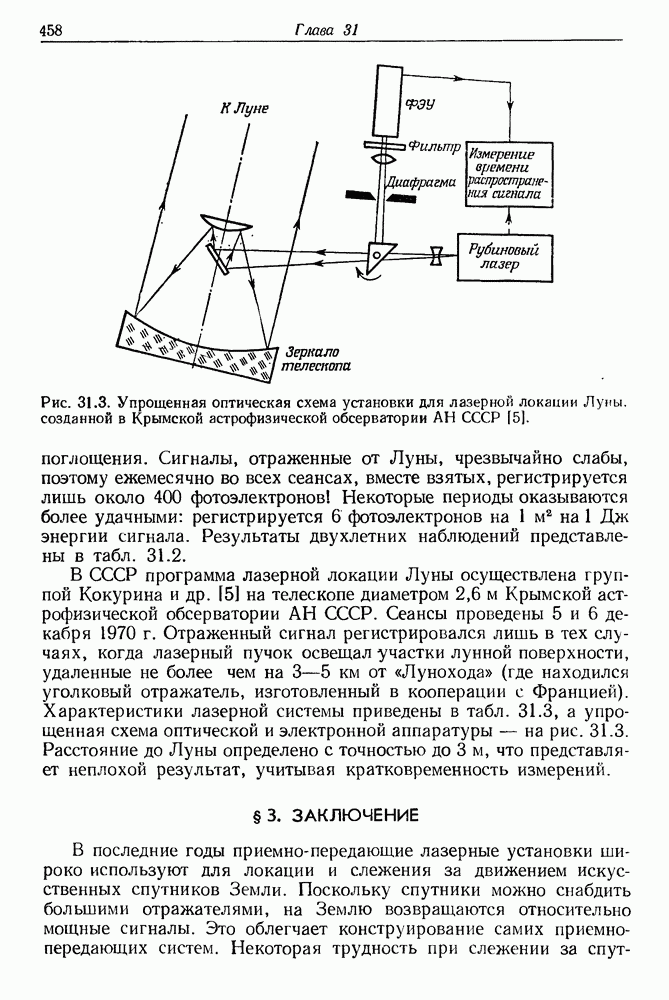
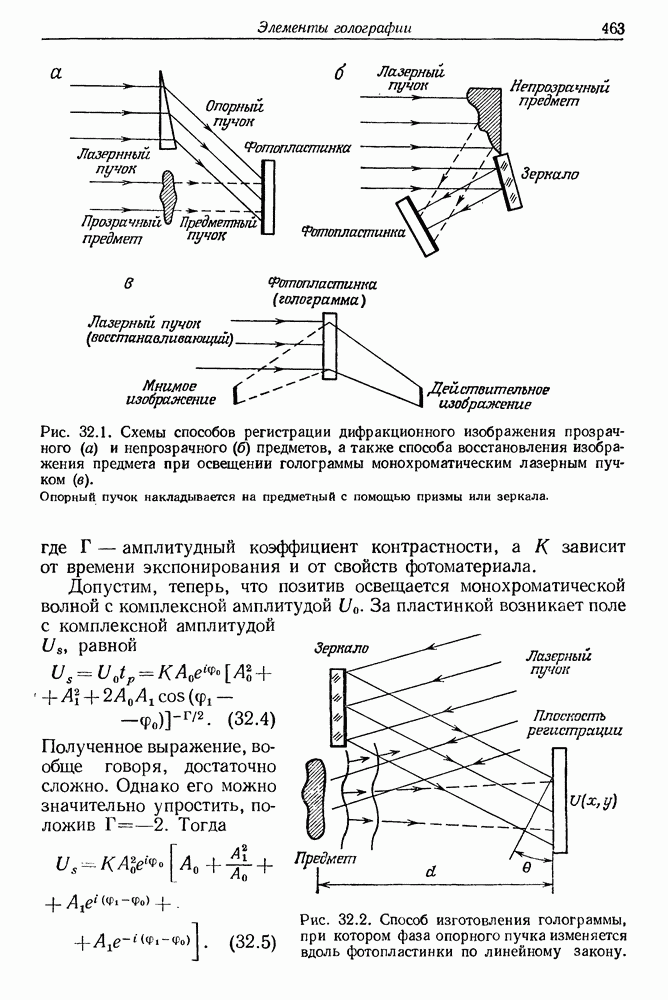
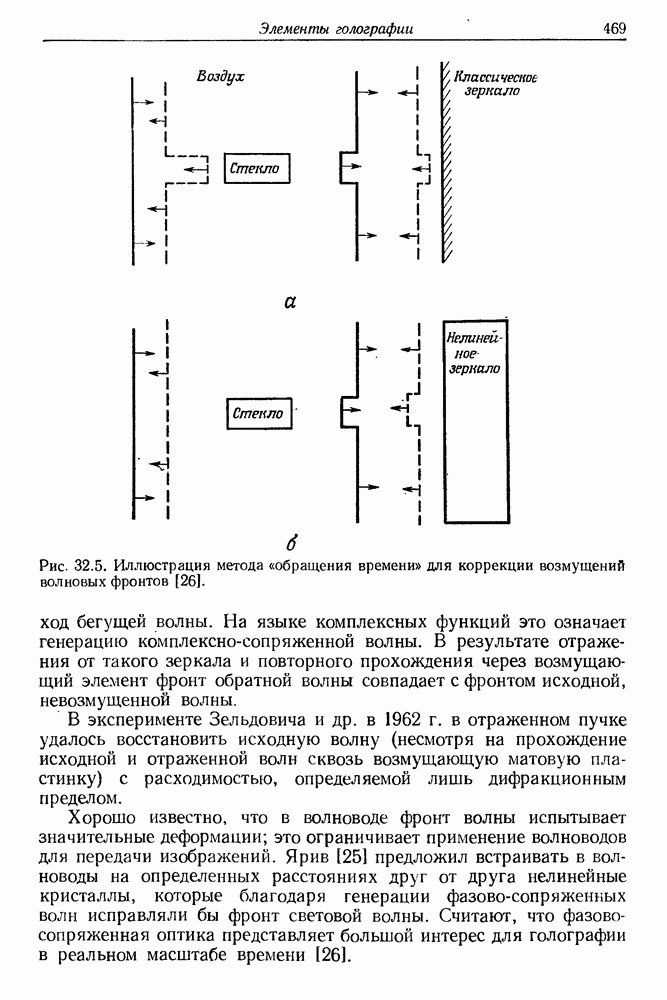
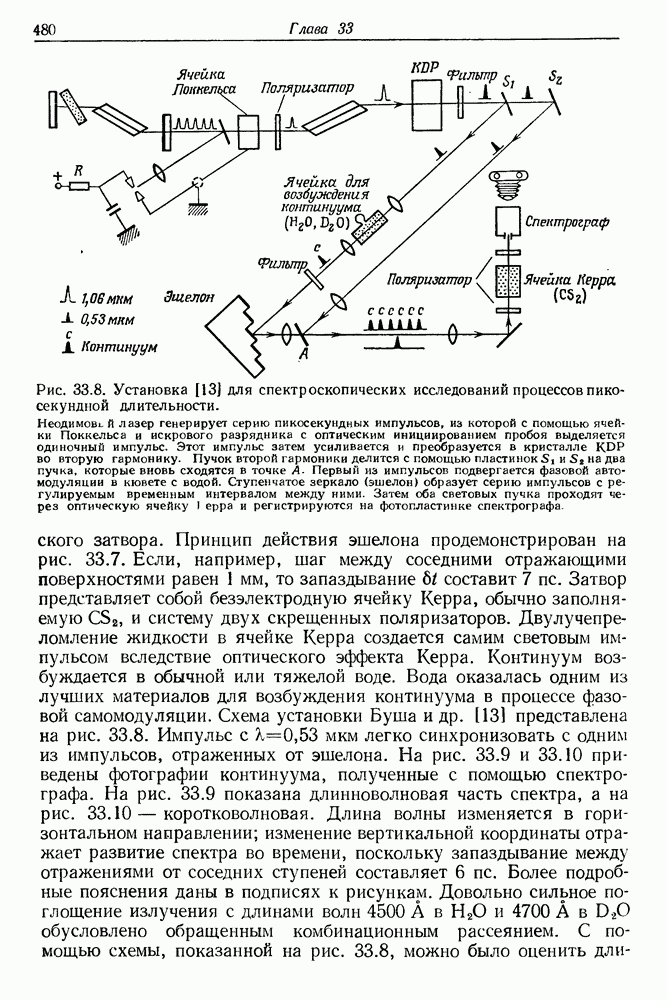
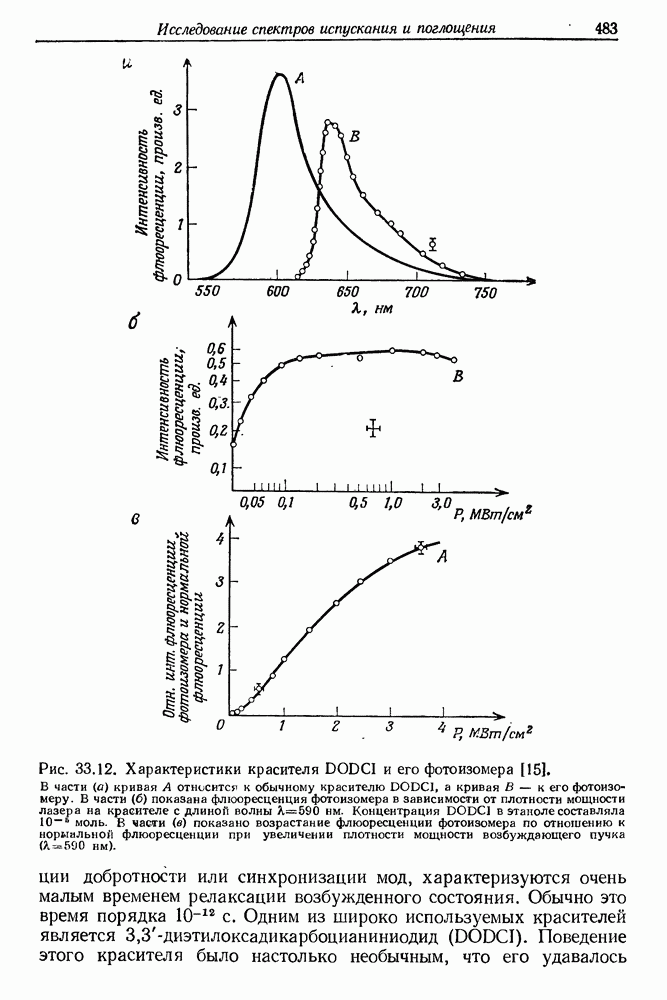
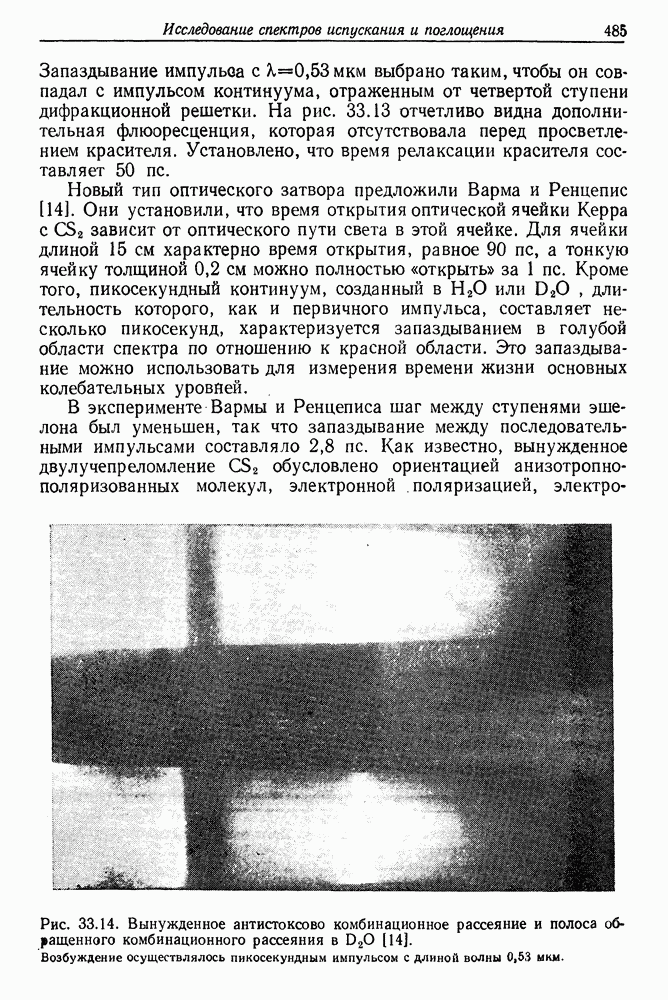
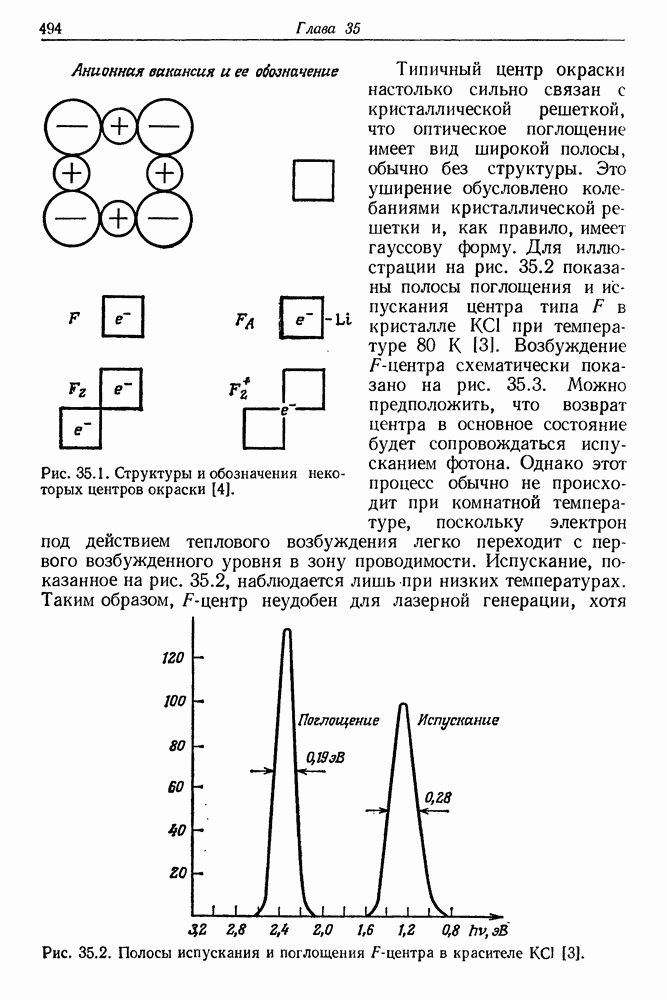
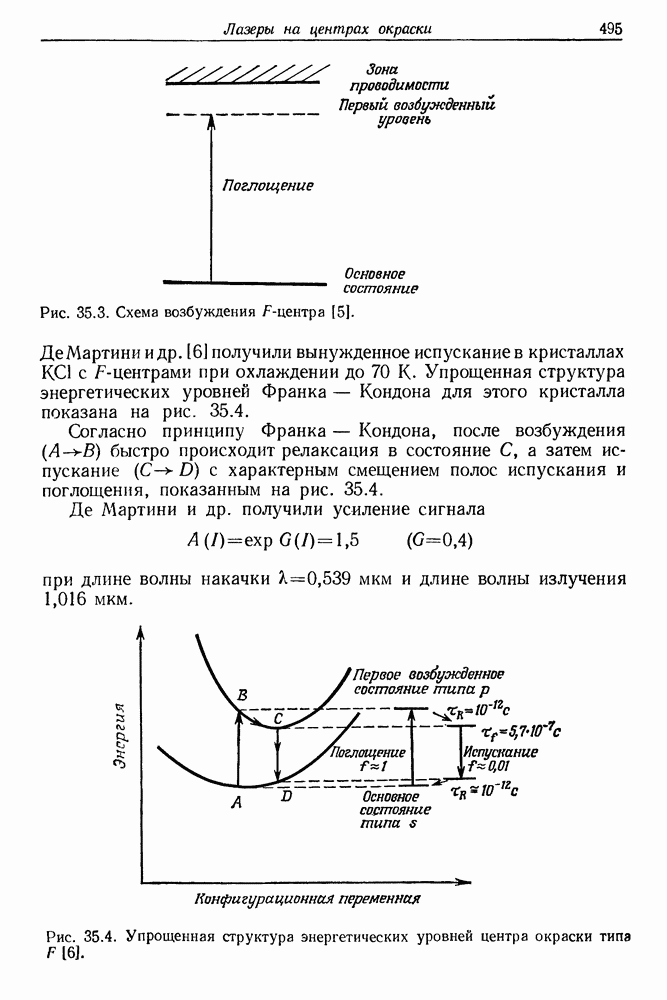
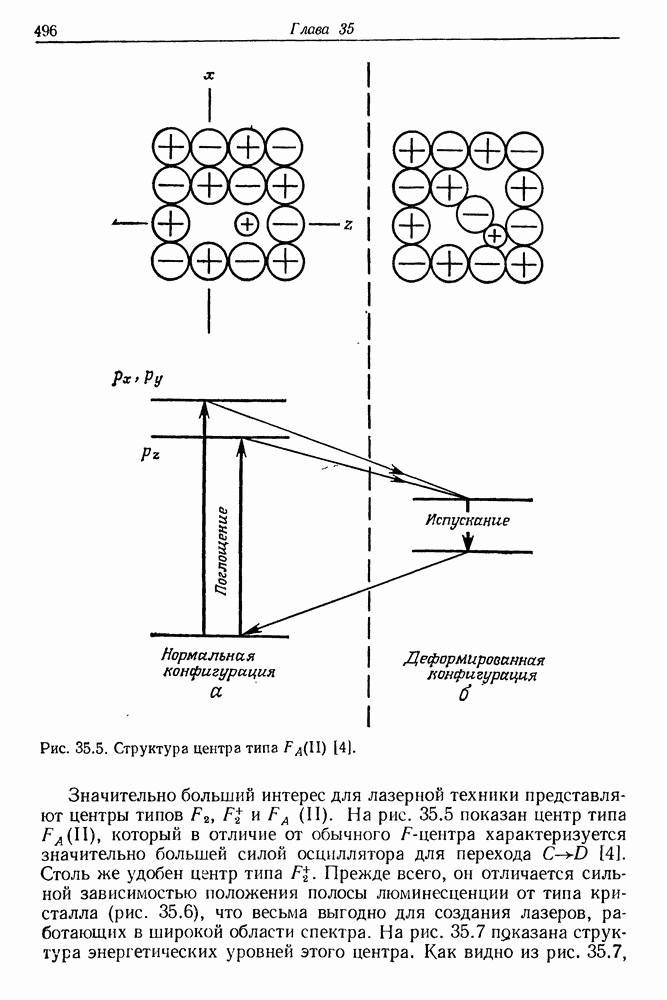
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
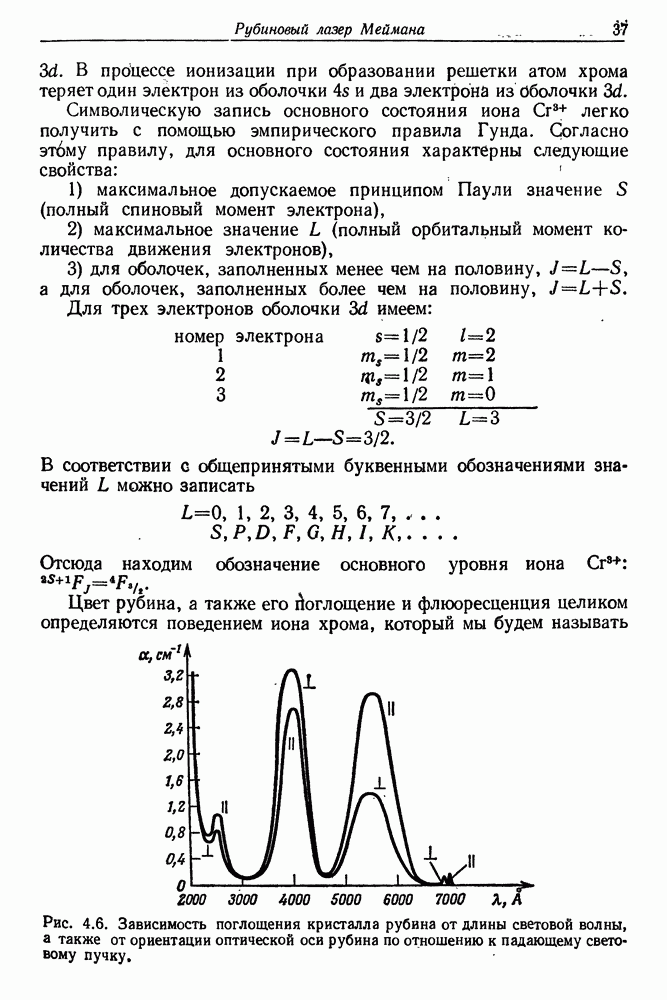
36
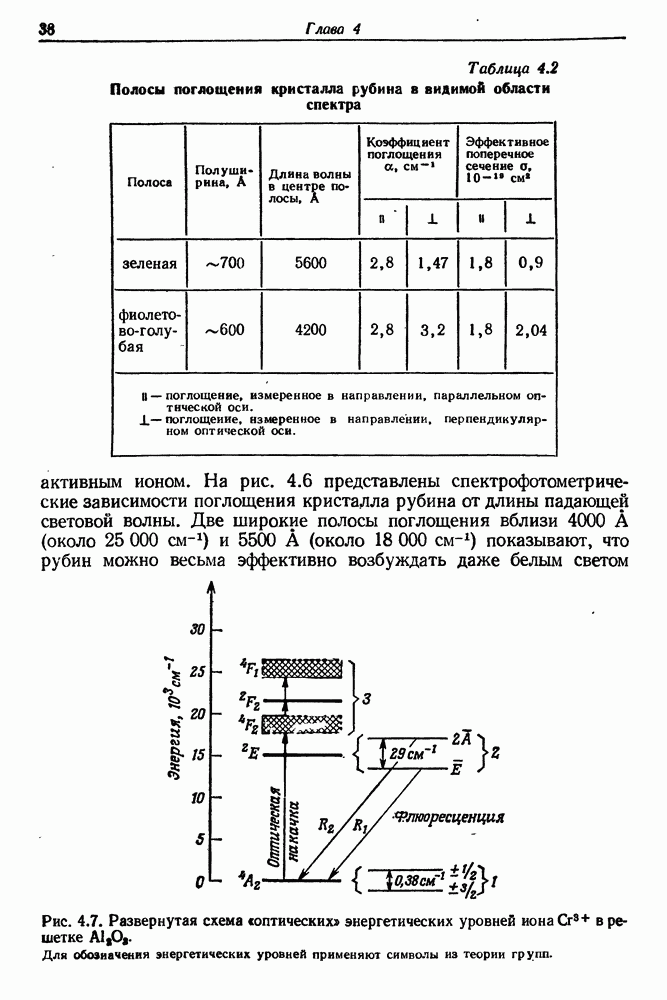
37
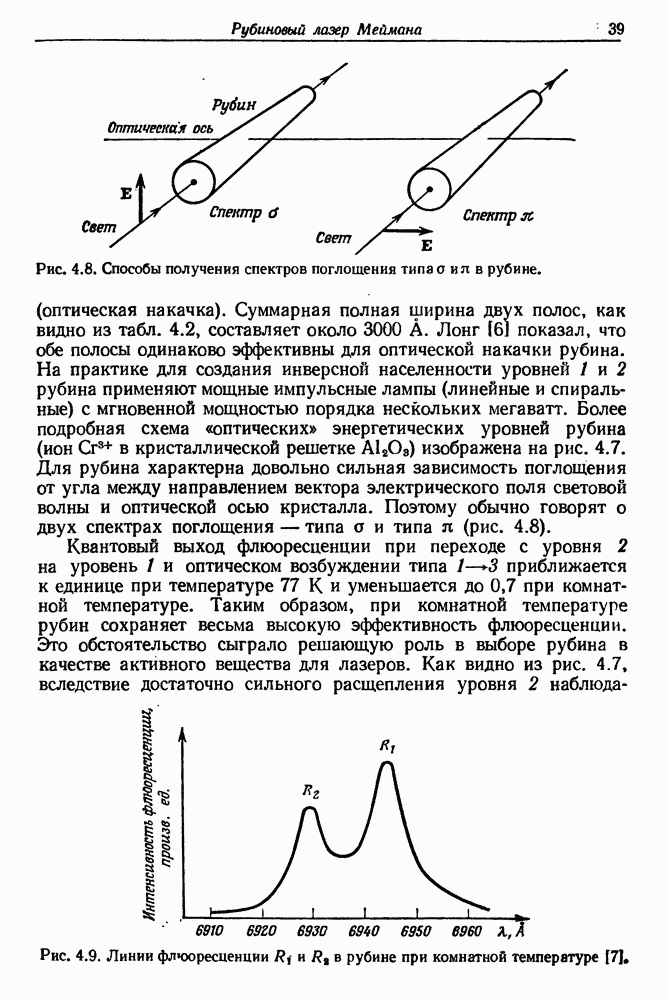
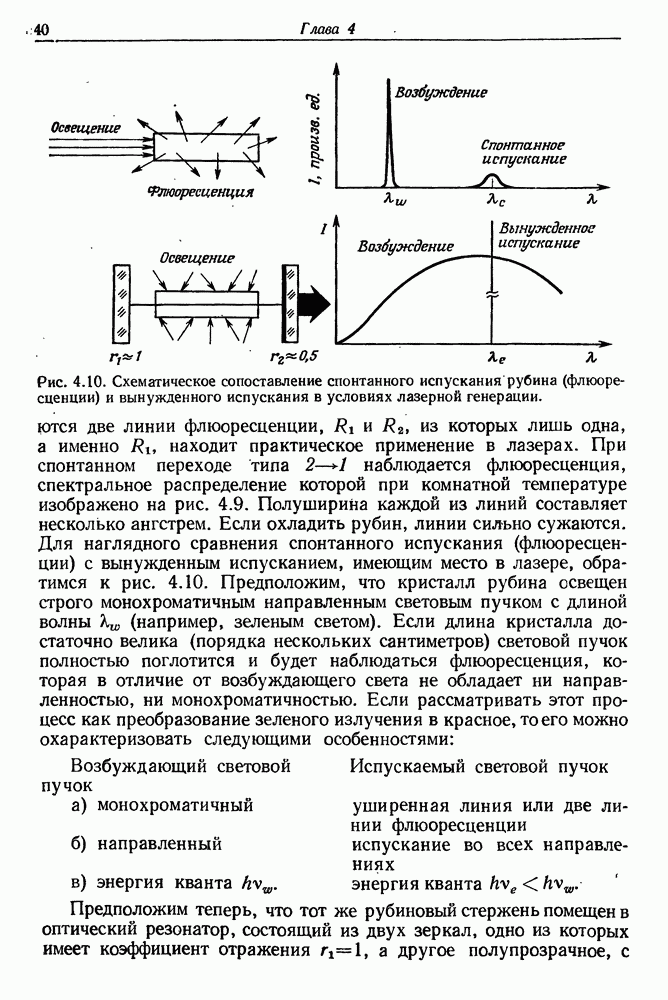
38
39
40
41
42
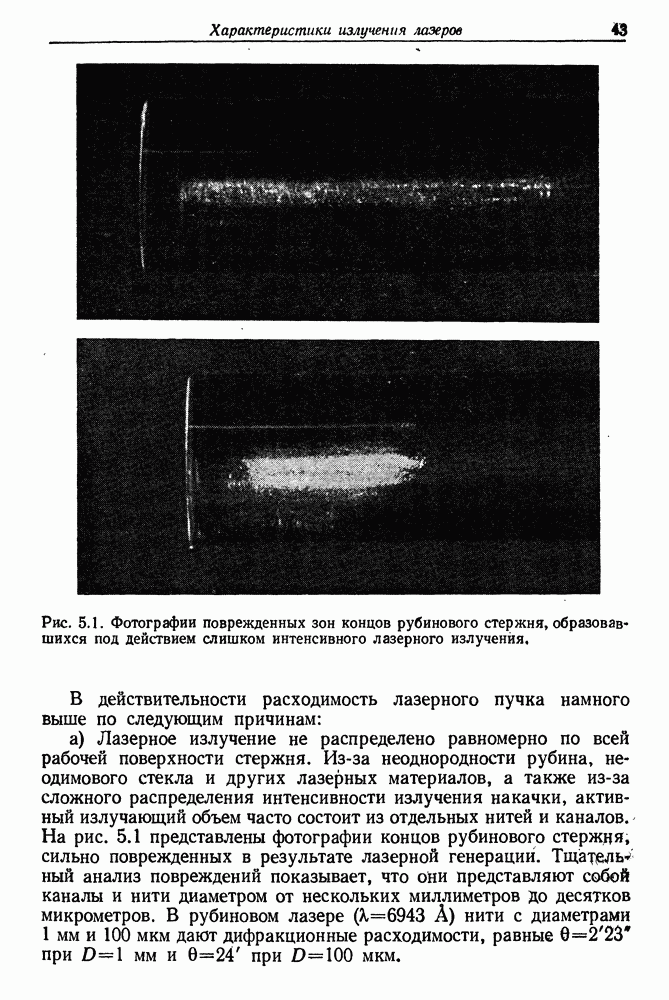
43
44
45
46
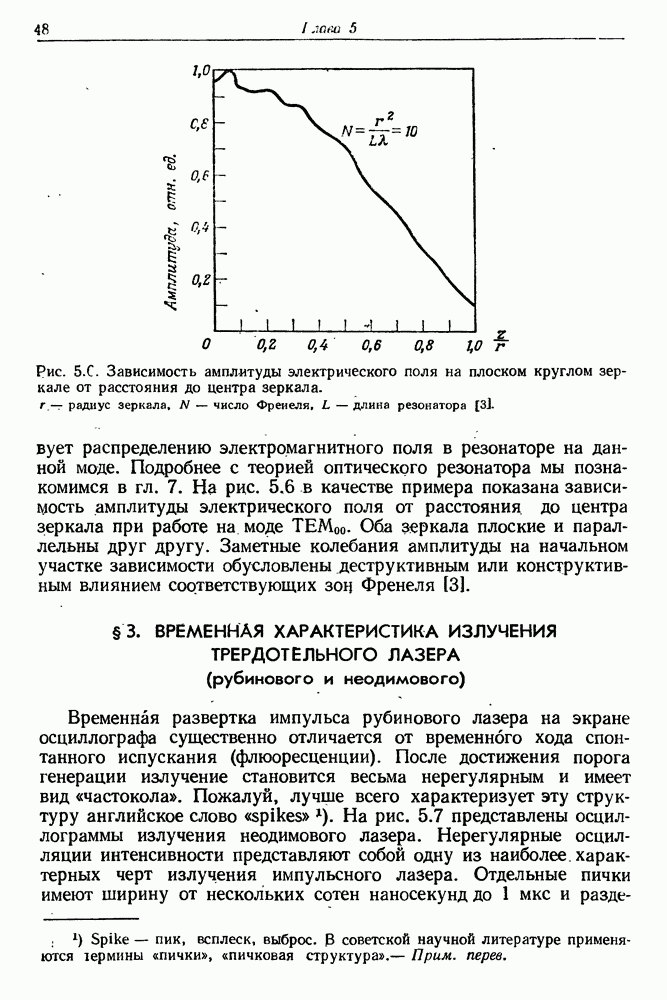
47
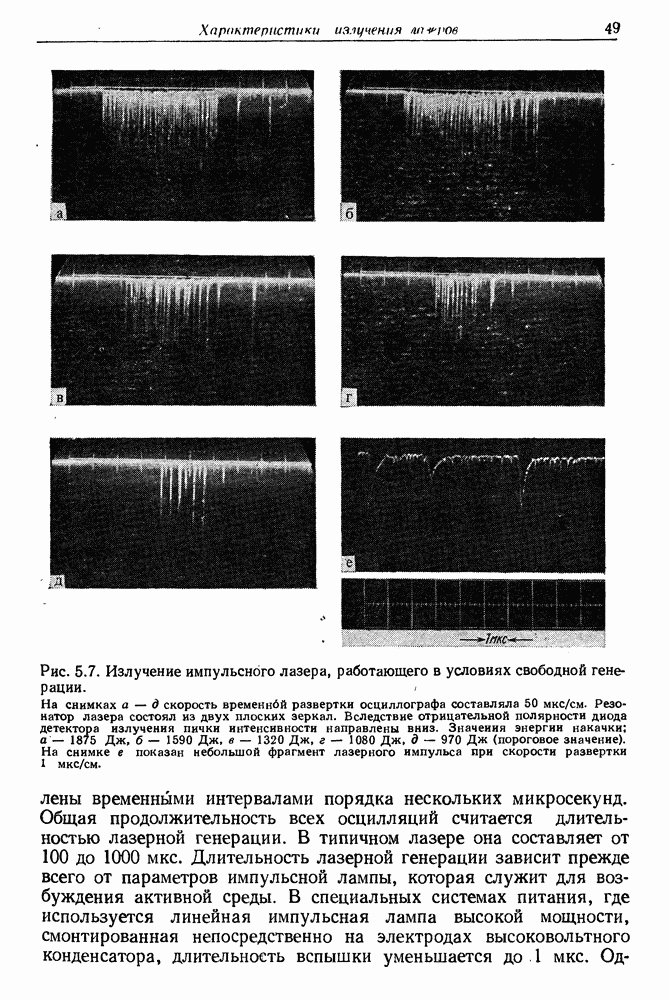
48
49
50
51
52
53
54
55
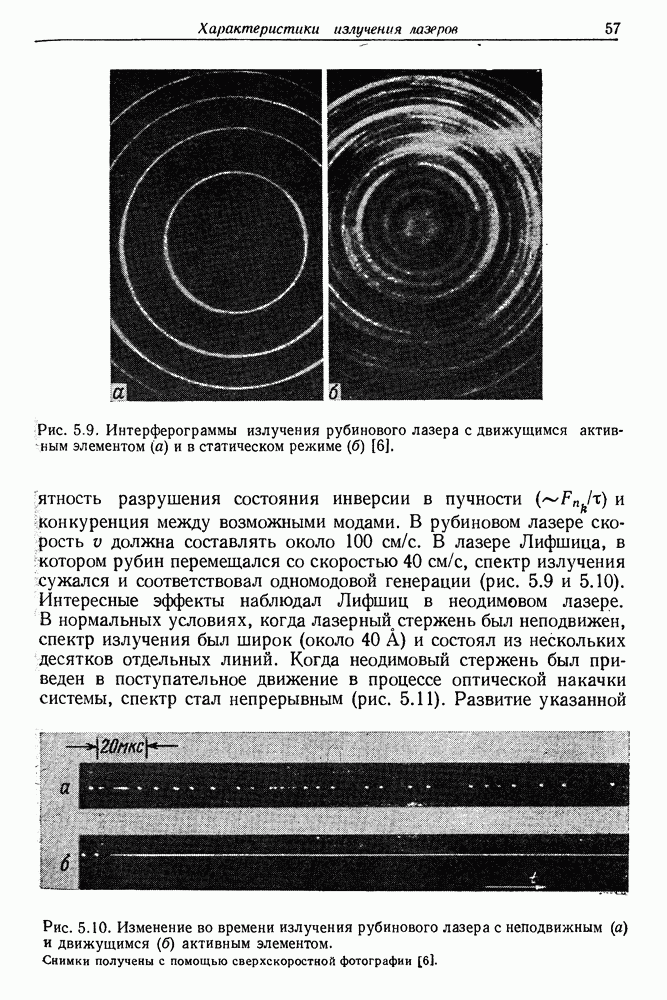
56
57
58
59
60
61
62
63
64
65
66
67
68
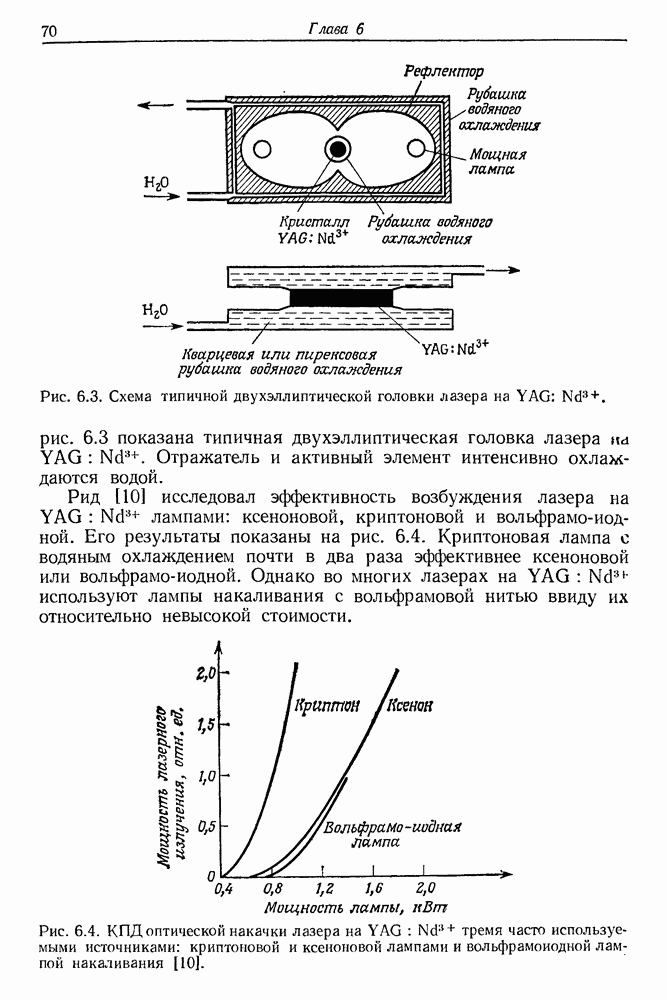
69
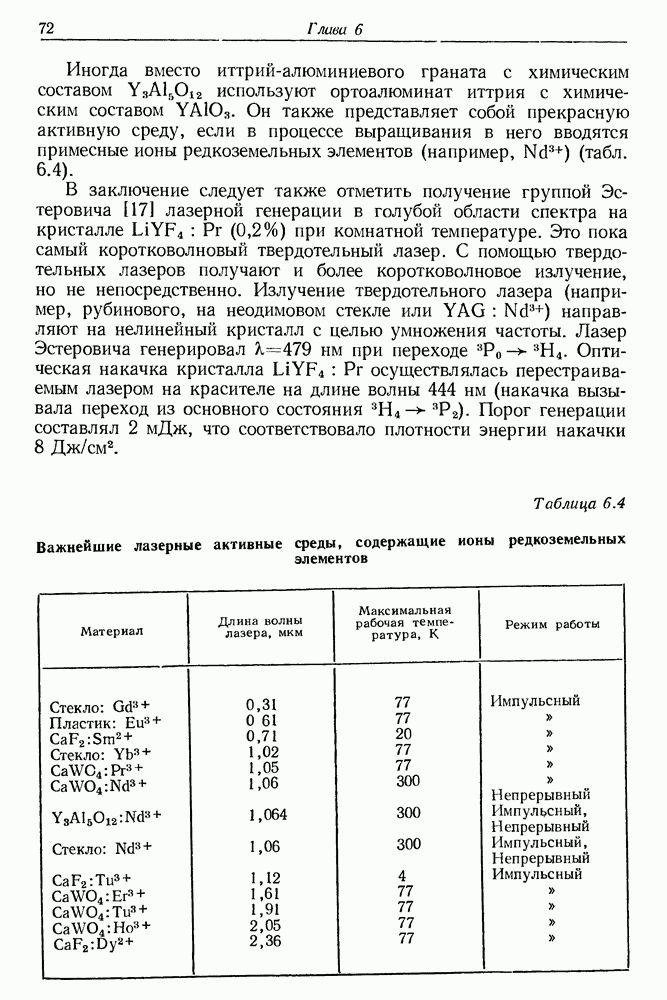
70
71
72
73
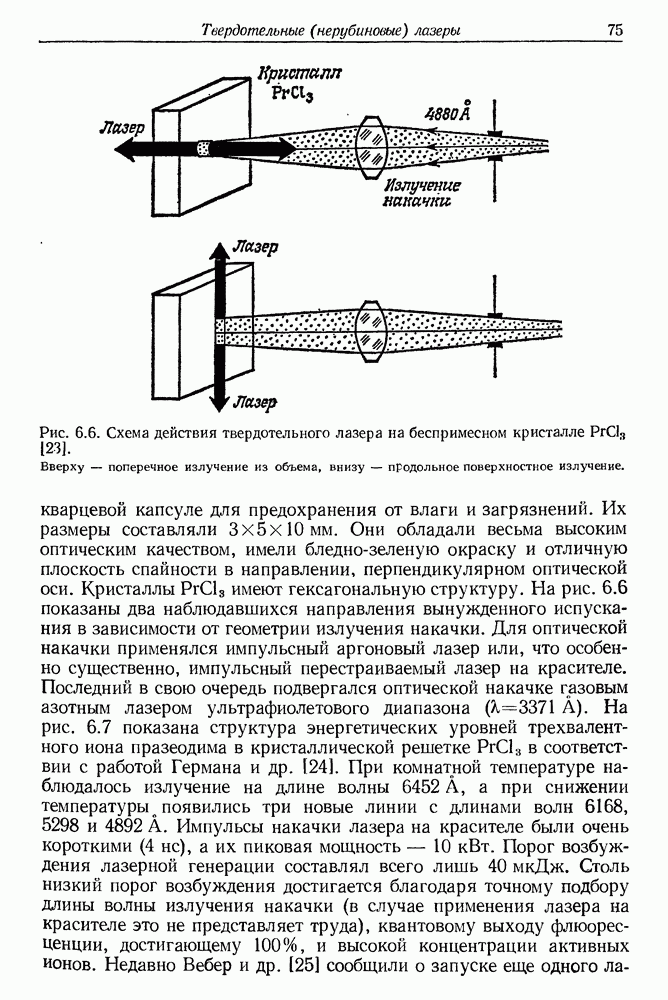
74
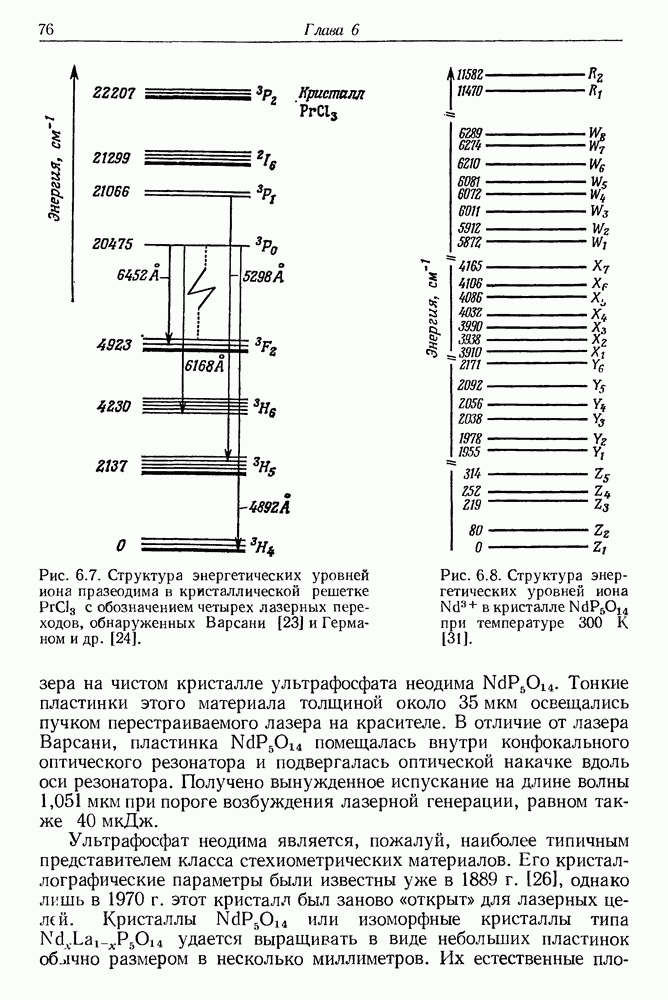
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
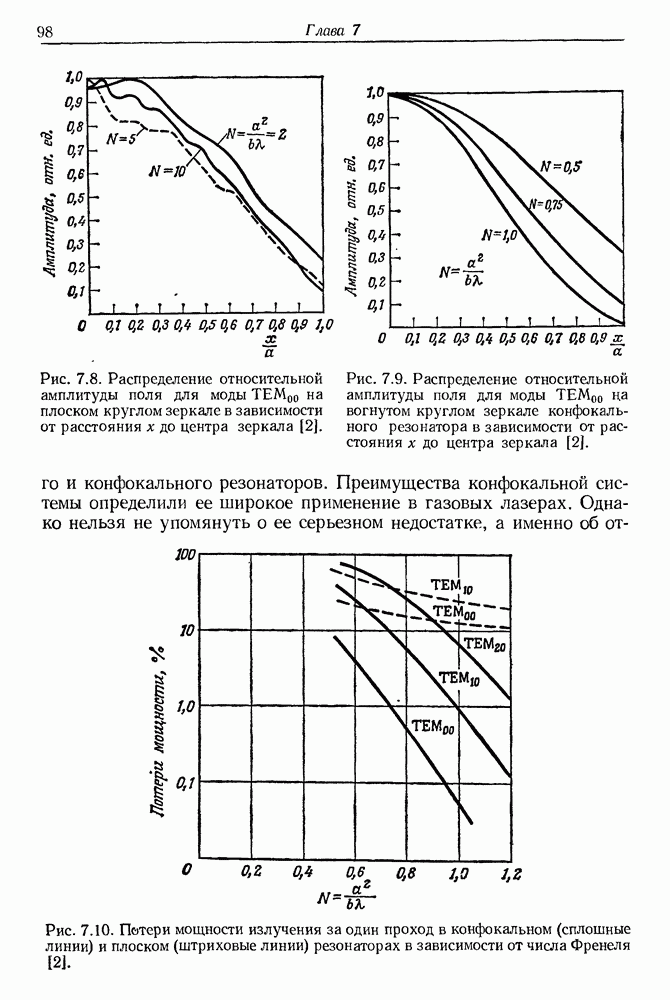
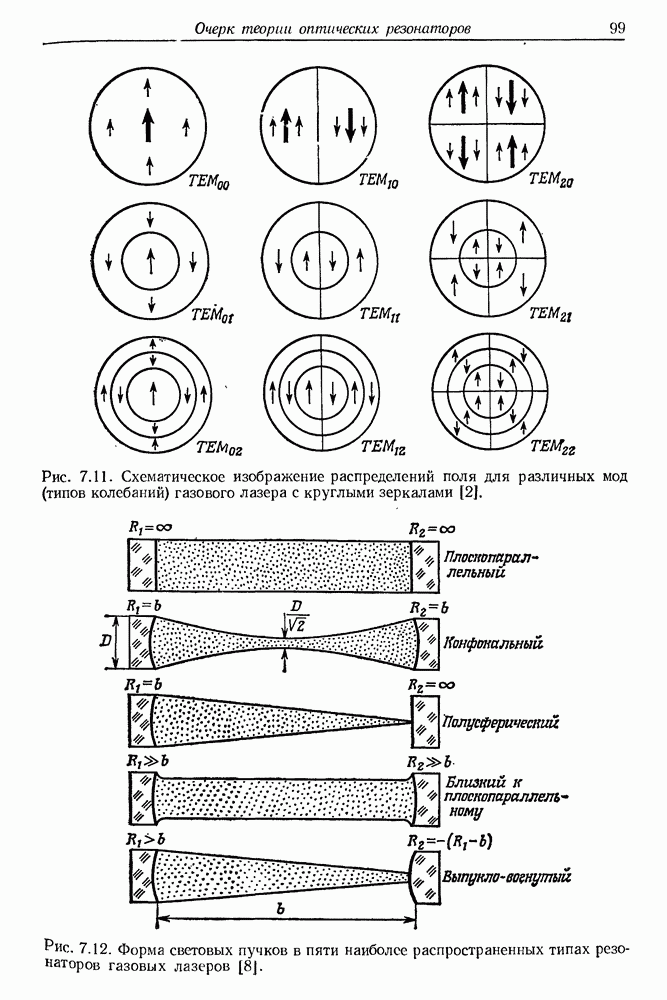
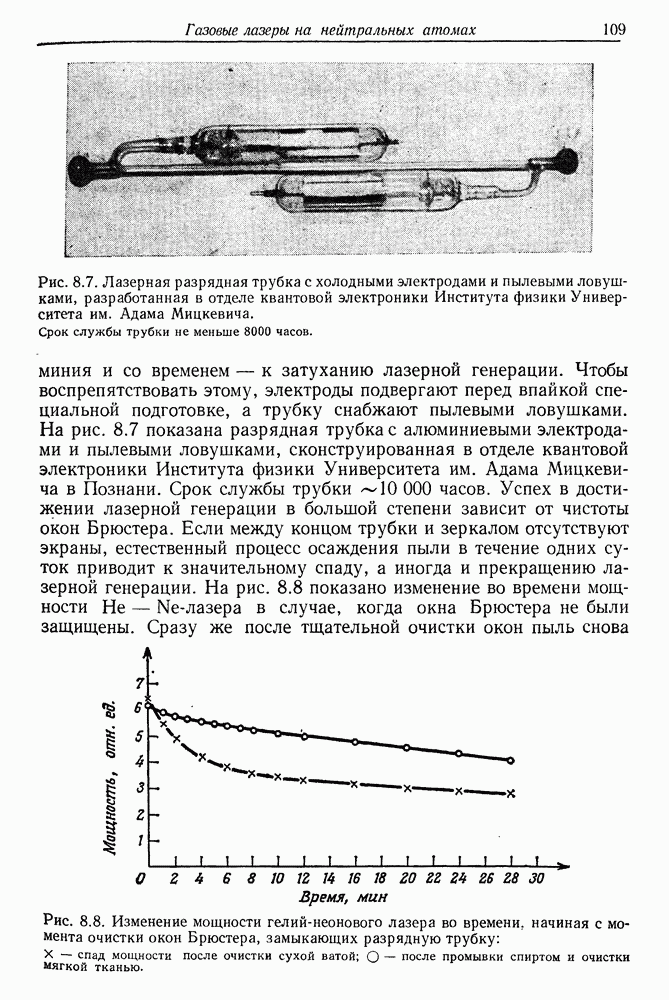
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
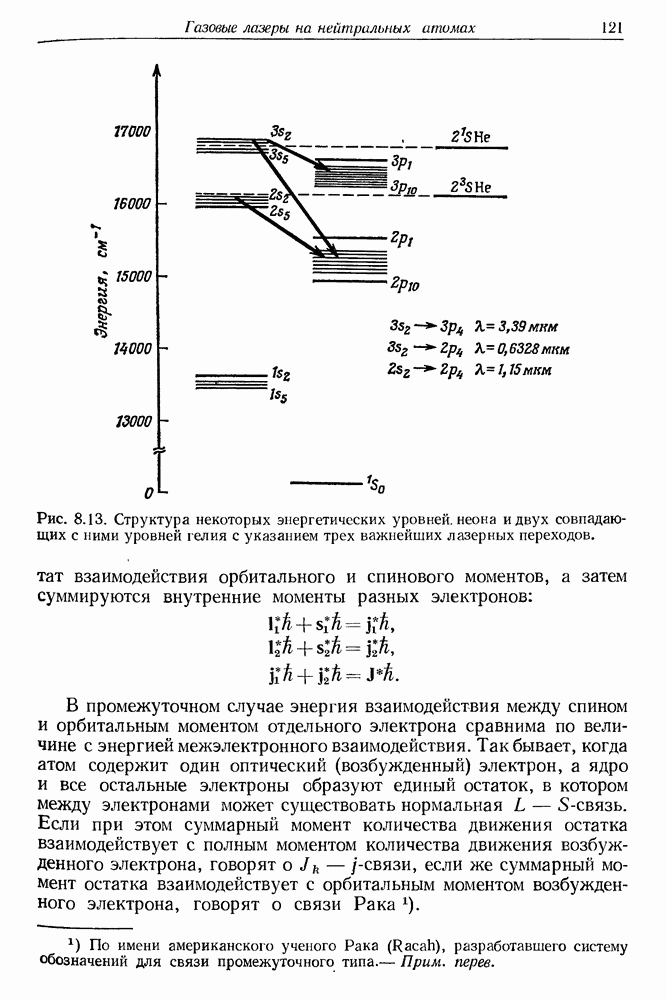
120
121
122
123
124
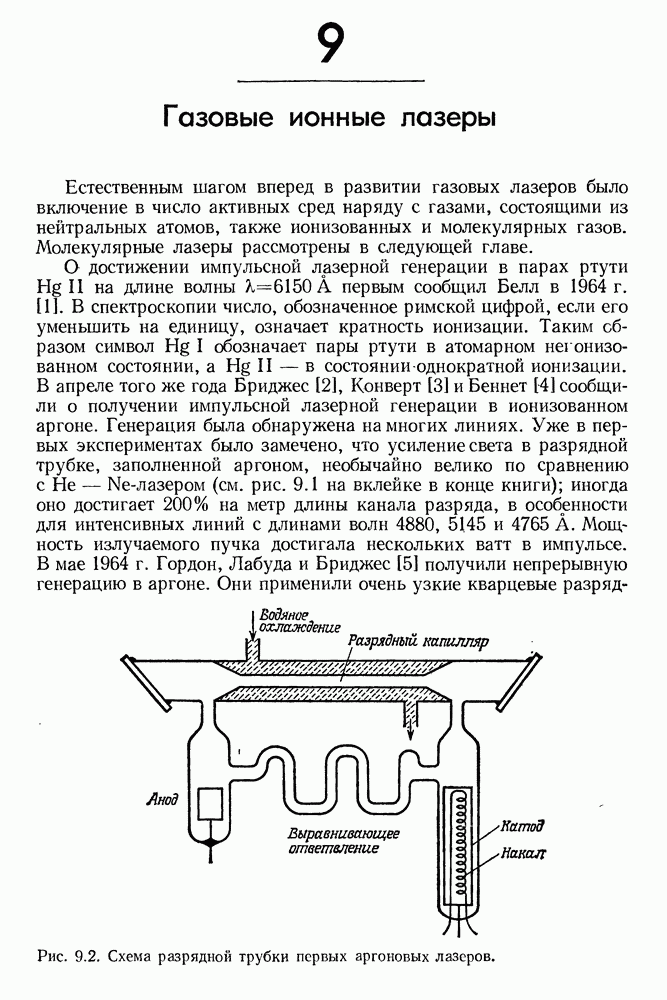
125
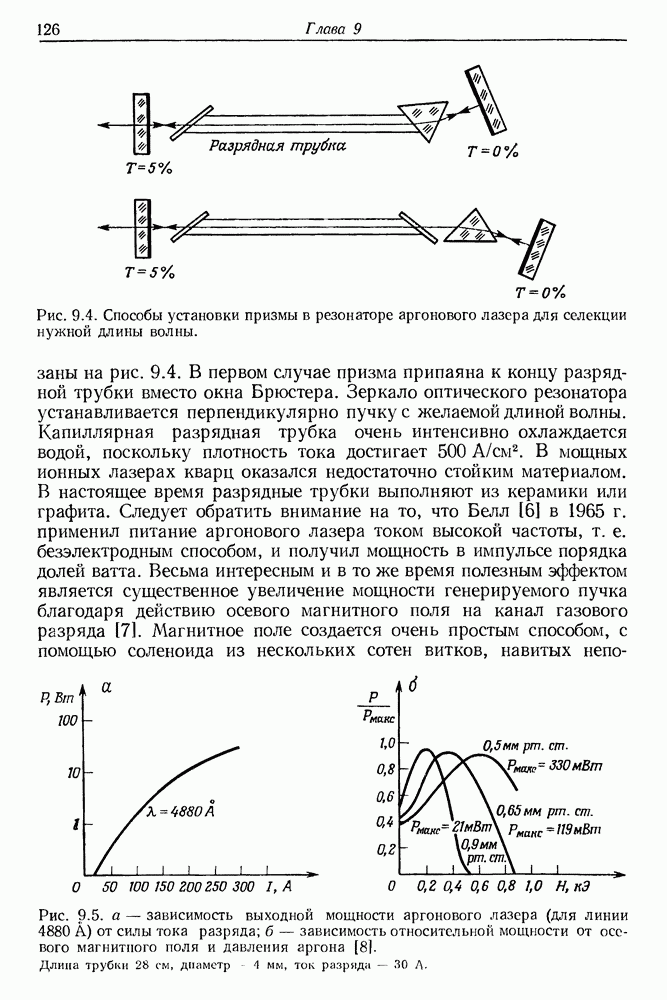
126
127
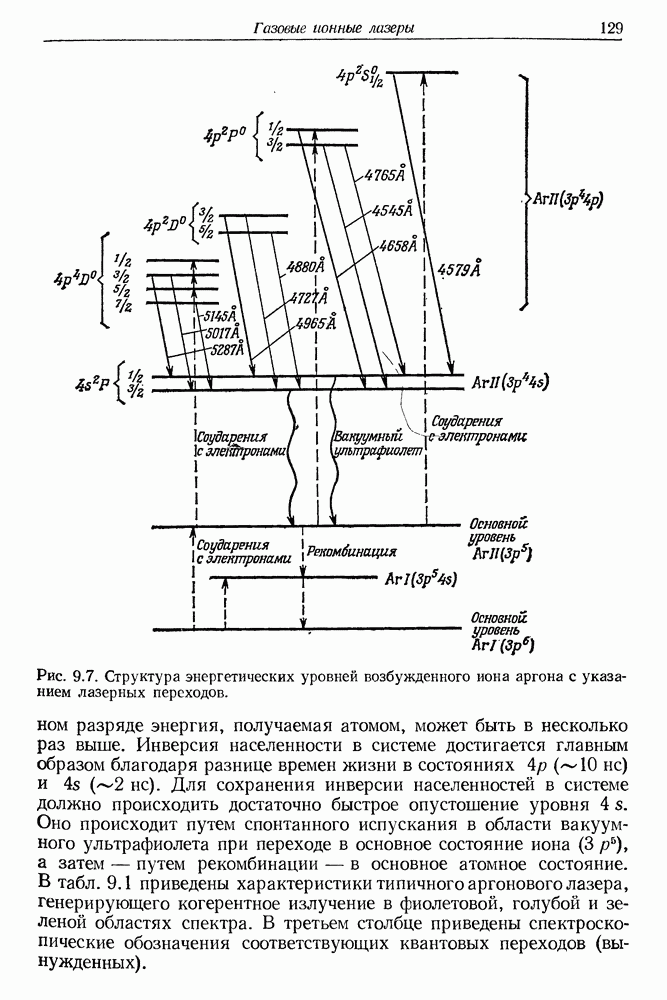
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
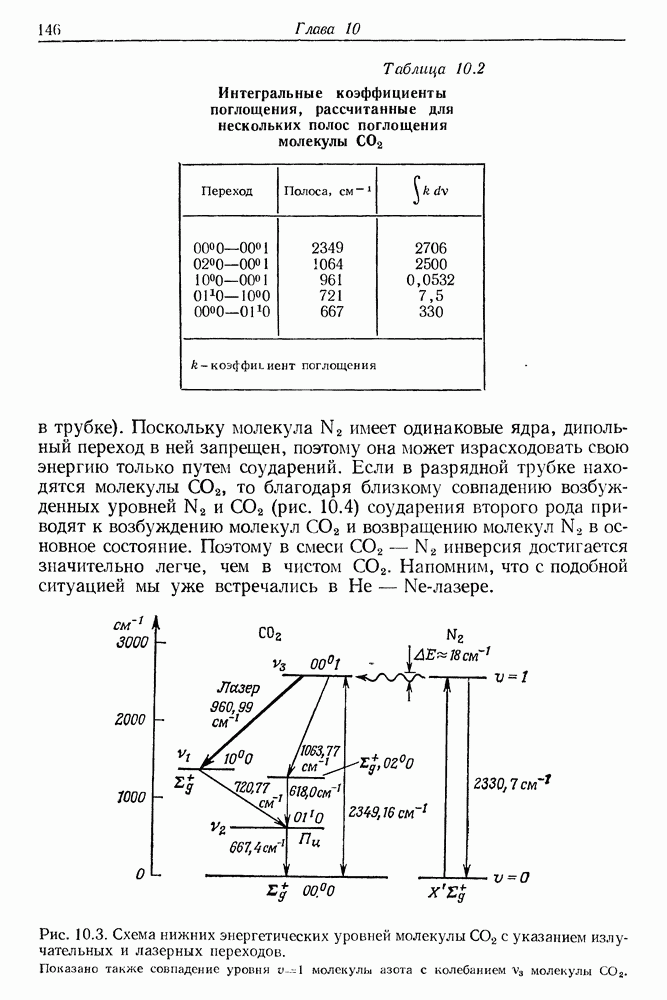
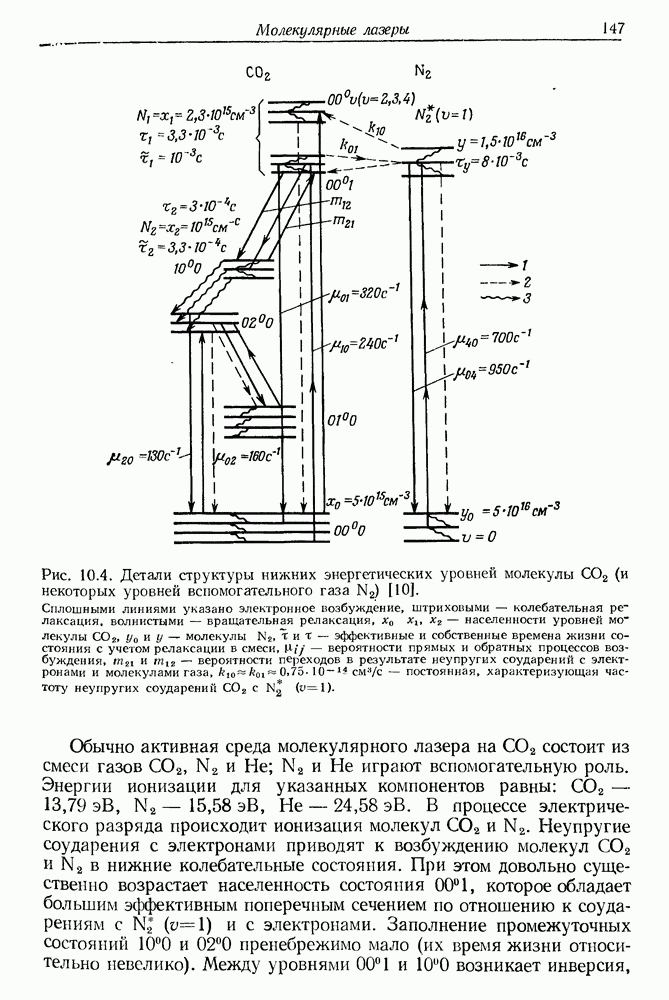
145
146
147
148
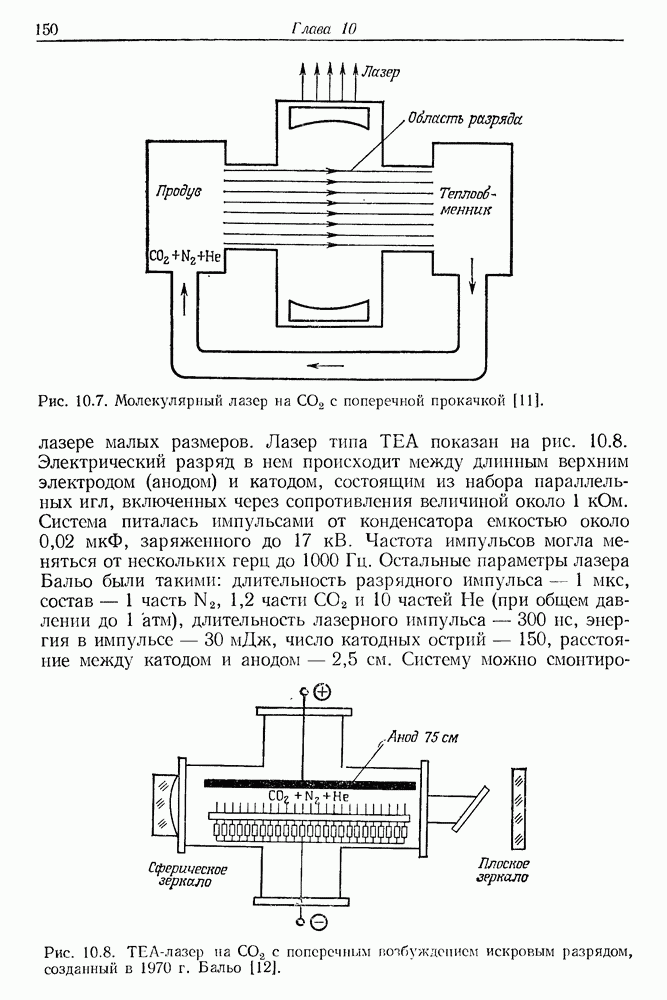
149
150
151
152
153
154
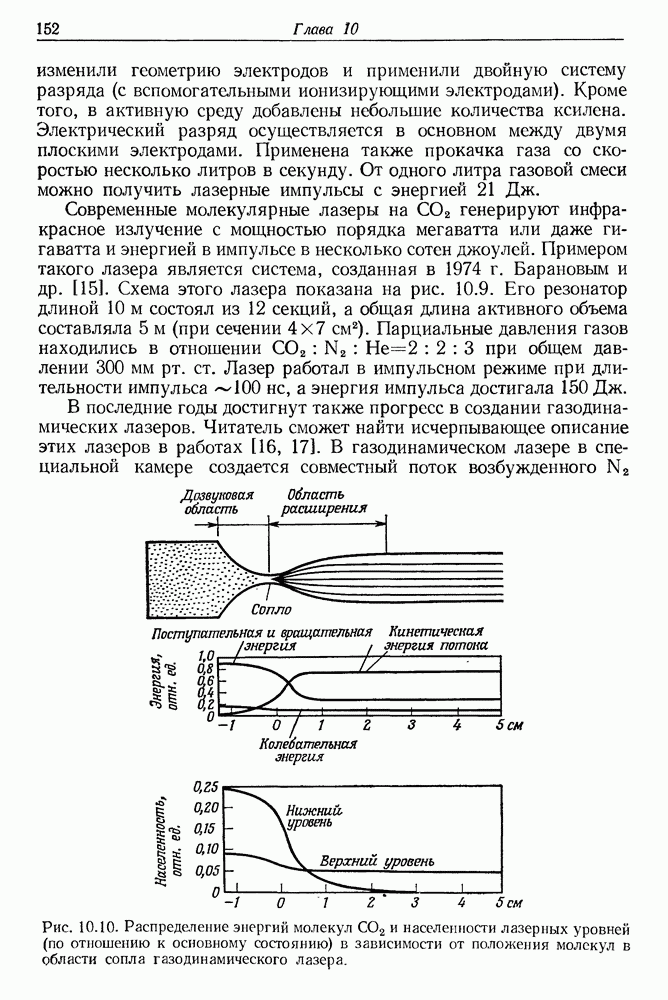
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
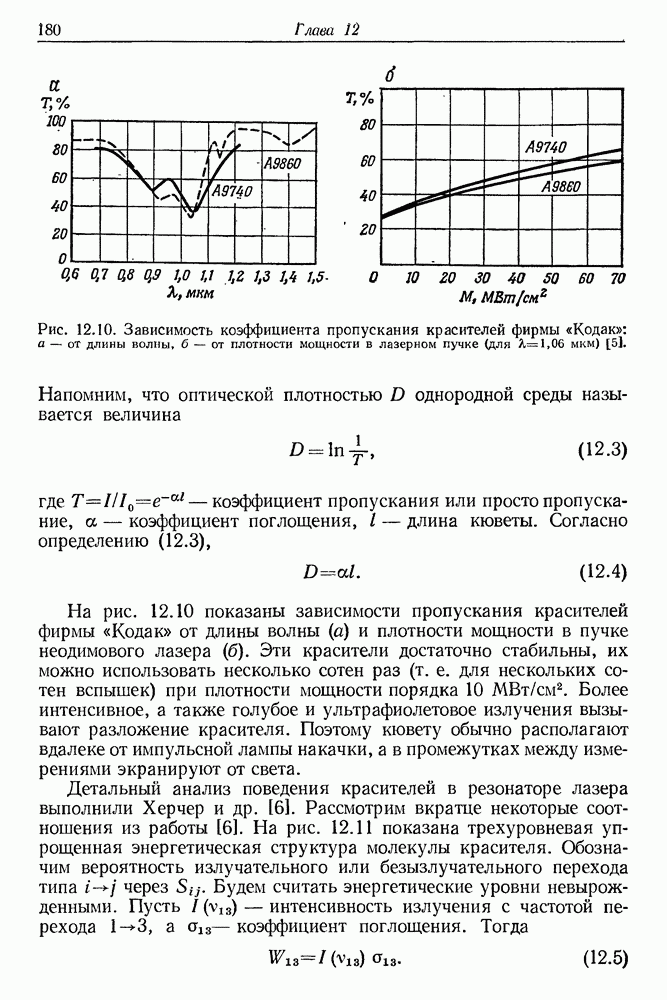
179
180
181
182
183
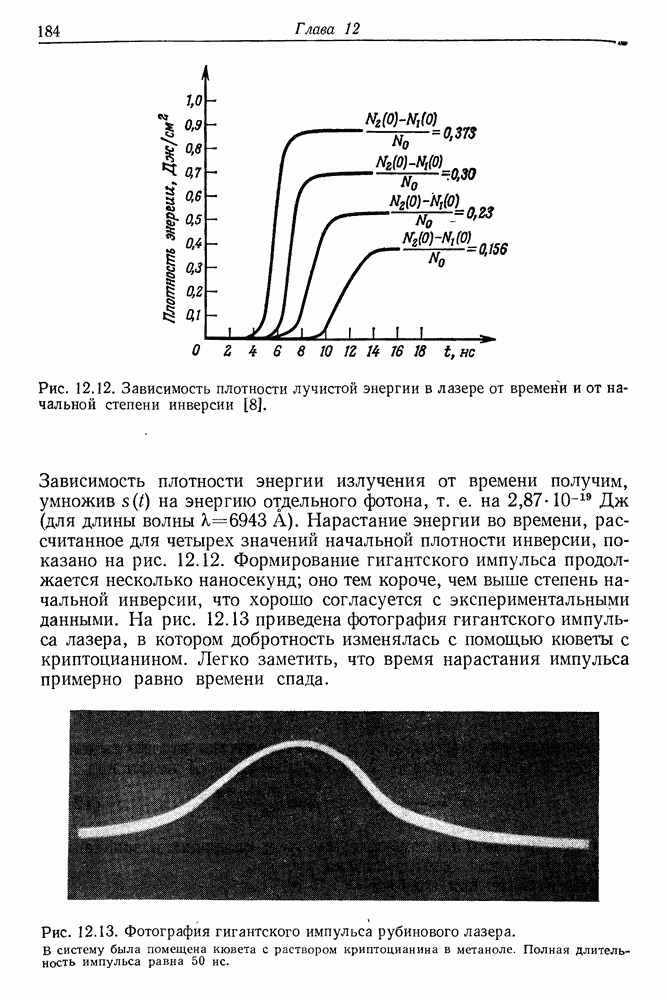
184
185
186
187
188
189
190
191
192
193
194
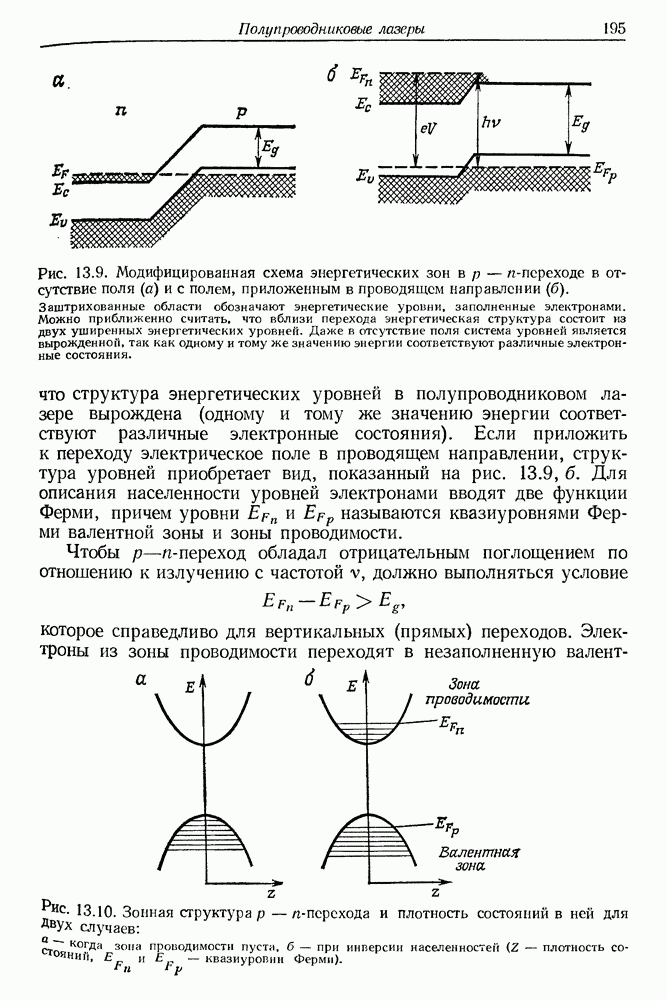
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
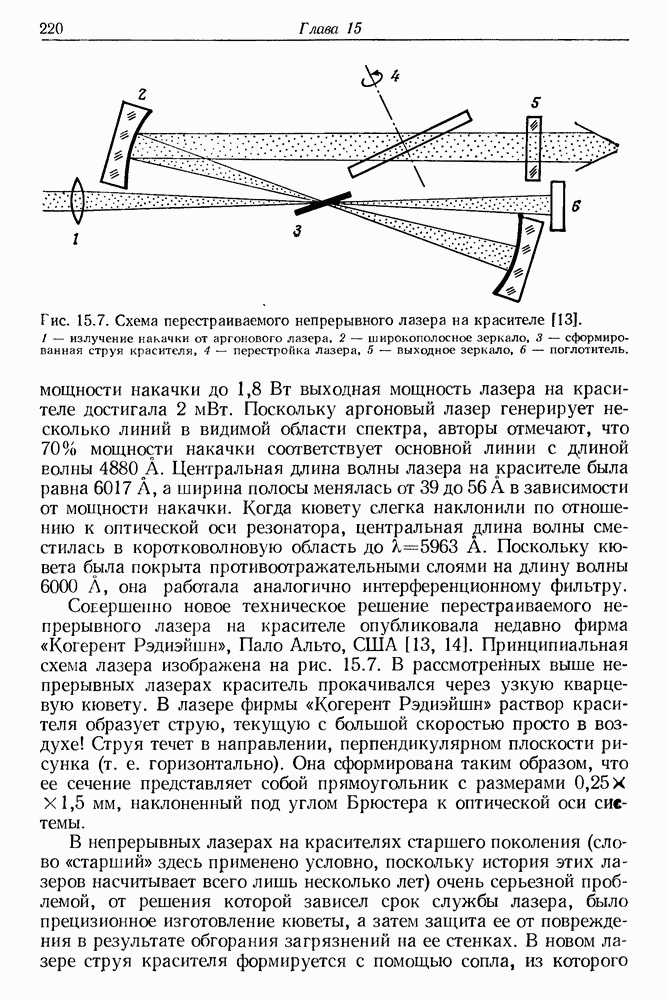
220
221
222
223
224
225
226
227
228
229
230
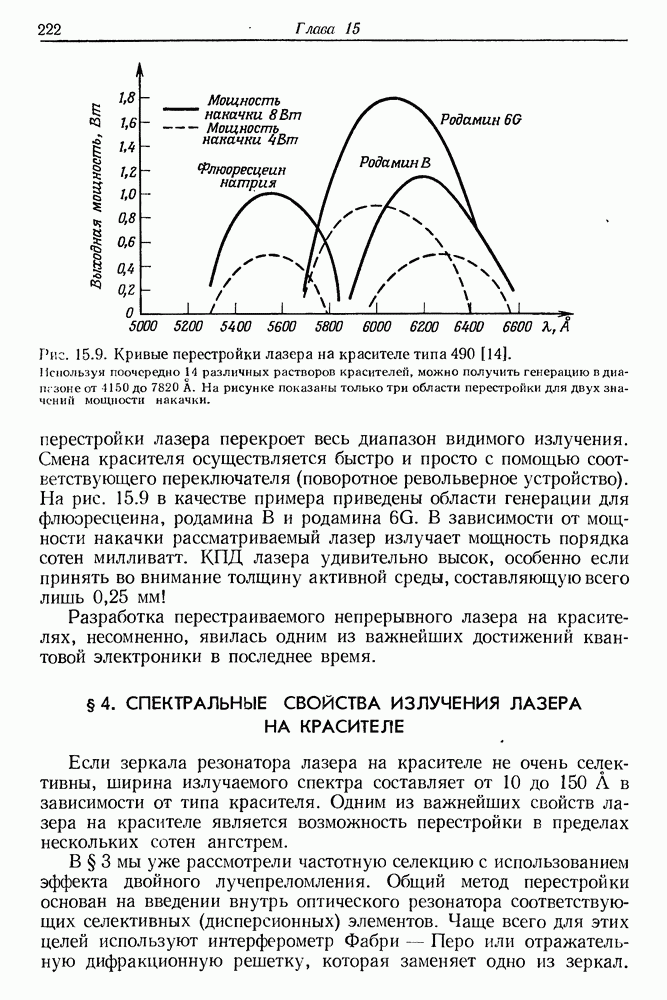
231
232
233
234
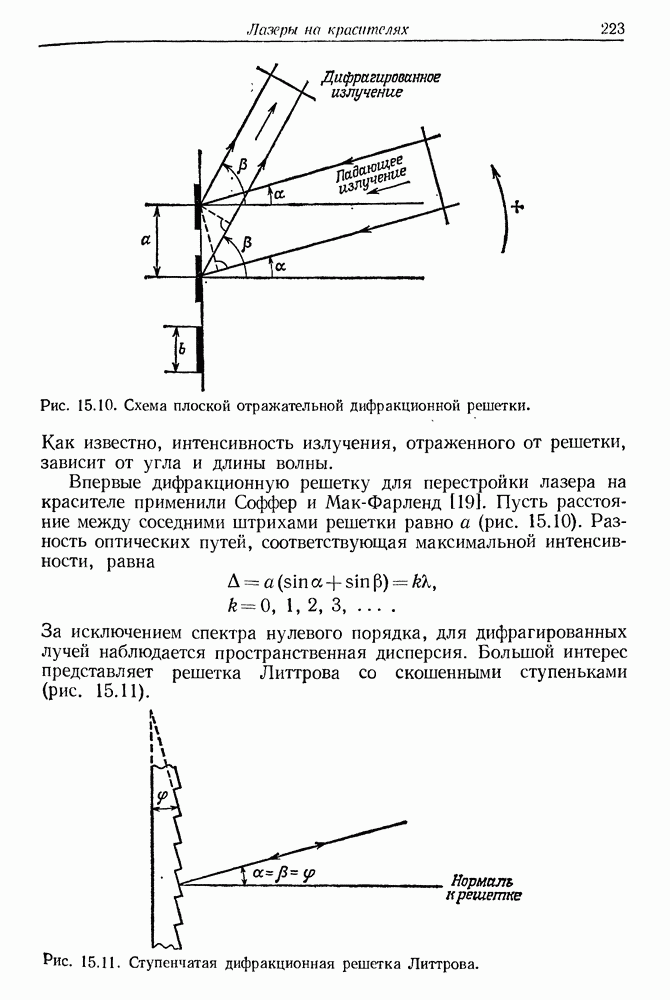
235
236
237
238
239
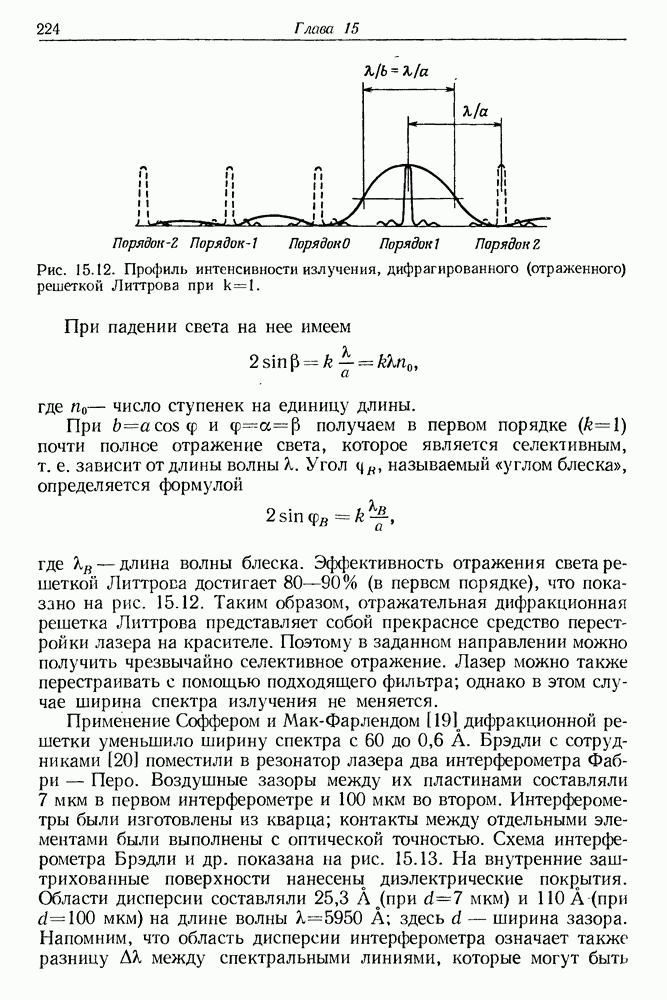
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
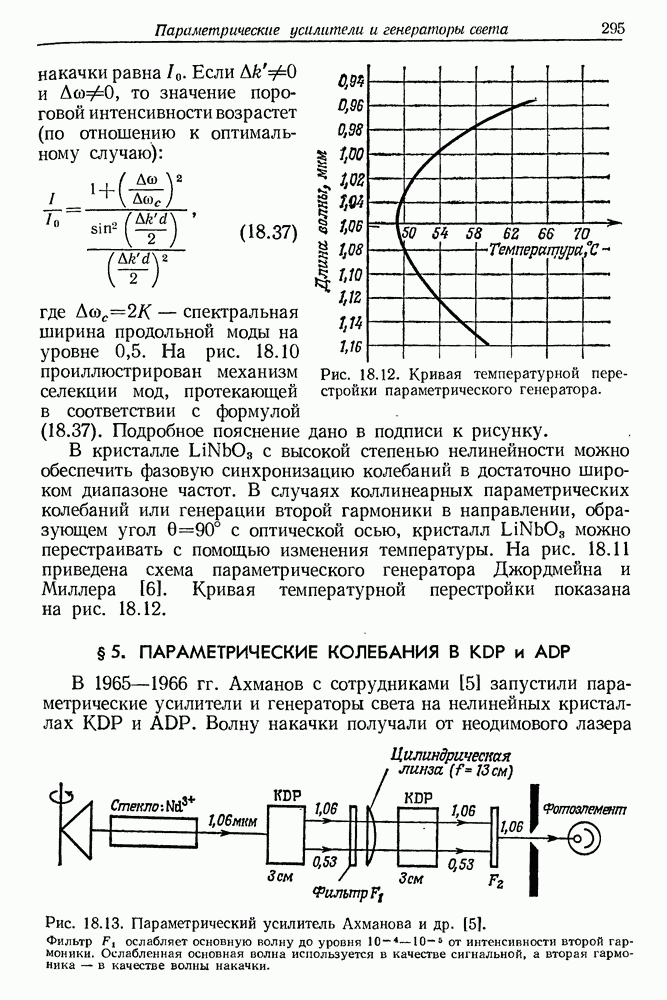
294
295
296
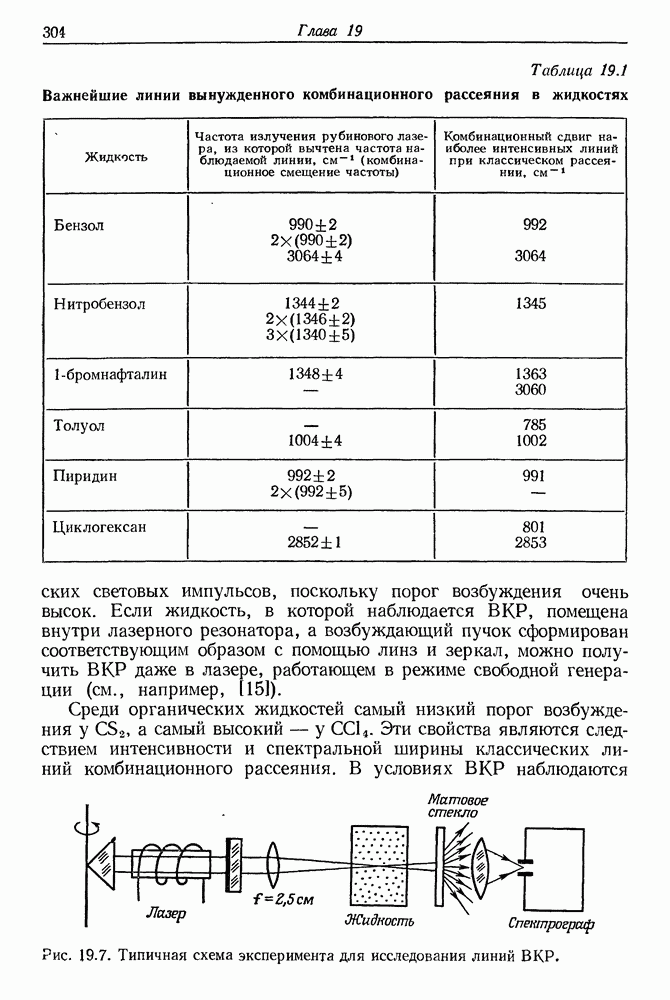
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
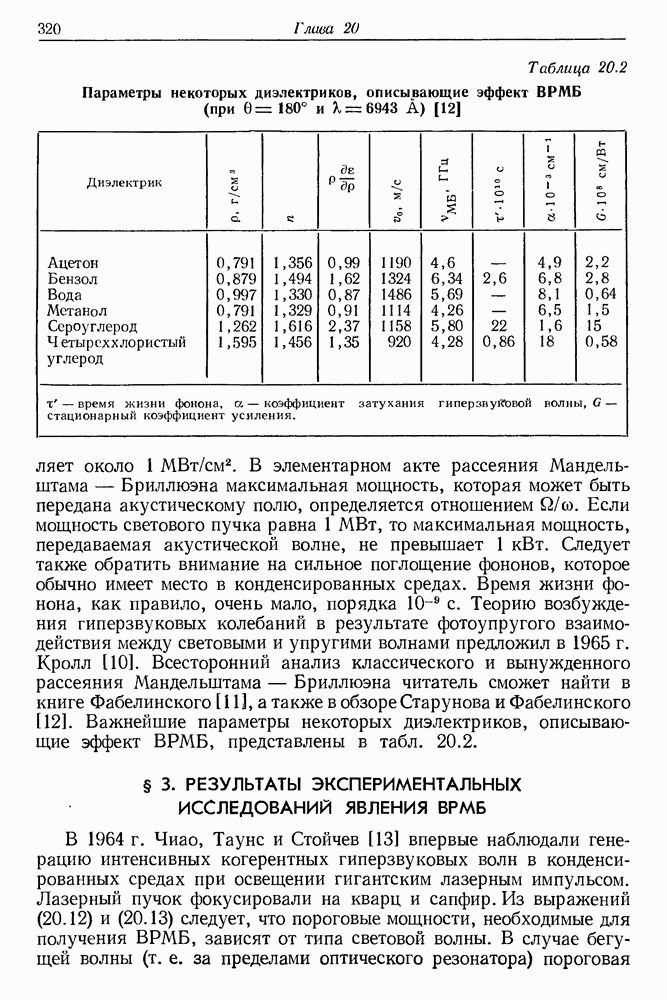
319
320
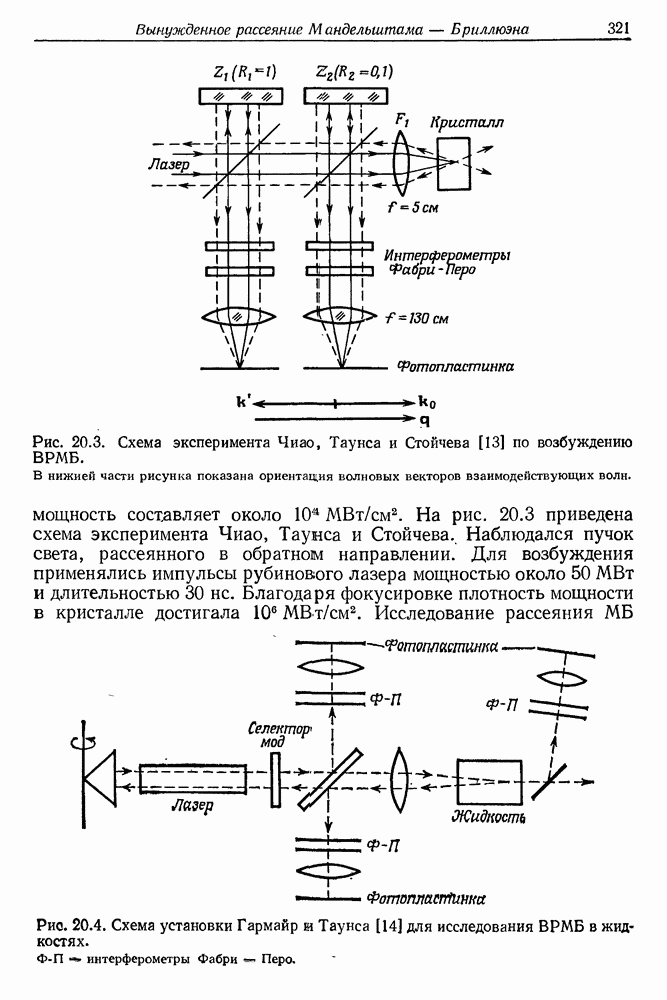
321
322
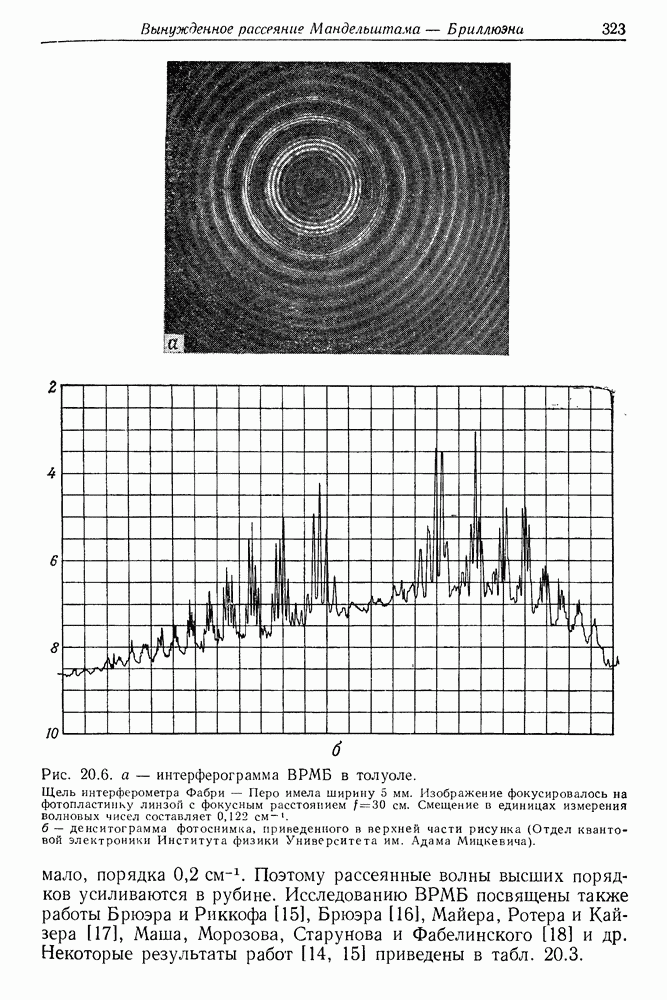
323
324
325
326
327
328
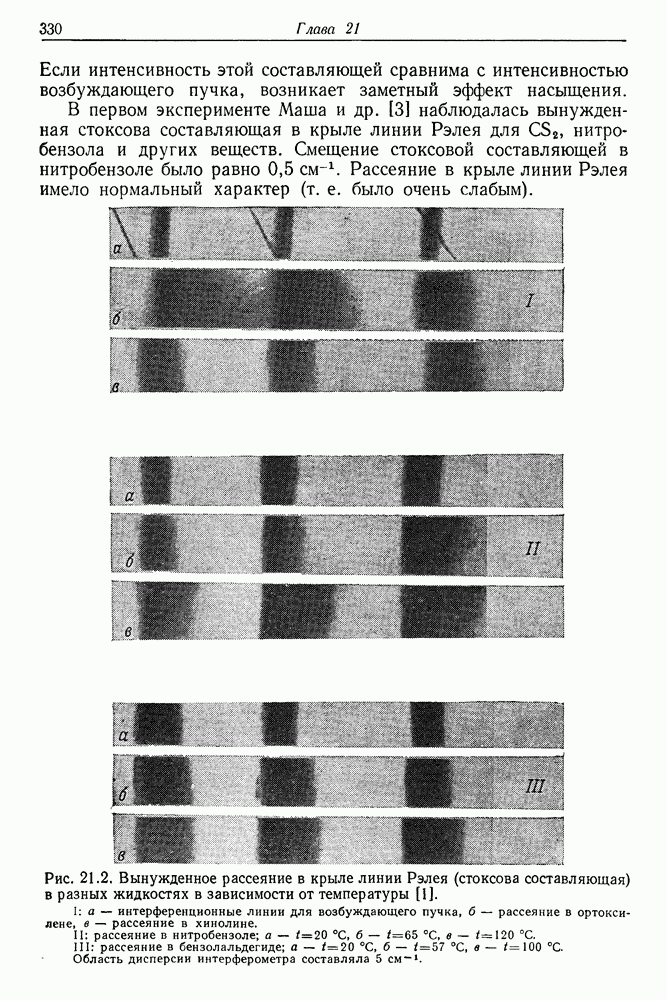
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
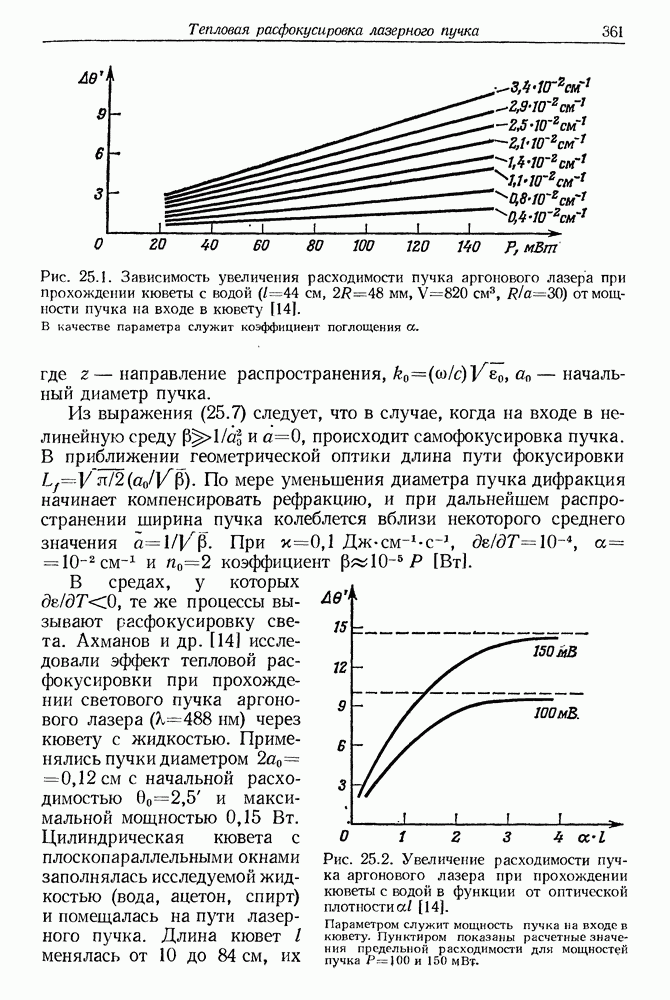
360
361
362
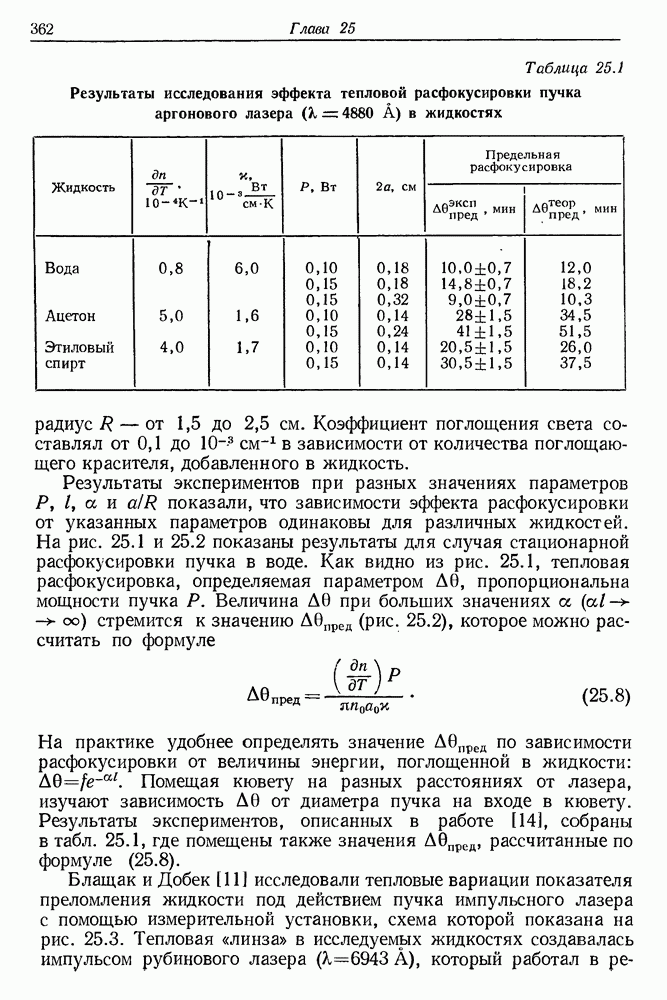
363
364
365
366
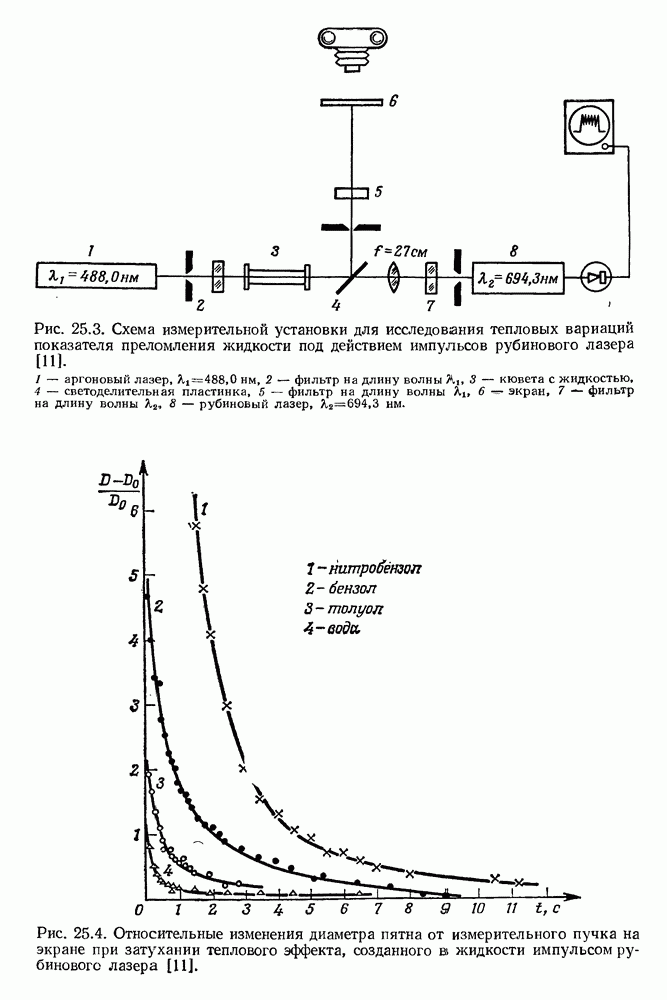
367
368
369
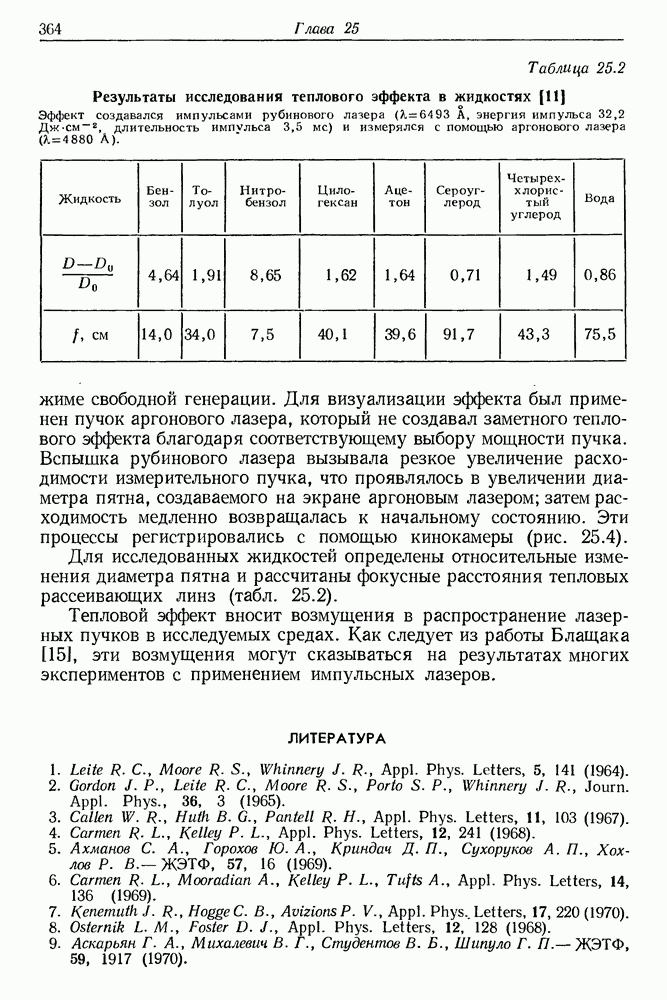
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
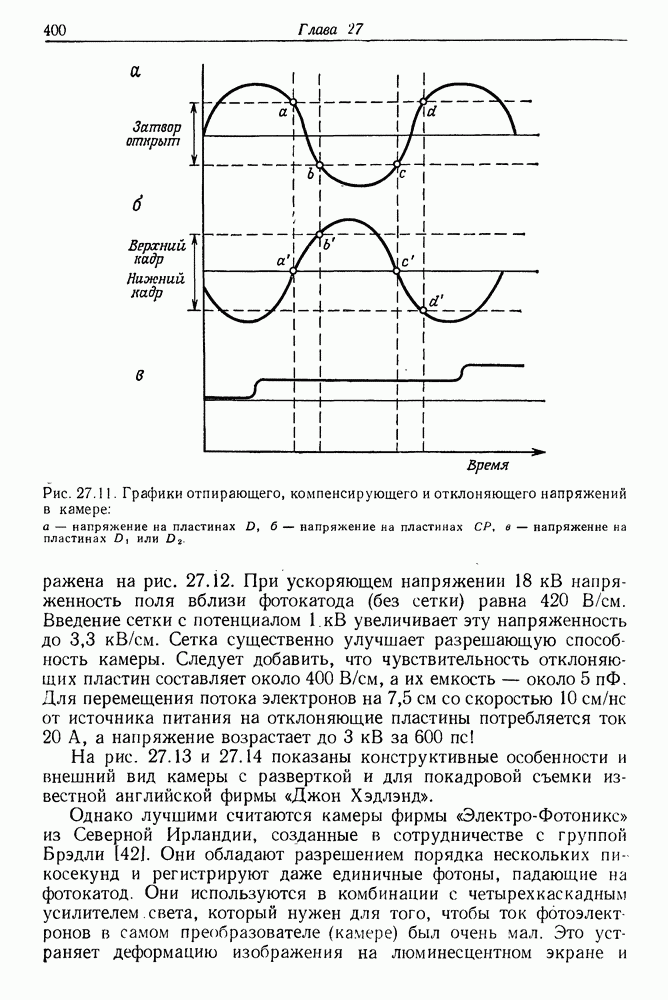
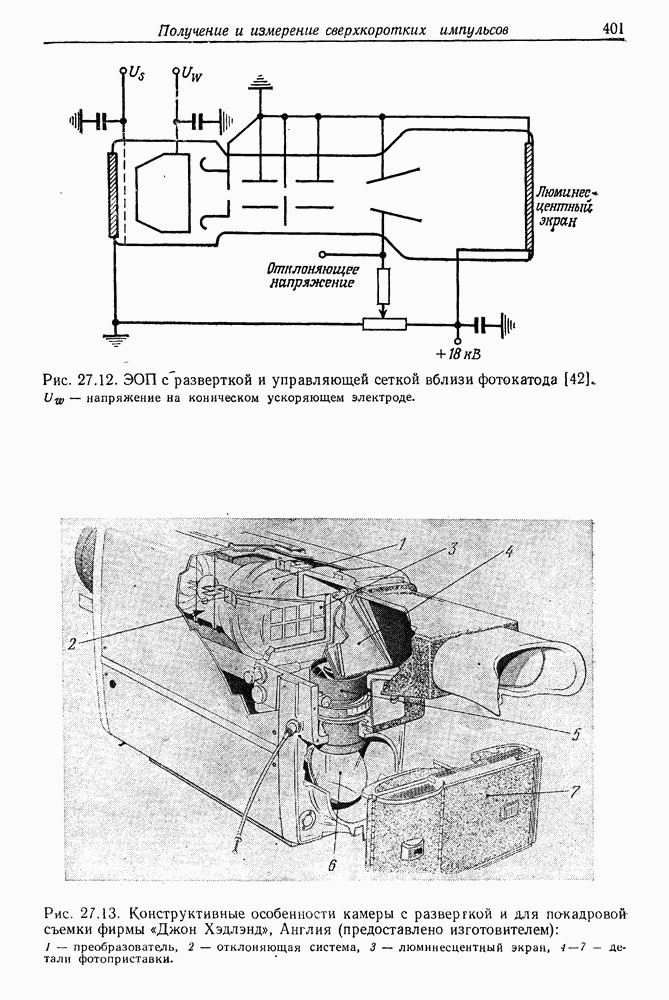
400
401
402
403
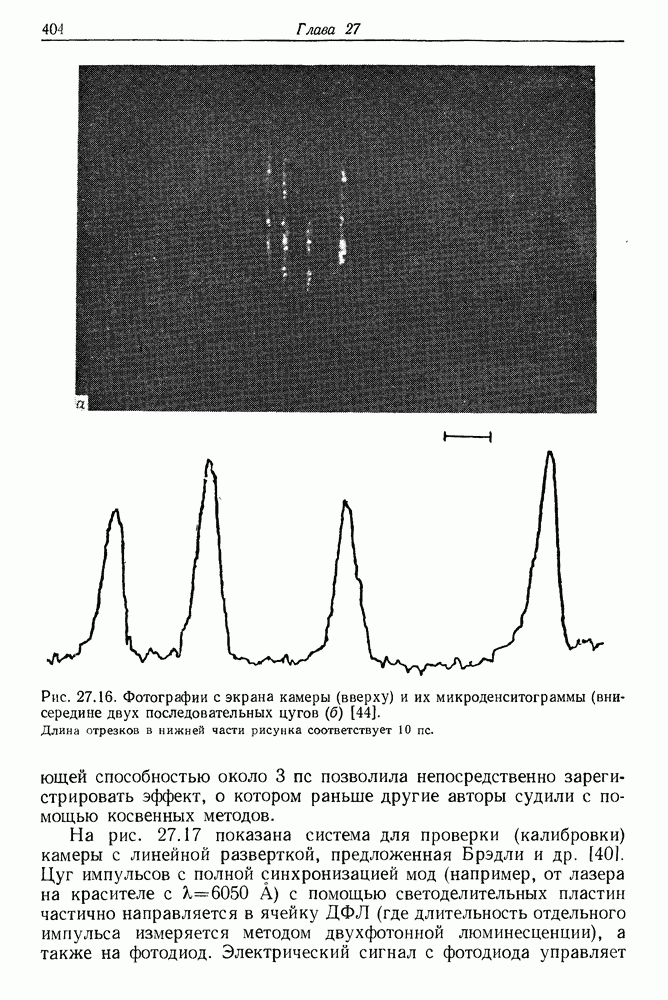
404
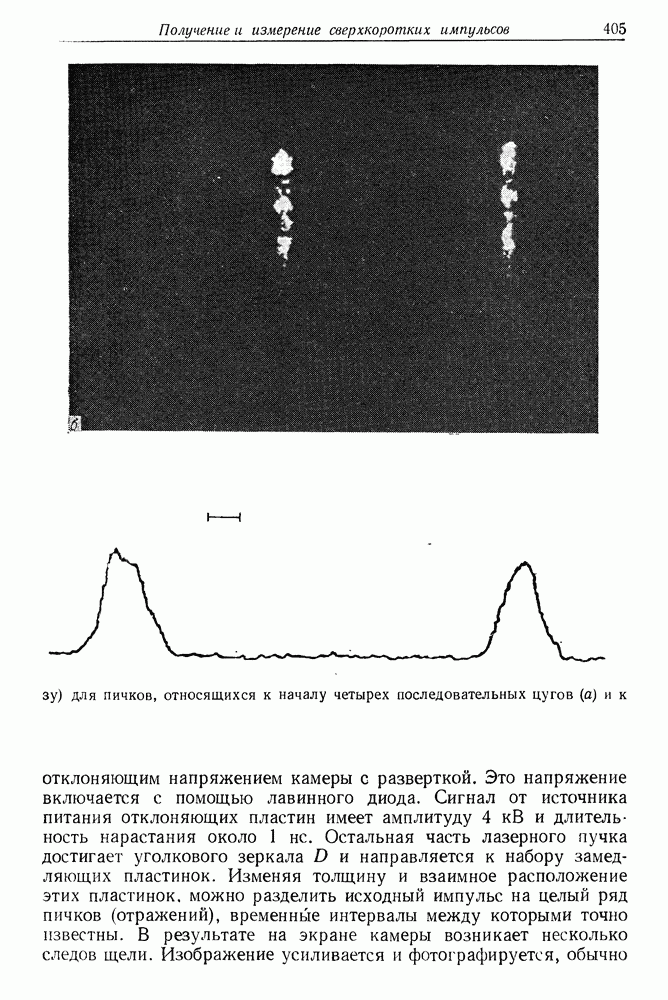
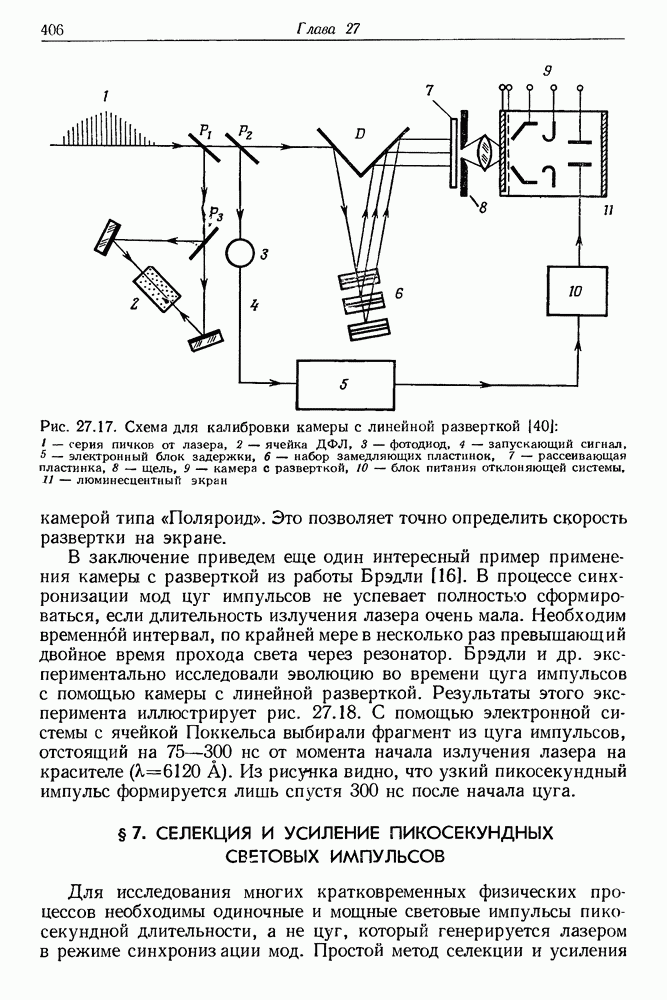
405
406
407
408
409
410
411
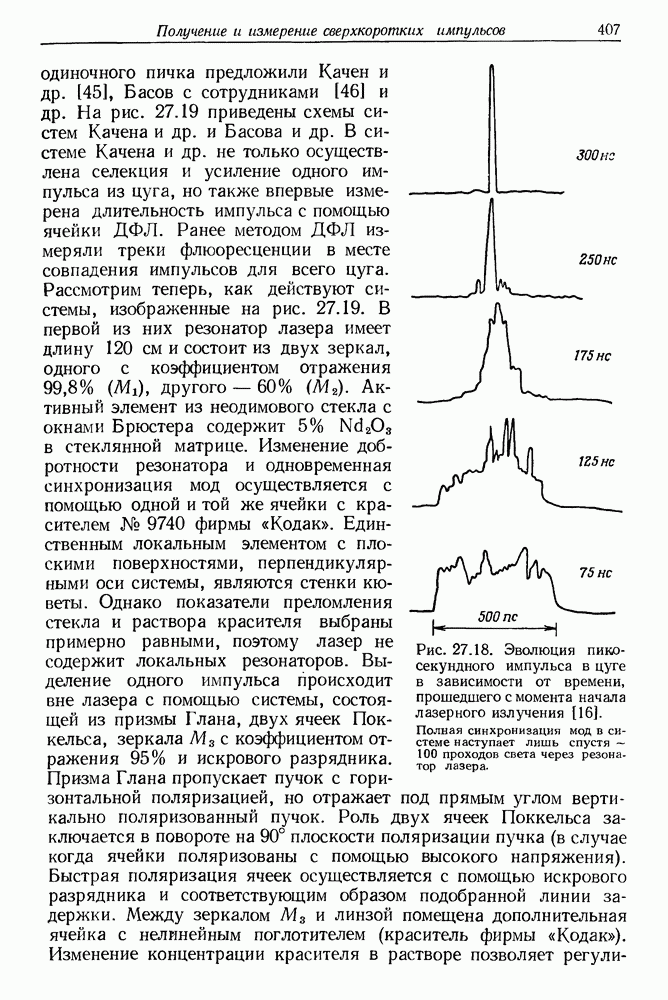
412
413
414
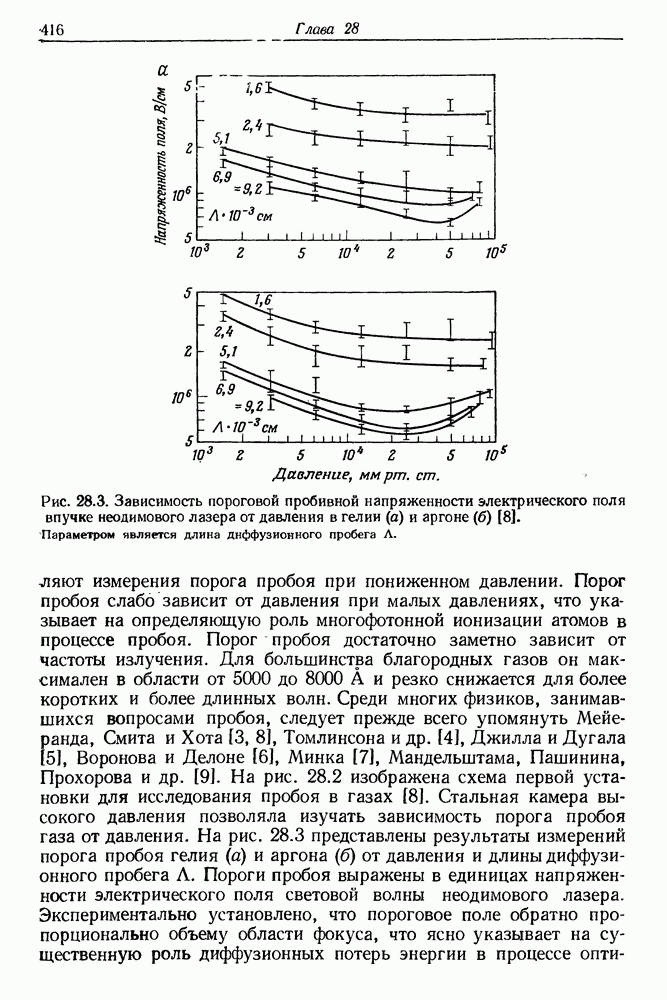
415
416
417
418
419
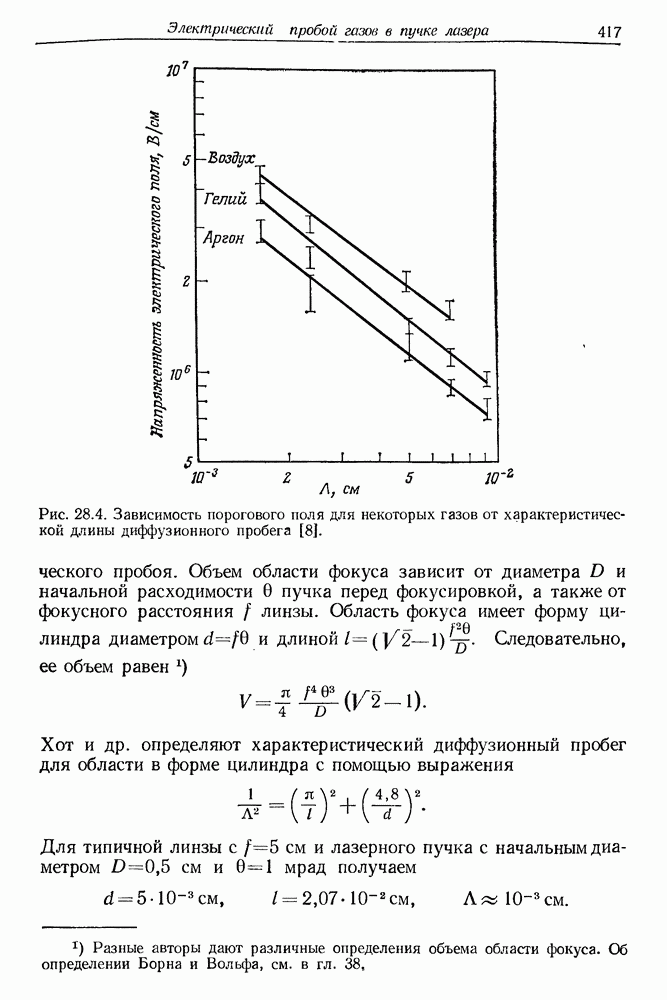
420
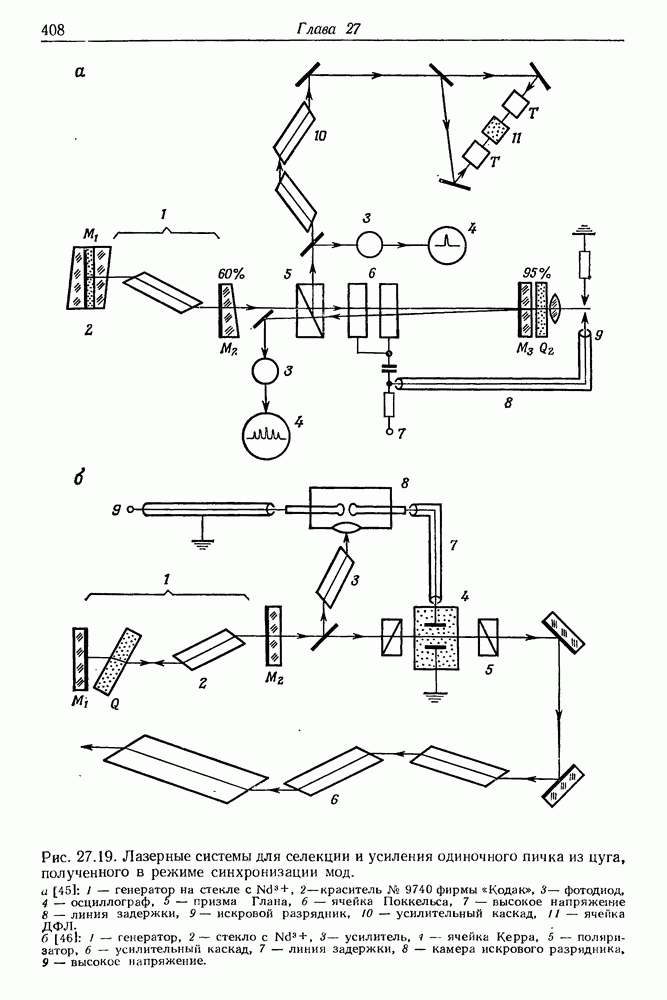
421
422
423
424
425
426
427
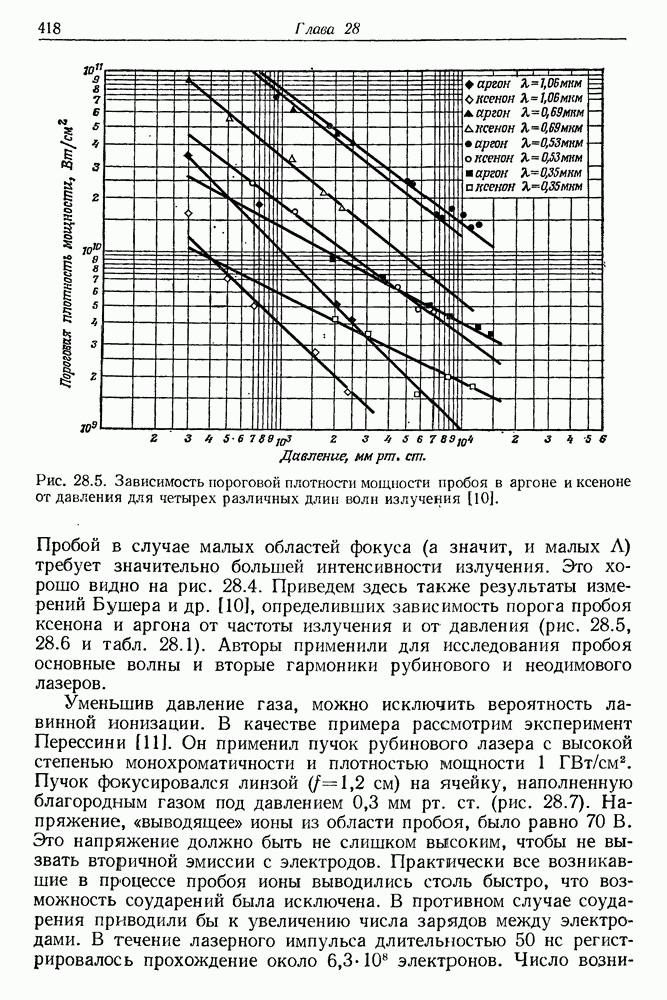
428
429
430
431
432
433
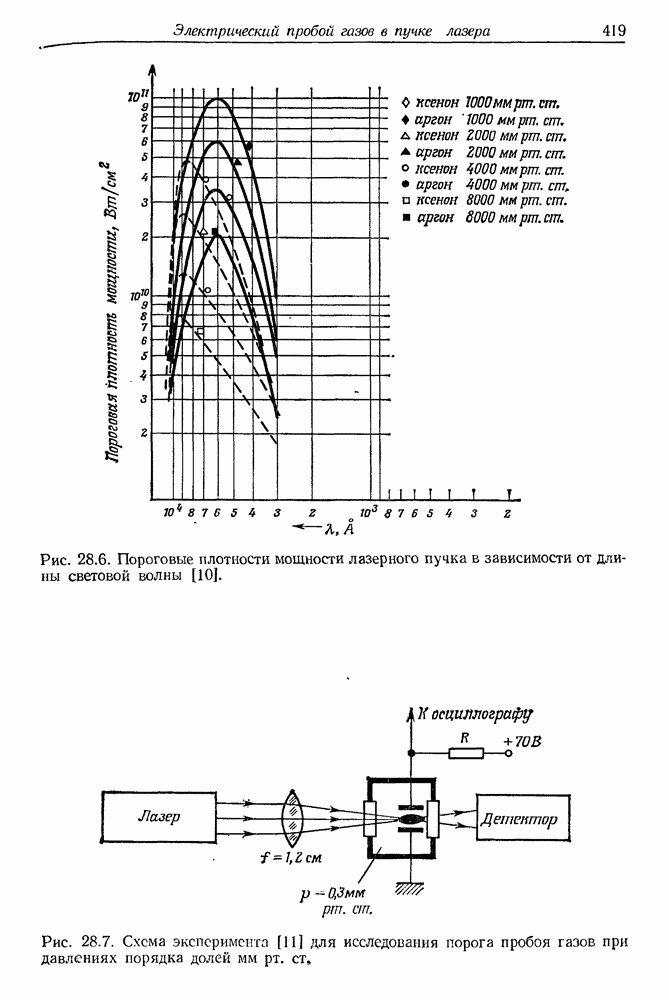
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
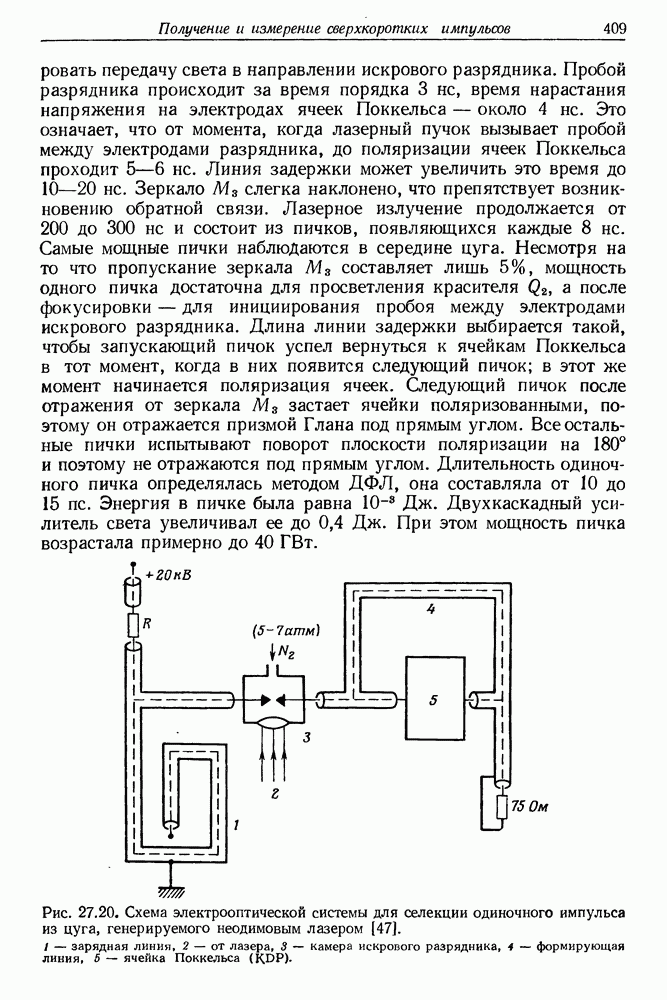
539
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
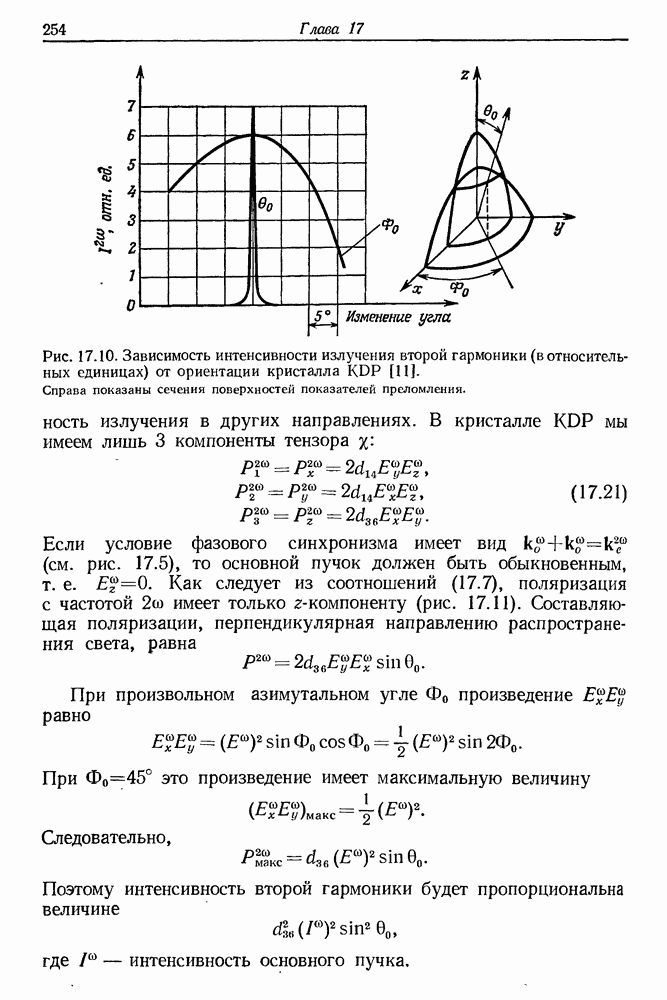
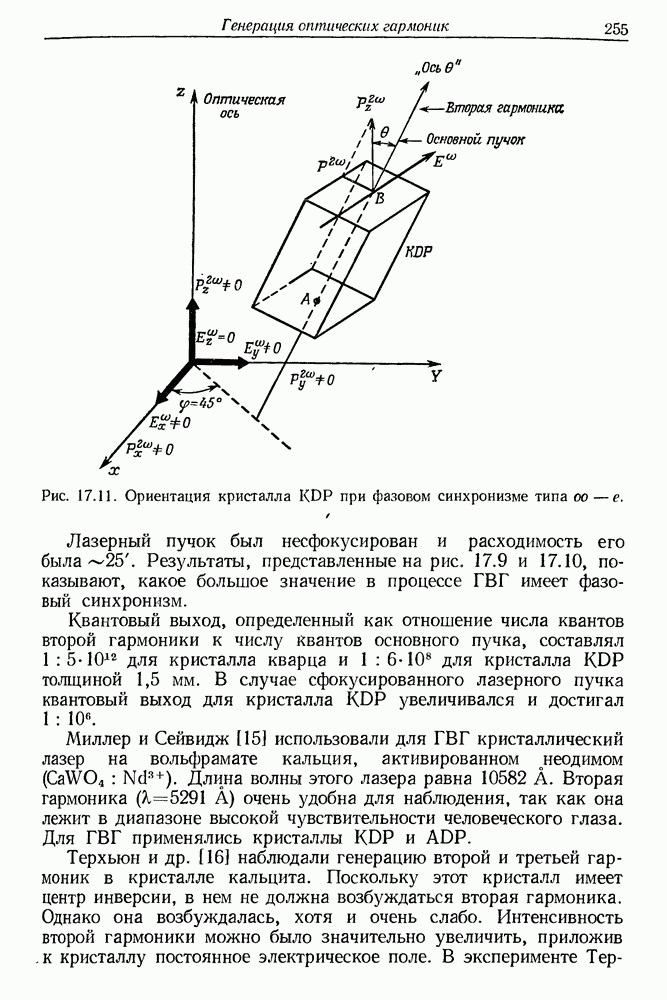
§ 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
Плотность потока энергии лазерного излучения в фокусе линзы может достигать  Для сравнения напомним, что для пробоя воздуха в электрическом поле световой волны необходима
Для сравнения напомним, что для пробоя воздуха в электрическом поле световой волны необходима
плотность энергии  Диаметр светового пятна в фокусе зависит прежде всего от начальной расходимости лазерного пучка. В короткофокусных линзах дифракционные потери играют меньшую роль. Допустим, что параллельный пучок света фокусируется идеальной линзой. В результате дифракции происходит размытие фокального пятна в направлении, перпендикулярном оптической оси, до значения
Диаметр светового пятна в фокусе зависит прежде всего от начальной расходимости лазерного пучка. В короткофокусных линзах дифракционные потери играют меньшую роль. Допустим, что параллельный пучок света фокусируется идеальной линзой. В результате дифракции происходит размытие фокального пятна в направлении, перпендикулярном оптической оси, до значения

где  — диаметр пучка,
— диаметр пучка,  — фокусное расстояние линзы. Для
— фокусное расстояние линзы. Для  мкм (рубиновый лазер)
мкм (рубиновый лазер)  , что часто имеет место при фокусировке лазерных пучков, получаем
, что часто имеет место при фокусировке лазерных пучков, получаем

Дифракционное уширение в этом случае настолько мало, что им можно пренебречь. Значительно большее размытие фокуса (в поперечном направлении) происходит при начальной расходимости
0 фокусируемого пучка. В этом случае

Для линзы с  см и начальной расходимости
см и начальной расходимости  рад, типичной для пучка рубинового лазера, получаем
рад, типичной для пучка рубинового лазера, получаем

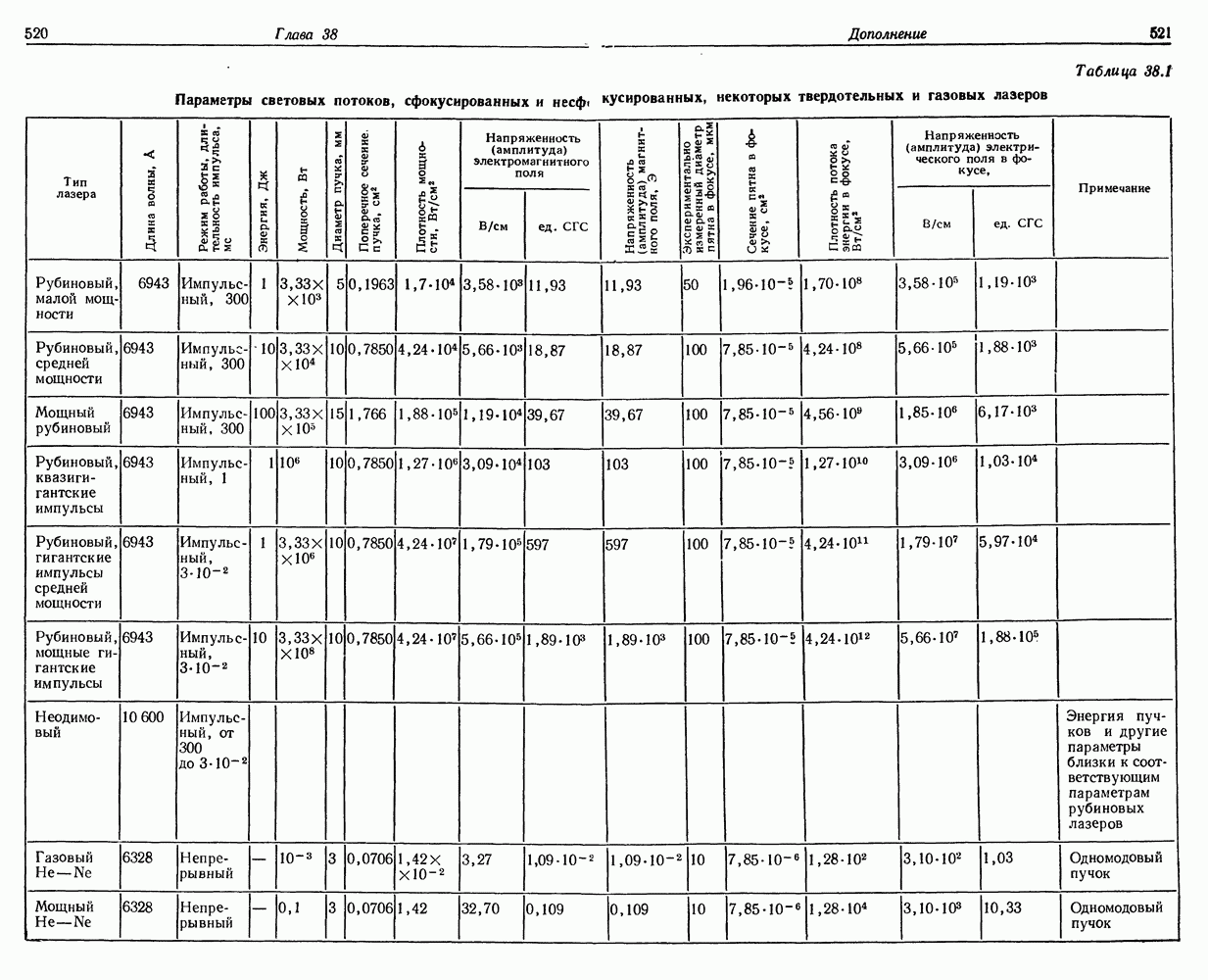
Наблюдаемые на практике диаметры световых пучков в фокусе обычно составляют от 100 до 200 мкм (для линз с  см) или несколько десятков микрометров (для линз с
см) или несколько десятков микрометров (для линз с  см). Размер фокального пятна устанавливается экспериментально, например путем измерений под микроскопом диаметра отверстия, прожженного в очень тонкой металлической фольге, установленной в фокальной плоскости. Считая, что мощность пучка с начальным диаметром
см). Размер фокального пятна устанавливается экспериментально, например путем измерений под микроскопом диаметра отверстия, прожженного в очень тонкой металлической фольге, установленной в фокальной плоскости. Считая, что мощность пучка с начальным диаметром  равна Р, находим в соответствии с формулой (38.2) интенсивность излучения в фокусе
равна Р, находим в соответствии с формулой (38.2) интенсивность излучения в фокусе

В случае газового лазера с плоским резонатором диаметр пучка в фокусе может составлять 10—20 мкм или даже меньше в зависимости от фокусного расстояния линзы.
Дифракция света, сфокусированного линзой, вызывает изменения его интенсивности в области фокуса не только в поперечном направлении, но и вдоль оптической оси. Можно ввести понятие объема фокуса. Область фокуса имеет форму цилиндра с диаметром основания, равным диаметру первого темного кольца, и высотой, равной расстоянию между точками на оптической оси, где
интенсивность света уменьшается до нуля. Эти точки располагаются симметрично относительно фокуса на расстояниях [1]

где  — диаметр пучка перед фокусировкой. Теперь находим объем фокуса
— диаметр пучка перед фокусировкой. Теперь находим объем фокуса

Если начальная расходимость пучка равна 0, то размытие фокуса в направлении оптической оси, рассчитанное методами геометрической оптики, равно

В случае линзы с  см и пучка рубинового лазера диаметром также в 1 см получаем:
см и пучка рубинового лазера диаметром также в 1 см получаем:
диаметр цилиндра  мкм,
мкм,
высота 
объем фокуса 
отношение высоты к диаметру 
Если определить размеры фокальной области по формулам (38.2) и (38.6), то объем ее составит

При  , этот объем равен
, этот объем равен

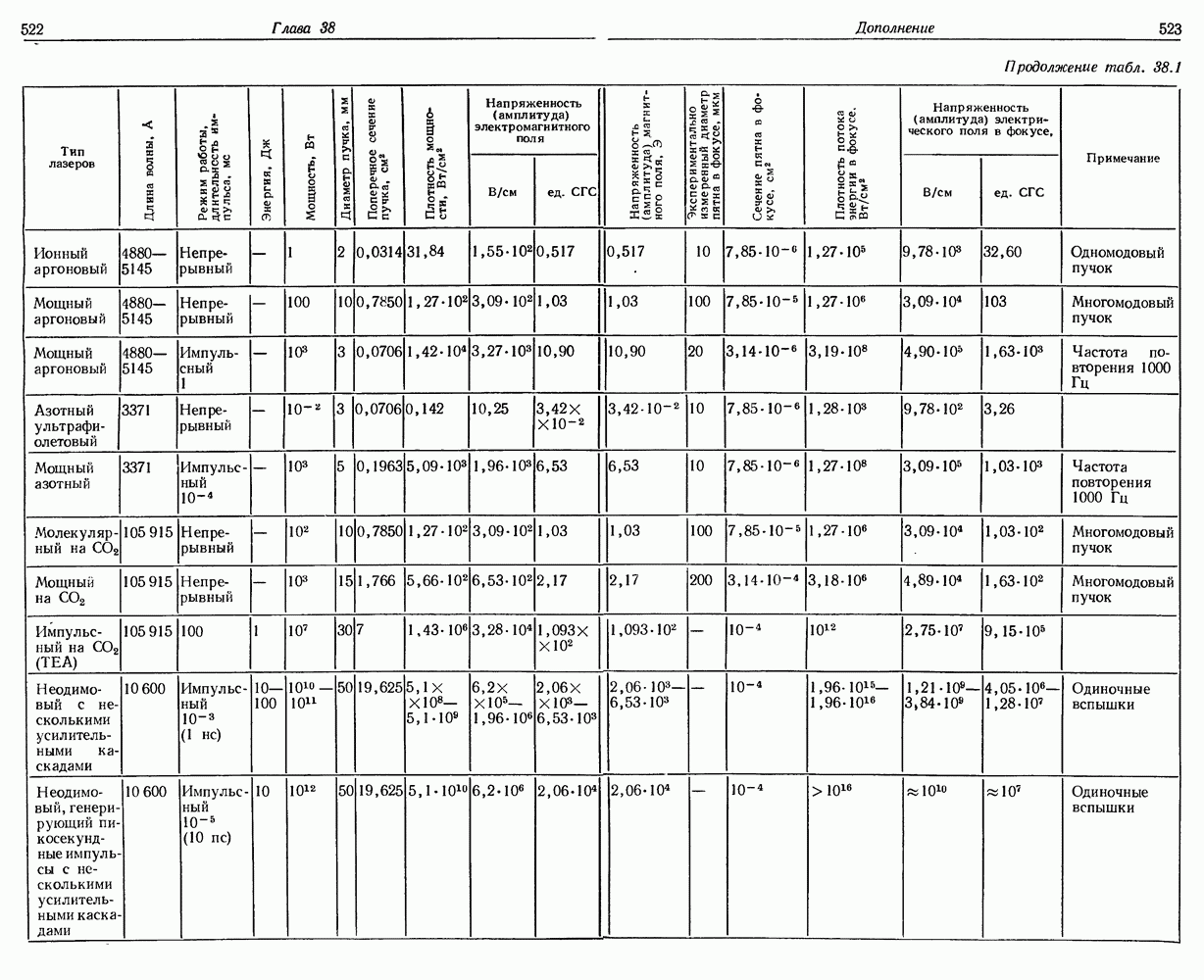
В табл. 38.1 приведены диаметры фокальных пятен лазеров, измеренные экспериментально; они существенно отличаются от результатов теоретических расчетов. Эти различия объясняются, в частности, несовершенством линз и начальными расходимостями лазерного пучка. В явлении фокусировки светового пучка большую роль играет сферическая аберрация. Ее влияние на формирование фокуса детально проанализировали Аарон, Айленд и Морган [2] и Морган [3]. Они определили с помощью интеграла Кирхгофа — Френеля форму фокуса для разных значений сферической аберрации линзы. Теоретические результаты были подтверждены экспериментально методом двухфотонной люминесценции, который был впервые применен для этой цели Бункиным и др. [4]. Правильная
оценка истинных размеров фокуса чрезвычайно важна в многофотонных процессах, а также во многих областях нелинейной оптики. В идеальной оптической системе размеры фокуса зависят прежде всего от начальной расходимости пучка 0, а также от дифракции на линзе. Влияние дифракции уже рассмотрено выше [см. формулы (38.1) и  Реальная линза искажает сферический фронт волны. Аарон и др. описали это искажение с помощью некоторой функции аберрации Ф, зависящей от фокусного расстояния
Реальная линза искажает сферический фронт волны. Аарон и др. описали это искажение с помощью некоторой функции аберрации Ф, зависящей от фокусного расстояния  показателя преломления
показателя преломления  материала линзы и от диаметра
материала линзы и от диаметра  линзы, заполненного светом. Максимальное значение
линзы, заполненного светом. Максимальное значение  рассматривается как наибольшее отклонение действительного фронта волны от идеальной сферической формы. Удобнее всего представить значение Ф в единицах К. Опуская выкладки и достаточно громоздкие вычисления, приведем лишь основные результаты этих расчетов (табл. 38.2) для неодимового лазера
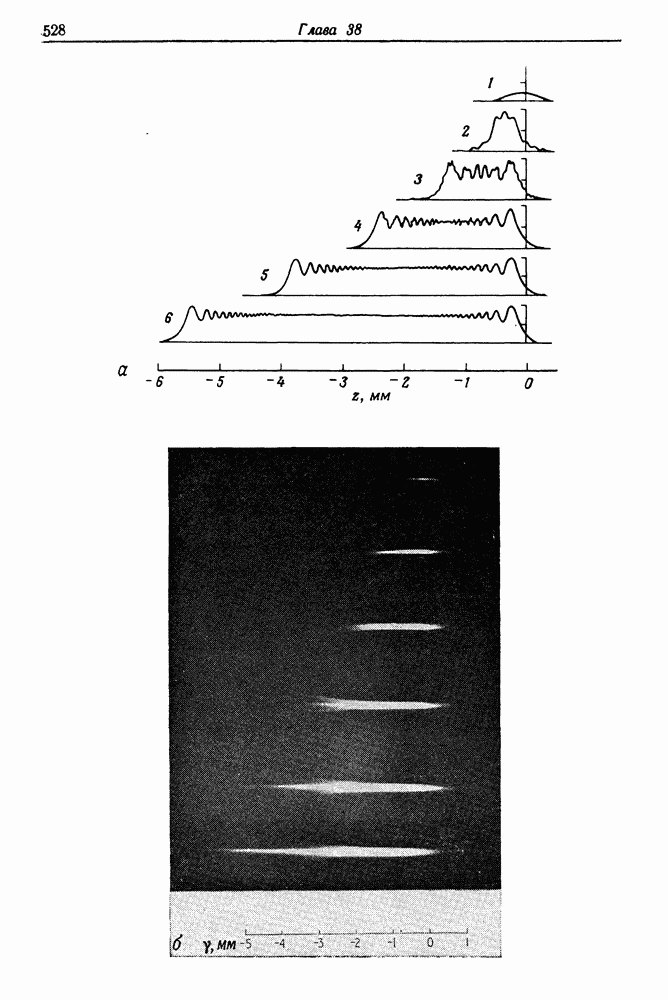
рассматривается как наибольшее отклонение действительного фронта волны от идеальной сферической формы. Удобнее всего представить значение Ф в единицах К. Опуская выкладки и достаточно громоздкие вычисления, приведем лишь основные результаты этих расчетов (табл. 38.2) для неодимового лазера  мкм). Искажение фронта волны, возникающее вблизи идеального фокуса линзы, приводит благодаря интерференции к значительным колебаниям интенсивности света и удлинению области действительного фокуса в направлении линзы. Этот эффект проиллюстрирован на рис. 38.1. В части а рисунка представлены результаты вычислений, а в части
мкм). Искажение фронта волны, возникающее вблизи идеального фокуса линзы, приводит благодаря интерференции к значительным колебаниям интенсивности света и удлинению области действительного фокуса в направлении линзы. Этот эффект проиллюстрирован на рис. 38.1. В части а рисунка представлены результаты вычислений, а в части  действительные размеры фокуса. Распределение лучистой энергии в области фокуса зарегистрировано методом ДФЛ. Световой пучок неодимового лазера фокусировался в кювету с родамином
действительные размеры фокуса. Распределение лучистой энергии в области фокуса зарегистрировано методом ДФЛ. Световой пучок неодимового лазера фокусировался в кювету с родамином  растворенным в этаноле. Места с высокой плотностью лучистой мощности отличались интенсивным оранжево-зеленым свечением, которое обусловлено двухфотонной люминесценцией. Анализ рис. 38.1 показывает, что при значении сферической аберрации, превышающем 100 К, понятие фокуса вообще теряет смысл.
растворенным в этаноле. Места с высокой плотностью лучистой мощности отличались интенсивным оранжево-зеленым свечением, которое обусловлено двухфотонной люминесценцией. Анализ рис. 38.1 показывает, что при значении сферической аберрации, превышающем 100 К, понятие фокуса вообще теряет смысл.
Из работы Аарона и др. следуют важные выводы, которые нужно всегда иметь в виду при фокусировке интенсивных лазерных
Таблица 38.2 (см. скан) Значения аберрации  (в единицах X), вносимой обычными сферическими линзами
(в единицах X), вносимой обычными сферическими линзами 

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
световых пучков. Во-первых, если  невозможно повысить плотность мощности в фокусе путем увеличения диаметра пучка или уменьшения фокусного расстояния линзы. Во-вторых, упрощенные формулы можно использовать для определения размеров фокуса только при
невозможно повысить плотность мощности в фокусе путем увеличения диаметра пучка или уменьшения фокусного расстояния линзы. Во-вторых, упрощенные формулы можно использовать для определения размеров фокуса только при 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
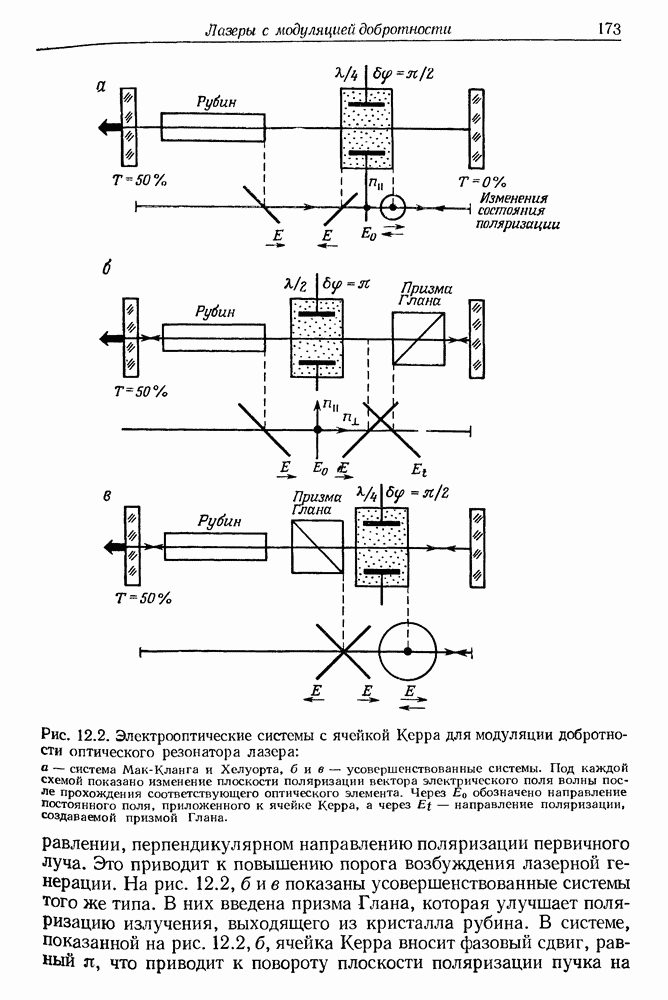
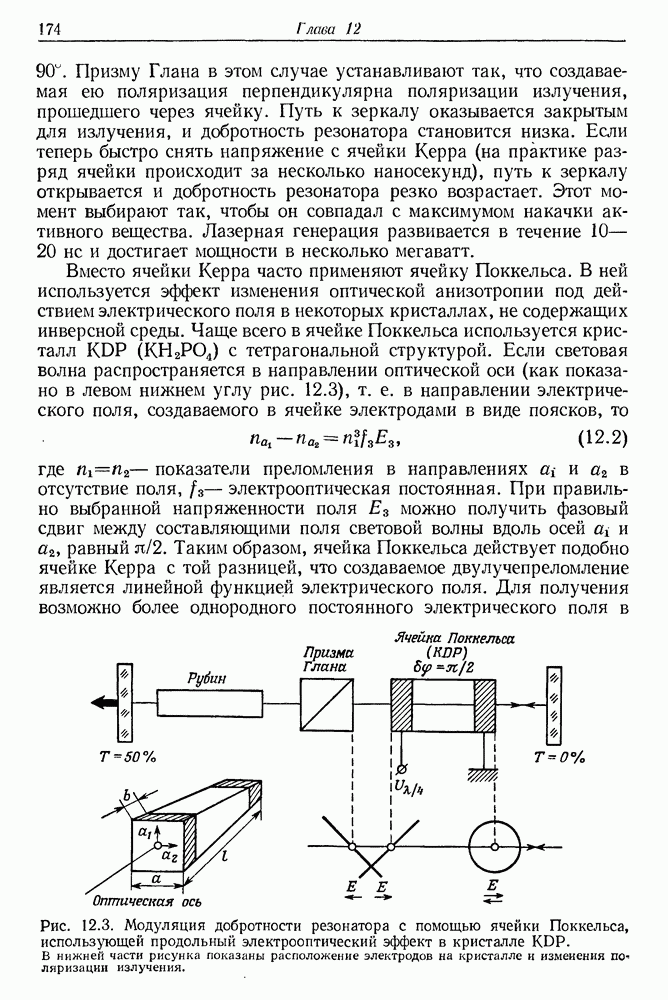
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
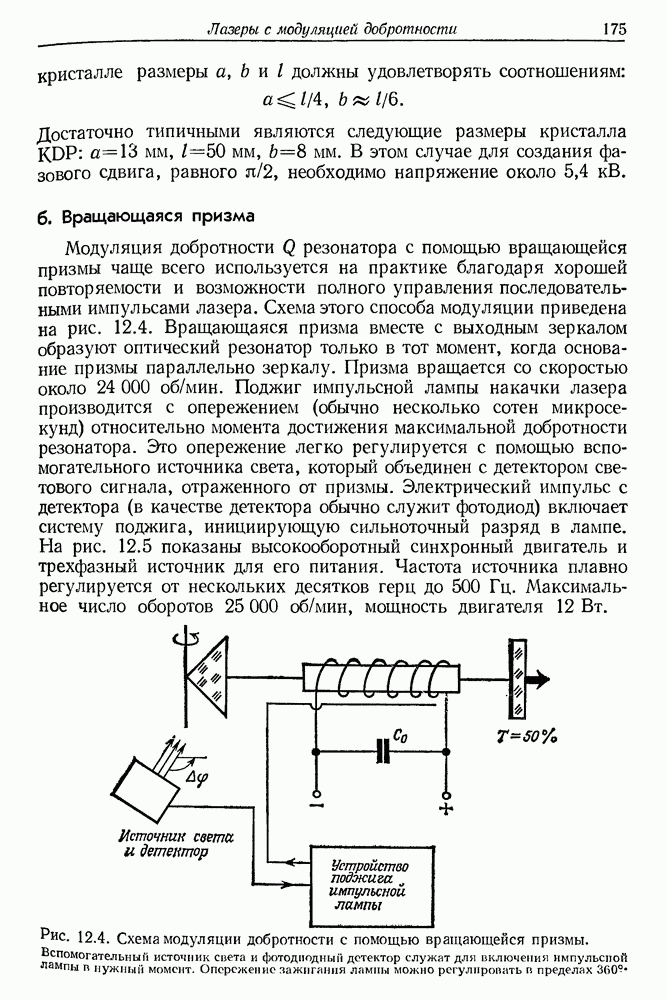
- б. Вращающаяся призма
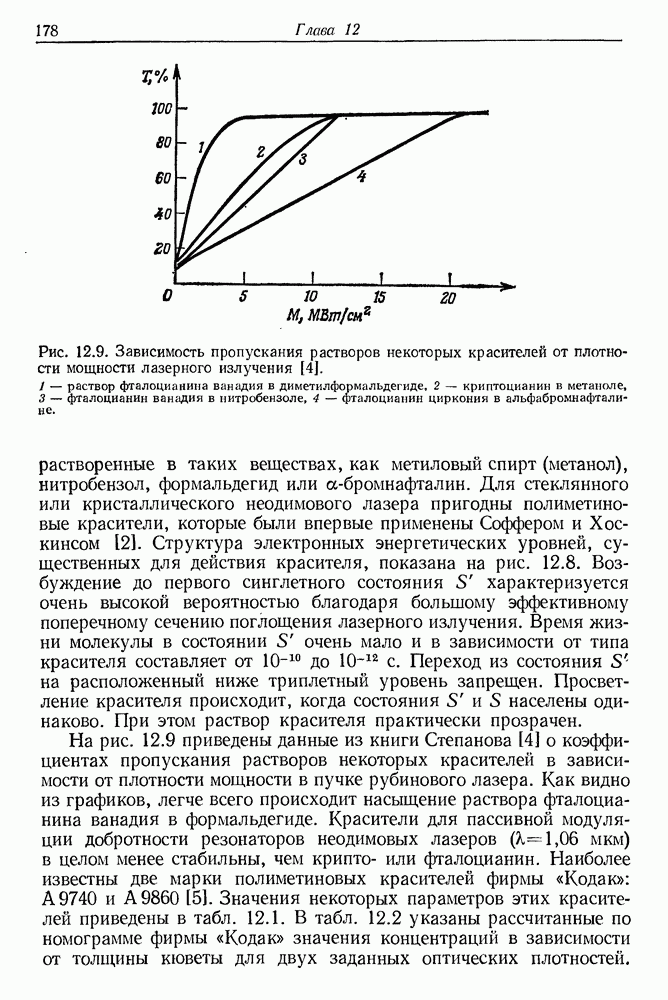
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
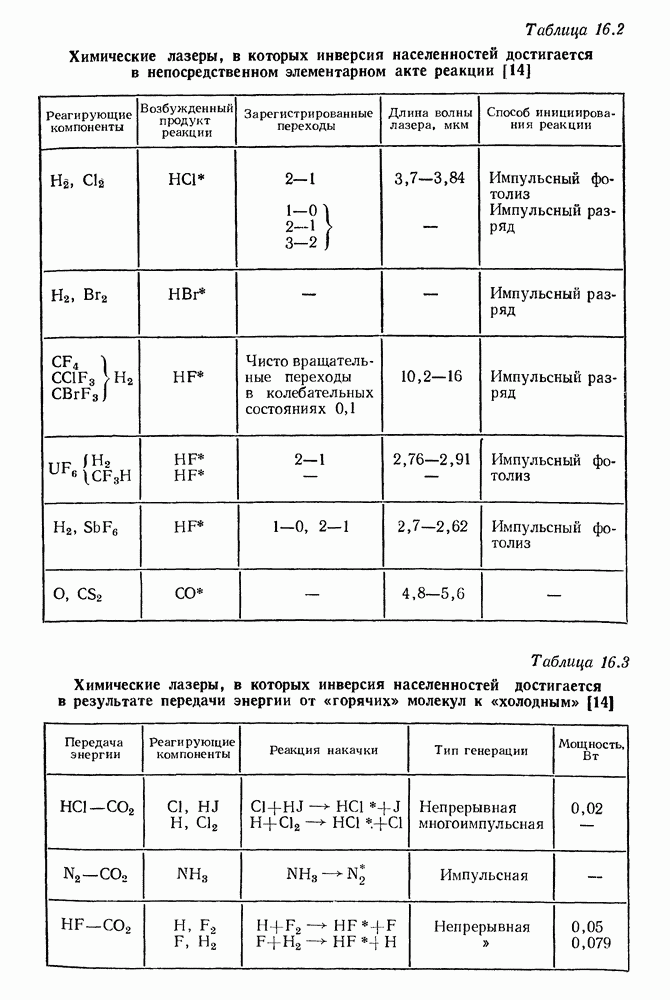
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
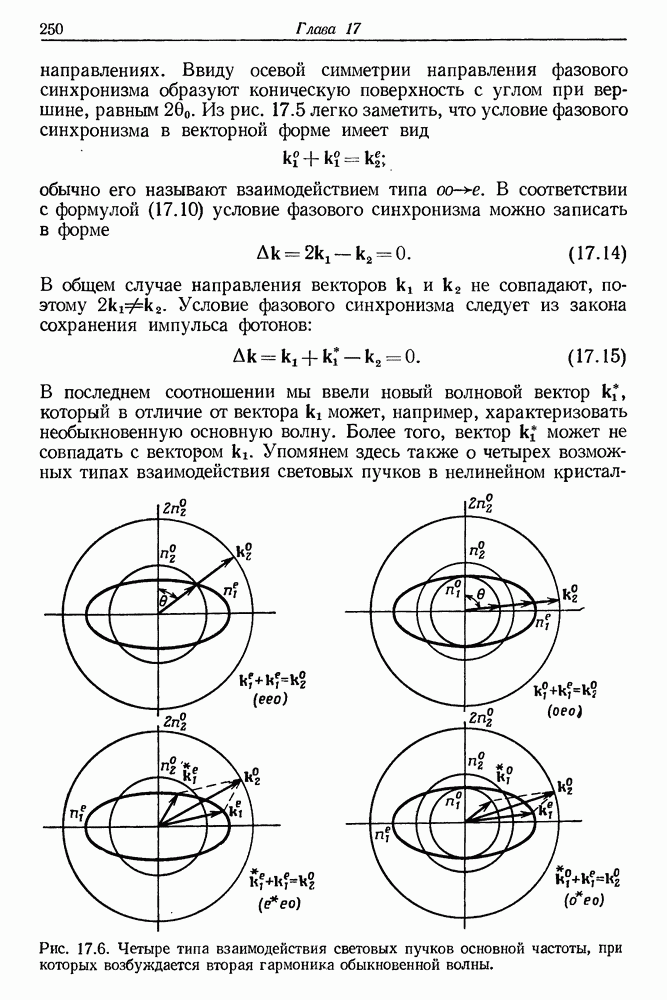
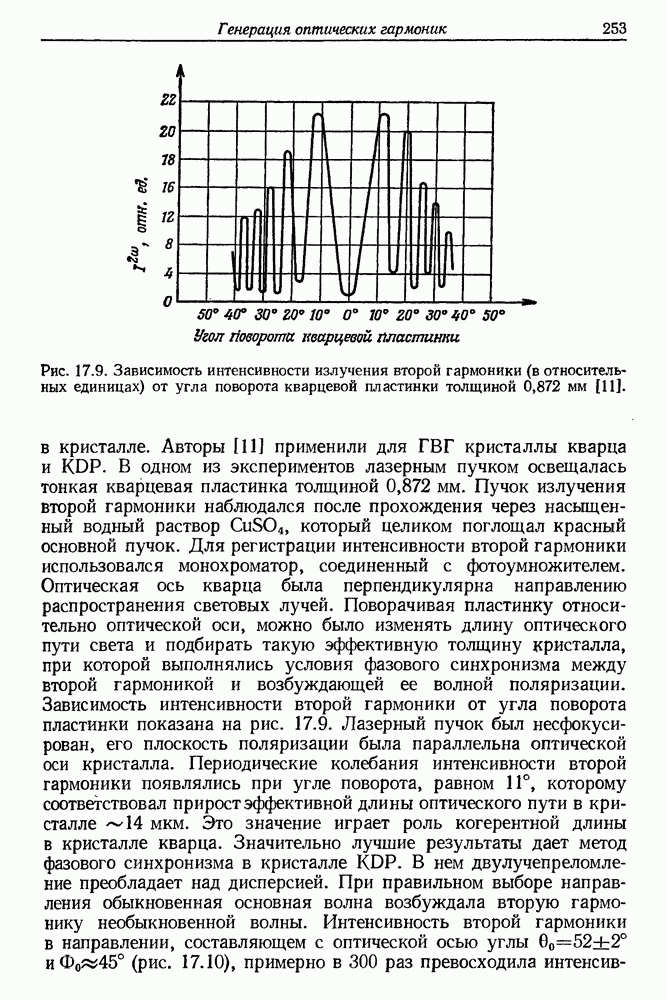
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
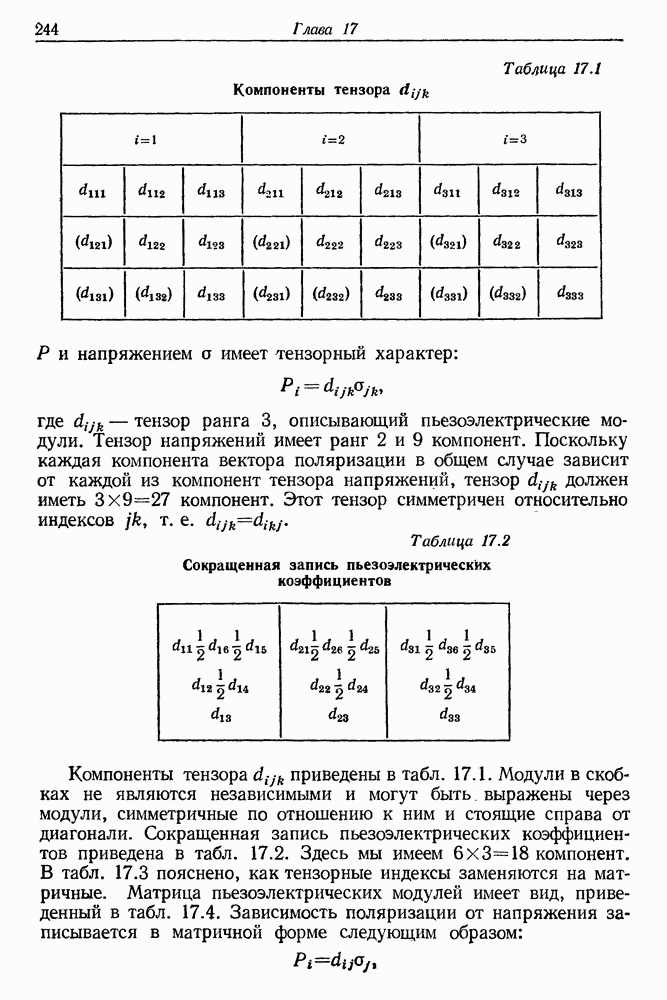
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
- 22. Параметрическая люминесценция (ПЛ)
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
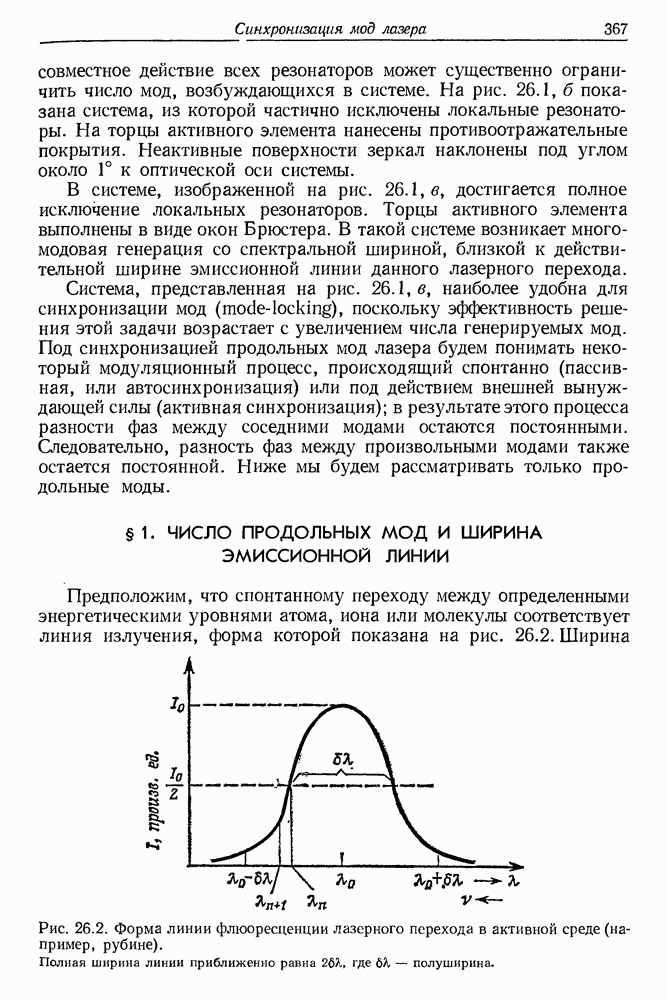
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
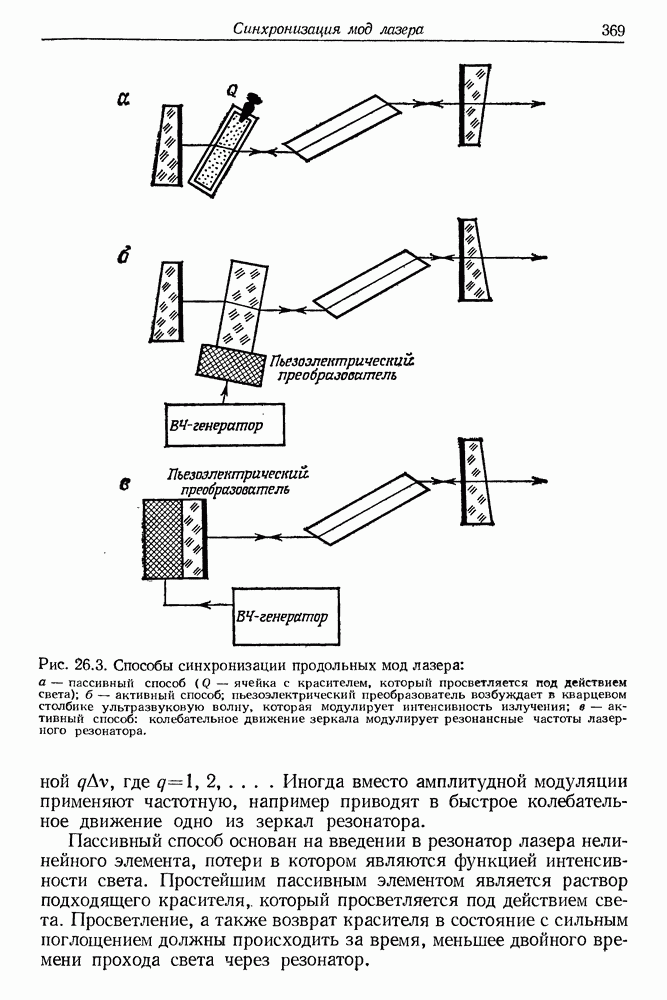
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
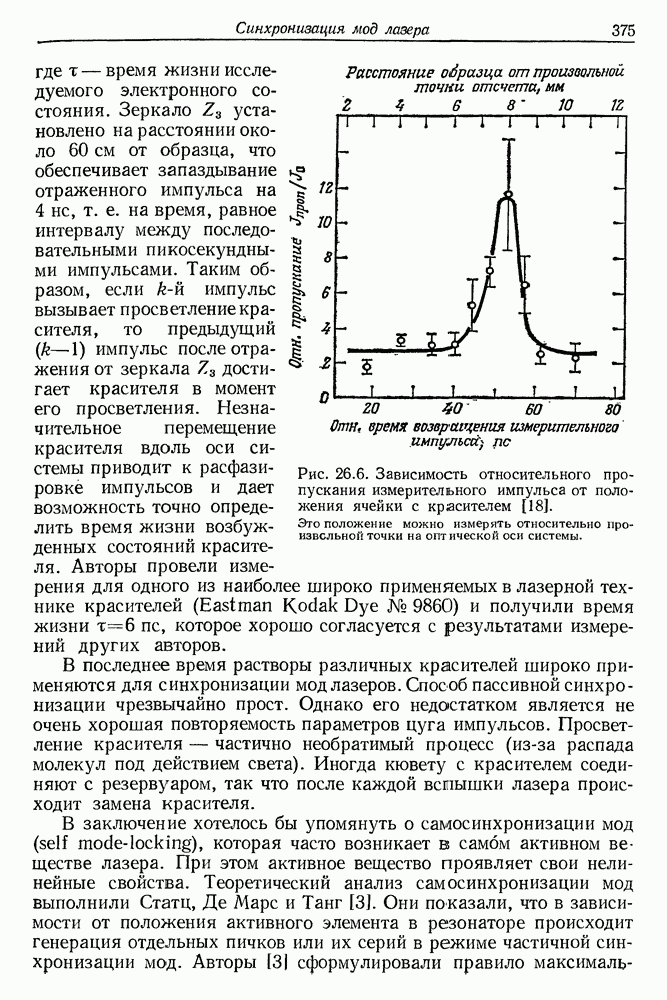
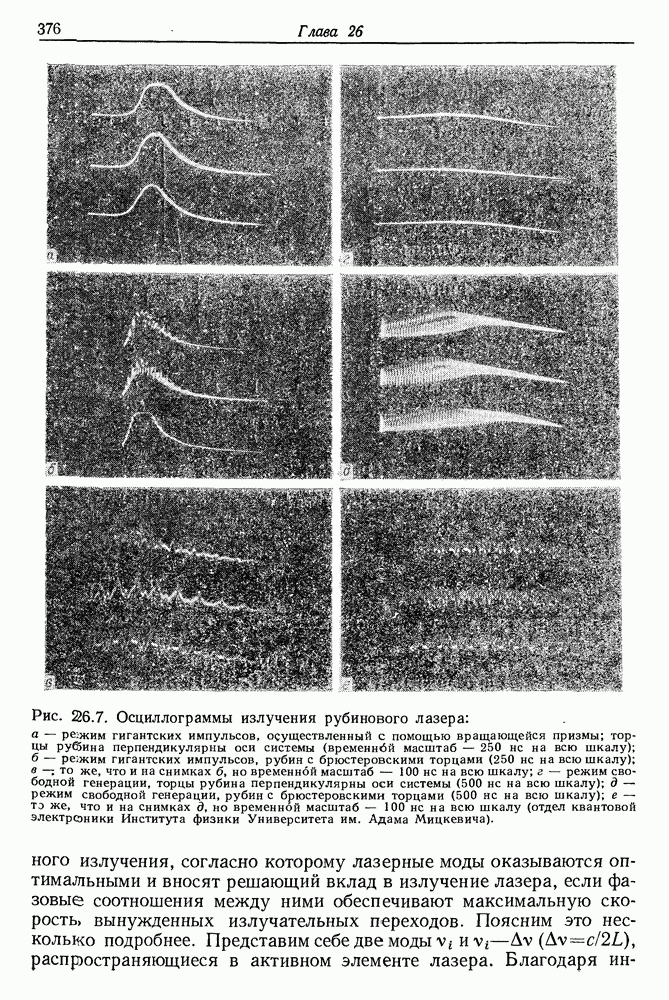
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
- в. Примеры использования камеры с разверткой
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
- 35. Лазеры на центрах окраски
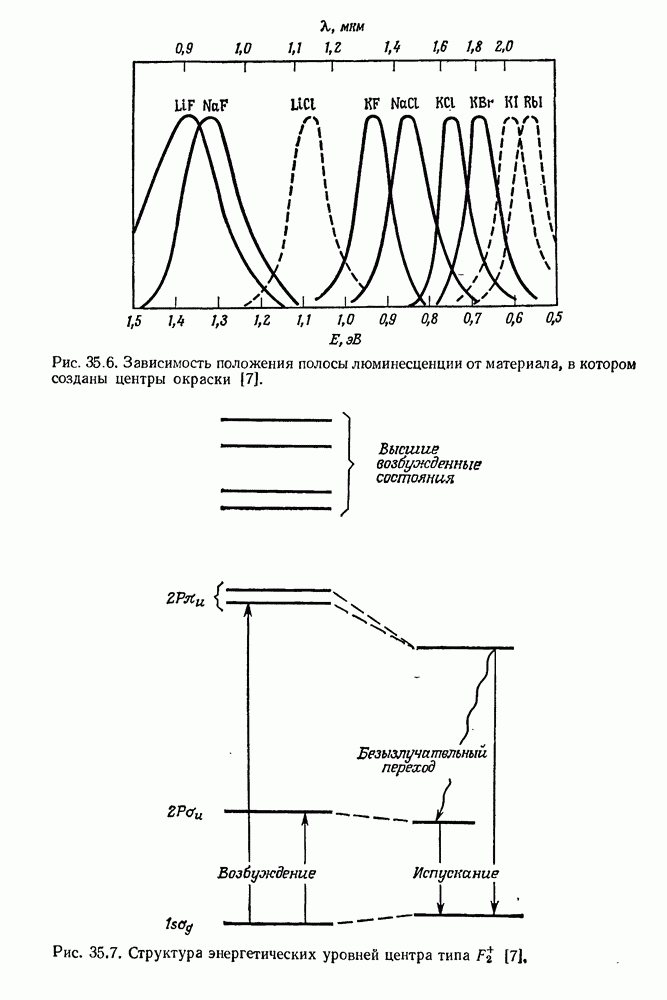
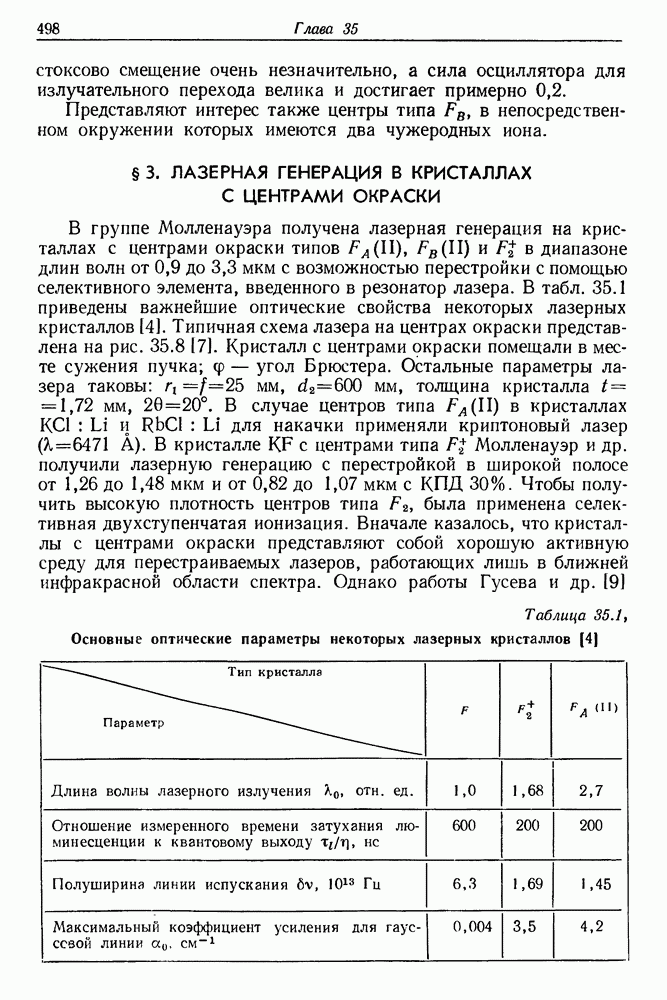
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
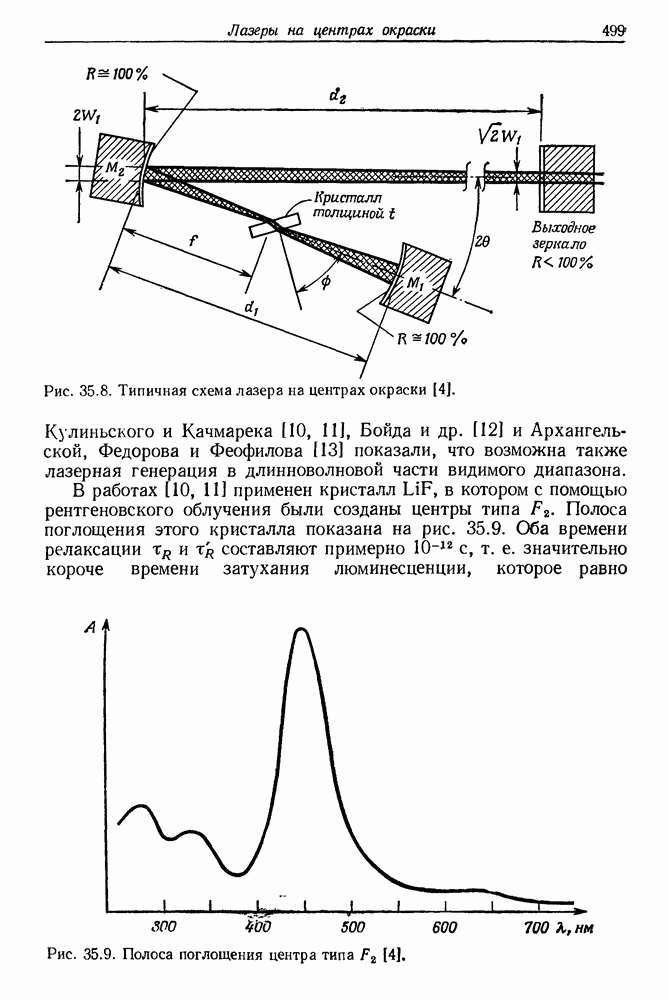
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
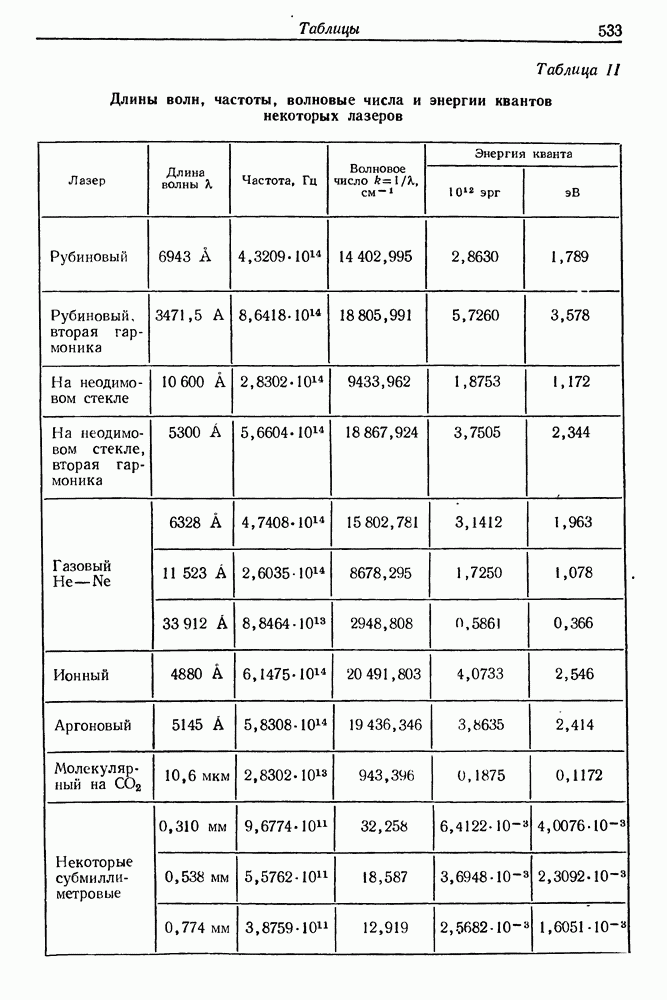
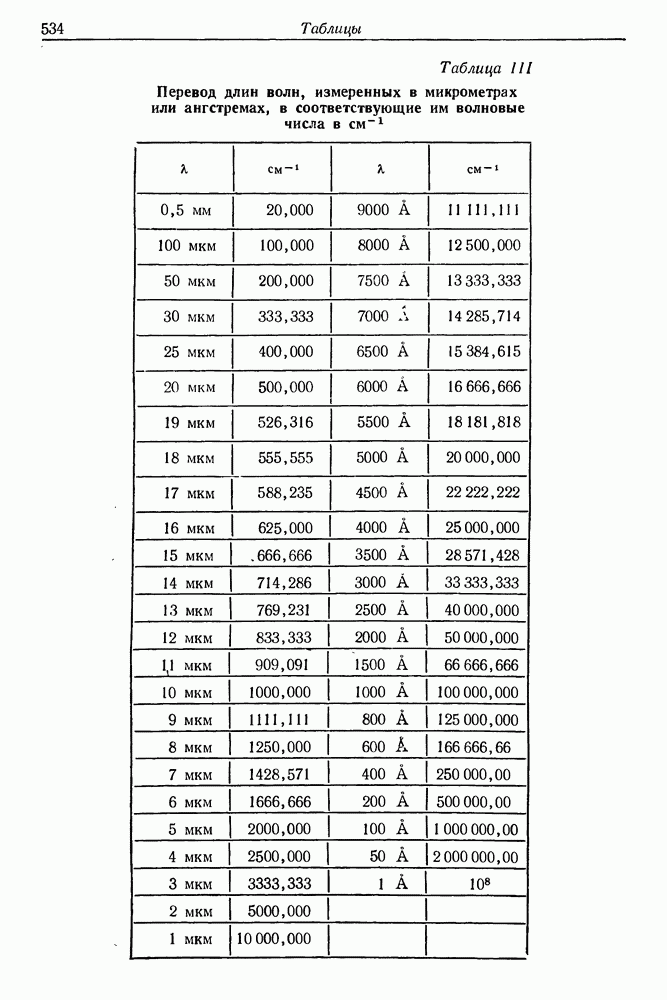
- Таблицы