| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. ОЧЕРК ТЕОРИИ ВКР
Увеличение числа фотонов в моде  с частотой
с частотой  можно описать следующим выражением:
можно описать следующим выражением:

Здесь символ  означает испускание фотона,
означает испускание фотона,  поглощение,
поглощение,  — населенности уровней
— населенности уровней  — характерное время релаксации фотонов моды
— характерное время релаксации фотонов моды  — постоянная. С учетом распределения Больцмана
— постоянная. С учетом распределения Больцмана

выражение (19.11) принимает вид

Граничное условие возникновения излучения в моде  имеет вид
имеет вид

Если разница энергий  невелика, то порог возбуждения моды
невелика, то порог возбуждения моды  очень высок.
очень высок.
Увеличение интенсивности  -рассеяния можно охарактеризовать выражением
-рассеяния можно охарактеризовать выражением

С учетом формулы (19.12) получаем

Вынужденное испускание в моде  на частоте
на частоте  невозможно, поскольку коэффициент при произведении
невозможно, поскольку коэффициент при произведении  отрицателен. Введем обозначения: X — сечение пучка в жидкости,
отрицателен. Введем обозначения: X — сечение пучка в жидкости,  — коэффициент усиления моды
— коэффициент усиления моды  — суммарная интенсивность двух пучков (распространяющихся вправо и влево),
— суммарная интенсивность двух пучков (распространяющихся вправо и влево),  — время прохождения света через резонатор,
— время прохождения света через резонатор,  — потери при отражении,
— потери при отражении,  — длина кюветы с веществом. Пренебрегая спонтанным испусканием, можно записать для стоксова рассеяния
— длина кюветы с веществом. Пренебрегая спонтанным испусканием, можно записать для стоксова рассеяния

Коэффициент усиления  легко связать с числом фотонов
легко связать с числом фотонов  в возбуждающем пучке
в возбуждающем пучке

следовательно,

где

Согласно работе Хелуорта [22], коэффициент усиления равен

где  — разностное эффективное поперечное сечение рассеяния основного пучка
— разностное эффективное поперечное сечение рассеяния основного пучка  на пучке
на пучке  Удобно принять, что
Удобно принять, что  представляет собой число фотонов на
представляет собой число фотонов на  за секунду.
за секунду.
Классическая теория ВКР формулируется следующим образом. Пусть в соответствии с выражением (19.4)

где через  обозначена потенциальная энергия, а
обозначена потенциальная энергия, а

В выражении (19.22) первый член относится к первичному пучку, а второй — к рассеянному. Формула (19.21) содержит осциллирующий член с частотой  Если
Если  эти осцилляции окажутся в резонансе с собственными колебаниями молекулы. Обозначим затухание в системе через
эти осцилляции окажутся в резонансе с собственными колебаниями молекулы. Обозначим затухание в системе через  Тогда получаем
Тогда получаем 

Соответствующий этим колебаниям электрический дипольный момент равен

Мощность, которую воспринимает рассеянная волна Е от основной волны  рассчитывается путем следующего усреднения по времени:
рассчитывается путем следующего усреднения по времени:

или

Для стоксова рассеяния  поэтому мощность пучка Е возрастает. Для линии
поэтому мощность пучка Е возрастает. Для линии  поэтому мощность пучка
поэтому мощность пучка  уменьшается.
уменьшается.
Для правильного описания ВКР антистоксова типа необходимо рассмотреть три взаимодействующие волны. Стоксово рассеяние имеет диффузный характер; угловая зависимость рассеяния и его состояние поляризации определяются членом  Существование порога возбуждения стоксовой линии обусловлено тем, что как потери в системе, так и мощность излучения пропорциональны
Существование порога возбуждения стоксовой линии обусловлено тем, что как потери в системе, так и мощность излучения пропорциональны 
Для рассеяния  положим
положим 

Мощности рассеянных пучков равны


Рис. 19.9. Схема спонтанного (а) и вынужденного (б) комбинационного рассеяния [23].
Если  то интенсивность линии
то интенсивность линии  может возрастать при условии, что
может возрастать при условии, что

Первое из условий (19.25) эквивалентно закону сохранения импульса. Оно может выполняться в жидкостях благодаря наличию дисперсии. Таким образом, антистоксово рассеяние может обладать селективной угловой структурой. Угол рассеяния 0 можно определить из соотношения

В то же время пучок взаимодействует с  под углом
под углом  равным
равным

Присутствие стоксова рассеяния необходимо для возбуждения антистоксова рассеяния. Отчетливый порог возбуждения в данном случае отсутствует, поскольку мощность излучения пропорциональна  , а потери
, а потери  .
.
Наглядное пояснение разницы между спонтанным и вынужденным рассеянием дано на рис. 19.9 [23]. В первом случае молекула вещества поглощает квант возбуждающего излучения  а затем испускает квант
а затем испускает квант  с уменьшенной энергией (стоксова линия). Во втором случае в веществе сосуществуют по меньшей мере два световых пучка: возбуждающий с энергией кванта
с уменьшенной энергией (стоксова линия). Во втором случае в веществе сосуществуют по меньшей мере два световых пучка: возбуждающий с энергией кванта  и стоксов. Испускание дополнительного кванта носит вынужденный характер и увеличивает интенсивность рассеяния. Лазерный пучок служит для возбуждения молекул до высших энергетических состояний. При стоксовом рассеянии молекула вещества переходит в возбужденное колебательное состояние, что в свою очередь создает условия для возникновения антистоксова рассеяния. В соответствии с рис. 19.9, описание ВКР на языке квантовой механики сводится к расчету вероятности перехода поля излучения с частотой
и стоксов. Испускание дополнительного кванта носит вынужденный характер и увеличивает интенсивность рассеяния. Лазерный пучок служит для возбуждения молекул до высших энергетических состояний. При стоксовом рассеянии молекула вещества переходит в возбужденное колебательное состояние, что в свою очередь создает условия для возникновения антистоксова рассеяния. В соответствии с рис. 19.9, описание ВКР на языке квантовой механики сводится к расчету вероятности перехода поля излучения с частотой  от числа квантов
от числа квантов  к числу
к числу  Эта вероятность пропорциональна
Эта вероятность пропорциональна 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
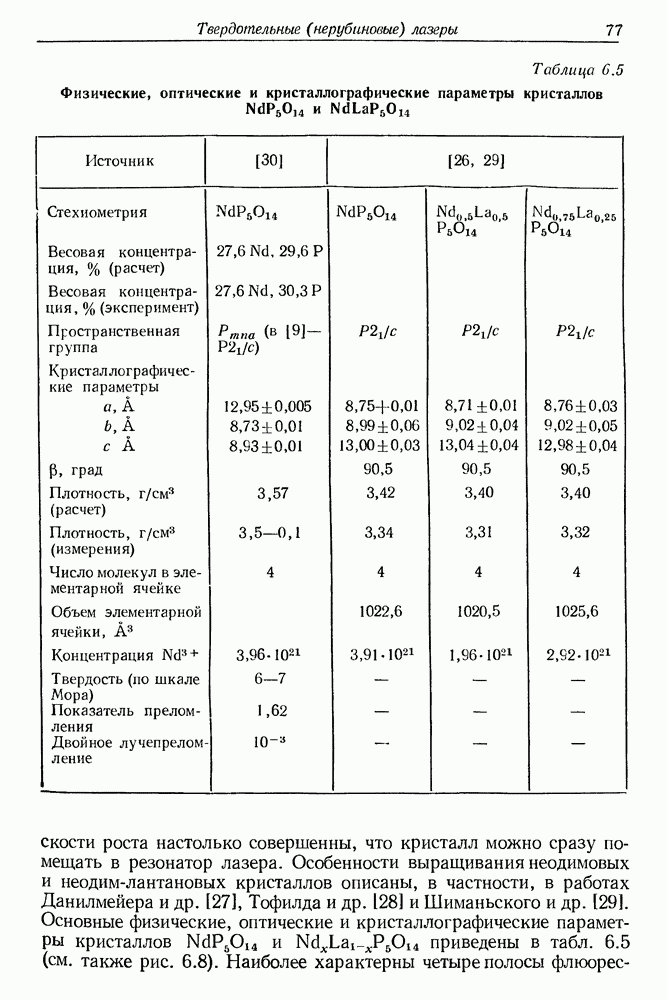
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
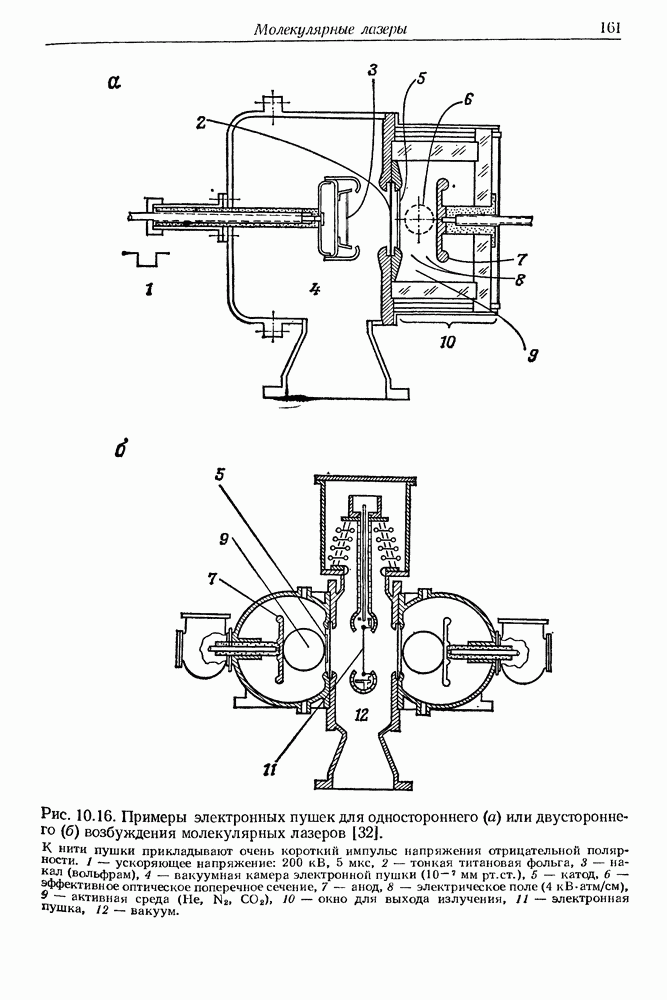
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
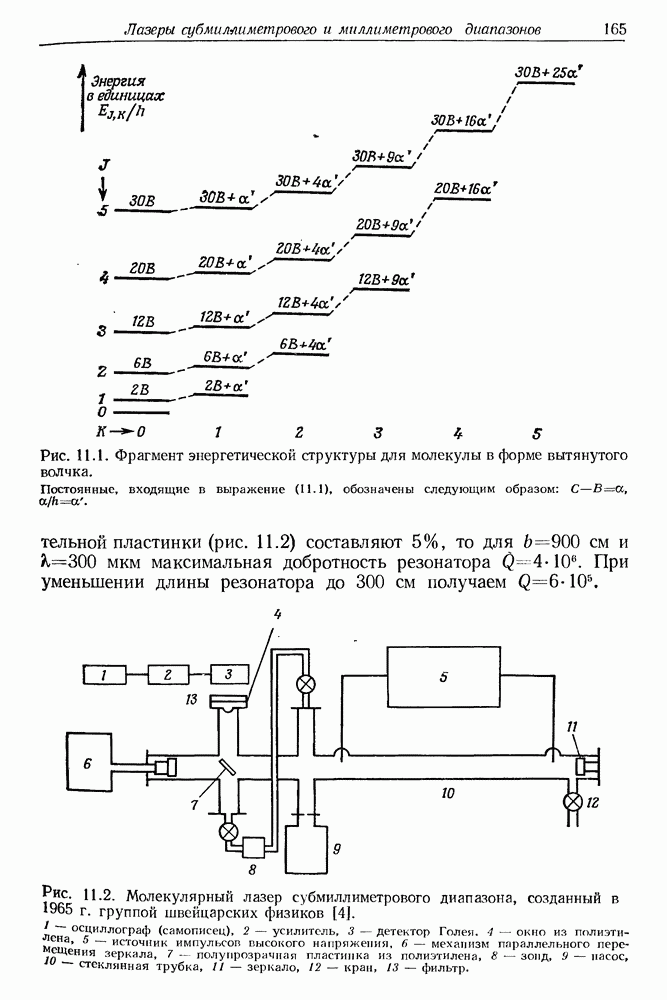
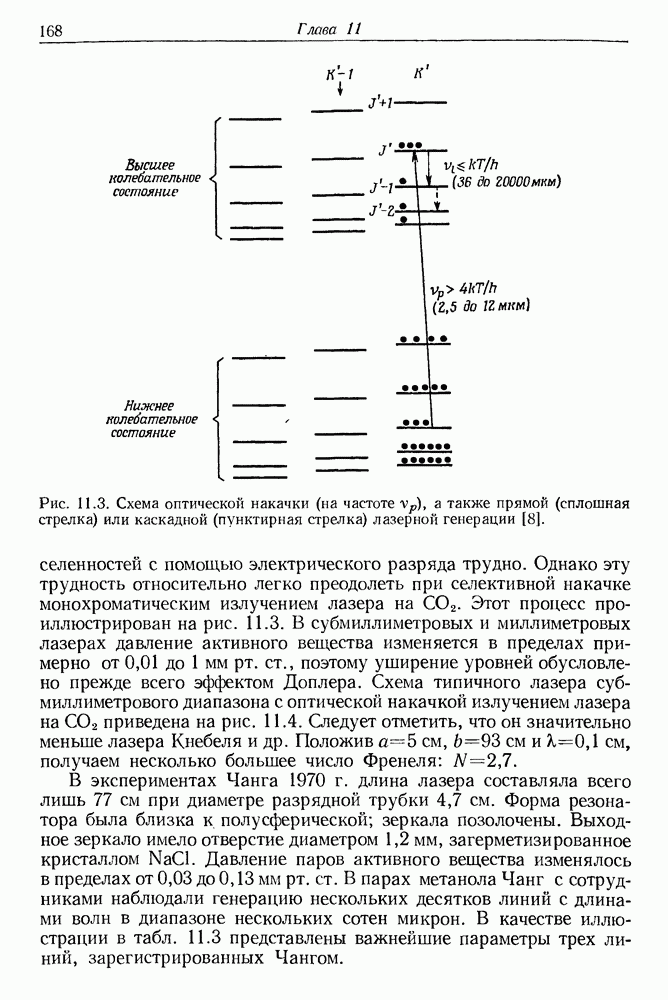
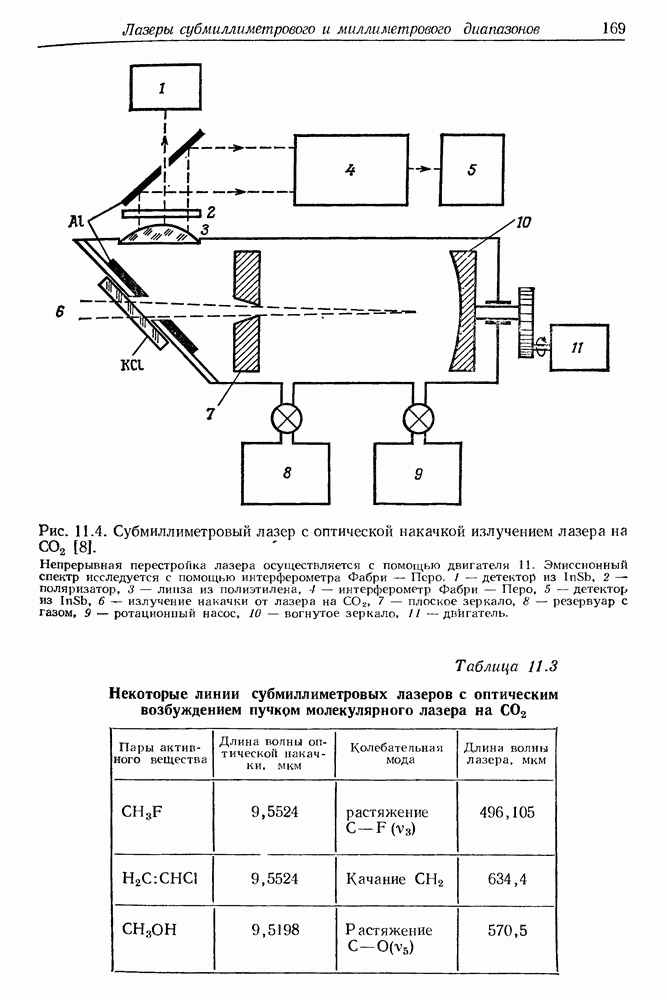
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
- б. Вращающаяся призма
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
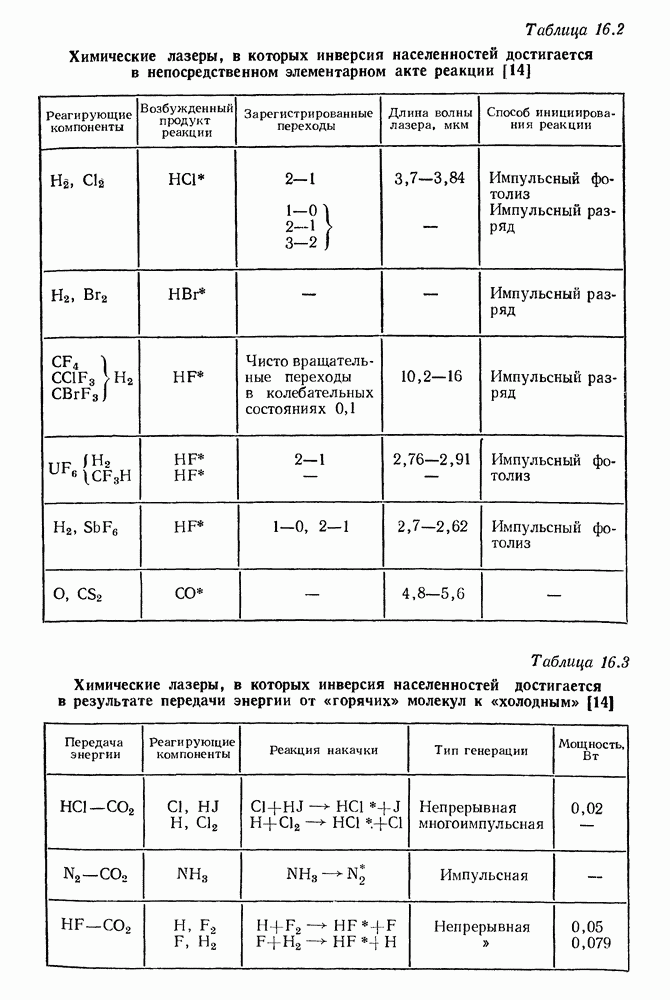
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
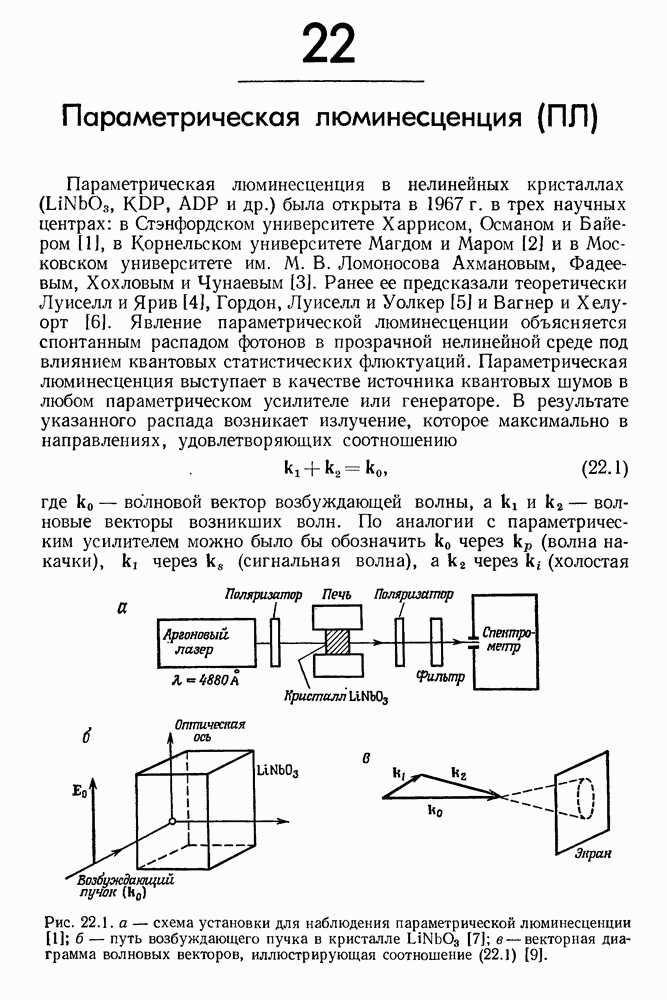
- 22. Параметрическая люминесценция (ПЛ)
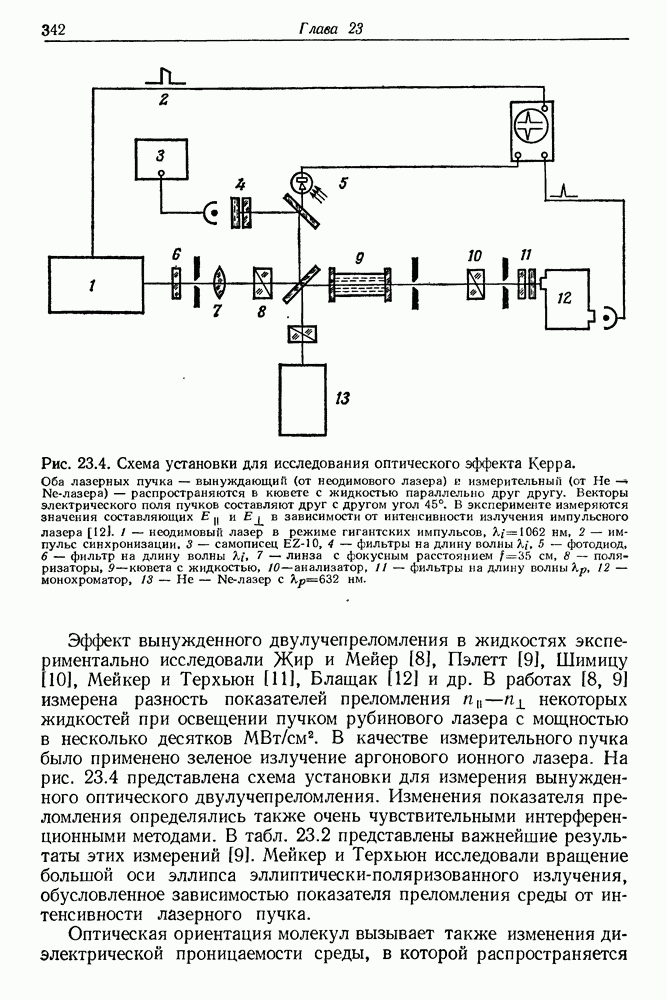
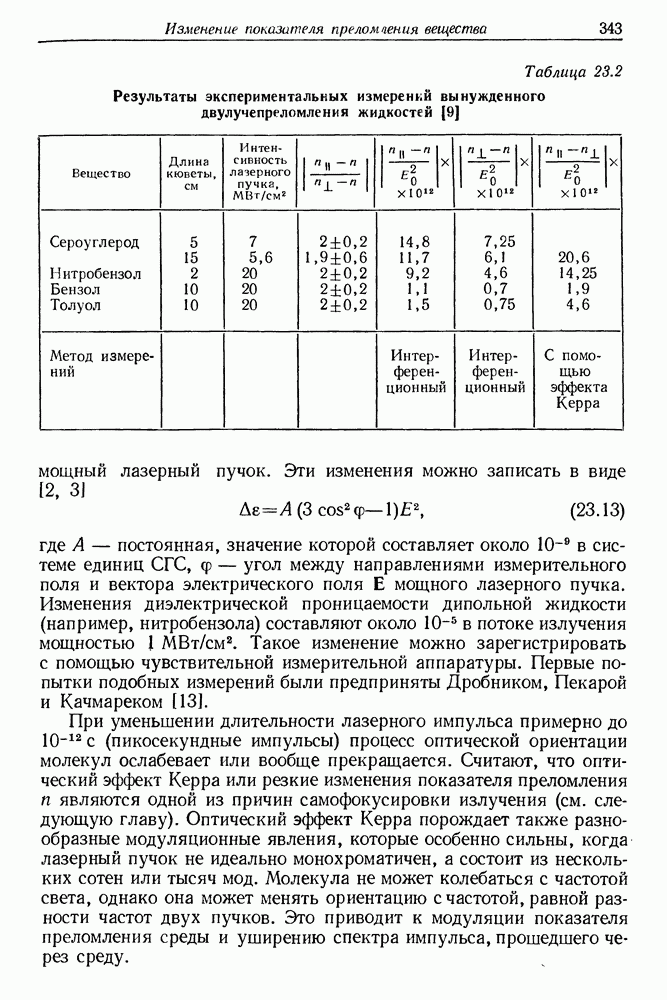
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
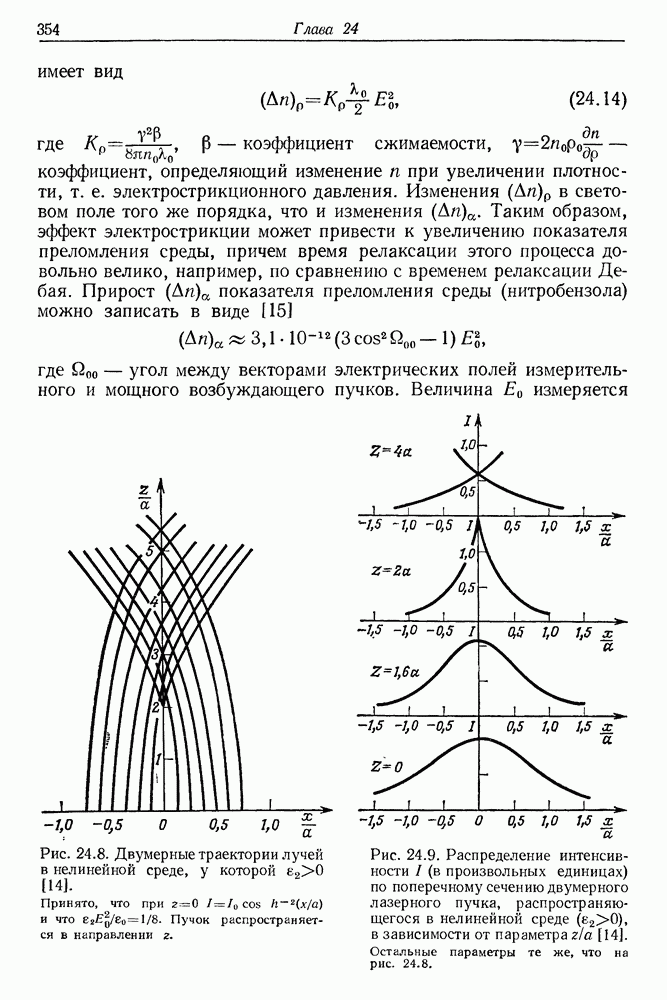
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
- в. Примеры использования камеры с разверткой
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
- 35. Лазеры на центрах окраски
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
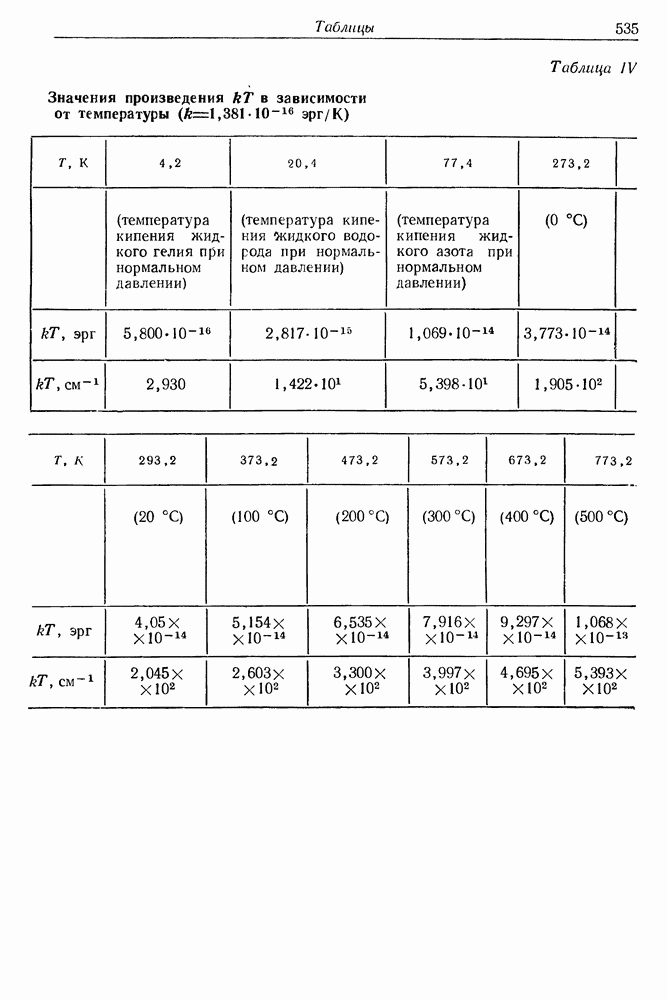
- Таблицы