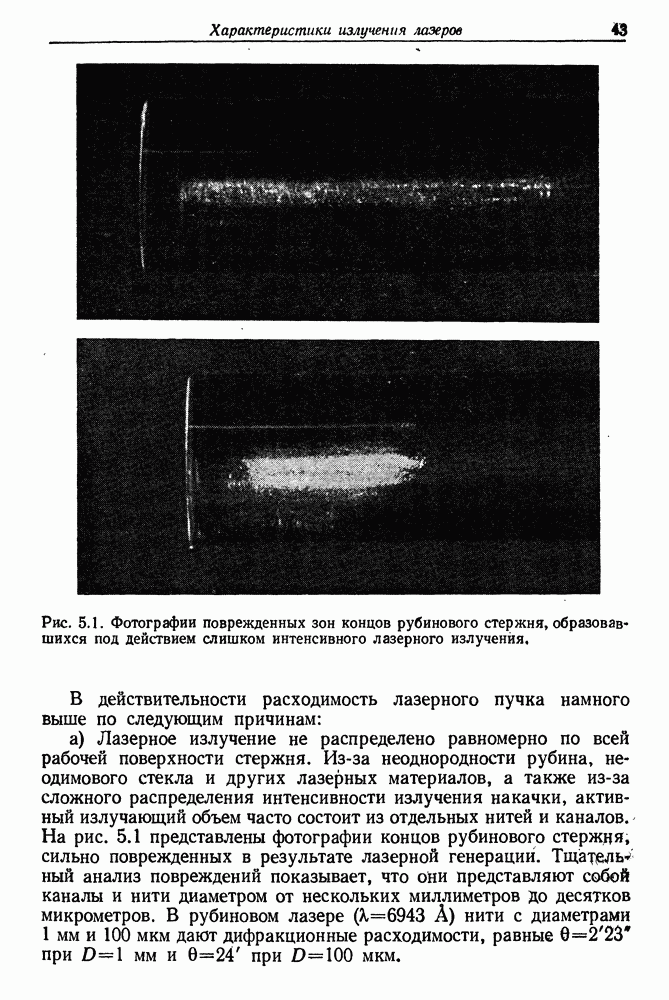
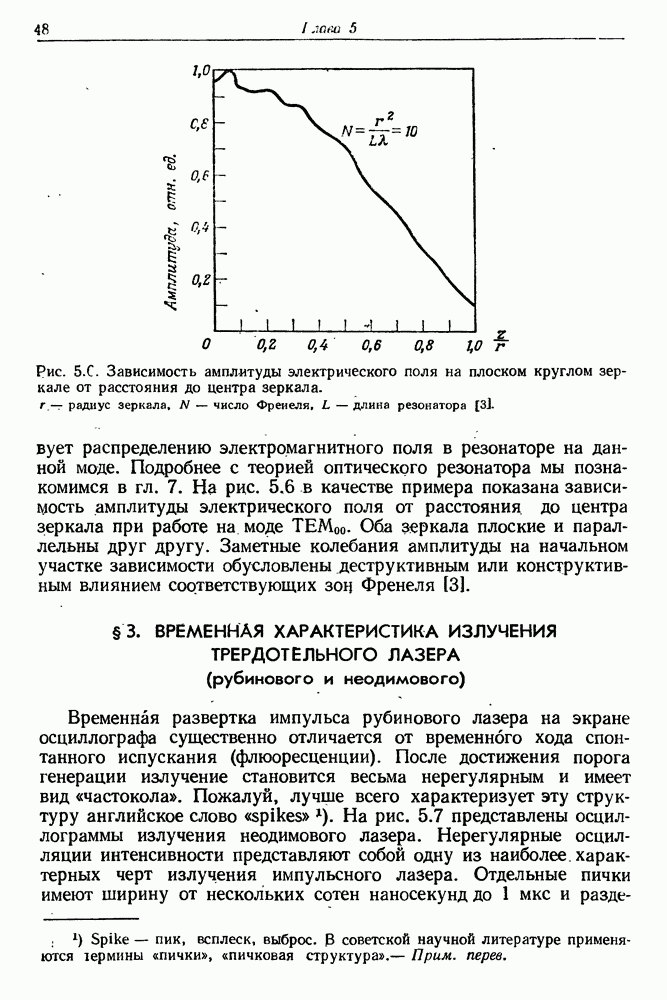
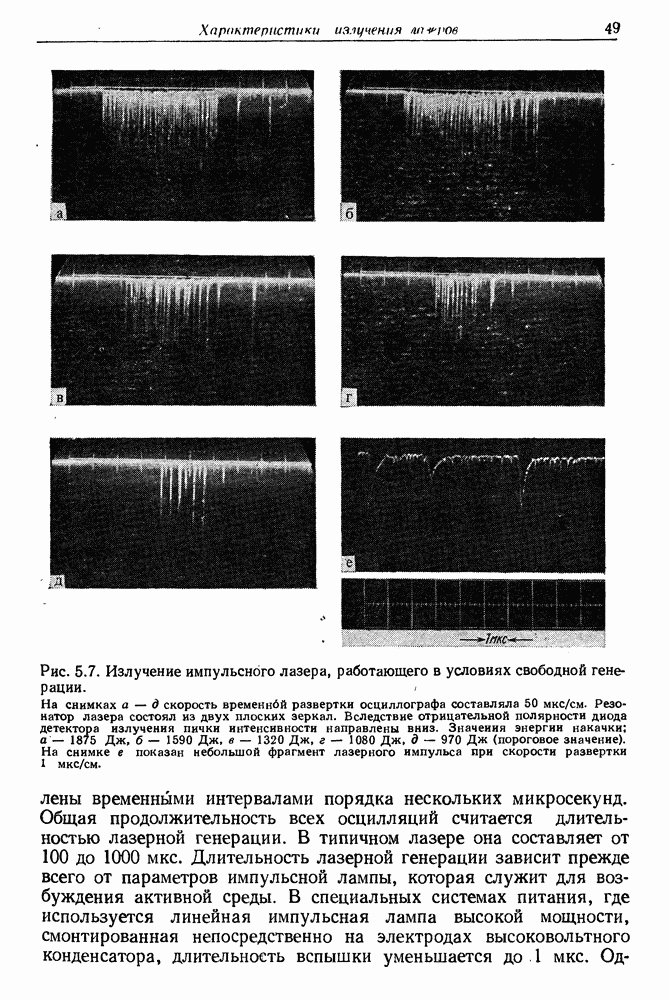
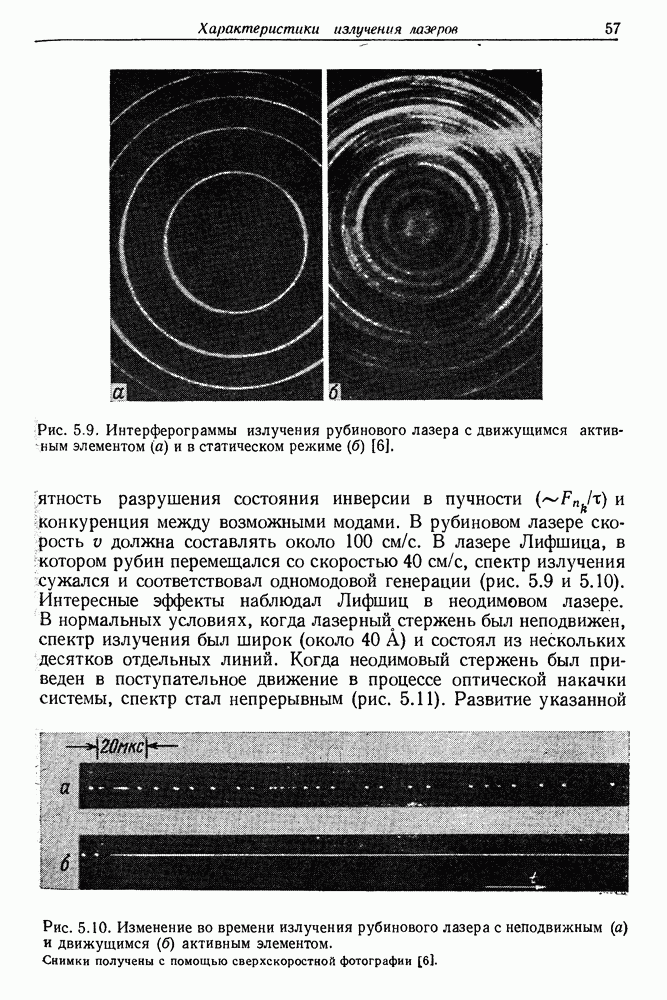
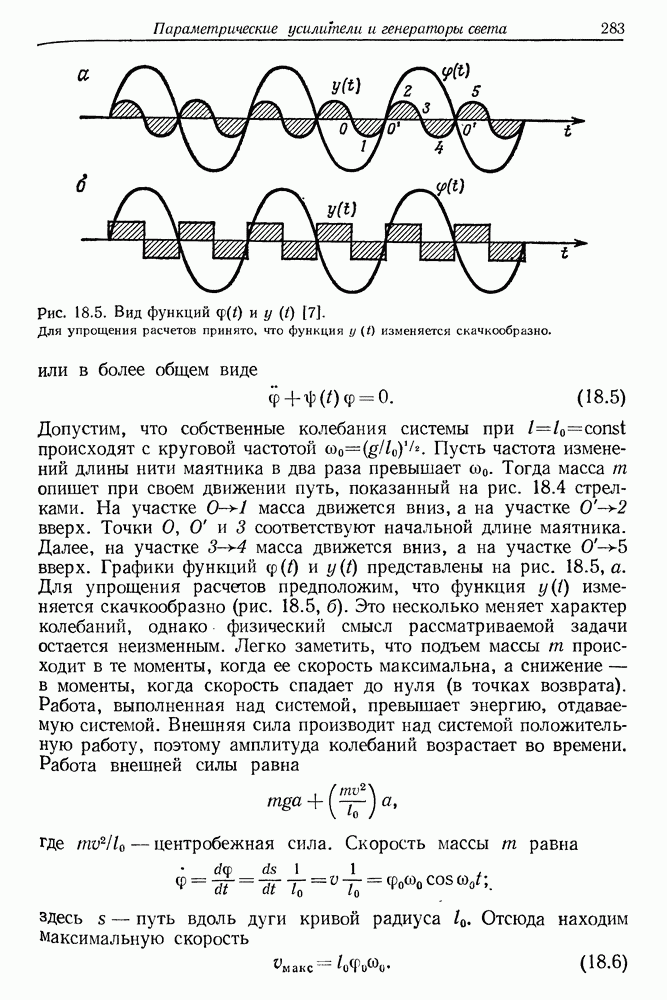
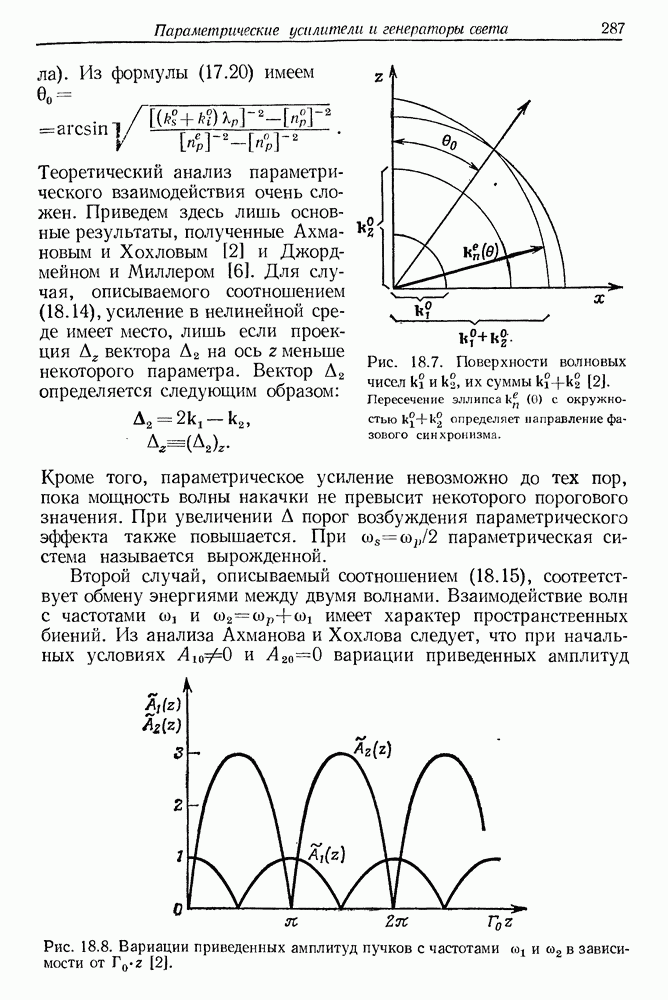
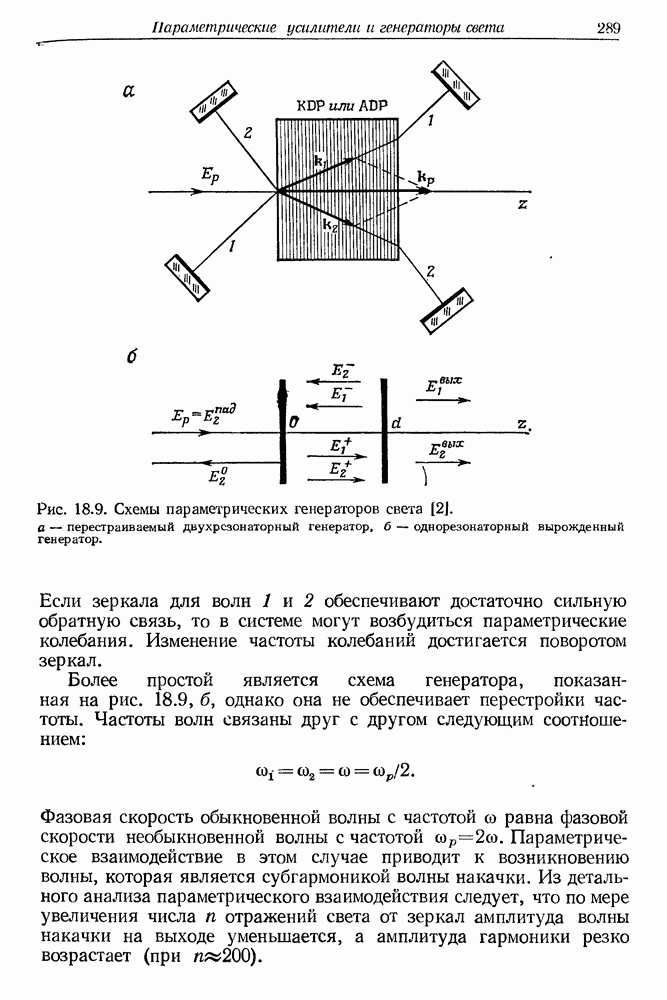
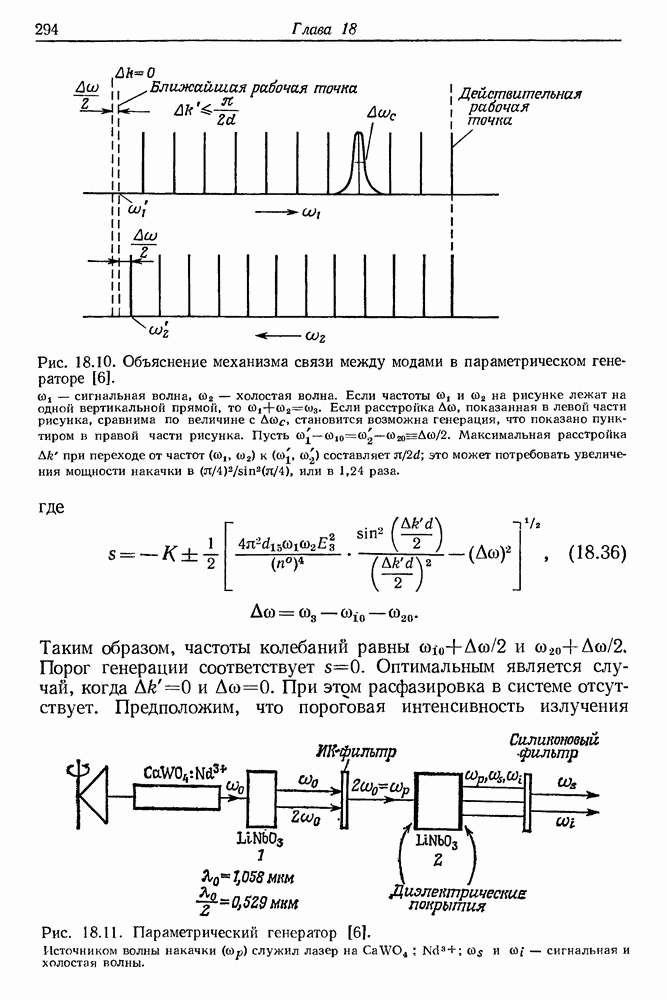
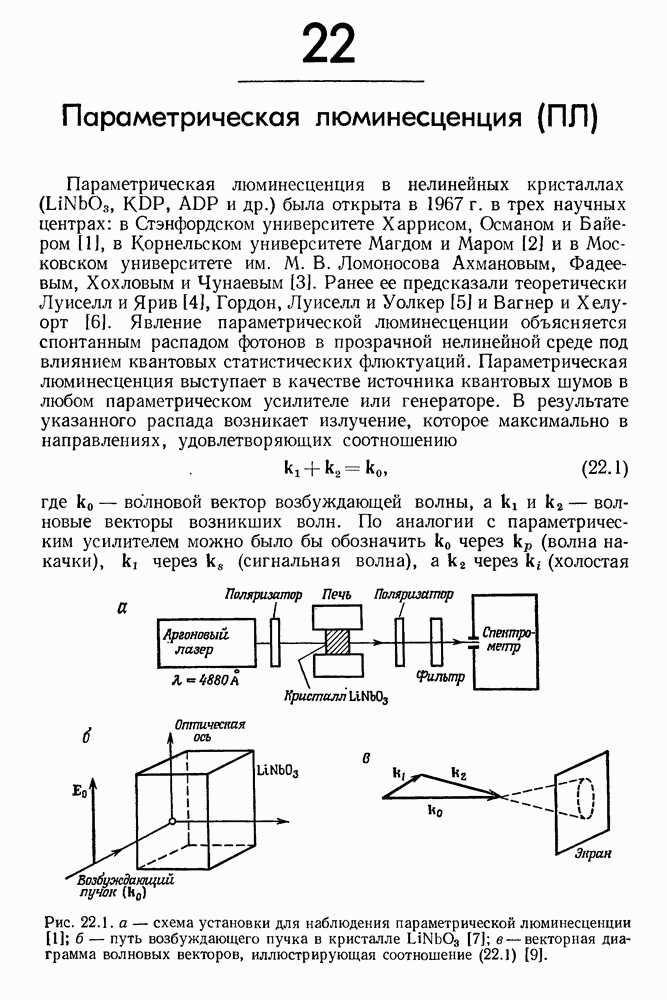
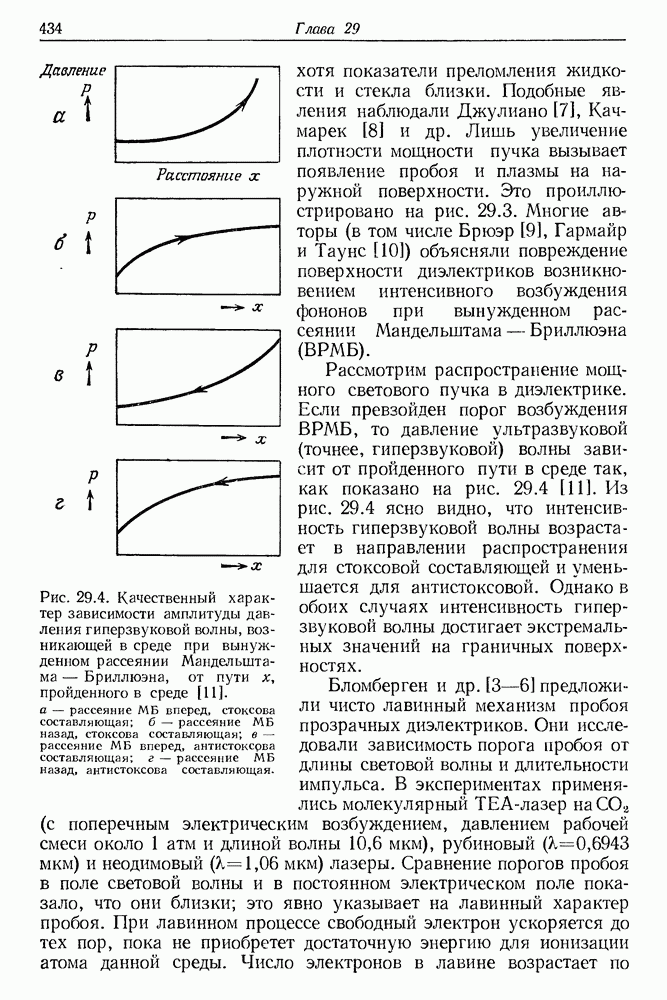
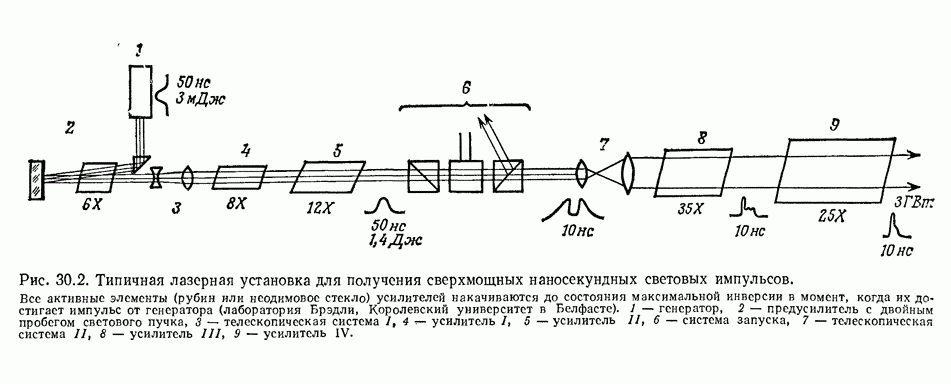
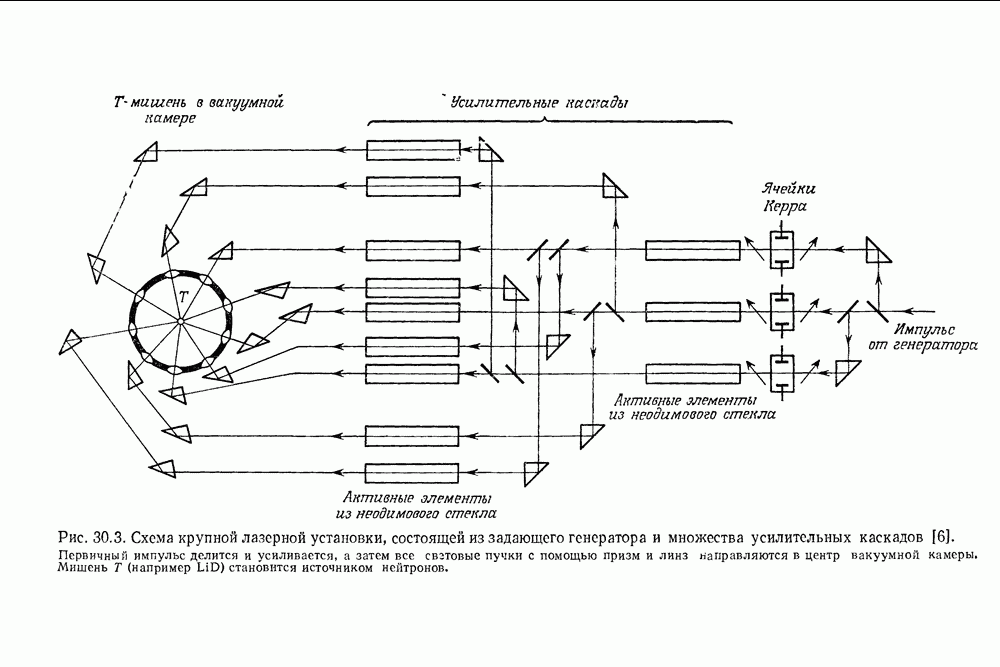
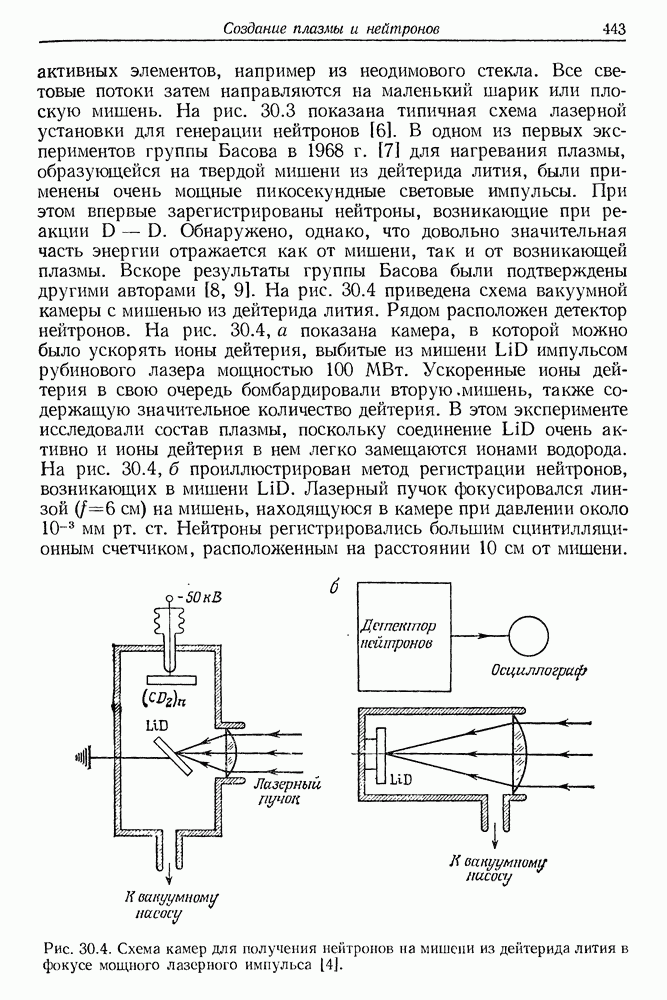
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
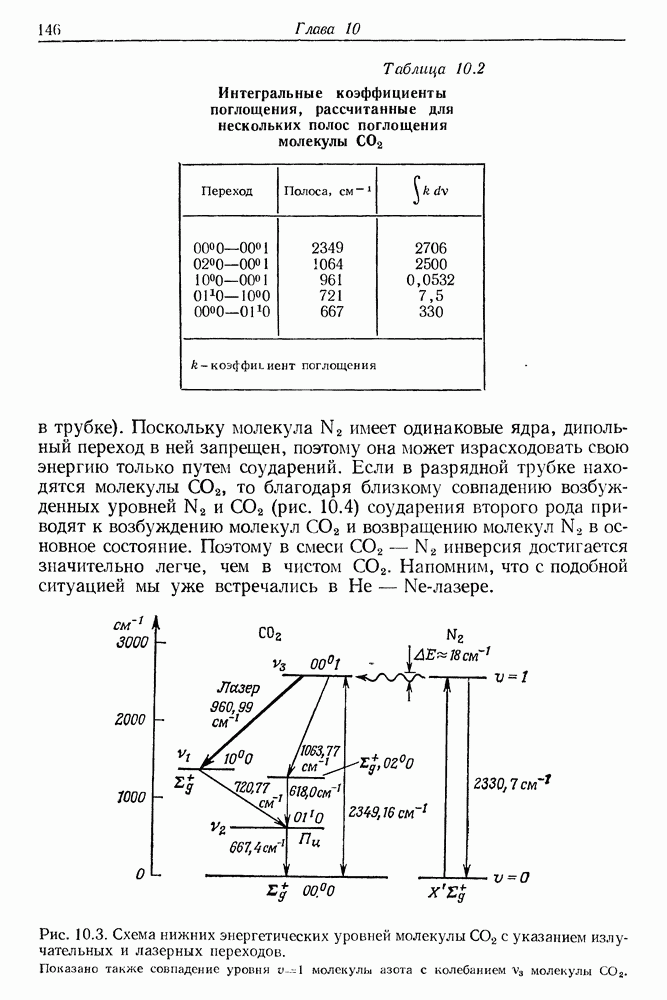
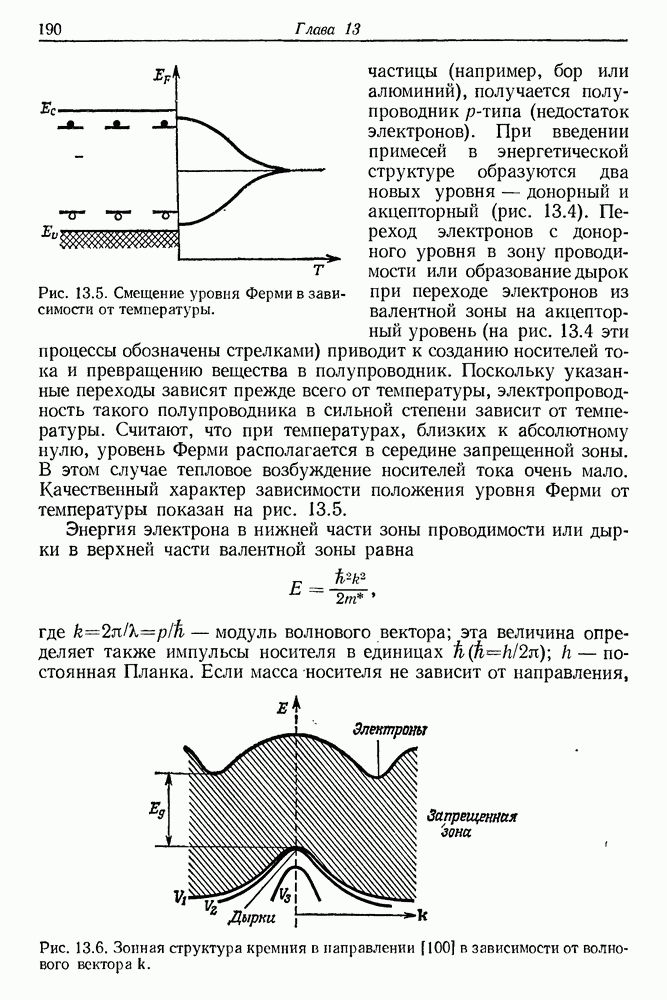
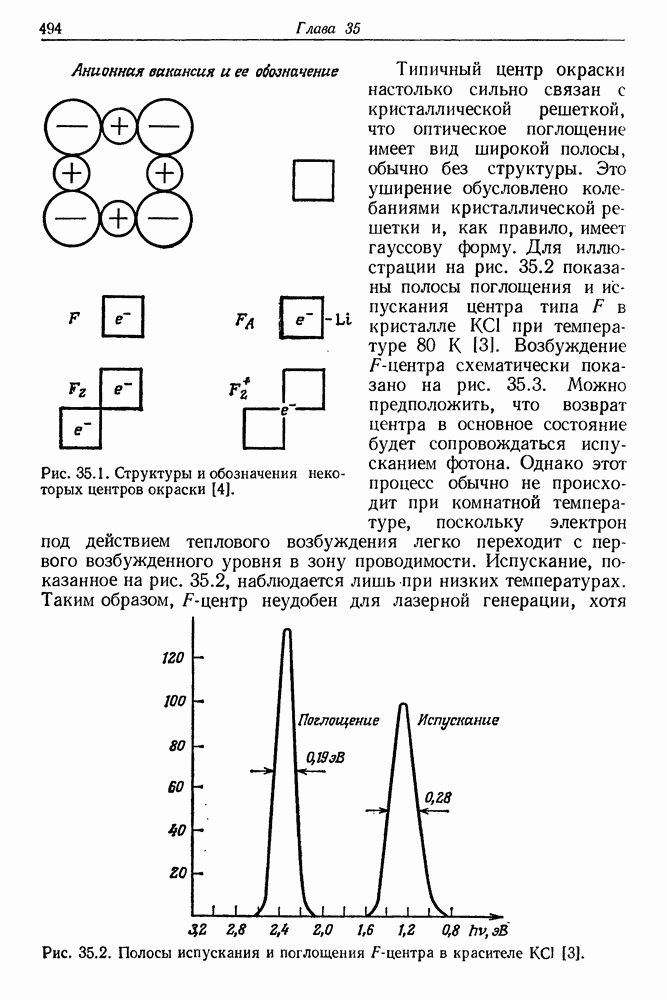
Бакингэм [1] впервые обратил внимание на возможность ориентации молекул с помощью мощного лазерного излучения. Ориентация в свою очередь приводит к возникновению вынужденного двулучепреломления, которое обычно называют оптическим эффектом Керра. Пекара и Келих [2, 3], а затем Келих [4, 5] разработали общую теорию воздействия мощного лазерного пучка на показатель преломления вещества и на его магнитную и диэлектрическую проницаемость. Явление вынужденного двулучепреломления представляет собой один из ее частных случаев. Не вникая в детали этой достаточно сложной теории, приведем здесь ее элементарное изложение, которое позволяет разобраться в основных физических процессах, определяющих анизотропию среды. С этой целью рассмотрим осесимметричную молекулу с анизотропной поляризуемостью, находящуюся в начале декартовой системы координат (рис. 23.1). Предположим, что на молекулу действует быстро изменяющееся электрическое поле Е световой волны. Компоненты вектора Е и вектора индуцированной поляризации Р запишем в линейном приближении в следующем виде:

Согласно нашему предположению, молекула не обладает постоянным дипольным моментом и совершает только вращательное движение. В тензорной записи выражения (23.1) значительно упрощаются:

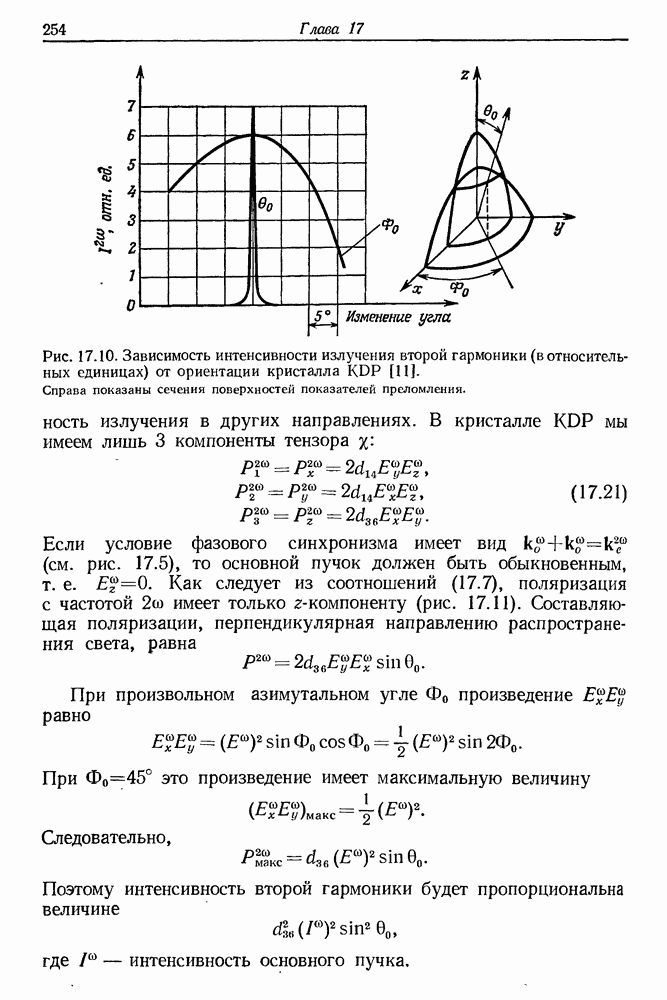
Здесь  — тензор оптической восприимчивости ранга 2. Выражения (23.1) говорят о том, что каждая составляющая вектора поляризации зависит от всех составляющих поля. В оптическом поле имеет место лишь электронная поляризация. Направления векторов Р и Е в общем случае не совпадают, как показано на рис. 23.1. Предположим теперь, что световой пучок линейно поляризован
— тензор оптической восприимчивости ранга 2. Выражения (23.1) говорят о том, что каждая составляющая вектора поляризации зависит от всех составляющих поля. В оптическом поле имеет место лишь электронная поляризация. Направления векторов Р и Е в общем случае не совпадают, как показано на рис. 23.1. Предположим теперь, что световой пучок линейно поляризован  Для выяснения эффекта ориентации молекул рассмотрим упрощенную модель молекулы, восприимчивость которой в направлении
Для выяснения эффекта ориентации молекул рассмотрим упрощенную модель молекулы, восприимчивость которой в направлении 

Рис. 23.1. Положение вектора индуцированной поляризации Р в электрическом поле Е.
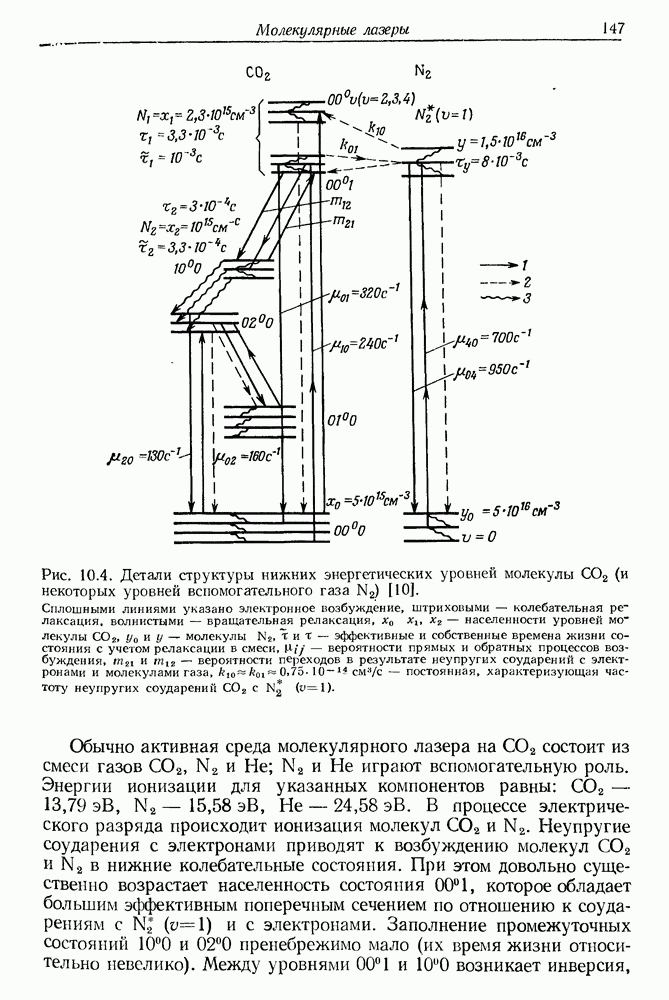
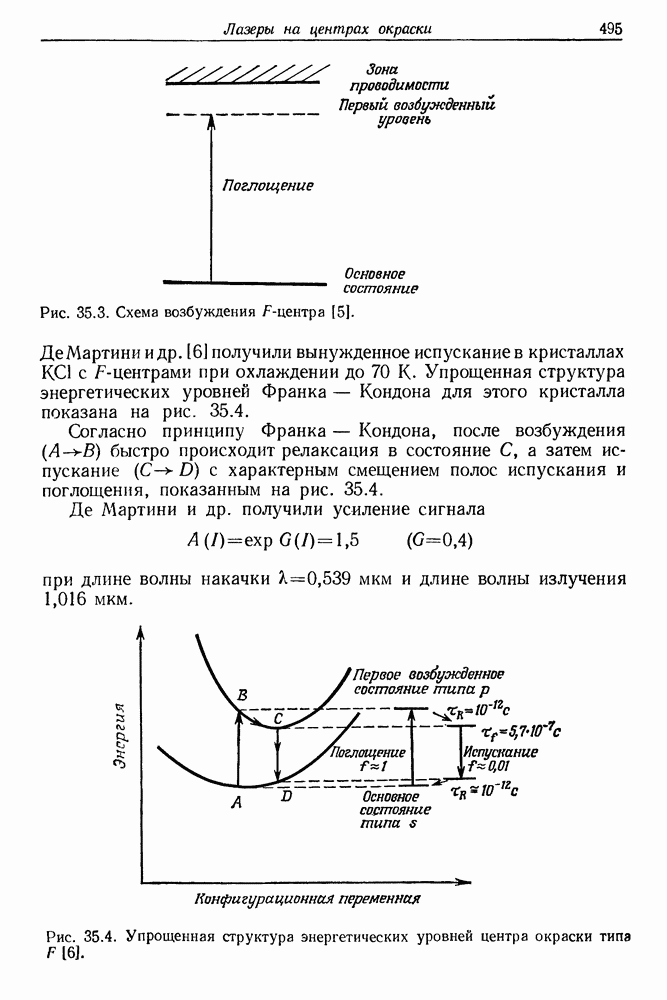
максимальна, а в направлении  минимальна (рис. 23.2). Пусть вектор Е образует в некоторый момент времени угол
минимальна (рис. 23.2). Пусть вектор Е образует в некоторый момент времени угол  с направлением оси
с направлением оси  . Направления вектора Р показаны на рис. 23.2 для обоих направлений вращения вектора электрического поля световой волны. Механический момент, действующий на молекулу, равен
. Направления вектора Р показаны на рис. 23.2 для обоих направлений вращения вектора электрического поля световой волны. Механический момент, действующий на молекулу, равен

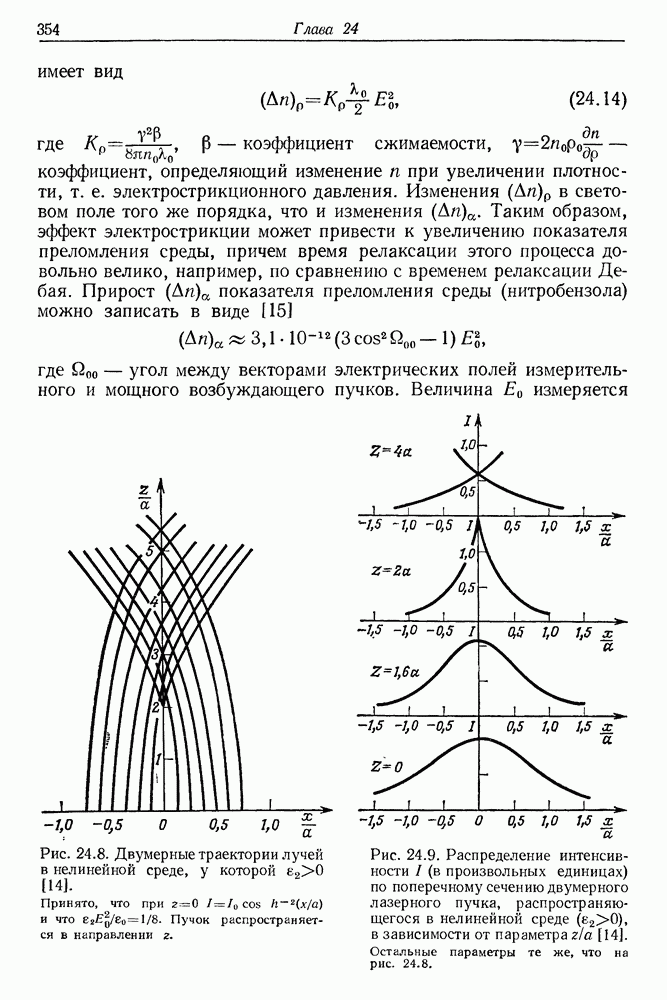
Он действует в одном и том же направлении независимо от направления вращения вектора электрического поля и стремится повернуть молекулу так, чтобы ее ось максимальной поляризуемости совпала с направлением вектора Е. Такому состоянию соответствует минимум энергии взаимодействия молекулы с полем. Полному упорядочению ориентации молекул в поле препятствует их хаотическое тепловое движение, а также взаимодействие между наведенными диполями. Возможное наличие у молекулы постоянного дипольного момента не влияет на величину ориентирующего момента М, поскольку время релаксации для дипольной ориентации обычно составляет от  до
до  , т. е. на несколько порядков величины превышает период колебаний электрического поля световой волны
, т. е. на несколько порядков величины превышает период колебаний электрического поля световой волны  .
.
Обозначим компоненты электрического поля вдоль осей  молекулы через
молекулы через  Аналогичные обозначения применяются для компонент наведенной поляризации вдоль тех же осей:
Аналогичные обозначения применяются для компонент наведенной поляризации вдоль тех же осей:  Элементарная поляризация в направлении оси
Элементарная поляризация в направлении оси  наведенная полем, рассчитывается следующим образом [6]:
наведенная полем, рассчитывается следующим образом [6]:


Рис. 23.2. Пояснение направления действия момента силы, возникающего в переменном поле (например, оптическом) с напряженностью Е. Этот момент вызывает поворот молекулы;  система координат, связанная с молекулой.
система координат, связанная с молекулой.
Далее имеем

Предположим, что длительность лазерного импульса существенно превышает характеристические времена как дебаевской релаксации  и релаксации анизотропии
и релаксации анизотропии  Постоянное во времени значение
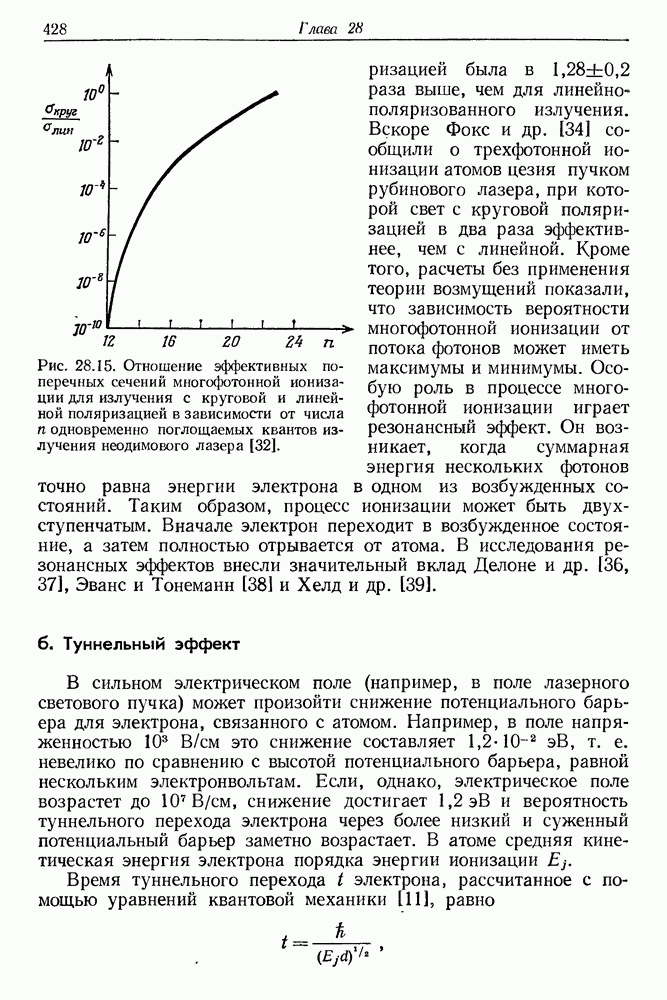
Постоянное во времени значение  находим путем усреднения функции
находим путем усреднения функции  в условиях термодинамического равновесия:
в условиях термодинамического равновесия:

Если  избранное направление отсутствует
избранное направление отсутствует  . В общем случае, когда
. В общем случае, когда  можно принять
можно принять

где S — параметр ориентации. На тензорном языке S представляет собой первый диагональный элемент матрицы анизотропии. С учетом (23.6) выражение (23.5) принимает вид

Согласно Френкелю [71, параметр S удовлетворяет соотношению

где

В общем случае расчет значения средней наведенной поляризации в направлении оси  является нелегкой задачей, поскольку ориентирующее поле не остается постоянным, а меняется с частотой
является нелегкой задачей, поскольку ориентирующее поле не остается постоянным, а меняется с частотой  Гц. Для конденсированной среды следует еще учитывать эффективное локальное поле, которое действует на рассматриваемую
Гц. Для конденсированной среды следует еще учитывать эффективное локальное поле, которое действует на рассматриваемую

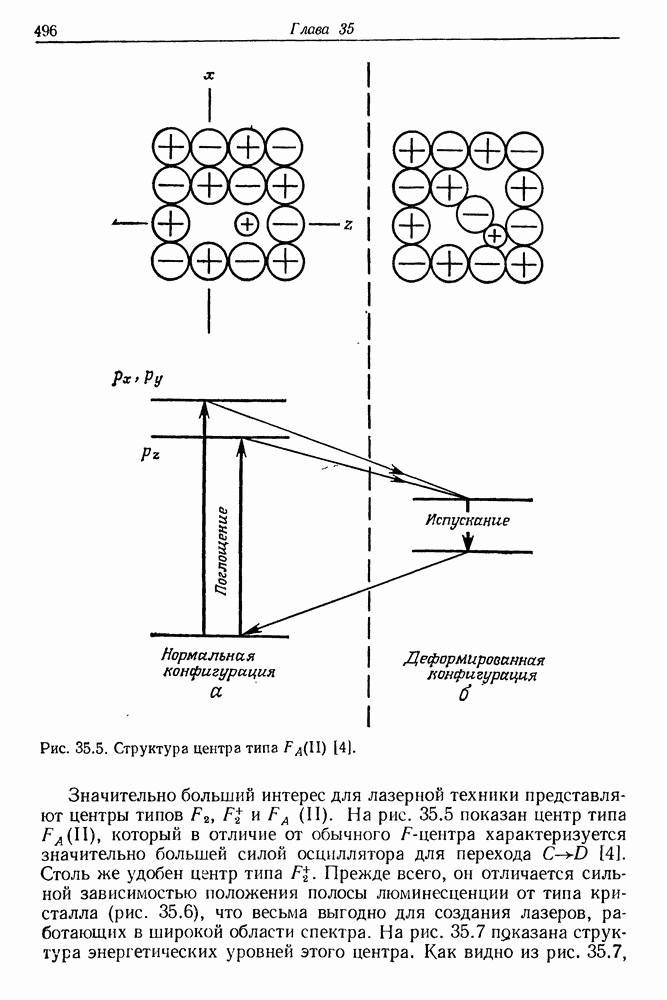
Рис. 23.3. Поляризованный лазерный пучок  создает оптическое двулучепреломление среды в направления х и z.
создает оптическое двулучепреломление среды в направления х и z.
молекулу. Электронная поляризация связана простым соотношением с показателем преломления среды.
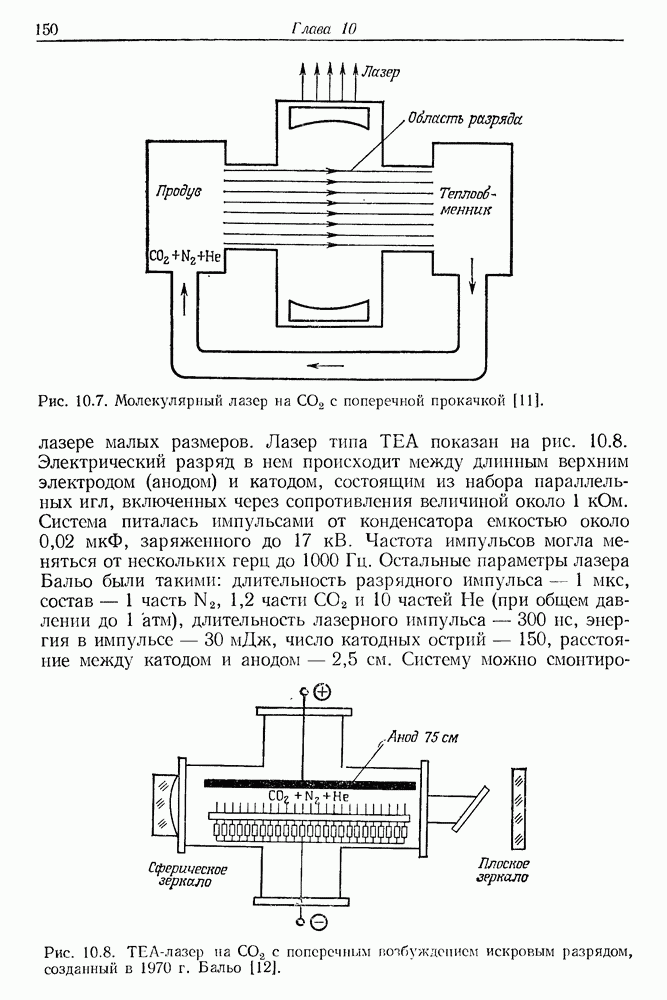
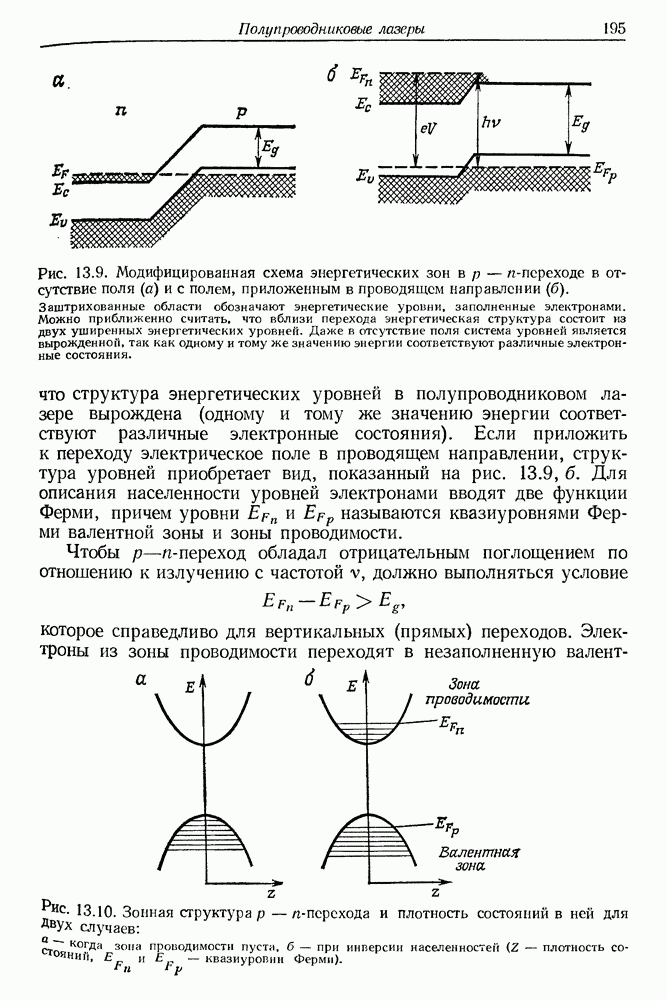
Предположим, что поляризованный лазерный пучок распространяется в прозрачной жидкости (например, в  в направлении оси у (рис. 23.3). Пусть вектор электрического поля
в направлении оси у (рис. 23.3). Пусть вектор электрического поля  будет параллелен оси
будет параллелен оси  Оптическая ориентация молекул с анизотропной поляризуемостью приводит к уменьшению показателя преломления в направлении оси х и его увеличению в направлении оси
Оптическая ориентация молекул с анизотропной поляризуемостью приводит к уменьшению показателя преломления в направлении оси х и его увеличению в направлении оси  Мерой индуцированной лазерным излучением анизотропии будет разность
Мерой индуцированной лазерным излучением анизотропии будет разность  которую легко измерить с помощью маломощного вспомогательного лазерного пучка. Вынужденная анизотропия показателя преломления зависит от квадрата напряженности поля. Обычно ее записывают в виде [5]
которую легко измерить с помощью маломощного вспомогательного лазерного пучка. Вынужденная анизотропия показателя преломления зависит от квадрата напряженности поля. Обычно ее записывают в виде [5]

где  — символ Кронекера
— символ Кронекера  , В — постоянная вынужденной оптической анизотропии,
, В — постоянная вынужденной оптической анизотропии,  — составляющая поля в направлении
— составляющая поля в направлении  — показатель преломления среды в отсутствие поля. Для примера, показанного на рис. 23.3, имеем
— показатель преломления среды в отсутствие поля. Для примера, показанного на рис. 23.3, имеем

Следовательно,

Далее имеем

и

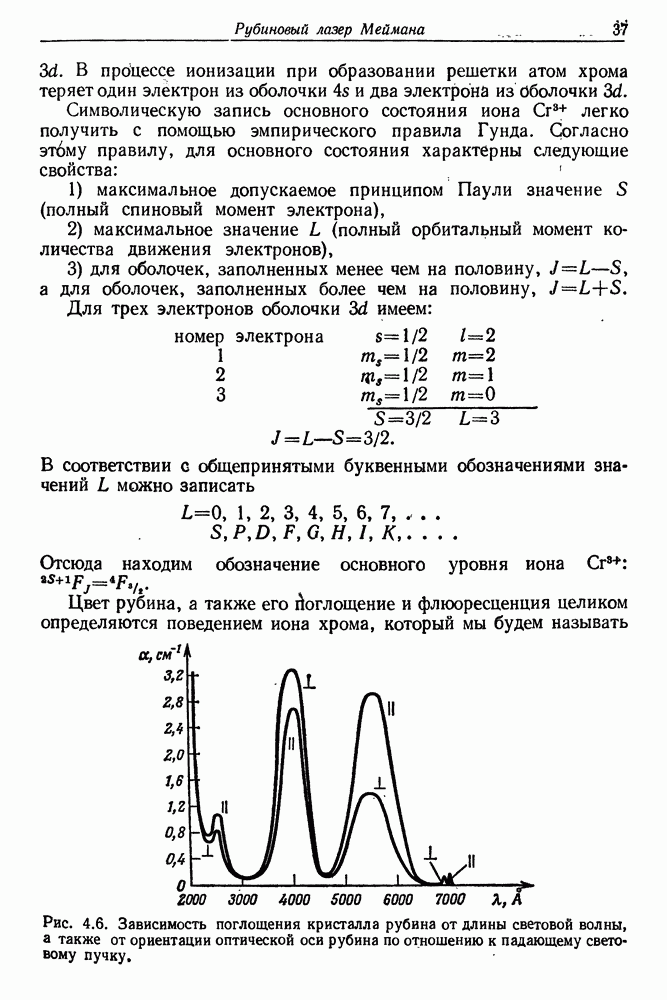
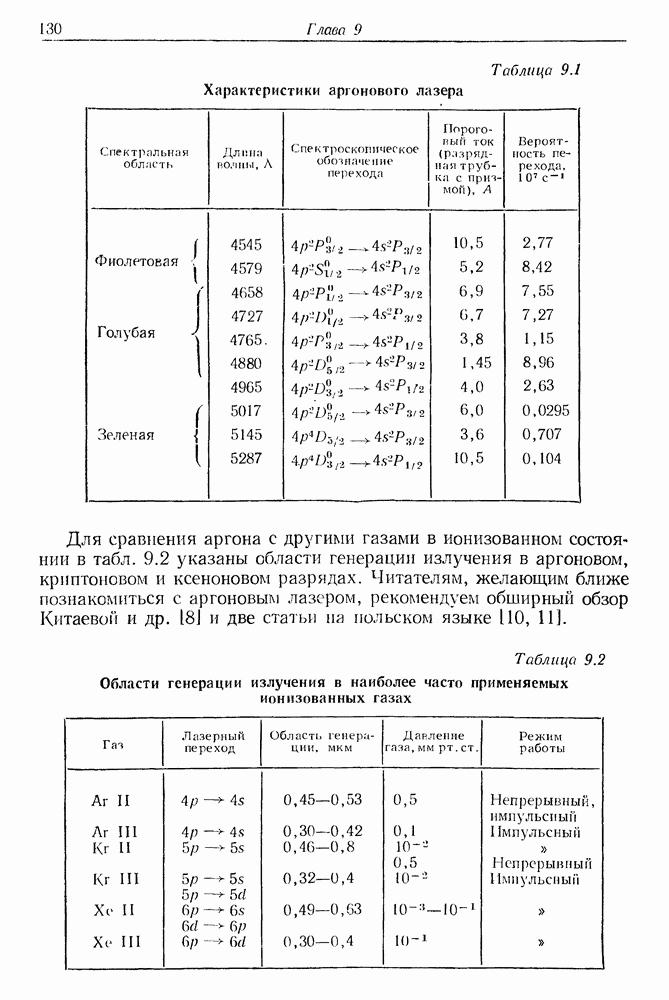
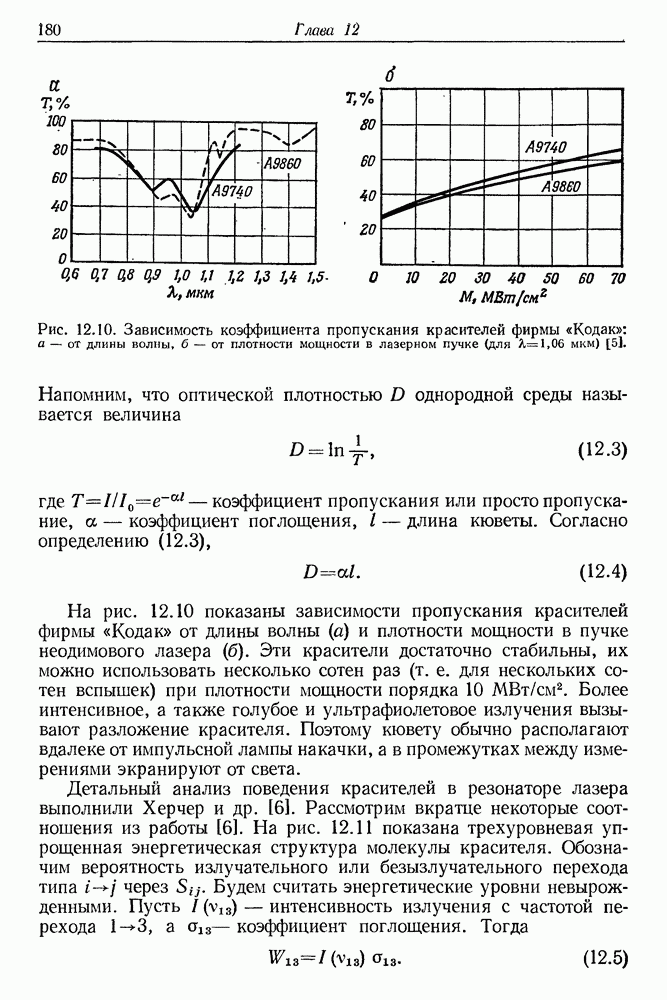
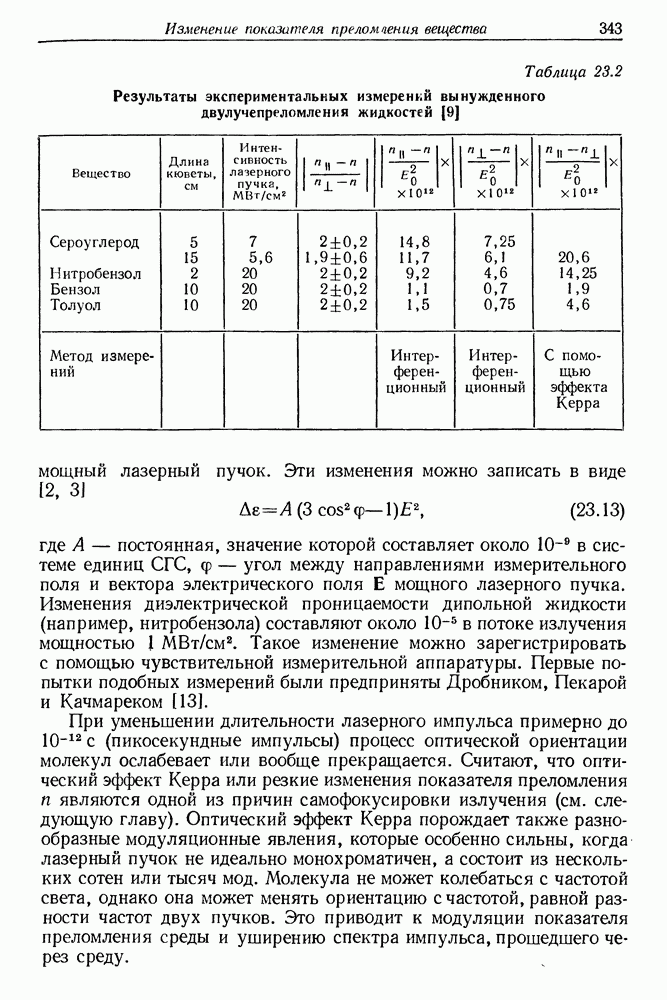
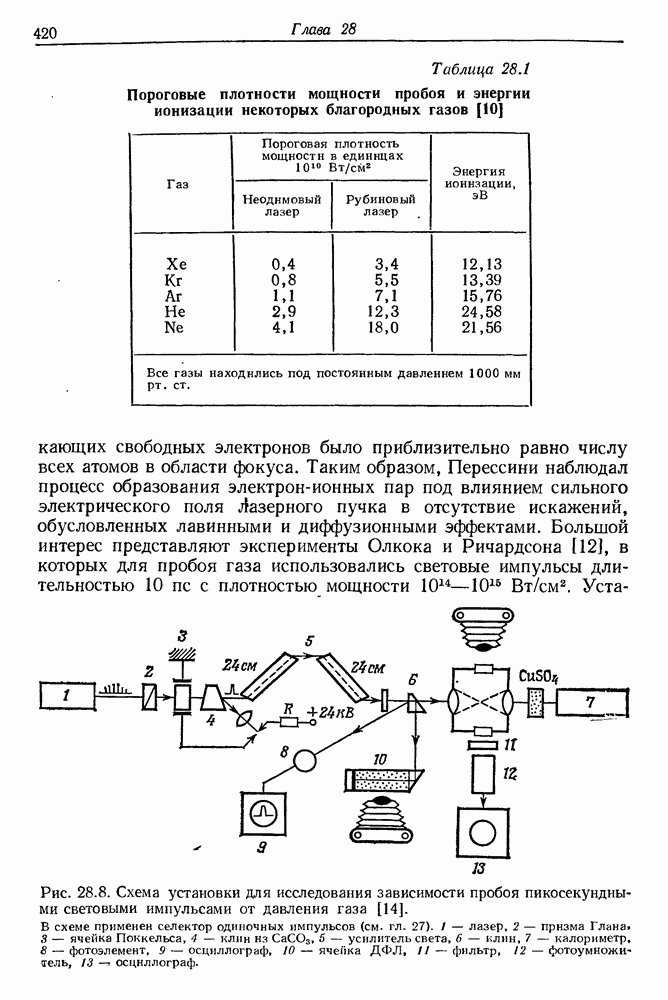
В табл. 23.1 приведены значения постоянной В для ряда известных жидкостей [4]. Особенно большой анизотропией оптической поляризуемости обладают молекулы сероуглерода.
Таблица 23.1 Значения постоянной вынужденной оптической анизотропии для ряда жидкостей [4]


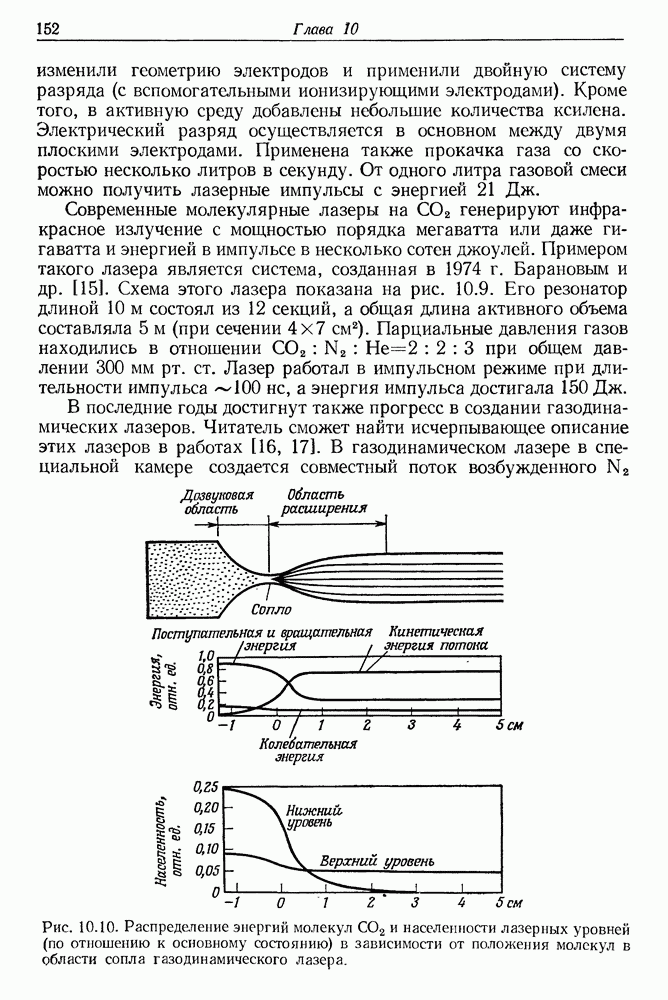
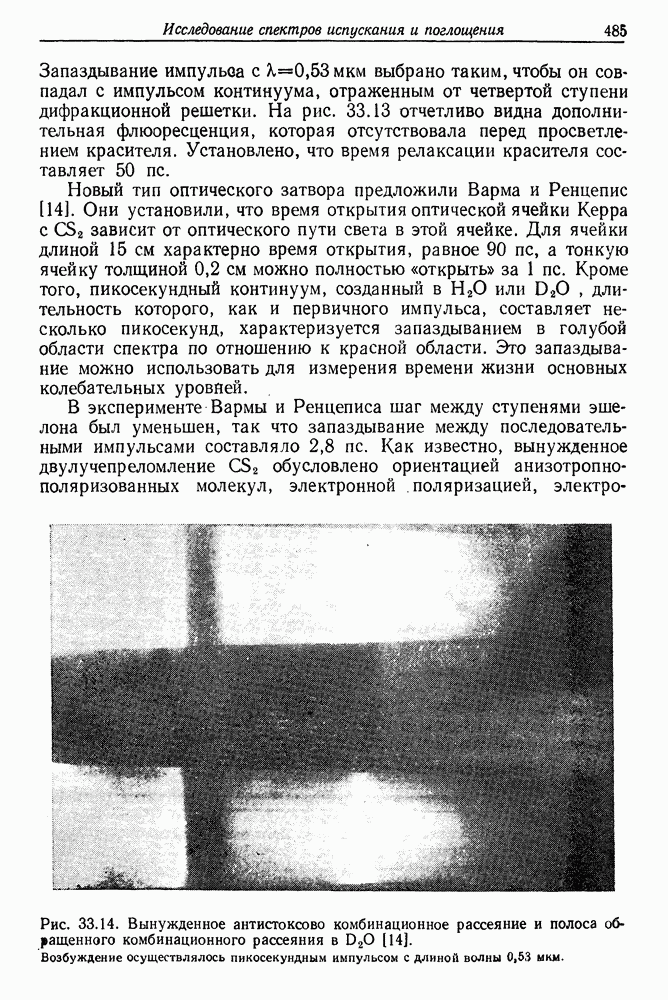
Рис. 23.4. Схема установки для исследования оптического эффекта Керра. Оба лазерных пучка — вынуждающий (от неодимового лазера) в измерительный (от Не Ne-лазера) — распространяются в кювете с жидкостью параллельно друг другу. Векторы электрического поля пучков составляют друг с другом угол 45°. В эксперименте измеряются значения составляющих  и в зависимости от интенсивности излучения импульсного лазера [12]. 1 — неодимовый лазер в режиме гигантских импульсов,
и в зависимости от интенсивности излучения импульсного лазера [12]. 1 — неодимовый лазер в режиме гигантских импульсов,  нм, 2 — импульс синхронизации, 3 — самописец
нм, 2 — импульс синхронизации, 3 — самописец  фильтры на длину волны 5 — фотодиод, 6 — фильтр на длину волны
фильтры на длину волны 5 — фотодиод, 6 — фильтр на длину волны  линза с фокусным расстоянием
линза с фокусным расстоянием  см, 8 — поляризаторы, 9 - кювета с жидкостью, 10-анализатор, 11 — фильтры на длину волны
см, 8 — поляризаторы, 9 - кювета с жидкостью, 10-анализатор, 11 — фильтры на длину волны  монохроматор, 13 — Не — Ne-лазер с
монохроматор, 13 — Не — Ne-лазер с  нм.
нм.
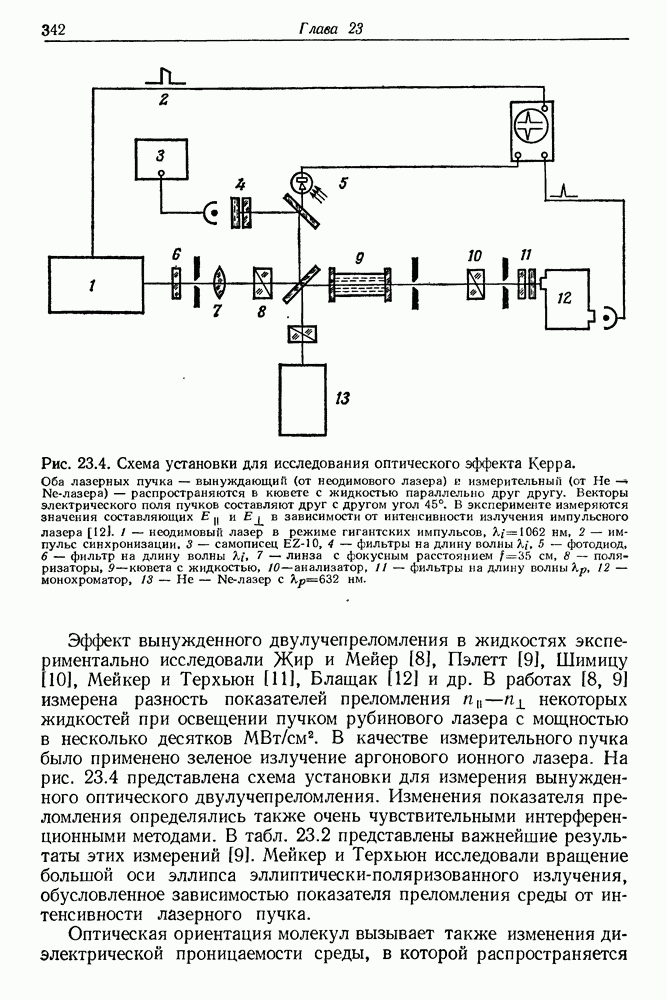
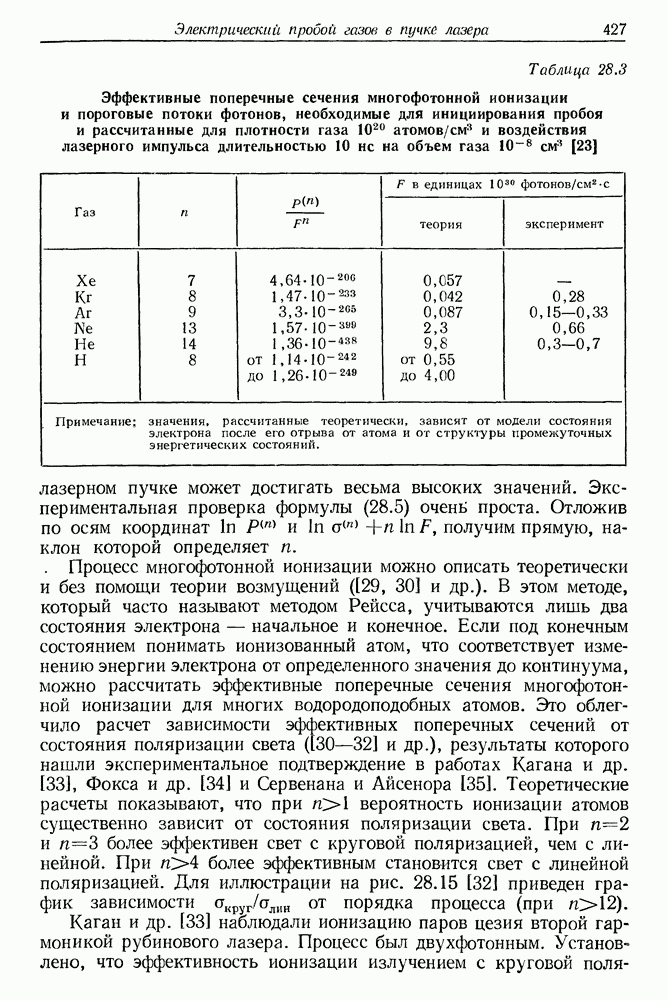
Эффект вынужденного двулучепреломления в жидкостях экспериментально исследовали Жир и Мейер [8], Пэлетт [9], Шимицу [10], Мейкер и Терхьюн [11], Блащак [12] и др. В работах [8, 9] измерена разность показателей преломления  некоторых жидкостей при освещении пучком рубинового лазера с мощностью в несколько десятков
некоторых жидкостей при освещении пучком рубинового лазера с мощностью в несколько десятков  В качестве измерительного пучка было применено зеленое излучение аргонового ионного лазера. На рис. 23.4 представлена схема установки для измерения вынужденного оптического двулучепреломления. Изменения показателя преломления определялись также очень чувствительными интерференционными методами. В табл. 23.2 представлены важнейшие результаты этих измерений [9]. Мейкер и Терхьюн исследовали вращение большой оси эллипса эллиптически-поляризованного излучения, обусловленное зависимостью показателя преломления среды от интенсивности лазерного пучка.
В качестве измерительного пучка было применено зеленое излучение аргонового ионного лазера. На рис. 23.4 представлена схема установки для измерения вынужденного оптического двулучепреломления. Изменения показателя преломления определялись также очень чувствительными интерференционными методами. В табл. 23.2 представлены важнейшие результаты этих измерений [9]. Мейкер и Терхьюн исследовали вращение большой оси эллипса эллиптически-поляризованного излучения, обусловленное зависимостью показателя преломления среды от интенсивности лазерного пучка.
Оптическая ориентация молекул вызывает также изменения диэлектрической проницаемости среды, в которой распространяется
Таблица 23.2 (см. скан) Результаты экспериментальных измерений вынужденного двулучепреломления жидкостей [9]
мощный лазерный пучок. Эти изменения можно записать в виде [2, 3]

где А — постоянная, значение которой составляет около  в системе единиц СГС,
в системе единиц СГС,  — угол между направлениями измерительного поля и вектора электрического поля Е мощного лазерного пучка. Изменения диэлектрической проницаемости дипольной жидкости (например, нитробензола) составляют около
— угол между направлениями измерительного поля и вектора электрического поля Е мощного лазерного пучка. Изменения диэлектрической проницаемости дипольной жидкости (например, нитробензола) составляют около  в потоке излучения мощностью
в потоке излучения мощностью  Такое изменение можно зарегистрировать с помощью чувствительной измерительной аппаратуры. Первые попытки подобных измерений были предприняты Дробником, Пекарой и Качмареком [13].
Такое изменение можно зарегистрировать с помощью чувствительной измерительной аппаратуры. Первые попытки подобных измерений были предприняты Дробником, Пекарой и Качмареком [13].
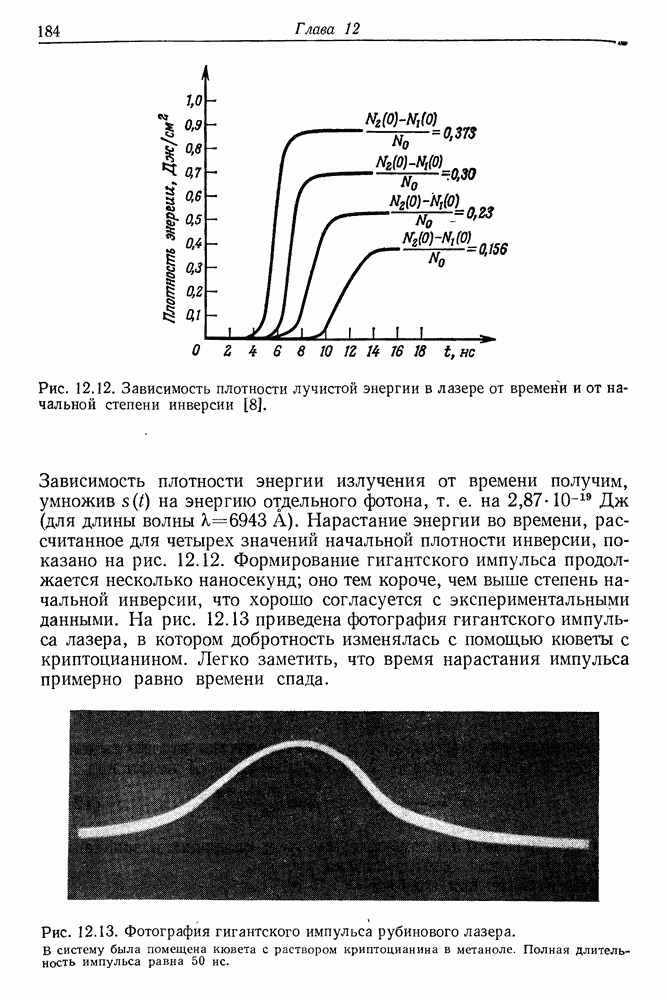
При уменьшении длительности лазерного импульса примерно до 10-12 с (пикосекундные импульсы) процесс оптической ориентации молекул ослабевает или вообще прекращается. Считают, что оптический эффект Керра или резкие изменения показателя преломления  являются одной из причин самофокусировки излучения (см. следующую главу). Оптический эффект Керра порождает также разнообразные модуляционные явления, которые особенно сильны, когда лазерный пучок не идеально монохроматичен, а состоит из нескольких сотен или тысяч мод. Молекула не может колебаться с частотой света, однако она может менять ориентацию с частотой, равной разности частот двух пучков. Это приводит к модуляции показателя преломления среды и уширению спектра импульса, прошедшего через среду.
являются одной из причин самофокусировки излучения (см. следующую главу). Оптический эффект Керра порождает также разнообразные модуляционные явления, которые особенно сильны, когда лазерный пучок не идеально монохроматичен, а состоит из нескольких сотен или тысяч мод. Молекула не может колебаться с частотой света, однако она может менять ориентацию с частотой, равной разности частот двух пучков. Это приводит к модуляции показателя преломления среды и уширению спектра импульса, прошедшего через среду.
Таблица 23.3 (см. скан) Сопоставление роли оптической ориентации молекул, электрострикции и электрокалорического эффекта в изменениях показателя преломления вещества [16]
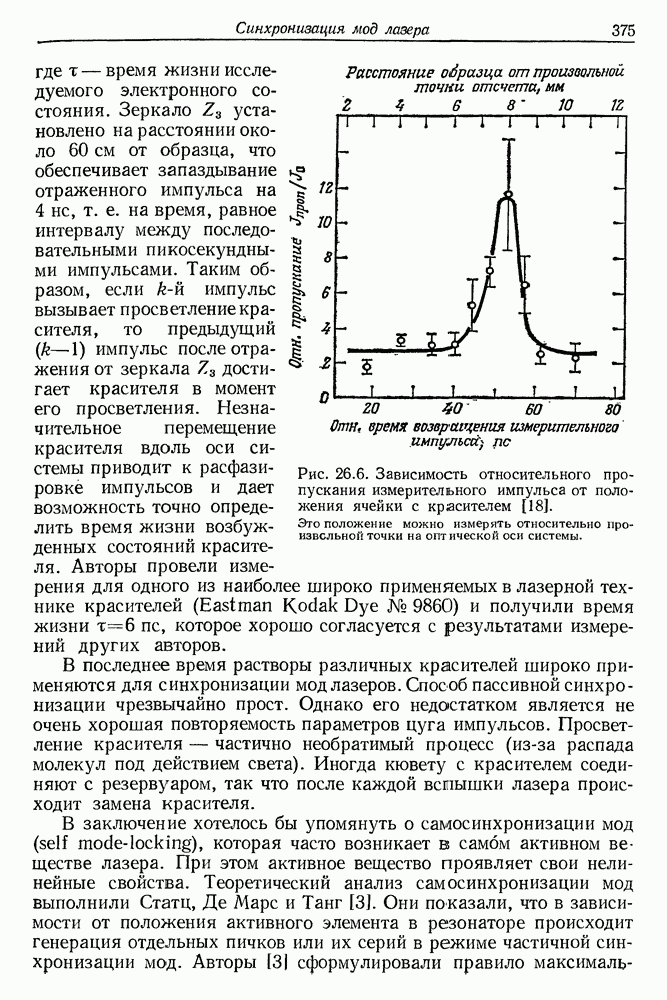
Вынужденное двулучепреломление в жидкости нашло интересное применение в оптической ячейке Керра 114]. В настоящее время такая ячейка является основным элементом аппаратуры для пикосекундной спектроскопии (см. гл. 33). Лоссад и Ярив [6] и Дальстрем [15] применили оптический эффект Керра также для синхронизации мод лазера.
Показатель преломления вещества в присутствии мощного лазерного излучения выражается формулой

или

где  — показатель преломления, измеренный при малой интенсивности излучения, а коэффициент
— показатель преломления, измеренный при малой интенсивности излучения, а коэффициент  описывает нелинейные свойства вещества. Значение
описывает нелинейные свойства вещества. Значение  определяется процессом оптической ориентации молекул, перераспределением молекул, электрострикцией, электрокалорическим и другими эффектами. В некоторых случаях сильная нелинейность среды связана с образованием плазмы вдоль пути светового пучка в рассматриваемой среде (см. гл. 29). Явление электрострикции уже обсуждалось в гл. 20, поскольку оно играет существенную роль в рассеянии Мандельштама — Бриллюэна. Влияние электрокалорического эффекта, который является следствием термодинамических свойств среды, рассчитано Келихом [16]. Процесс перераспределения молекул в жидкости, рассмотренный теоретически Келихом [5] и Хелуортом [17], возникает в результате взаимодействия диполей, наведенных сильным электрическим полем световой волны. Он представляет собой перегруппировку молекул при их поступательном движении в пределах взаимодействия
определяется процессом оптической ориентации молекул, перераспределением молекул, электрострикцией, электрокалорическим и другими эффектами. В некоторых случаях сильная нелинейность среды связана с образованием плазмы вдоль пути светового пучка в рассматриваемой среде (см. гл. 29). Явление электрострикции уже обсуждалось в гл. 20, поскольку оно играет существенную роль в рассеянии Мандельштама — Бриллюэна. Влияние электрокалорического эффекта, который является следствием термодинамических свойств среды, рассчитано Келихом [16]. Процесс перераспределения молекул в жидкости, рассмотренный теоретически Келихом [5] и Хелуортом [17], возникает в результате взаимодействия диполей, наведенных сильным электрическим полем световой волны. Он представляет собой перегруппировку молекул при их поступательном движении в пределах взаимодействия
ближнего порядка. В конденсированной среде это приводит к измеримым изменениям показателя преломления. Роль этих и других молекулярно-статистических процессов была выяснена в недавних измерениях оптического эффекта Керра [18, 19]. В заключение приводим табл. 23.3, в которой сопоставлены роли вышеупомянутых процессов в изменениях показателя преломления ряда веществ [16].
Литература
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
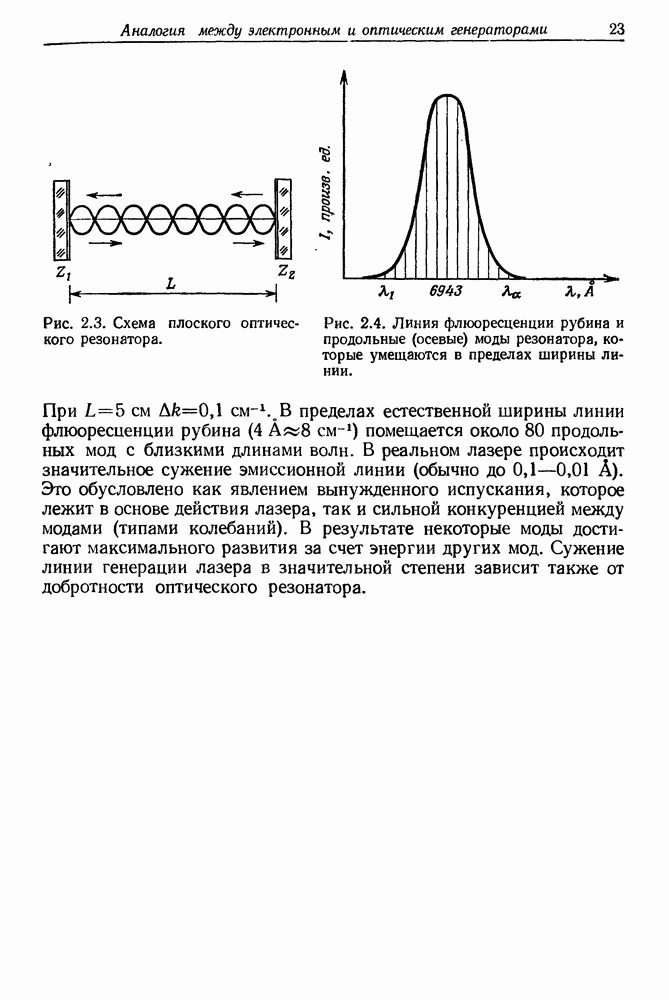
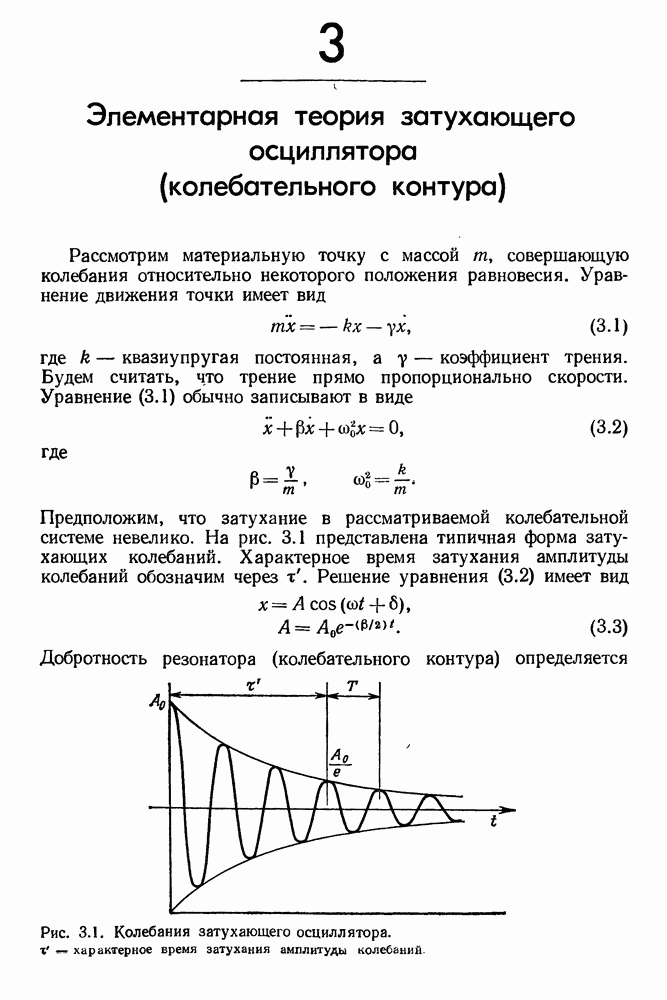
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
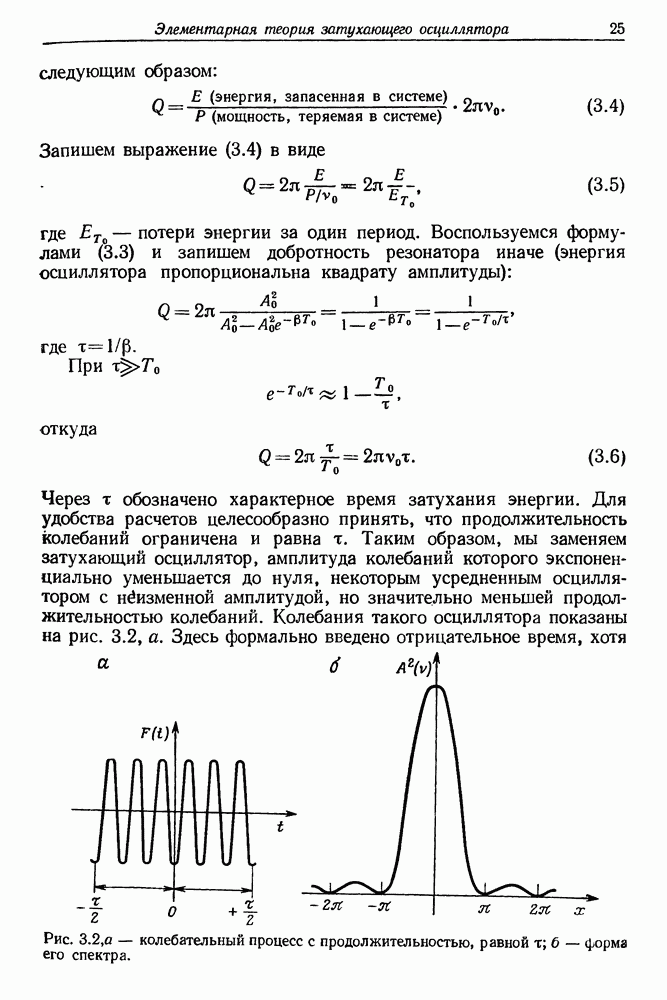
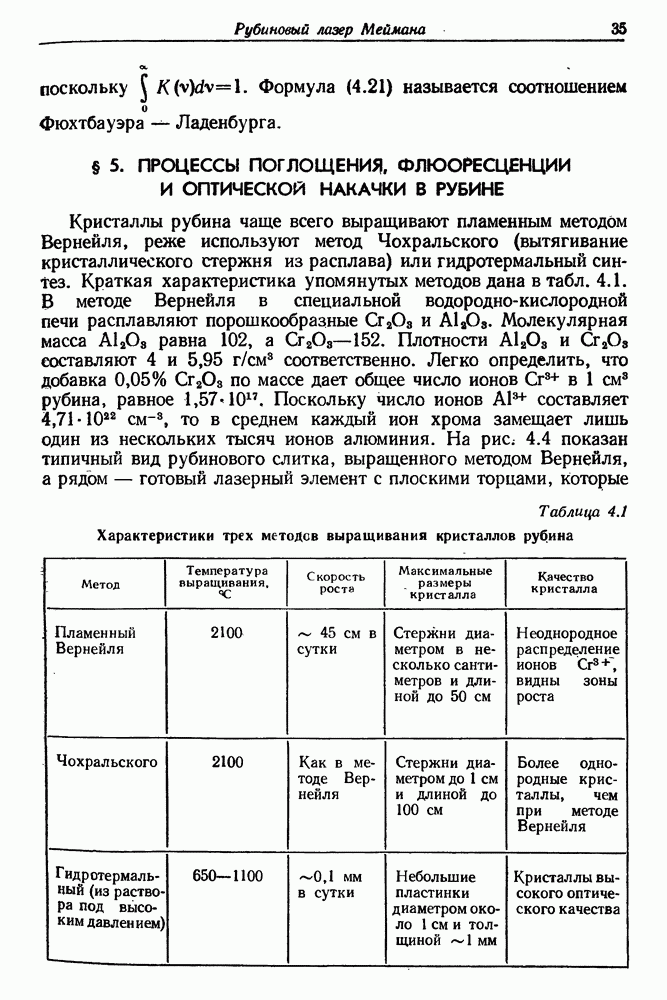
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
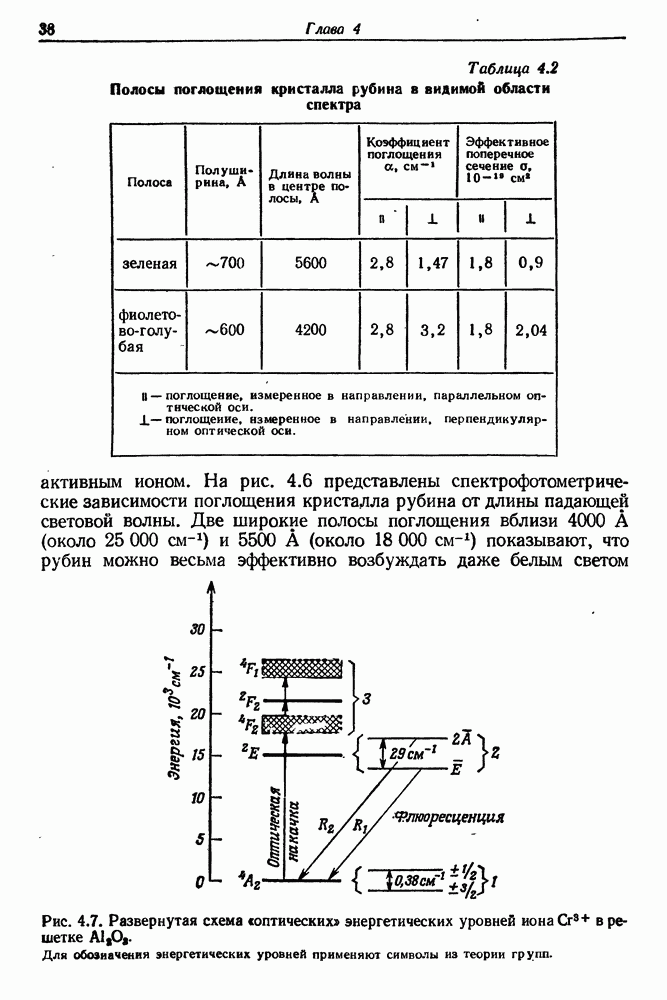
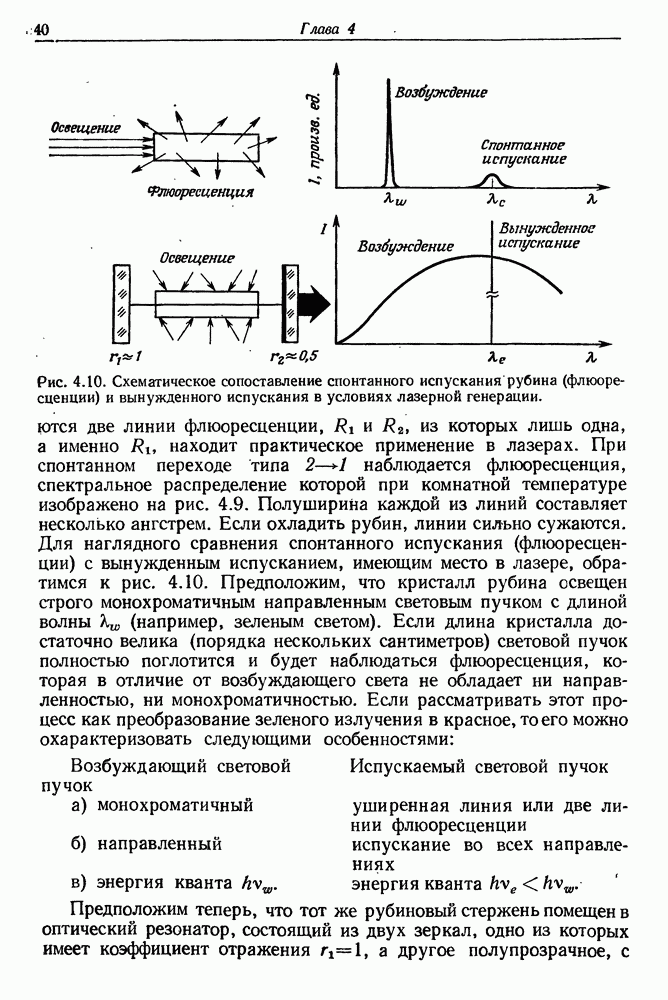
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
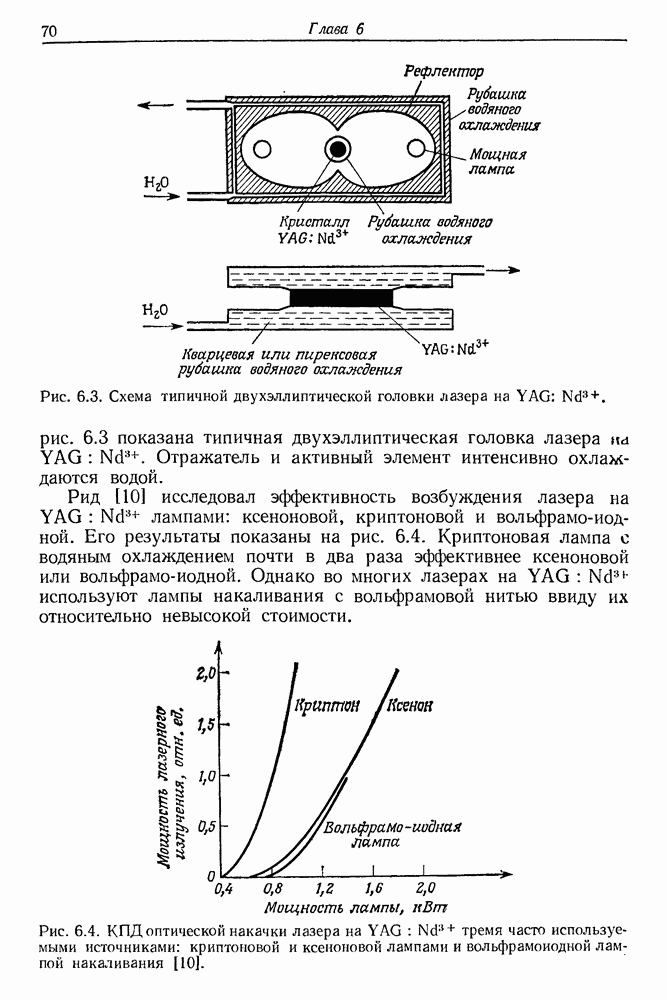
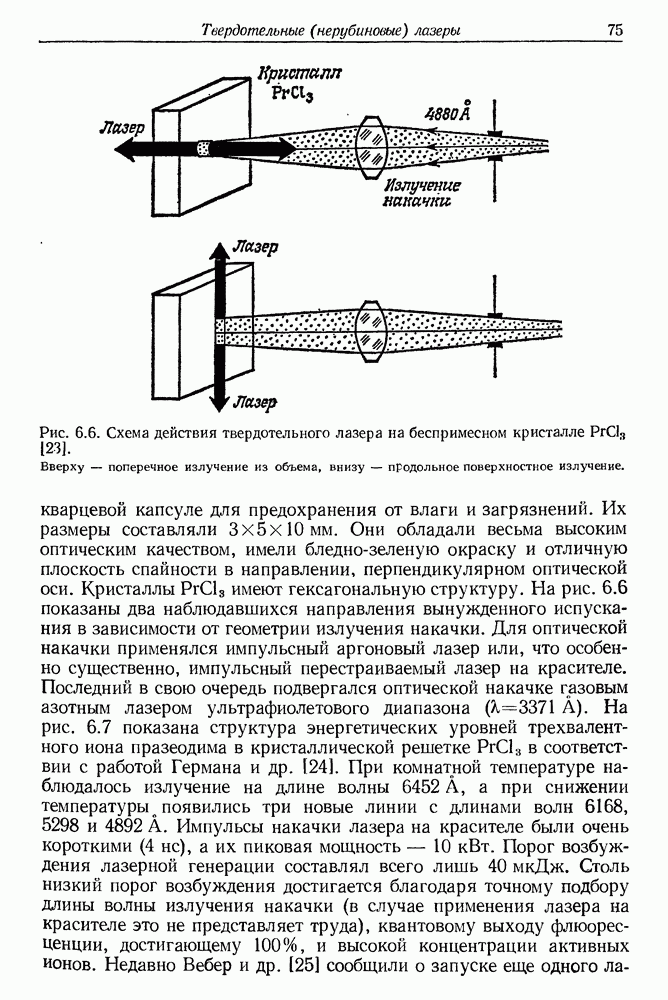
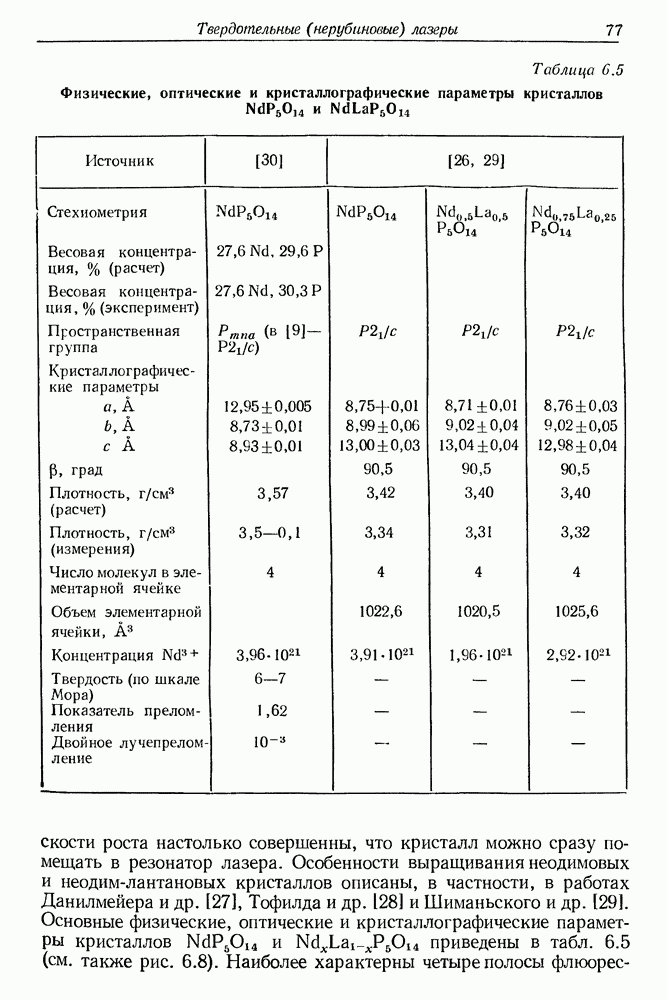
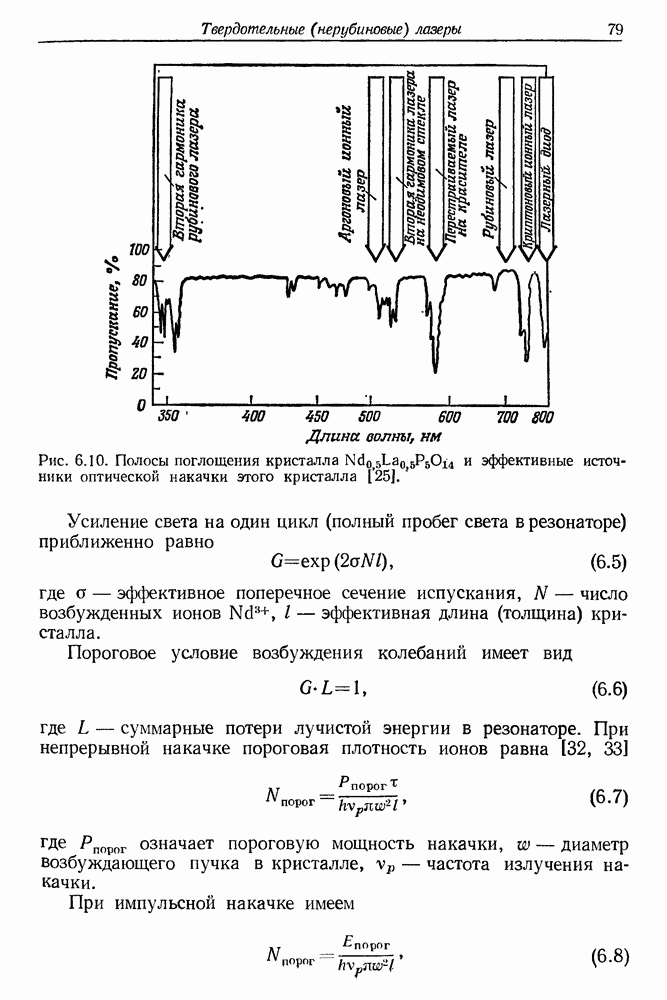
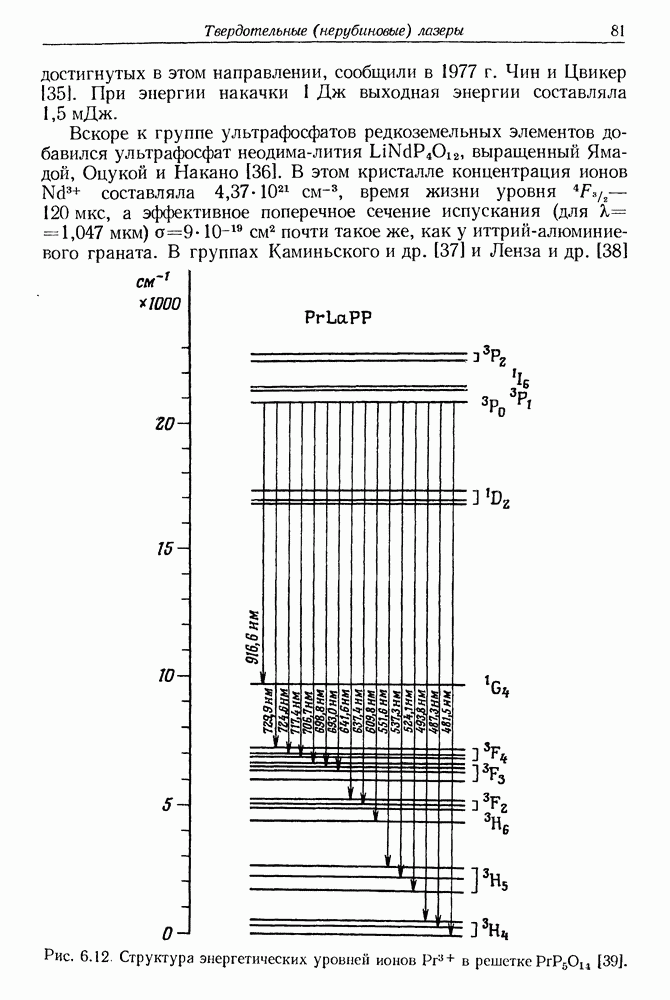
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
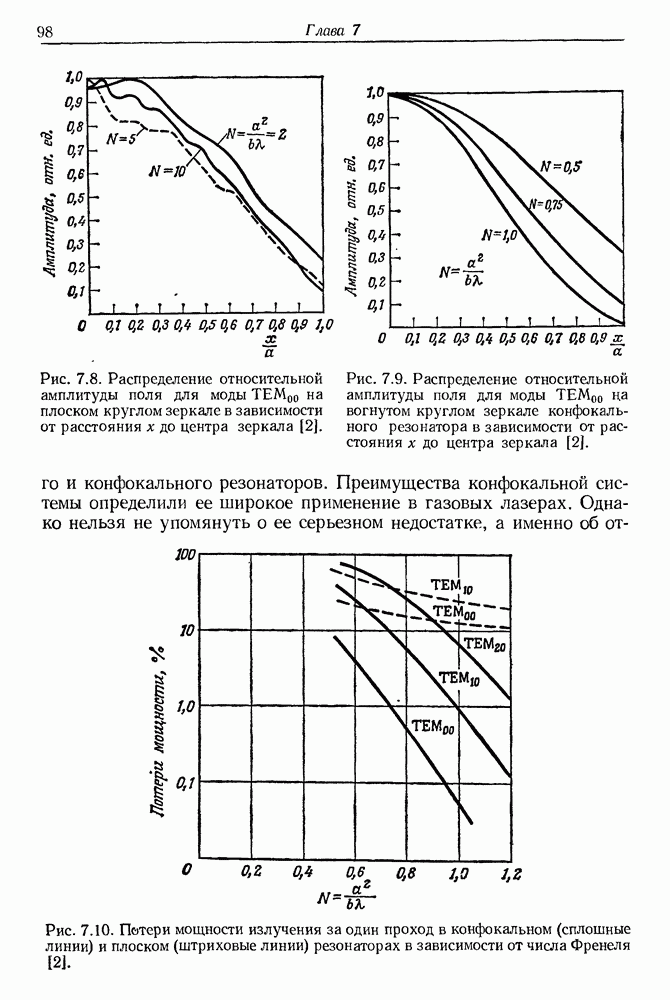
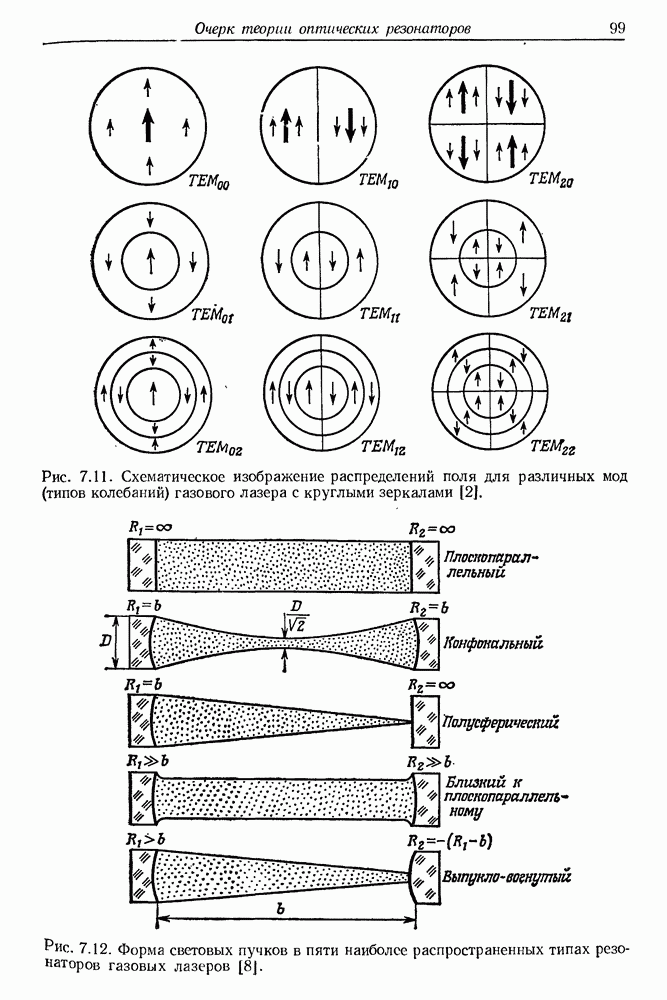
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
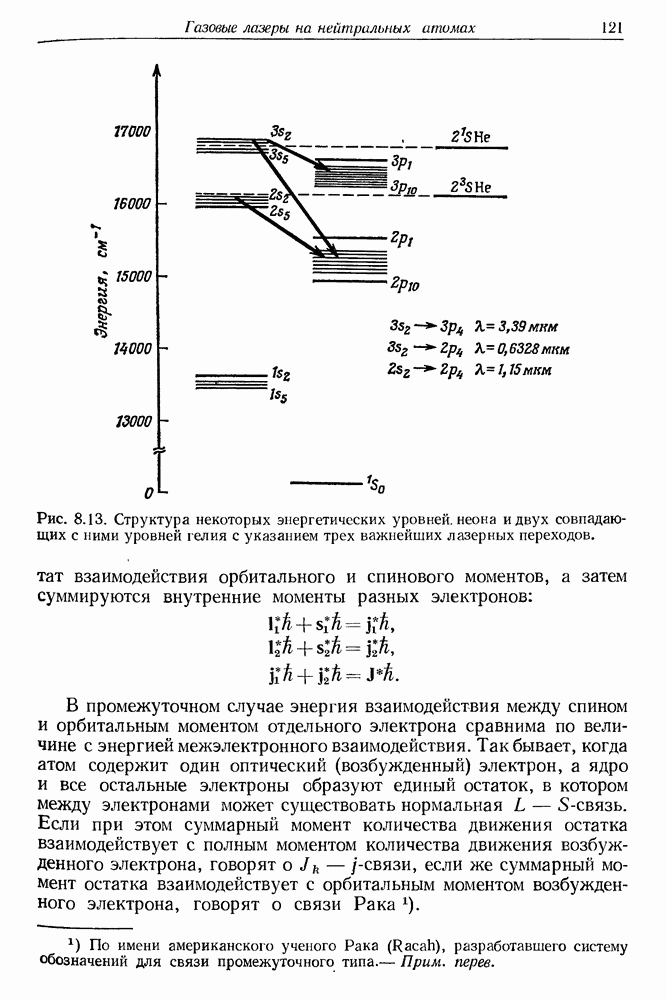
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
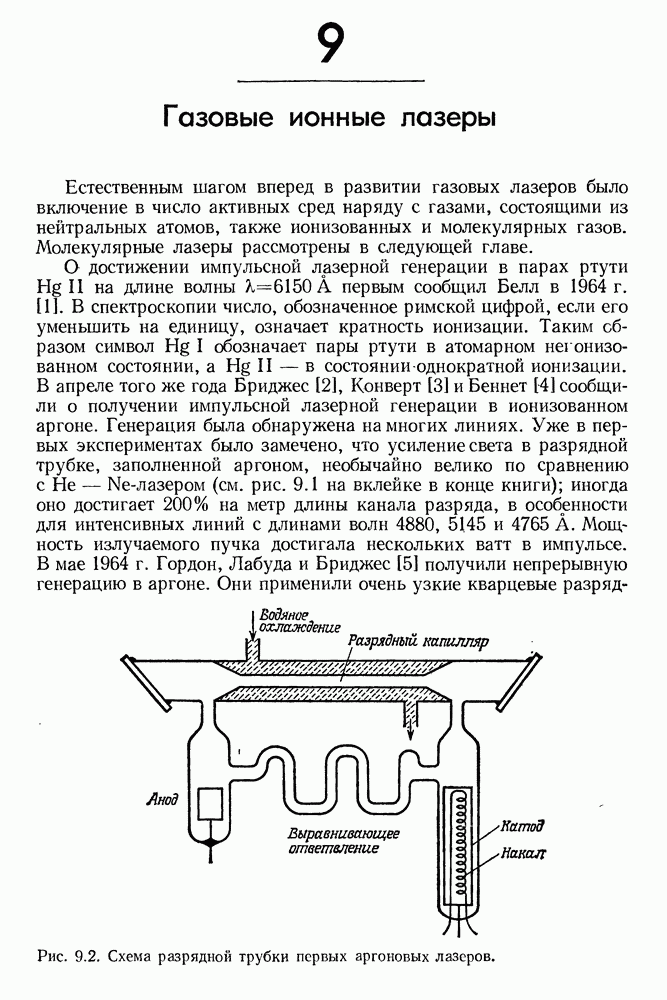
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
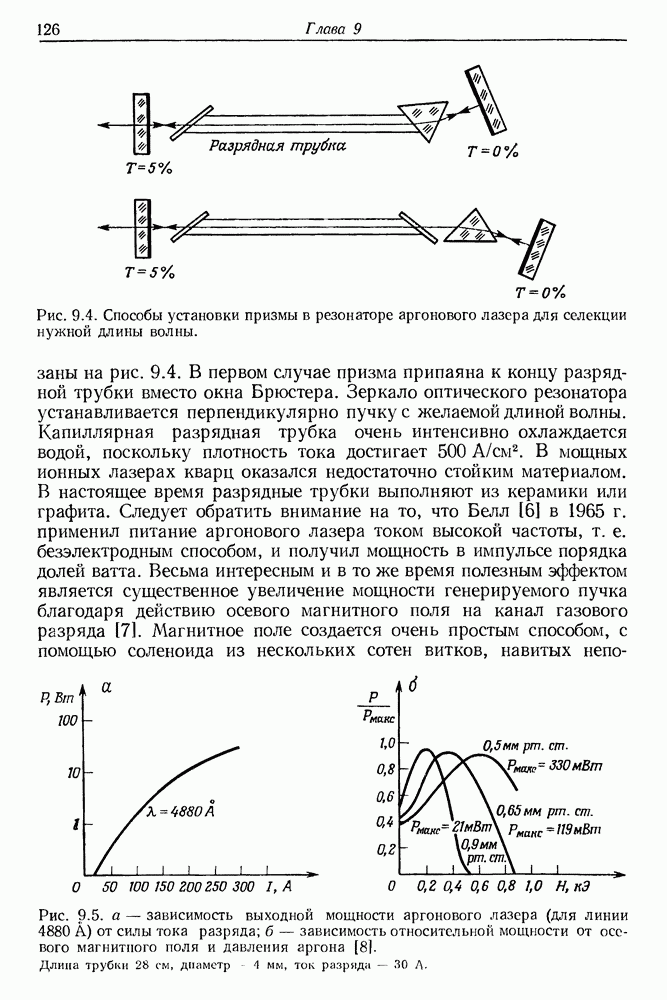
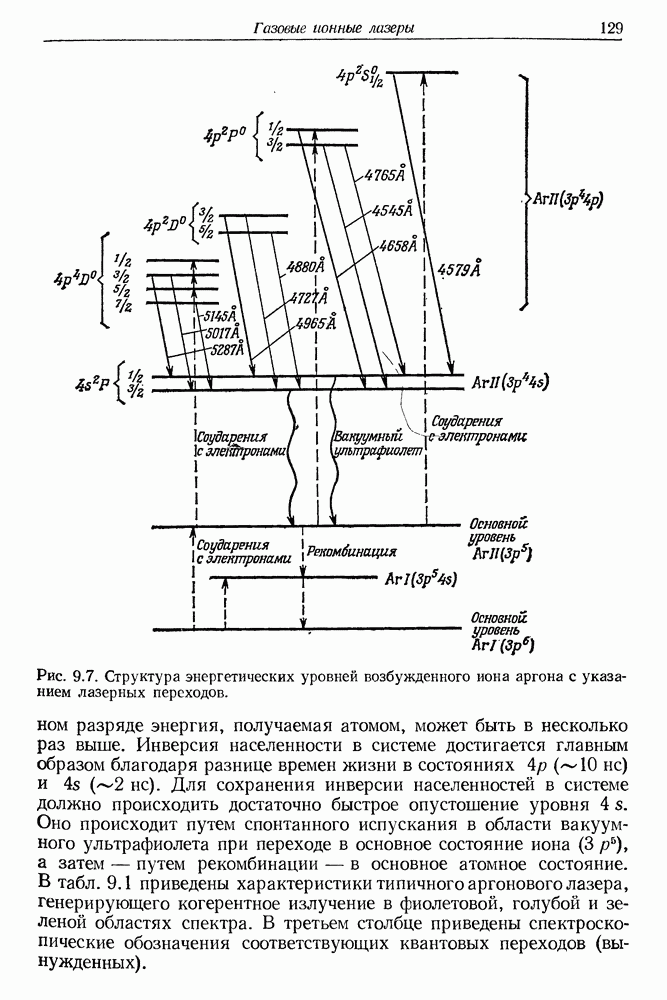
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
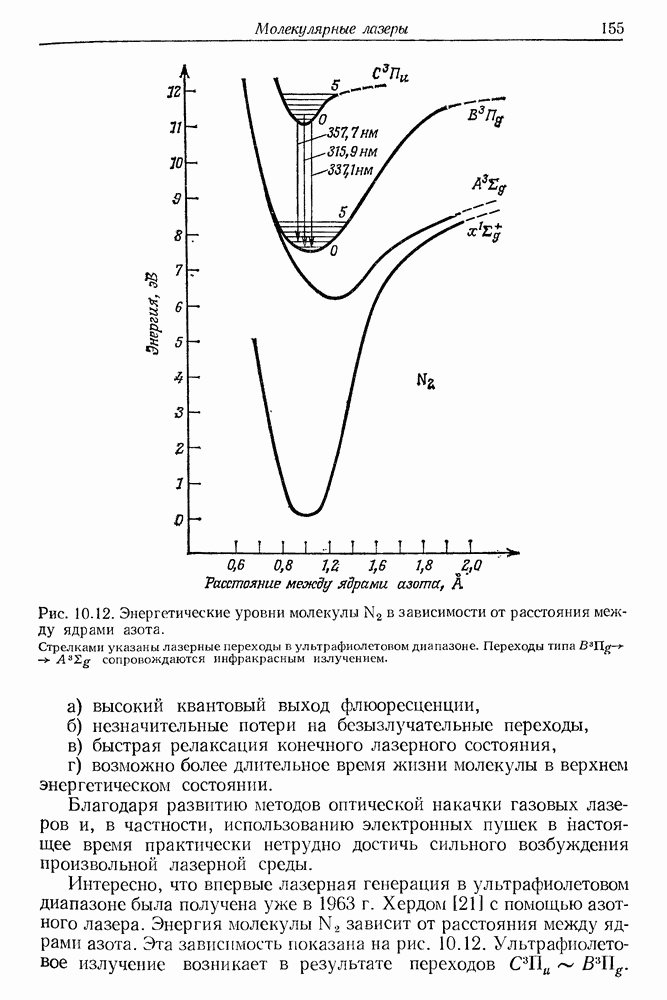
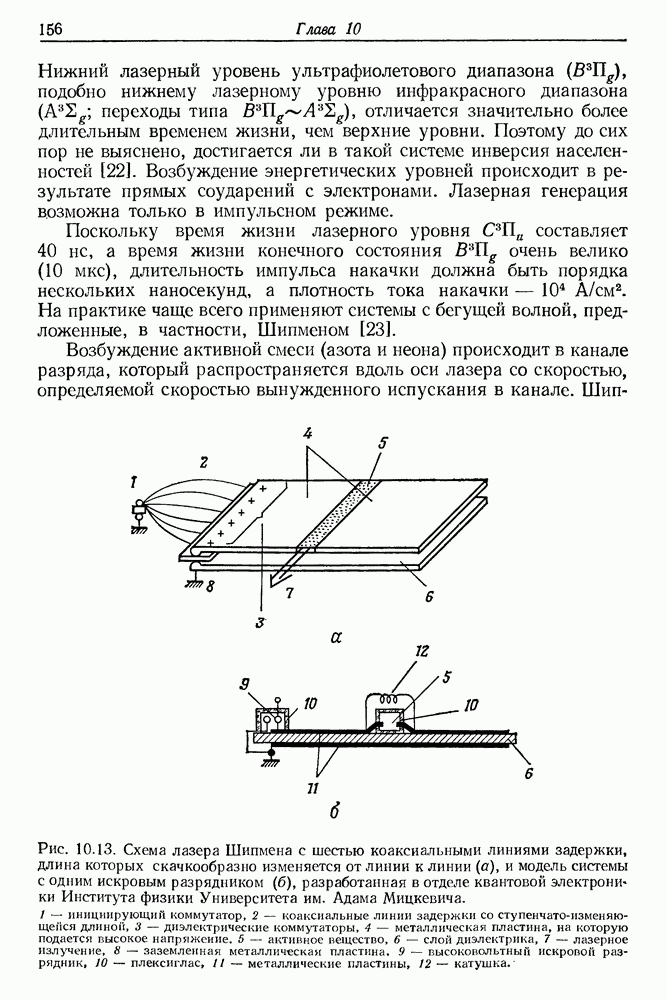
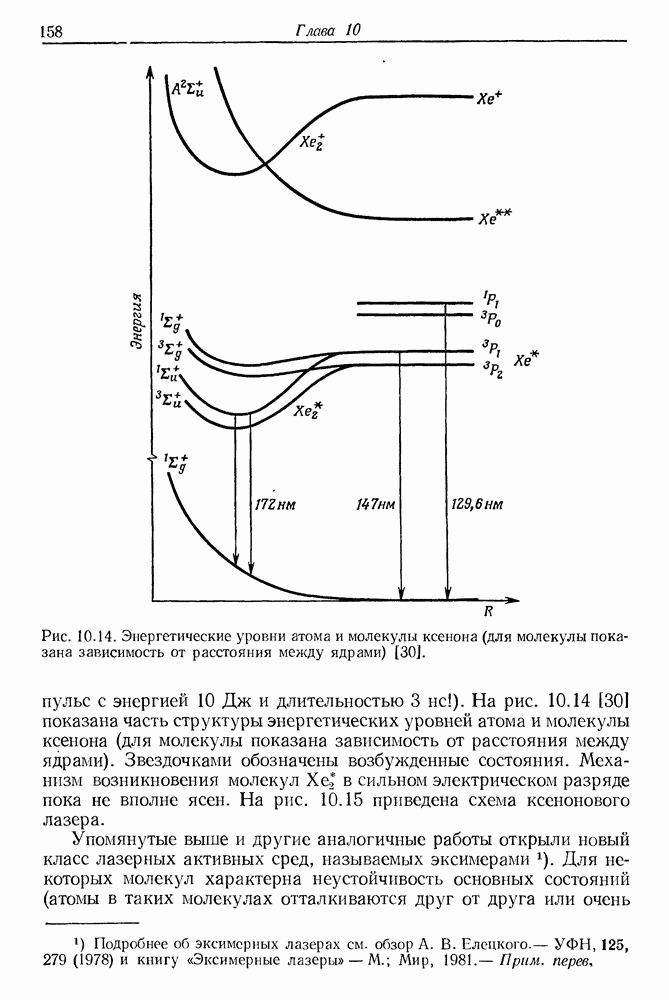
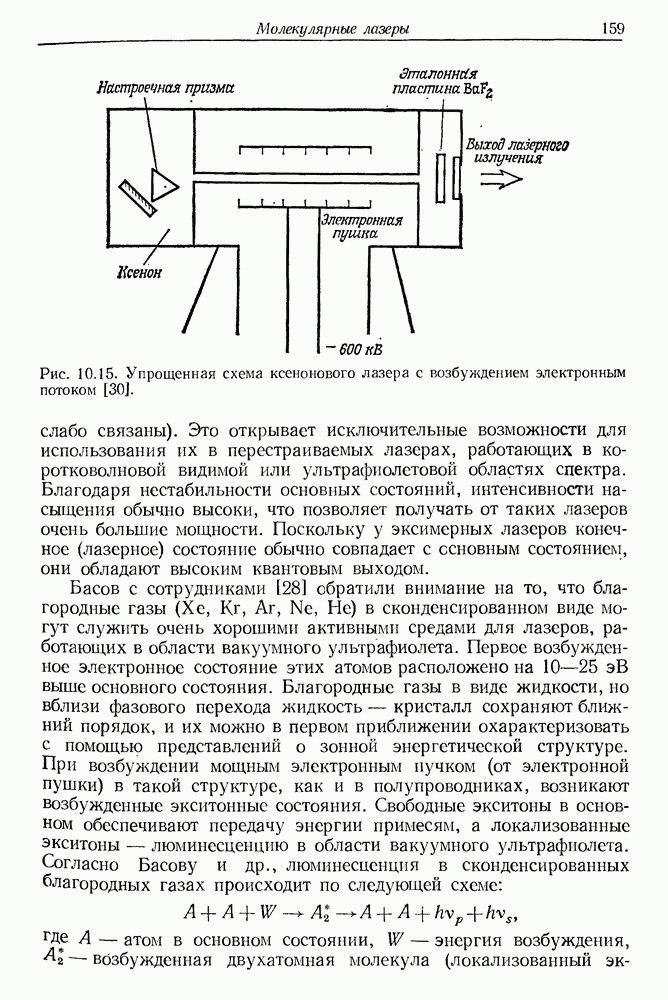
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
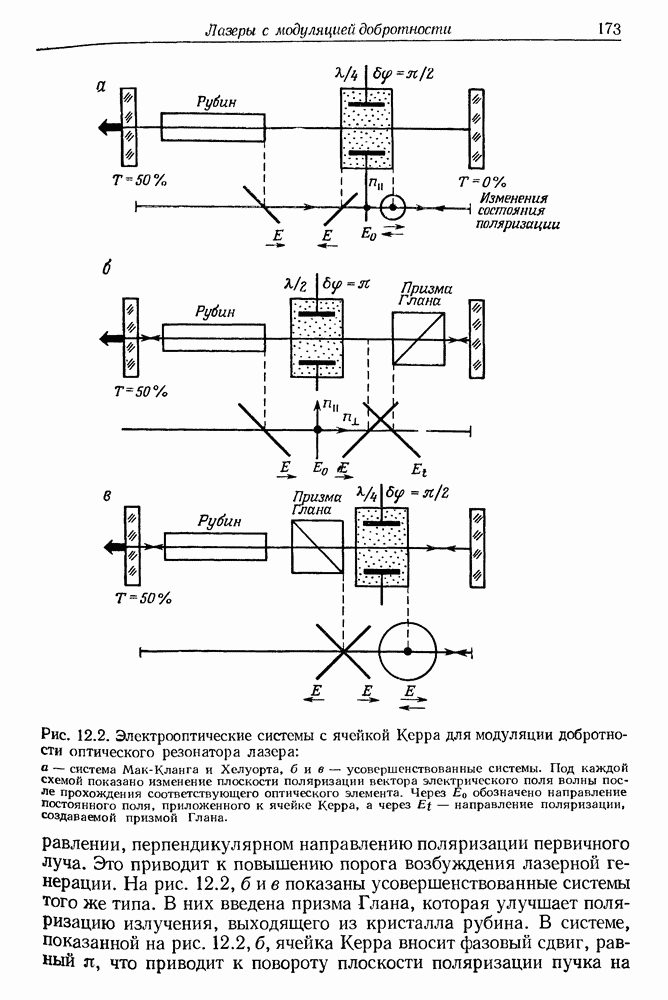
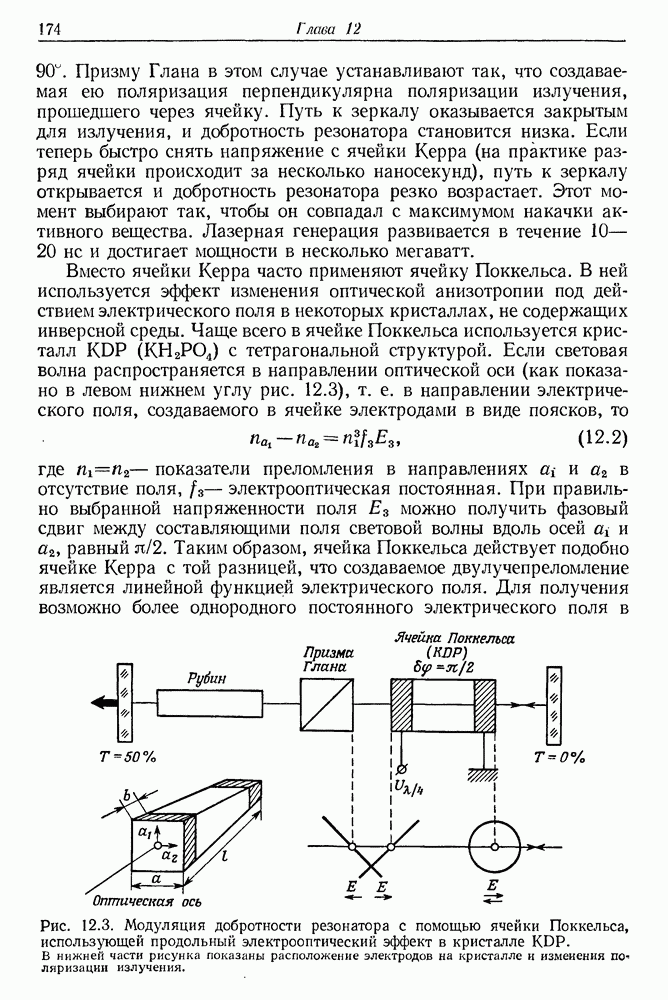
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
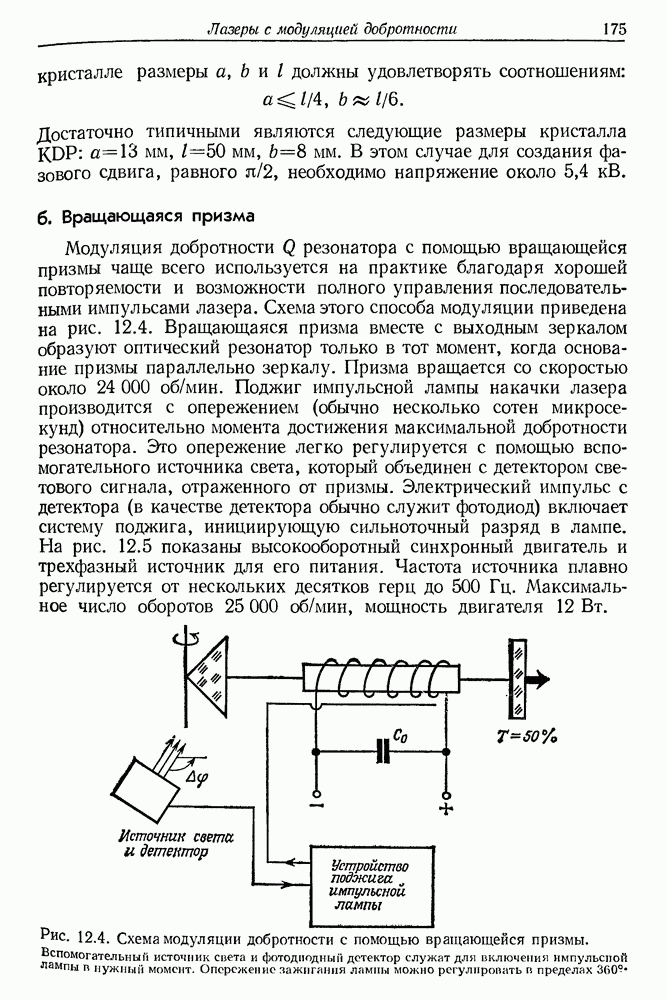
- б. Вращающаяся призма
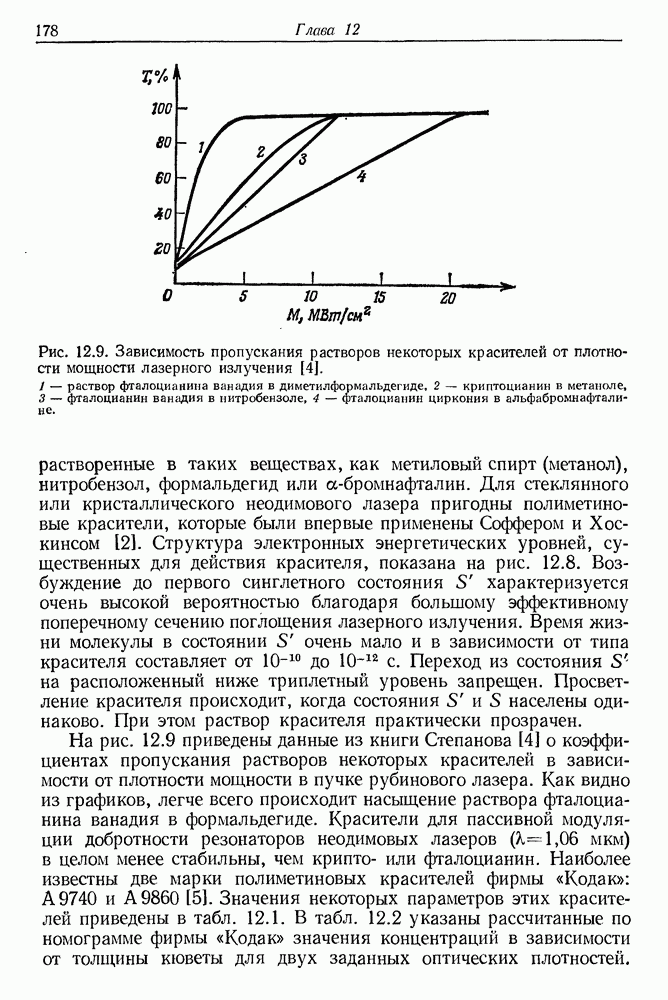
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
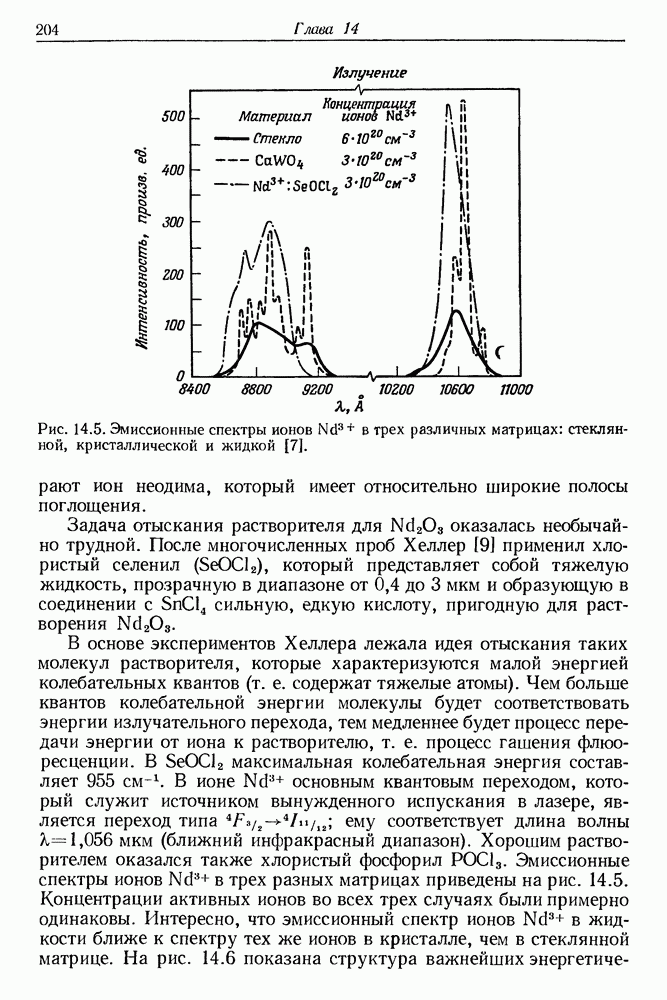
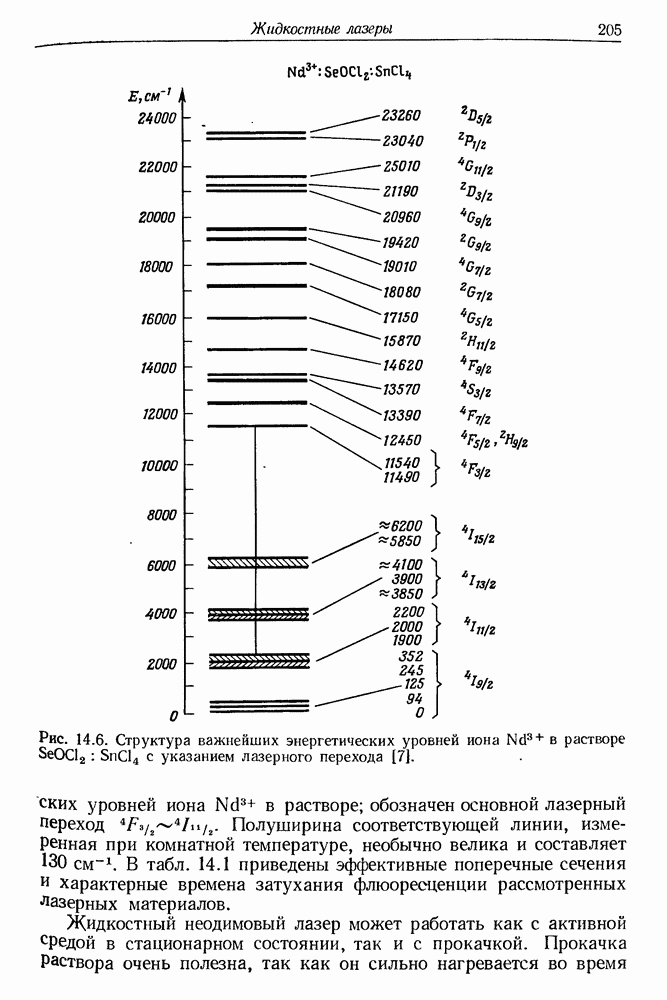
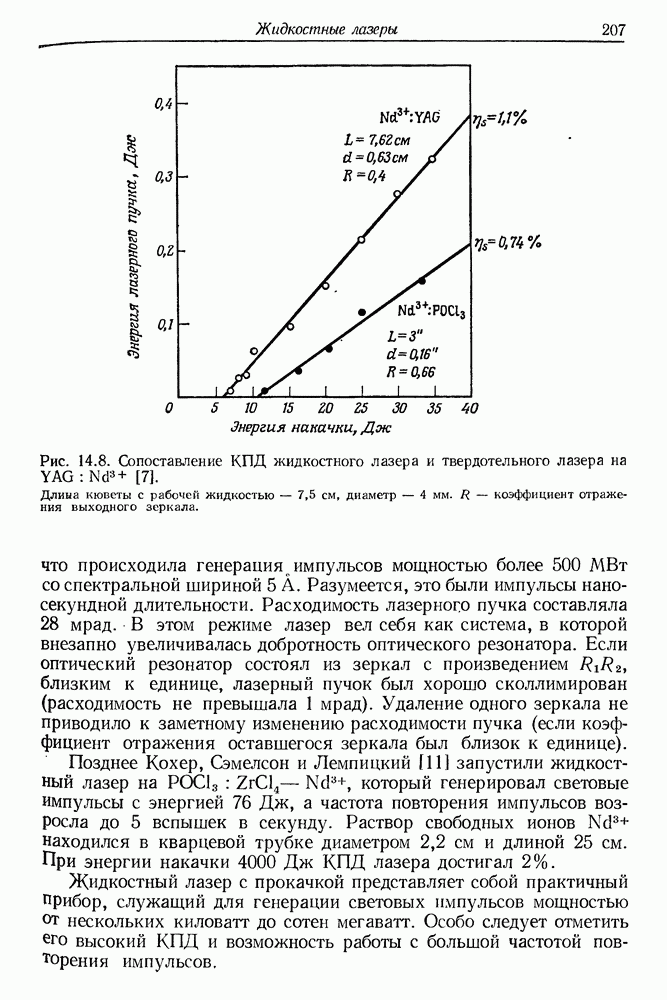
- 14. Жидкостные лазеры
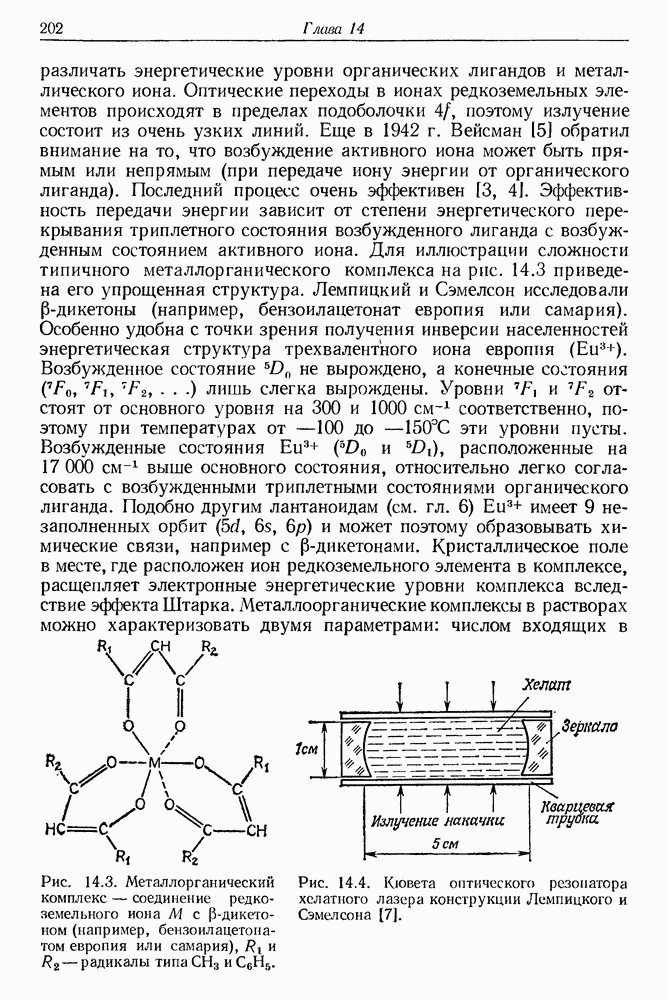
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
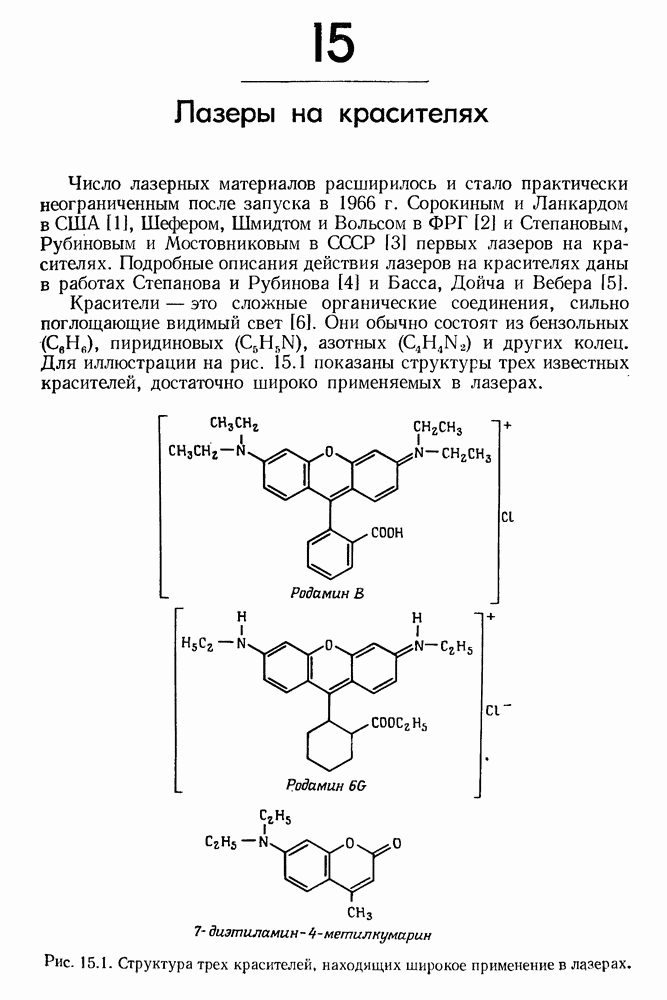
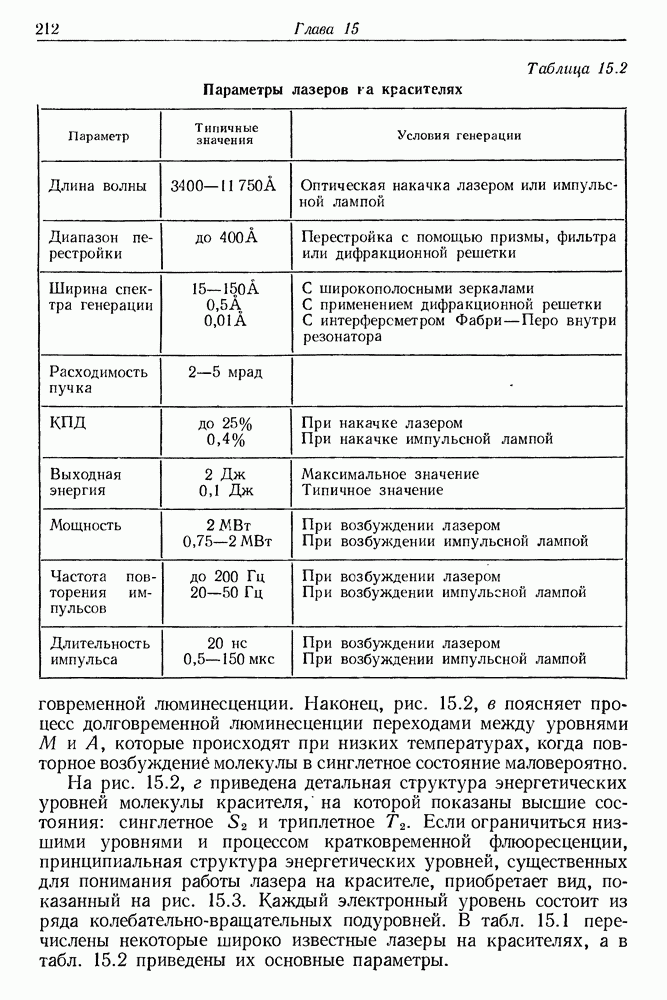
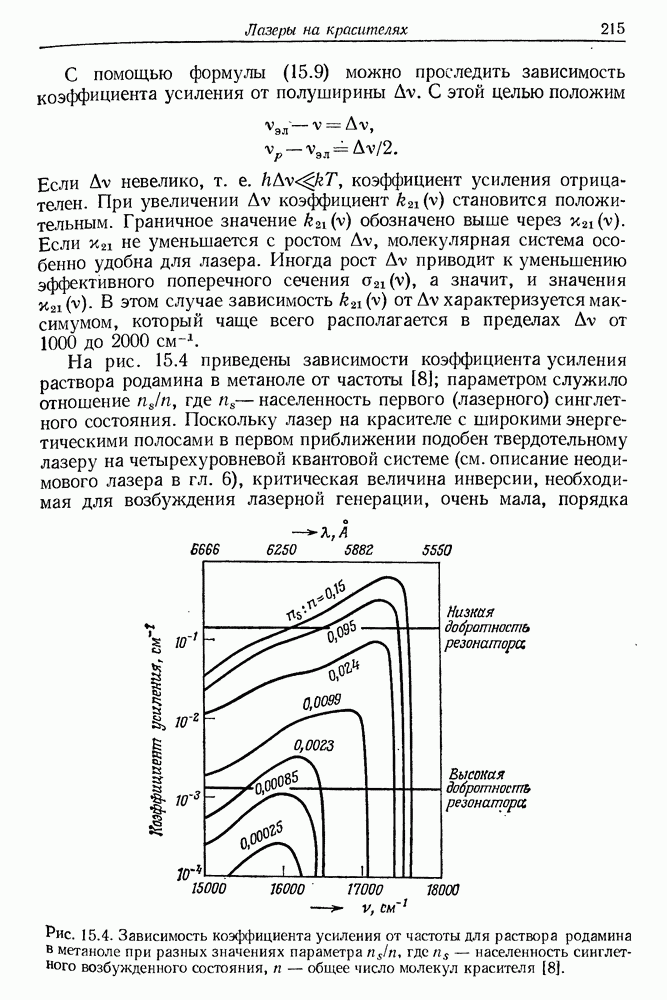
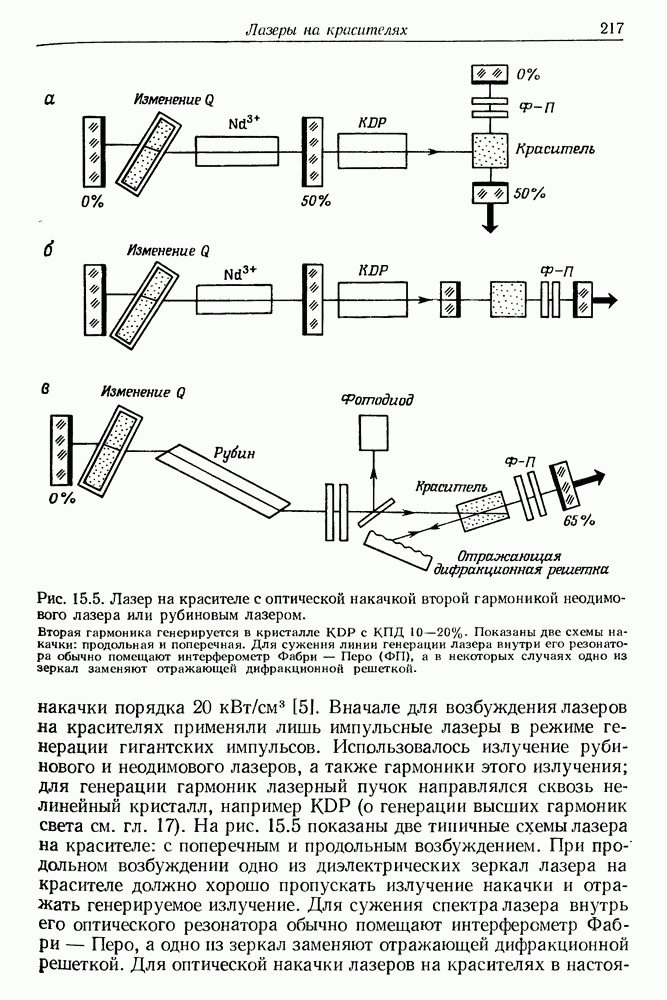
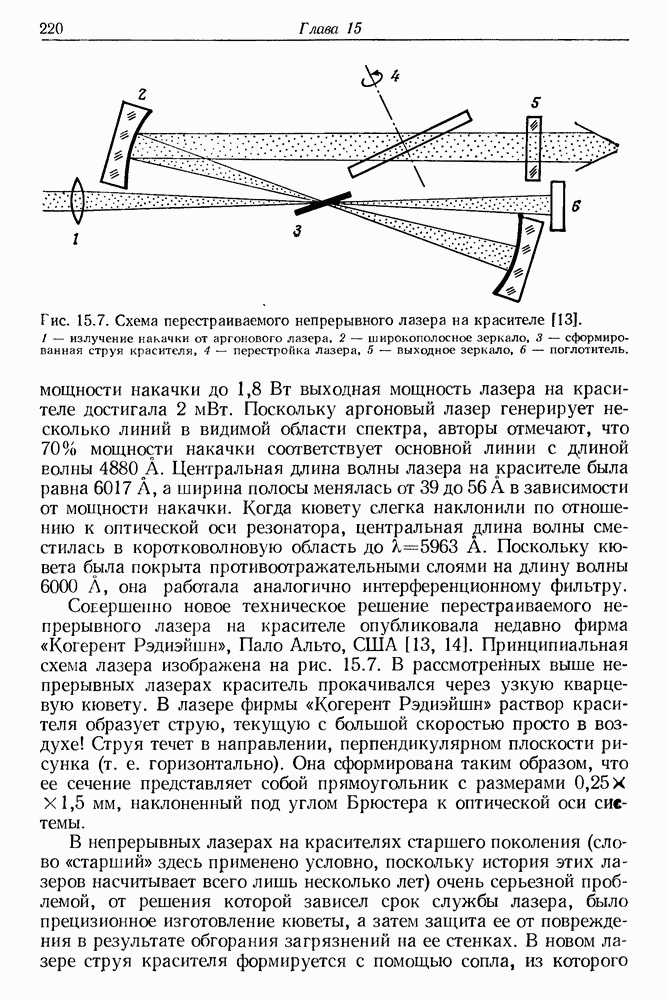
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
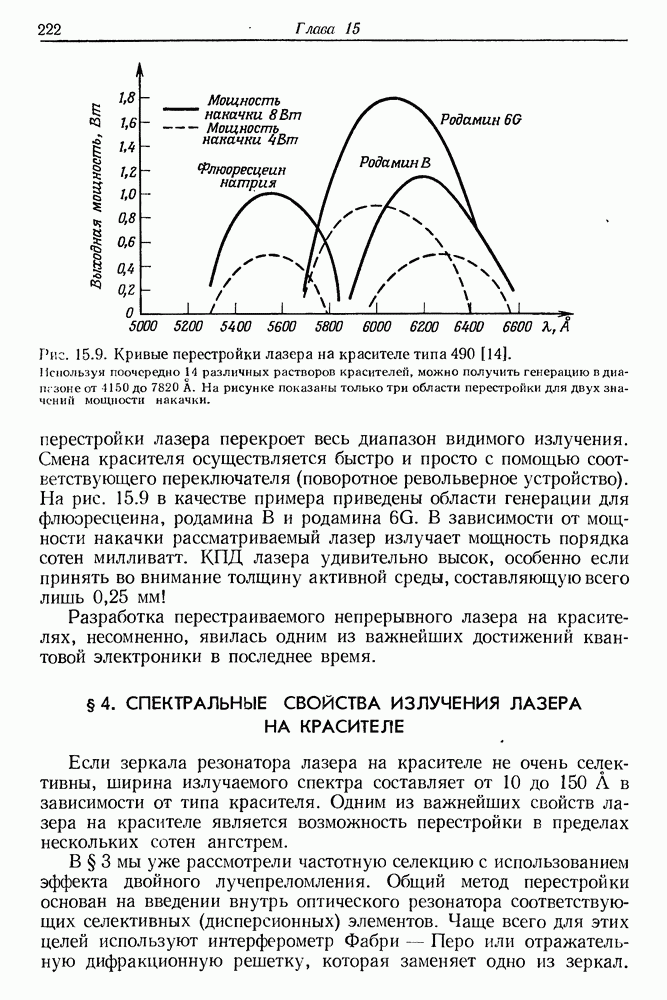
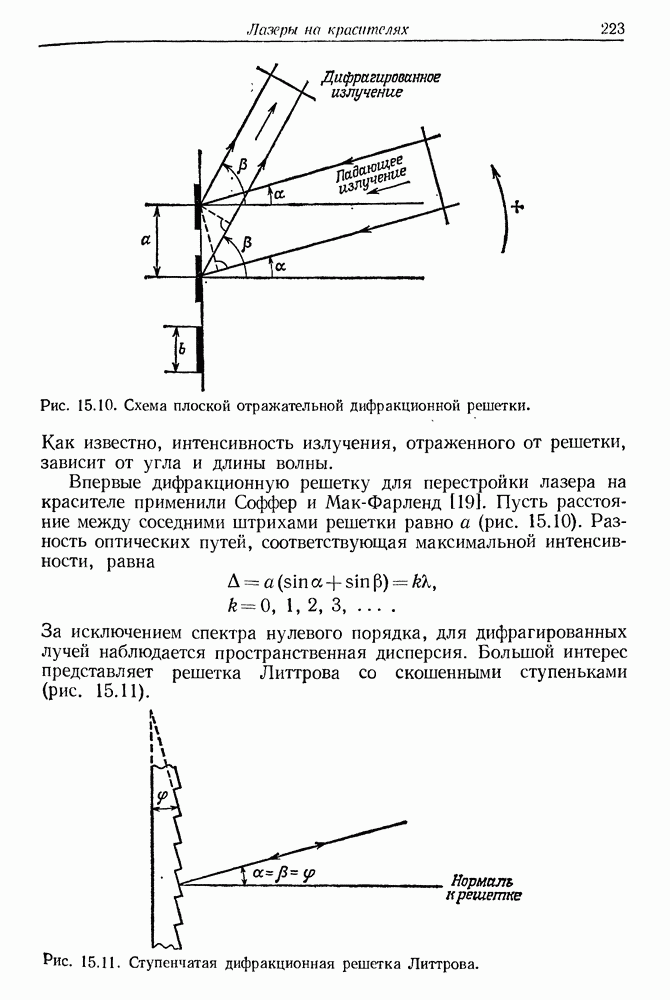
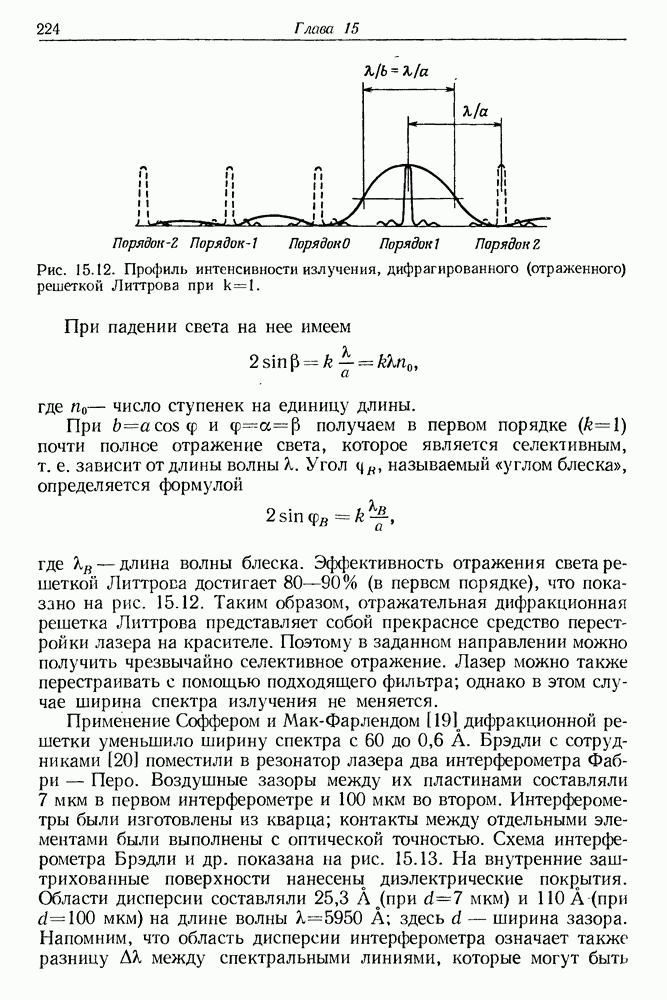
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
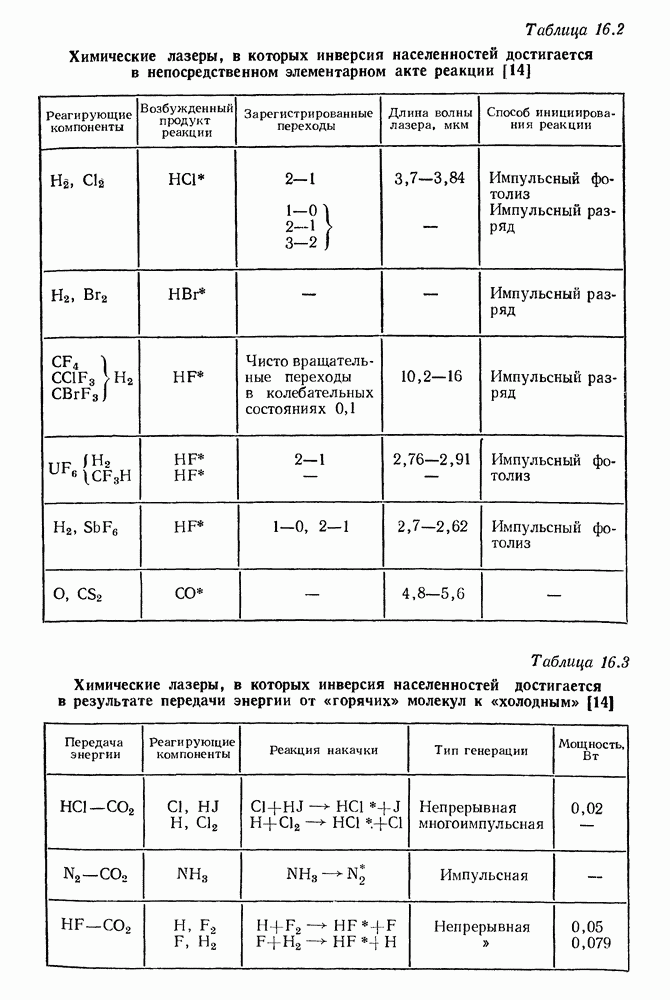
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
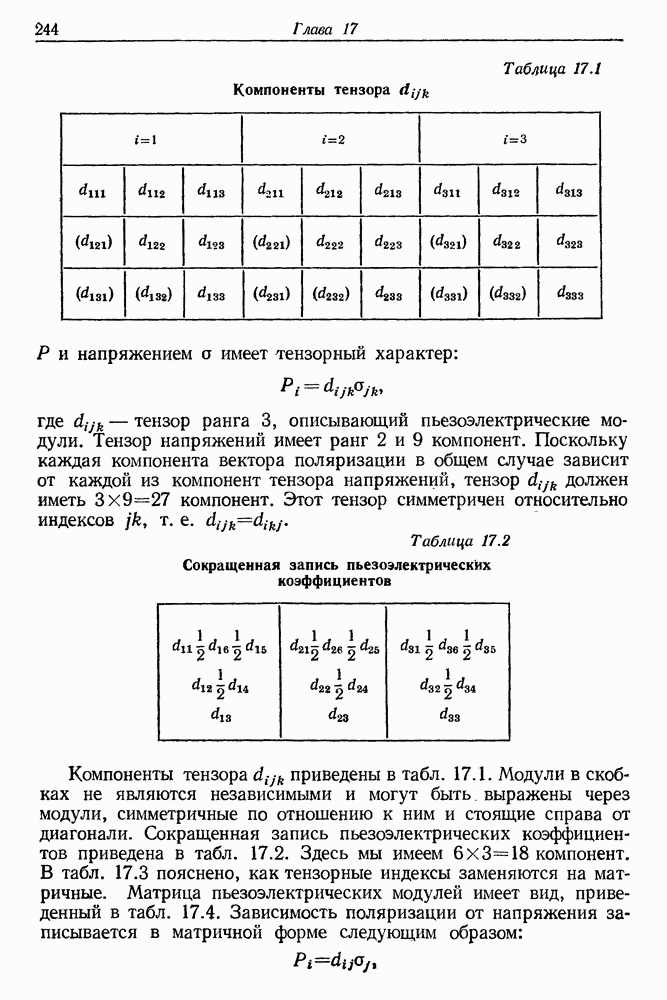
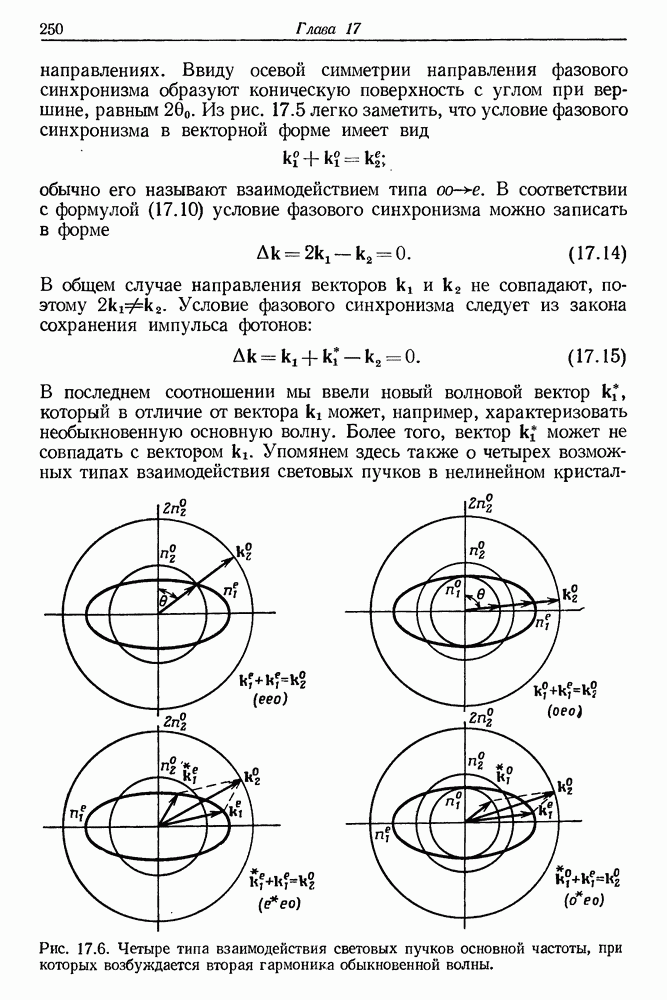
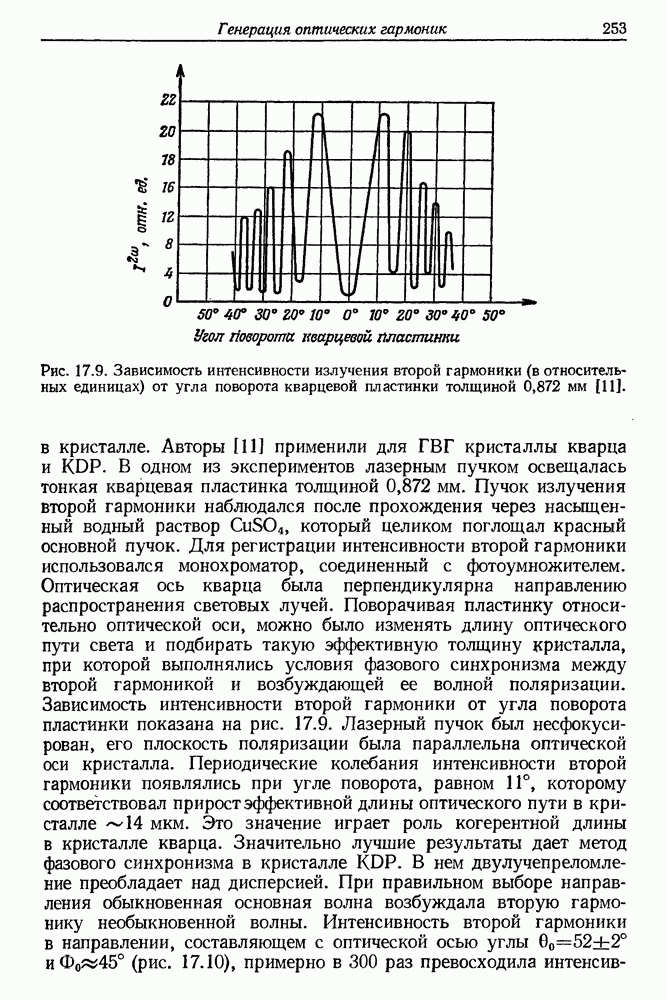
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
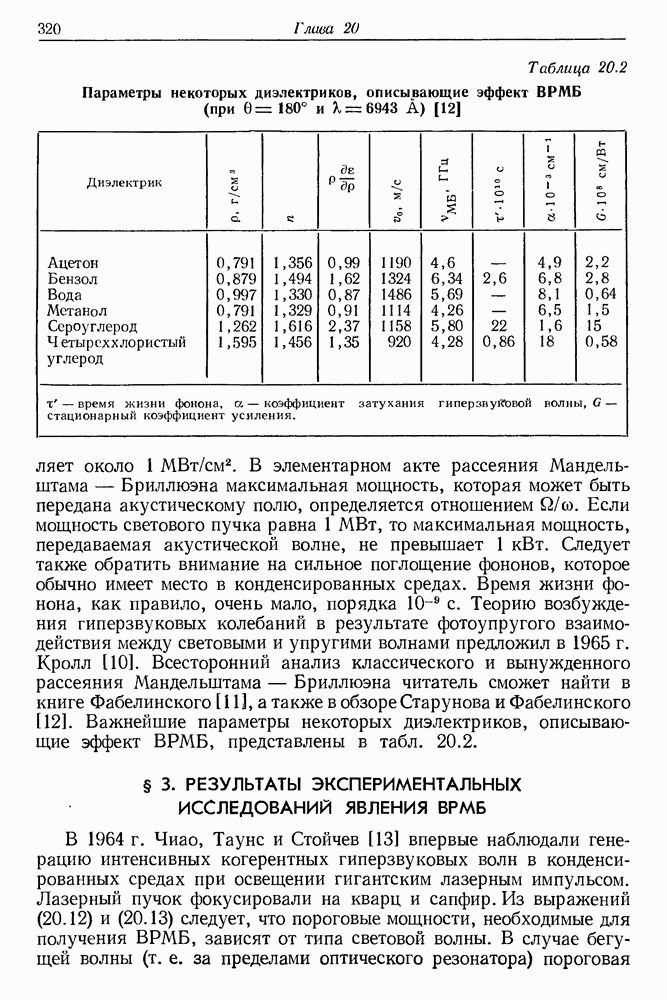
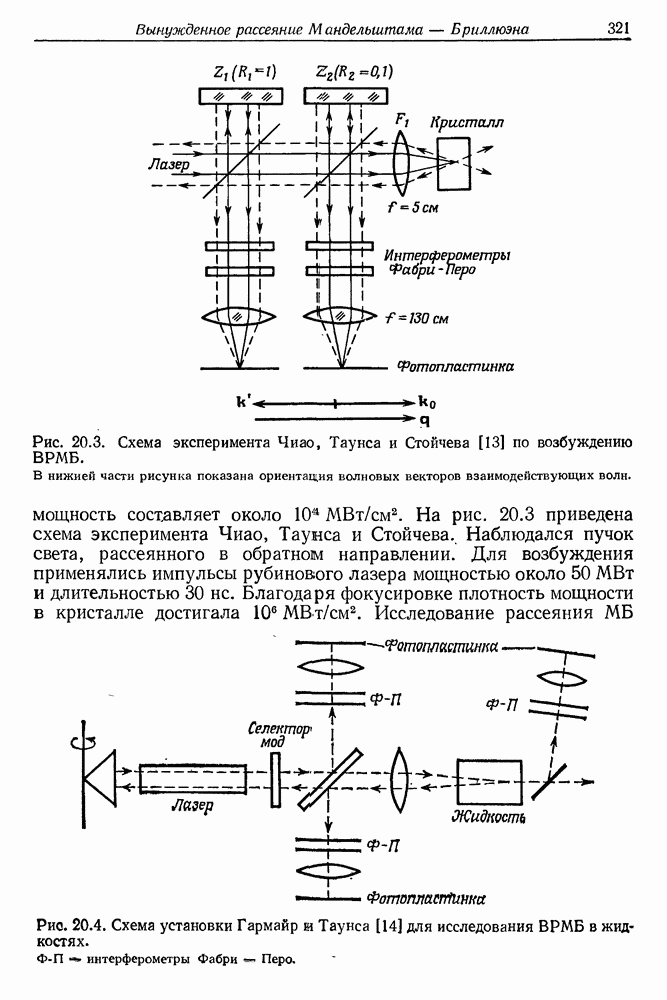
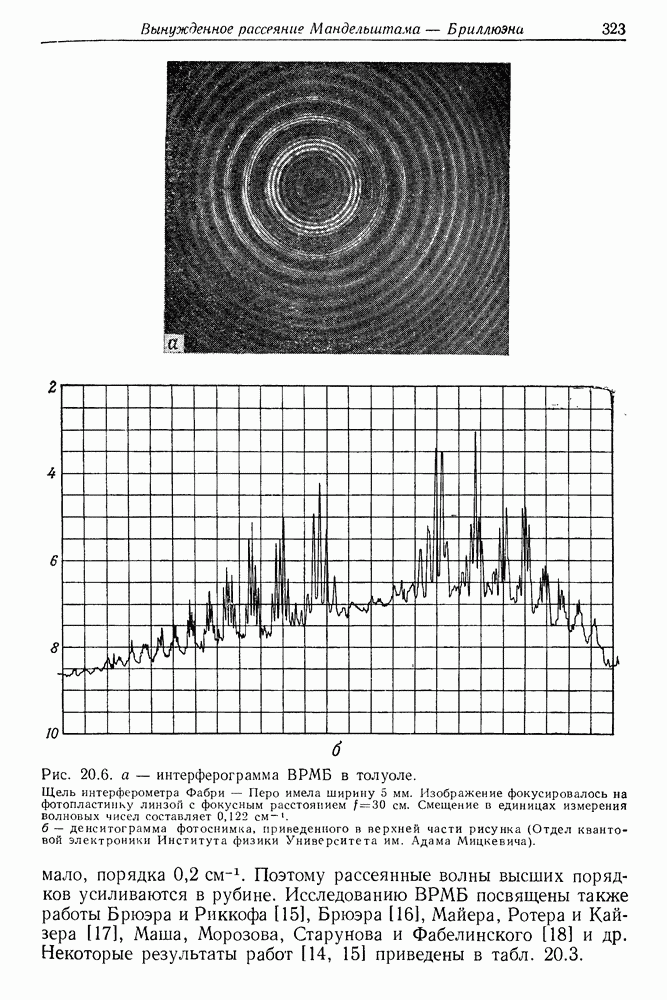
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
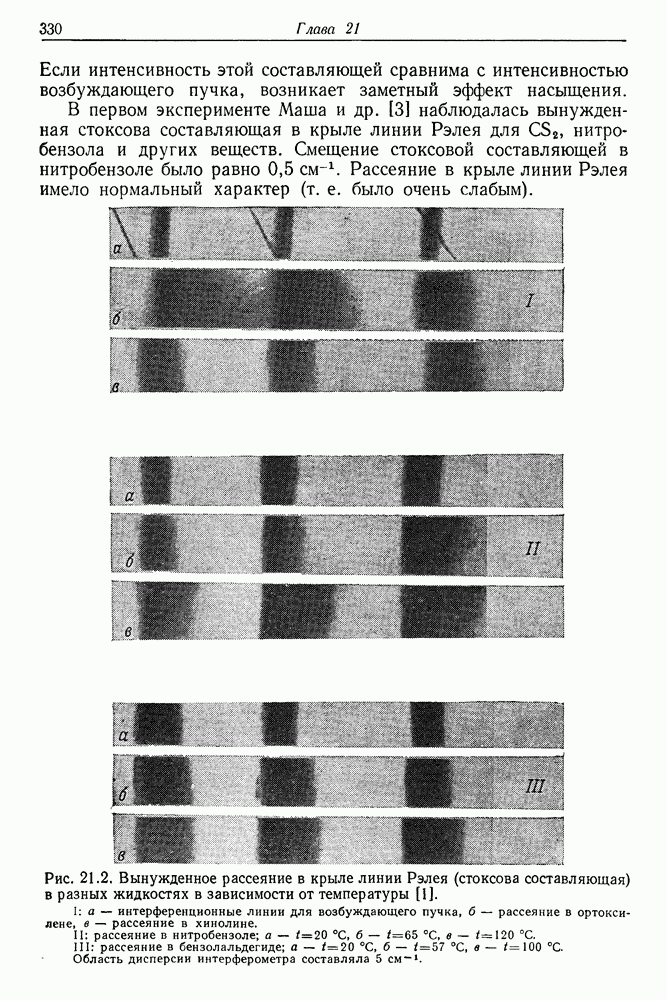
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
- 22. Параметрическая люминесценция (ПЛ)
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
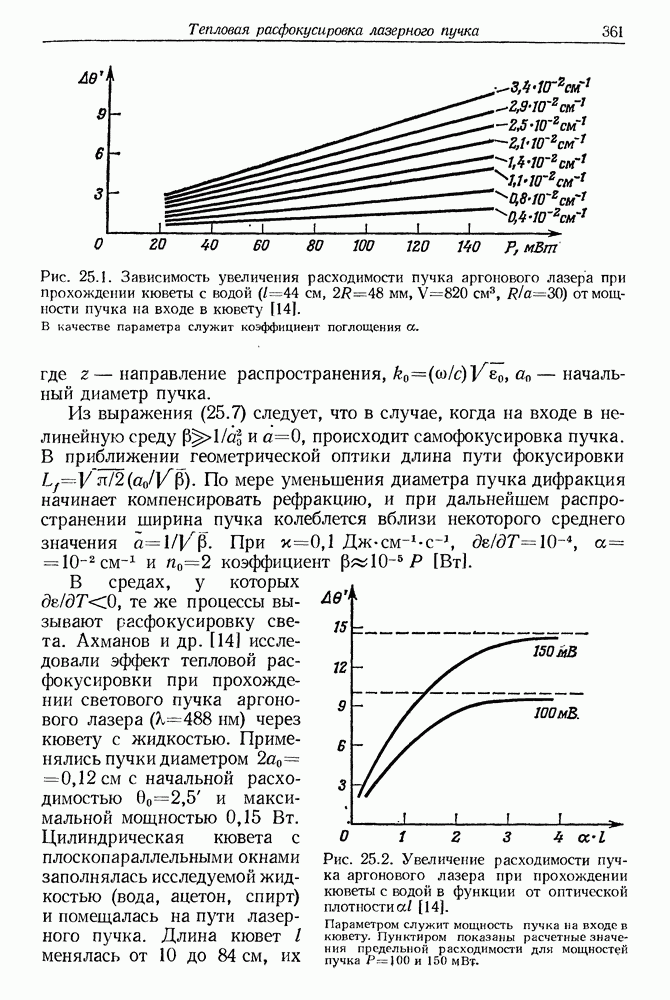
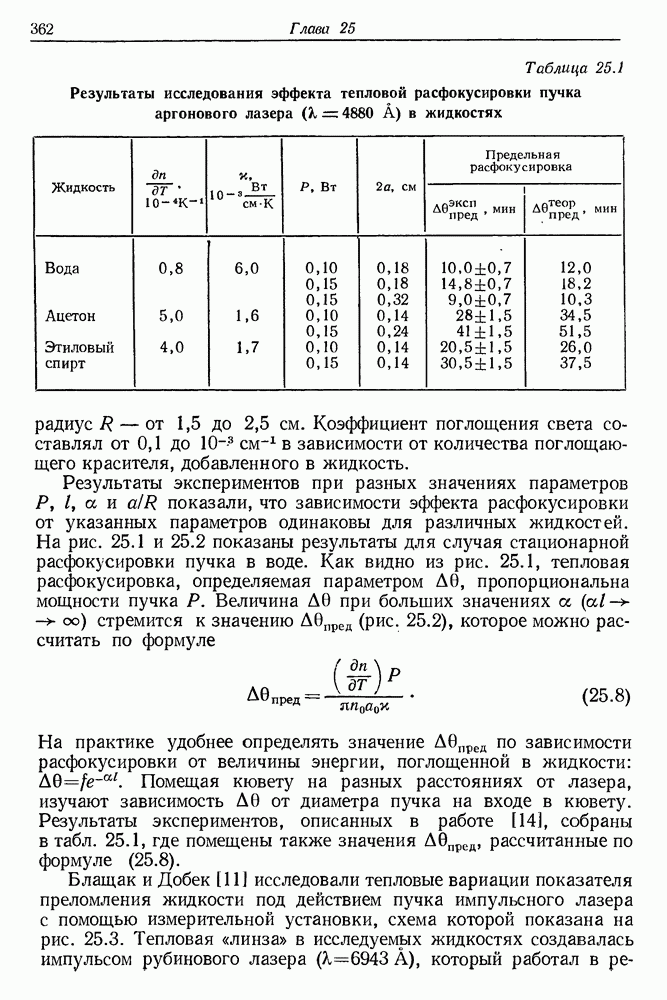
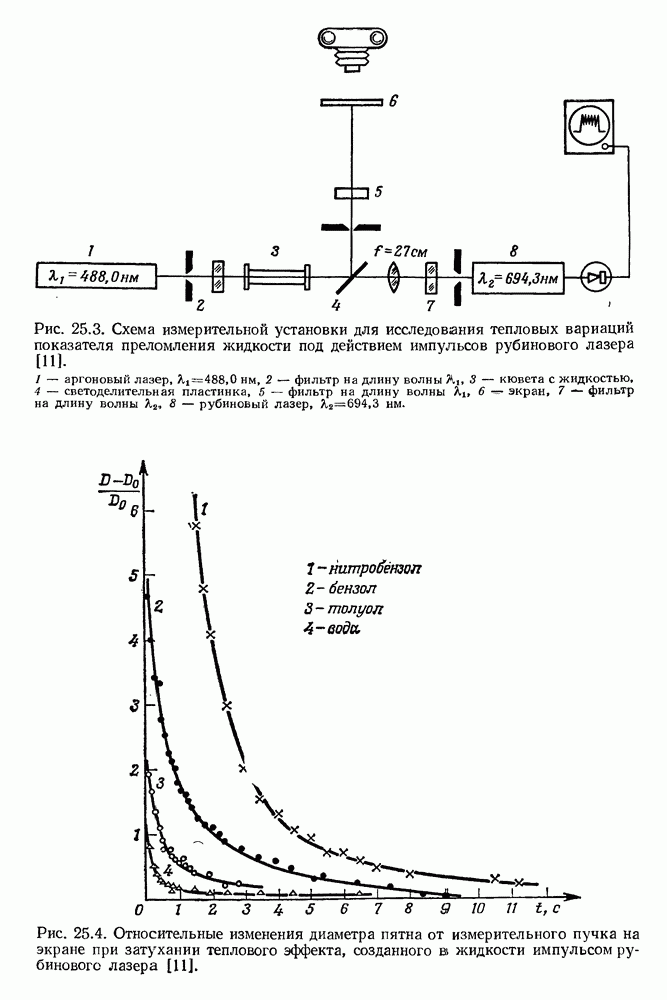
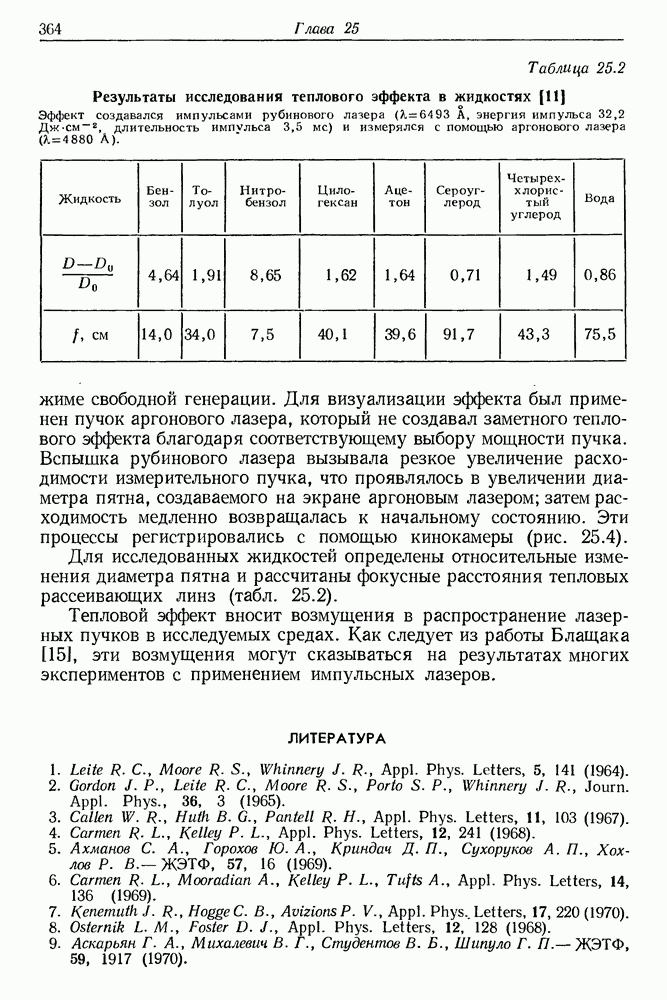
- 25. Тепловая расфокусировка лазерного пучка
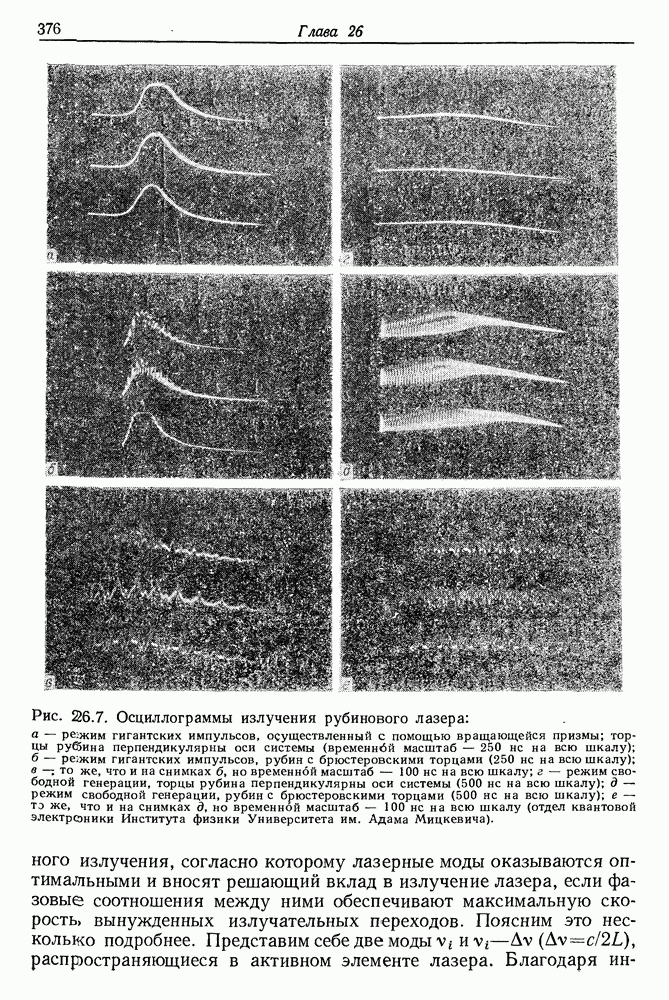
- 26. Синхронизация мод лазера
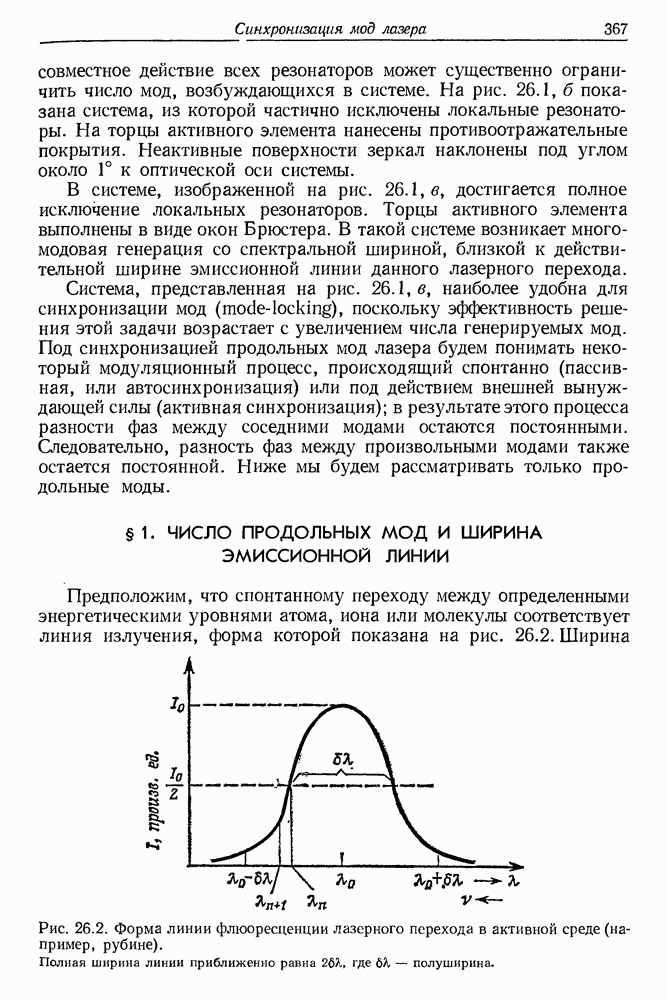
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
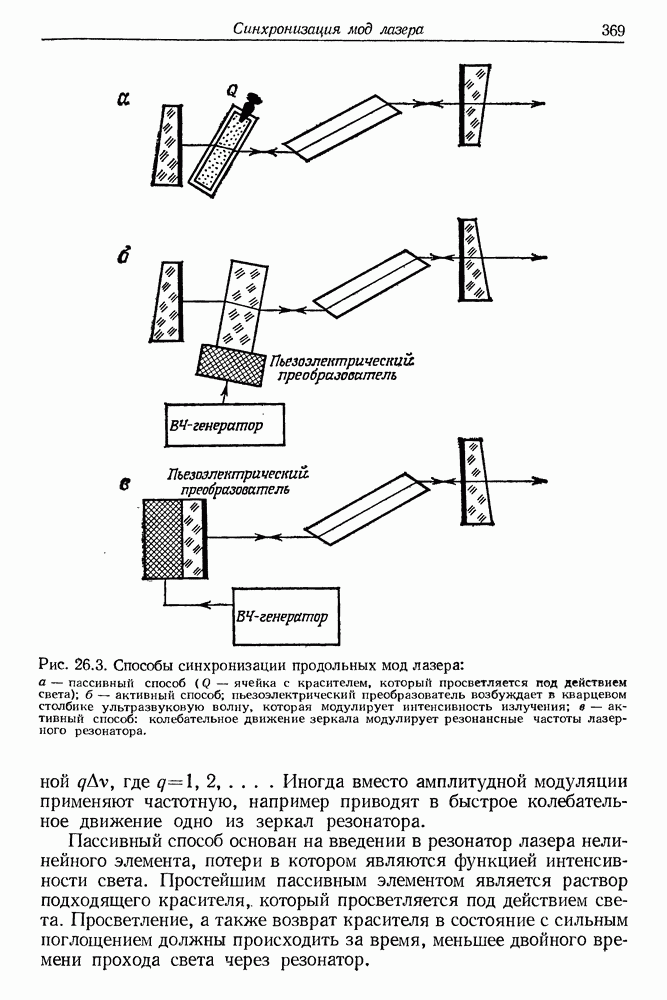
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
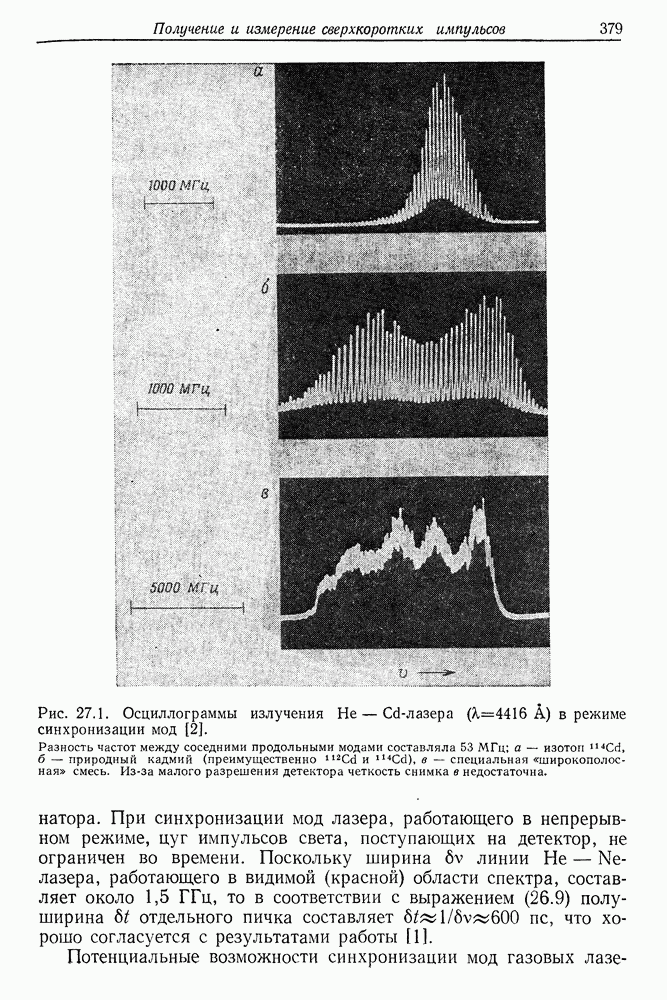
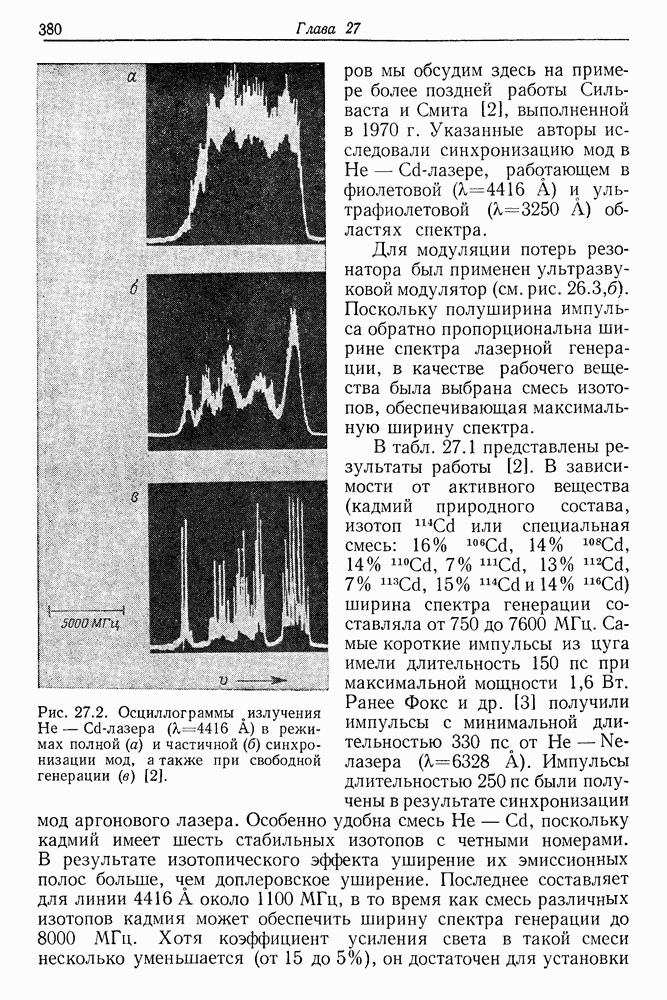
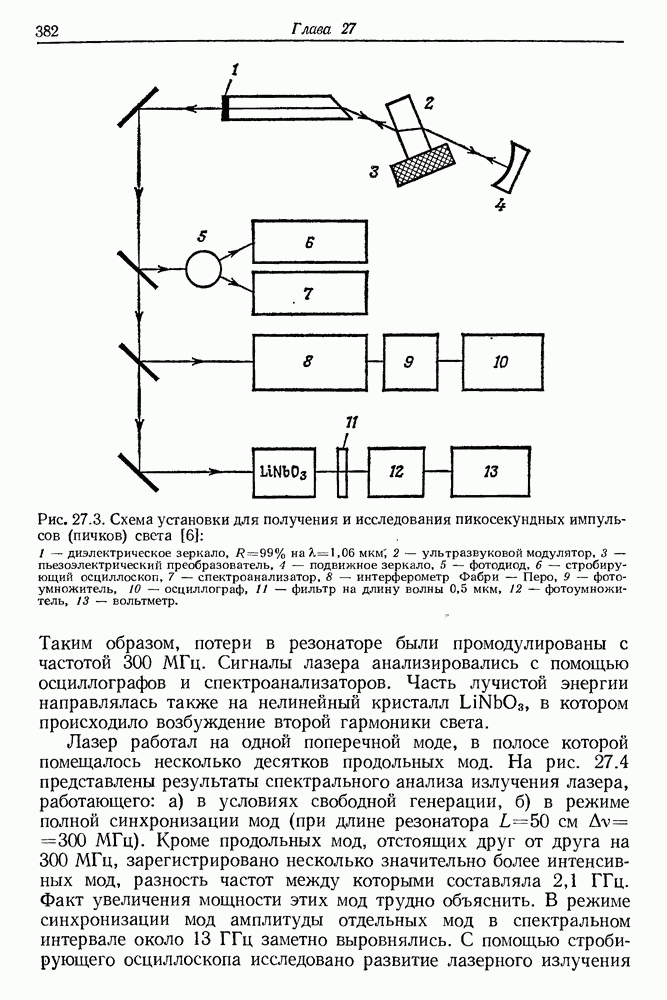
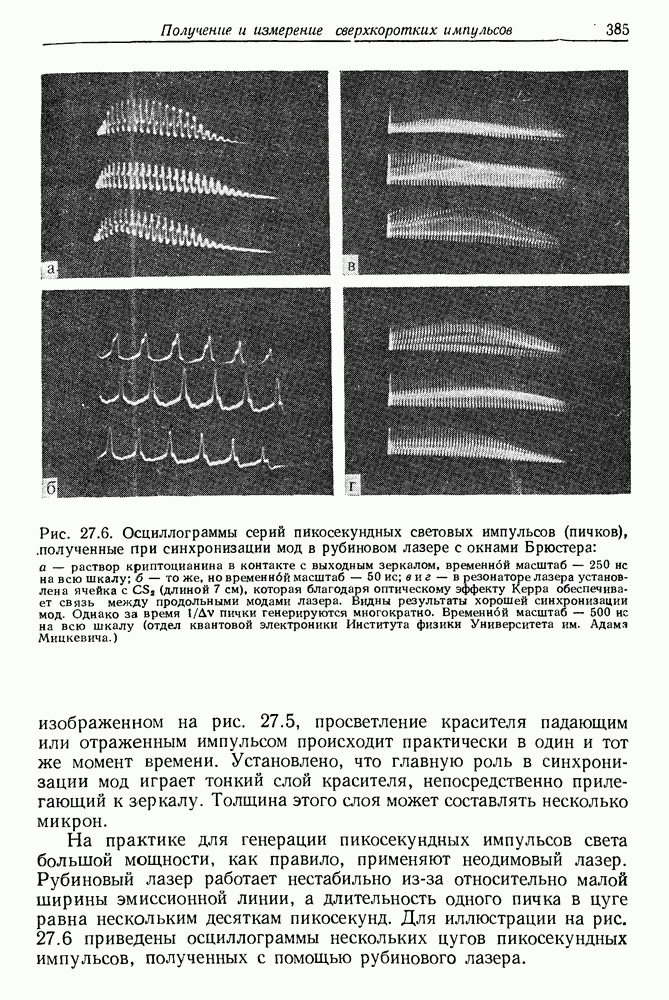
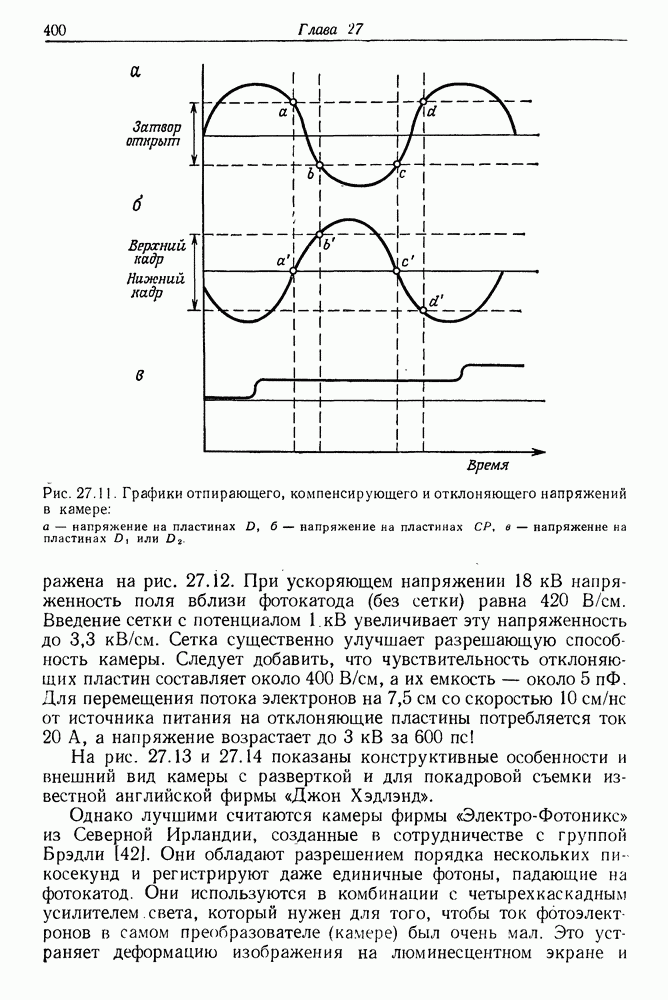
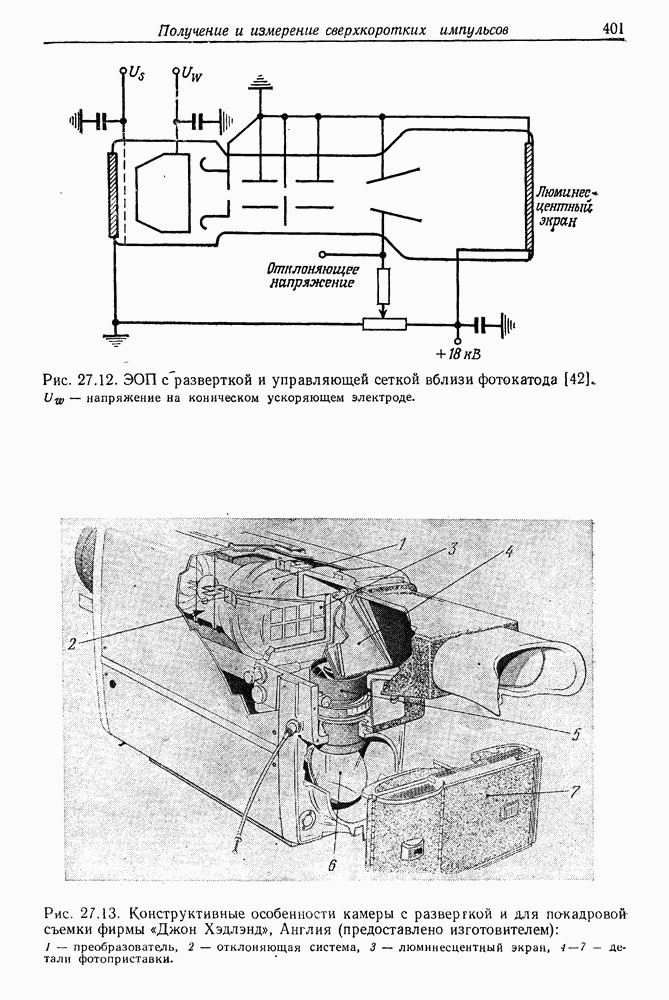
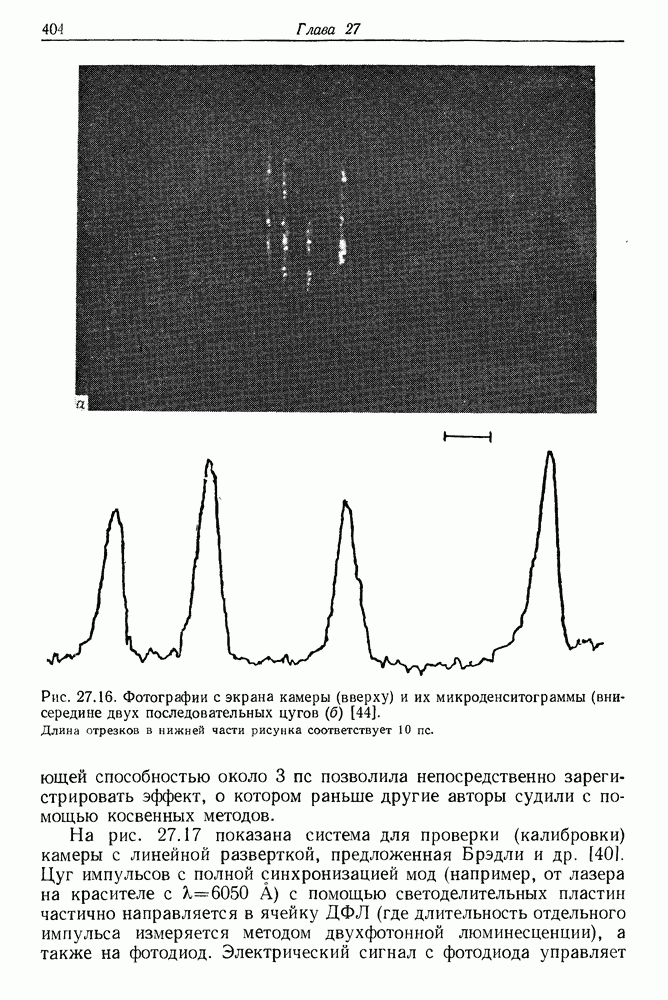
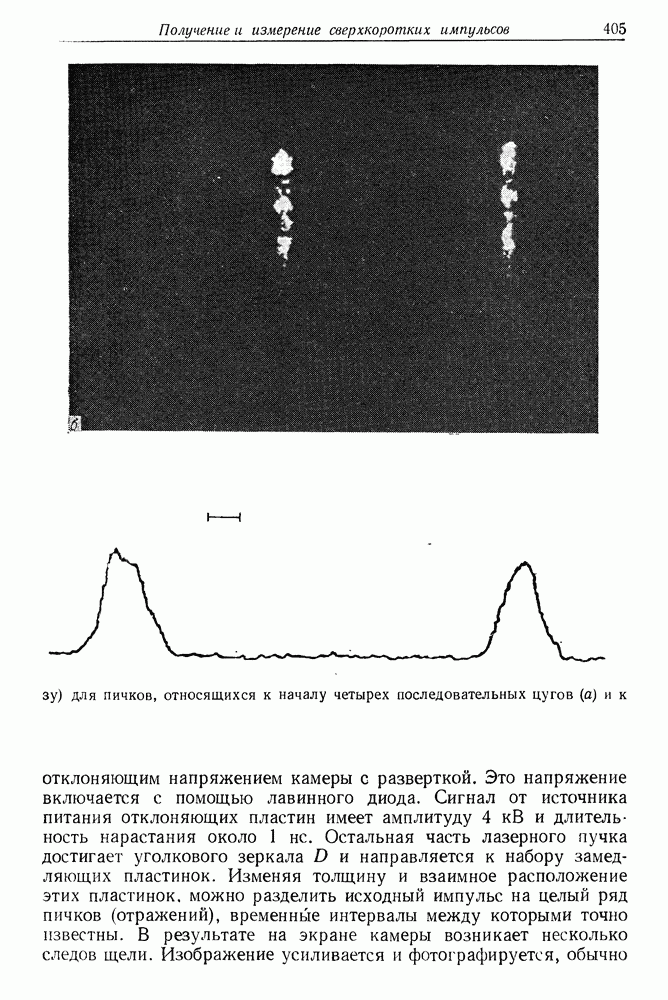
- 27. Получение и измерение сверхкоротких импульсов света
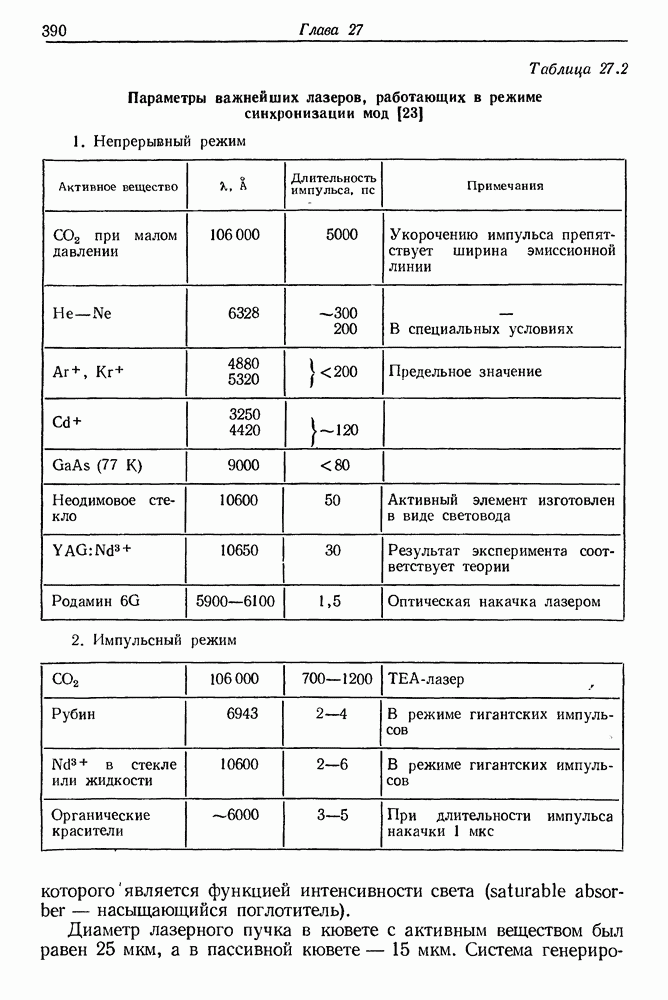
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
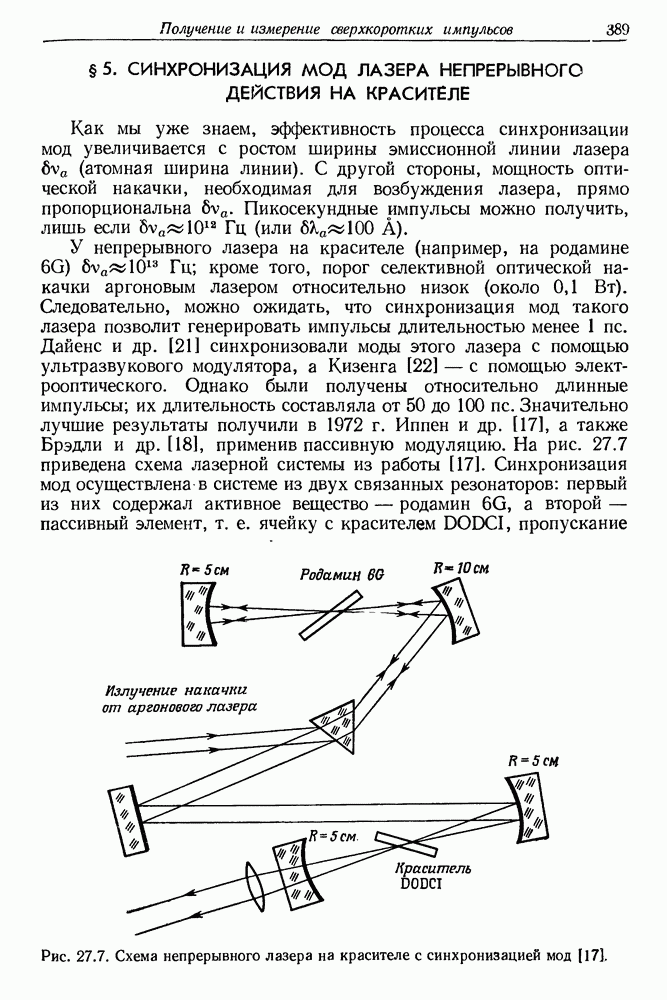
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
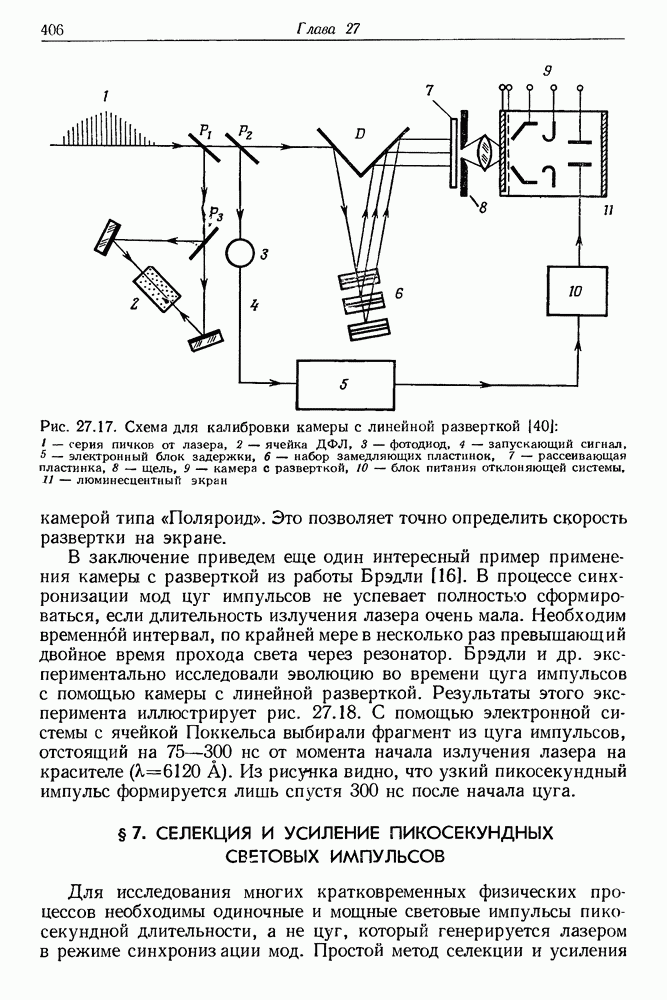
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
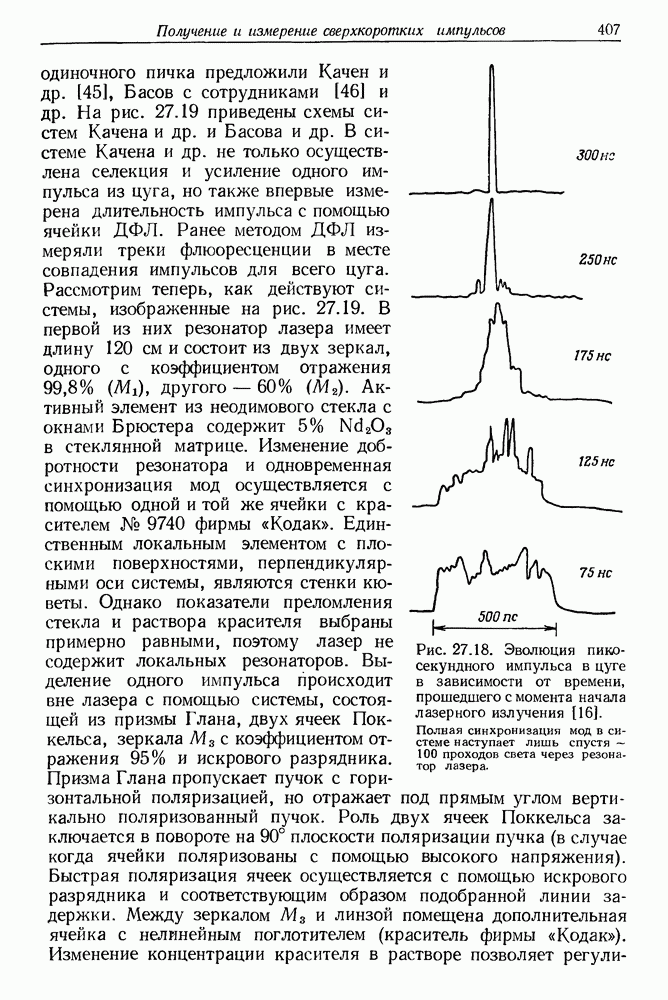
- в. Примеры использования камеры с разверткой
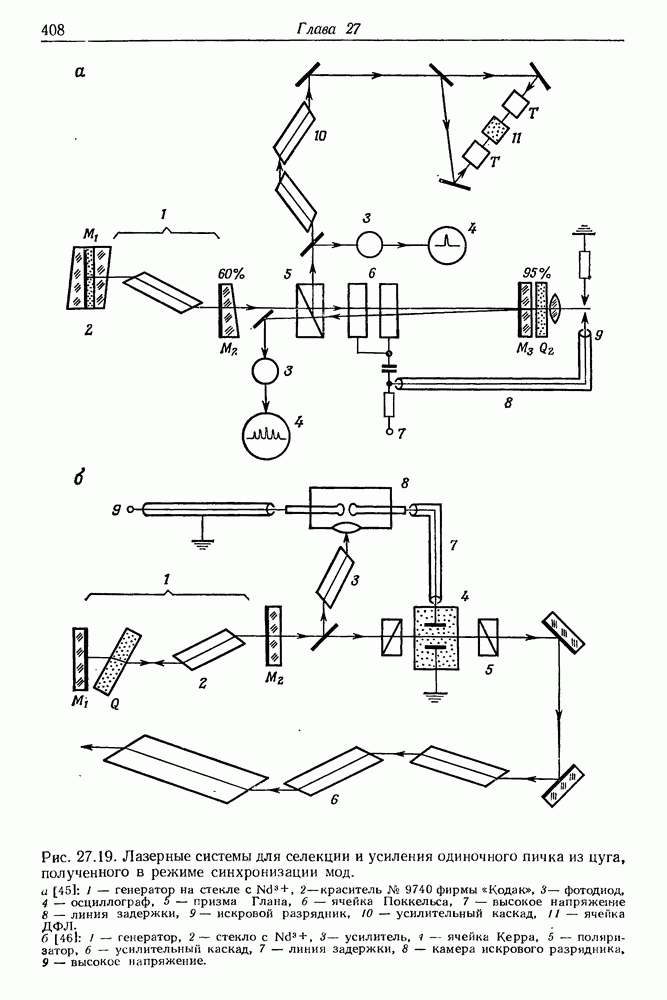
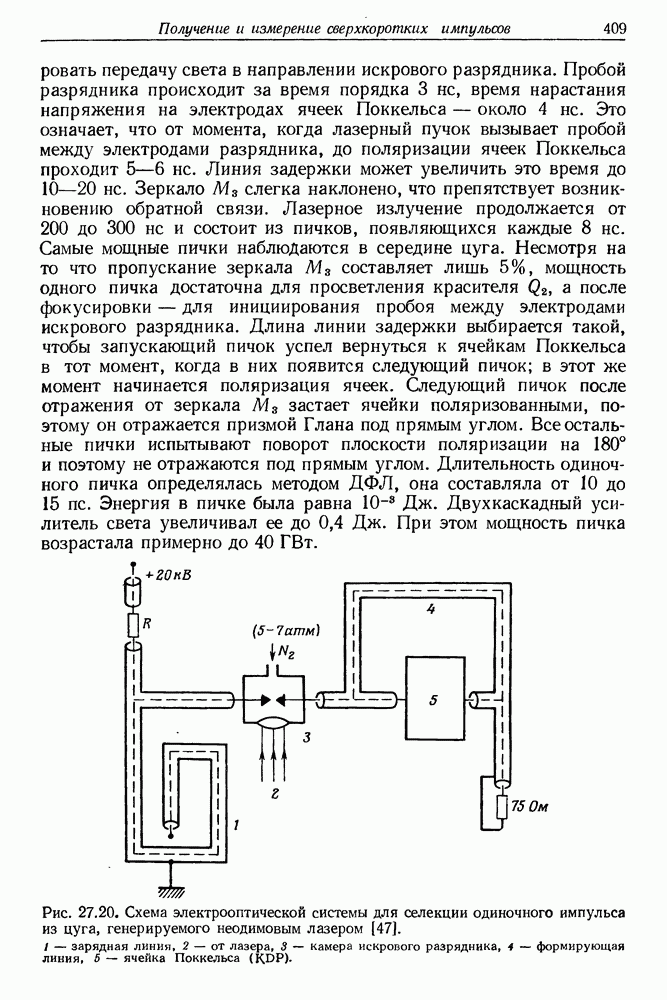
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
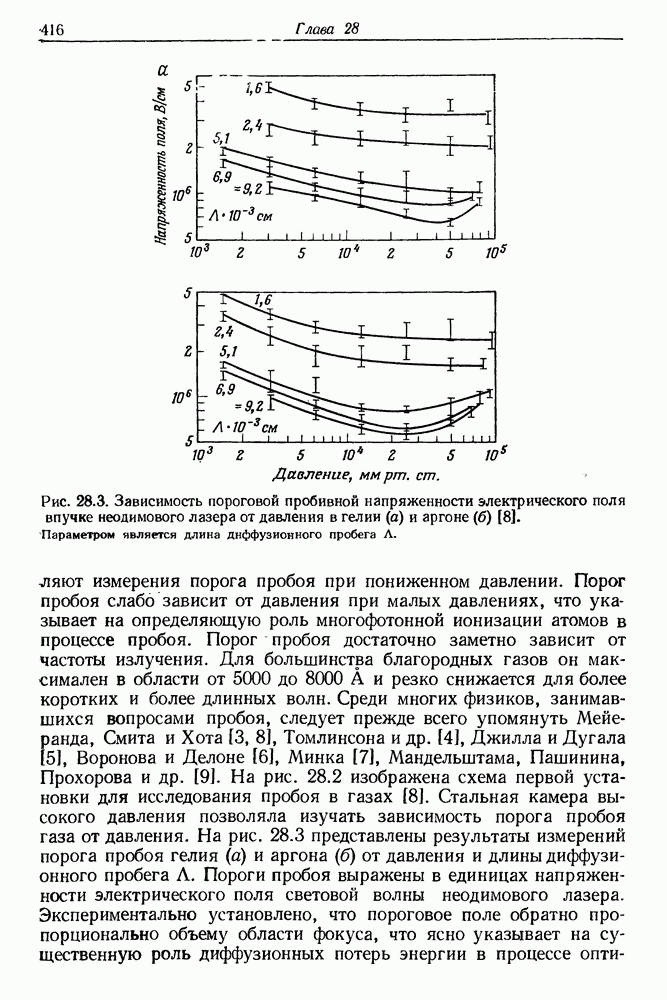
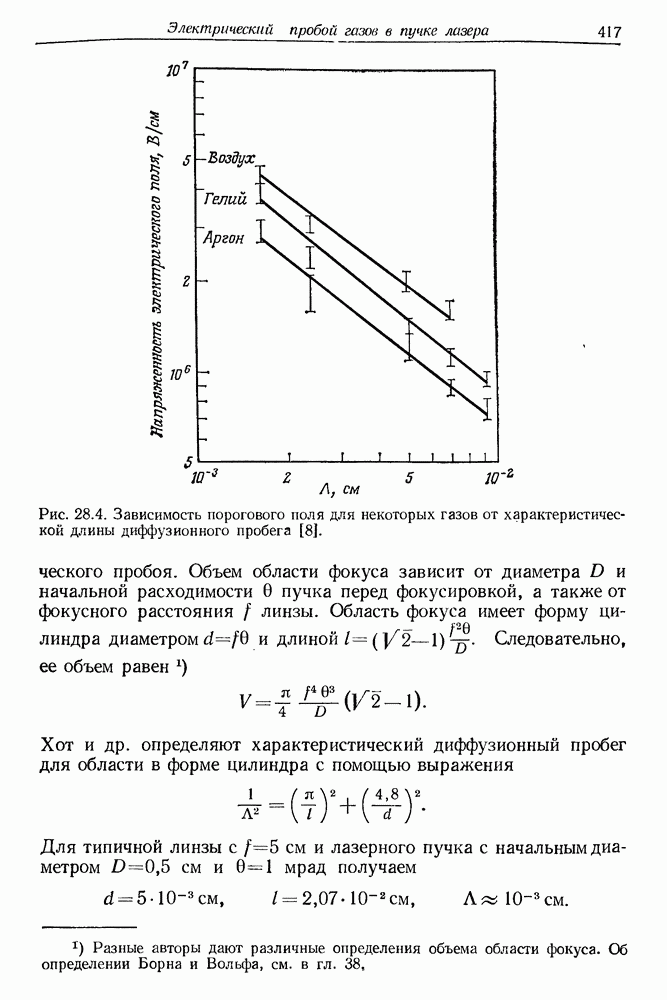
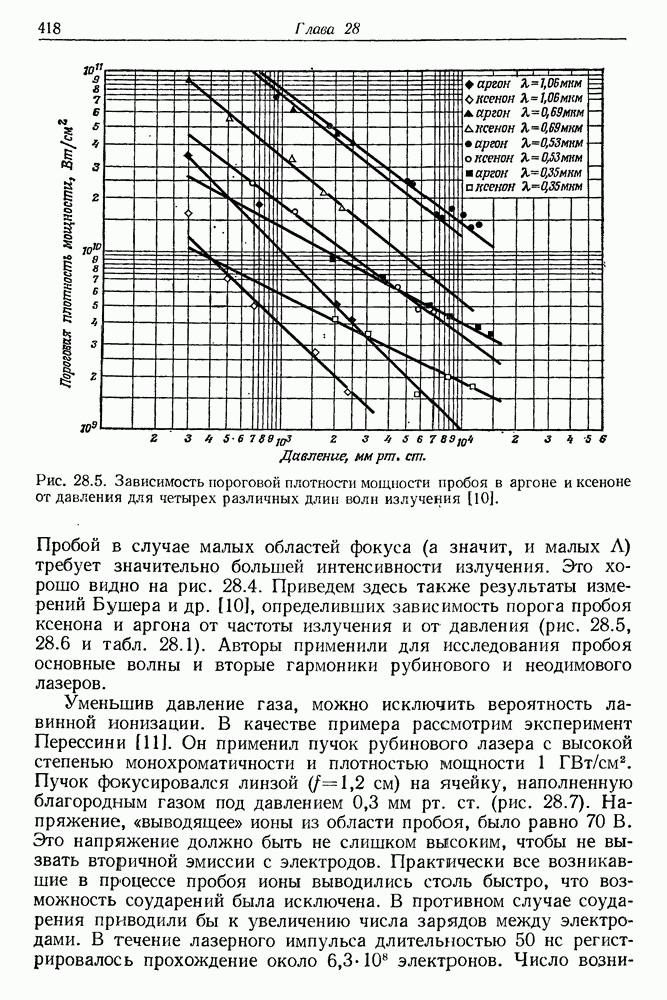
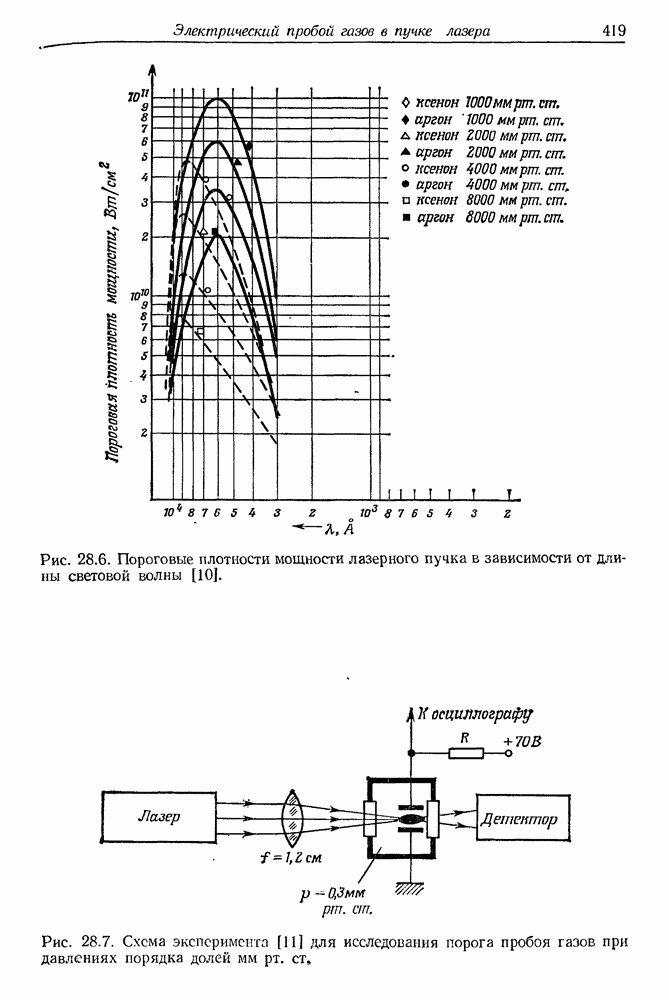
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
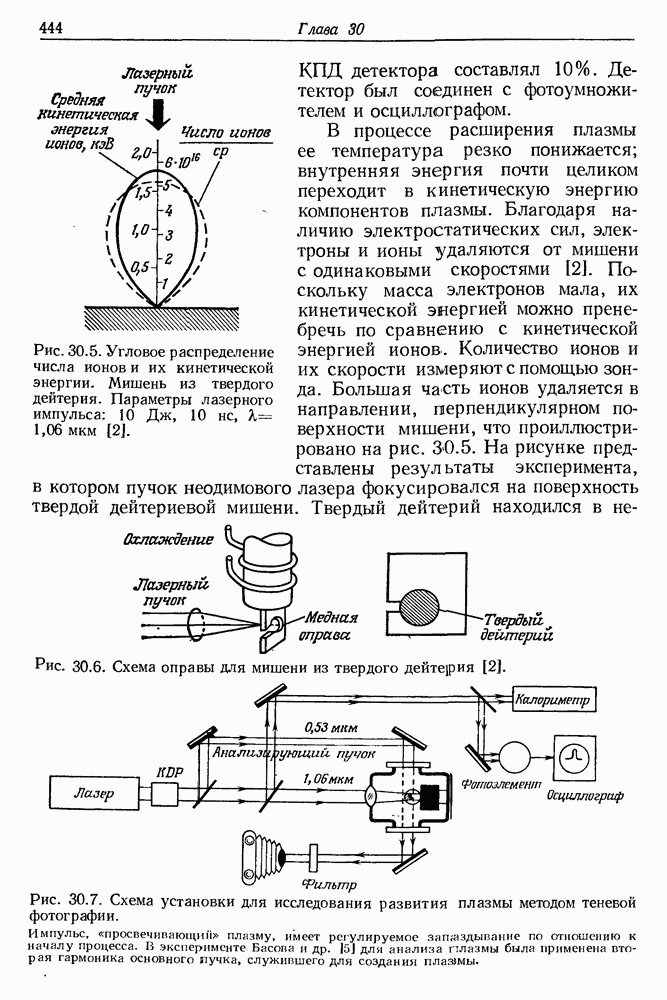
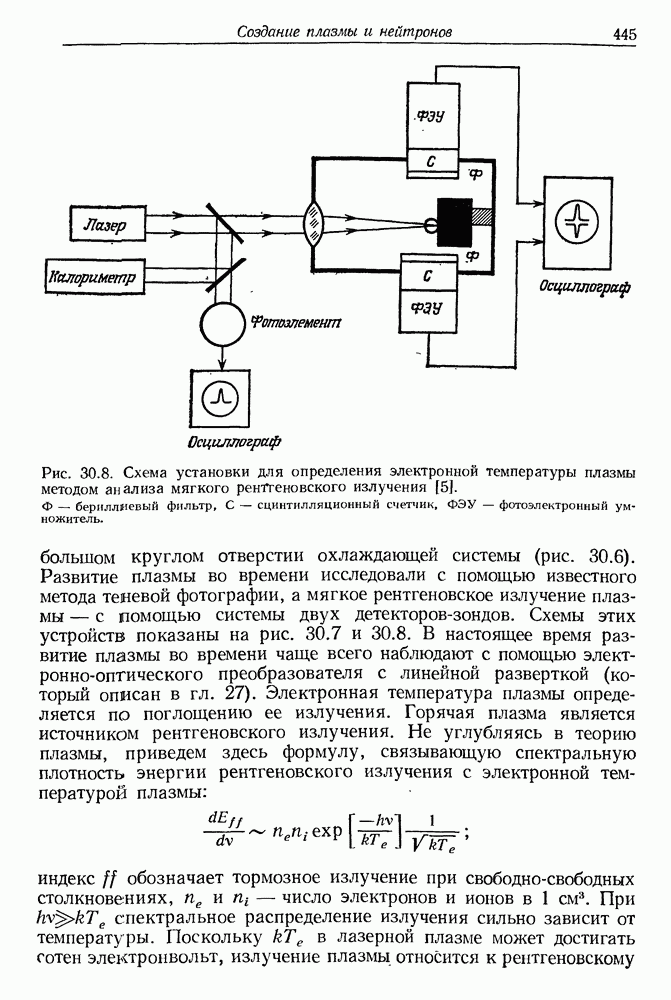
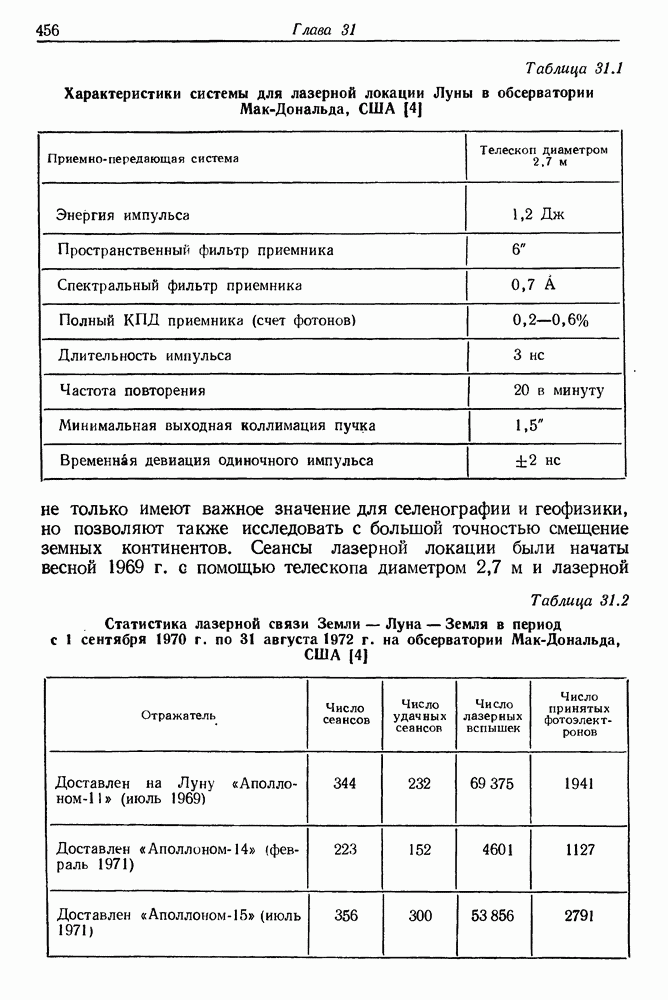
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
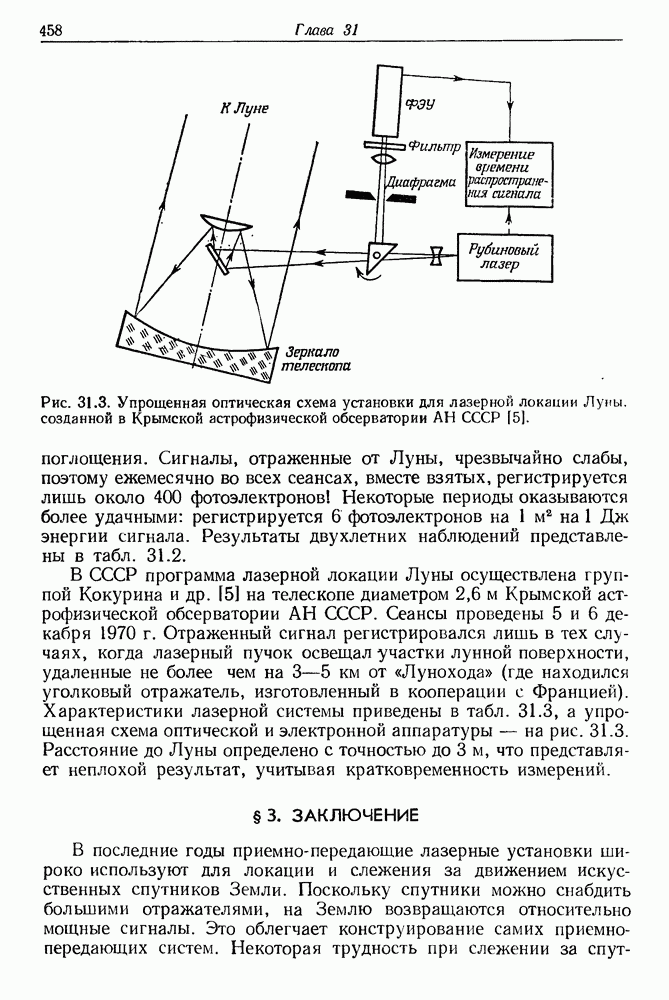
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
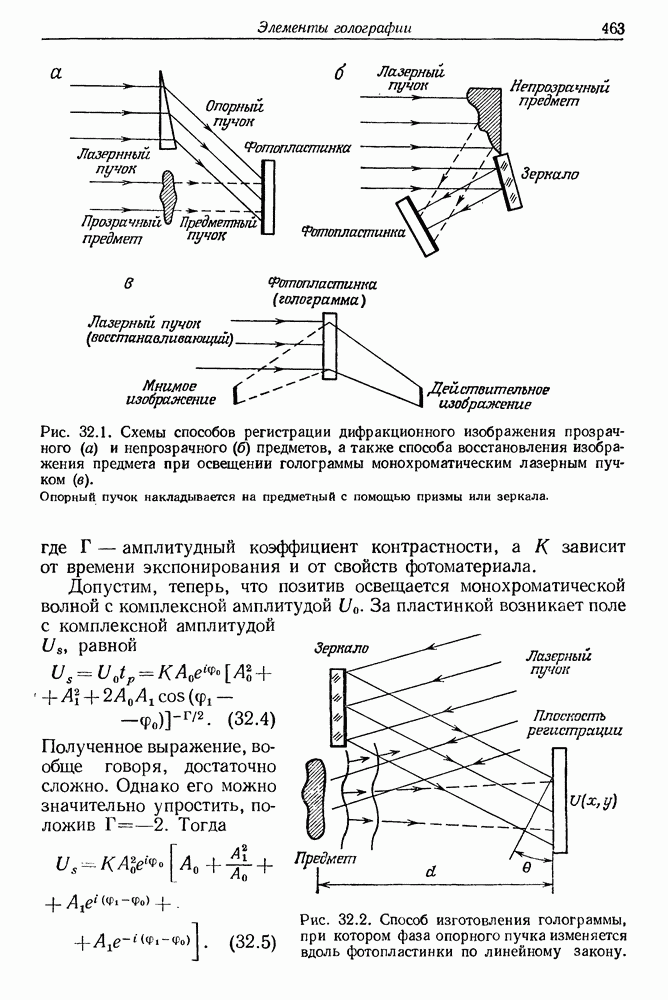
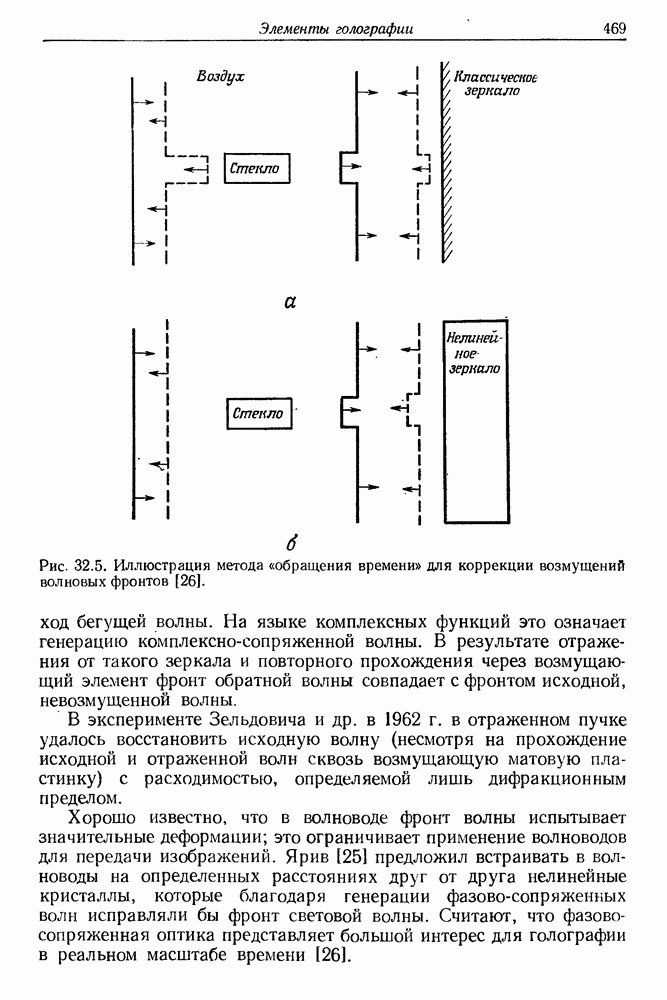
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
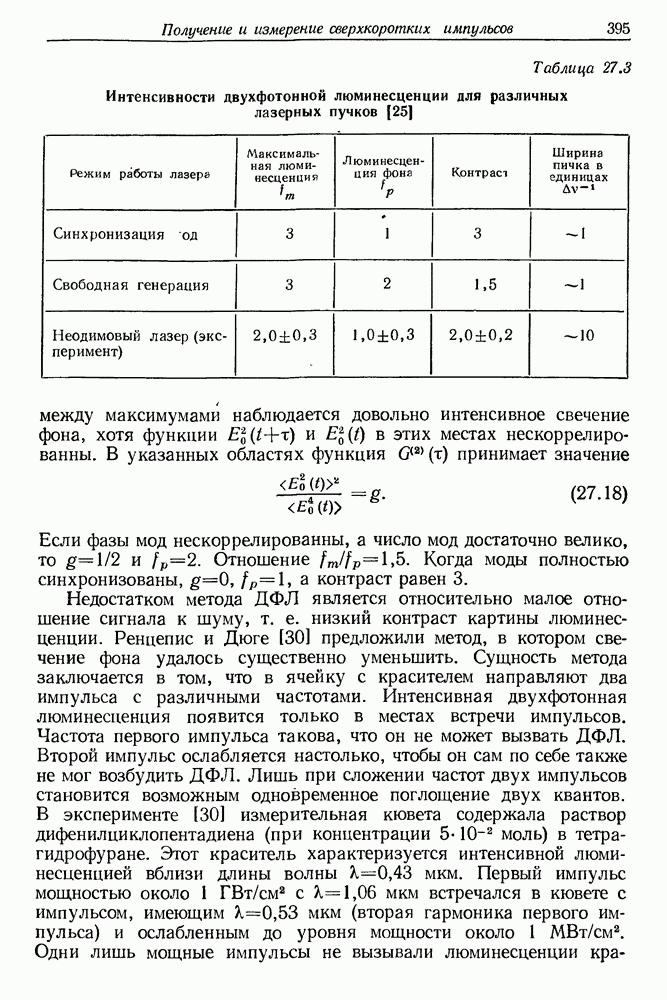
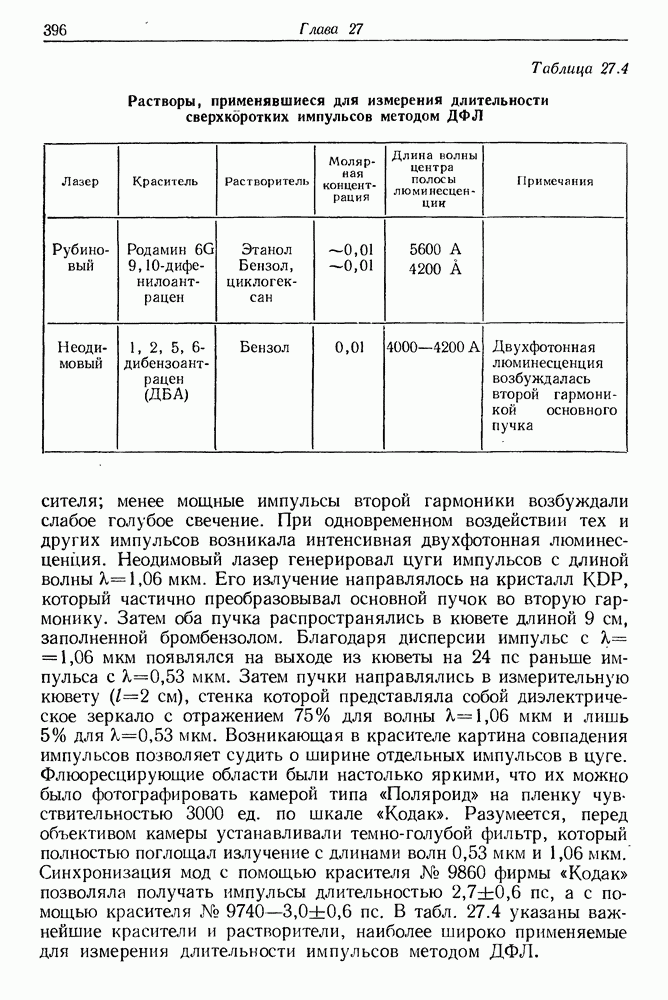
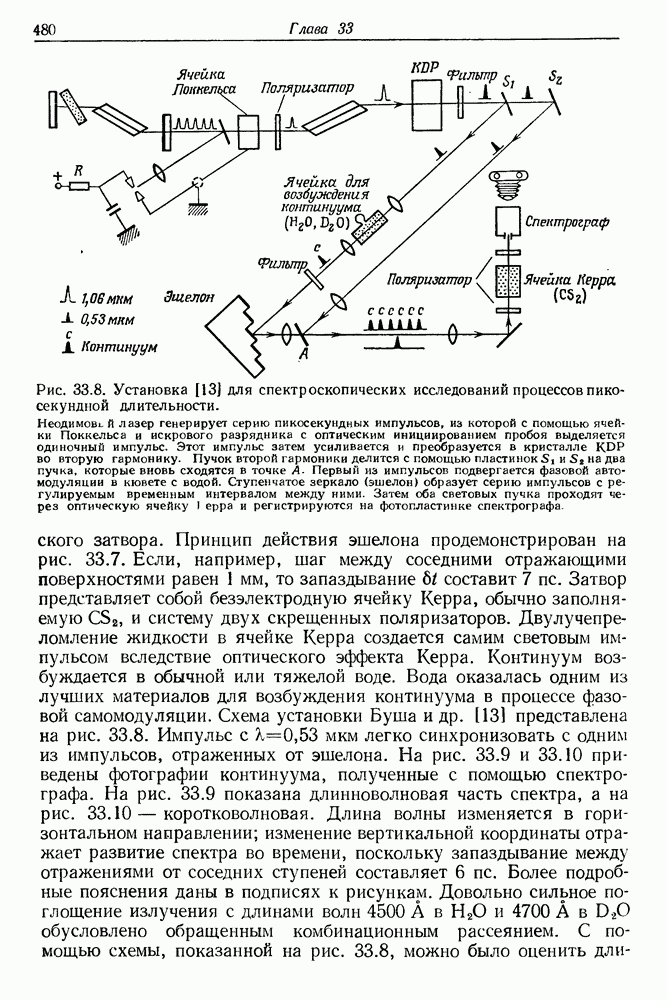
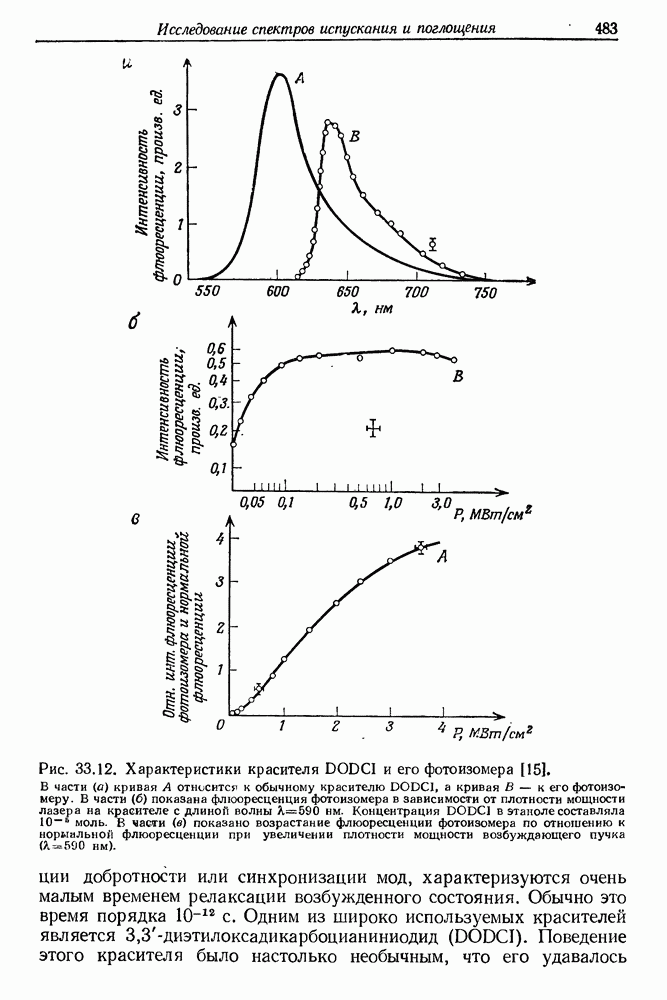
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
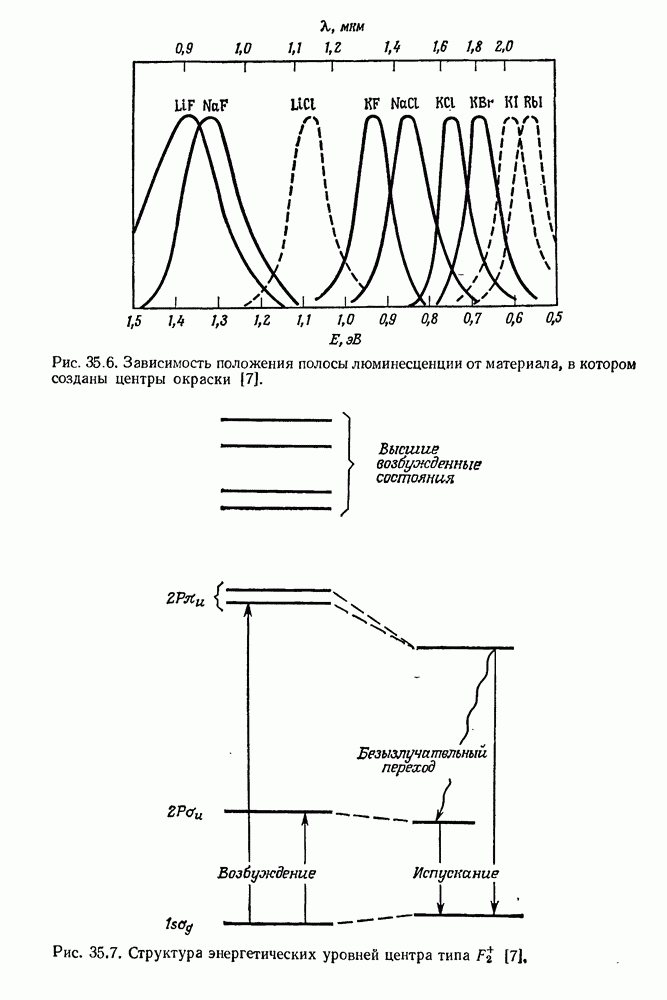
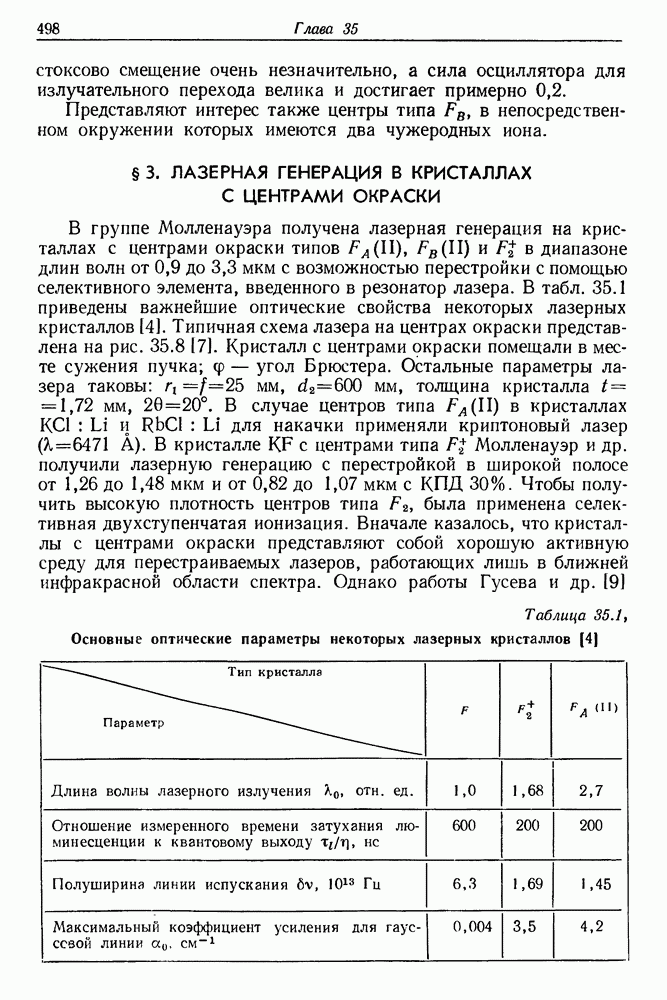
- 35. Лазеры на центрах окраски
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
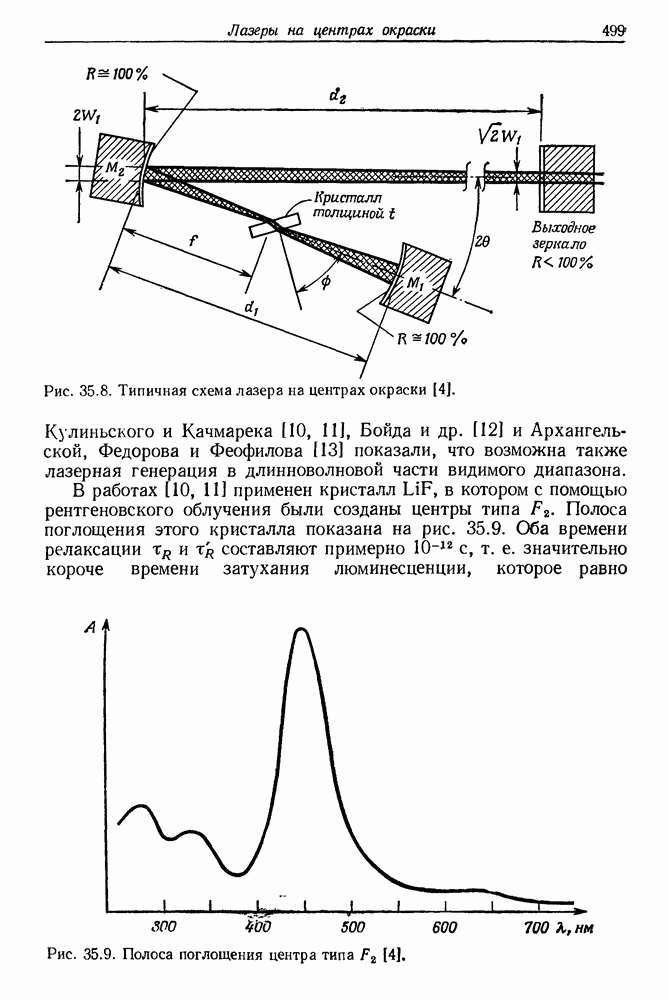
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
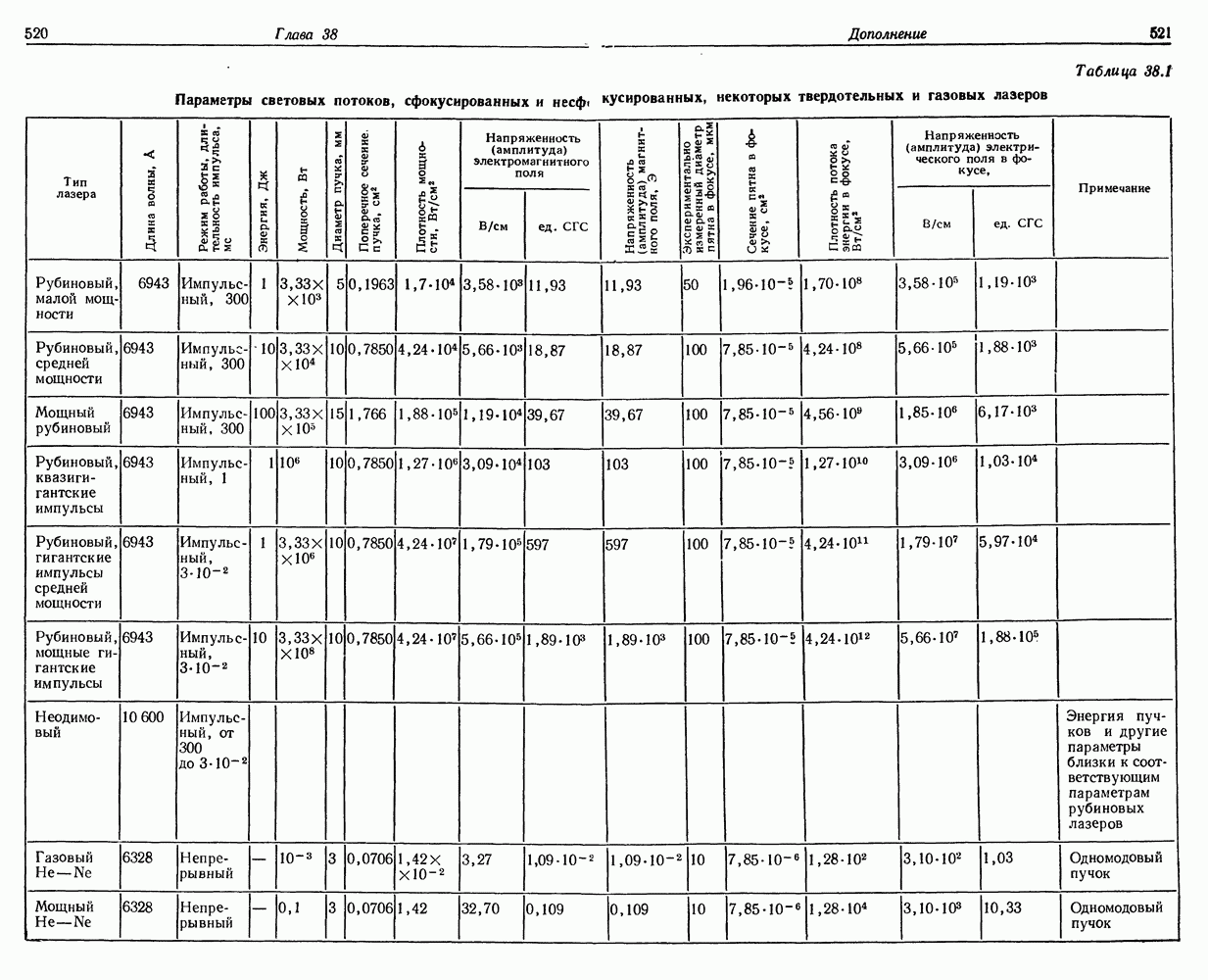
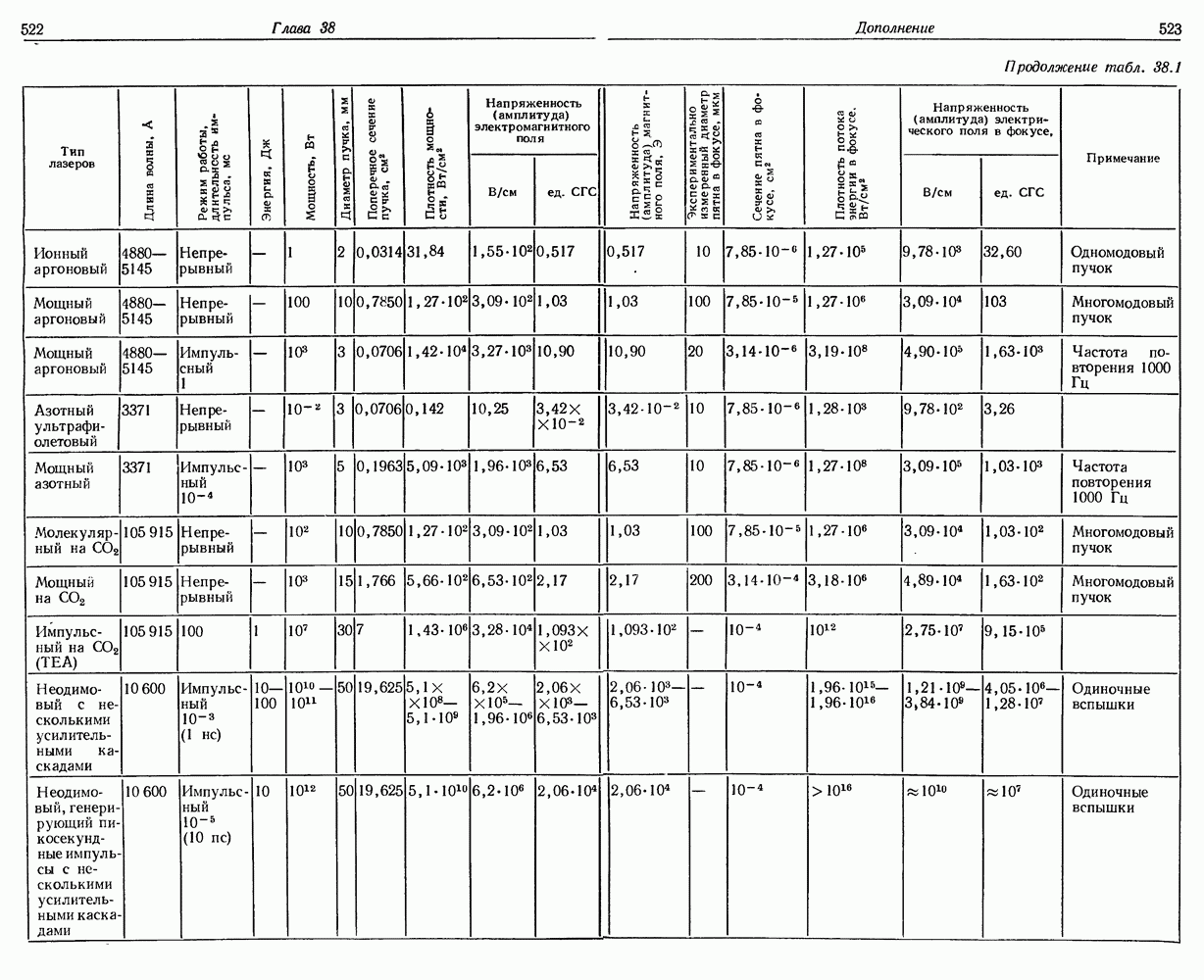
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
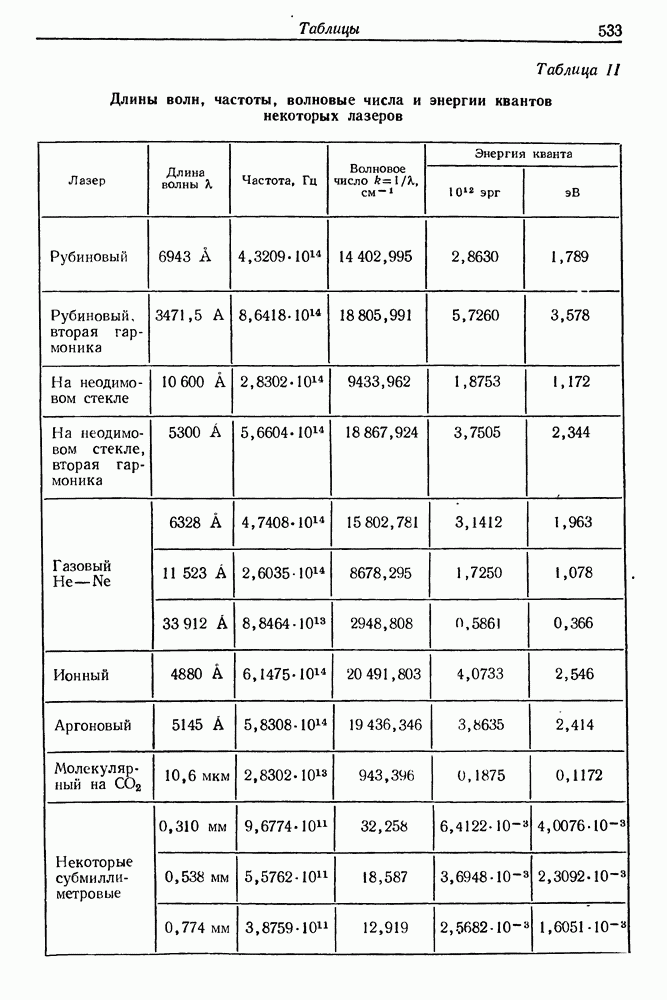
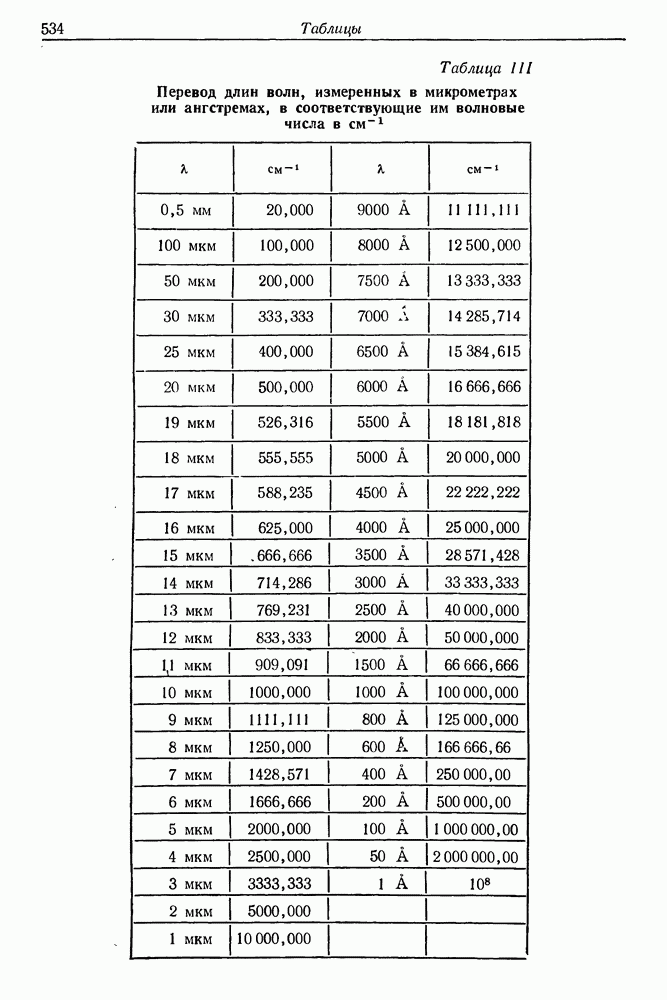
- Таблицы