| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
Чиао, Гармайр и Таунс [6] рассмотрели условия, при которых свет может создать в нелинейной среде волновод и затем распространяться по нему без дифракционных потерь. Приведем здесь некоторые результаты из работы [6], а также из обзора Ахманова и др. [14].
Пусть световой пучок распространяется в канале с увеличенным показателем преломления под углом  к его оси (рис. 24.6). Условие полного внутреннего отражения от границы между областями с различными показателями преломления будет выполнено для угла
к его оси (рис. 24.6). Условие полного внутреннего отражения от границы между областями с различными показателями преломления будет выполнено для угла  равного
равного


Рис. 24.6. Распространение света в канале с увеличенным показателем преломления. При некоторых углах  происходит полное внутреннее отражение от границы областей с различными показателями преломления.
происходит полное внутреннее отражение от границы областей с различными показателями преломления.

Рис. 24.7. Распространение светового пучка в нелинейной среде (вверху), а также в эквивалентной схеме (внизу) [14].
Действие среды эквивалентно действию собирающей линзы с фокусным расстоянием  хотя реальные траектории лучей искривлены.
хотя реальные траектории лучей искривлены.
Благодаря дифракции, световой пучок диаметром 2 а будет иметь расходимость

где  — длина световой волны в вакууме. Если
— длина световой волны в вакууме. Если  пучок при распространении в среде будет расходиться, но несколько медленнее, чем в линейной среде. При
пучок при распространении в среде будет расходиться, но несколько медленнее, чем в линейной среде. При  вклад нелинейности среды настолько велик, что полностью компенсирует дифракционную расходимость. В последнем случае пучок сужается в нелинейной среде (самофокусировка), а траектории лучей искривляются (рис. 24.7). На некотором расстоянии
вклад нелинейности среды настолько велик, что полностью компенсирует дифракционную расходимость. В последнем случае пучок сужается в нелинейной среде (самофокусировка), а траектории лучей искривляются (рис. 24.7). На некотором расстоянии  пучок проходит через фокус и далее распространяется в узком канале уже без дифракционных потерь (автоколлимация). С помощью формулы (24.3) находим амплитуду электрического поля световой волны, испытывающей автоколлимацию:
пучок проходит через фокус и далее распространяется в узком канале уже без дифракционных потерь (автоколлимация). С помощью формулы (24.3) находим амплитуду электрического поля световой волны, испытывающей автоколлимацию:

Здесь использовано разложение функции  в ряд (для малых
в ряд (для малых  ). В общем виде мощность излучения записывается в виде
). В общем виде мощность излучения записывается в виде

где 
В случае  из выражений (24.4) — (24.6) находим пороговую мощность, необходимую для автоколлимации пучка
из выражений (24.4) — (24.6) находим пороговую мощность, необходимую для автоколлимации пучка

Все величины выражены в единицах СГС. Введем по Ахманову и др. [14] дифракционную длину в виде

Из рис. 24.6 и 24.7 видно, что условие  эквивалентно выражению
эквивалентно выражению

Величину  можно рассматривать как длину (путь) самофокусировки. В эквивалентной схеме процесса естественную дифракцию можно представить в виде рассеивающей линзы с фокусным расстоянием
можно рассматривать как длину (путь) самофокусировки. В эквивалентной схеме процесса естественную дифракцию можно представить в виде рассеивающей линзы с фокусным расстоянием 
Рассмотрим вкратце роль электрострикции, а также оптической ориентации молекул в процессе сужения светового пучка. Предположим, что зависимость диэлектрической проницаемости от поля имеет вид

Запишем подобное выражение для показателя преломления

Поскольку  то или
то или 
Если в результате электрострикции изменяется плотность вещества, то меняется и его показатель преломления. Эти две величины связаны формулой Клаузиуса — Моссоти

где а — электронная поляризуемость.
Использование формулы (24.12) для конденсированных сред носит довольно ограниченный характер, поэтому дальнейшее рассмотрение является приближенным.
Пусть  Положим в первом приближении
Положим в первом приближении

Тогда

Поправку  рассчитывают, решая уравнение для акустических волн. Можно показать, что стационарное решение этого уравнения
рассчитывают, решая уравнение для акустических волн. Можно показать, что стационарное решение этого уравнения
имеет вид

где  — коэффициент сжимаемости,
— коэффициент сжимаемости,  — коэффициент, определяющий изменение
— коэффициент, определяющий изменение  при увеличении плотности, т. е. электрострикционного давления. Изменения
при увеличении плотности, т. е. электрострикционного давления. Изменения  в световом поле того же порядка, что и изменения
в световом поле того же порядка, что и изменения  Таким образом, эффект электрострикции может привести к увеличению показателя преломления среды, причем время релаксации этого процесса довольно велико, например, по сравнению с временем релаксации Дебая. Прирост
Таким образом, эффект электрострикции может привести к увеличению показателя преломления среды, причем время релаксации этого процесса довольно велико, например, по сравнению с временем релаксации Дебая. Прирост  показателя преломления среды (нитробензола) можно записать в виде [15]
показателя преломления среды (нитробензола) можно записать в виде [15]

где  — угол между векторами электрических полей измерительного и мощного возбуждающего пучков. Величина
— угол между векторами электрических полей измерительного и мощного возбуждающего пучков. Величина  измеряется
измеряется

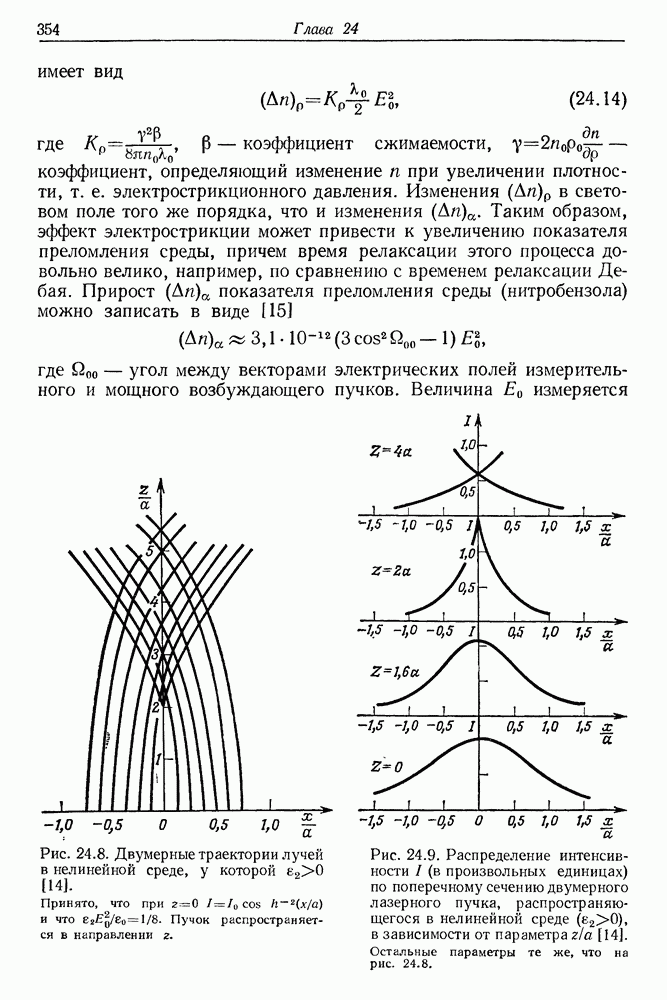
Рис. 24.8. Двумерные траектории лучей в нелинейной среде, у которой  Принято, что при
Принято, что при  и что
и что  Пучок распространяется в направлении
Пучок распространяется в направлении 

Рис. 24.9. Распределение интенсивности  (в произвольных единицах) по поперечному сечению двумерного лазерного пучка, распространяющегося в нелинейной среде
(в произвольных единицах) по поперечному сечению двумерного лазерного пучка, распространяющегося в нелинейной среде  в зависимости от параметра
в зависимости от параметра  Остальные параметры те же, что на рис. 24.8.
Остальные параметры те же, что на рис. 24.8.
в единицах СГСЭ. В этом случае время релаксации процесса составляет  с. Общее решение задачи самофокусировки или автоколлимации получают с помощью уравнений Максвелла при определенных начальных условиях (диаметр пучка, распределение напряженности поля по сечению пучка, поляризация излучения, форма волнового фронта). Можно также воспользоваться обобщенными уравнениями геометрической оптики.
с. Общее решение задачи самофокусировки или автоколлимации получают с помощью уравнений Максвелла при определенных начальных условиях (диаметр пучка, распределение напряженности поля по сечению пучка, поляризация излучения, форма волнового фронта). Можно также воспользоваться обобщенными уравнениями геометрической оптики.
На рис. 24.8 и 24.9 проиллюстрированы результаты таких решений [14]. Первый рисунок показывает траектории световых лучей в нелинейной среде, в которой  Сужение светового пучка эквивалентно увеличению плотности энергии вблизи оси пучка, что хорошо видно на рис. 24.9.
Сужение светового пучка эквивалентно увеличению плотности энергии вблизи оси пучка, что хорошо видно на рис. 24.9.
Очень интересную идею бегущих фокусов, объясняющую возникновение автоколлимированных нитей с микронными диаметрами, предложили Дышко, Луговой и Прохоров [16]. Экспериментальное подтверждение этой идеи получено Коробкиным, Прохоровым и Щелевым [17] и др. Длительность существования микронных автоколлимированных нитей составляет 0,5 не или даже меньше. Они возникают и изчезают в различных точках нелинейной среды. Зарегистрировано также перемещение отдельных светящихся точек со скоростью порядка 109 см/с. Количество нитей в поперечном сечении лазерного пучка зависит от его максимальной мощности [18]. Если мощность лазера лишь незначительно превышает некоторое пороговое значение, то появляется только одна автоколлимированная нить.
Предположив более сложную зависимость показателя преломления нелинейной среды от напряженности поля,

Пекара [19] дал вполне удовлетворительное объяснение эффекта автоколлимации света. Развитие процесса зависит не только от значений коэффициентов  но прежде всего от их знаков. Необходимым условием возникновения автоколлимации является
но прежде всего от их знаков. Необходимым условием возникновения автоколлимации является  При
При  автоколлимация не наступает. Она возможна, лишь если
автоколлимация не наступает. Она возможна, лишь если  или
или  Принимая во внимание угловую корреляцию молекул с анизотропной поляризуемостью, Келих [20] рассчитал эти коэффициенты. Например, коэффициент
Принимая во внимание угловую корреляцию молекул с анизотропной поляризуемостью, Келих [20] рассчитал эти коэффициенты. Например, коэффициент  отрицателен для сероуглерода, ацетона, бромбензола и нитробензола и положителен для циклогексана, бензола и толуола.
отрицателен для сероуглерода, ацетона, бромбензола и нитробензола и положителен для циклогексана, бензола и толуола.
Интересное и весьма убедительное объяснение увеличения показателя преломления среды при воздействии лазерного импульса предложено Пекарой [21]. В модели Пекары коллективное состояние атомной решетки определяет изменения диэлектрической проницаемости (и показателя преломления) среды. Рассмотрим очень кратко эту модель на примере линейной цепочки атомов с изотропной поляризуемостью. Пусть цепочка находится в состоянии
колебаний (продольная мода оптической ветви), которое характеризуется волновым числом  Сильное электрическое поле световой волны индуцирует диполи в атомах цепочки. Взаимодействие диполей заставляет их смещаться, что приводит к увеличению амплитуды колебаний. Это в свою очередь сопровождается возрастанием оптической поляризуемости системы. Пекара использовал потенциал Ленарда-Джонса с учетом ангармоничности колебаний атомов цепочки и получил следующую формулу для изменения диэлектрической проницаемости:
Сильное электрическое поле световой волны индуцирует диполи в атомах цепочки. Взаимодействие диполей заставляет их смещаться, что приводит к увеличению амплитуды колебаний. Это в свою очередь сопровождается возрастанием оптической поляризуемости системы. Пекара использовал потенциал Ленарда-Джонса с учетом ангармоничности колебаний атомов цепочки и получил следующую формулу для изменения диэлектрической проницаемости:

Согласно оценкам, постоянные  для регулярной цепочки атомов могут быть достаточно велики для возникновения самофокусировки. Поскольку при этом учитывается лишь электронная поляризуемость атомов, процесс характеризуется незначительной инерционностью, что позволяет объяснить самофокусировку даже пикосекундных импульсов света.
для регулярной цепочки атомов могут быть достаточно велики для возникновения самофокусировки. Поскольку при этом учитывается лишь электронная поляризуемость атомов, процесс характеризуется незначительной инерционностью, что позволяет объяснить самофокусировку даже пикосекундных импульсов света.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
- б. Вращающаяся призма
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
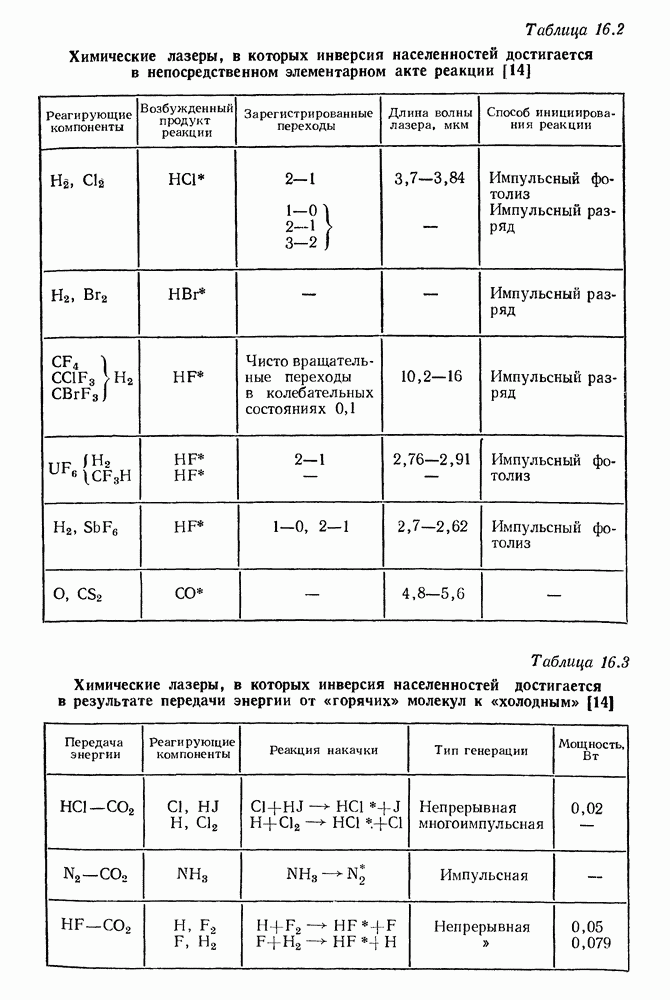
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
- 22. Параметрическая люминесценция (ПЛ)
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
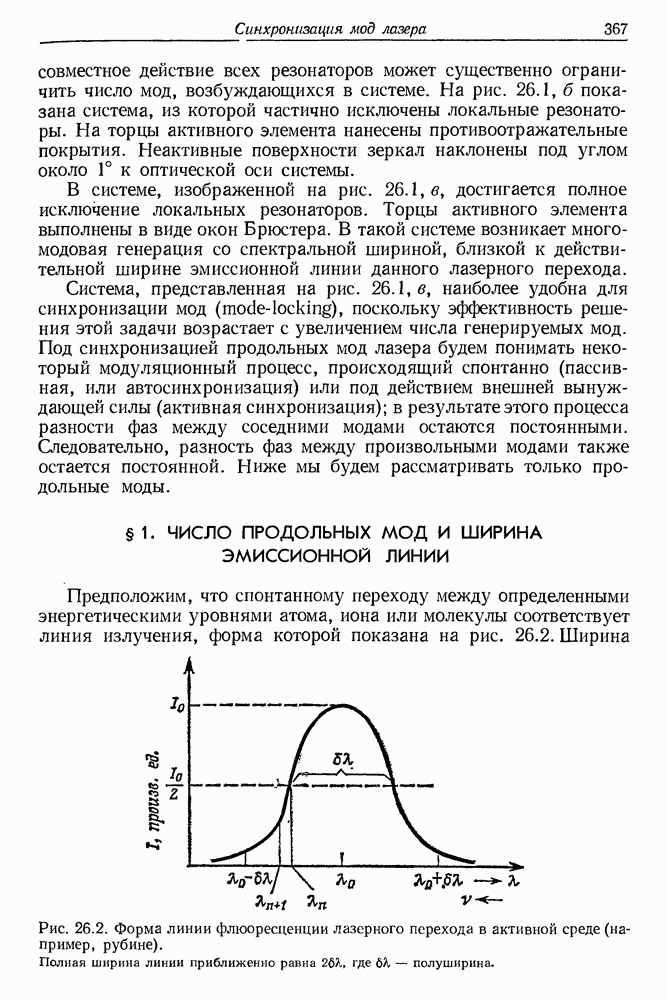
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
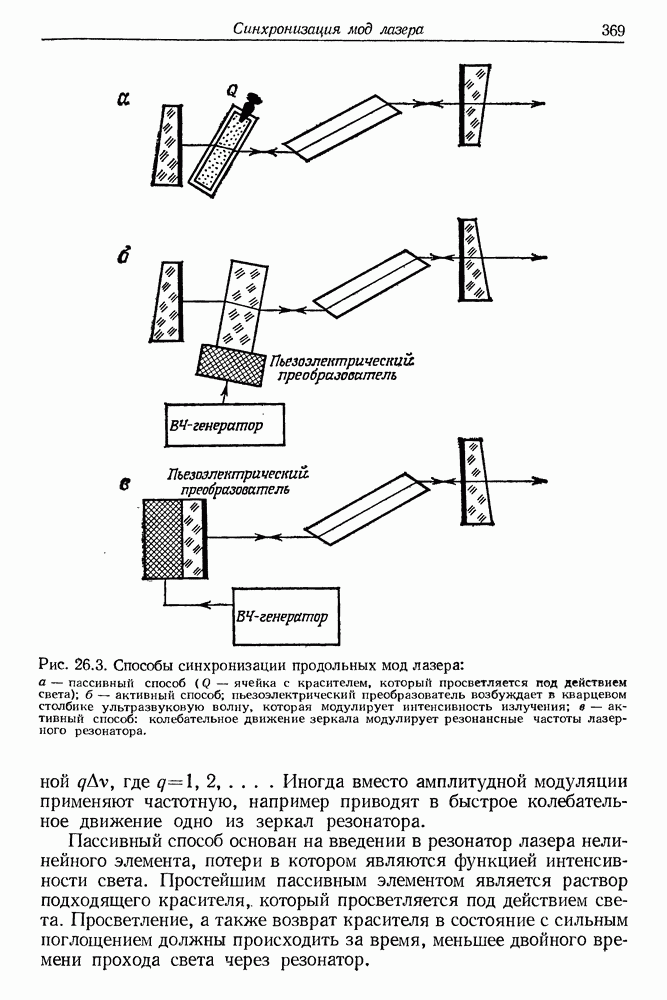
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
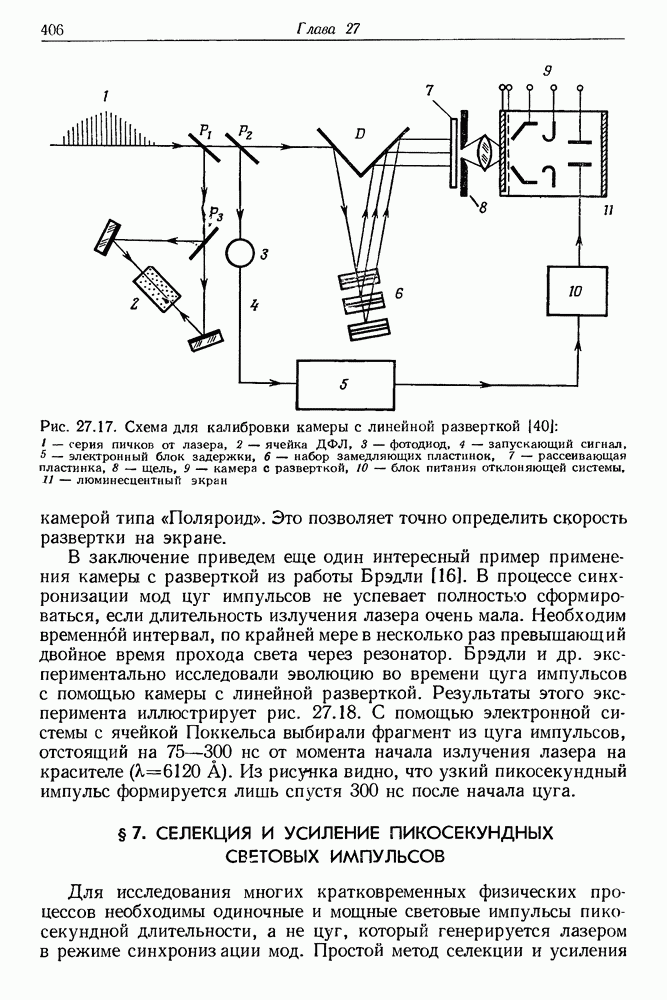
- в. Примеры использования камеры с разверткой
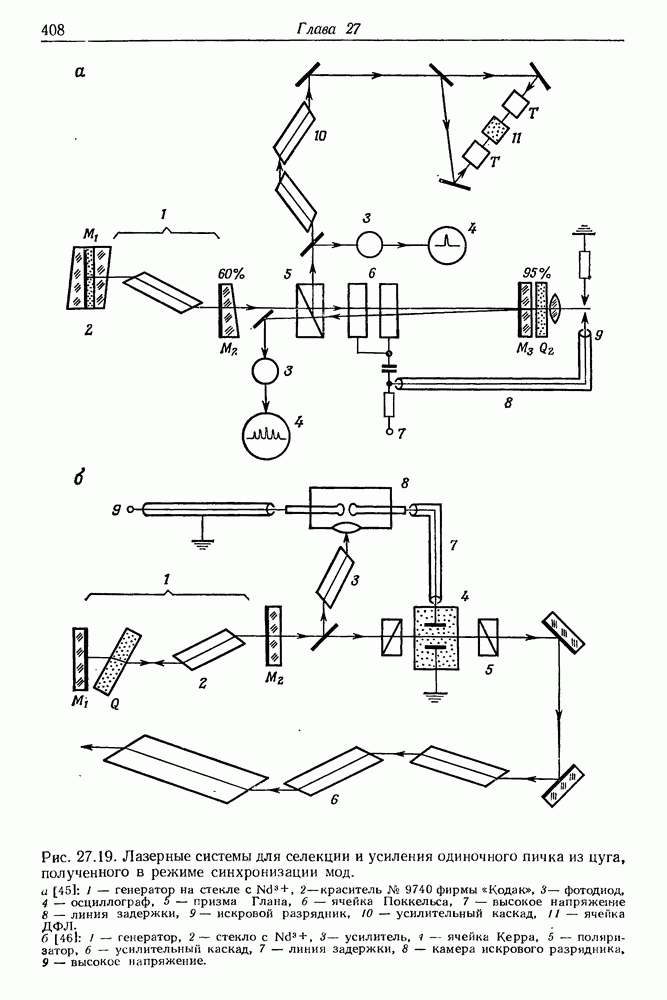
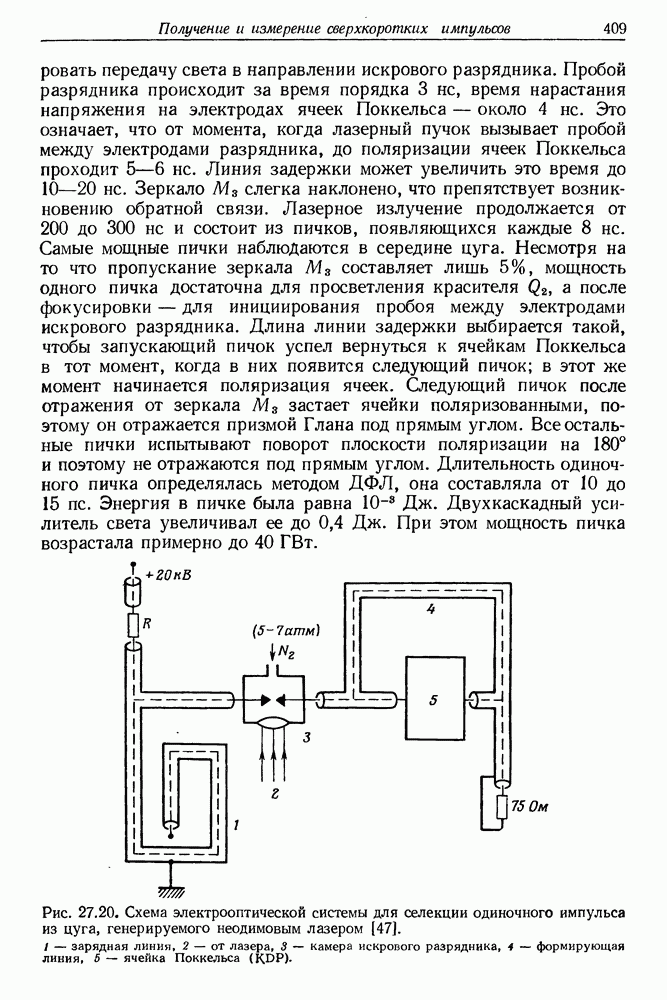
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
- 35. Лазеры на центрах окраски
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
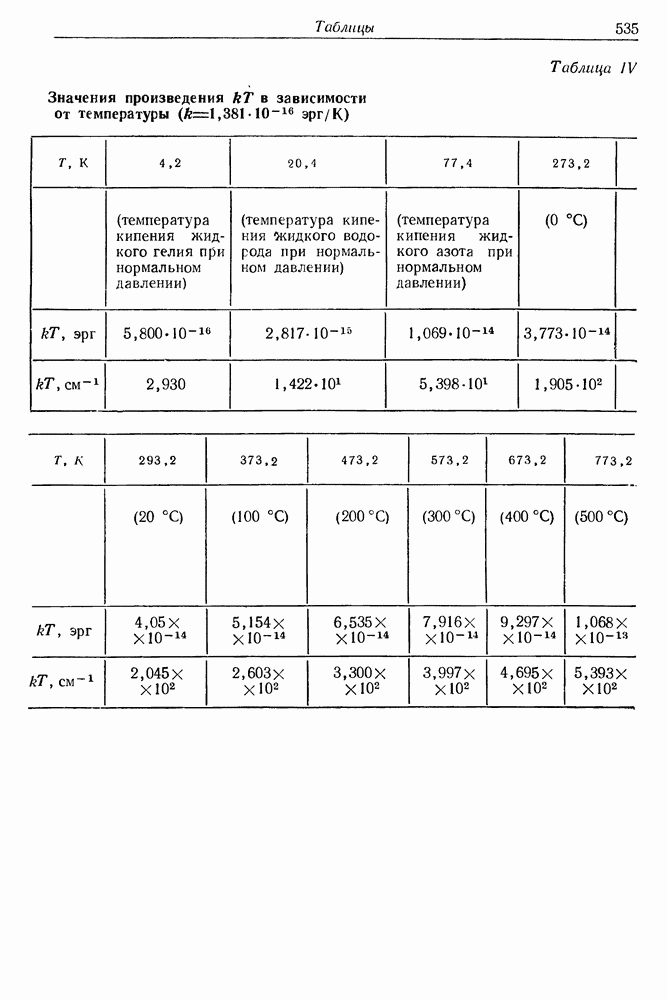
- Таблицы