| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. МАТРИЦА ПЛОТНОСТИ
С помощью матрицы плотности чаще всего рассчитывают средние значения и распределение вероятностей физических величин, если точная волновая функция системы неизвестна. В таких случаях говорят, что система находится в смешанном состоянии.
Допустим, что состояние системы можно описать волновой функцией 

где

 — полная ортонормированная последовательность функций. Пусть
— полная ортонормированная последовательность функций. Пусть  — оператор некоторой физической величины
— оператор некоторой физической величины  рассматриваемой системы. Среднее значение
рассматриваемой системы. Среднее значение  по определению равно
по определению равно

В матричной форме квантовой механики каждому оператору А ставится в соответствие матрица, определяемая следующим образом:

где  — полная ортонормированная последовательность функций. С учетом (36.39) выражение (36.38) принимает вид
— полная ортонормированная последовательность функций. С учетом (36.39) выражение (36.38) принимает вид

Допустим, что состояние системы точно не известно, т. е. невозможно определить коэффициенты  в формуле (36.37), а можно определить лишь средние значения произведения
в формуле (36.37), а можно определить лишь средние значения произведения  , т. е. стсп.
, т. е. стсп.
Тогда 

Положим 

Величины  называются элементами матрицы плотности. Теперь
называются элементами матрицы плотности. Теперь

Пользуясь правилом умножения элементов матрицы, запишем формулу (36.43) в виде

Сумма диагональных элементов матрицы называется ее следом. Его обычно обозначают символом 

Величина  называется также статистическим оператором. Чтобы найти его в явном виде, обычно пользуются связью между энтропией и матрицей плотности, а иногда и другими параметрами, описывающими состояние рассматриваемой системы. Поскольку точная волновая функция системы априори неизвестна, мы не располагаем полной информацией о системе. Основной величиной, которая служит мерой недостатка информации, является энтропия. В случае когда система полностью определена, энтропия тождественно равна нулю. Полная неопределенность системы соответствует максимальному значению энтропии. Максимализуя энтропию S при дополнительных условиях, которые отражают уровень нашей информации о системе, можно найти явный вид матрицы плотности. Воспользуемся с этой целью следующим уравнением квантовой статистики:
называется также статистическим оператором. Чтобы найти его в явном виде, обычно пользуются связью между энтропией и матрицей плотности, а иногда и другими параметрами, описывающими состояние рассматриваемой системы. Поскольку точная волновая функция системы априори неизвестна, мы не располагаем полной информацией о системе. Основной величиной, которая служит мерой недостатка информации, является энтропия. В случае когда система полностью определена, энтропия тождественно равна нулю. Полная неопределенность системы соответствует максимальному значению энтропии. Максимализуя энтропию S при дополнительных условиях, которые отражают уровень нашей информации о системе, можно найти явный вид матрицы плотности. Воспользуемся с этой целью следующим уравнением квантовой статистики:

и условием нормировки матрицы плотности

Допустим далее, что единственной известной величиной является средняя энергия системы:

При условиях (36.47) и (36.48) следует так выбрать  чтобы энтропия S была максимальной. Допуская возможность перестановки операций дифференцирования и
чтобы энтропия S была максимальной. Допуская возможность перестановки операций дифференцирования и  определим вариации выражений (36.46), (36.47) и (36.48):
определим вариации выражений (36.46), (36.47) и (36.48):

Однако условие максимума S требует, чтобы

После умножения уравнений (36.50) и (36.51) на неопределенные коэффициенты Лагранжа X и Р система уравнений (36.49) — (36.51) обращается в одно уравнение:

Оно справедливо только тогда, когда

или

Не определенный выше коэффициент  находится из условия нормировки (36.47); получаем
находится из условия нормировки (36.47); получаем

что с учетом (36.54) дает

Знаменатель в последнем выражении называется статистической суммой. Из формул (36.55) и (36.45) следует, что

Здесь остался не определенным параметр  Чтобы установить его физический смысл, рассмотрим резонатор, заполненный электромагнитным излучением, которое находится в равновесии со стенками, имеющими температуру Т. Рассчитаем среднюю энергию, заключенную в одной моде с частотой
Чтобы установить его физический смысл, рассмотрим резонатор, заполненный электромагнитным излучением, которое находится в равновесии со стенками, имеющими температуру Т. Рассчитаем среднюю энергию, заключенную в одной моде с частотой  . С этой целью воспользуемся гамильтонианом
. С этой целью воспользуемся гамильтонианом

который получается из более общего выражения (36.24) в пренебрежении энергией нулевых колебаний, т. е. членом В соответствии с (36.56) получаем

где

Ряд в знаменателе формулы (36.58) с учетом (36.59) сходится к

Если принять во внимание также, что

то формула (36.58) принимает следующий окончательный вид:

Это формула Планка. Из принципа соответствия известно, что в классическом пределе, т. е. при  должно определять энергию
должно определять энергию  классического гармонического осциллятора. С учетом этого, а также приближенного выражения
классического гармонического осциллятора. С учетом этого, а также приближенного выражения

определяем параметр (3:

где  — постоянная Больцмана. Таким образом, мы нашли явный вид матрицы плотности, соответствующий максимуму энтропии при условиях (36.47) и (36.48):
— постоянная Больцмана. Таким образом, мы нашли явный вид матрицы плотности, соответствующий максимуму энтропии при условиях (36.47) и (36.48):

Выражение (36.64) можно рассматривать как эквивалент классической функции распределения вероятностей. Однако это выражение справедливо лишь для системы, находящейся в стационарном состоянии, т. е. в состоянии термодинамического равновесия. Тогда гамильтониан  и матрица плотности
и матрица плотности  не изменяются во времени. В случае электромагнитного поля гамильтониан становится явной функцией времени, т. е. к части не зависящей от времени, следует добавить член
не изменяются во времени. В случае электромагнитного поля гамильтониан становится явной функцией времени, т. е. к части не зависящей от времени, следует добавить член  . В этом случае матрица плотности становится функцией времени, и ее эволюция описывается уравнением Неймана
. В этом случае матрица плотности становится функцией времени, и ее эволюция описывается уравнением Неймана

в котором скобки обозначают коммутатор. Если возмущение, вносимое полем, невелико, это уравнение можно решить методом последовательных приближений. Принимают, что в нулевом приближении, т. е. в отсутствие поля, формула (36.64) справедлива. В первом приближении матрицу плотности  находят из
находят из
уравнения

в котором  обозначает момент начала возмущения, а
обозначает момент начала возмущения, а  определяется выражением (36.64). Формула (36.66) вместе с (36.64) и (36.45) позволяет определять квантовомеханические средние значения любых физических величин в случае, когда система выведена возмущением из состояния равновесия.
определяется выражением (36.64). Формула (36.66) вместе с (36.64) и (36.45) позволяет определять квантовомеханические средние значения любых физических величин в случае, когда система выведена возмущением из состояния равновесия.
Чтобы проиллюстрировать применение уравнения движения Неймана, найдем изменение во времени элементов матрицы плотности для двухуровневого атома, возмущенного электромагнитным полем. Пусть энергии уровней равны

Соответствующие им стационарные волновые функции обозначим через  Поскольку система, согласно предположению, двухуровневая, ее матрица плотности будет состоять из двух строк и двух столбцов. В матричной форме уравнение (36.65) принимает вид
Поскольку система, согласно предположению, двухуровневая, ее матрица плотности будет состоять из двух строк и двух столбцов. В матричной форме уравнение (36.65) принимает вид

где введены обозначения

и использован тот факт, что  являются собственными функциями гамильтониана
являются собственными функциями гамильтониана  Считая, что
Считая, что  получаем
получаем

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

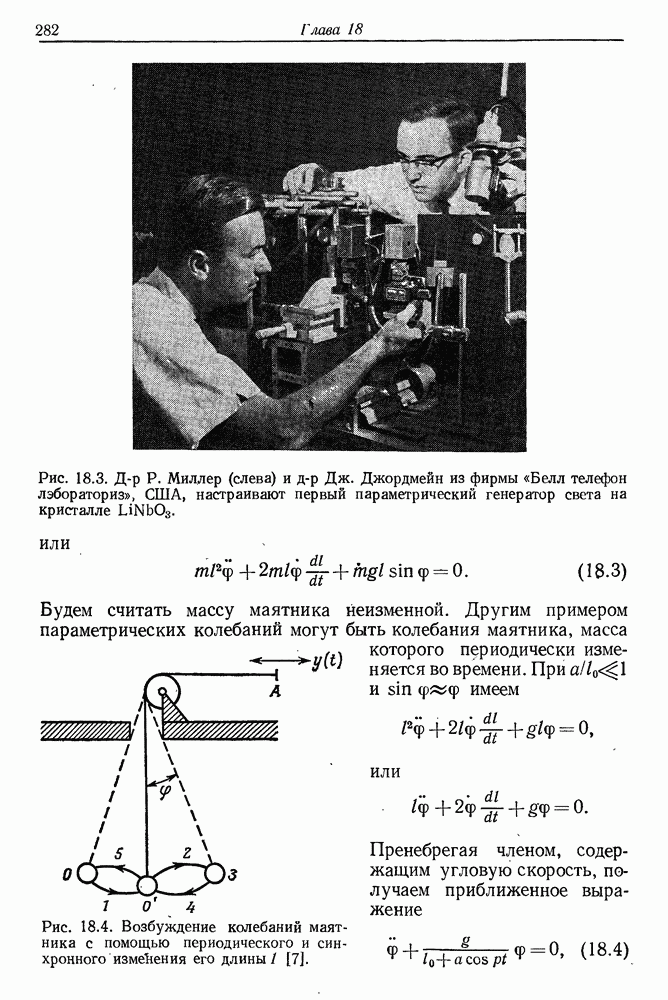
Рис. 36.1. Профессор В. Лэмб (младший) из Йельского университета (США). Создатель теории лазера, один из известных современных физиков.
систему из четырех уравнений:

Эта система с учетом релаксационных процессов (затухание возбужденных состояний атома) положена в основу теории газового лазера, развитой Лэмбом. Значение системы заключается в том, что хотя она относится к микроструктуре среды, она позволяет рассчитать макроскопическую поляризацию среды, выразив ее через недиагональные элементы матрицы  Численные расчеты выполняются методом последовательных приближений,
Численные расчеты выполняются методом последовательных приближений,
В приведенном ниже списке литературы указаны работы общего характера как по теоретическим основам квантовой электроники [1, 2, 4, 5, 6], так и по теории лазера [3, 7, 8].
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
- б. Вращающаяся призма
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
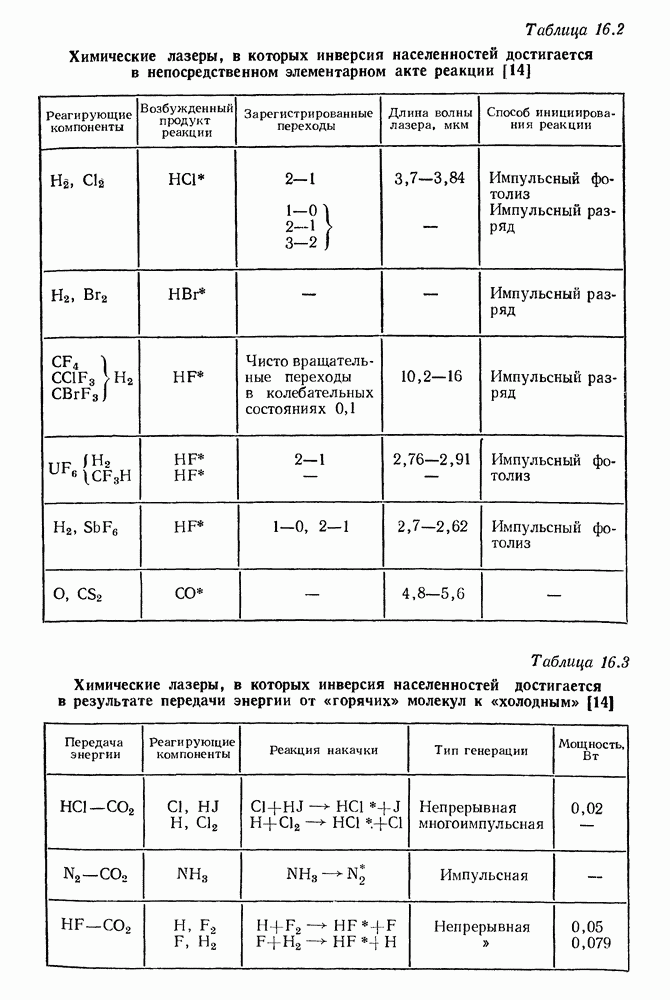
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
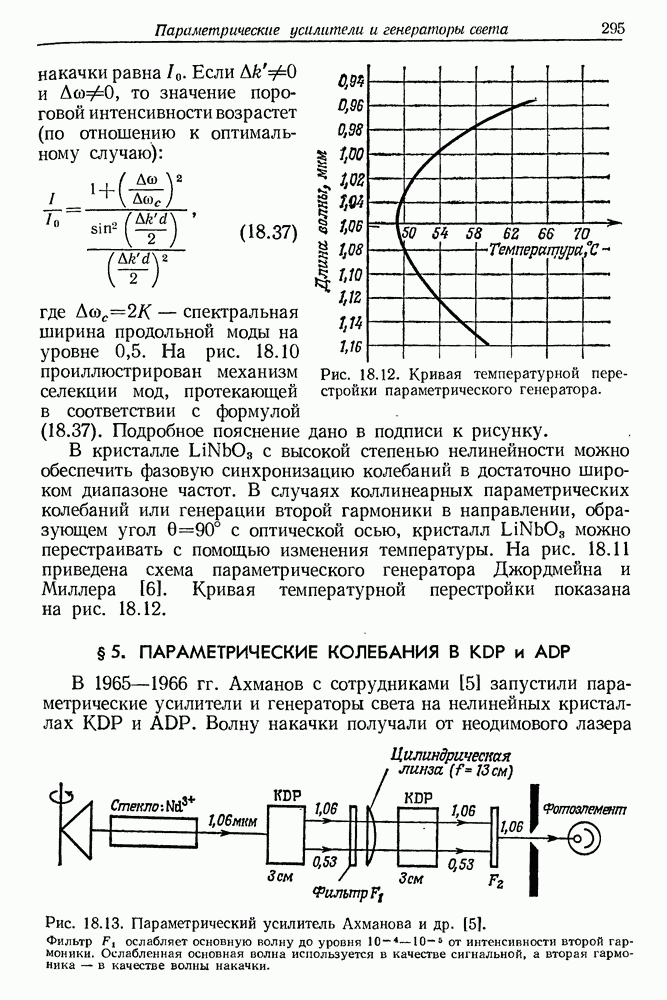
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
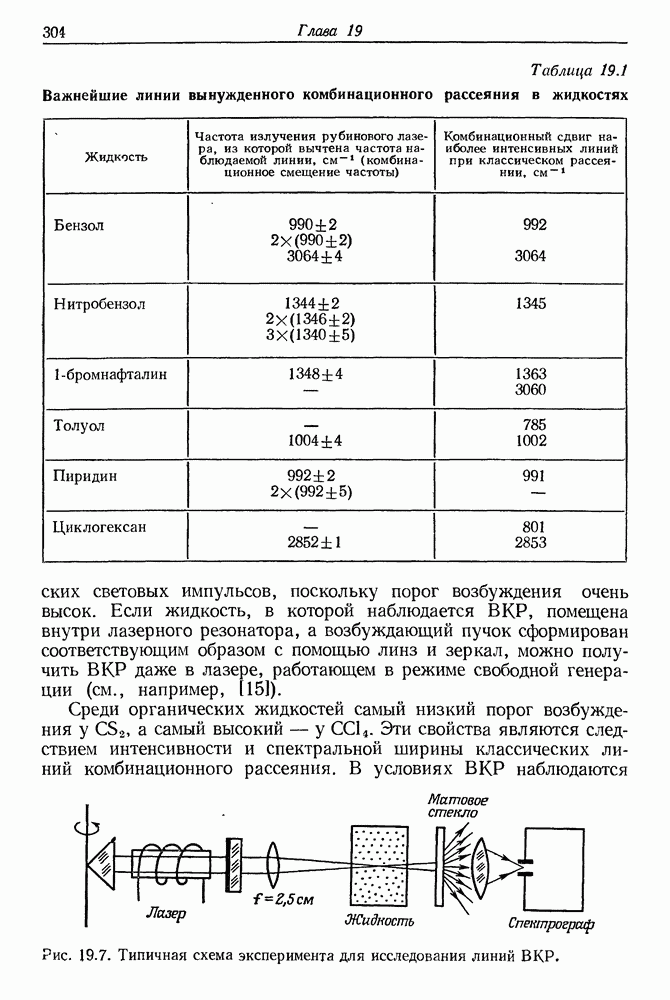
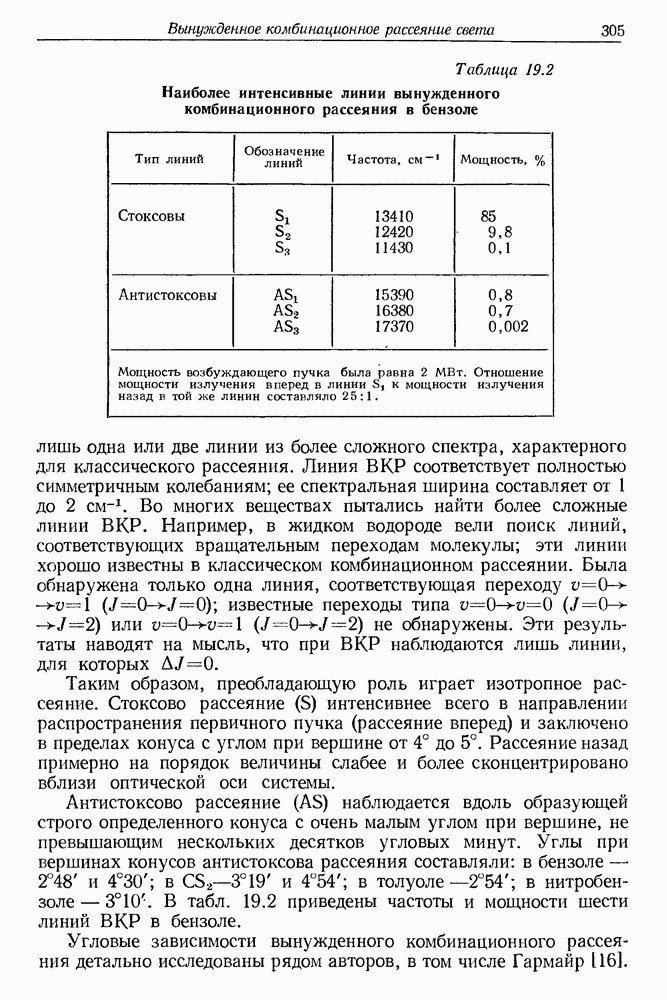
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
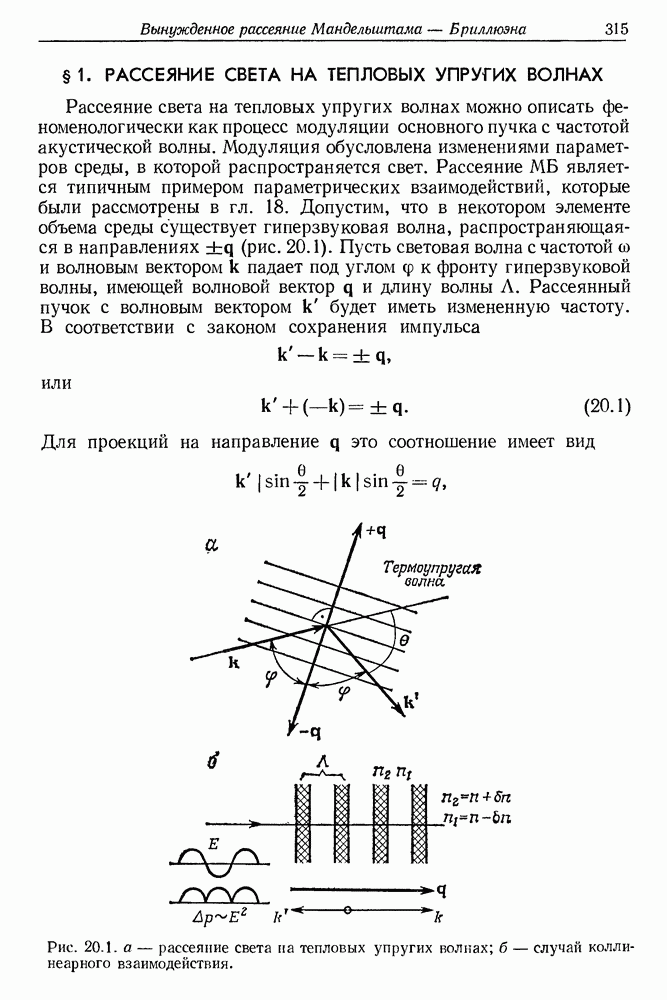
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
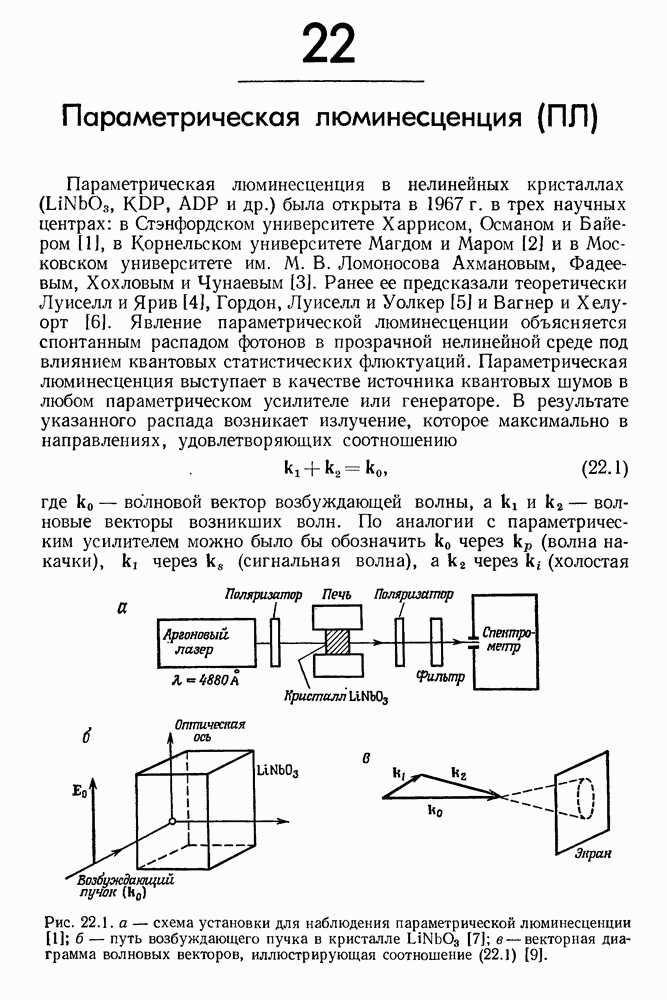
- 22. Параметрическая люминесценция (ПЛ)
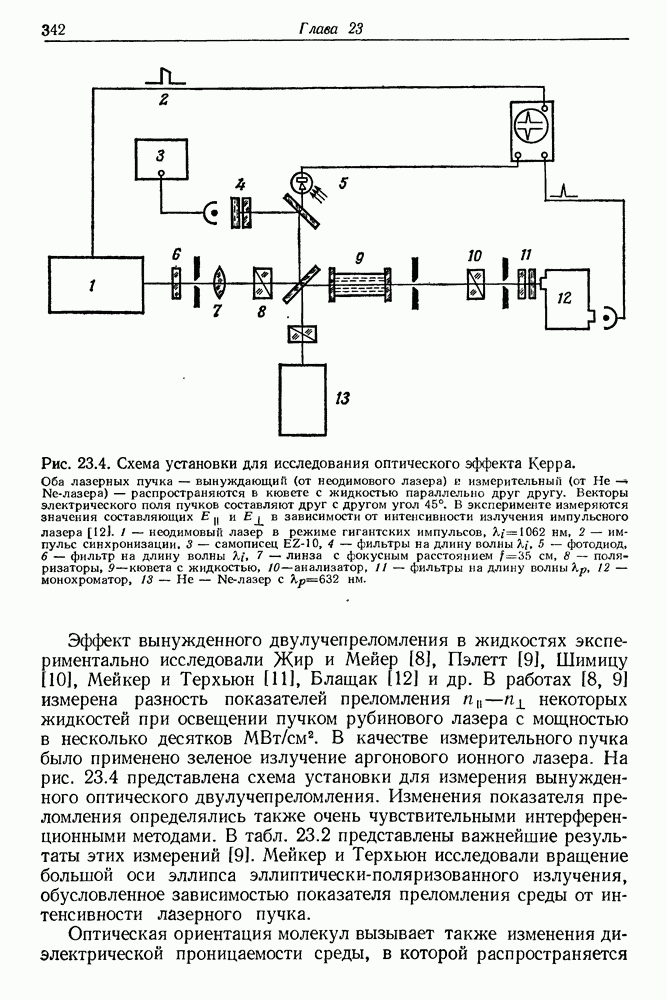
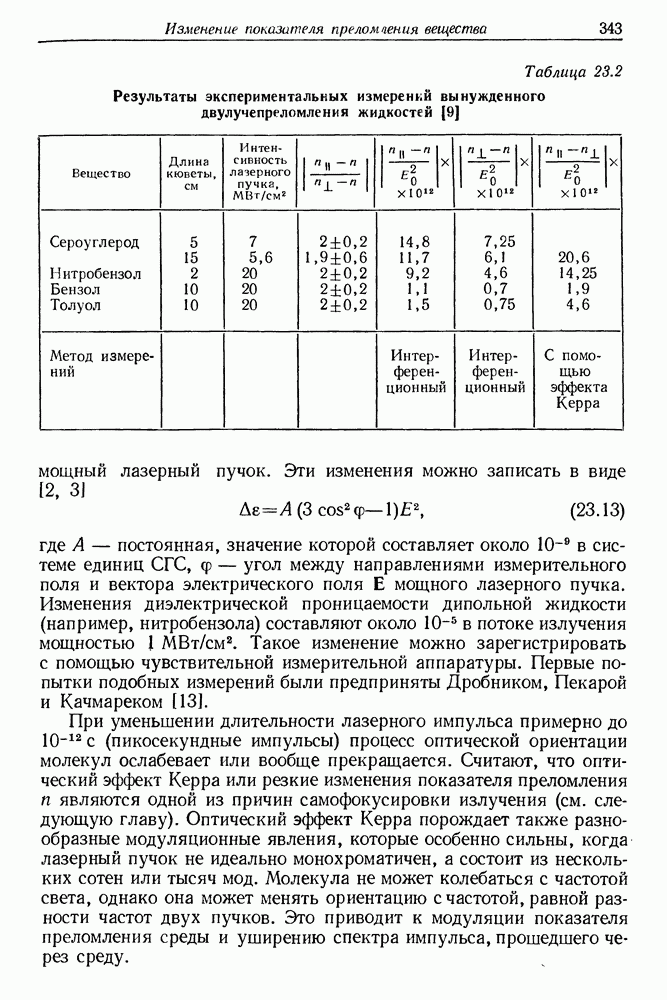
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
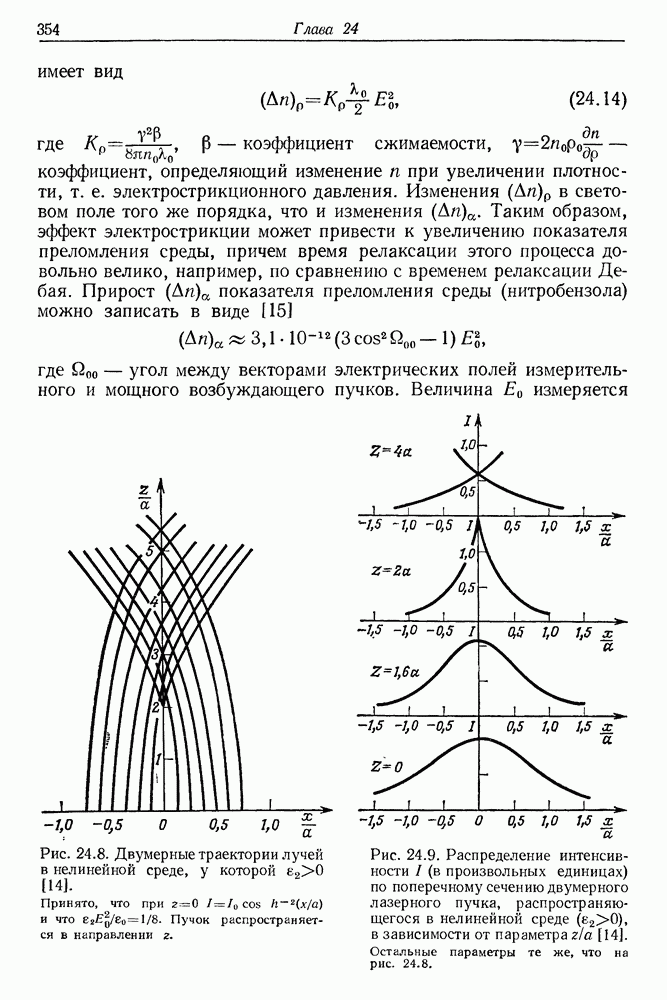
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
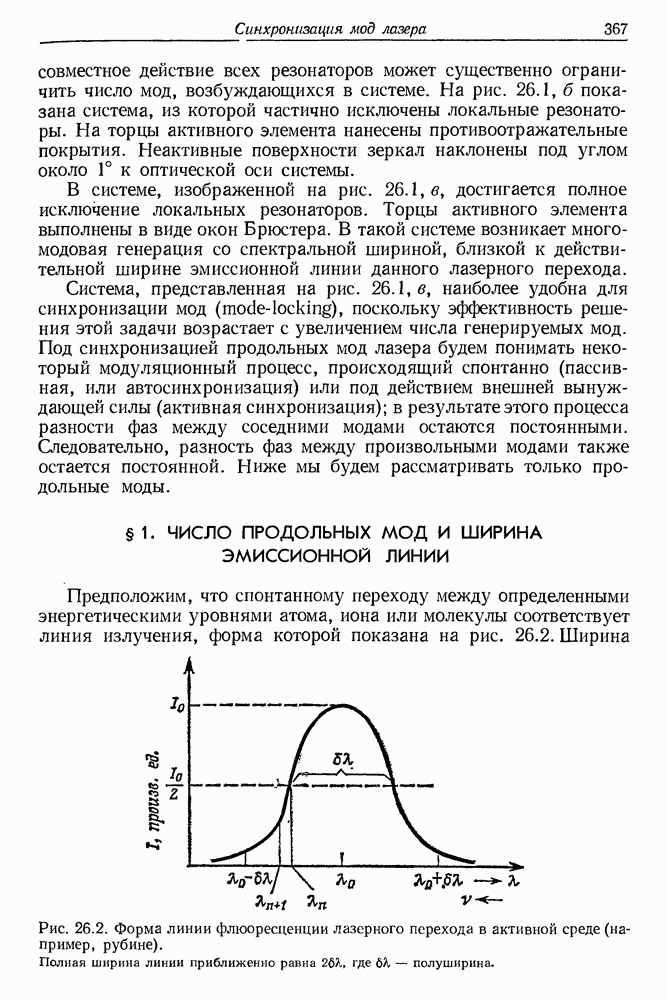
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
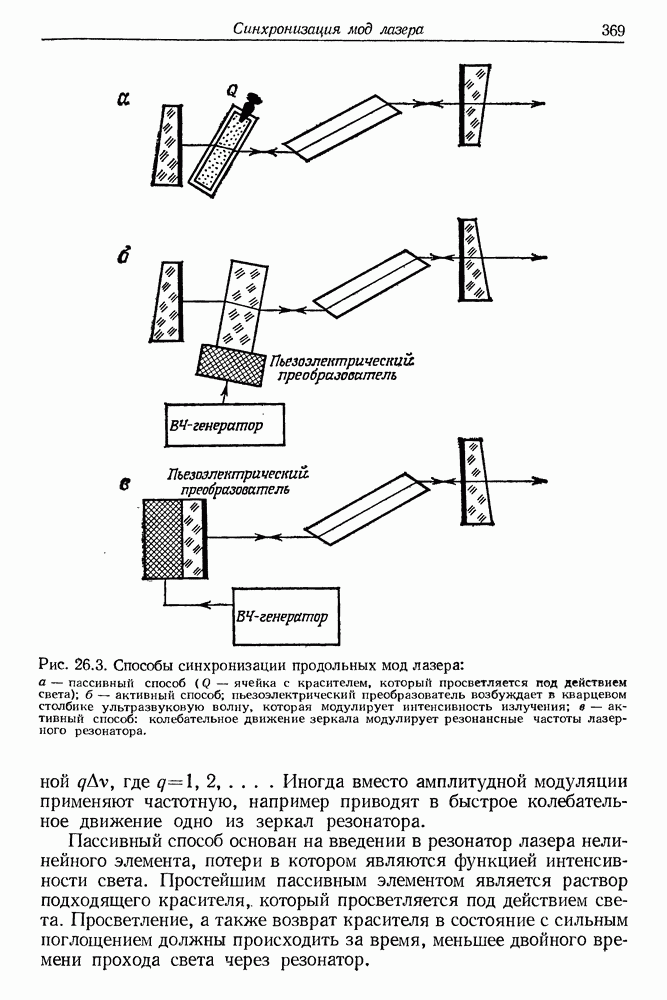
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
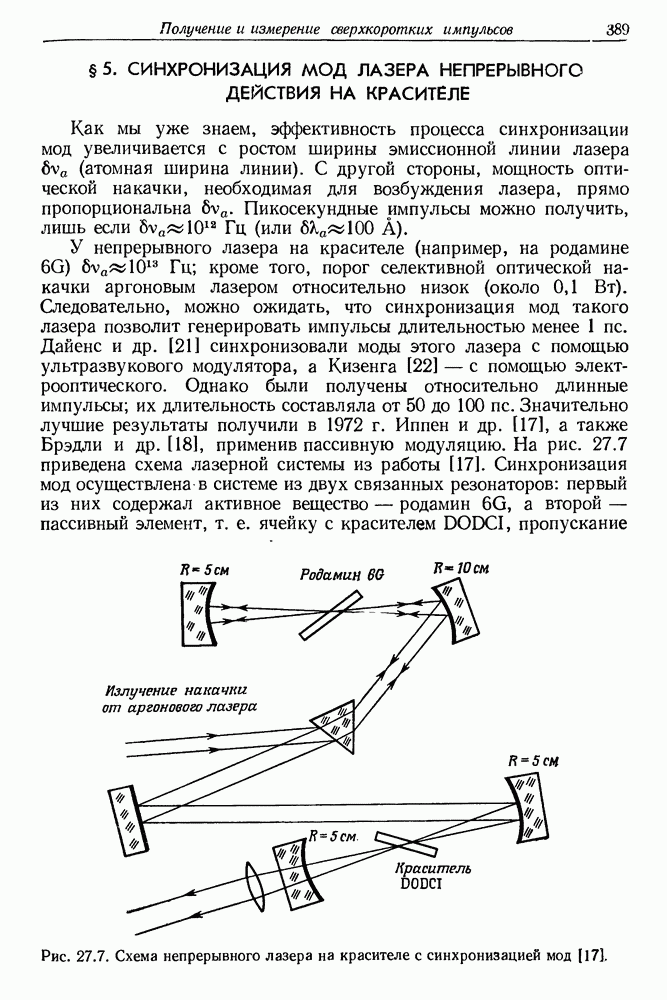
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
- в. Примеры использования камеры с разверткой
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
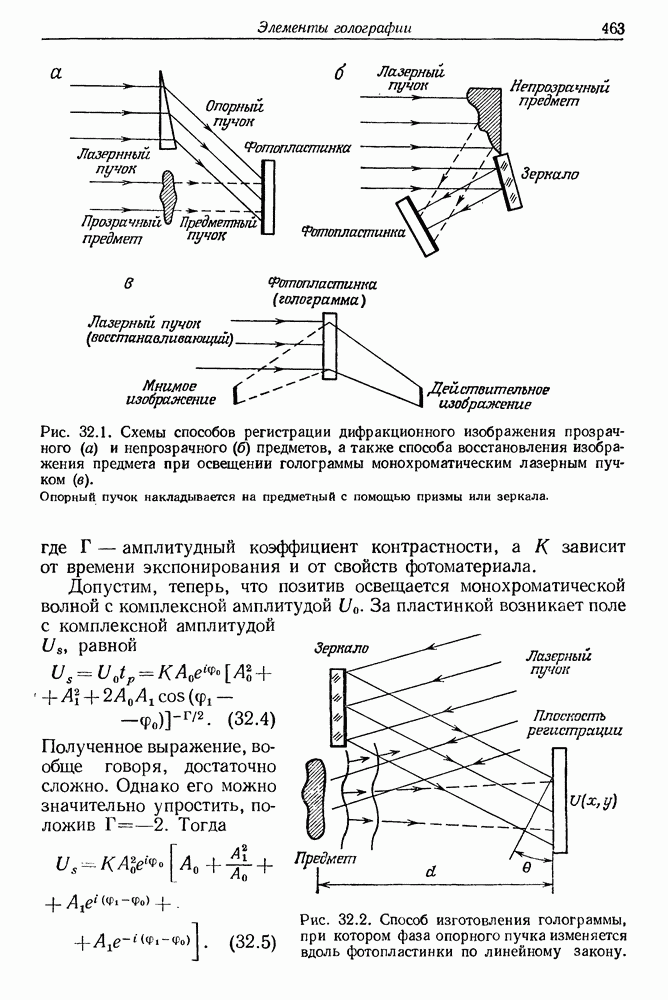
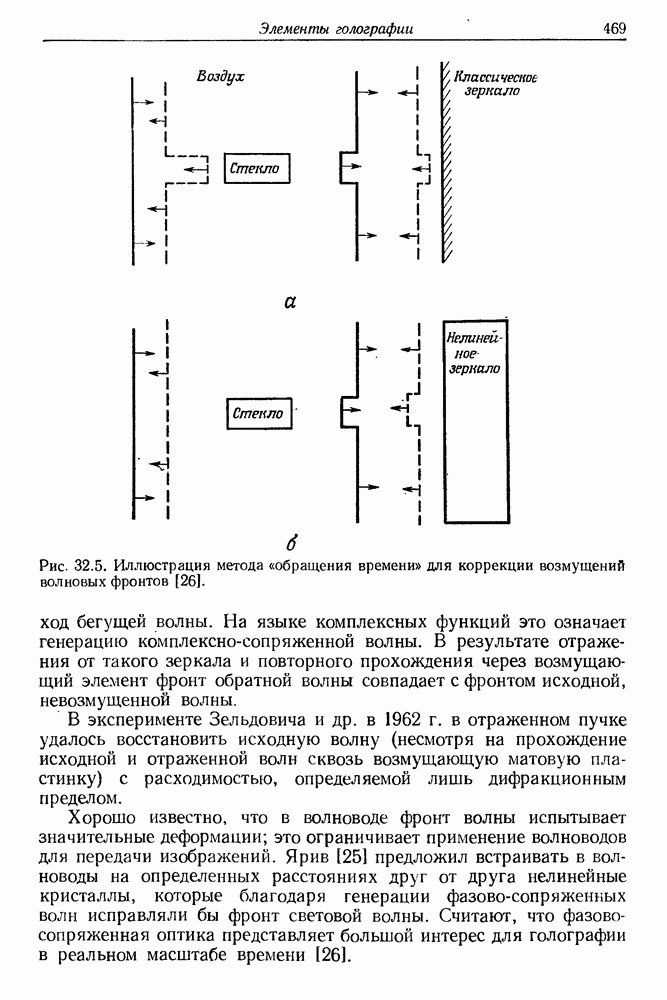
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
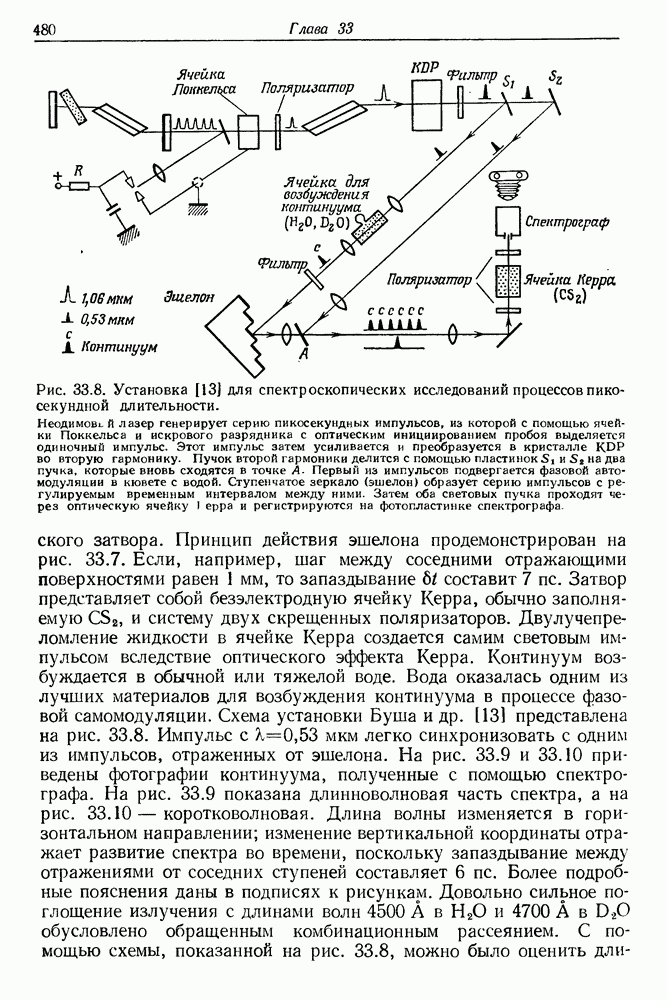
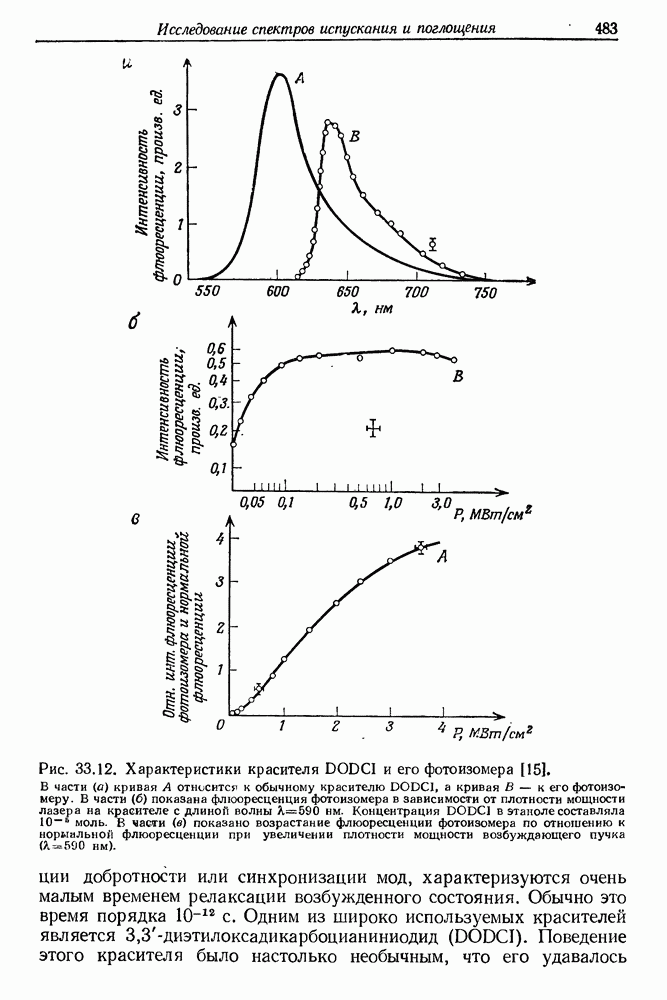
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
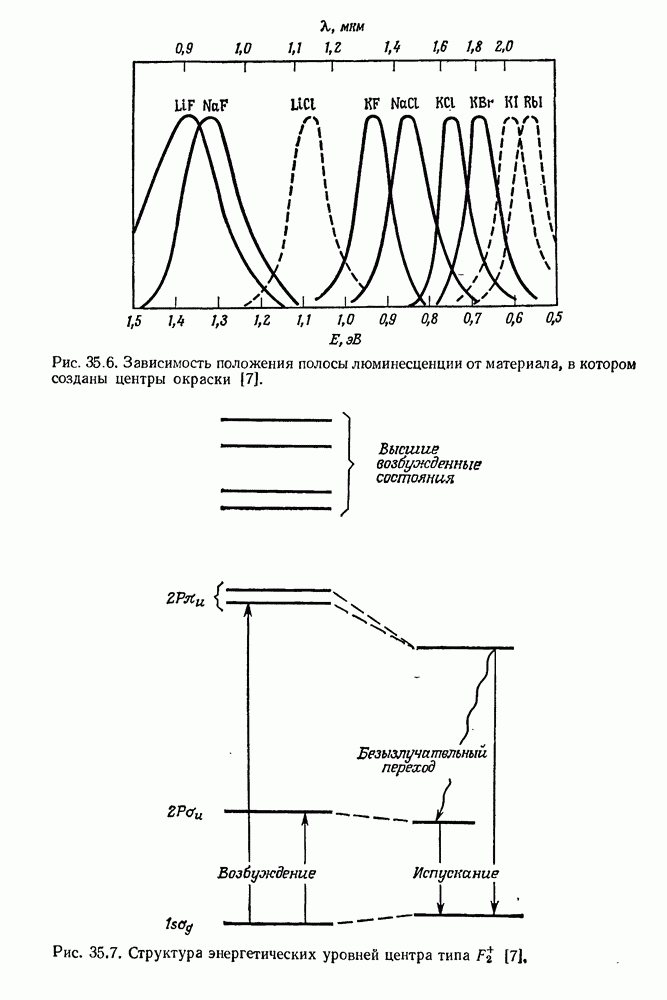
- 35. Лазеры на центрах окраски
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
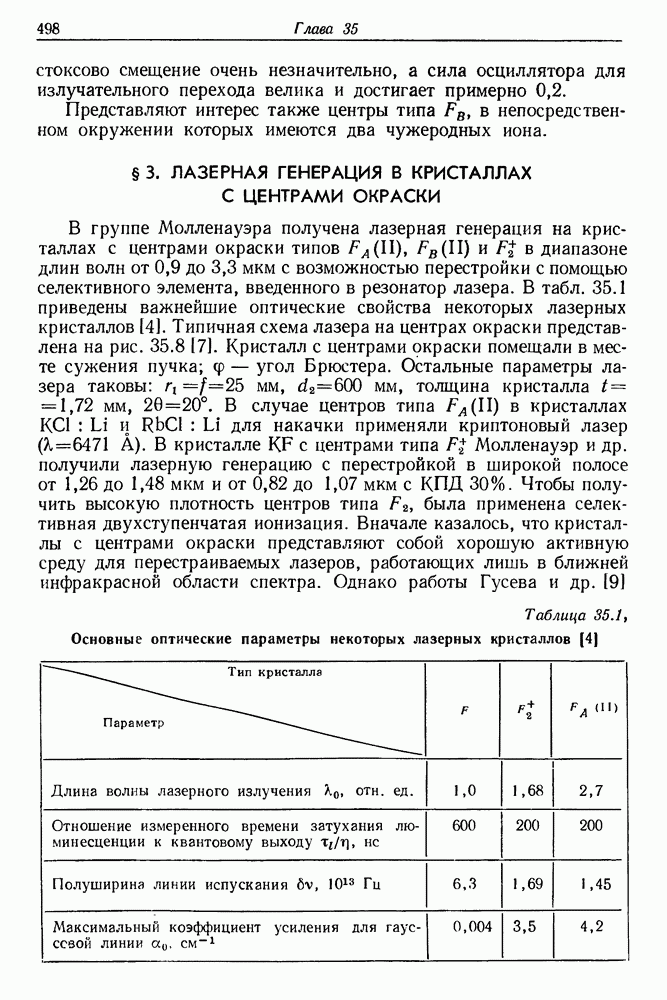
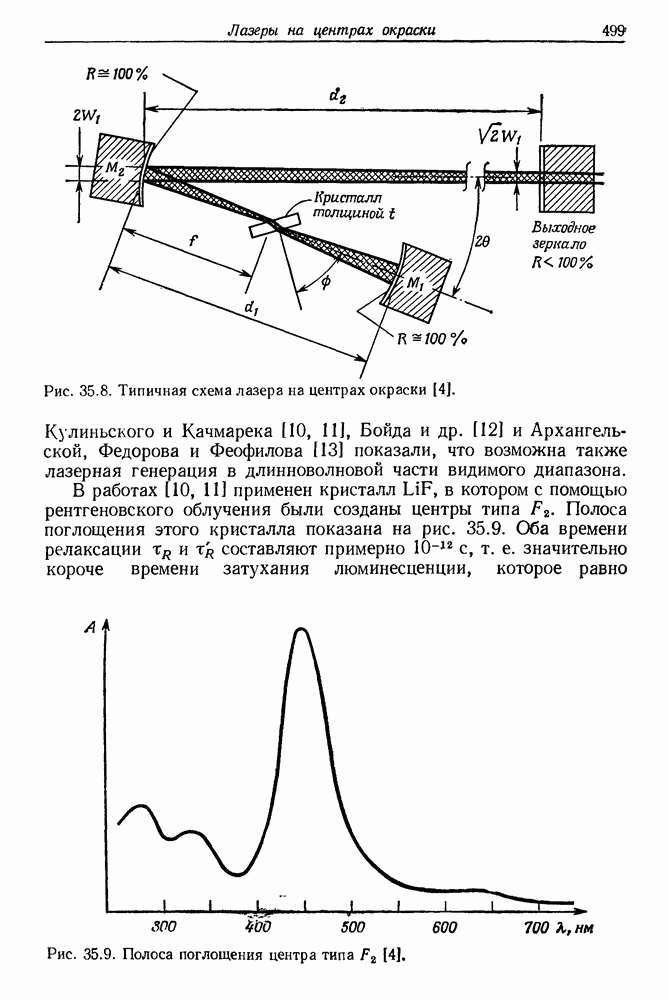
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
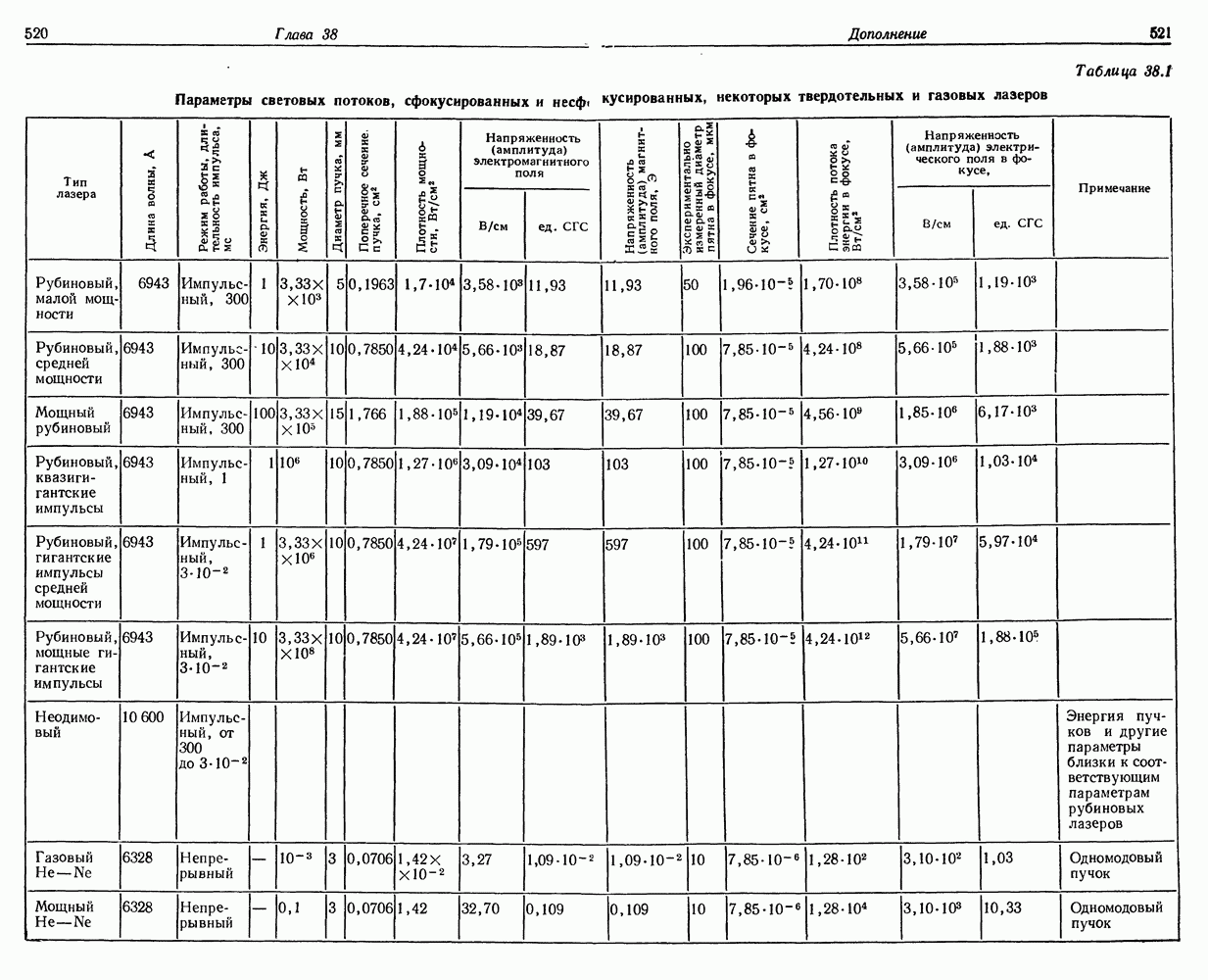
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
- Таблицы