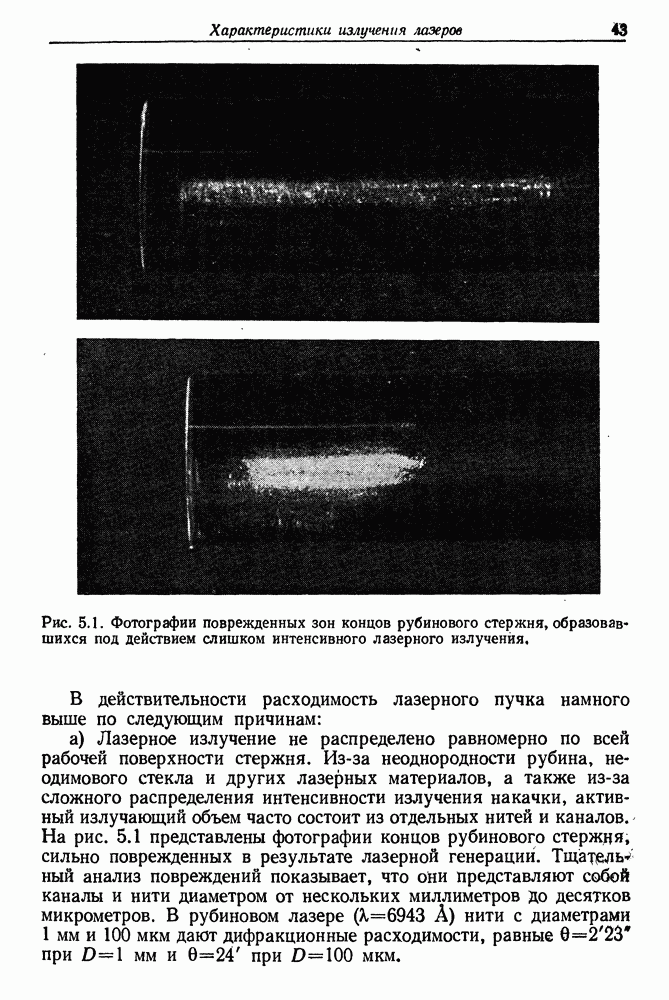
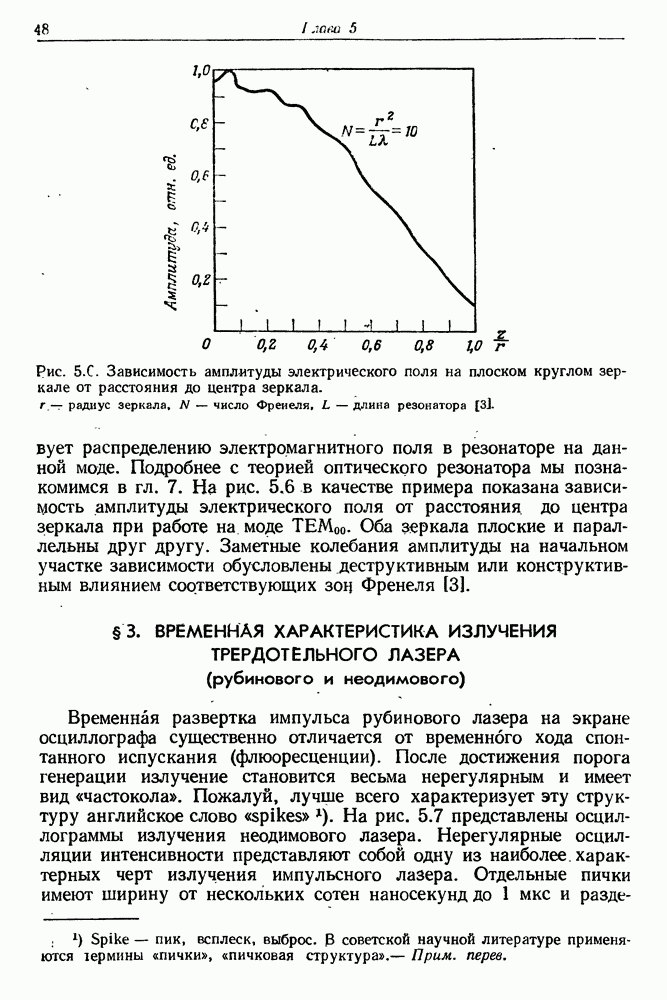
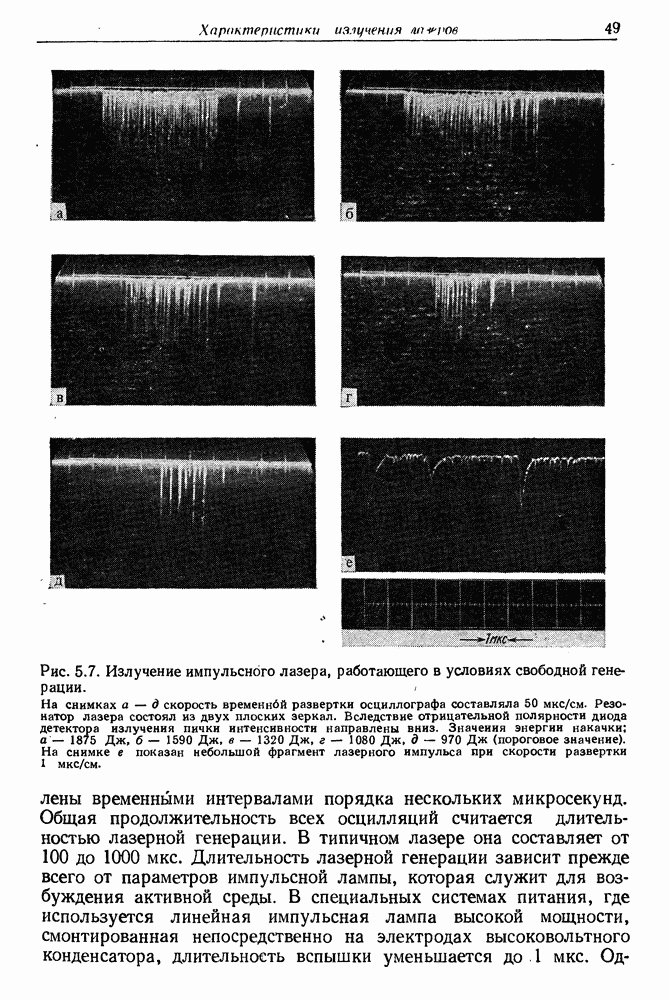
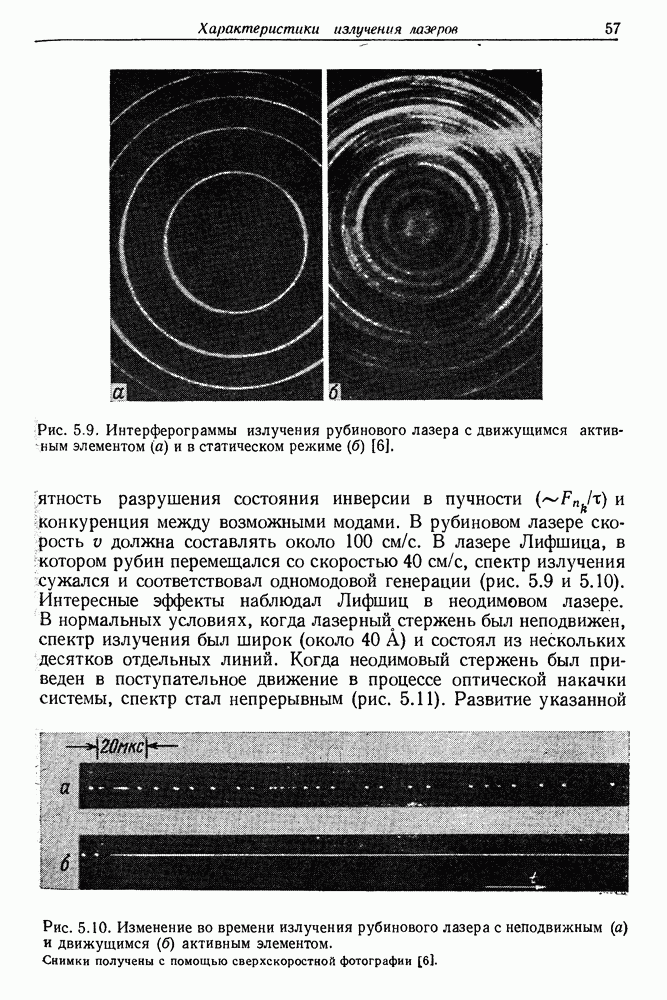
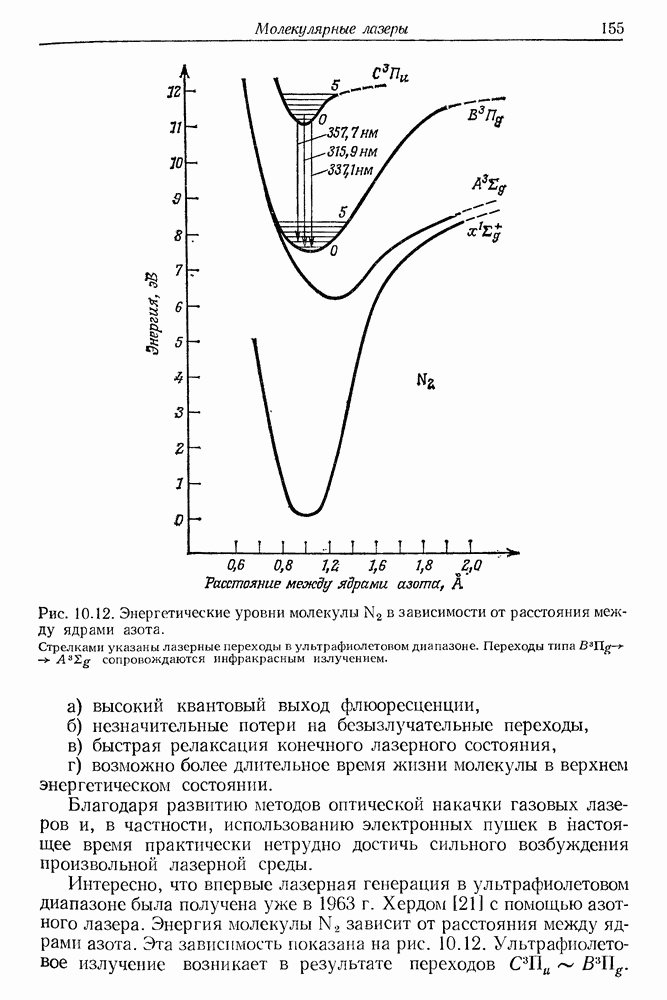
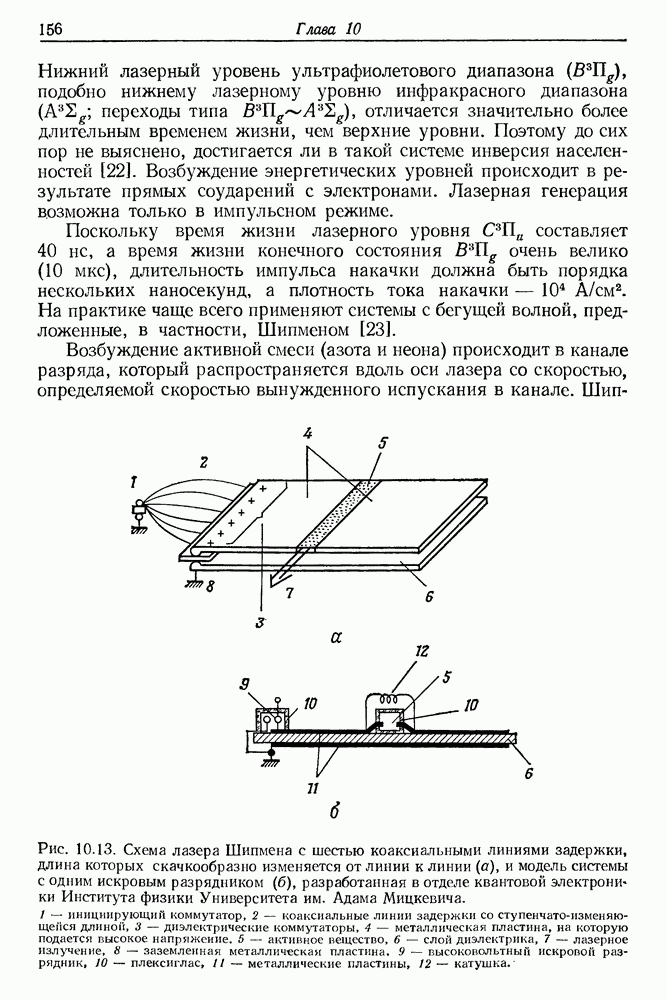
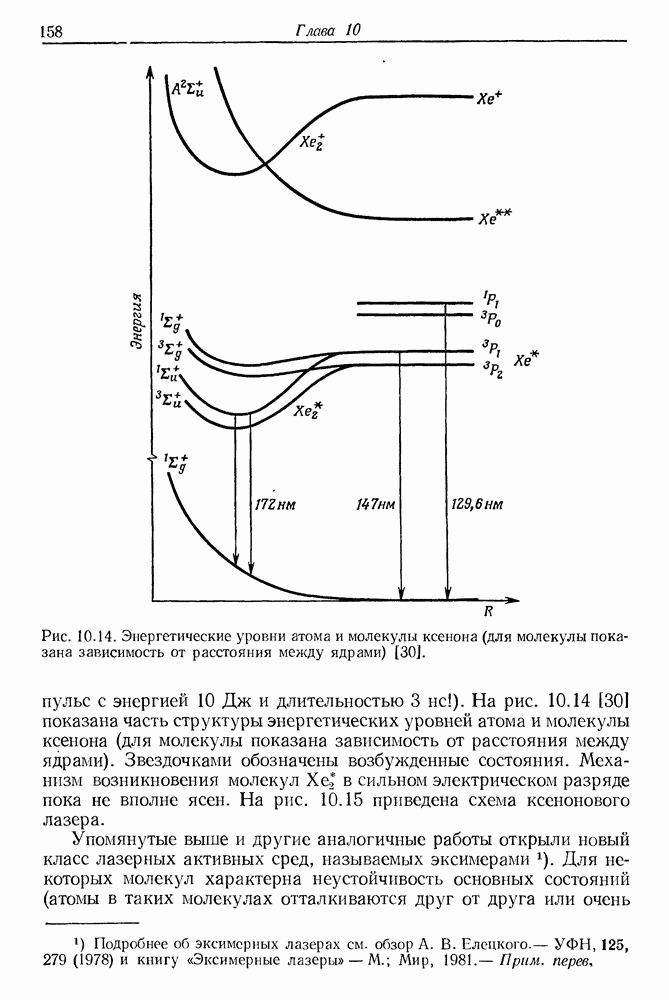
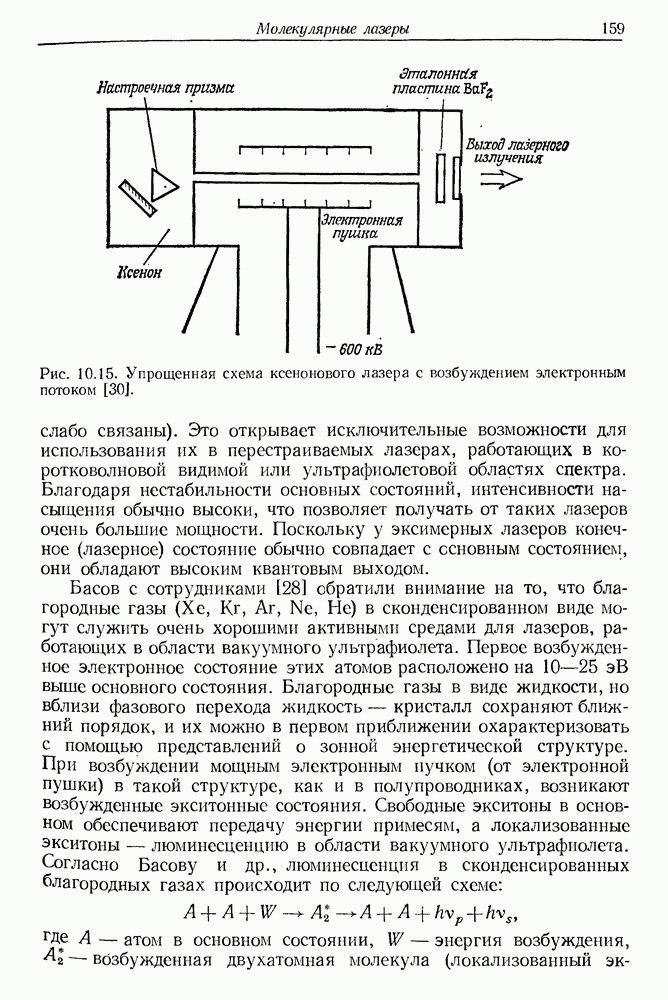
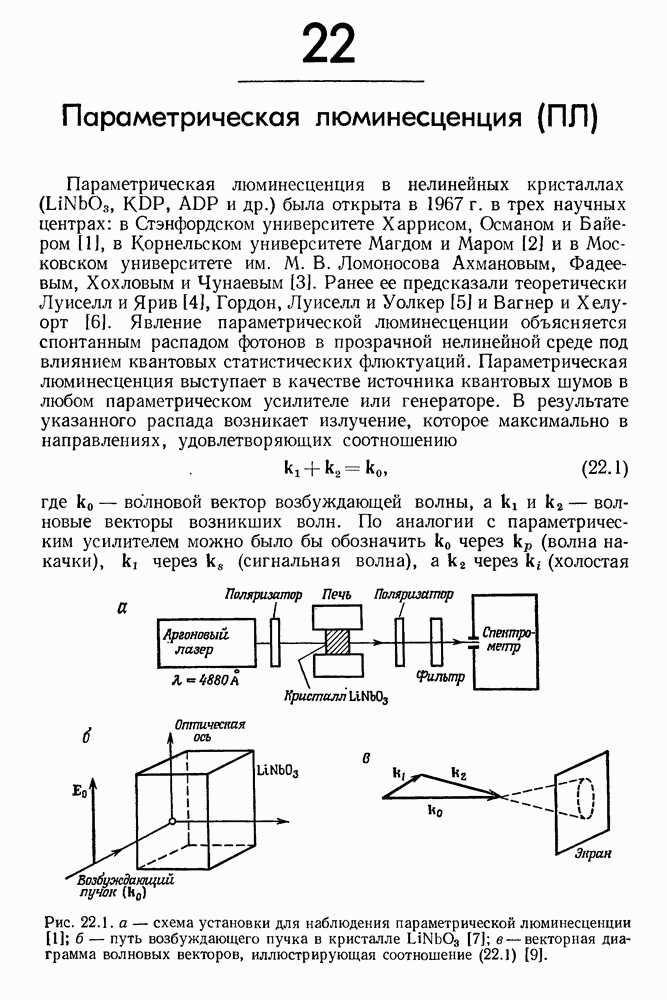
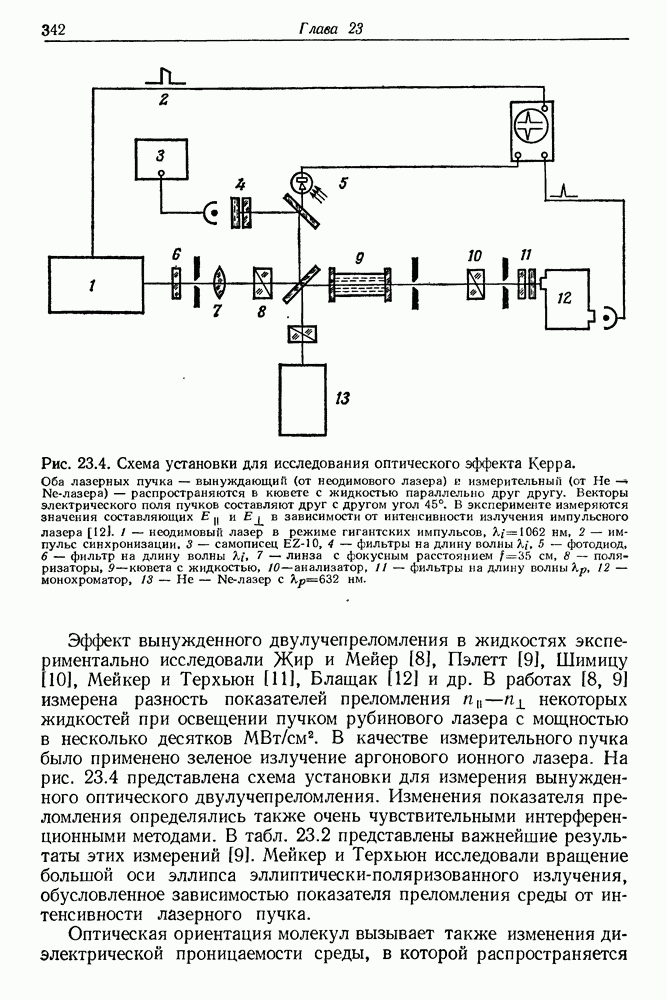
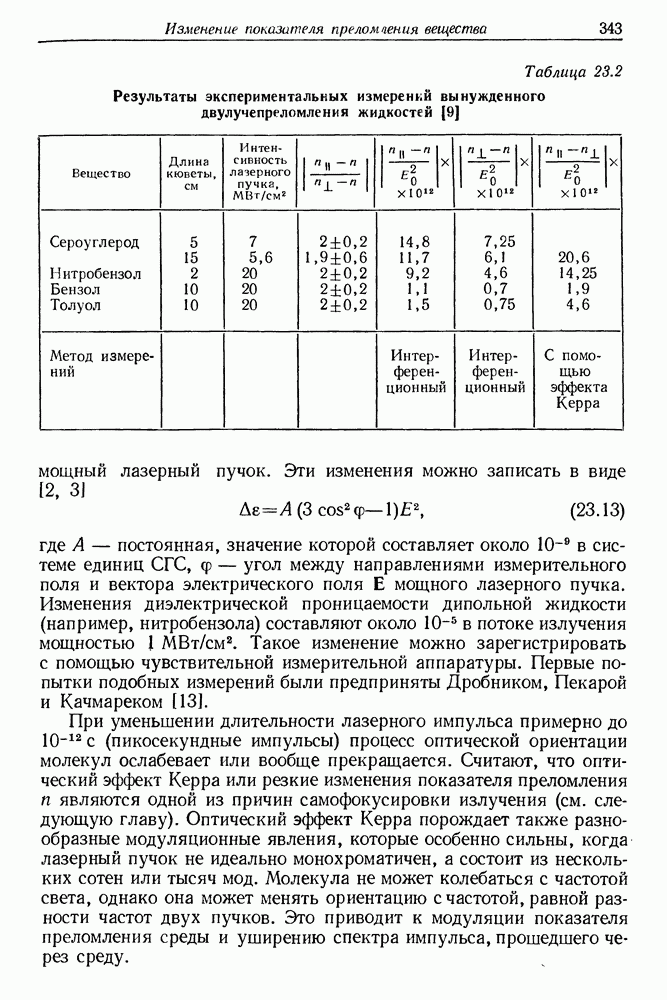
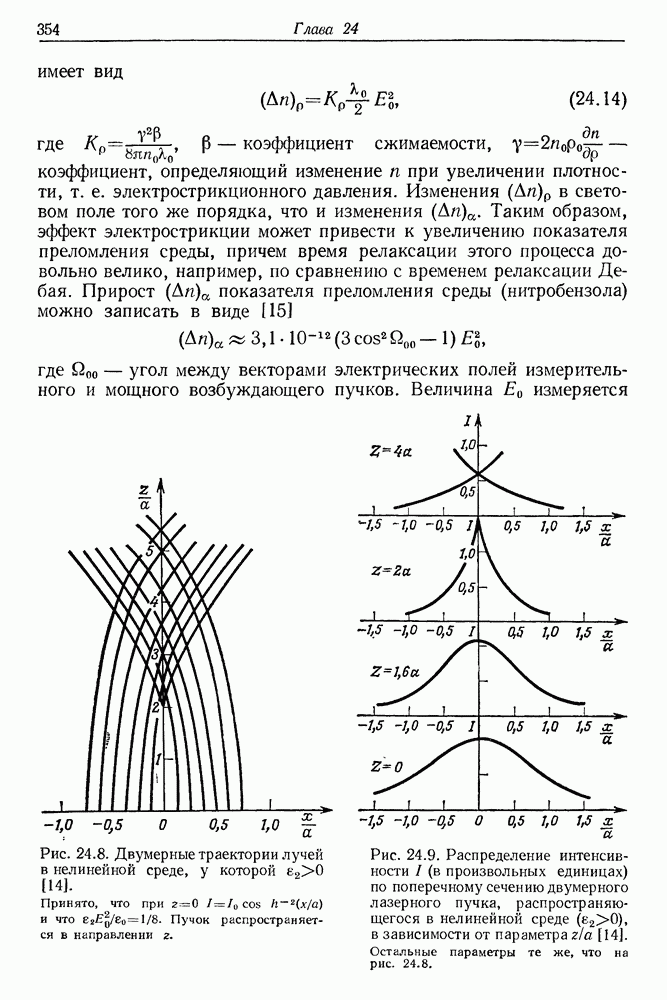
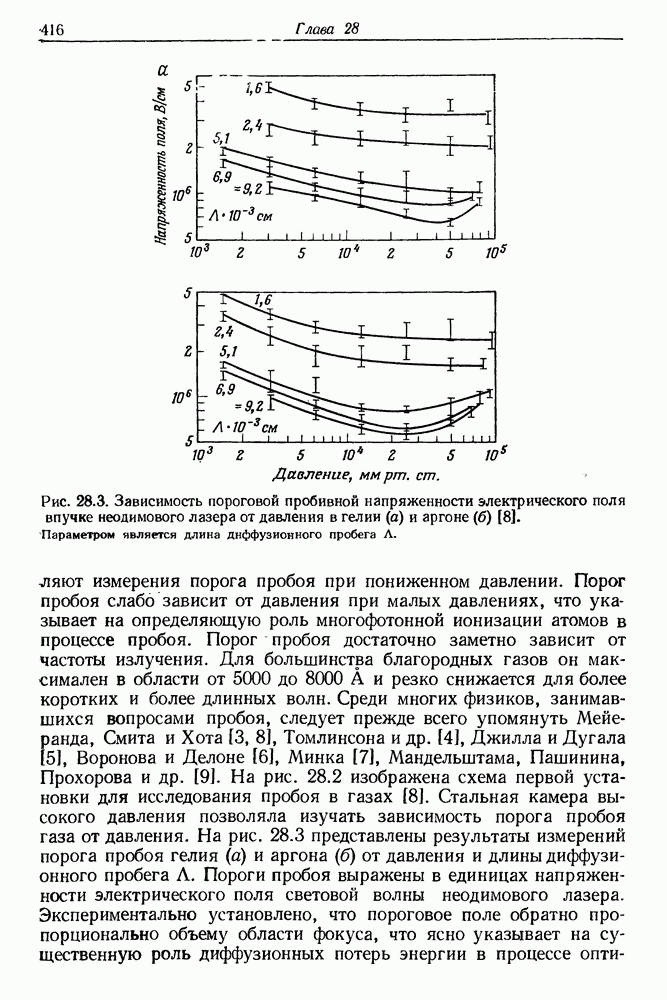
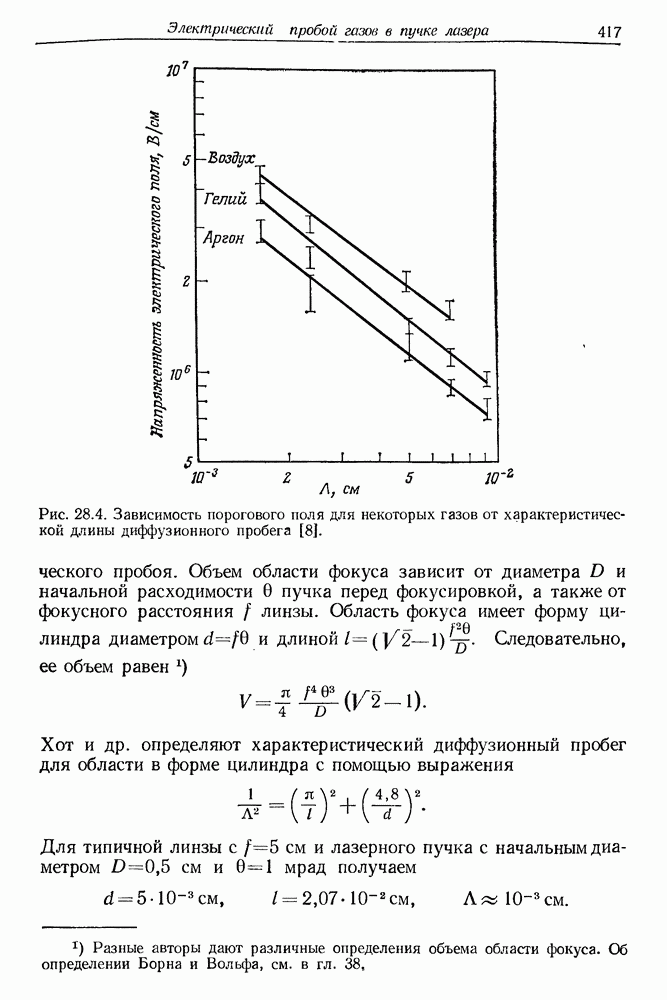
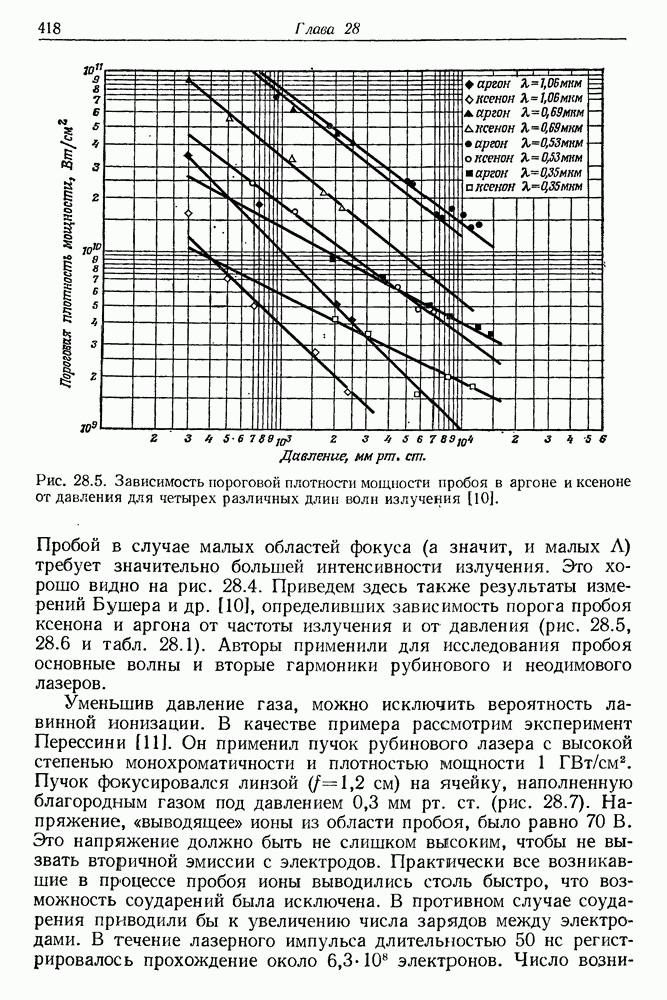
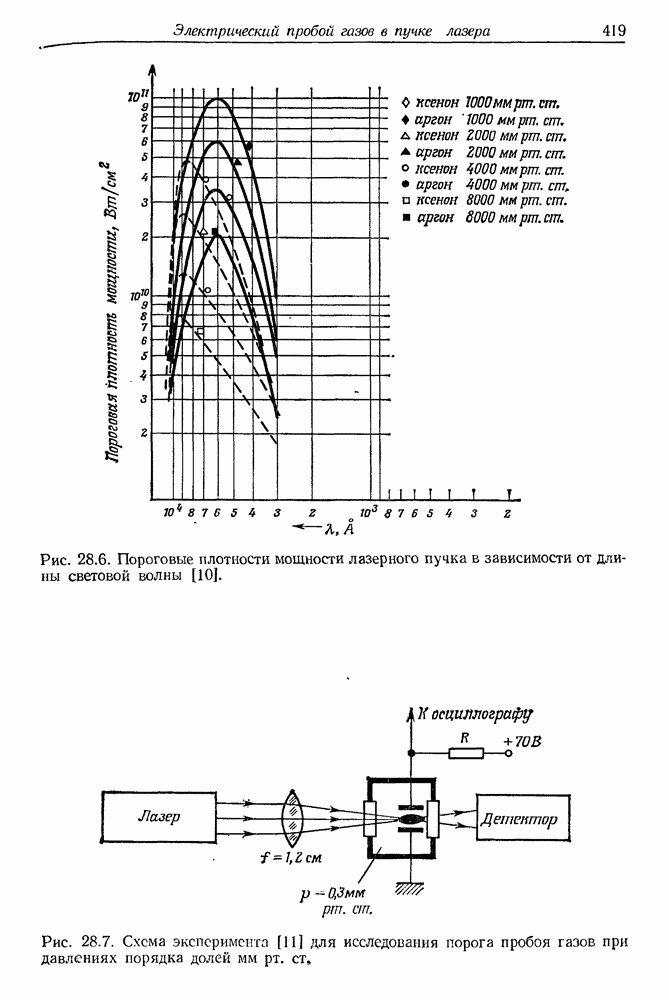
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
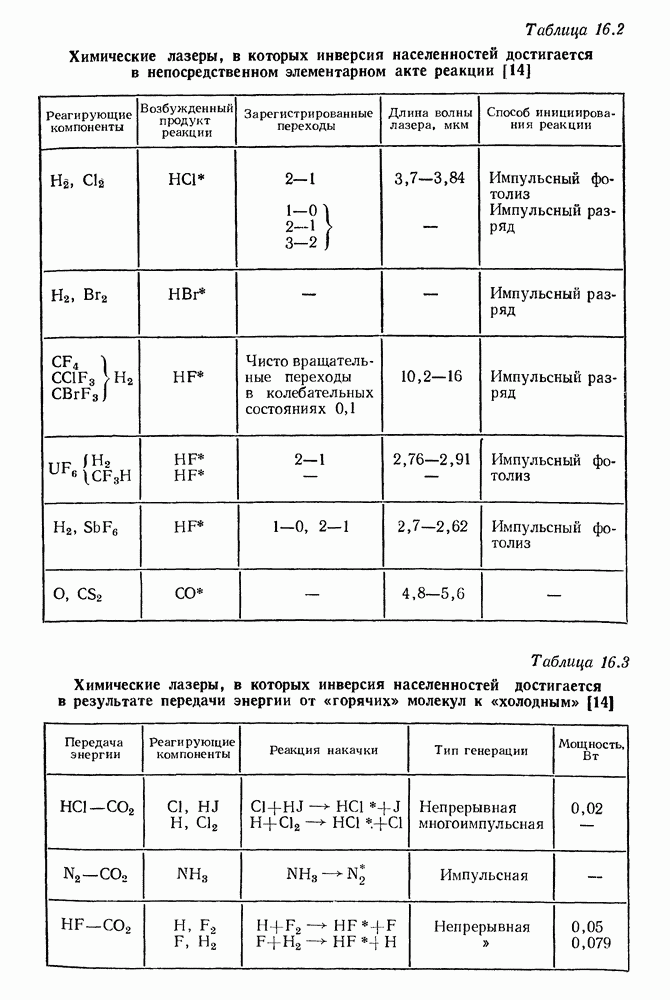
16. Химические лазеры
Еще в 1961 г. Полани [II обратил внимание на возможность использования химической энергии для возбуждения активной среды в лазере. Этот вопрос затем исследовали Ораевский [2], Юнг [3] и др. Первый химический лазер запустили в  Каспер и Пиментел [4]. В их лазере происходила следующая реакция:
Каспер и Пиментел [4]. В их лазере происходила следующая реакция:  звездочкой обозначена возбужденная молекула. Реакцию инициировали с помощью фотолиза. Давление смеси ионов составляло от 3 до 16 мм рт. ст.
звездочкой обозначена возбужденная молекула. Реакцию инициировали с помощью фотолиза. Давление смеси ионов составляло от 3 до 16 мм рт. ст.  Были получены световые импульсы длительностью около
Были получены световые импульсы длительностью около  с энергией
с энергией  Дж. Вскоре были созданы другие химические лазеры, в которых, в частности, использовались возбужденные молекулы СО (Поллак [5]) и HF (Компа, Пиментел [6]). Очень интересные результаты в этой области получили Мур и др. [7] и Хао-Лин-Чен и др. [8]. Они запустили лазер на
Дж. Вскоре были созданы другие химические лазеры, в которых, в частности, использовались возбужденные молекулы СО (Поллак [5]) и HF (Компа, Пиментел [6]). Очень интересные результаты в этой области получили Мур и др. [7] и Хао-Лин-Чен и др. [8]. Они запустили лазер на  в котором происходил процесс передачи колебательной энергии от возбужденной молекулы
в котором происходил процесс передачи колебательной энергии от возбужденной молекулы  молекуле
молекуле  При этом один квант колебательной энергии двухатомной молекулы превращался в два колебательных кванта многоатомной молекулы по схеме:
При этом один квант колебательной энергии двухатомной молекулы превращался в два колебательных кванта многоатомной молекулы по схеме:

В скобках указаны энергетические состояния молекул; система обозначений пояснена в гл. 10.
Источником энергии накачки в этом лазере были возбужденные молекулы  возникающие при химической реакции
возникающие при химической реакции  Подобный лазер был запущен также Гроссом и др. [9]. В их лазере передача энергии происходила между молекулами
Подобный лазер был запущен также Гроссом и др. [9]. В их лазере передача энергии происходила между молекулами  и
и  Как видим, энергия химической реакции используется для непосредственного возбуждения активных молекул в лазере или для возбуждения молекул другого газа, передающих затем энергию активным молекулам.
Как видим, энергия химической реакции используется для непосредственного возбуждения активных молекул в лазере или для возбуждения молекул другого газа, передающих затем энергию активным молекулам.
Химические лазеры могут работать как в импульсном, так и в непрерывном режимах. В первом случае химическая реакция инициируется вспышкой мощной лампы или электрическим разрядом. Для работы в непрерывном режиме в камеру лазера вводят компоненты, которые реагируют друг с другом, например, в присутствии непрерывного дугового разряда. При этом освобождается значительная химическая энергия, а значит, появляются возбужденные молекулы. Энергия импульсов первых химических лазеров была
невелика (несколько сотых джоуля). В непрерывном режиме мощность достигала нескольких ватт. В последнем разделе этой главы мы приведем примеры очень мощных современных химических лазеров.
§ 1. МЕХАНИЗМ ДЕЙСТВИЯ ХИМИЧЕСКОГО ЛАЗЕРА
В химическом лазере для возбуждения молекул активной среды используется энергия химических реакций. Необходимым условием лазерной генерации является создание инверсии населенностей соответствующих колебательно-вращательных состояний в системе. Критериями при выборе химической системы служат распределение энергии в молекулах, возникающих в результате химических реакций, и релаксационные процессы. Прежде всего прирост числа молекул, находящихся на высших энергетических уровнях, должен быть настолько велик, чтобы превосходить рост населенностей низших уровней. Кроме того, время жизни возбужденных молекул не должно быть малым по сравнению с длительностью реакции. Если исходное состояние активной среды химического лазера является метастабильным, химическую реакцию инициируют электрическим разрядом или вспышкой мощной лампы. Чаще всего для этой цели используют явление фотолиза.
В результате химических реакций в общем случае возбуждаются электронные, колебательные и вращательные состояния молекул. Пока в химических лазерах применяют лишь колебательные переходы. Джиджоев и др. [10] рассмотрели простую химическую реакцию типа

Здесь А В означает возбужденную молекулу,  — энергия реакции. В кинетике этой реакции различают три этапа:
— энергия реакции. В кинетике этой реакции различают три этапа:
1) приближение атома А к молекуле 
2) процесс сближения и ослабление связи между атомами В и С,
3) возникновение продуктов реакции А, В и С и удаление их друг от друга.
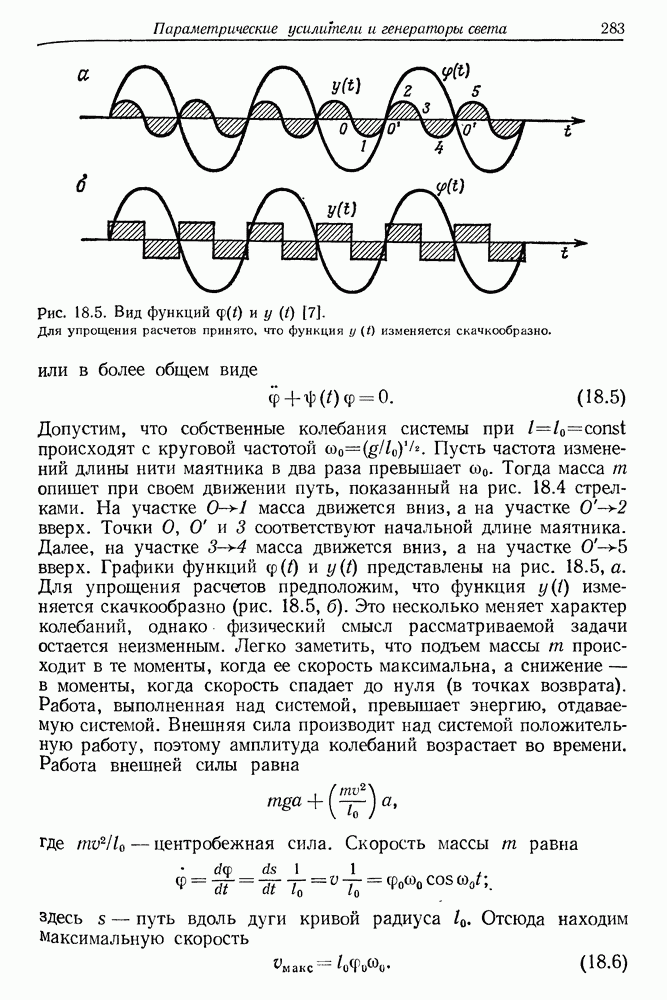
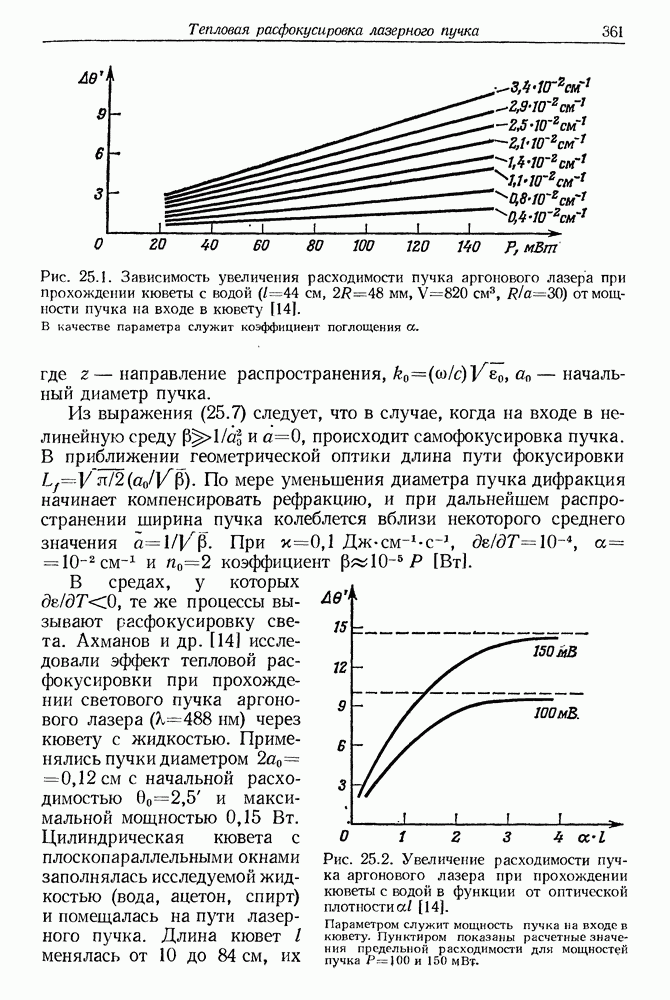
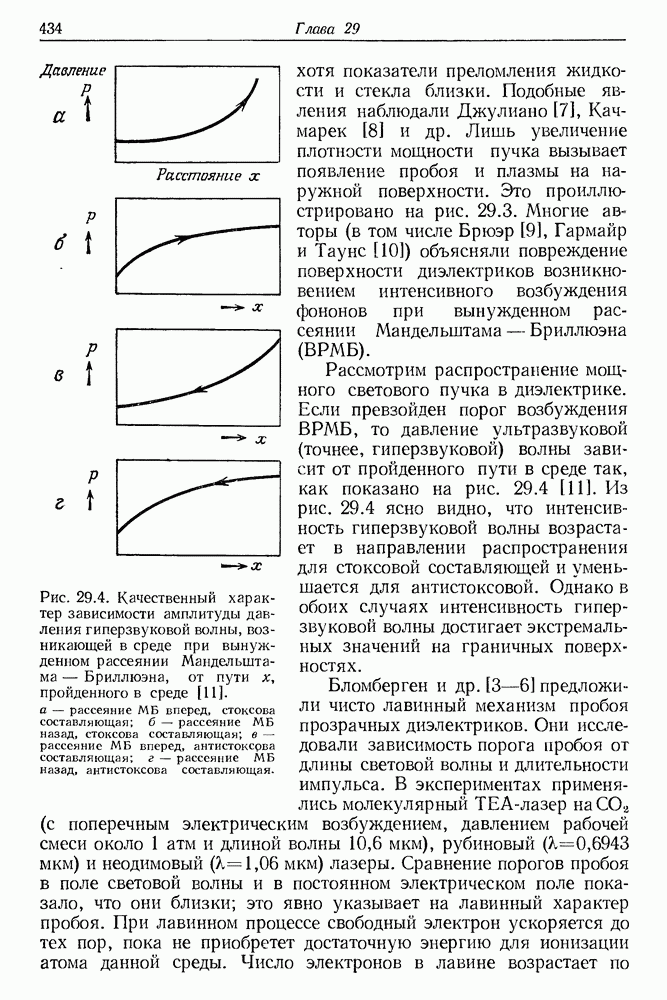
Энергии, соответствующие каждому из этапов, обозначим через  Наибольший интерес представляет этап реакции, на котором происходит обогащение молекул колебательной энергией; обычно это второй этап. Отношение прироста колебательной энергии к кинетической энергии тем выше, чем тяжелее атом А по отношению к атомам В и С. Ход реакции можно представить в виде изменений полной энергии химической системы. Согласно Пиментелу [11], этот процесс развивается так, как показано на рис. 16.1. Реакция является экзотермической; освобождающаяся энергия должна быть равна сумме
Наибольший интерес представляет этап реакции, на котором происходит обогащение молекул колебательной энергией; обычно это второй этап. Отношение прироста колебательной энергии к кинетической энергии тем выше, чем тяжелее атом А по отношению к атомам В и С. Ход реакции можно представить в виде изменений полной энергии химической системы. Согласно Пиментелу [11], этот процесс развивается так, как показано на рис. 16.1. Реакция является экзотермической; освобождающаяся энергия должна быть равна сумме  . В большинстве химических реакций скорость релаксационных процессов превышает скорость
. В большинстве химических реакций скорость релаксационных процессов превышает скорость

Рис. 16.1. Кинетика реакции в химическом лазере  постоянные коэффициенты, которые характеризуют отдельные возбужденные состояния молекулы с различной кинетикой.
постоянные коэффициенты, которые характеризуют отдельные возбужденные состояния молекулы с различной кинетикой.
реакции; в таких системах получение инверсии населенностей невозможно.
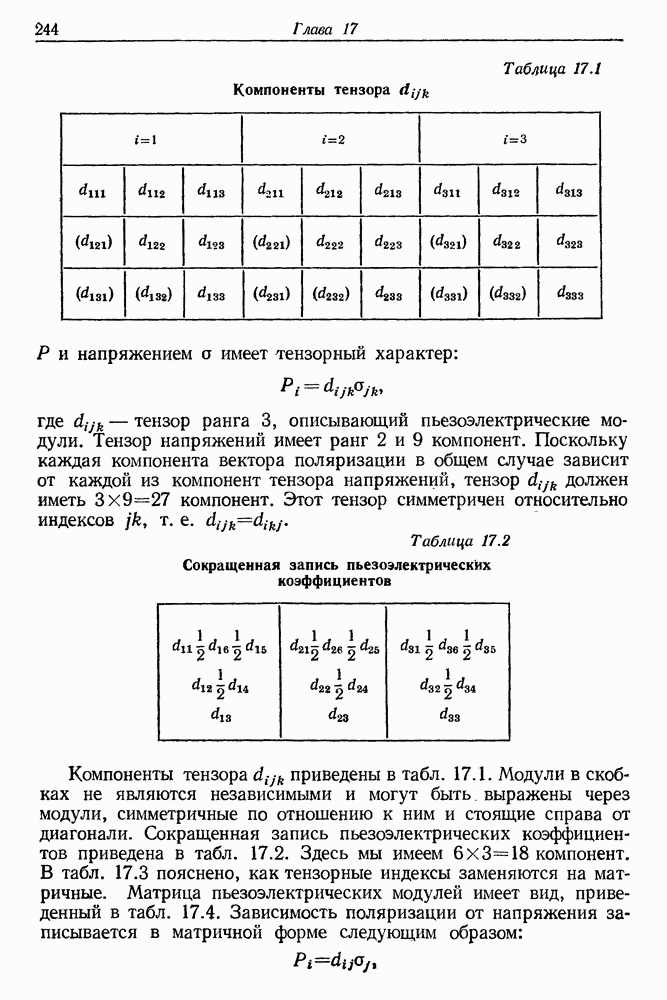
В главе 10 мы рассмотрели колебательно-вращательные движения молекул. В процессе дипольных переходов изменение вращательного квантового числа равно 
Эксперимент показал, что колебательная энергия молекулы в возбужденном состоянии очень медленно превращается в поступательную.
В верхней части рис. 16.1 указана постоянная, которую можно определить из кинетики реакции. С точки зрения использования в лазере важно знать отдельные постоянные  описывающие различные возбужденные состояния молекулы, которая участвует в химической реакции.
описывающие различные возбужденные состояния молекулы, которая участвует в химической реакции.
Вращательная энергия молекулы очень быстро преобразуется в поступательную. Если известна температура химической реакции  можно рассчитать населенности отдельных вращательных уровней, связанных с заданным состоянием колебательной энергии молекулы. Это позволяет оценить усиление химического вещества как отношение соответствующих коэффициентов
можно рассчитать населенности отдельных вращательных уровней, связанных с заданным состоянием колебательной энергии молекулы. Это позволяет оценить усиление химического вещества как отношение соответствующих коэффициентов  (см. рис. 16.1). Допустим, например, что мы рассматриваем переход в молекуле
(см. рис. 16.1). Допустим, например, что мы рассматриваем переход в молекуле  (см. рис. 10.1), обозначенный символом
(см. рис. 10.1), обозначенный символом  Колебательное квантовое число при этом уменьшается на единицу
Колебательное квантовое число при этом уменьшается на единицу  а вращательное возрастает на единицу
а вращательное возрастает на единицу  Согласно Пиментелу [11], отношение
Согласно Пиментелу [11], отношение  приближенно равно
приближенно равно

где В — вращательная постоянная.
В выражении (16.2) предполагается, что температура реакции равна «вращательной температуре», т. е. при соударениях второго рода соблюдается термодинамическое равновесие. В момент мощной вспышки лампы, которая инициирует экзотермическую реакцию, вращательная температура может превышать комнатную. Опишем вкратце условия возникновения инверсии в системе [10].
Колебательно-вращательные энергетические состояния описываются набором колебательных и вращательных квантовых чисел. Обозначим для краткости набор колебательных чисел через  а набор вращательных чисел через
а набор вращательных чисел через  Ограничим
Ограничим
рассмотрение, как и в гл. 10, линейной молекулой. Энергия молекулы в первом приближении равна

Если измерять вращательную постоянную в  то вращательная энергия будет равна
то вращательная энергия будет равна

Следует отметить, что обычно вращательная постоянная также является функцией V. В результате соударений устанавливается некоторое состояние равновесия населенностей отдельных вращательных уровней. Запишем это состояние в виде

Здесь  — кинетическая температура системы. Коэффициенты
— кинетическая температура системы. Коэффициенты  и а равны единице для молекулы, не имеющей центра инверсии; для молекул с центром инверсии
и а равны единице для молекулы, не имеющей центра инверсии; для молекул с центром инверсии  а коэффициент
а коэффициент  зависит от симметрии уровня и его значение лежит в границах между 0 и 1. Под кинетической температурой здесь понимается температура вращательных и поступательных степеней свободы молекулы.
зависит от симметрии уровня и его значение лежит в границах между 0 и 1. Под кинетической температурой здесь понимается температура вращательных и поступательных степеней свободы молекулы.
Интересно, что изменение распределения энергии между различными молекулами системы, но для одной и той же степени свободы, происходит в результате резонансной передачи энергии при соударениях. Подобный обмен энергиями происходит относительно быстро. Передача же кванта колебательной энергии другой степени свободы, отличающейся от исходной, является в общем случае нерезонансным процессом. Его вероятность значительно меньше, чем вероятность резонансного процесса. Отсюда следует, что скорость изменения распределения энергии между различными степенями свободы меньше, чем в пределах одной степени свободы. Проиллюстрируем это на примере линейной молекулы  . Больцмановское распределение энергии между антисимметричными колебательными состояниями (см. рис. 10.2) устанавливается примерно за
. Больцмановское распределение энергии между антисимметричными колебательными состояниями (см. рис. 10.2) устанавливается примерно за  а распределение между всеми степенями свободы — за время, превышающее
а распределение между всеми степенями свободы — за время, превышающее  т. е. времена весьма существенно отличаются друг от друга.
т. е. времена весьма существенно отличаются друг от друга.
Состояние инверсии населенностей уровней  записывается следующим образом:
записывается следующим образом:

где  означает степень вырождения данного уровня.
означает степень вырождения данного уровня.
Обычно определяют два состояния инверсии: первое состояние (так называемая полная инверсия) связано с инверсией колебательных уровней, второе — с колебательно-вращательными
уровнями (частичная инверсия). В первом случае

Б этом неравенстве мы приняли, что  Инверсия (полная) относительно просто достигается в среде, состоящей из многоатомных молекул, между уровнями, относящимися к различным степеням свободы. Пусть реализуется переход между состояниями
Инверсия (полная) относительно просто достигается в среде, состоящей из многоатомных молекул, между уровнями, относящимися к различным степеням свободы. Пусть реализуется переход между состояниями  Достижение инверсии возможно при
Достижение инверсии возможно при  для
для  где Т и
где Т и  температура и частота данного типа колебаний. Однако переход такого типа является запрещенным, поэтому его вероятность очень мала (в гармоническом приближении). Из общего рассмотрения проблемы статистического распределения энергии следует, что высокая степень инверсии, а значит, и высокое усиление в системе легче достигаются в ансамбле молекул с малым числом атомов и небольшим моментом инерции. Наиболее удобны для химического лазера линейные трехатомные молекулы. В случае частичной инверсии имеем
температура и частота данного типа колебаний. Однако переход такого типа является запрещенным, поэтому его вероятность очень мала (в гармоническом приближении). Из общего рассмотрения проблемы статистического распределения энергии следует, что высокая степень инверсии, а значит, и высокое усиление в системе легче достигаются в ансамбле молекул с малым числом атомов и небольшим моментом инерции. Наиболее удобны для химического лазера линейные трехатомные молекулы. В случае частичной инверсии имеем

Такое состояние инверсии особенно важно в двухатомных моле кулах, для которых полная инверсия возможна лишь на очень короткое время; это время определяется установлением равновесия в одном колебательном состоянии.
В случае водородсодержащих молекул, например  и др., частичная инверсия может быть достаточно значительной и система обладает высоким усилением, поскольку в гармоническом приближении переходы
и др., частичная инверсия может быть достаточно значительной и система обладает высоким усилением, поскольку в гармоническом приближении переходы  являются раздельными и вероятность их велика.
являются раздельными и вероятность их велика.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
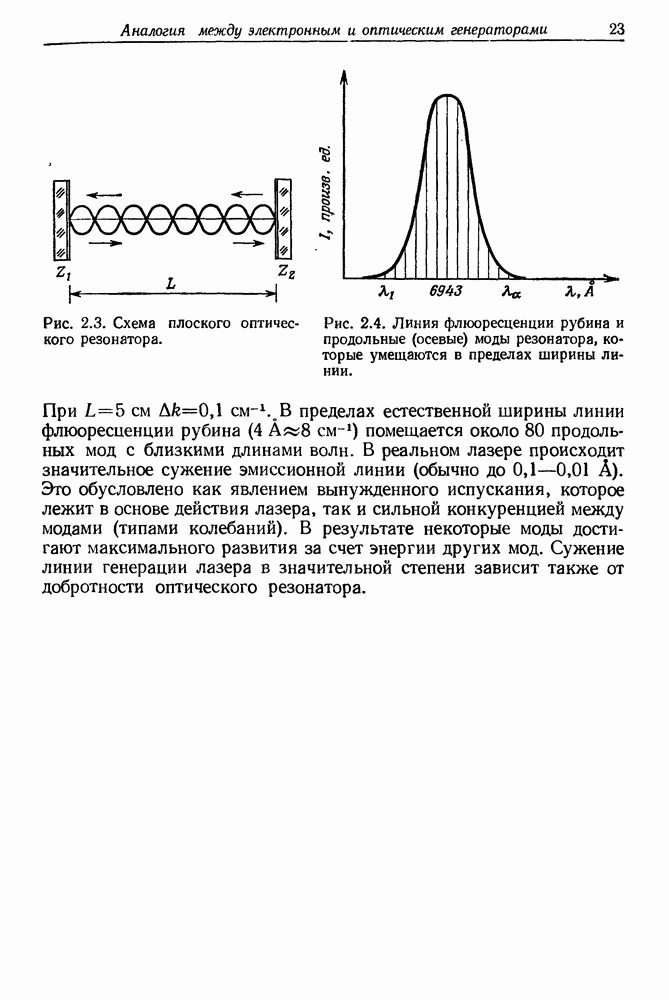
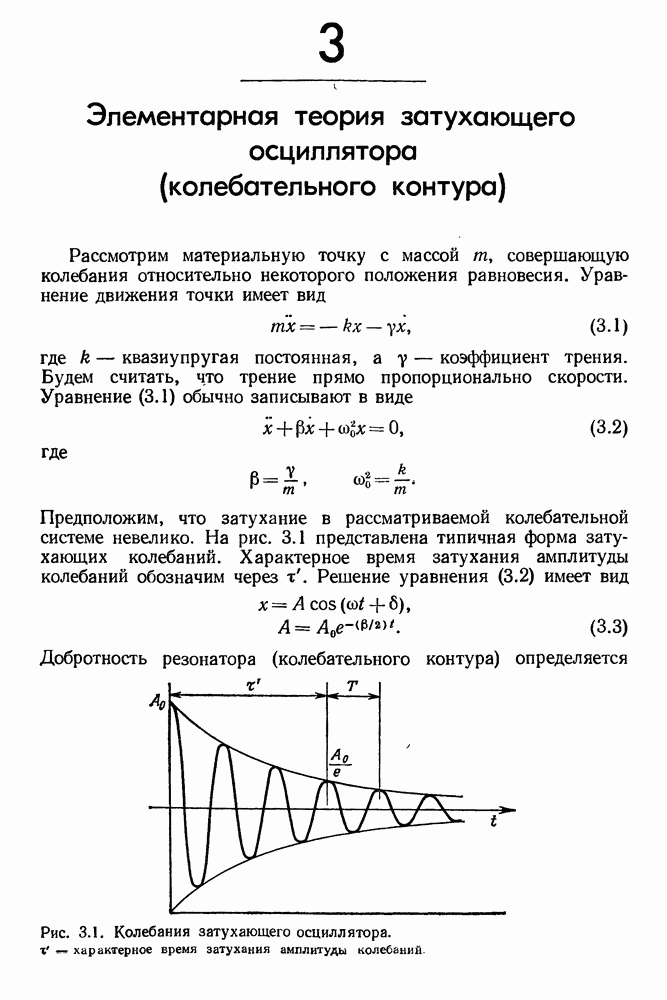
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
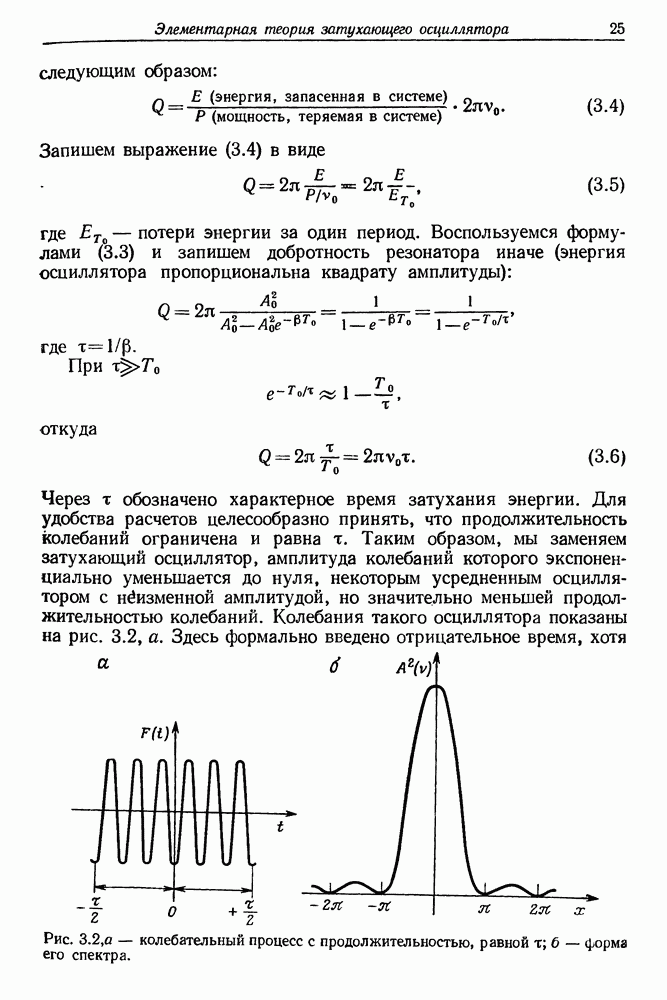
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
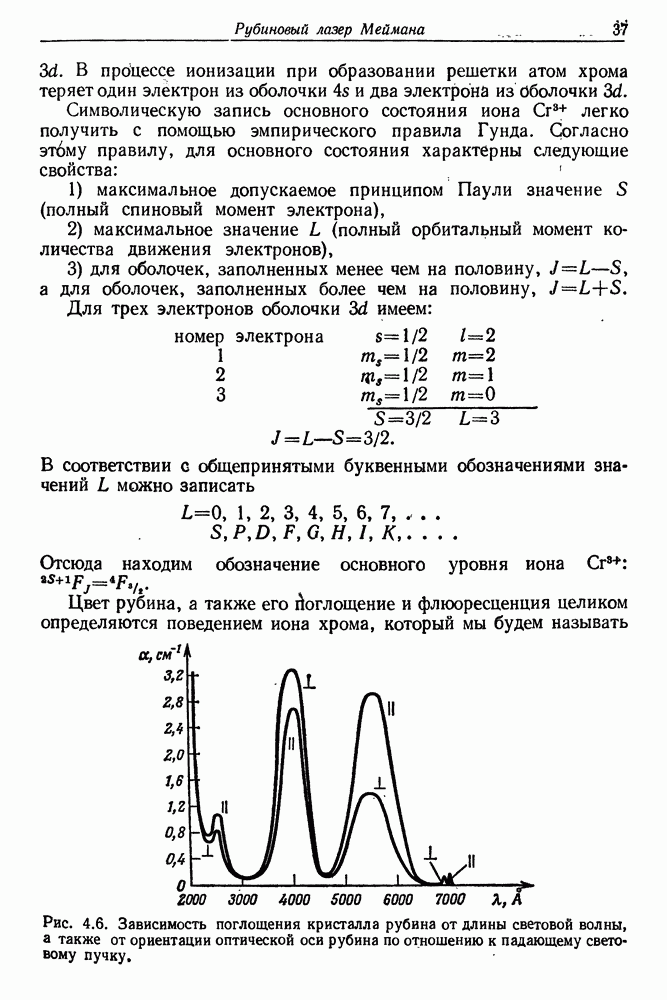
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
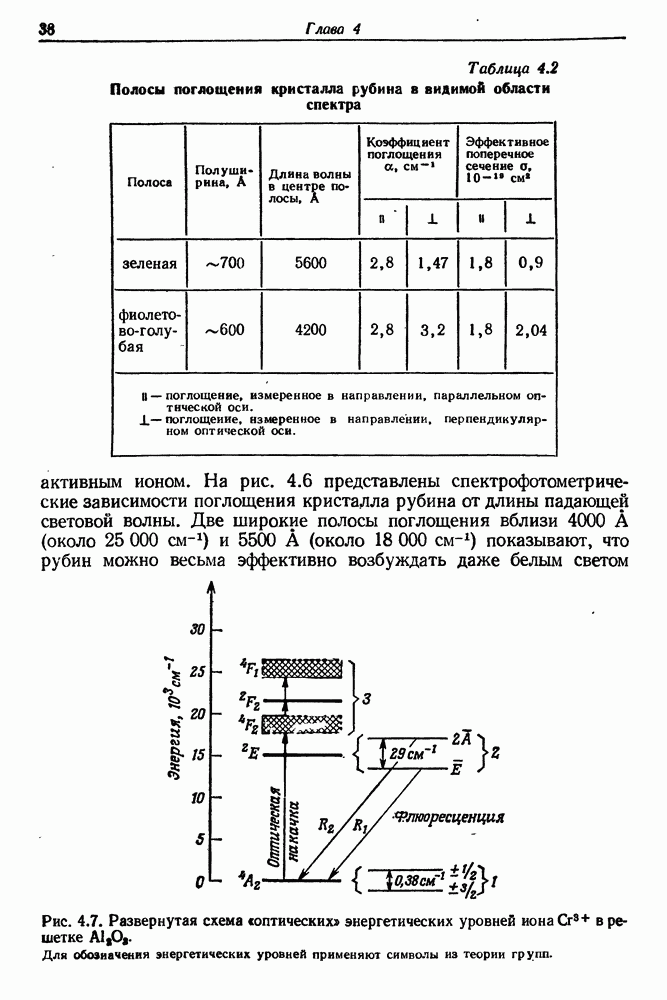
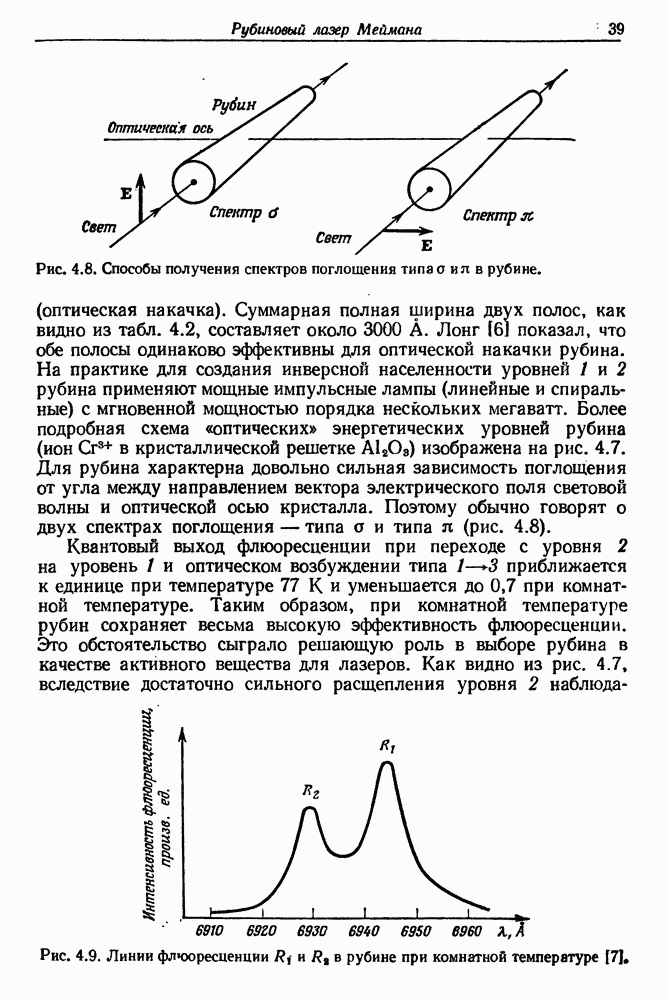
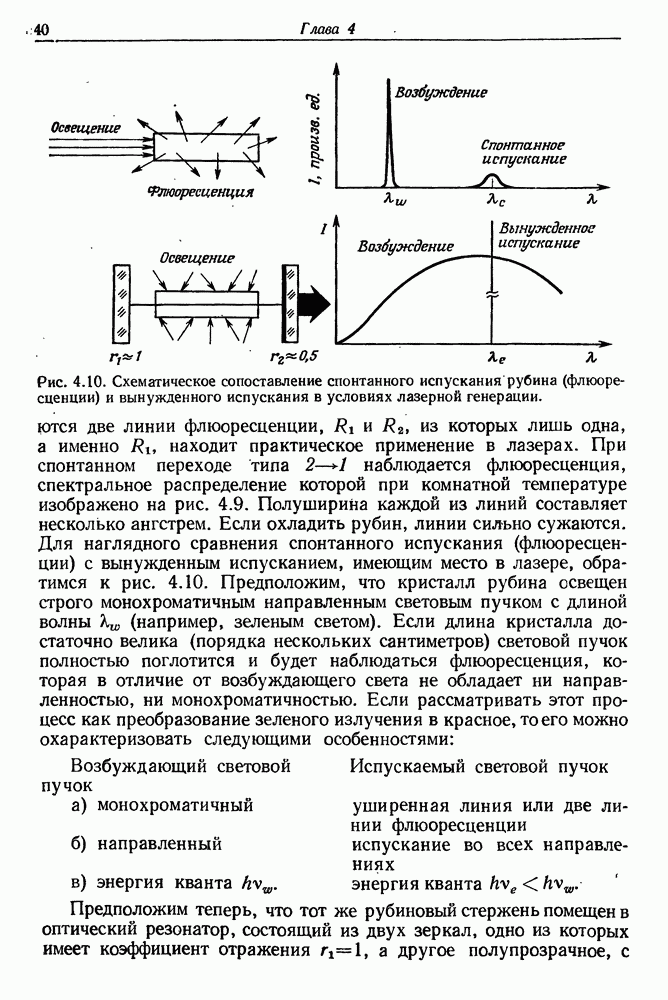
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
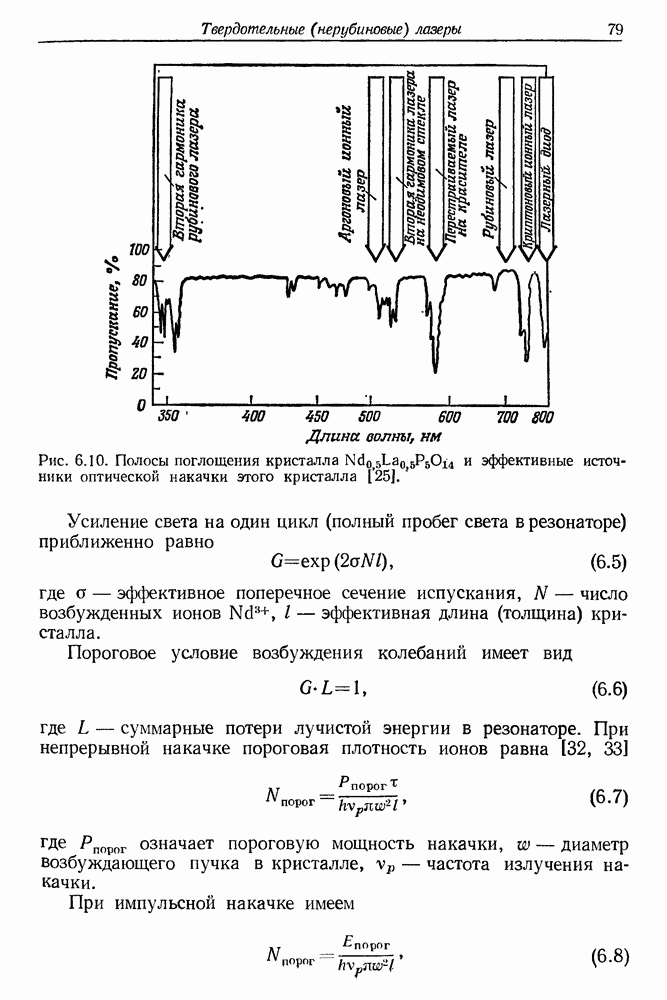
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
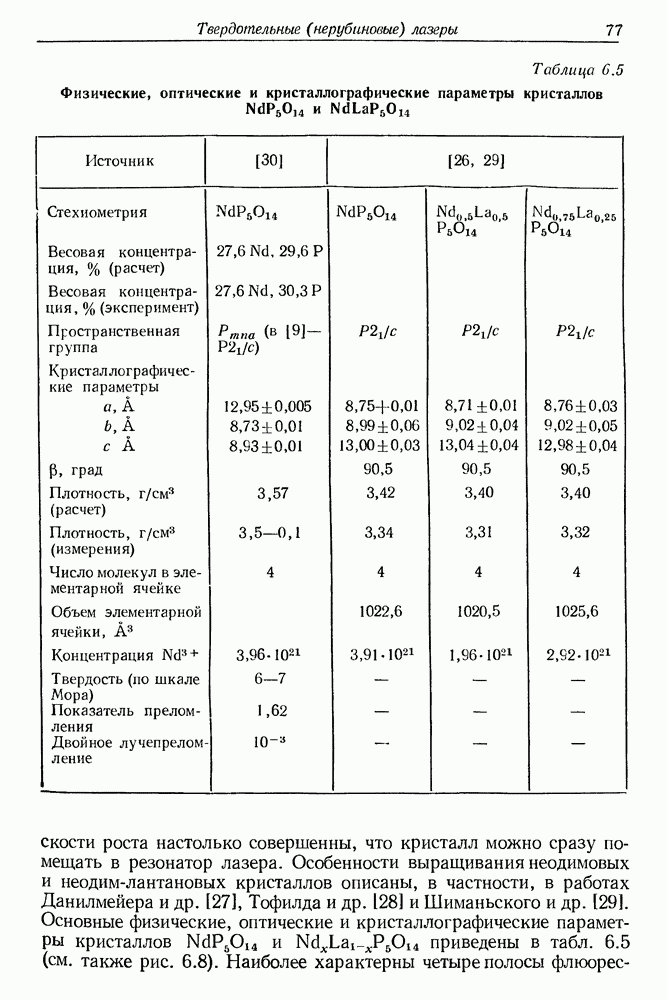
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
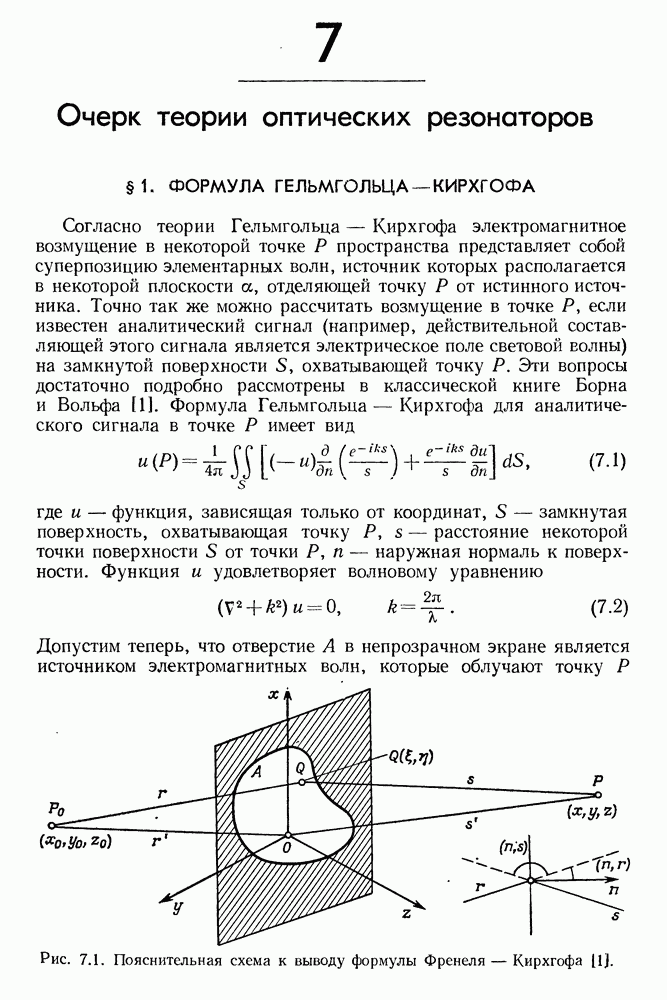
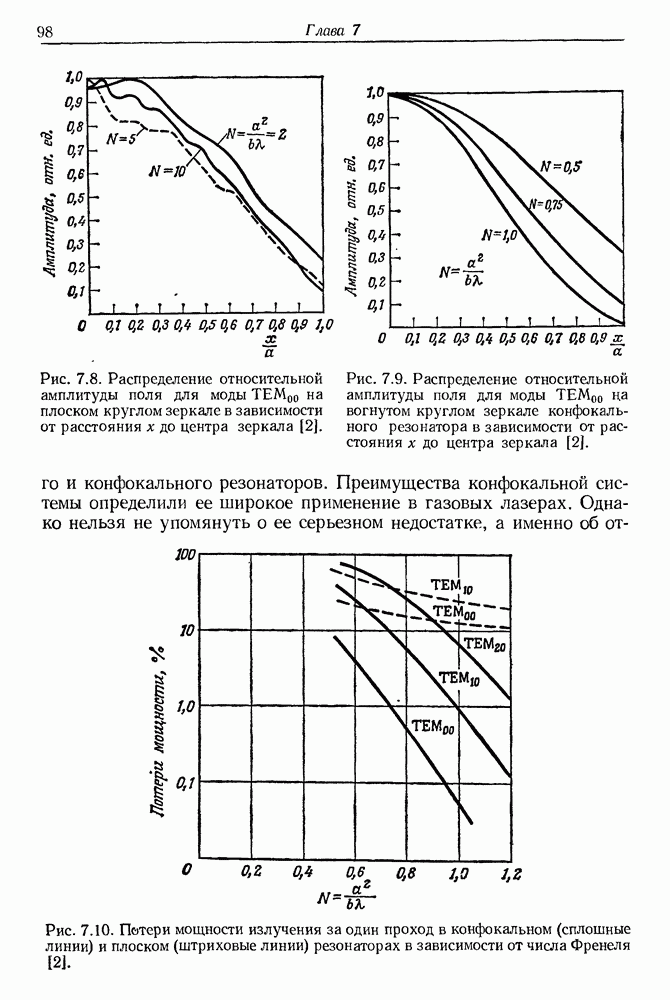
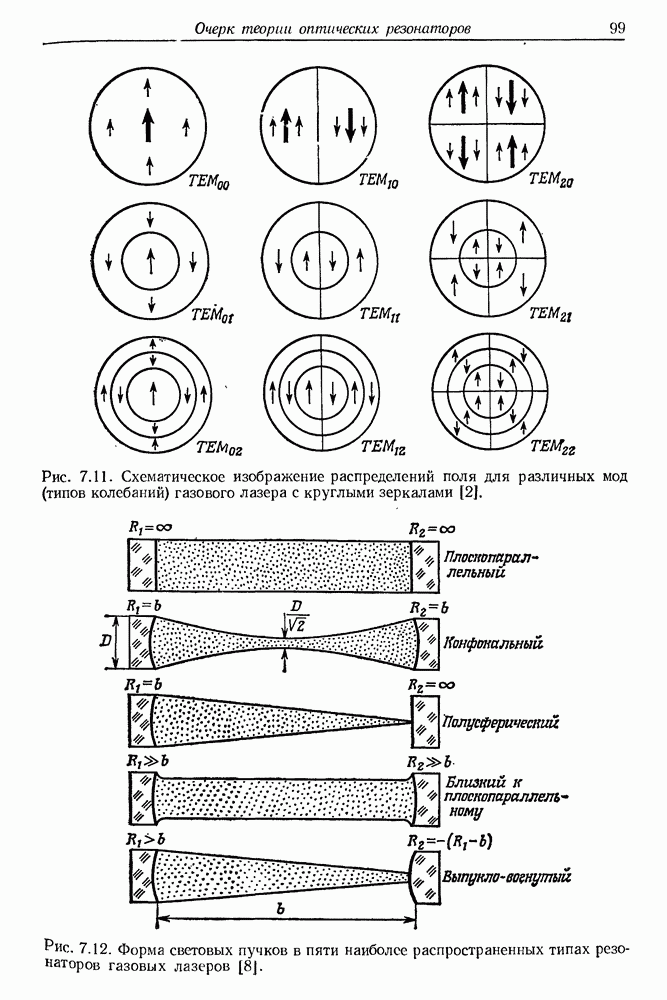
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
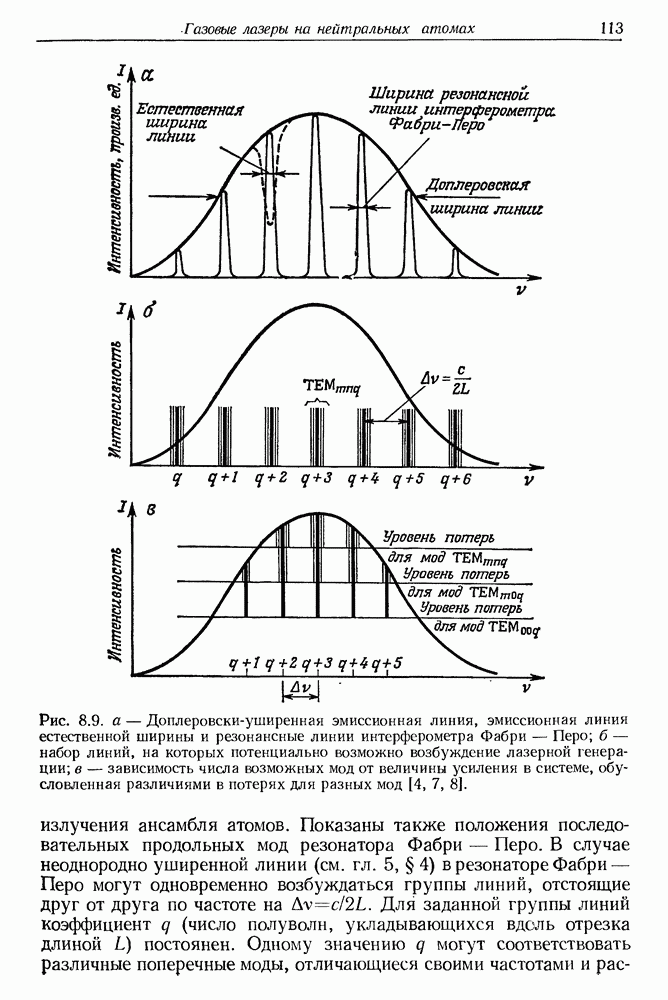
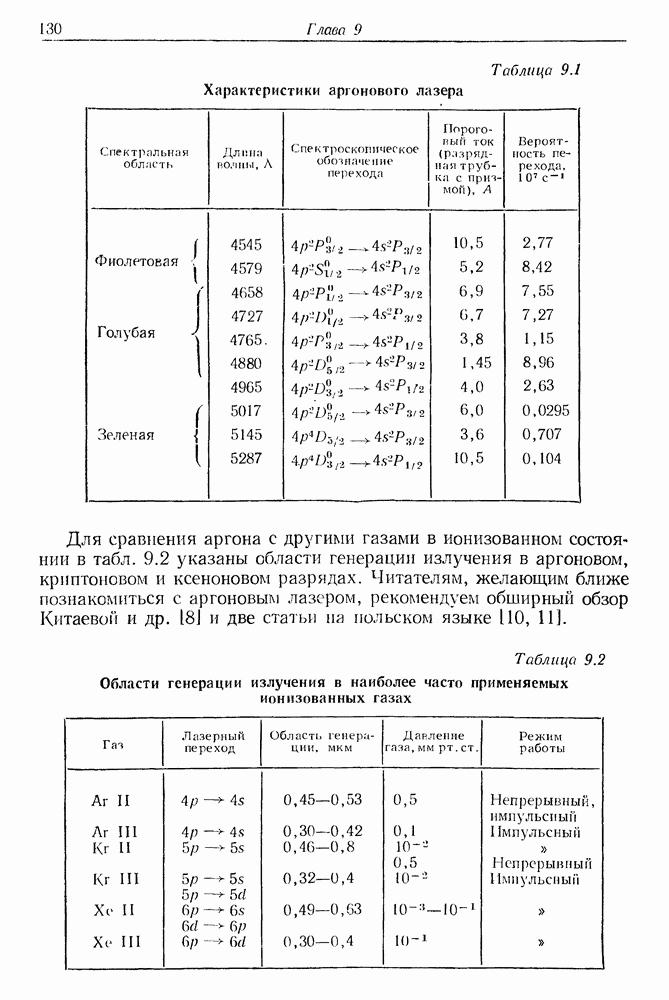
- 9. Газовые ионные лазеры
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
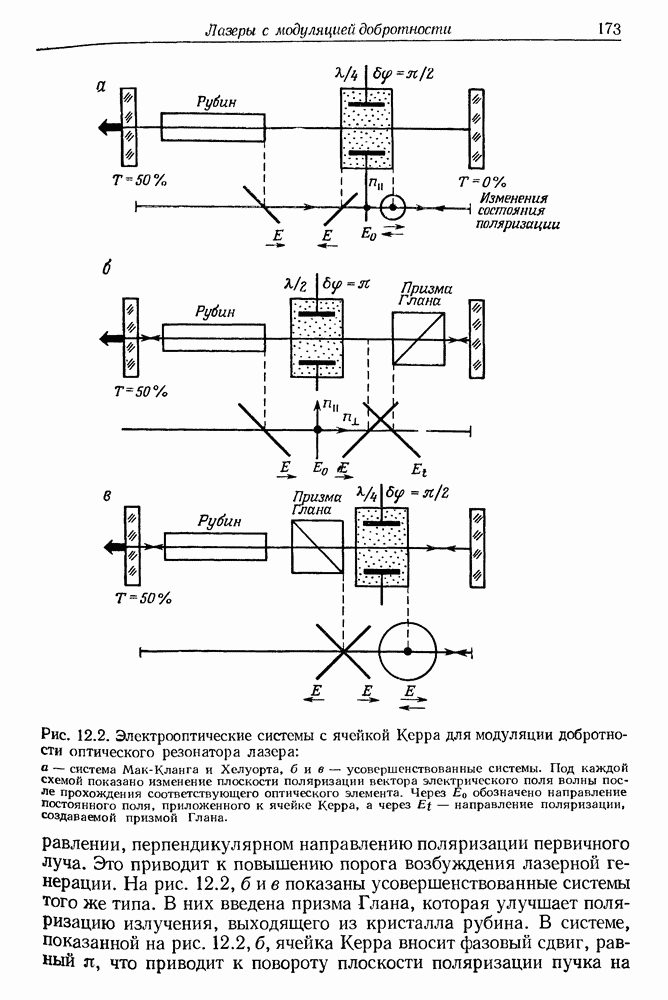
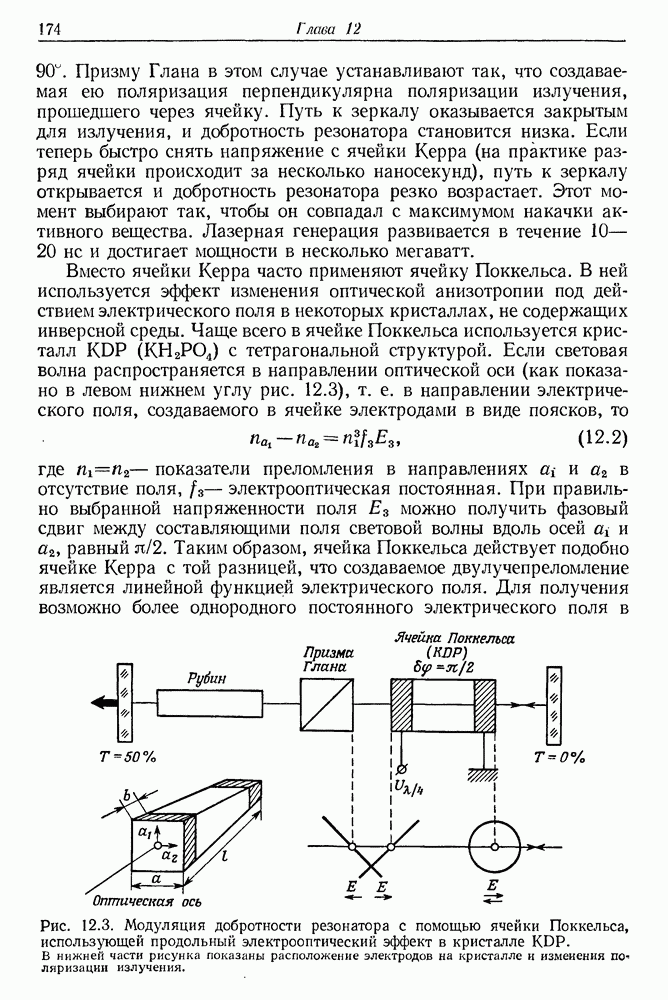
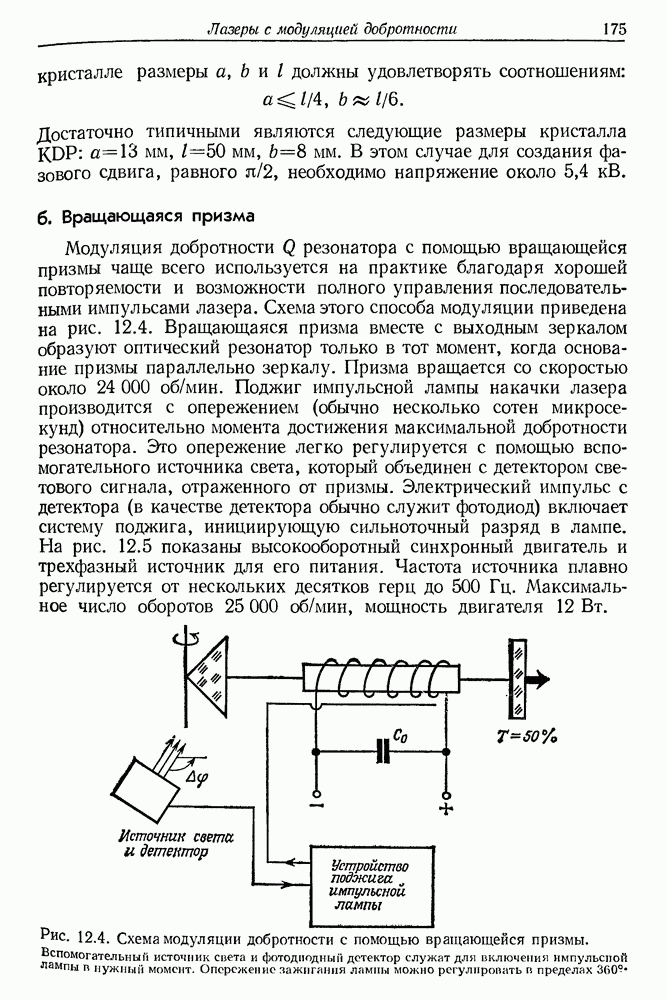
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
- б. Вращающаяся призма
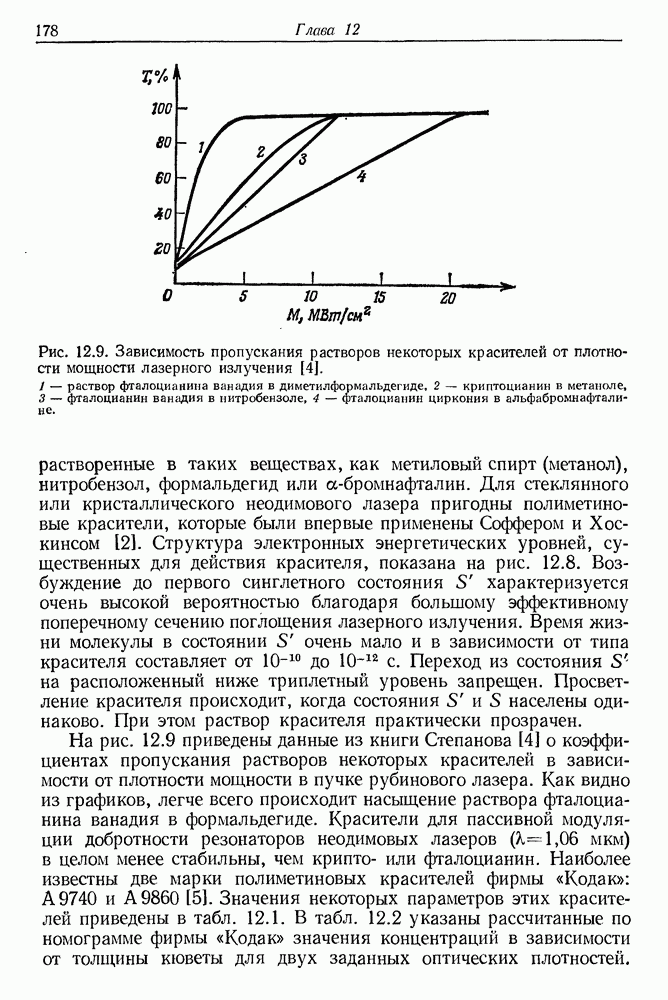
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
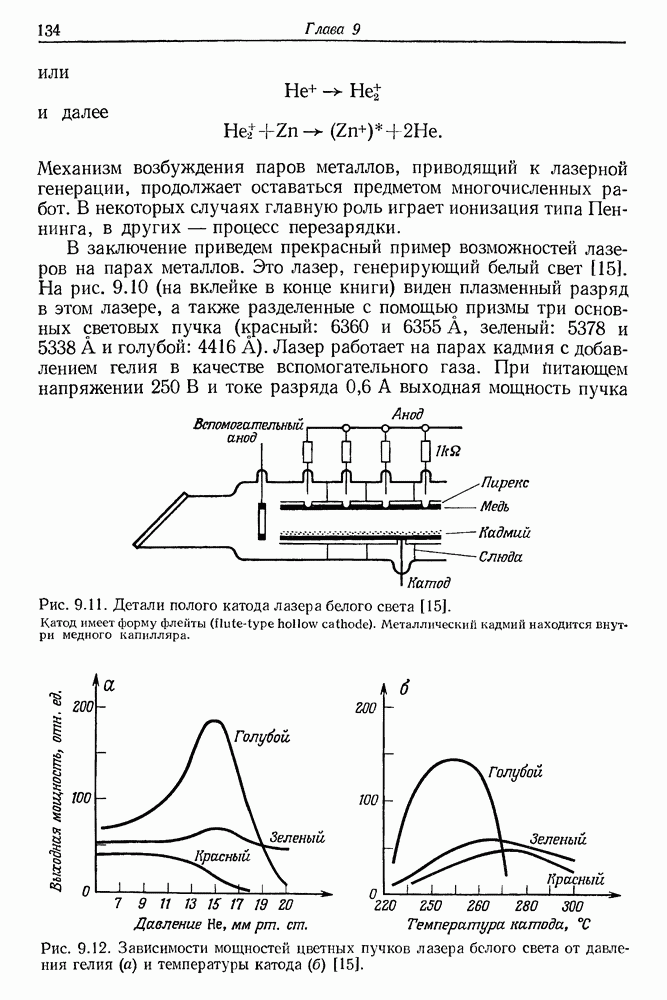
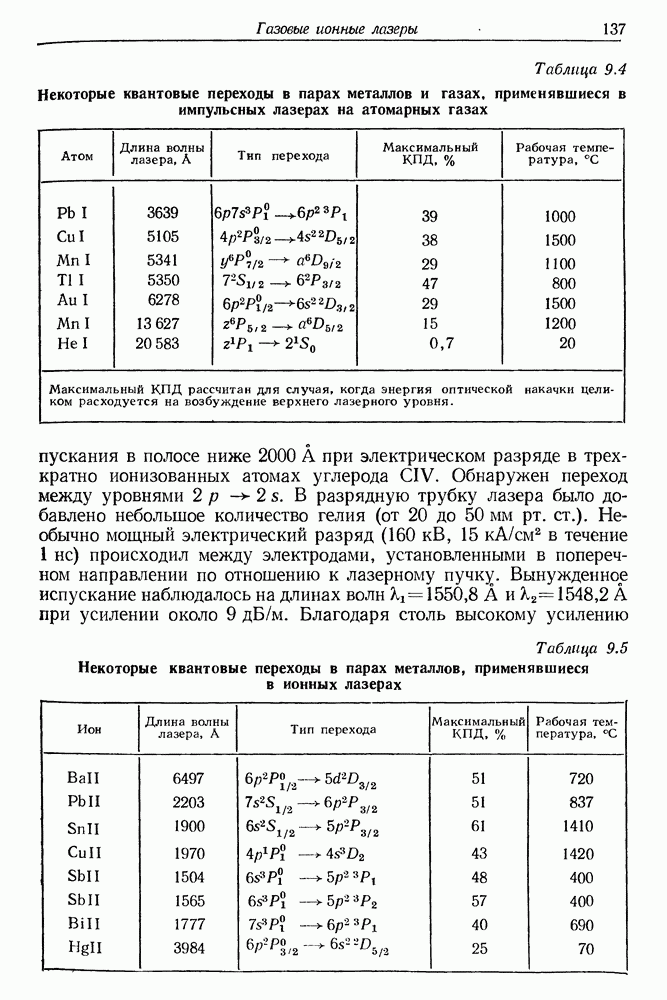
- 14. Жидкостные лазеры
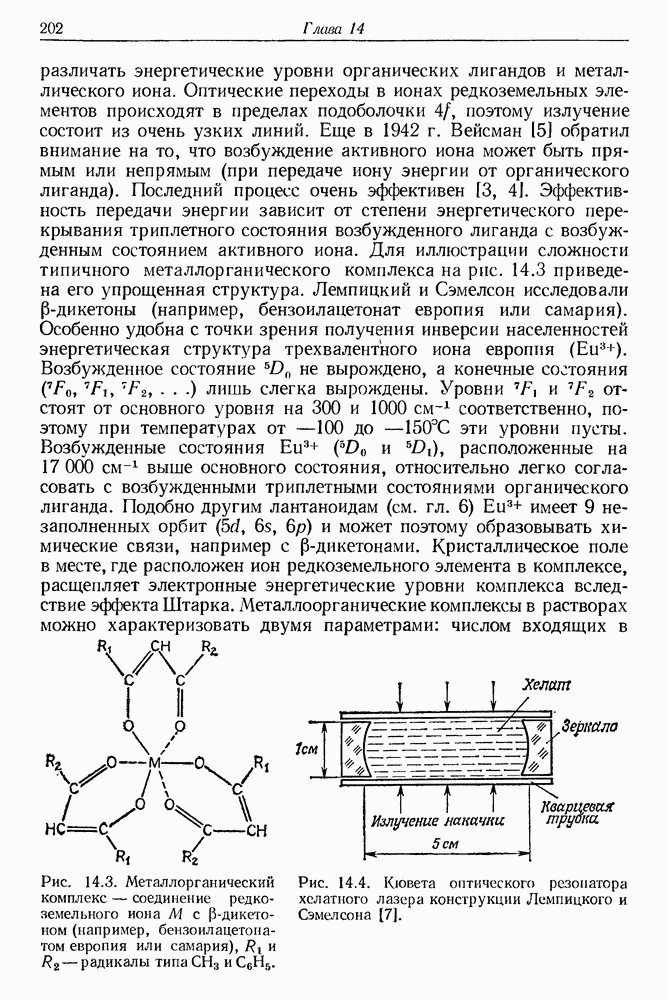
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
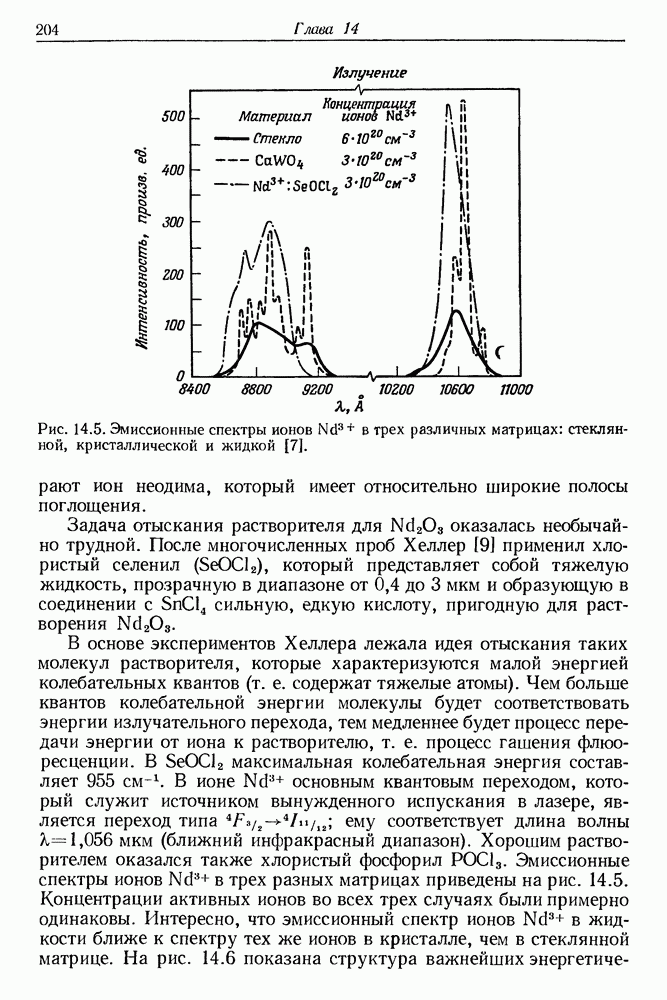
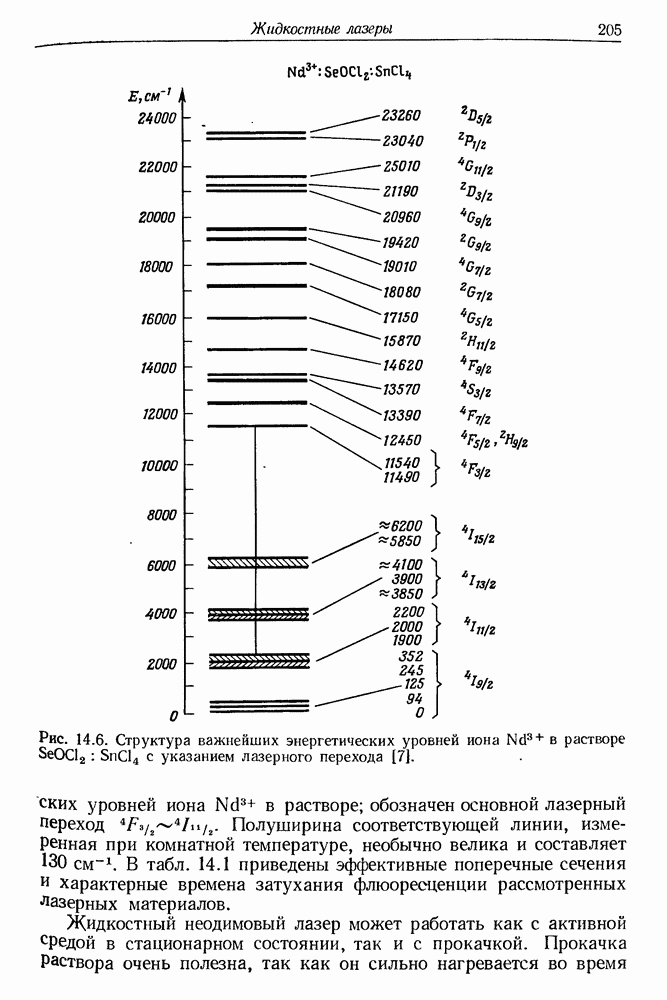
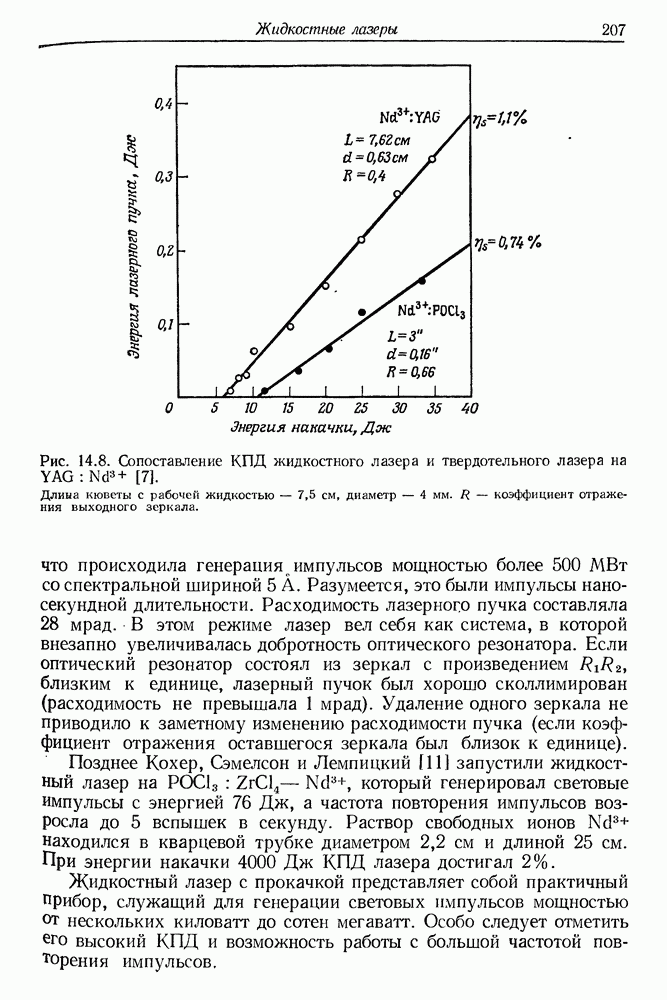
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
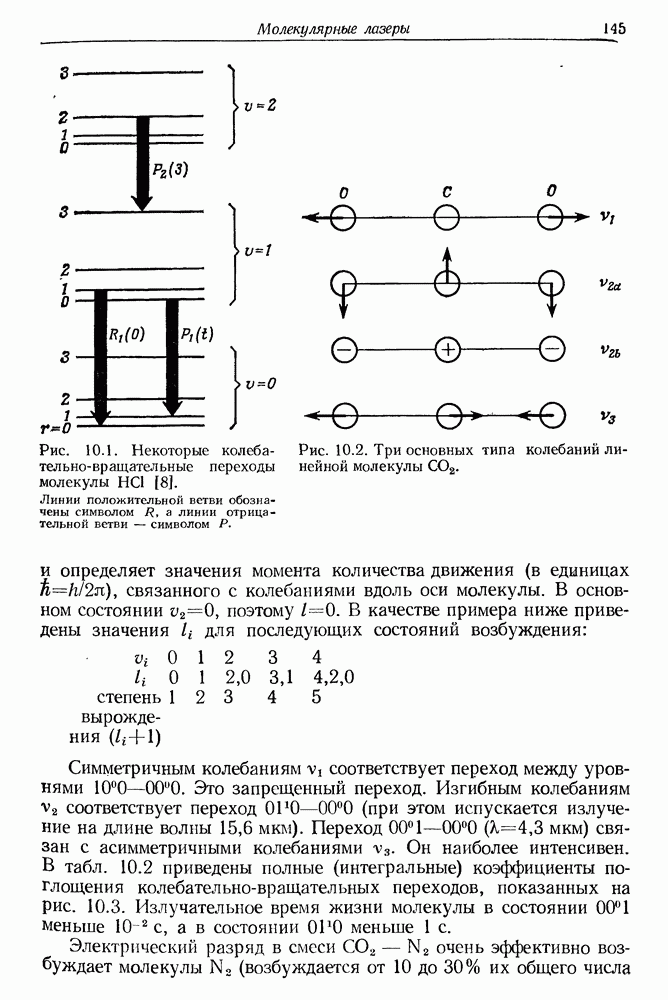
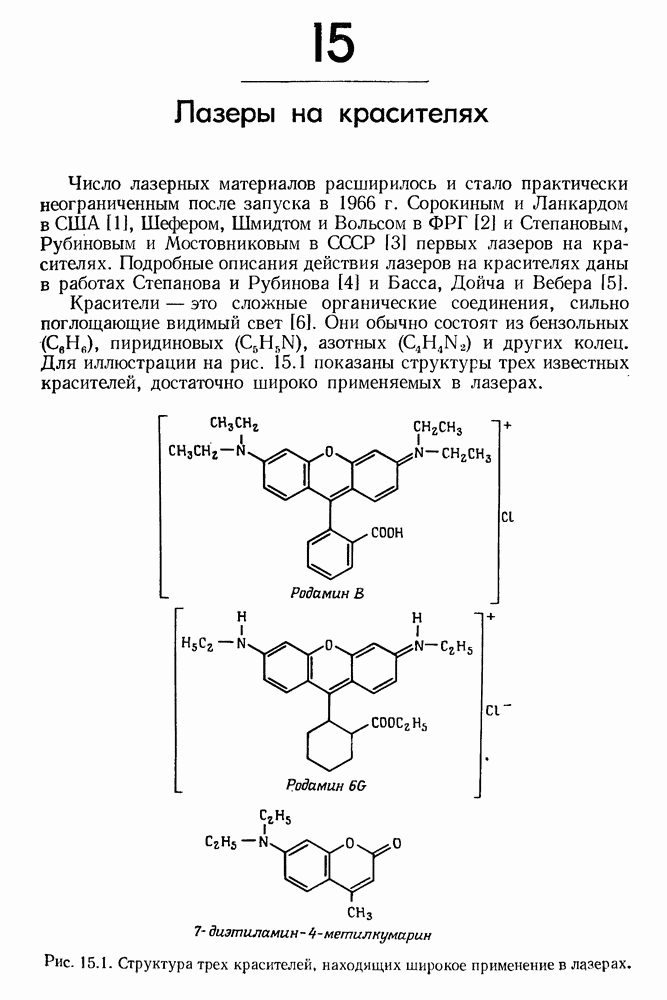
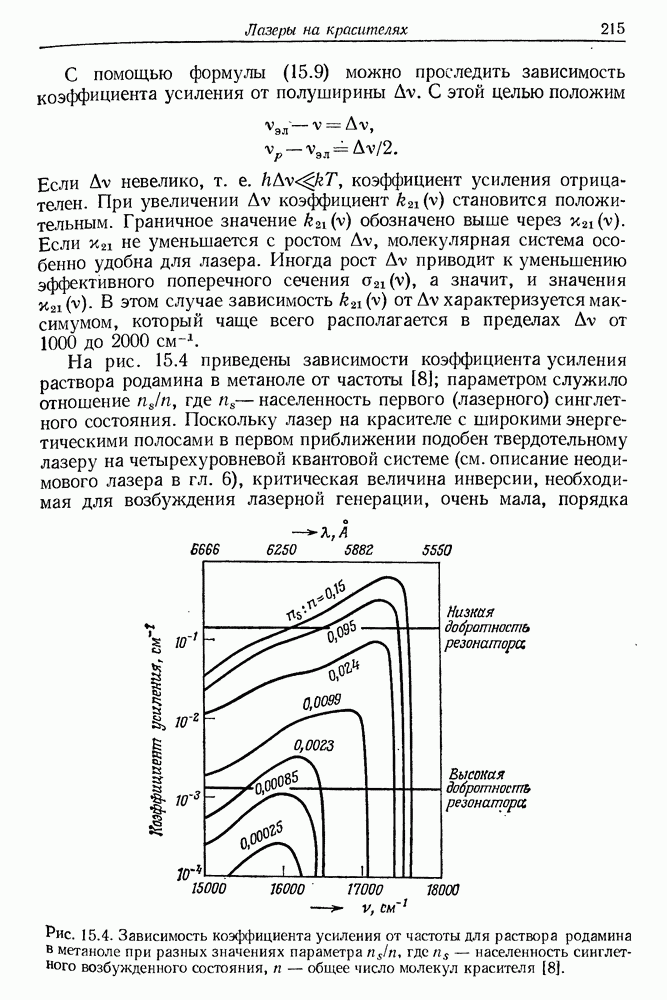
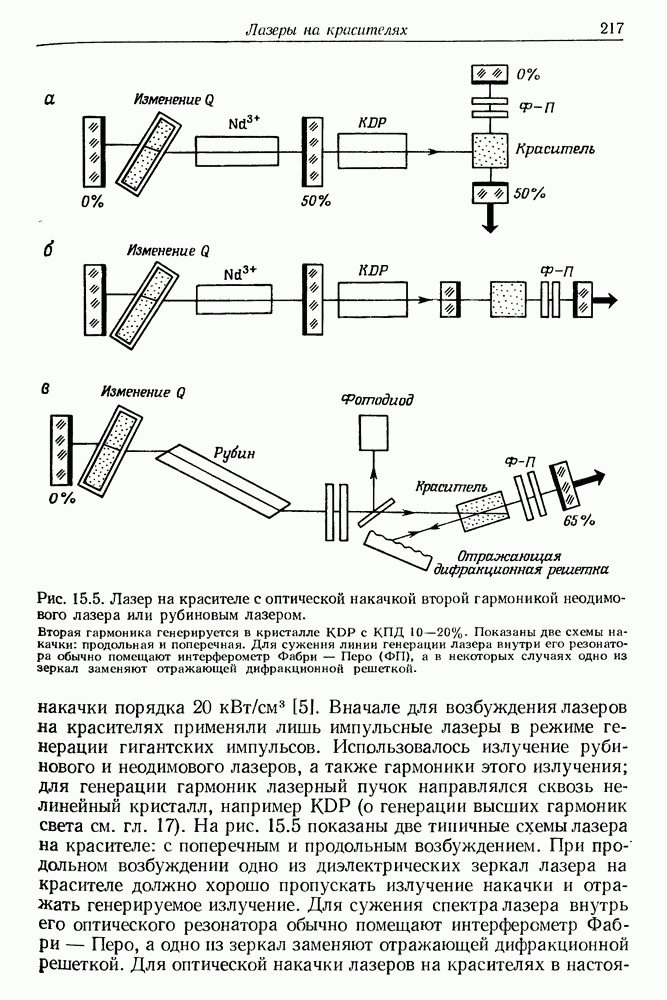
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
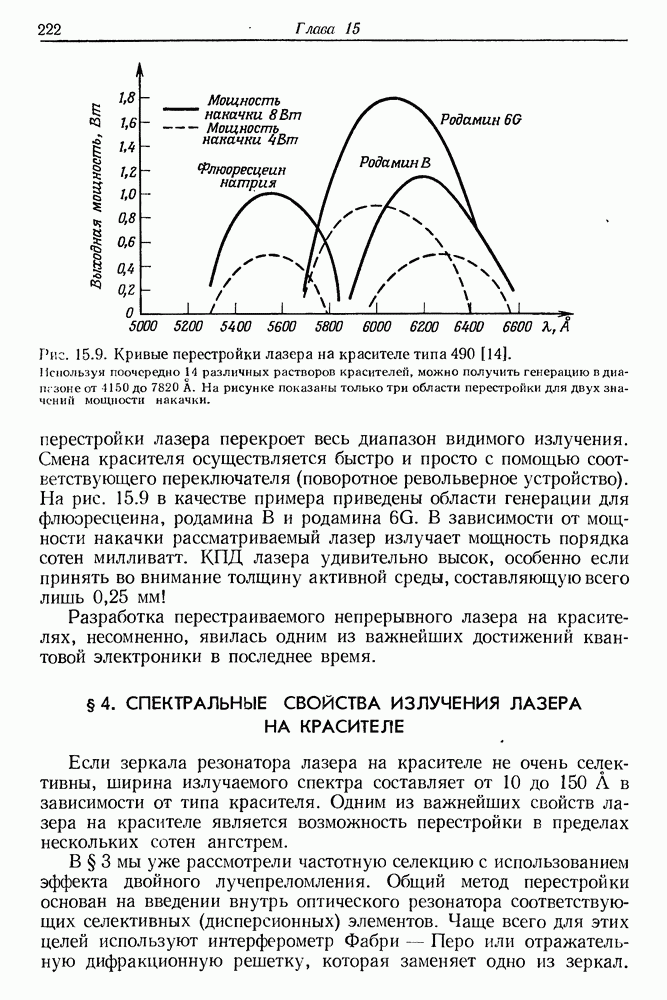
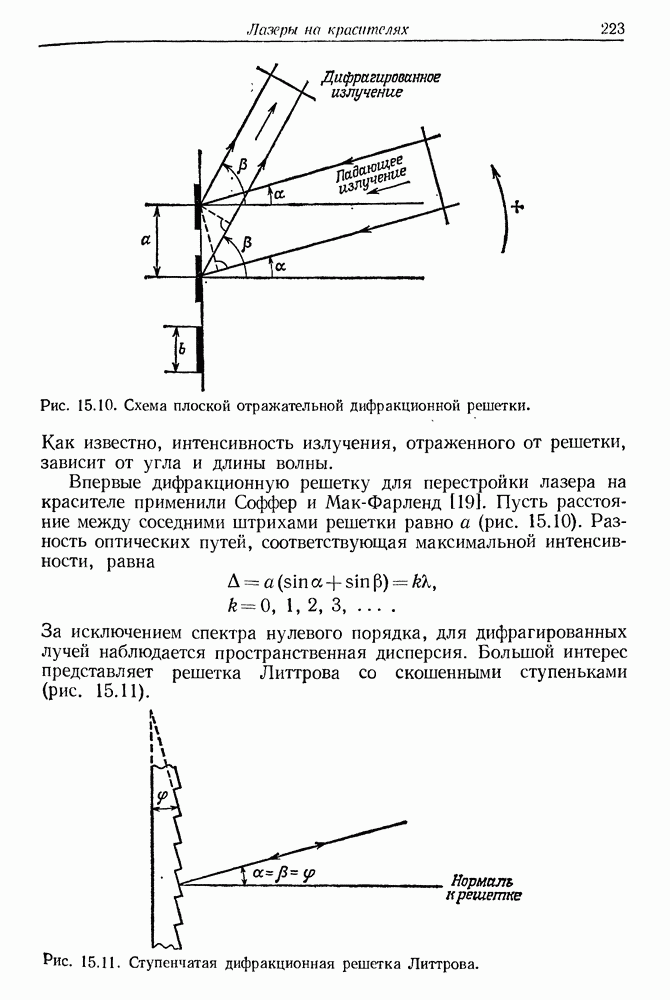
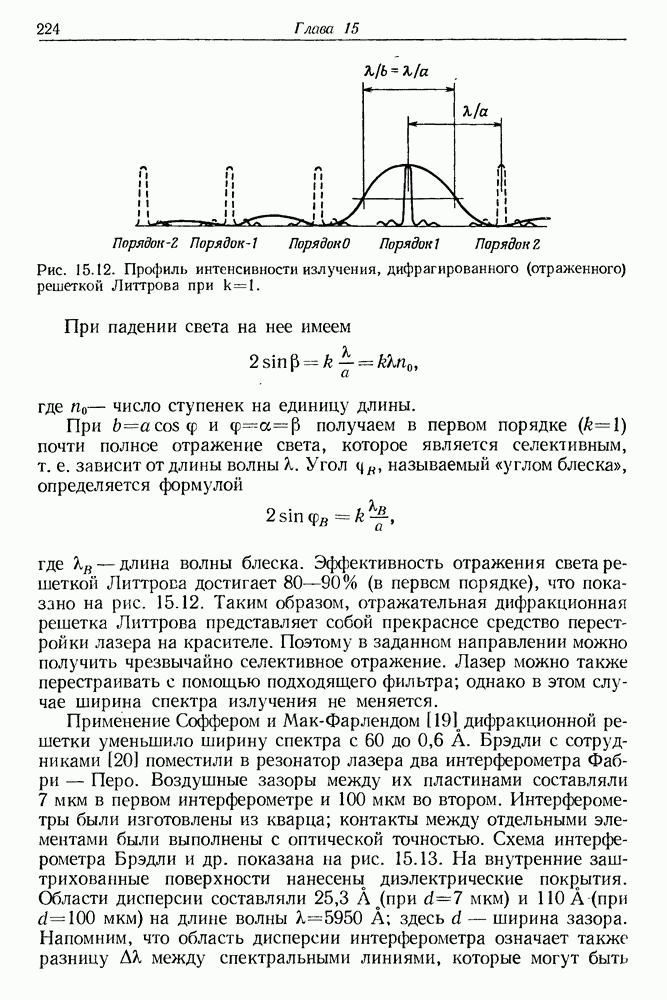
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
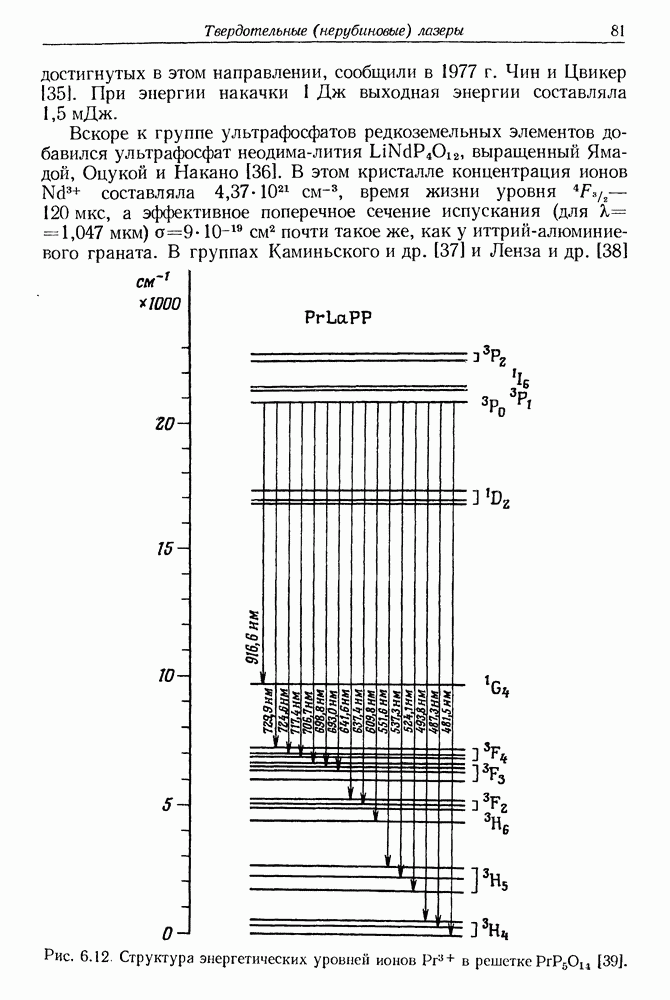
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
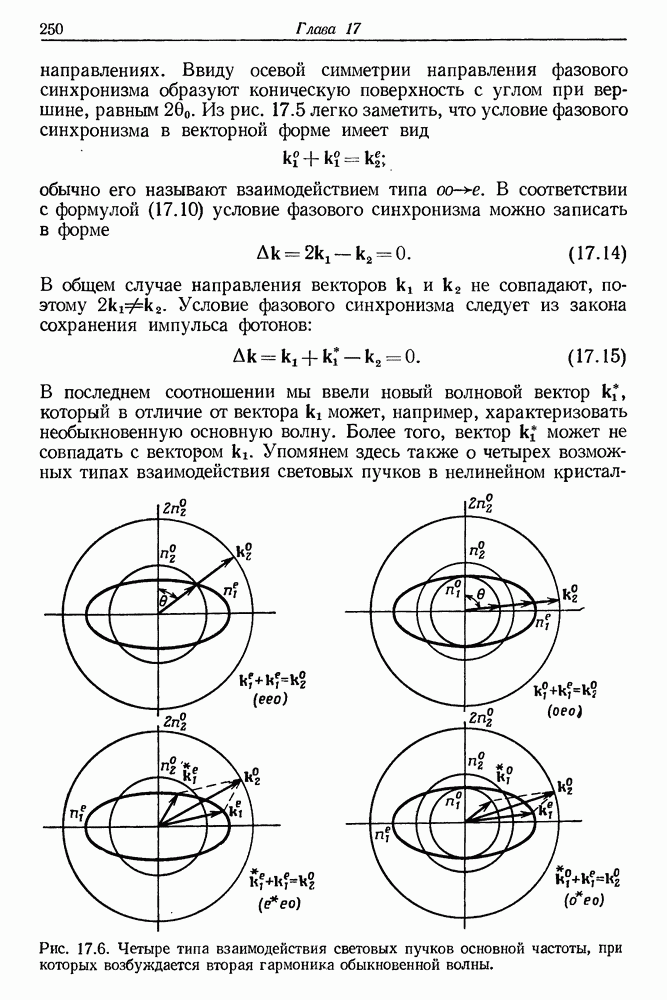
- 17. Генерация оптических гармоник
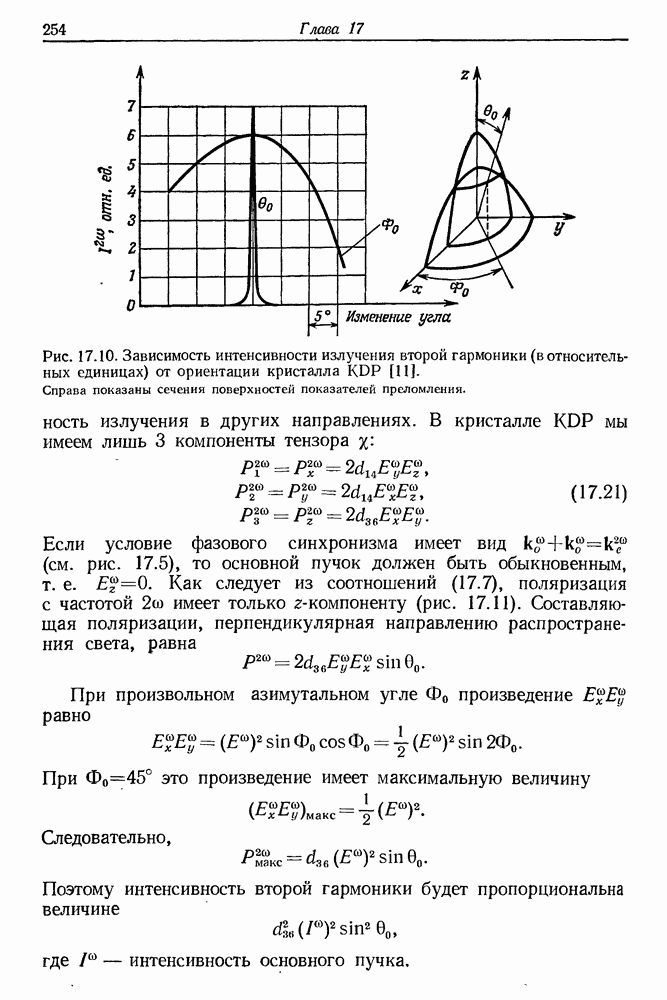
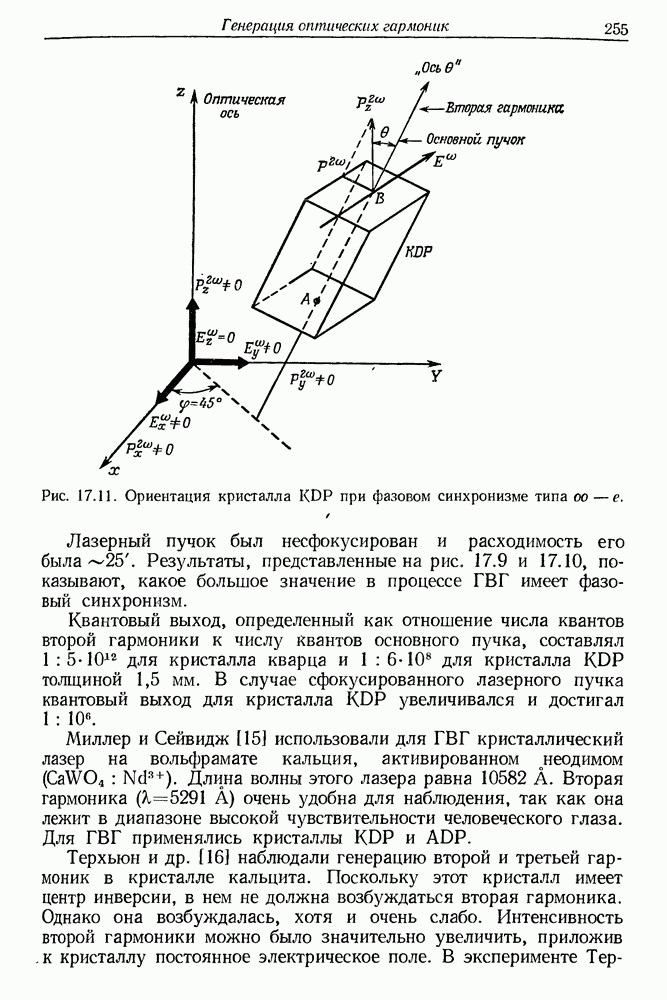
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
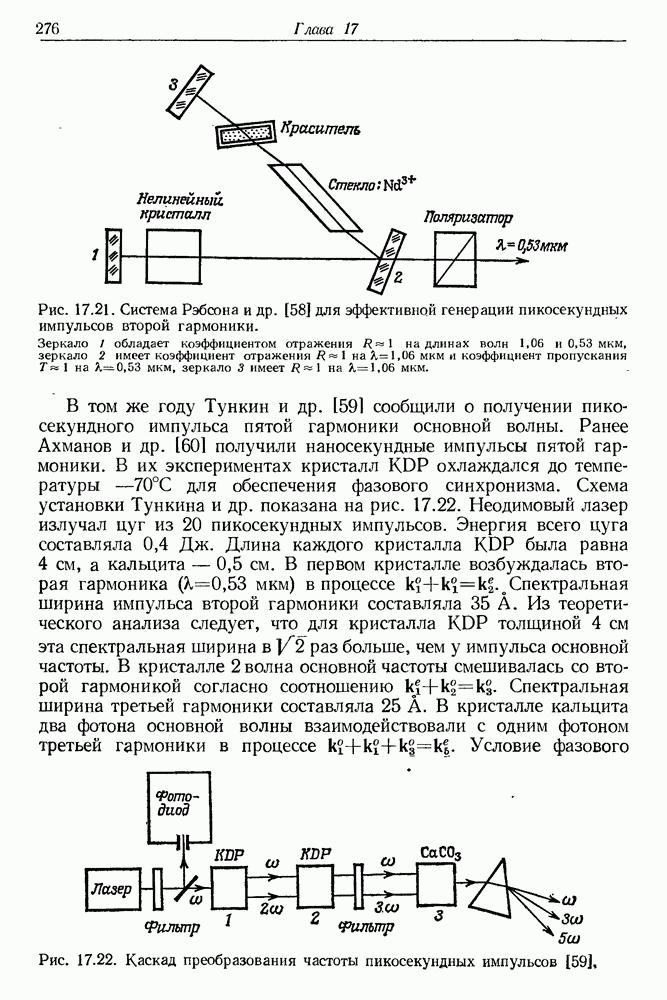
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
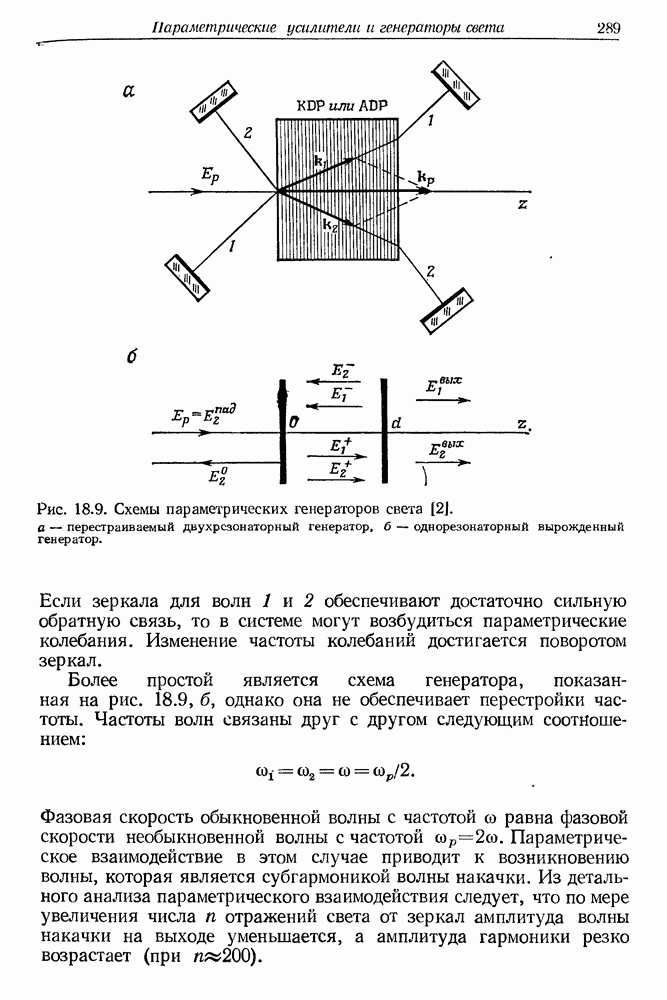
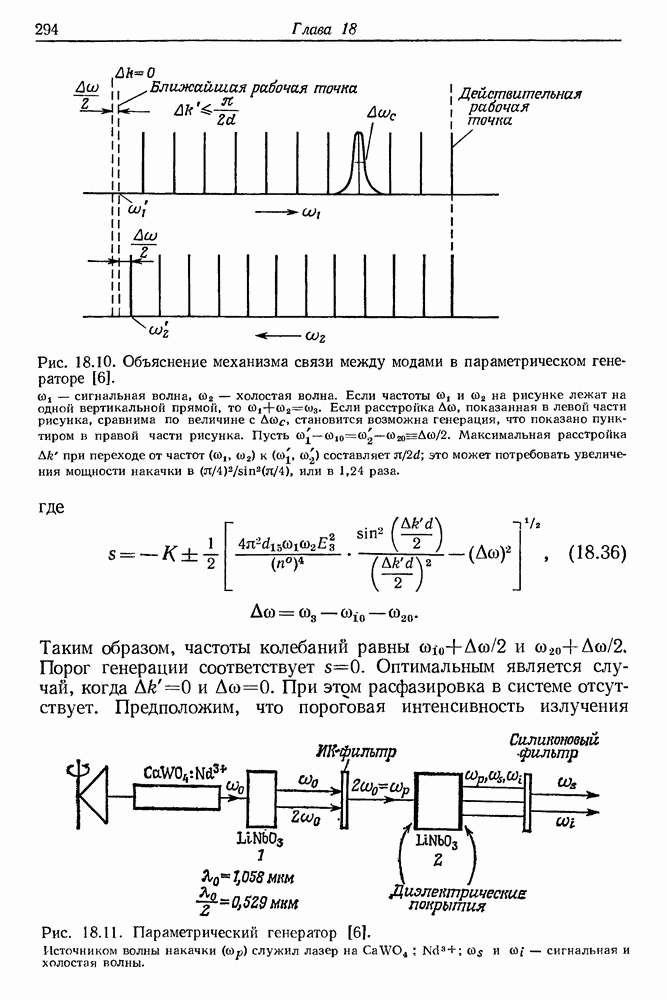
- 18. Параметрические усилители и генераторы света
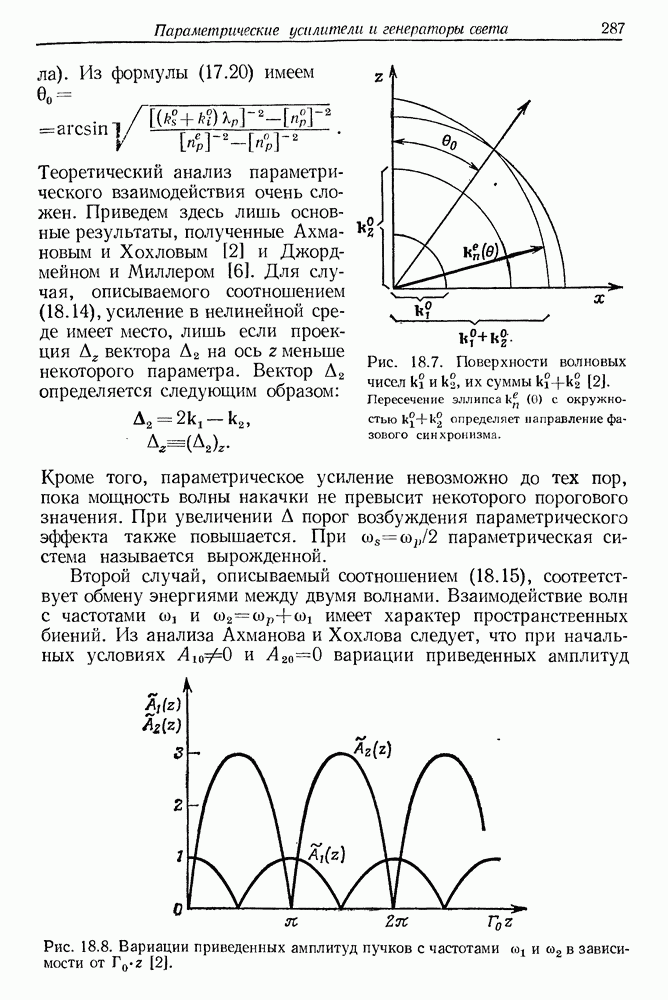
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
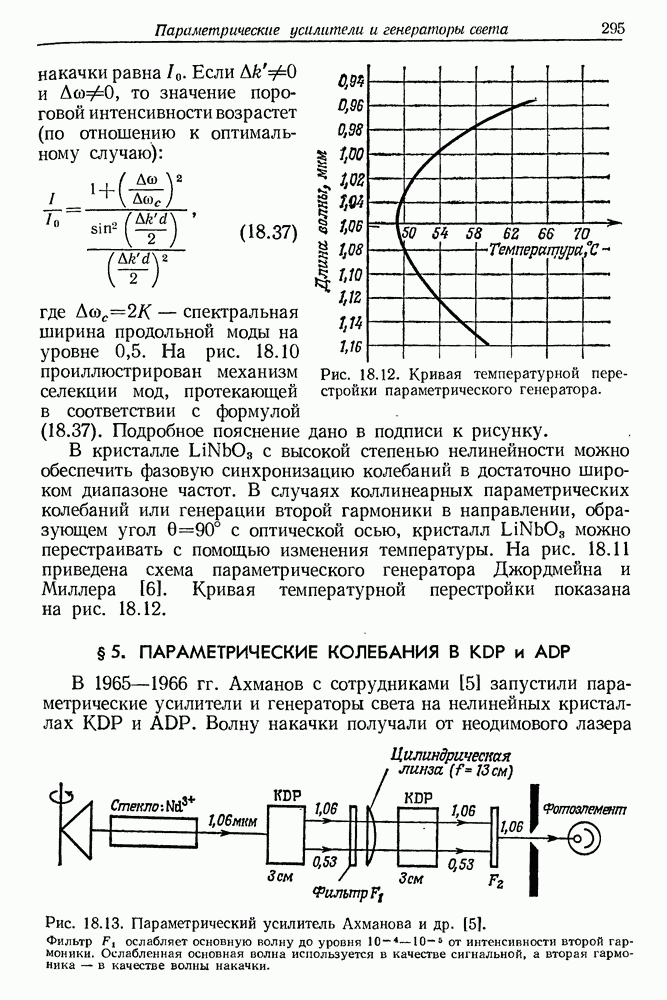
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
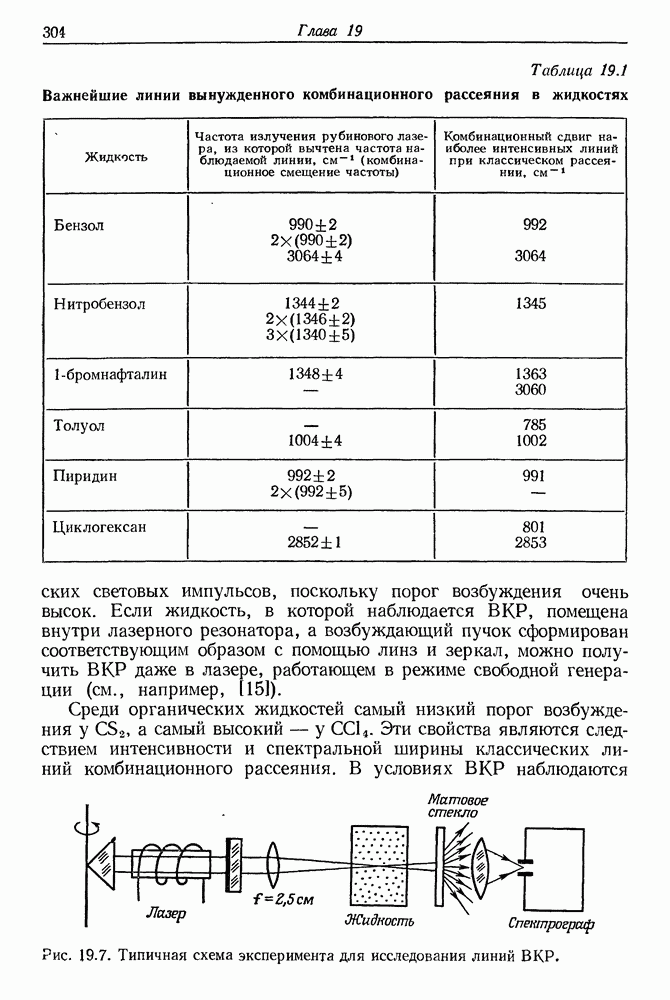
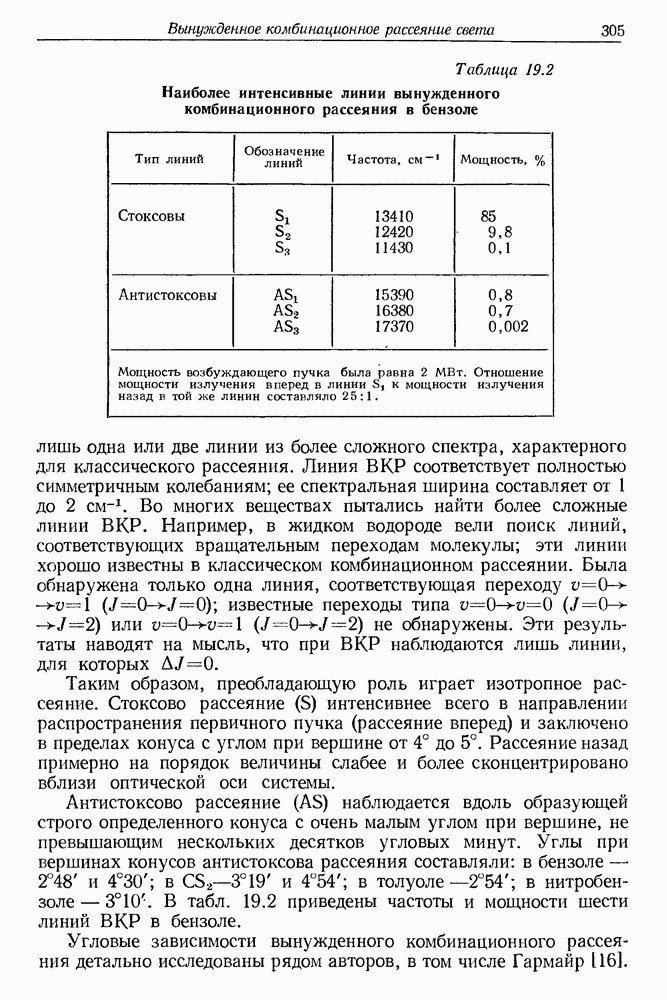
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
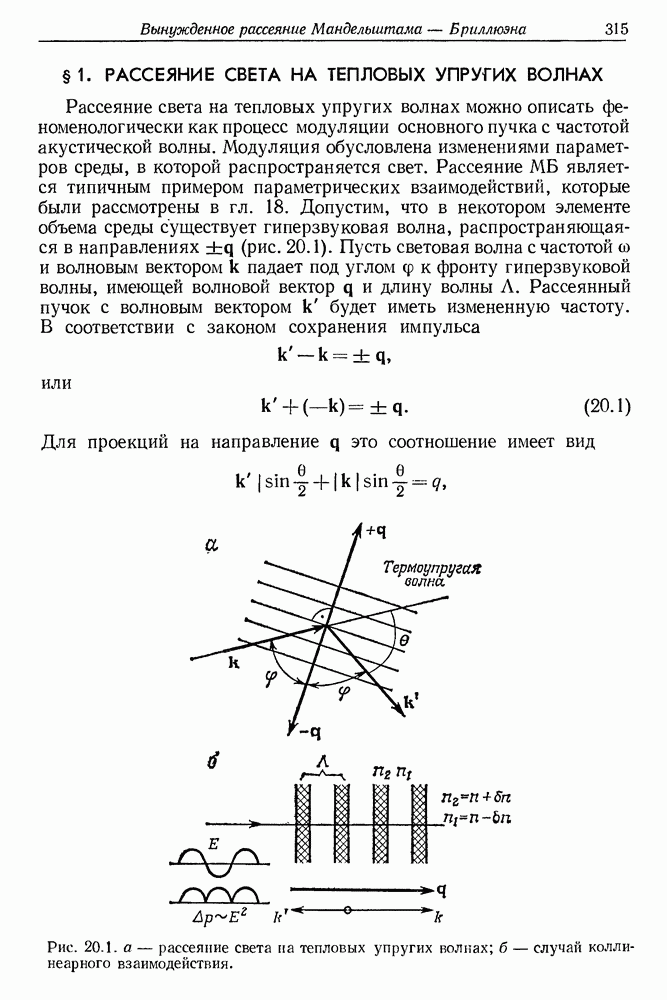
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
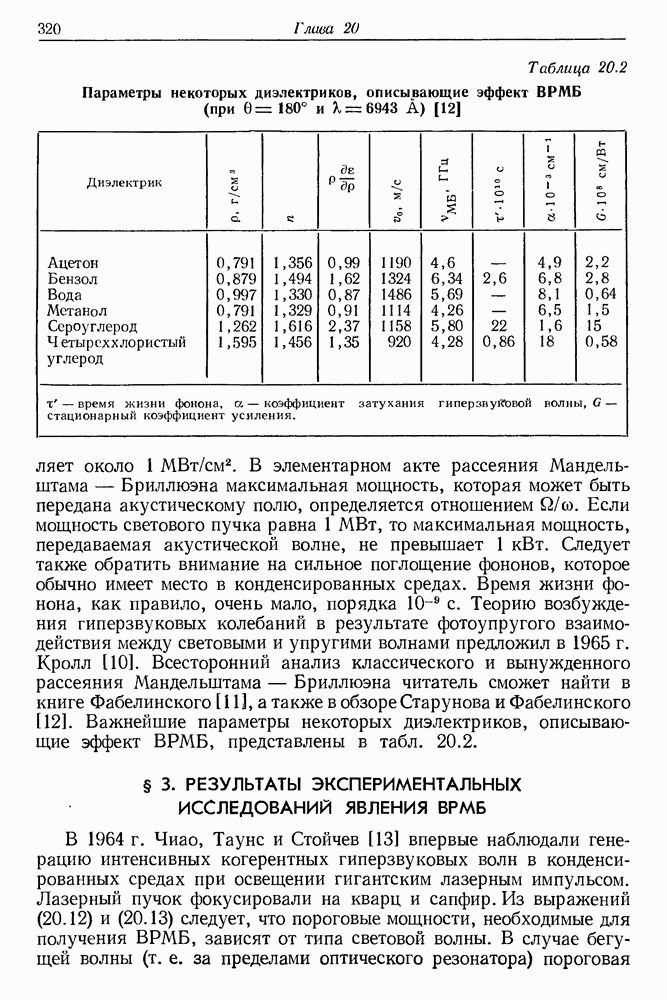
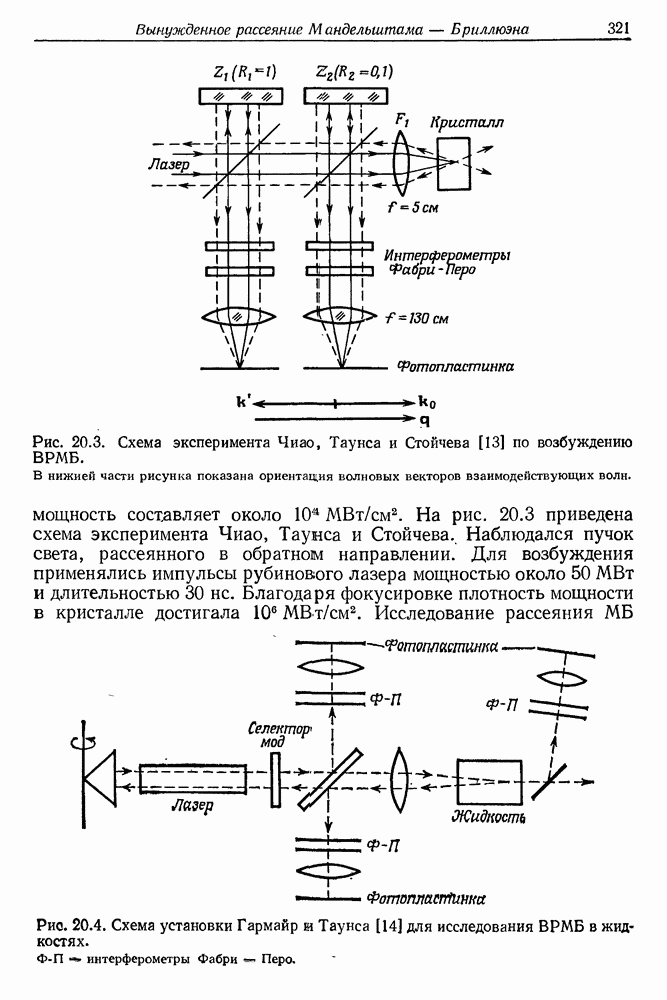
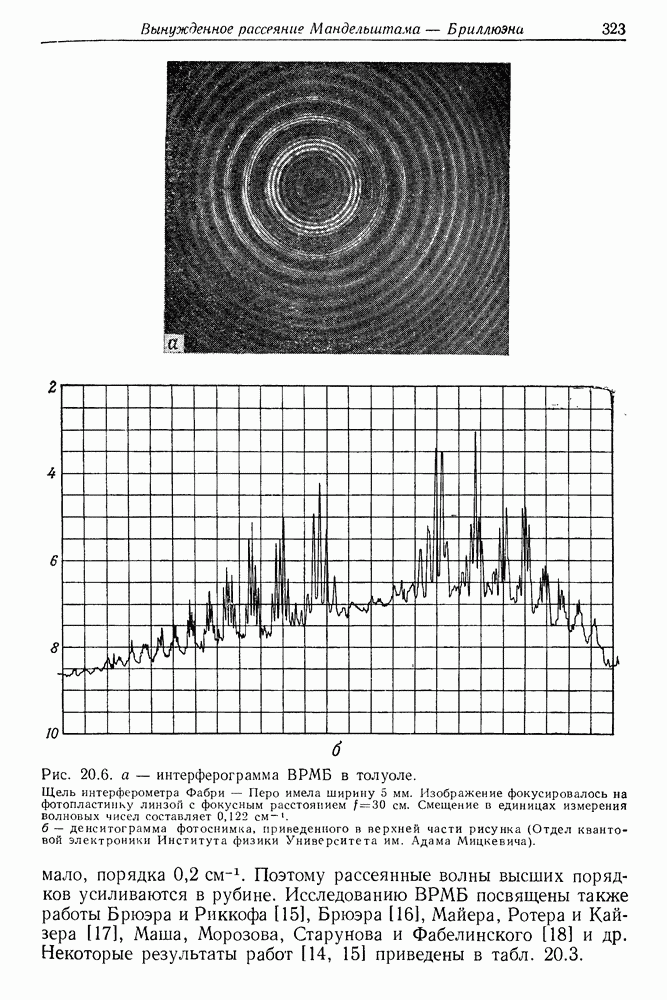
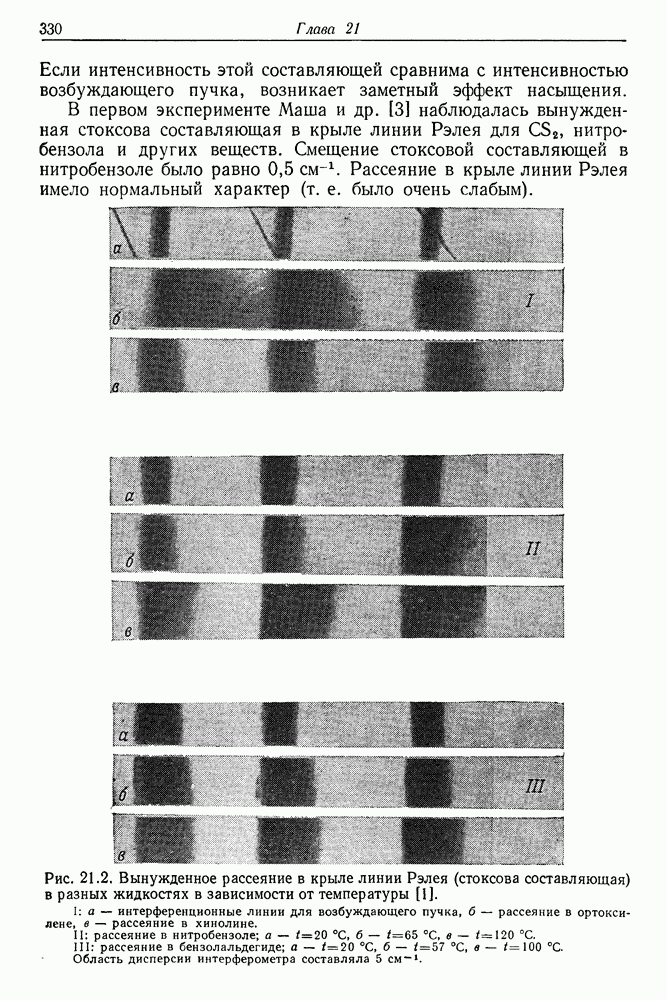
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
- 22. Параметрическая люминесценция (ПЛ)
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
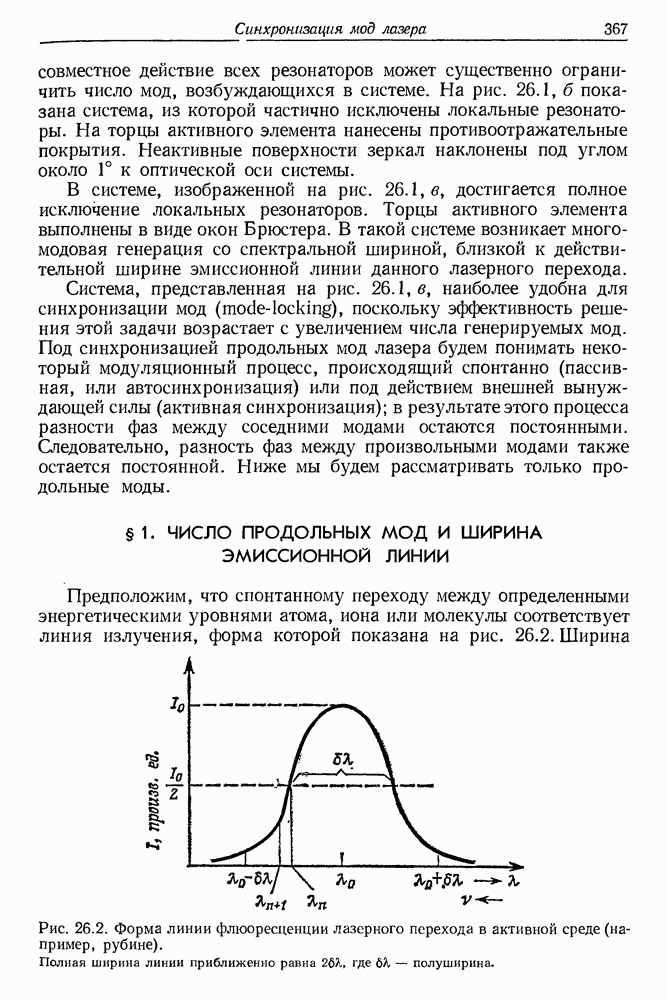
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
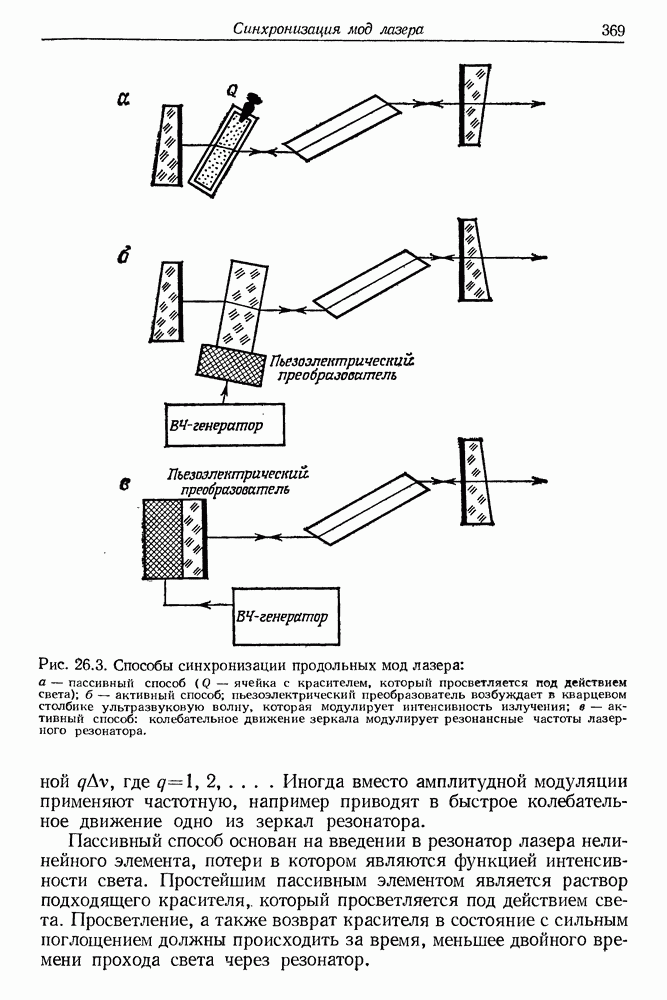
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
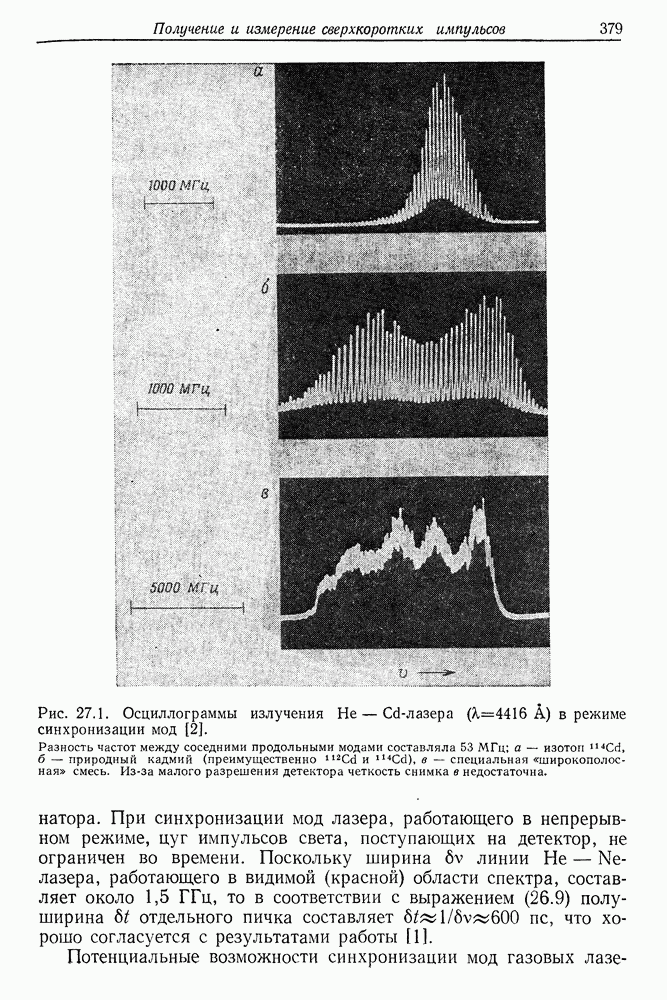
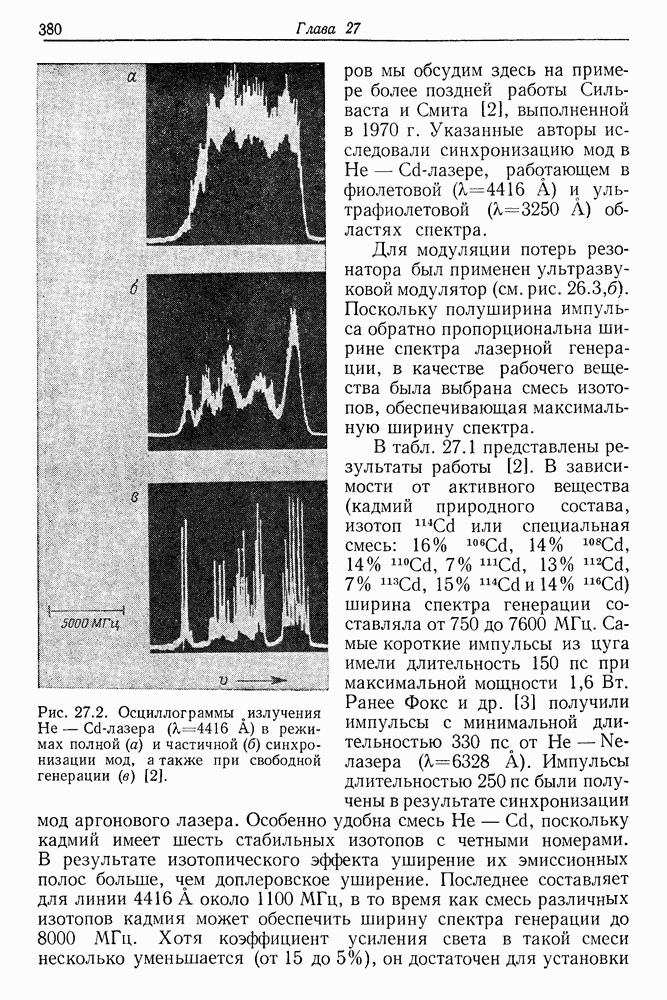
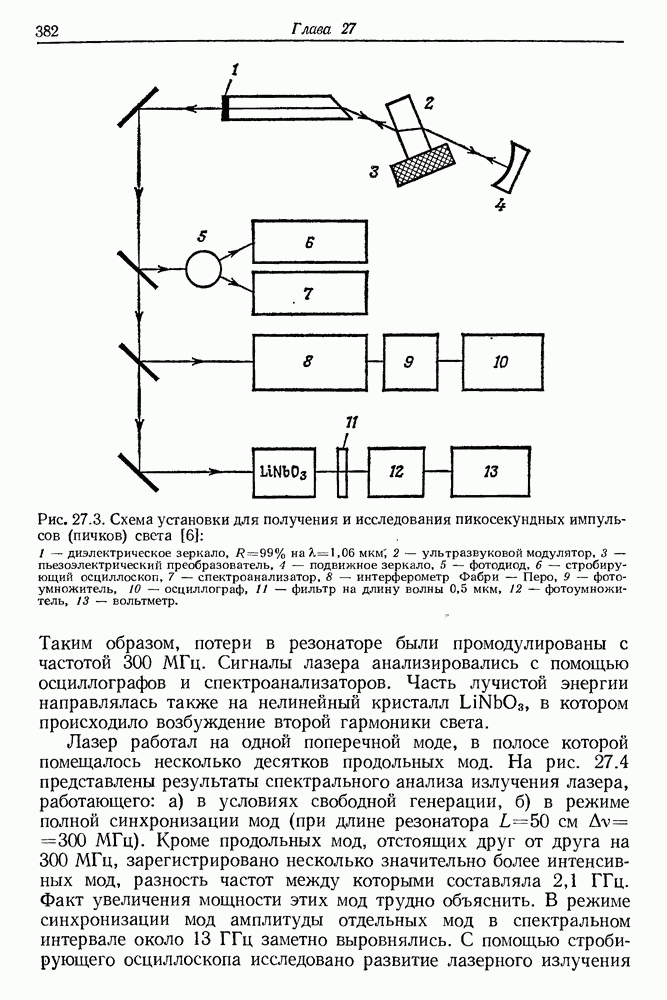
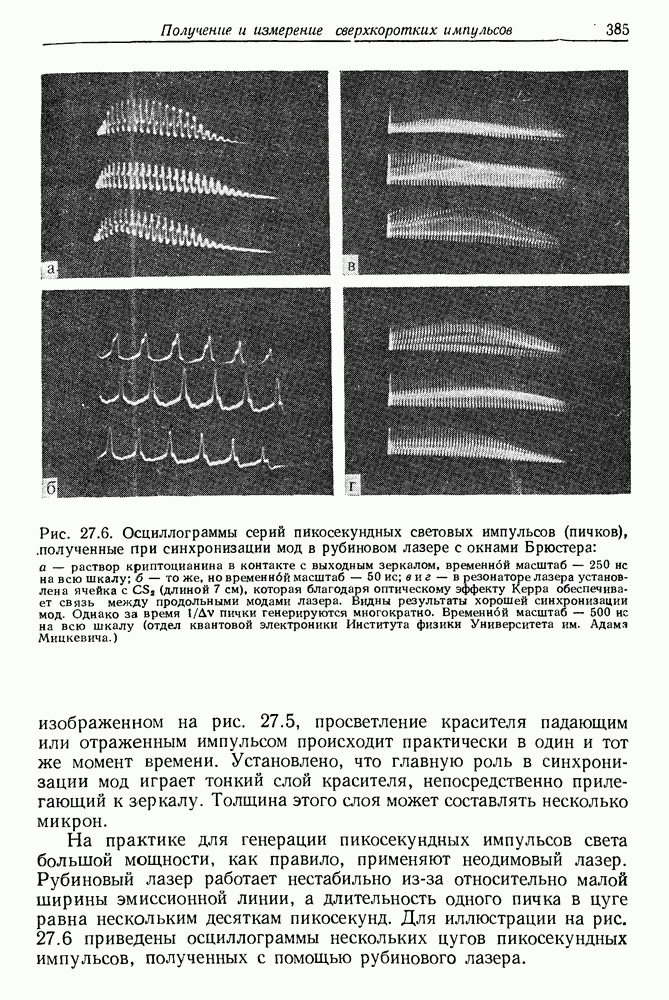
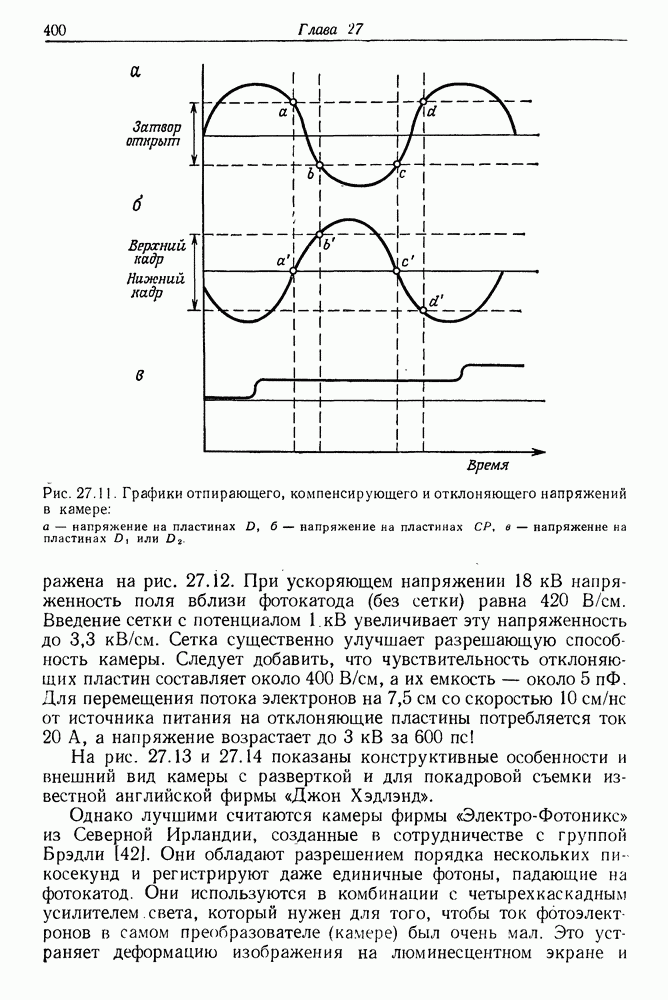
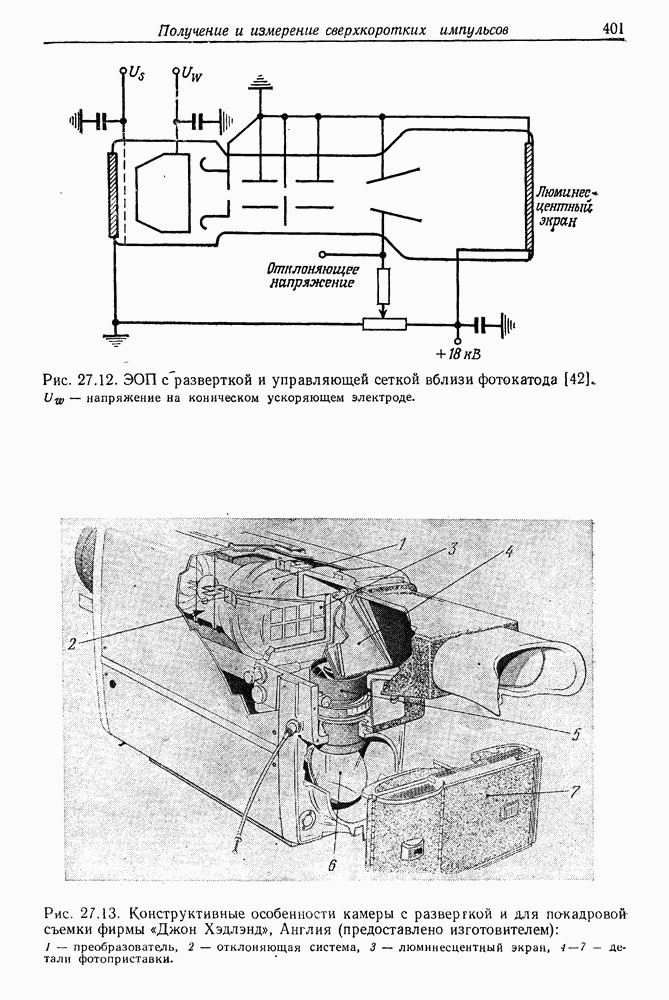
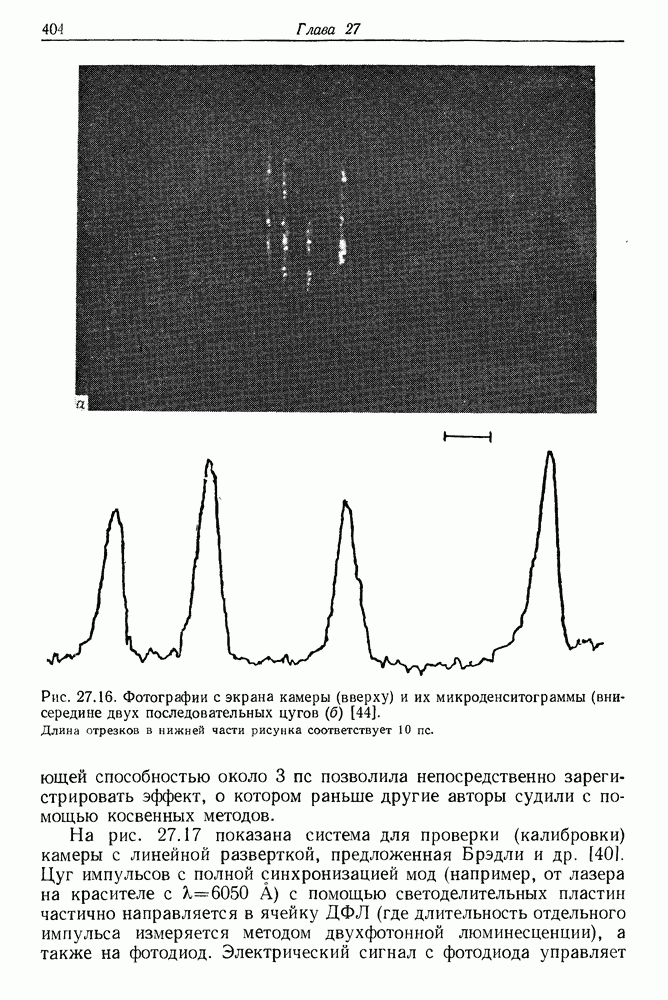
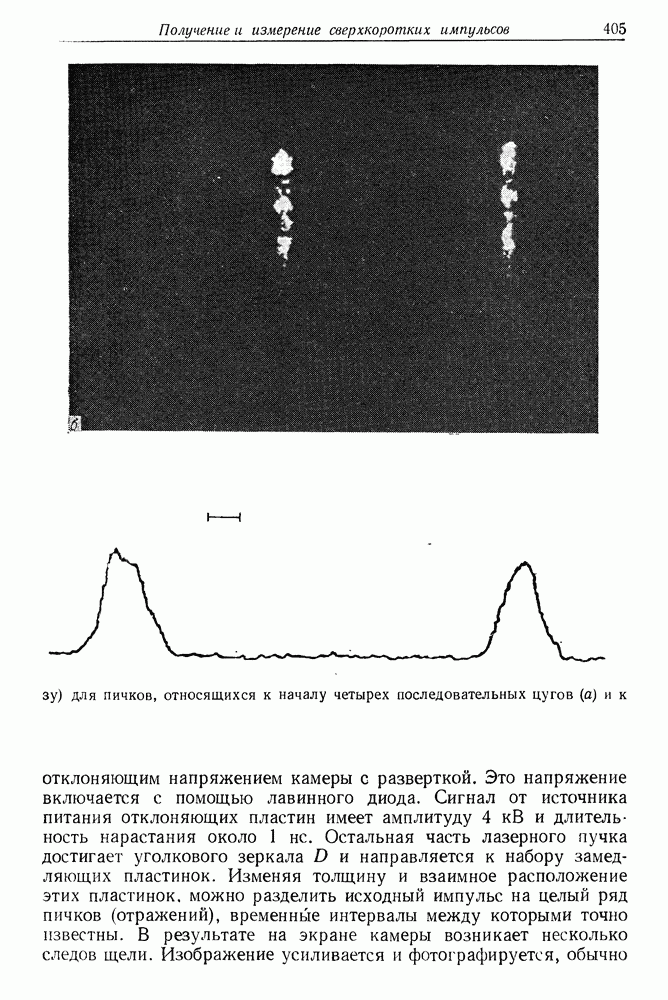
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
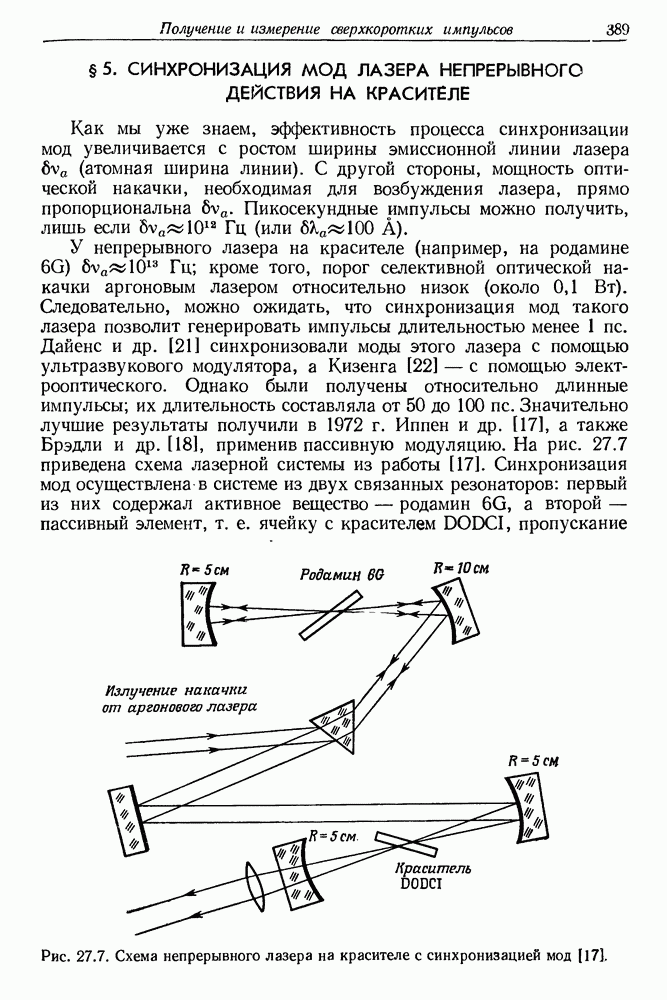
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
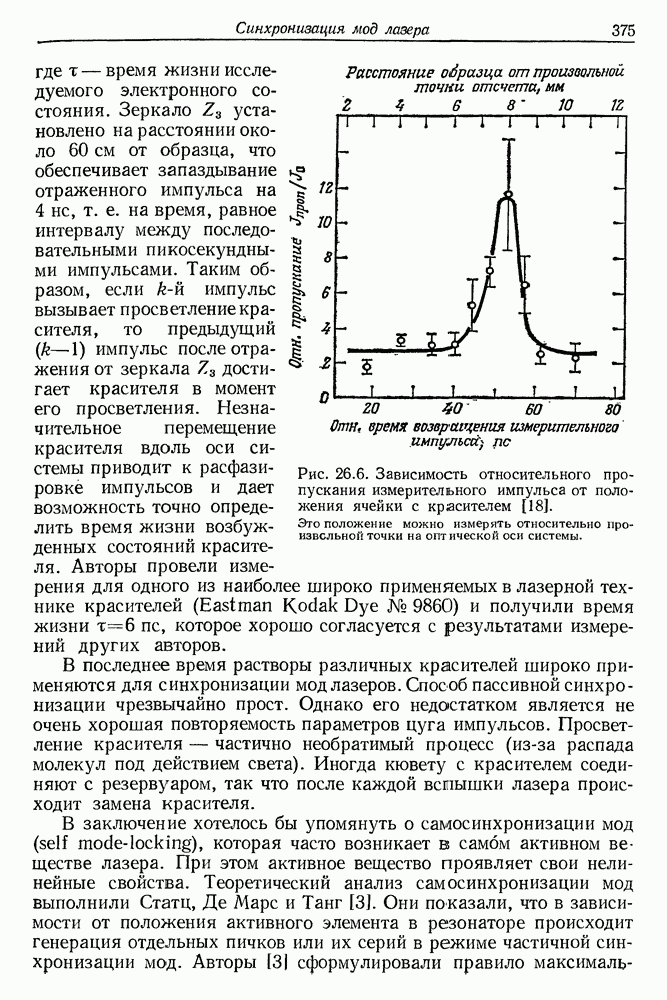
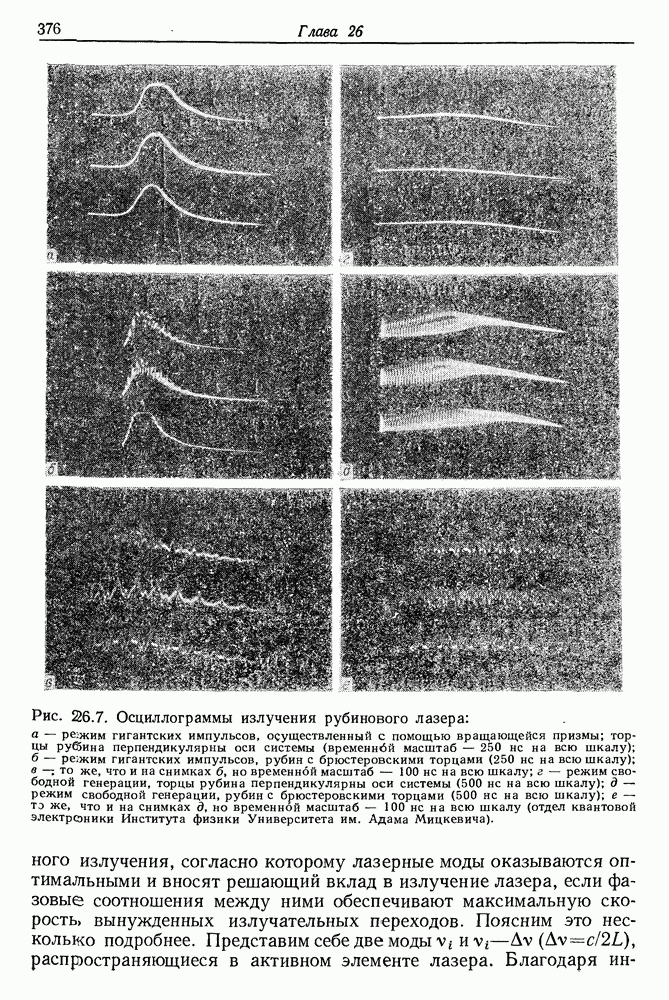
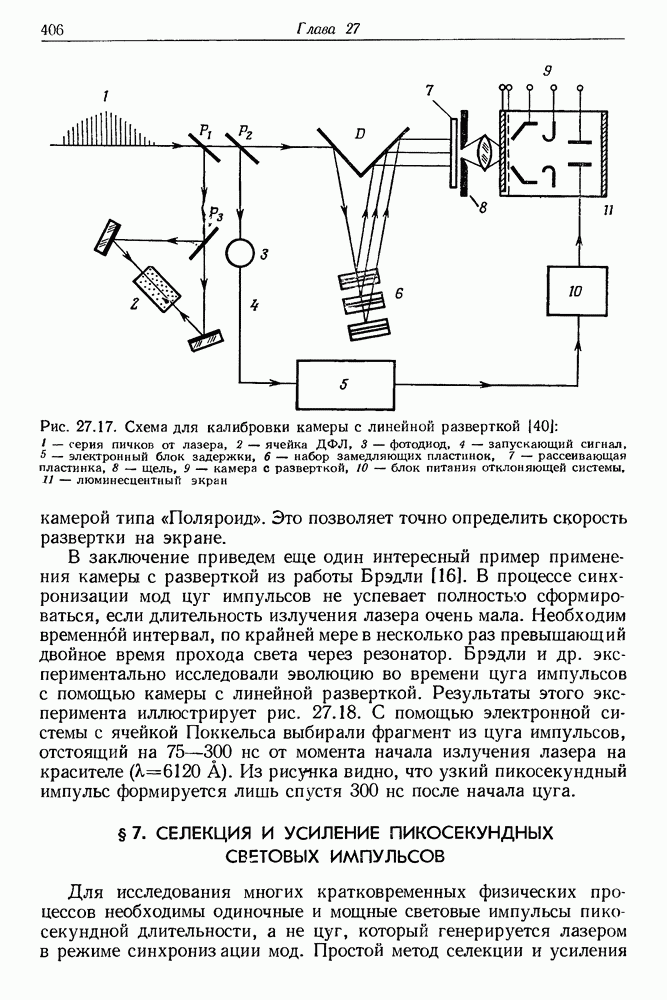
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
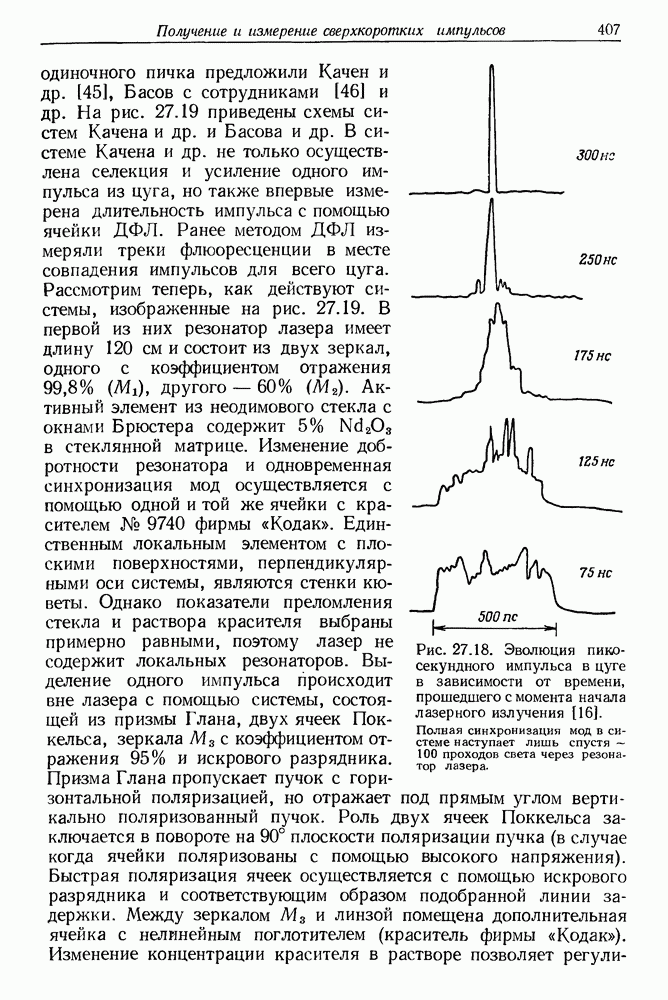
- в. Примеры использования камеры с разверткой
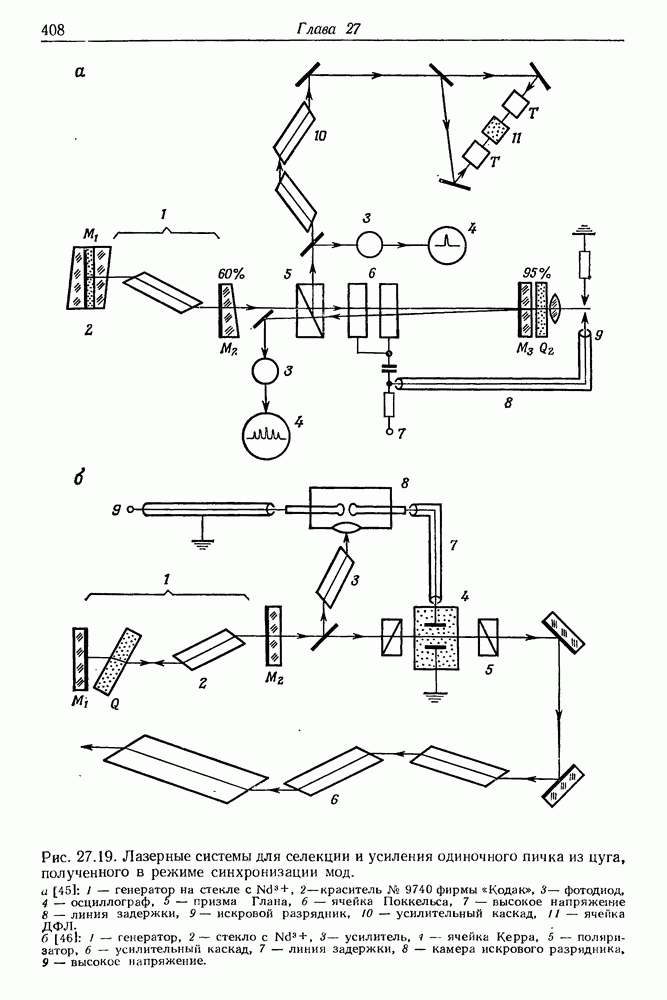
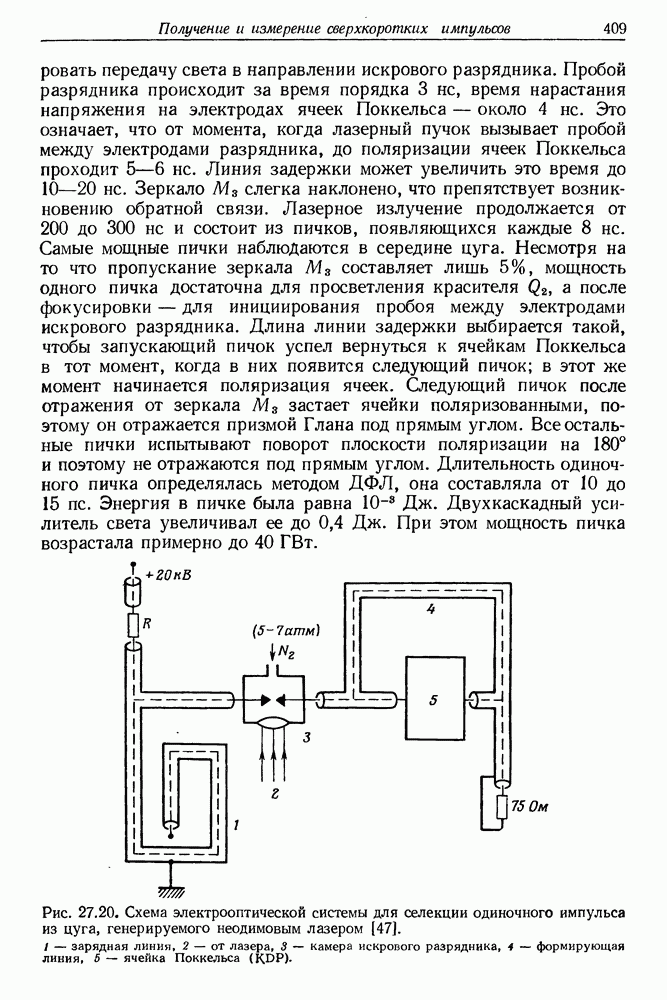
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
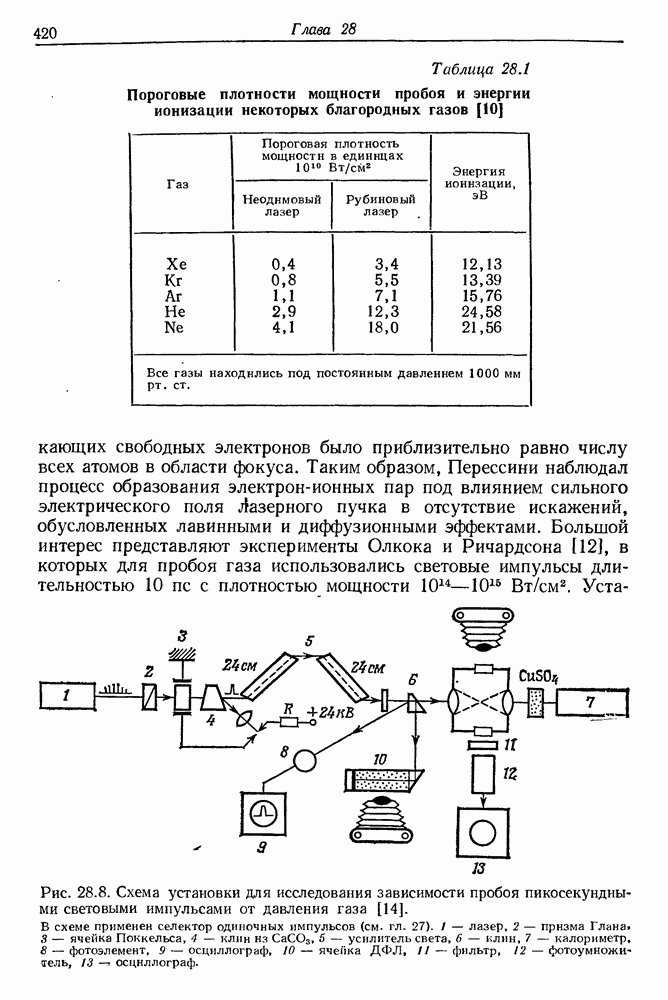
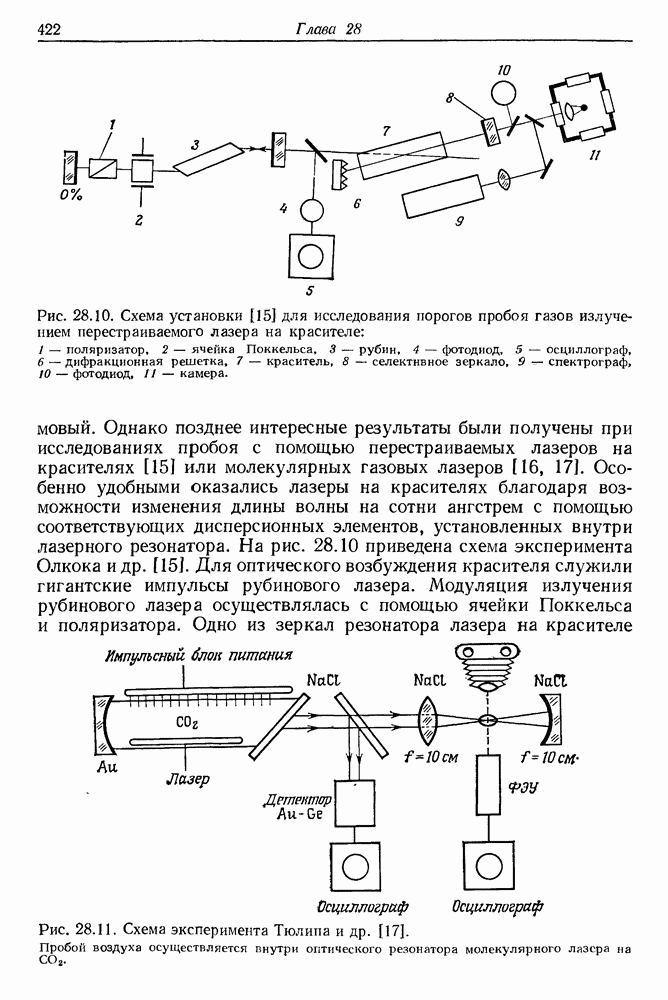
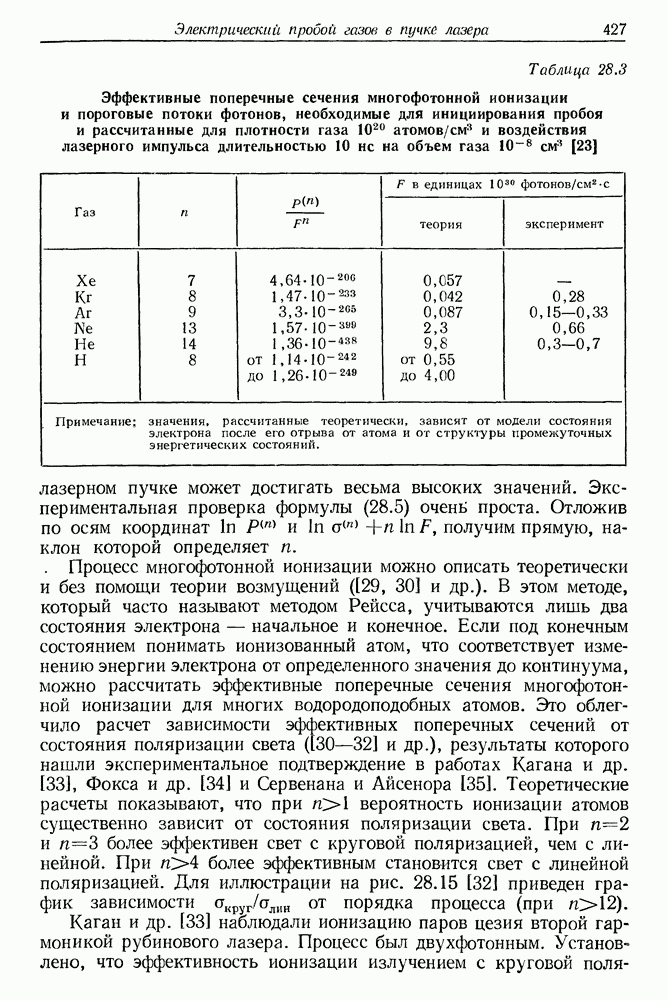
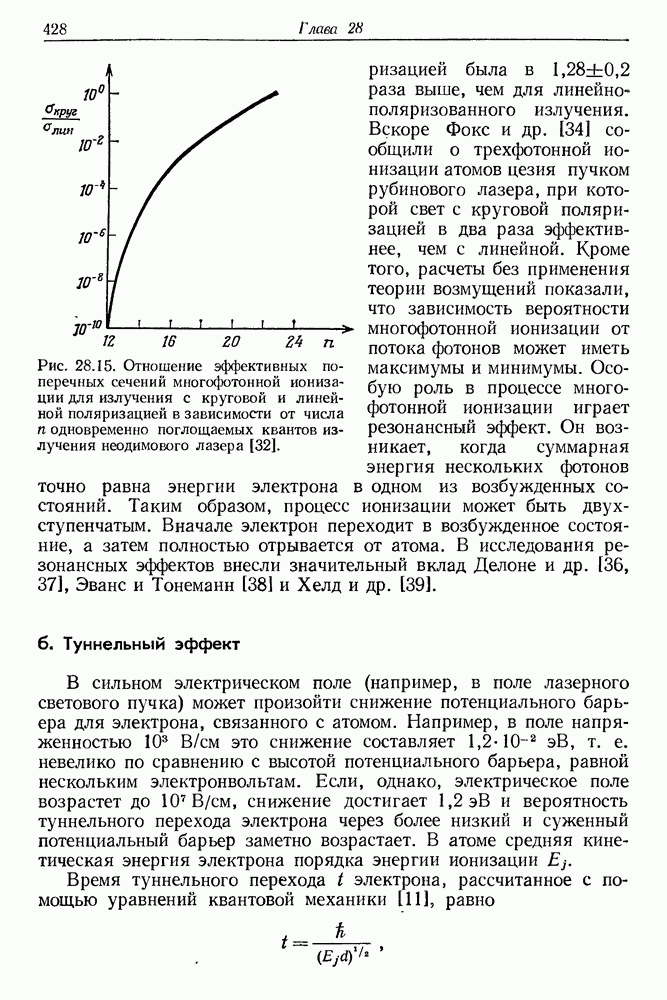
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
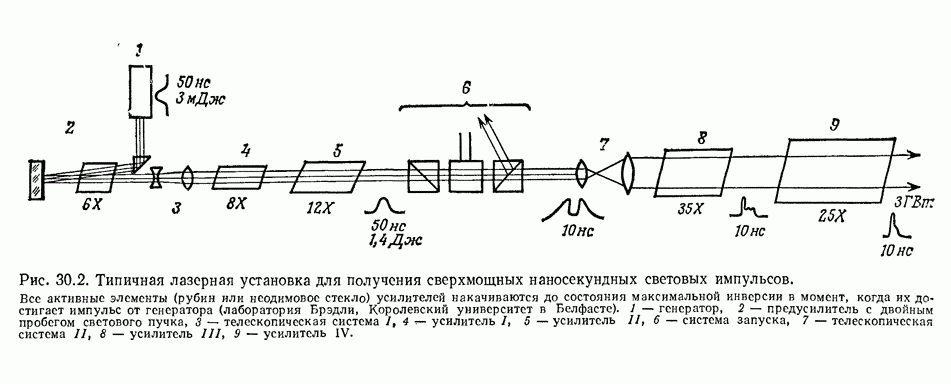
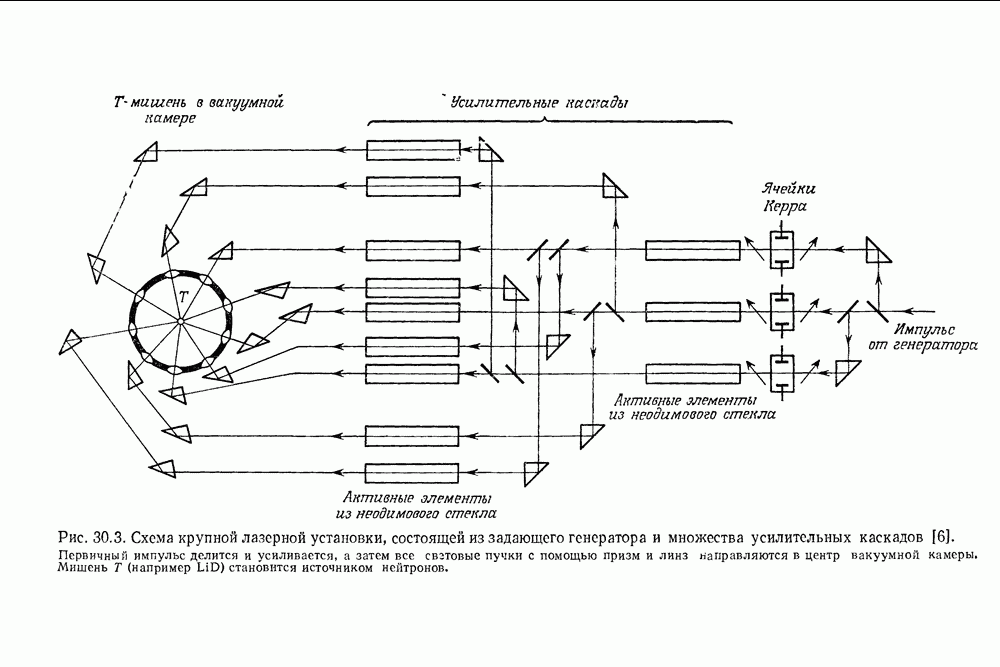
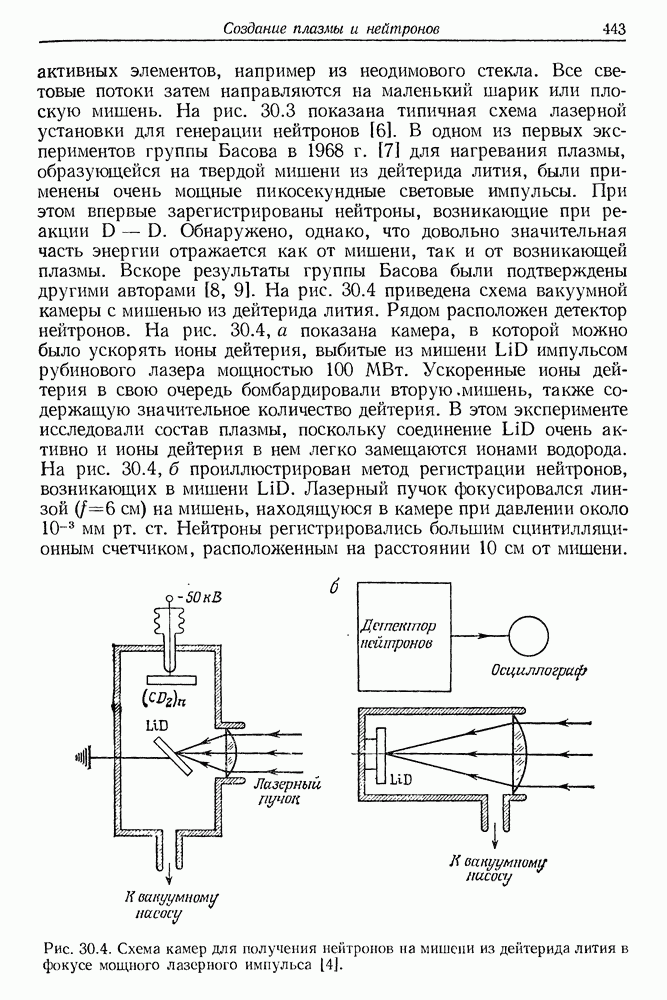
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
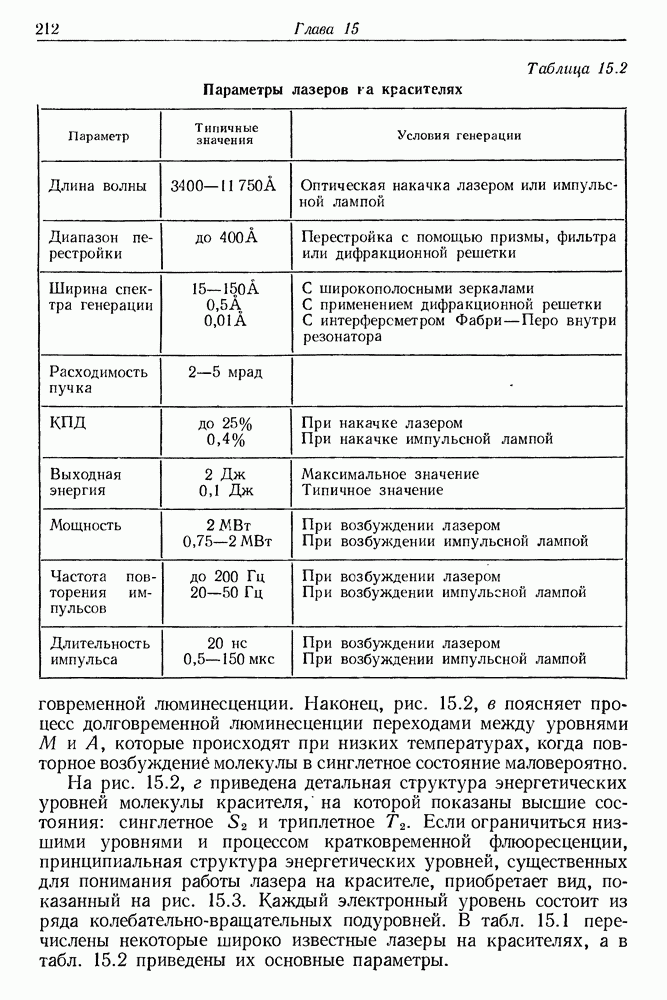
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
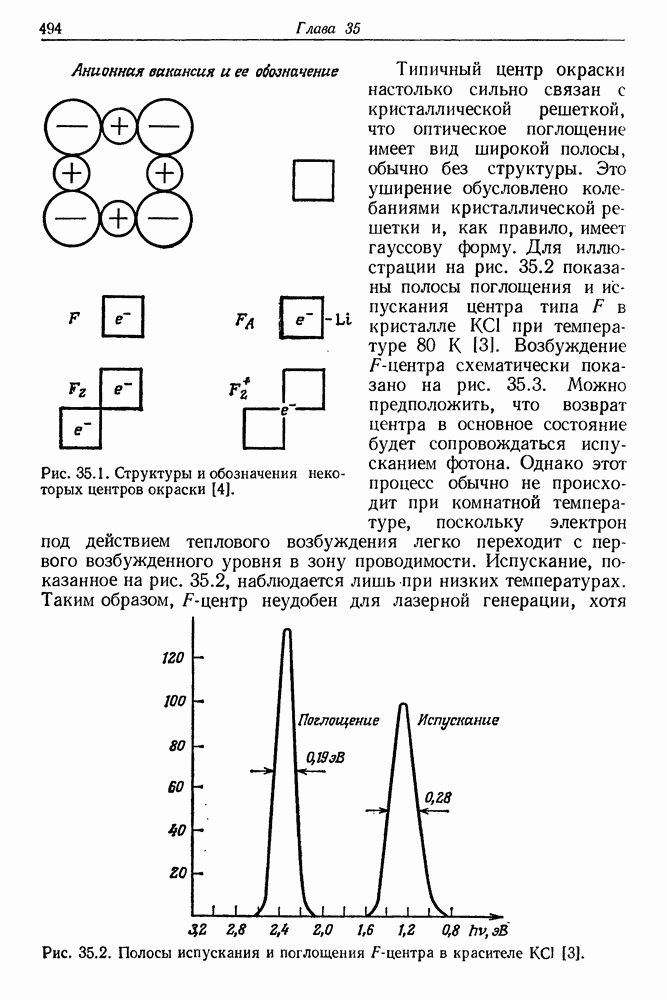
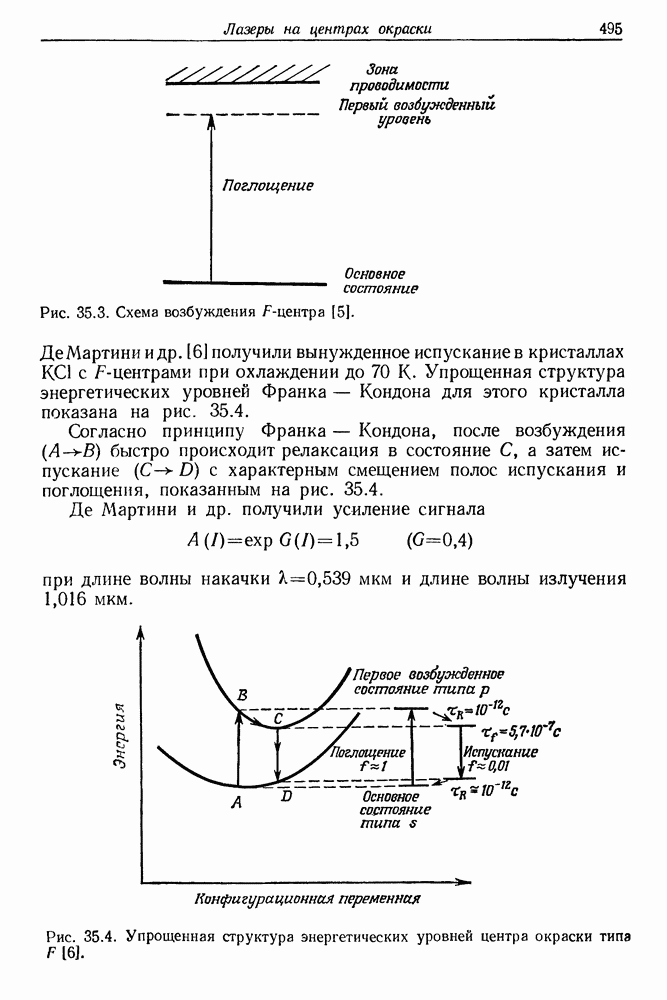
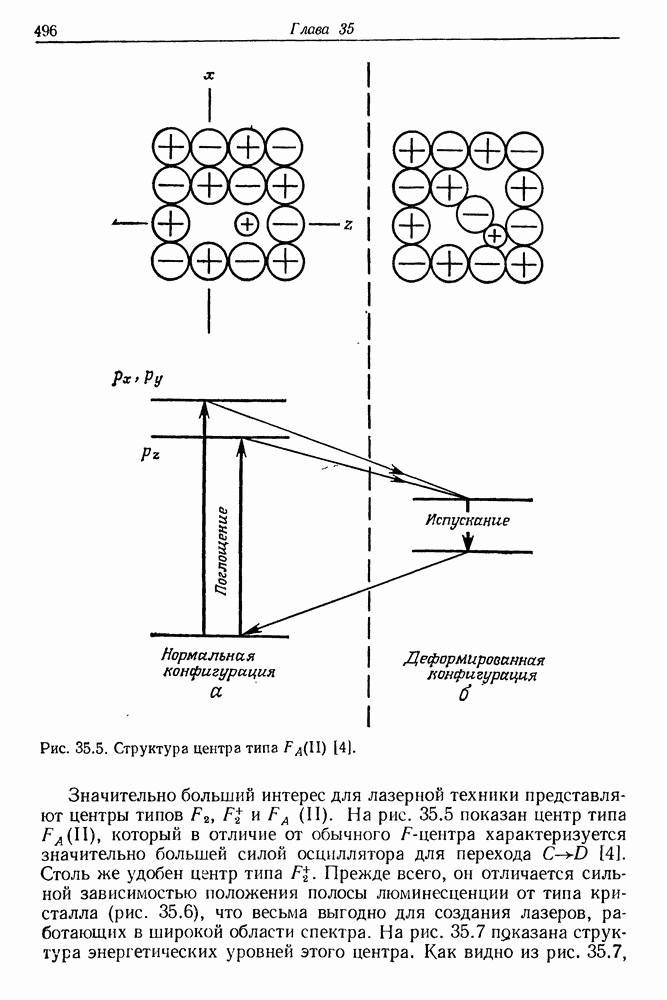
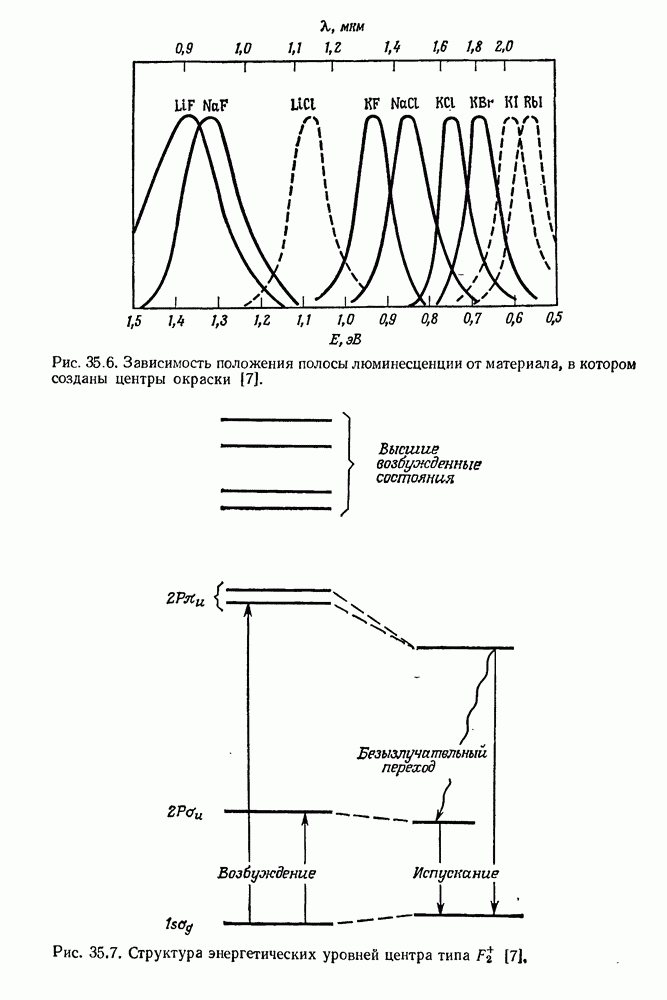
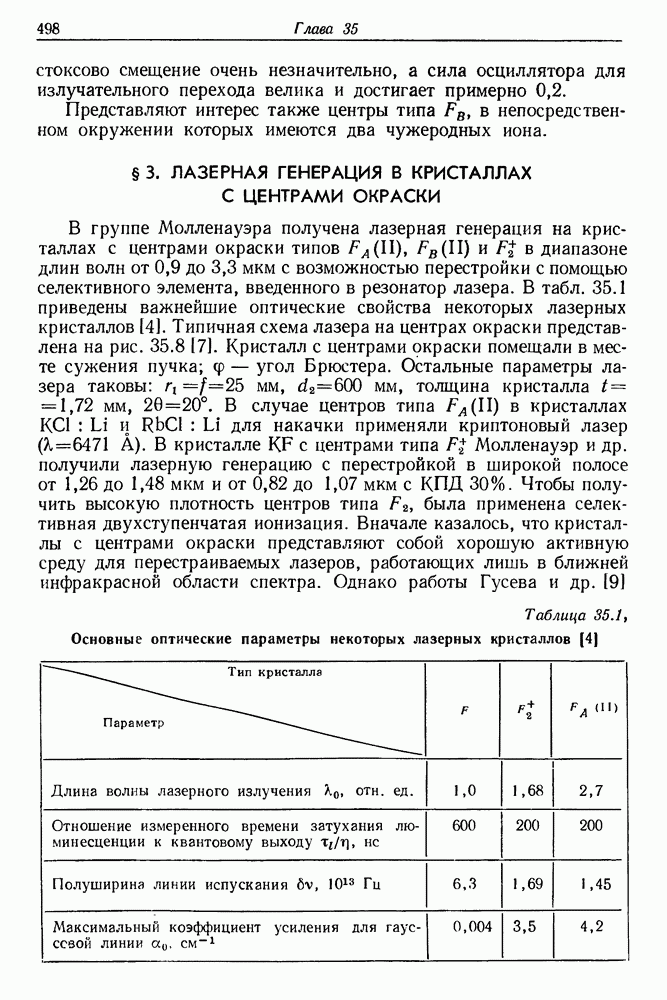
- 35. Лазеры на центрах окраски
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
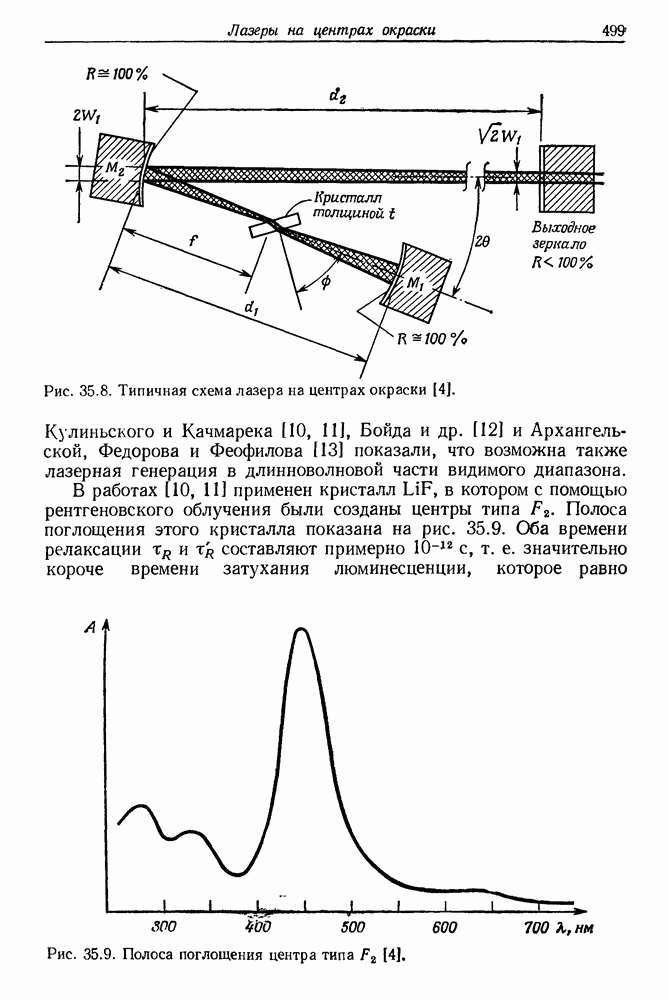
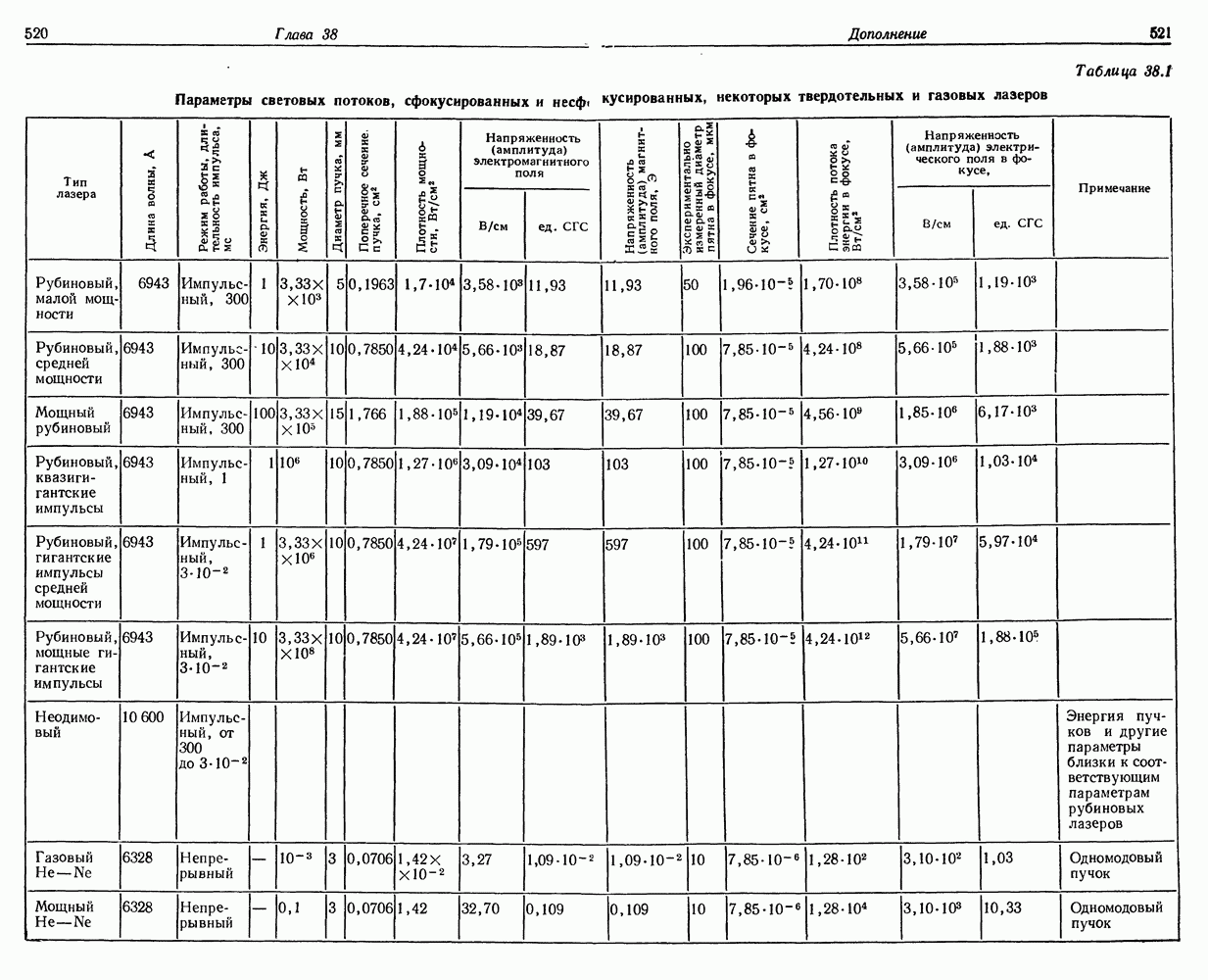
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
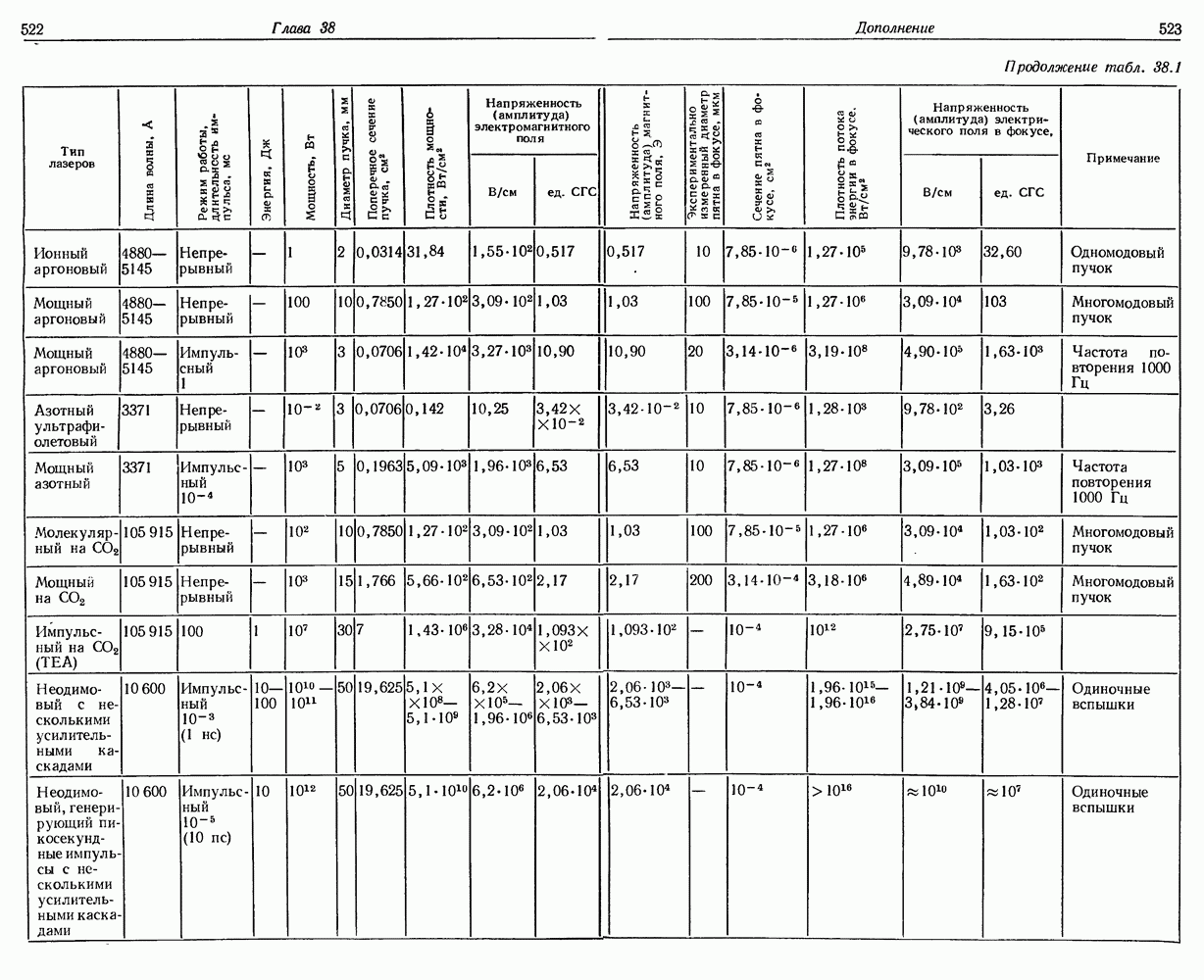
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
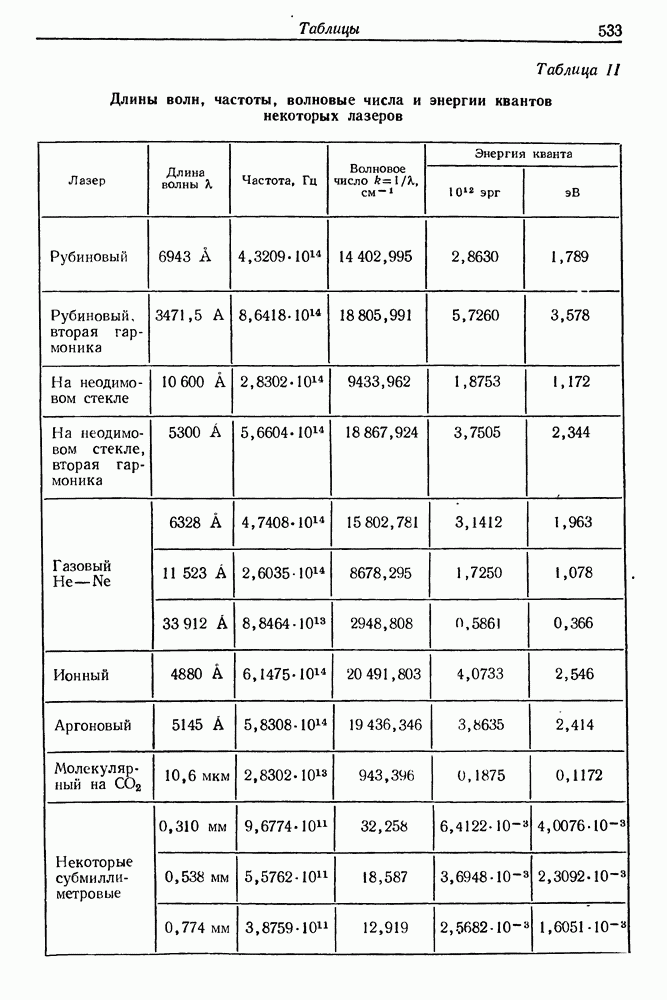
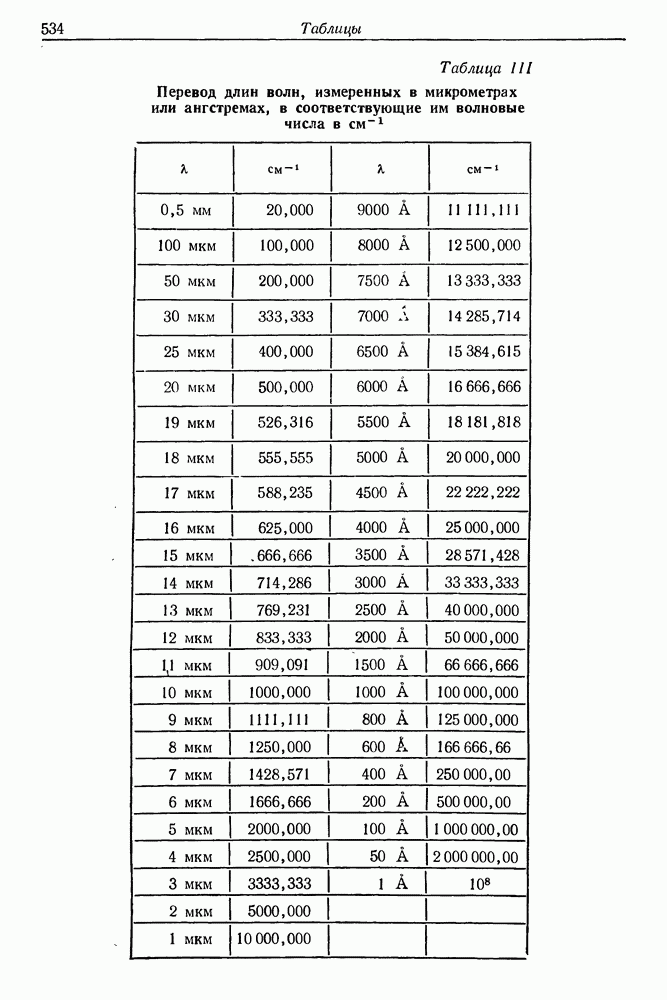
- Таблицы