| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
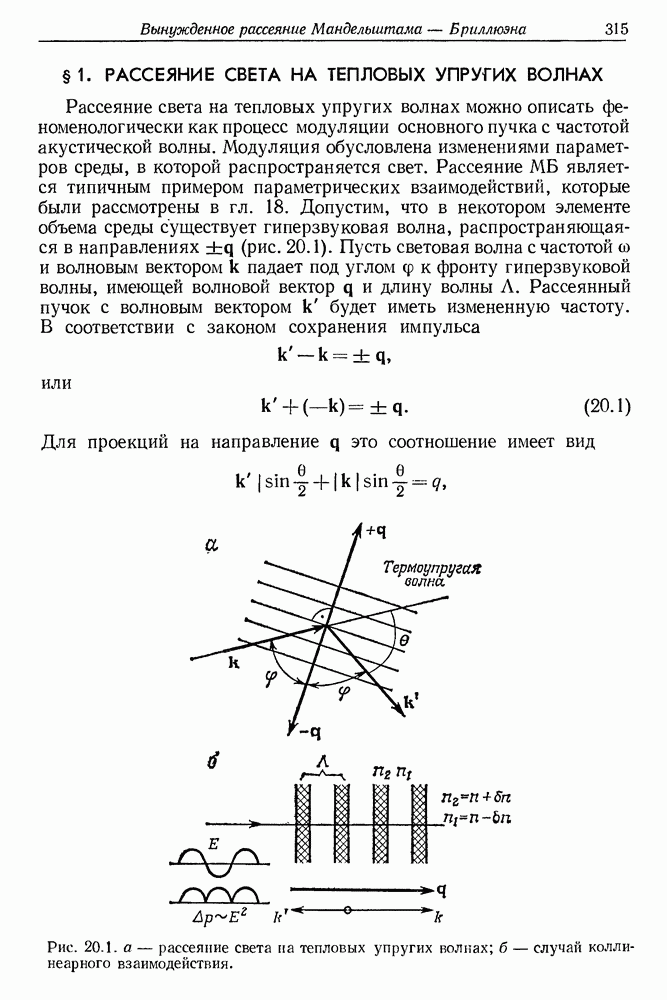
Спектральный состав света при молекулярном рассеянии дает ценную информацию о кинетике микропроцессов в среде (флюктуациях плотности, термоупругих волнах, продольных, поперечных и сдвиговых колебаниях и их комбинациях и т. п.). Каждый вид тепловых флюктуаций некоторым образом отражается в спектре рассеянного света (Зайцев [1], Фабелинский [2]). Медленные изобарические флюктуации плотности или концентрации среды приводят к появлению центральной линии. Адиабатические флюктуации дают тонкие смещенные компоненты (линии Мандельштама—Бриллюэна). При рассеянии в жидкостях по обе стороны от основной линии имеются спадающие крылья с непрерывным деполяризованным спектром, которые иногда простираются на  Они называются крыльями линии Рэлея. Относительно широкие спектральные области, образующие крылья линии Рэлея, часто называют «шумом» рассеяния из-за его деполяризованного характера. Этот шум возникает в результате быстрых флюктуаций анизотропии в среде (модуляционный эффект).
Они называются крыльями линии Рэлея. Относительно широкие спектральные области, образующие крылья линии Рэлея, часто называют «шумом» рассеяния из-за его деполяризованного характера. Этот шум возникает в результате быстрых флюктуаций анизотропии в среде (модуляционный эффект).
В 1965 г. Маш, Морозов, Старунов и Фабелинский [3] открыли вынужденное рассеяние в крыле линии Рэлея, а спустя два года Зайцев, Кызыласов, Старунов и Фабелинский [4] обнаружили вынужденное энтропийное (температурное) рассеяние,

Рис. 21.1. Член-корр. АН СССР И. Я. Фабелинский из Физического института им. П. Н. Лебедева АН СССР, один из крупнейших специалистов в области классического и вынужденного рассеяния света. Вместе со своими сотрудниками открыл вынужденное температурное (энтропийное) рассеяние и вынужденное рассеяние в крыле линии Рэлея.
обусловленное электрокалорическим эффектом. Этот эффект был также обнаружен Рэнком, Чо, Фольцем и Уиггинсом [5] как результат чистого поглощения света в жидкости.
Согласно Фабелинскому и Старунову [61, вынужденное температурное рассеяние вызывается электрокалорическим эффектом, а также прямым поглощением света в среде. Благодаря флюктуациям анизотропии и ориентации анизотропно-поляризованных молекул в электрическом поле световой волны (электрооптический эффект Керра) возникает еще один эффект, связанный с первым, а именно вынужденное рассеяние в крыле линии Рэлея.
§ 1. ВЫНУЖДЕННОЕ РАССЕЯНИЕ В КРЫЛЕ ЛИНИИ РЭЛЕЯ
Уширение спектральной линии рассеянного света обусловлено главным образом релаксационными процессами в жидкости: ширина крыла линии Рэлея обратно пропорциональна времени релаксации дипольного момента молекулы. Теория рассеяния света Леонтовича [7] объясняет возникновение крыла как результат флюктуаций анизотропии. В этой теории предполагается, что состояние произвольной точки жидкости можно описать с помощью тензора деформаций  температуры и тензора анизотропии
температуры и тензора анизотропии  последний характеризует отклонения осей анизотропии молекул от хаотического распределения. Основное уравнение, связывающее изменения во времени тензора анизотропии с изменениями тензора деформаций, выводится с помощью термодинамических представлений из условия минимума свободной энергии системы (см., например, [2]), Уравнение имеет вид
последний характеризует отклонения осей анизотропии молекул от хаотического распределения. Основное уравнение, связывающее изменения во времени тензора анизотропии с изменениями тензора деформаций, выводится с помощью термодинамических представлений из условия минимума свободной энергии системы (см., например, [2]), Уравнение имеет вид

С помощью этого уравнения Леонтович получил формулу для распределения интенсивности излучения в крыле линии Рэлея:

где  — модуль сдвига,
— модуль сдвига,  — коэффициент вязкости среды), А — некоторая постоянная. В модели жидкости Дебая время релаксации анизотропии равно [8]
— коэффициент вязкости среды), А — некоторая постоянная. В модели жидкости Дебая время релаксации анизотропии равно [8]

где  время релаксации дипольного момента молекул жидкости,
время релаксации дипольного момента молекул жидкости,  — радиус молекулы. Отсюда получаем полуширину крыла линии
— радиус молекулы. Отсюда получаем полуширину крыла линии
Индексы 0, 1, 2 относятся соответственно к возбуждающей волне, стоксовой и антистоксовой составляющим; к. с. - комплексно-сопряженные члены. Принято, что правая часть выражения (21.8) много меньше единицы.
Старунов [9] рассчитал параметр ориентации 

где

Параметр ориентации S промодулирован частотой  Полное решение получают с привлечением уравнений Максвелла, в которых положено:
Полное решение получают с привлечением уравнений Максвелла, в которых положено:

где  — амплитудный коэффициент затухания,
— амплитудный коэффициент затухания,  — значение волнового вектора.
— значение волнового вектора.
Решение уравнений Максвелла в общем виде с учетом нелинейной поляризации и возможного поглощения света в среде очень сложно. Из-за недостатка места приведем здесь лишь важнейшие результаты из работы Старунова.
Флюктуации анизотропии с характерным временем релаксации  приводят к модуляции параметров рассеивающей среды. В поле мощного лазерного пучка изменения анизотропии промодулированы регулярным образом. Смещение частоты стоксовой составляющей (относительно центральной линии) связано с временем релаксации
приводят к модуляции параметров рассеивающей среды. В поле мощного лазерного пучка изменения анизотропии промодулированы регулярным образом. Смещение частоты стоксовой составляющей (относительно центральной линии) связано с временем релаксации  простым соотношением
простым соотношением

Интенсивность стоксовой составляющей в случае, когда  нарастает экспоненциально. Очевидно, в спектре рассеянного излучения даже в условиях вынужденного рассеяния непрерывно возникают волны, длины которых не удовлетворяют соотношению (21.11). Однако усиление составляющей с частотой со максимально.
нарастает экспоненциально. Очевидно, в спектре рассеянного излучения даже в условиях вынужденного рассеяния непрерывно возникают волны, длины которых не удовлетворяют соотношению (21.11). Однако усиление составляющей с частотой со максимально.
Рэлея

В области высоких частот  уравнение (21.1) требует некоторой модификации. Следует дополнительно учесть влияние инерции
уравнение (21.1) требует некоторой модификации. Следует дополнительно учесть влияние инерции

где а — параметр инерции молекулы. Тогда распределение интенсивности в крыле линии Рэлея приобретает вид

В высокочастотной области крыла линии Рэлея  следует также учитывать зависимость вязкости от частоты.
следует также учитывать зависимость вязкости от частоты.
Предположим, что среда (например, жидкость) состоит из анизотропно поляризованных осесимметричных молекул. Мощный лазерный импульс создает в среде направляющие (ориентирующие) силы, которые пропорциональны величине

где  — основные поляризуемости молекулы, Е — сумма напряженностей возбуждающего и рассеянного полей. Низкочастотная составляющая указанных сил создает анизотропию среды как единого целого. В неподвижной системе координат ориентация молекулы определяется углами
— основные поляризуемости молекулы, Е — сумма напряженностей возбуждающего и рассеянного полей. Низкочастотная составляющая указанных сил создает анизотропию среды как единого целого. В неподвижной системе координат ориентация молекулы определяется углами  . В этом случае тензор анизотропии
. В этом случае тензор анизотропии  имеет вид
имеет вид

Пусть световая волна линейно-поляризована:  Предположим, что она распространяется в направлении оси х. Анизотропия среды, изменившаяся под действием силы
Предположим, что она распространяется в направлении оси х. Анизотропия среды, изменившаяся под действием силы  , равна
, равна

где  (см. гл. 23).
(см. гл. 23).
Положим

Если интенсивность этой составляющей сравнима с интенсивностью возбуждающего пучка, возникает заметный эффект насыщения.
В первом эксперименте Маша и др. [3] наблюдалась вынужденная стоксова составляющая в крыле линии Рэлея для  нитробензола и других веществ. Смещение стоксовой составляющей в нитробензоле было равно
нитробензола и других веществ. Смещение стоксовой составляющей в нитробензоле было равно  Рассеяние в крыле линии Рэлея имело нормальный характер (т. е. было очень слабым).
Рассеяние в крыле линии Рэлея имело нормальный характер (т. е. было очень слабым).
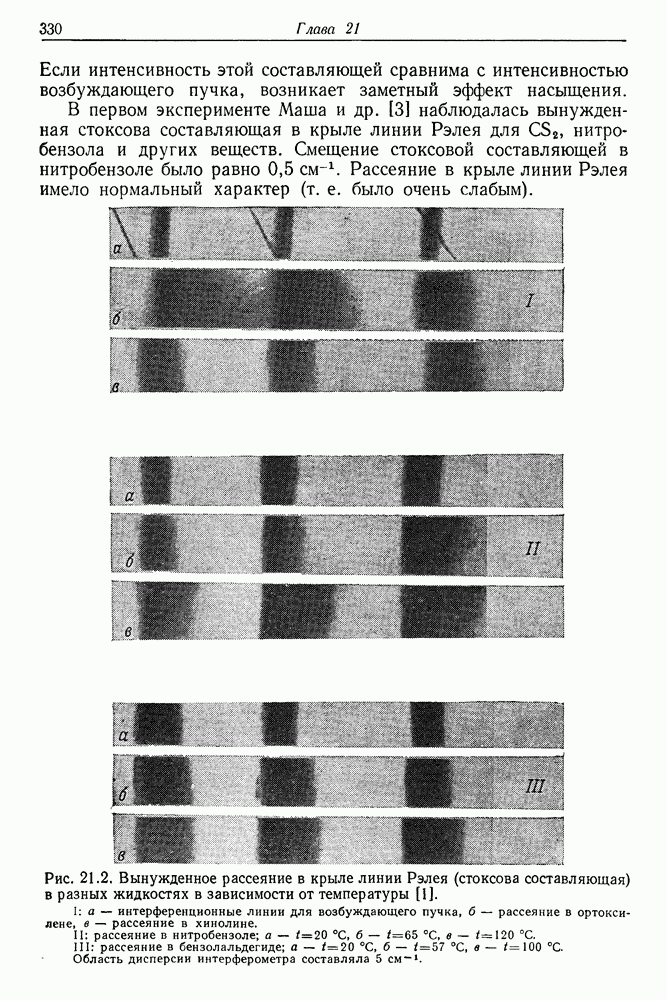
Рис. 21.2. (см. скан) Вынужденное рассеяние в крыле линии Рэлея (стоксова составляющая) в разных жидкостях в зависимости от температуры [1]. I: а — интерференционные линии для возбуждающего пучка,  — рассеяние в ортоксилене, в — рассеяние в хинолине. II: рассеяние в нитробензоле;
— рассеяние в ортоксилене, в — рассеяние в хинолине. II: рассеяние в нитробензоле;  III: рассеяние в бензолальдегиде;
III: рассеяние в бензолальдегиде;  Область дисперсии интерферометра составляла
Область дисперсии интерферометра составляла 
Чо с сотрудниками [10] также исследовали стоксову часть крыла линии Рэлея. Они обнаружили, что при увеличении температуры от 285 до 390 К смещение  изменилось от 0,09 до
изменилось от 0,09 до 
Обширное исследование вынужденного рассеяния в крыле линии Рэлея опубликовал в 1972 г. Зайцев [1]. На рис. 21.2 представлены спектры стоксова рассеяния в крыле линии Рэлея в нитробензоле и бензолальдегиде в зависимости от температуры. Область дисперсии интерферометра Фабри — Перо составляла  . В довольно размытом спектре интенсивного стоксова рассеяния с трудом удается различить основную составляющую, частота которой определяется формулой (21.11).
. В довольно размытом спектре интенсивного стоксова рассеяния с трудом удается различить основную составляющую, частота которой определяется формулой (21.11).
Фотографии, приведенные на рис. 21.2, свидетельствуют также о том, что механизм вынужденного рассеяния в крыле линии Рэлея очень сложен. Обычно исследуют рассеяние вперед или назад по отношению к направлению распространения возбуждающего пучка. Власов и Фабелинский [11] исследовали рассеяние под углом 90° и открыли тонкую структуру вынужденного рассеяния в крыле линии Рэлея.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
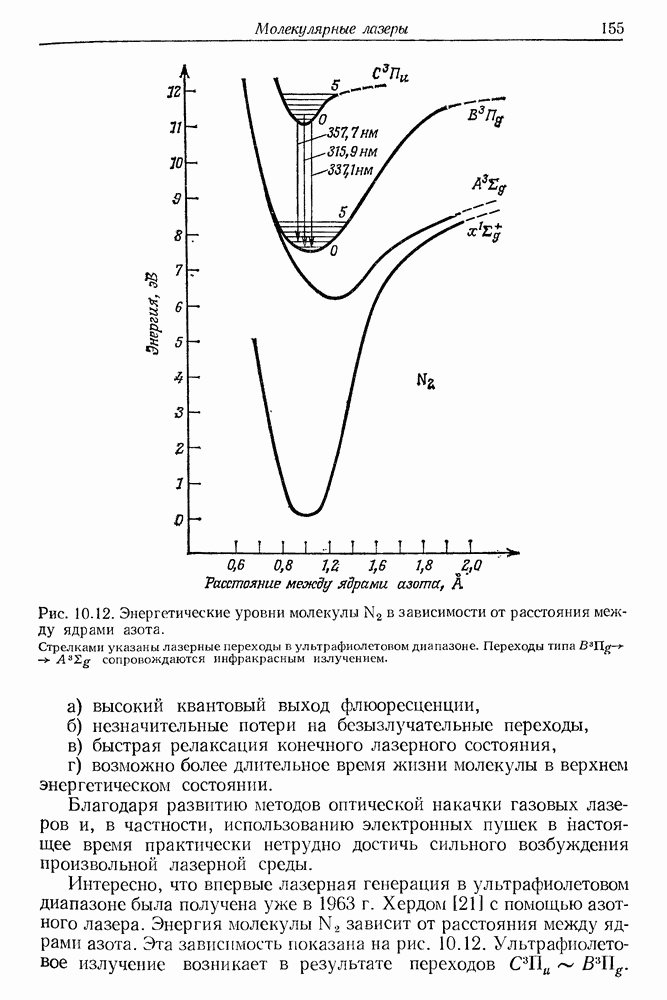
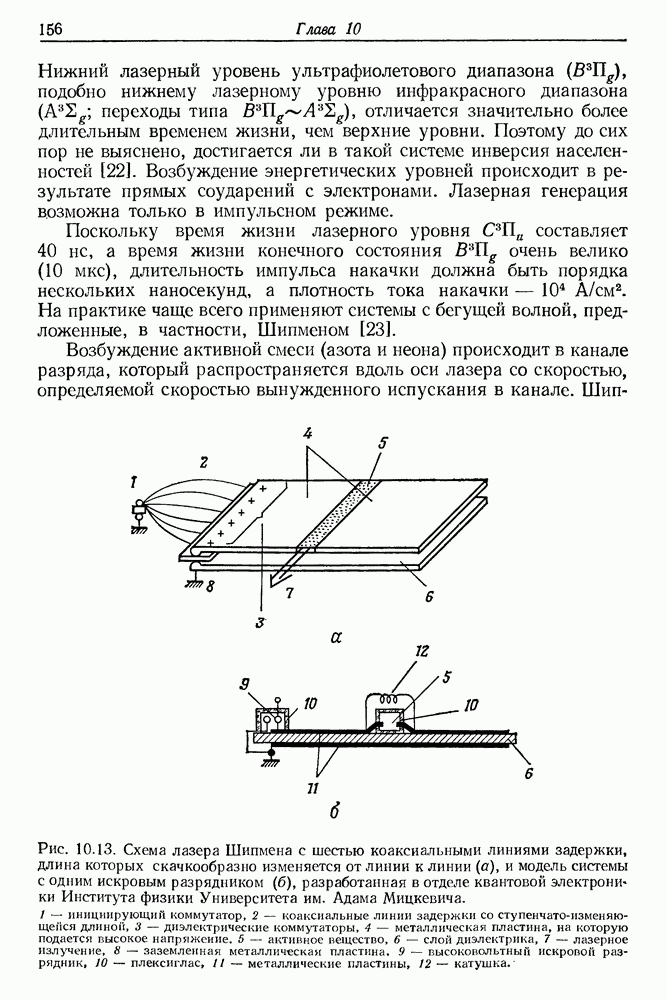
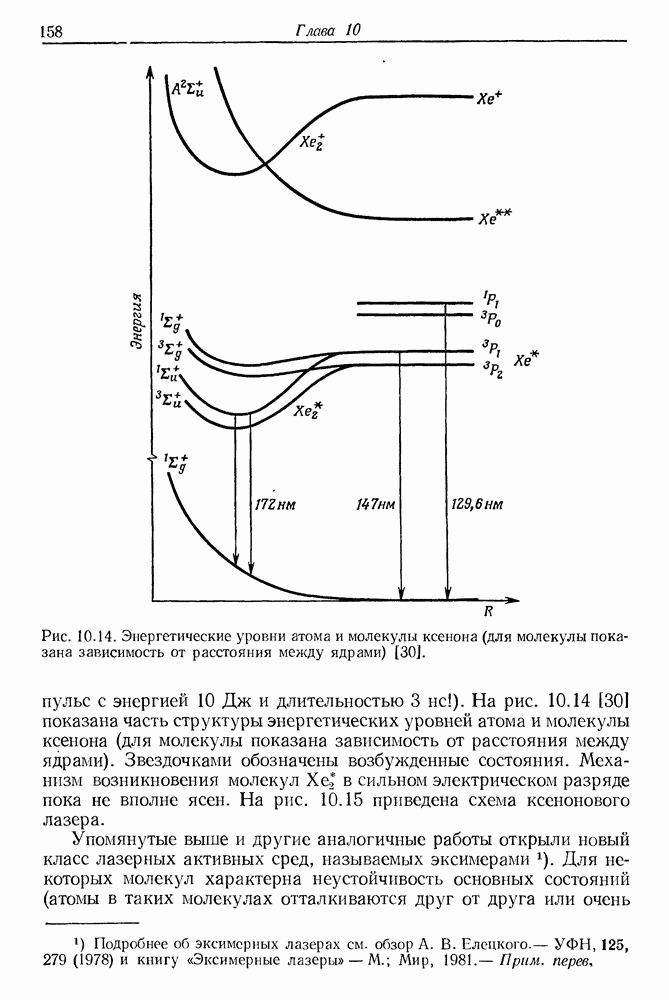
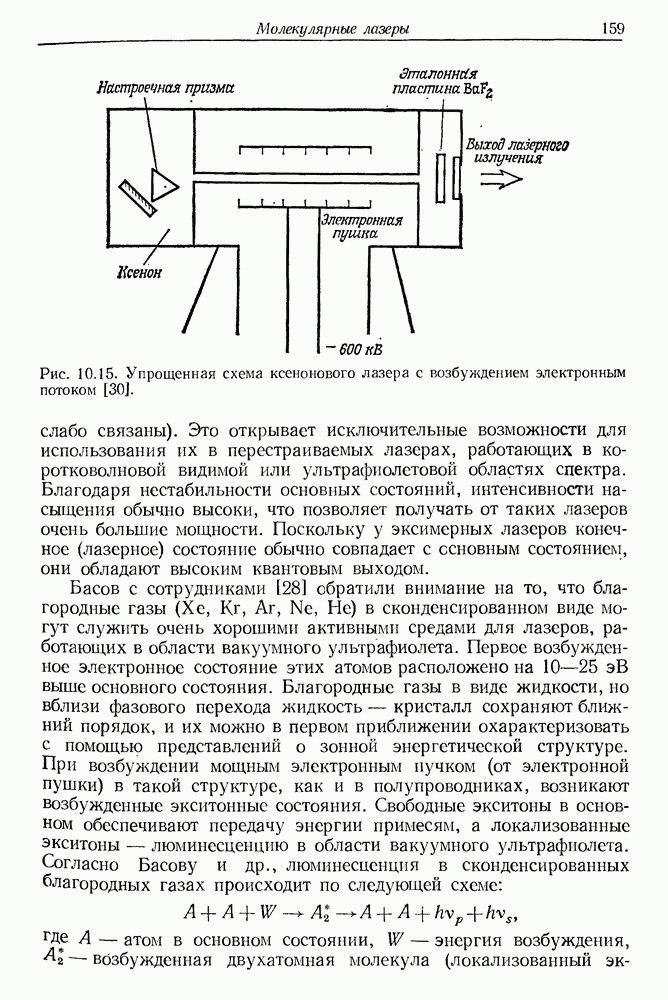
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
- б. Вращающаяся призма
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
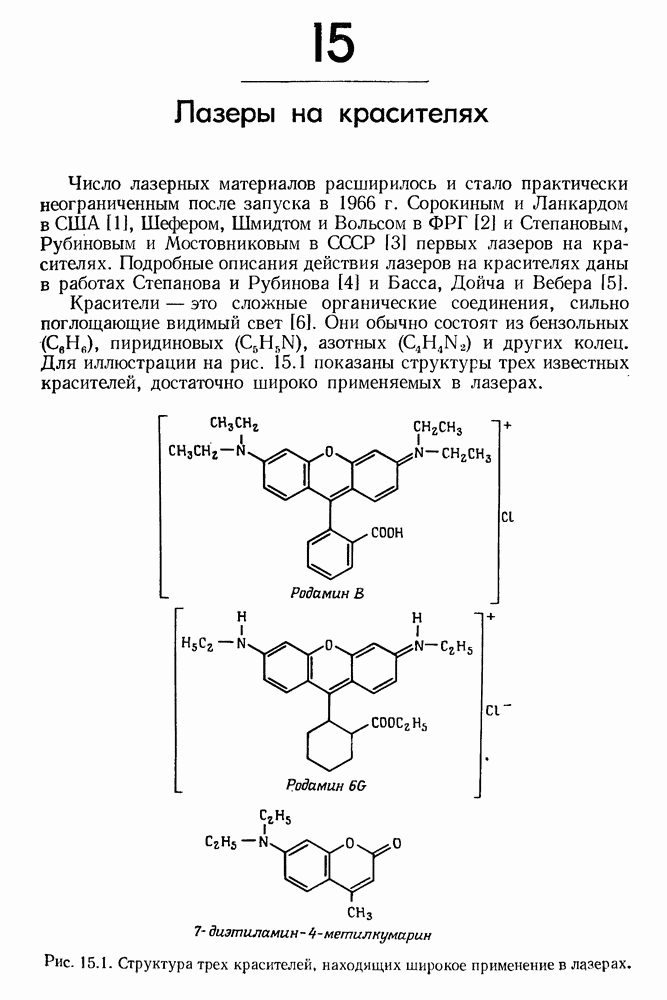
- 15. Лазеры на красителях
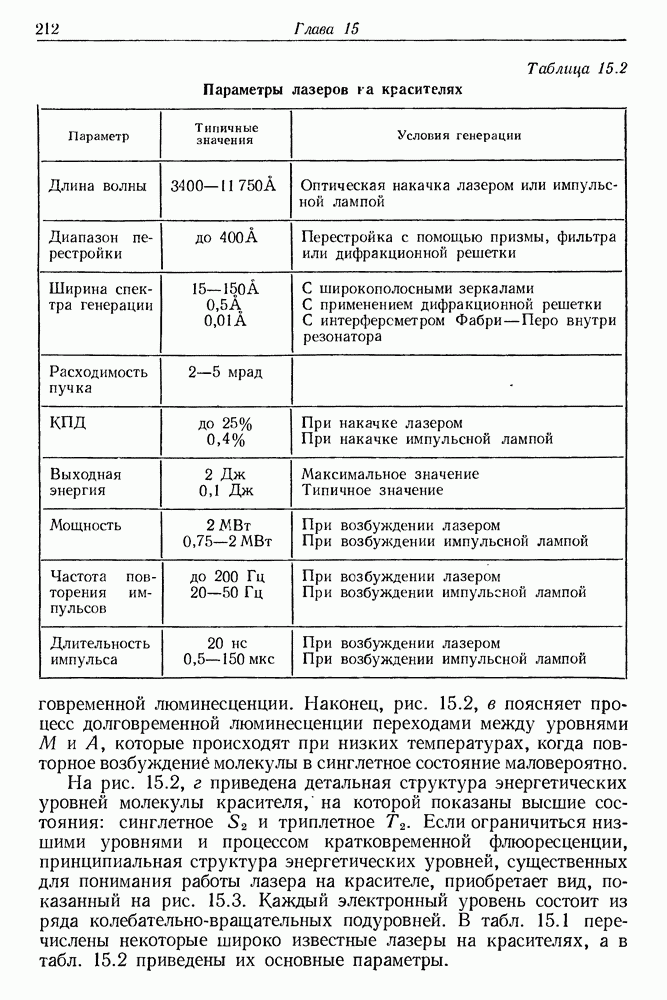
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
- 22. Параметрическая люминесценция (ПЛ)
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
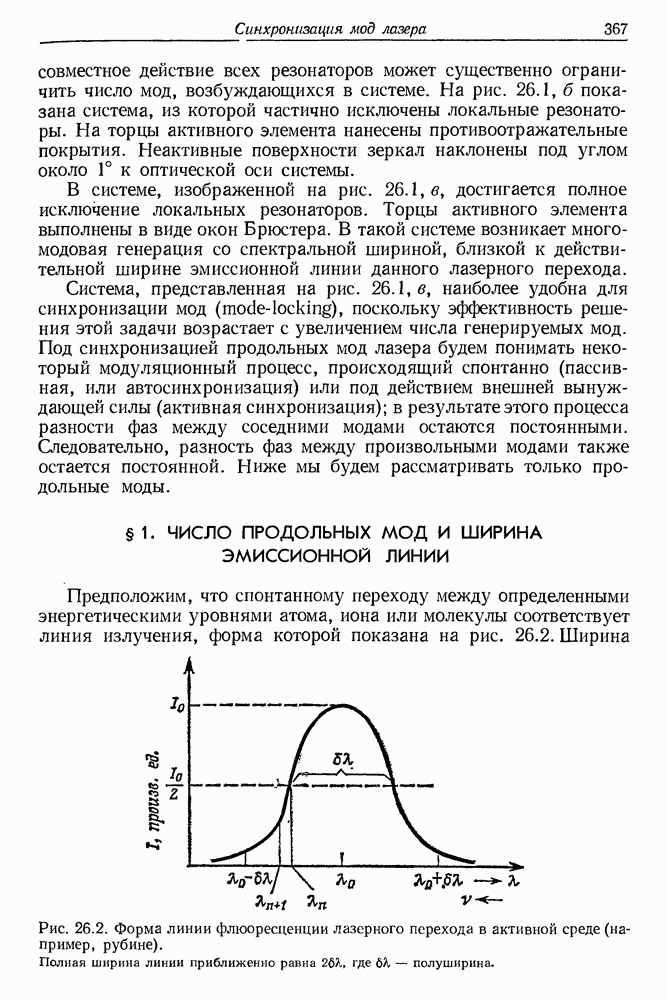
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
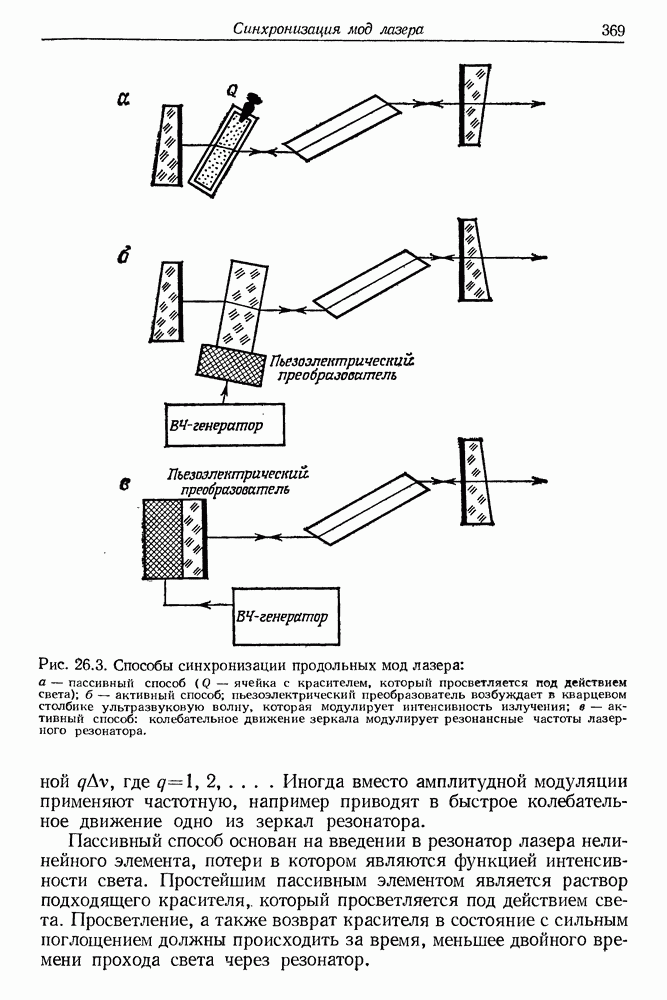
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
- в. Примеры использования камеры с разверткой
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
- 35. Лазеры на центрах окраски
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
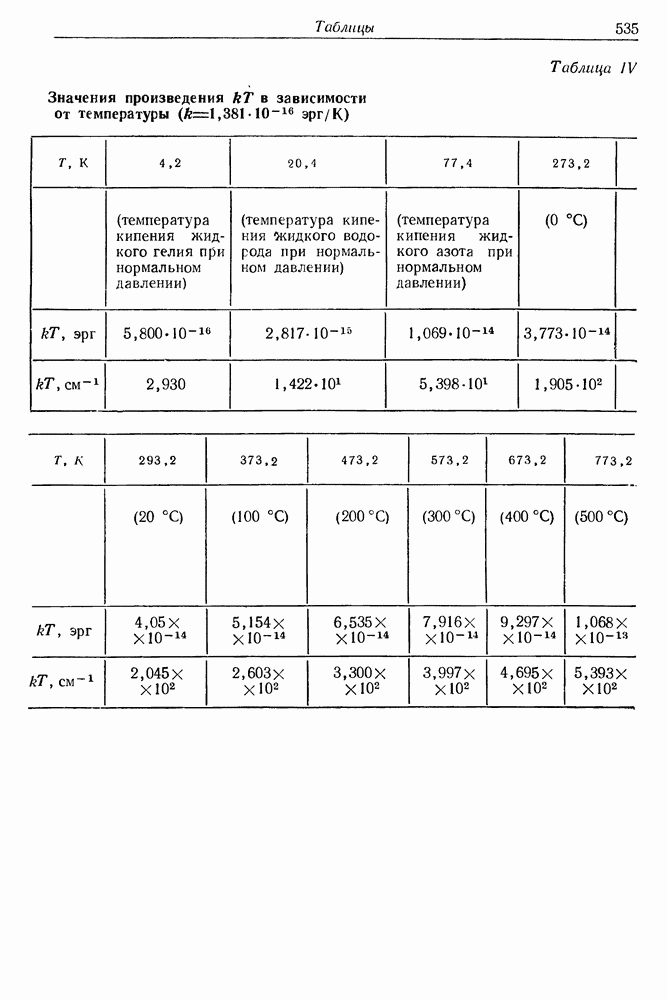
- Таблицы