| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
37. Когерентность света
До создания лазеров трудно было получить отчетливое представление о когерентности света. Действительно, наблюдая световые пятна или потоки от классических источников света, мы не в состоянии были сказать, удастся ли отличить это обычно некогерентное излучение от когерентного. Не удивительно, что следы красных пучков первых газовых лазеров произвели ошеломляющее впечатление. Сразу стало очевидно, что мы видим совершенно иной тип излучения, мерцавшего перед нашими глазами, как парча, тысячами светящихся точек.
В классической оптике известно много способов оценки степени когерентности света (определение когерентности мы дадим несколько ниже), хотя — и это следует подчеркнуть — во многих экспериментах некогерентное излучение давало такие же эффекты, как и когерентное. Следовательно, к оценке степени когерентности света следует подходить весьма осторожно.
§ 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
В гл. 3 мы рассматривали свет, испускаемый атомом как цуг затухающих электромагнитных волн. Там же была дана оценка длительности испускания т. Представим себе, что два таких цуга волн, распространяющихся в различных направлениях, встретились в точке Р (рис. 37.1). Будем считать, что фазы колебаний в обоих цугах в точке расположения источника одинаковы. Это означает, что два цуга взаимно когерентны. Через некоторое время  фронт первого цуга достигнет точки Р, в то время как фронт второго цуга, распространяющегося по более длинному пути, будет вдали от этой точки. Очевидно, что в этих условиях нельзя говорить о взаимодействии, т. е. об интерференции двух волн в точке Р. Взаимодействие будет возможно, лишь если длина цуга превышает разность оптических путей. Поскольку длительность испускания
фронт первого цуга достигнет точки Р, в то время как фронт второго цуга, распространяющегося по более длинному пути, будет вдали от этой точки. Очевидно, что в этих условиях нельзя говорить о взаимодействии, т. е. об интерференции двух волн в точке Р. Взаимодействие будет возможно, лишь если длина цуга превышает разность оптических путей. Поскольку длительность испускания  , длина цуга должна быть равна
, длина цуга должна быть равна


Рис. 37.1. Относительная расфазировка в точке Р двух цугов волн, излученных атомом в различных направлениях.
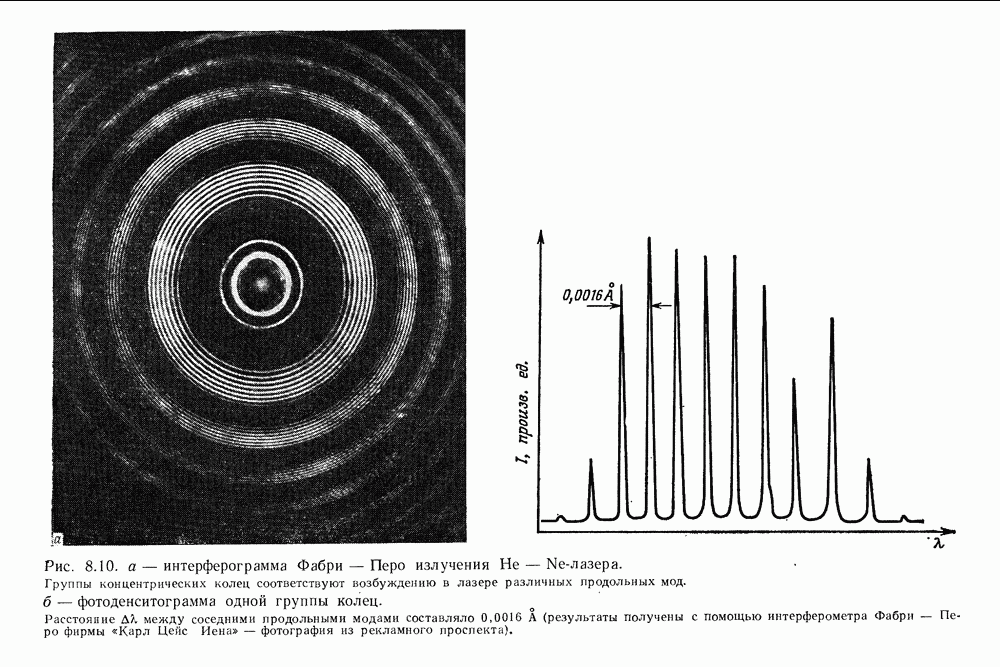
На практике хорошие интерференционные картины обычно получаются в условиях, когда разность путей невелика, порядка миллиметра или меньше. Однако иногда, например в известном интер ферометре Фабри — Перо, наблюдаются интерференционные полосы высших порядков; в этом случае разность путей достигает десяткой сантиметров. В плоском интерферометре Фабри — Перо разность оптических путей приближенно равна

где  — целое число,
— целое число,  — расстояние между параллельными зеркалами. Предполагается, что свет падает на зеркала почти перпендикулярно их поверхности. Положив
— расстояние между параллельными зеркалами. Предполагается, что свет падает на зеркала почти перпендикулярно их поверхности. Положив  см, получаем (для
см, получаем (для 

При квантовомеханическом описании электромагнитного поля его обычно представляют с помощью квантованных гармонических осцилляторов. В предыдущей главе было показано, что точно определить число фотонов и их фазы для одного и того же момента времени невозможно. Этому препятствует соотношение неопределенностей

где  — неопределенность числа фотонов,
— неопределенность числа фотонов,  — девиация фазы. Таким образом, идеальная когерентность светового потока невозможна.
— девиация фазы. Таким образом, идеальная когерентность светового потока невозможна.
С точки зрения квантовой механики атом может испустить фотон в произвольном направлении. В этом смысле атом, очевидно, не излучает сферическую волну. Однако если число актов испускания велико, то в среднем во всех направлениях будет излучаться одинаковое число фотонов, и можно сказать, что при этом мы имеем дело со сферической волной. Интерференционные явления выглядят очень просто, если пользоваться неким усредненным представлением об излучении. Мы говорим о световых пучках и лучах, не уточняя значения этих понятий. Эксперимент подтверждает правомерность такого подхода. С помощью источников света, которые можно лишь с большой натяжкой считать точечными, а также щелей и призм мы легко получаем хорошие интерференционные картины (полосы). Наблюдая результаты этих экспериментов, трудно понять утверждение, что согласно работе Дирака [2] два разных фотона не могут интерферировать друг с другом: фотон может интерферировать лишь с самим собой. Однако Поль [3] показал, что возможна интерференция с участием даже большего числа фотонов, чем два. Эти вопросы очень сложны и в то же время чрезвычайно увлекательны. Интересное и доступное их обсуждение содержится в книге «Квантовая физика» Вихмана [4].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- 1. Период перед открытием лазеров
- 2. Аналогия между электронным генератором электромагнитных колебаний и оптическим квантовым генератором — лазером
- 3. Элементарная теория затухающего осциллятора (колебательного контура)
- 4. Рубиновый лазер Меймана
- § 1. ВЫНУЖДЕННОЕ ИСПУСКАНИЕ В РУБИНЕ
- § 2. СВЯЗЬ МЕЖДУ КОЭФФИЦИЕНТОМ ПОГЛОЩЕНИЯ И ЭФФЕКТИВНЫМ СЕЧЕНИЕМ ПОГЛОЩЕНИЯ
- § 3. ИЗЛУЧАЕМАЯ МОЩНОСТЬ ПРИ ВЫНУЖДЕННОМ ИСПУСКАНИИ
- § 4. УПРОЩЕННОЕ ПОРОГОВОЕ УСЛОВИЕ ГЕНЕРАЦИИ СВЕТА
- § 5. ПРОЦЕССЫ ПОГЛОЩЕНИЯ ФЛЮОРЕСЦЕНЦИИ И ОПТИЧЕСКОЙ НАКАЧКИ В РУБИНЕ
- 5. Пространственные, временные и спектральные характеристики излучения лазеров на рубине и неодимовом стекле
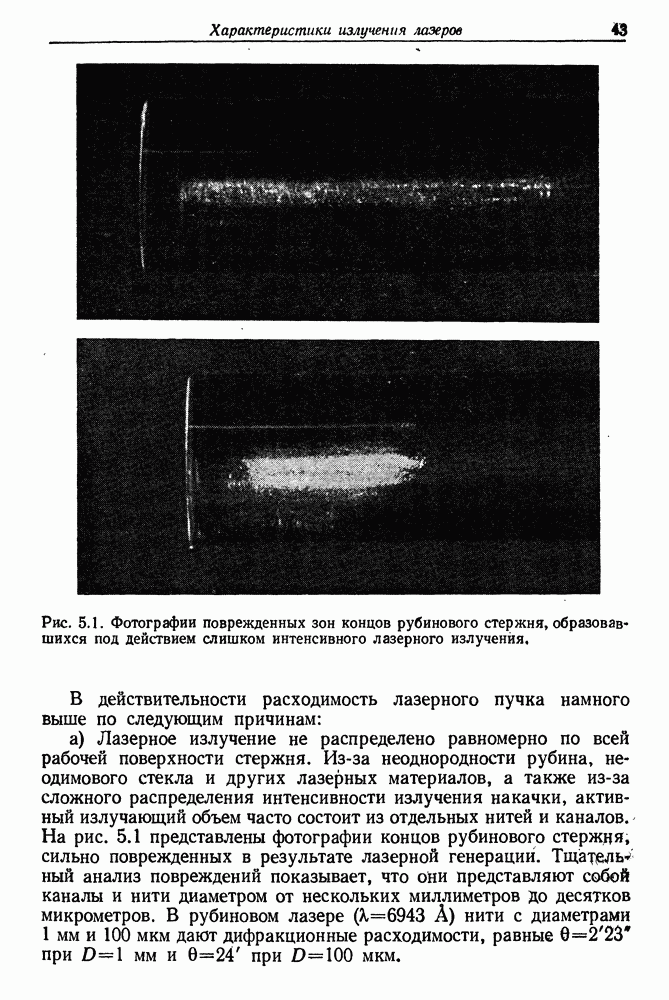
- § 1. РАСХОДИМОСТЬ ЛАЗЕРНОГО ПУЧКА
- § 2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО ПОПЕРЕЧНОМУ СЕЧЕНИЮ ПУЧКА
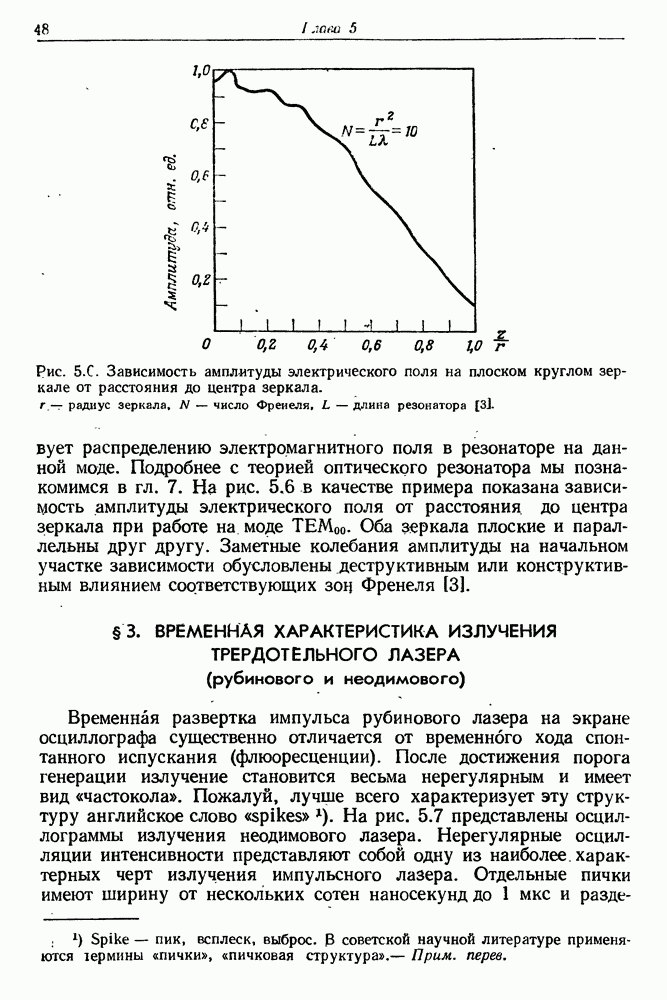
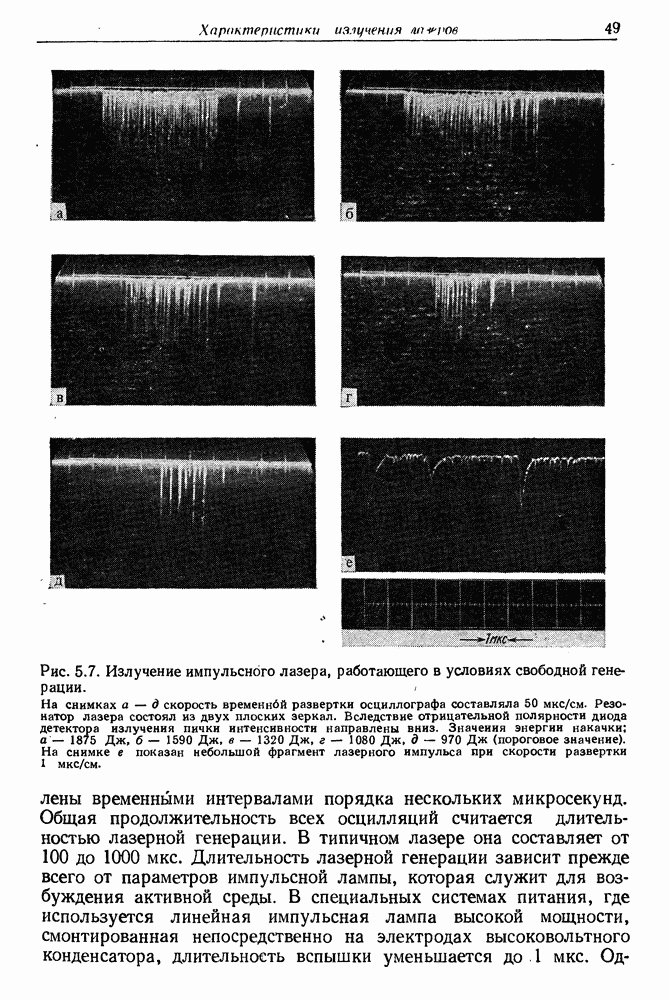
- § 3. ВРЕМЕННАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ТРЕРДОТЕЛЬНОГО ЛАЗЕРА (рубинового и неодимового)
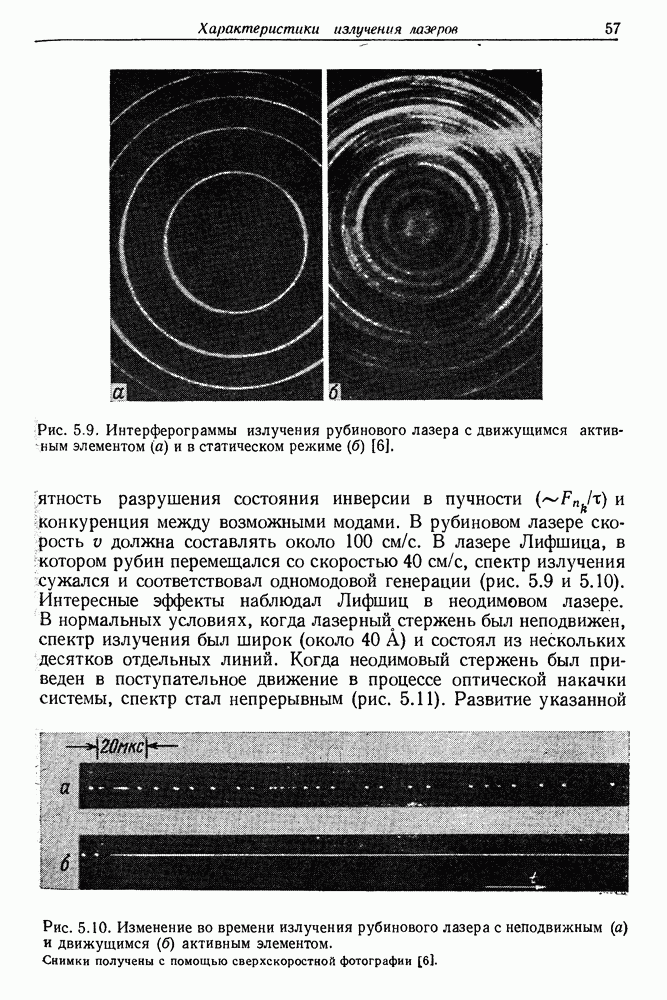
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 6. Твердотельные (нерубиновые) импульсные и непрерывные лазеры
- § 2. ОПТИЧЕСКАЯ НАКАЧКА И ВЫНУЖДЕННОЕ ИСПУСКАНИЕ
- § 3. РАБОЧИЕ ВЕЩЕСТВА С БОЛЬШОЙ КОНЦЕНТРАЦИЕЙ АКТИВНЫХ ИОНОВ (примесные и стехиометрические материалы)
- 7. Очерк теории оптических резонаторов
- § 2. РЕЗОНАТОР ФАБРИ—ПЕРО
- § 3. ТЕОРИЯ ОПТИЧЕСКОГО РЕЗОНАТОРА ФОКСА И ЛИ
- б. Плоский резонатор с круглыми зеркалами
- в. Конфокальный резонатор
- г. Численные расчеты распределений поля на зеркалах резонатора
- 8. Газовые лазеры на нейтральных атомах (гелий-неоновый лазер Джавана)
- § 2. КОНСТРУКЦИЯ ГЕЛИЙ-НЕОНОВОГО ЛАЗЕРА
- § 3. УСЛОВИЕ ВОЗБУЖДЕНИЯ ЛАЗЕРНОЙ ГЕНЕРАЦИИ
- § 4. СПЕКТРАЛЬНАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ГАЗОВОГО ЛАЗЕРА
- § 5. СТРУКТУРА «ОПТИЧЕСКИХ» ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ
- § 6. МЕТАСТАБИЛЬНЫЕ СОСТОЯНИЯ
- 9. Газовые ионные лазеры
- § 1. РАЗРЯДНЫЕ ТРУБКИ АРГОНОВЫХ ЛАЗЕРОВ
- § 2. ОПТИЧЕСКОЕ ВОЗБУЖДЕНИЕ ИОНОВ АРГОНА И ДРУГИХ ГАЗОВ
- § 3. ИОННЫЕ ЛАЗЕРЫ НА ПАРАХ МЕТАЛЛОВ
- § 4. ГАЗОВЫЕ ИМПУЛЬСНЫЕ ЛАЗЕРЫ (ионные и на нейтральных атомах)
- 10. Молекулярные лазеры
- § 1. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ ДВИЖЕНИЯ МОЛЕКУЛ
- б. Вращательные движения молекул
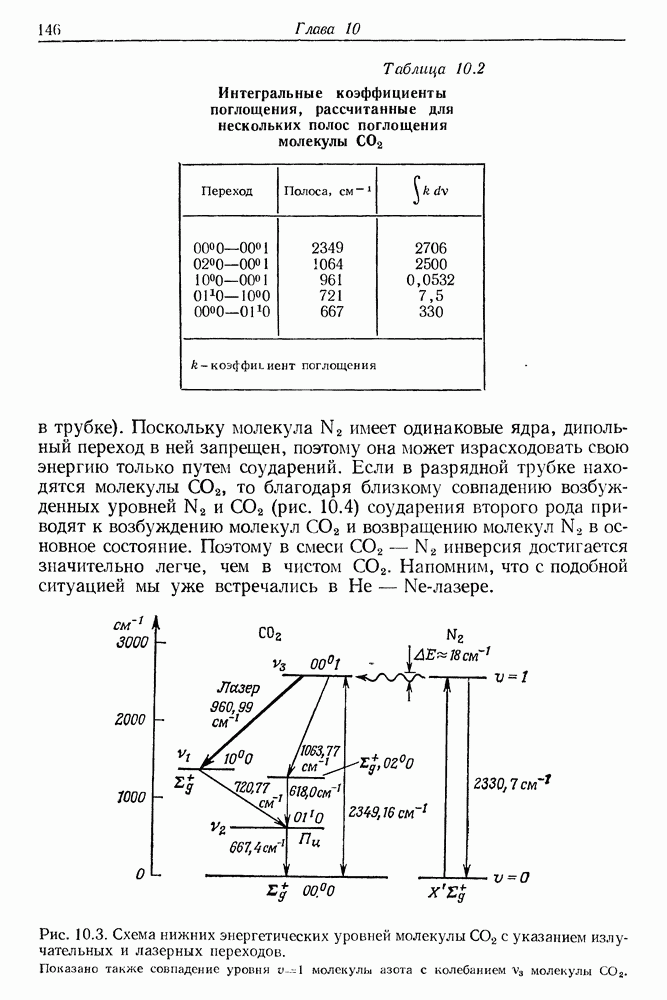
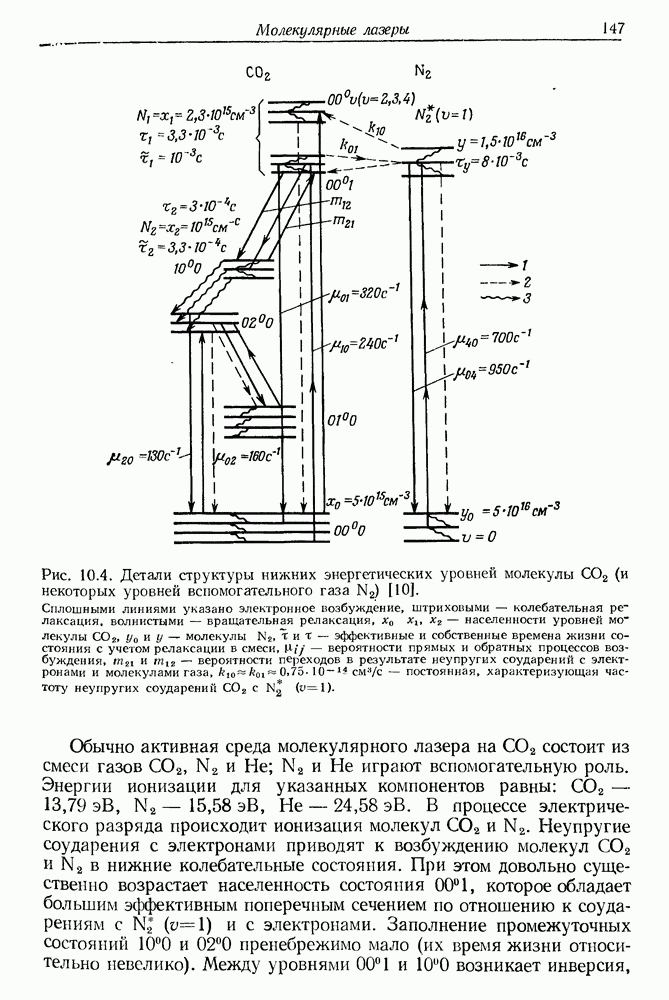
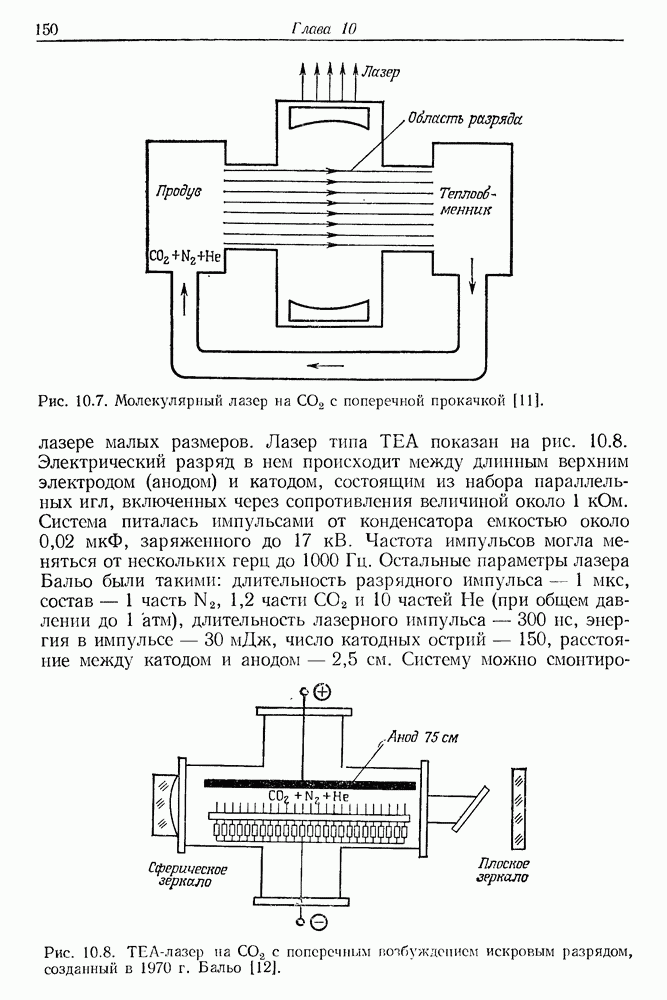
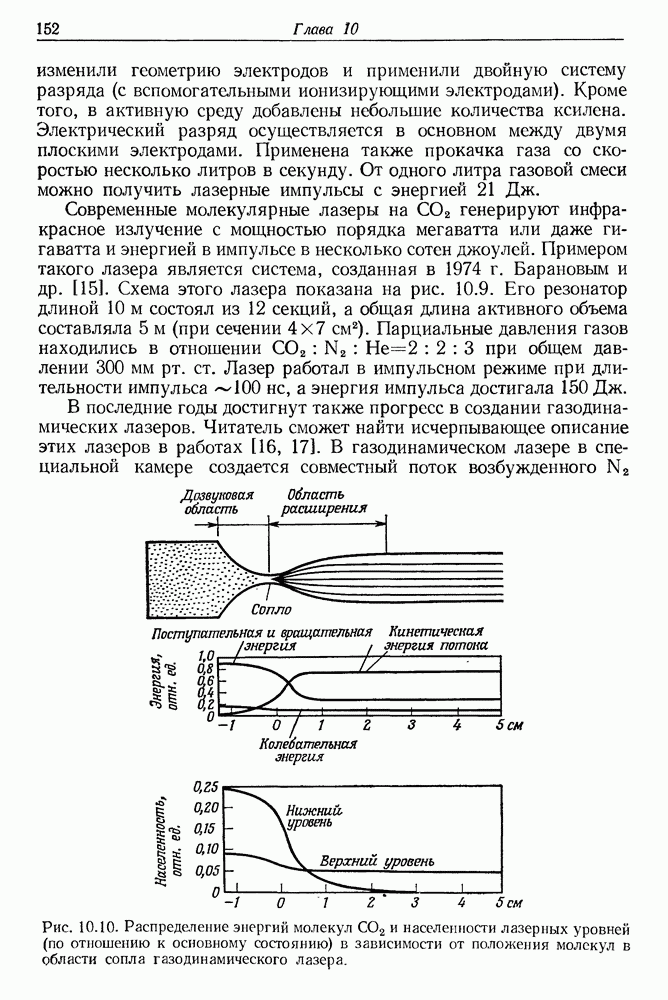
- § 2. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО2
- § 3. МОЛЕКУЛЯРНЫЙ ЛАЗЕР НА СО
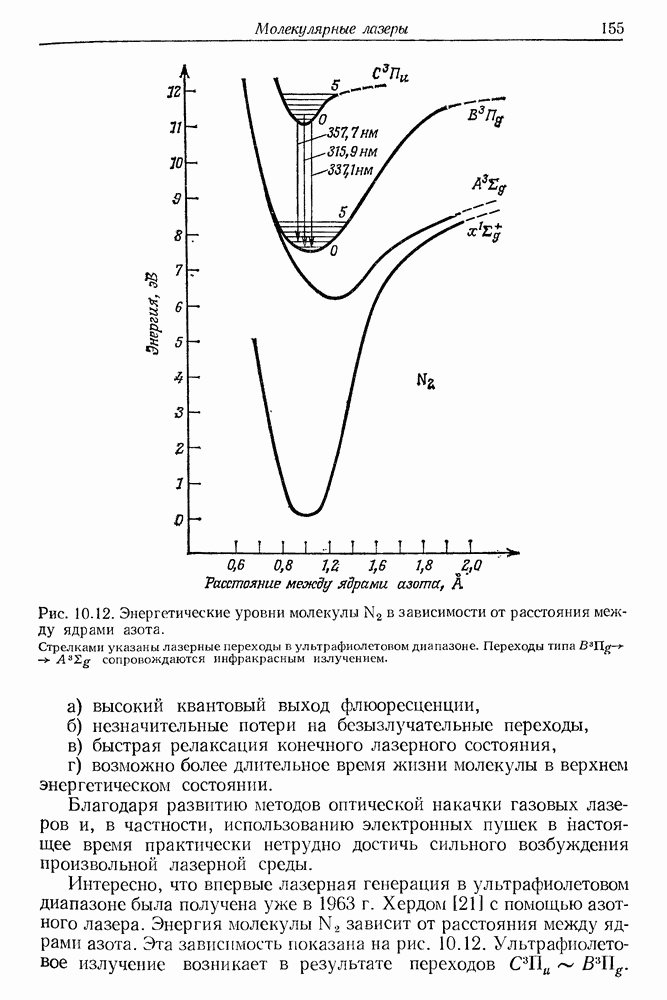
- § 4. МОЛЕКУЛЯРНЫЕ ЛАЗЕРЫ УЛЬТРАФИОЛЕТОВОГО ДИАПАЗОНА
- 11. Молекулярные лазеры субмиллиметрового и миллиметрового диапазонов
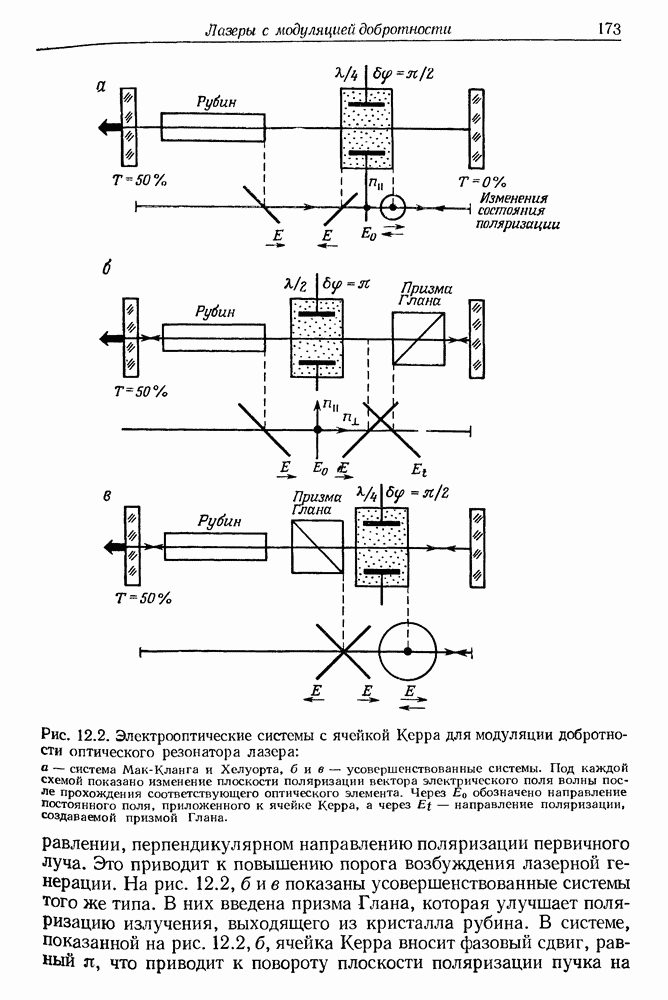
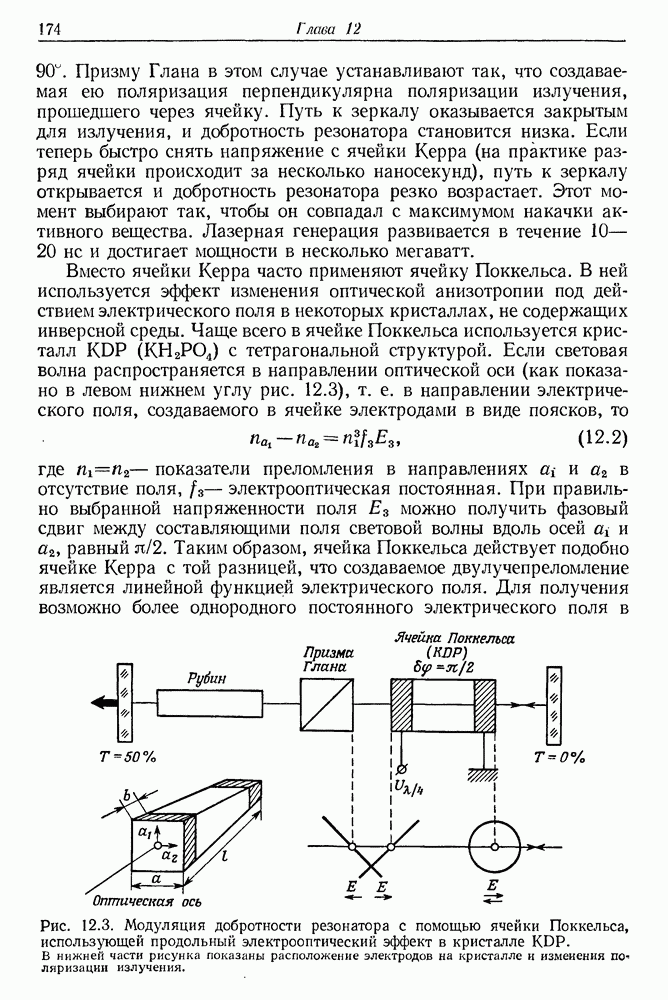
- 12. Твердотельные лазеры с модуляцией добротности оптического резонатора
- § 1. МОДУЛЯЦИЯ ДОБРОТНОСТИ Q ОПТИЧЕСКИХ РЕЗОНАТОРОВ ЛАЗЕРОВ
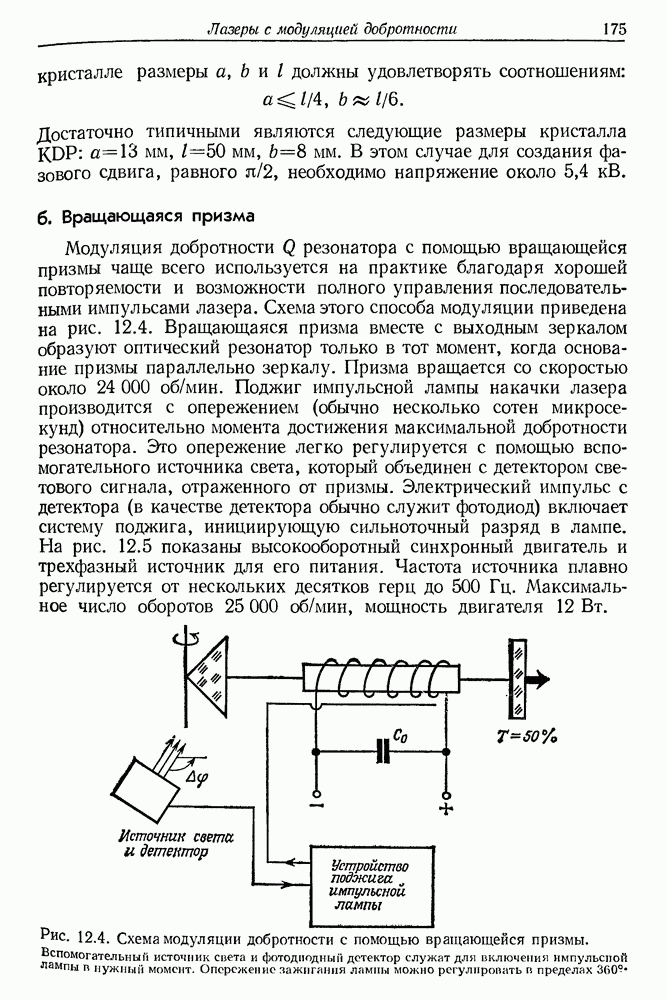
- б. Вращающаяся призма
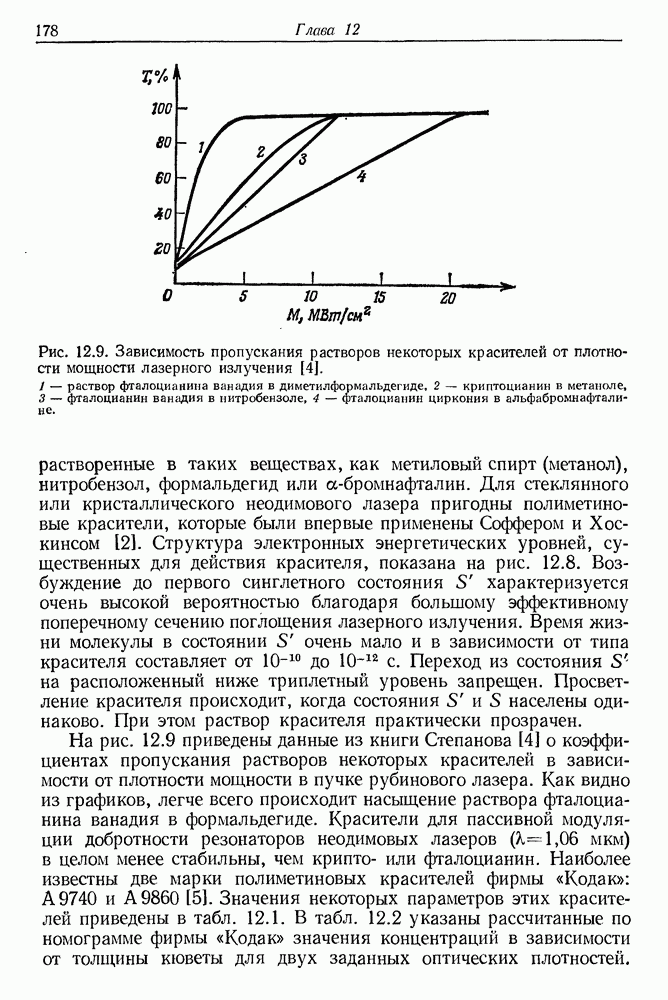
- в. Пассивная модуляция Q с помощью красителей
- § 2. РАЗВИТИЕ ГИГАНТСКОГО ИМПУЛЬСА В ЛАЗЕРЕ
- 13. Полупроводниковые лазеры
- § 1. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ НОСИТЕЛЕЙ ТОКА В ДИЭЛЕКТРИКАХ И ПОЛУПРОВОДНИКАХ
- § 2. ПОЛУЧЕНИЕ ИНВЕРСИИ НАСЕЛЕННОСТЕЙ В р-n-ПЕРЕХОДЕ
- § 3. КРАТКАЯ ХАРАКТЕРИСТИКА ИЗЛУЧЕНИЯ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- 14. Жидкостные лазеры
- § 2. ХЕЛАТЫ РЕДКОЗЕМЕЛЬНЫХ ЭЛЕМЕНТОВ
- § 3. ЖИДКОСТНЫЕ ЛАЗЕРЫ НА СВОБОДНЫХ РЕДКОЗЕМЕЛЬНЫХ ИОНАХ
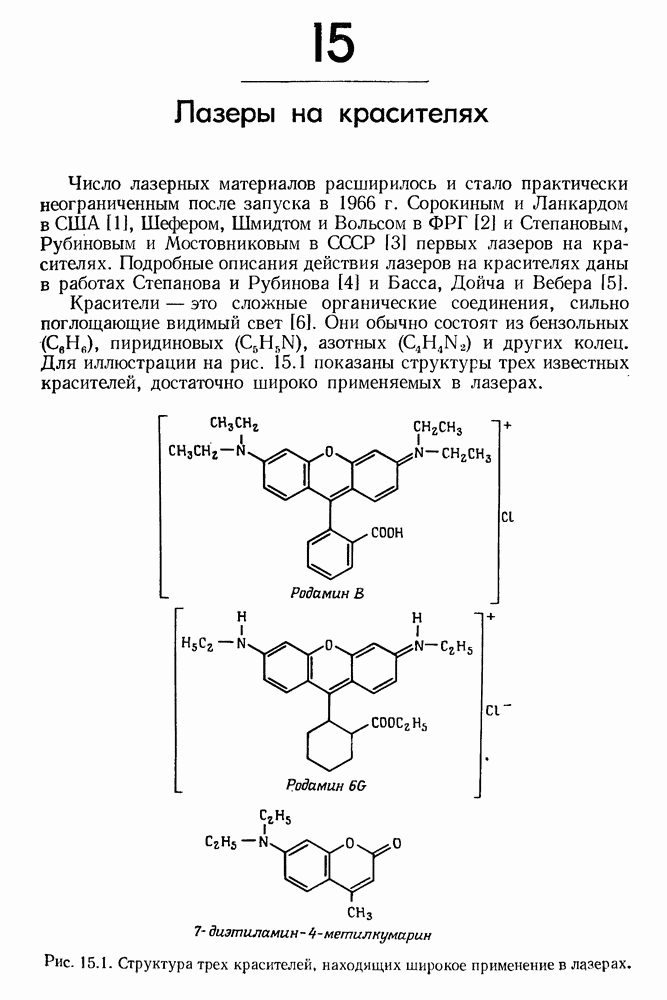
- 15. Лазеры на красителях
- § 1. УСЛОВИЯ ГЕНЕРАЦИИ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 2. ВЛИЯНИЕ РАСТВОРИТЕЛЯ И ТУШИТЕЛЕЙ НА ОПТИЧЕСКИЕ СВОЙСТВА КРАСИТЕЛЯ
- § 3. ОПТИЧЕСКАЯ НАКАЧКА ЛАЗЕРА НА КРАСИТЕЛЕ
- § 4. СПЕКТРАЛЬНЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
- § 5. ДРУГИЕ ОСОБЕННОСТИ ИЗЛУЧЕНИЯ ЛАЗЕРА НА КРАСИТЕЛЕ
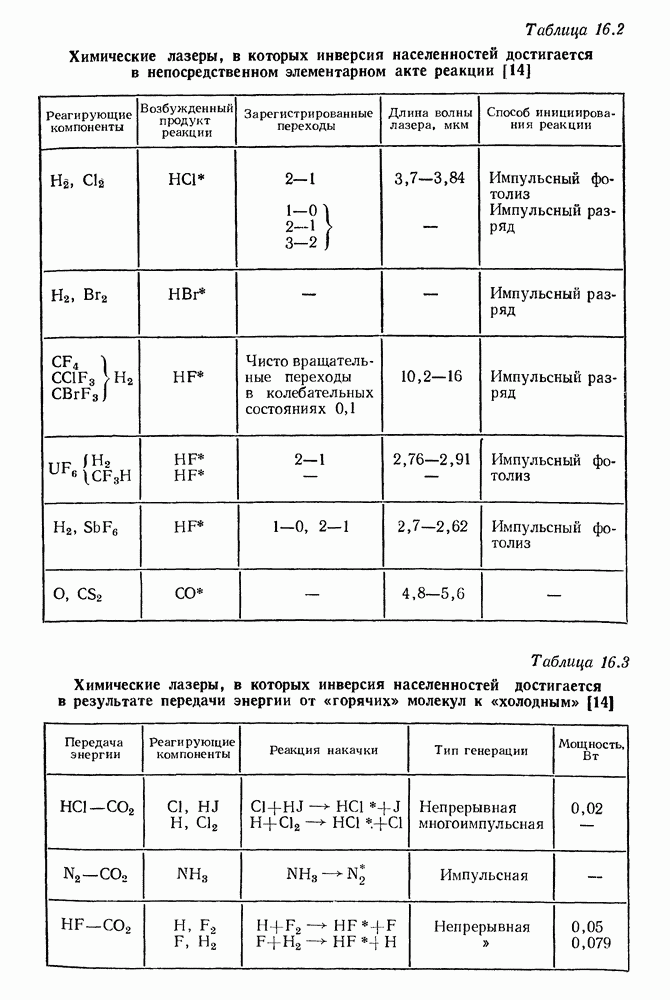
- 16. Химические лазеры
- § 2. УСТРОЙСТВО И ДЕЙСТВИЕ НЕКОТОРЫХ ХИМИЧЕСКИХ ЛАЗЕРОВ
- § 3. ВАЖНЕЙШИЕ ХИМИЧЕСКИЕ ЛАЗЕРЫ
- 17. Генерация оптических гармоник
- § 2. РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ВОЛН В ДИСПЕРСИОННОЙ СРЕДЕ
- § 3. МЕТОД СОГЛАСОВАНИЯ ФАЗ ПРИ ГВГ
- § 4. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ЛАЗЕРОВ
- § 5. ВАЖНЕЙШИЕ КРИСТАЛЛЫ ДЛЯ ГЕНЕРАЦИИ ВЫСШИХ ГАРМОНИК СВЕТА
- § 6. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРОВ
- § 7. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ СВЕТА С ПОМОЩЬЮ ГАЗОВЫХ ЛАЗЕРОВ
- § 8. СМЕШЕНИЕ ДВУХ ВОЛН МОНОХРОМАТИЧЕСКОГО ИЗЛУЧЕНИЯ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ
- § 9. СТАТИЧЕСКАЯ ПОЛЯРИЗАЦИЯ НЕЛИНЕЙНЫХ КРИСТАЛЛОВ ПОД ДЕЙСТВИЕМ СВЕТА (оптическое детектирование)
- § 10. ГЕНЕРАЦИЯ ВТОРОЙ ГАРМОНИКИ С ПОМОЩЬЮ НЕЛИНЕЙНОГО КРИСТАЛЛА, ПОМЕЩЕННОГО ВНУТРЬ ОПТИЧЕСКОГО РЕЗОНАТОРА
- § 11. ГВГ В КРИСТАЛЛИЧЕСКИХ ПОРОШКАХ
- § 12. ГЕНЕРАЦИЯ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ГАРМОНИК
- § 13. ГЕНЕРАЦИЯ ВЫСШИХ ГАРМОНИК С ПОМОЩЬЮ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 14. ВОЗБУЖДЕНИЕ ВЫСШИХ ГАРМОНИК В ПАРАХ МЕТАЛЛОВ
- 18. Параметрические усилители и генераторы света
- § 2. ПАРАМЕТРИЧЕСКОЕ УСИЛЕНИЕ В ЭКСПЕРИМЕНТЕ ВАНГА И РЕЙСЕТТА
- § 3. ЭЛЕМЕНТЫ ТЕОРИИ ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ
- § 4. ОПТИЧЕСКИЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В КРИСТАЛЛЕ
- § 5. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ В KDP и ADP
- § 6. ЗАКЛЮЧЕНИЕ
- 19. Вынужденное комбинационное рассеяние света
- § 2. КРАТКИЙ ОЧЕРК ТЕОРИИ КЛАССИЧЕСКОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ
- § 3. ВЫНУЖДЕННОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА (экспериментальные результаты)
- § 4. ОЧЕРК ТЕОРИИ ВКР
- § 5. НЕЛИНЕЙНОЕ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- 20. Вынужденное рассеяние Мандельштама — Бриллюэна (ВРМБ)
- § 2. СВЯЗЬ ГИПЕРЗВУКОВЫХ И СВЕТОВЫХ ВОЛН
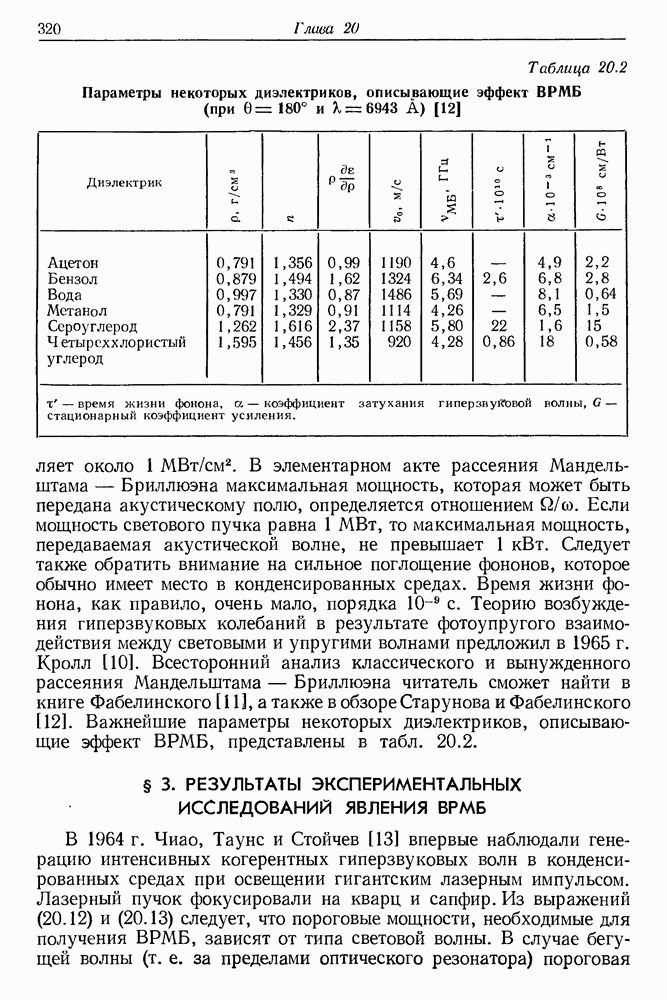
- § 3. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ ЯВЛЕНИЯ ВРМБ
- 21. Вынужденное энтропийное (температурное) рассеяние и вынужденное рассеяние в крыле линии Рэлея
- § 2. ВЫНУЖДЕННОЕ ЭНТРОПИЙНОЕ (температурное) РАССЕЯНИЕ СВЕТА В ЖИДКОСТЯХ
- 22. Параметрическая люминесценция (ПЛ)
- 23. Изменения показателя преломления вещества в поле интенсивного лазерного излучения
- 24. Явление автоколлимации и самофокусировки света
- § 2. ОБЪЯСНЕНИЕ ЭФФЕКТОВ АВТОКОЛЛИМАЦИИ И САМОФОКУСИРОВКИ ЛАЗЕРНОГО ПУЧКА
- § 3. САМОФОКУСИРОВКА И АВТОКОЛЛИМАЦИЯ ПУЧКА ЛАЗЕРА, РАБОТАЮЩЕГО В НЕПРЕРЫВНОМ РЕЖИМЕ
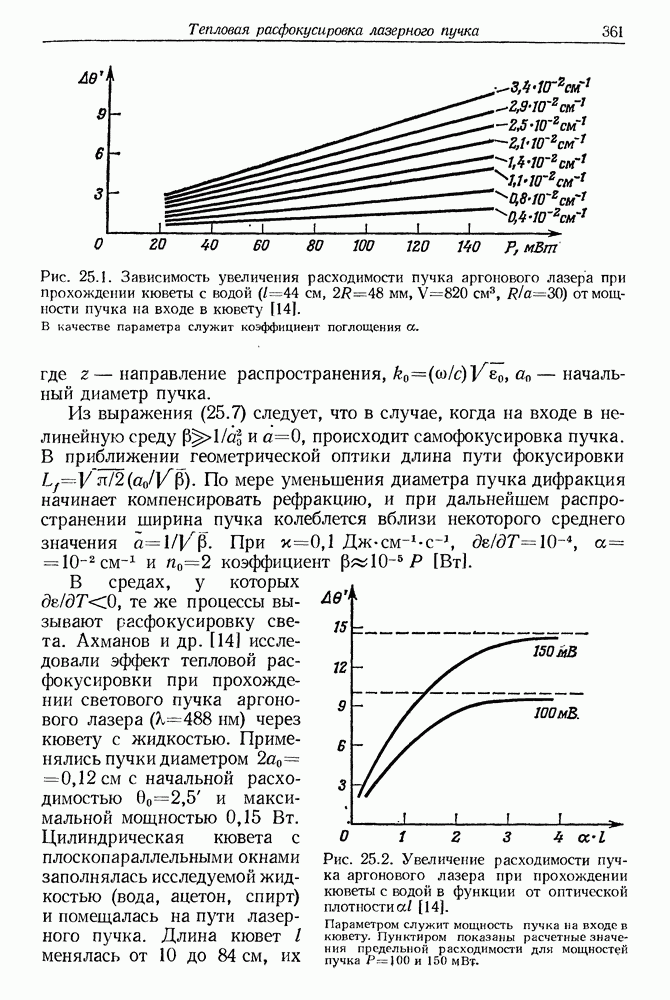
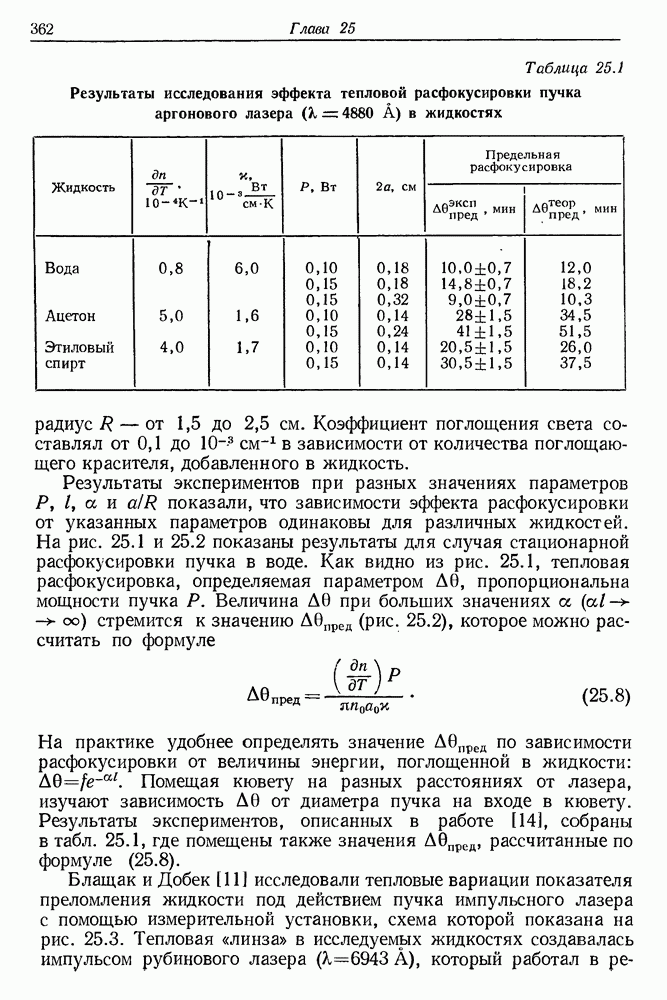
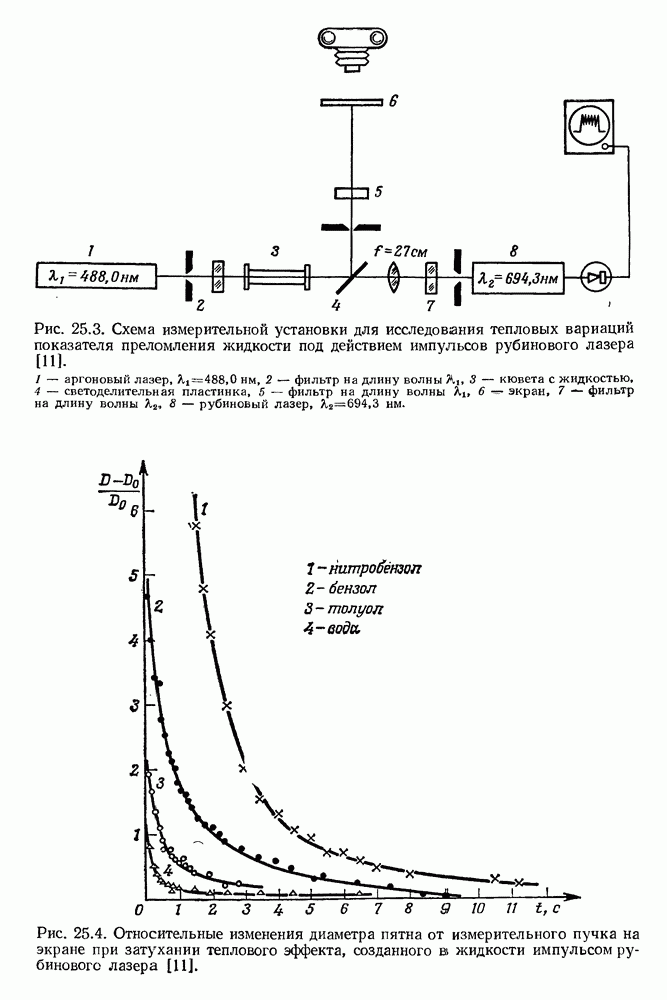
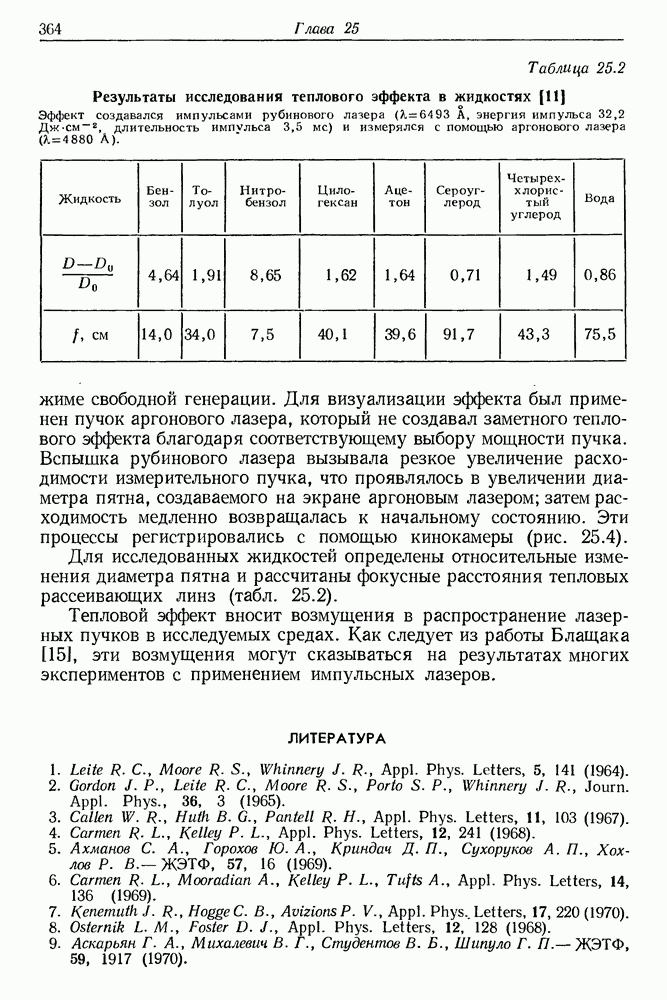
- 25. Тепловая расфокусировка лазерного пучка
- 26. Синхронизация мод лазера
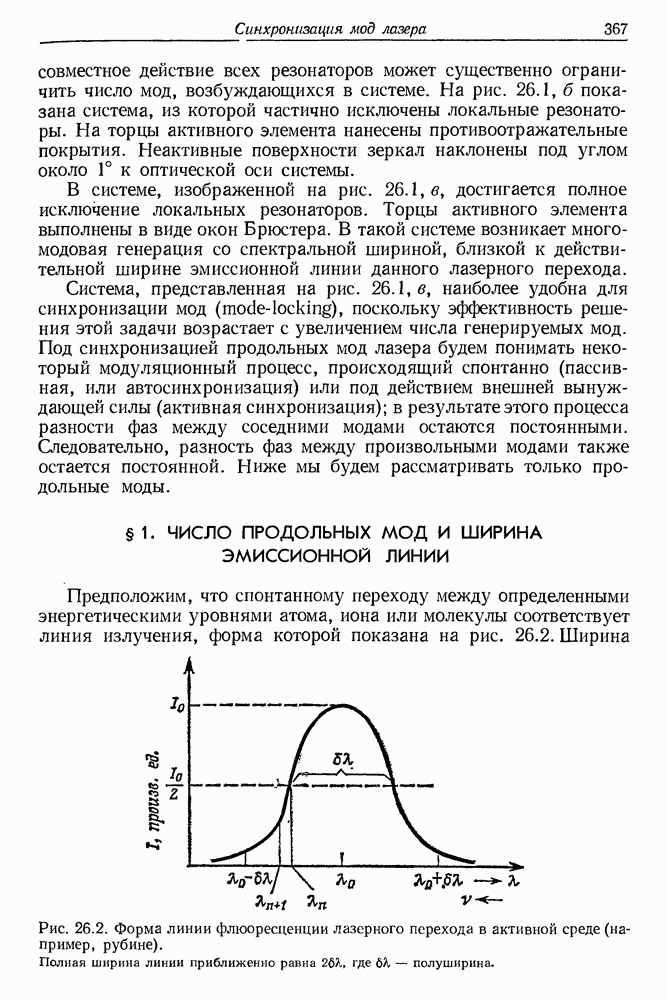
- § 1. ЧИСЛО ПРОДОЛЬНЫХ МОД И ШИРИНА ЭМИССИОННОЙ ЛИНИИ
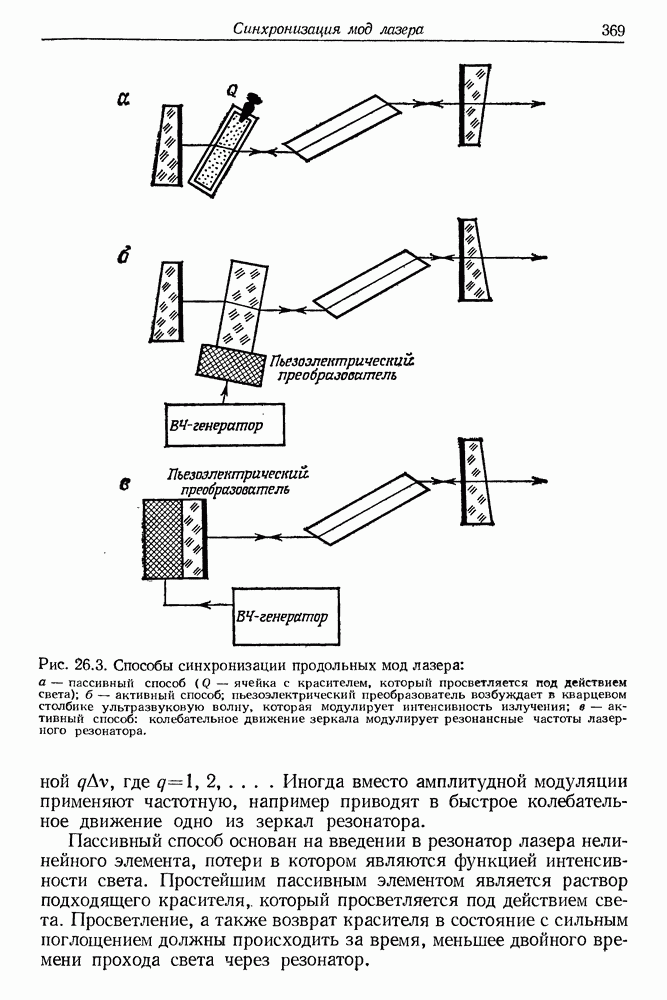
- § 2. СПОСОБЫ СИНХРОНИЗАЦИИ МОД ЛАЗЕРА
- § 3. ОБЪЯСНЕНИЕ ЭФФЕКТА СИНХРОНИЗАЦИИ МОД
- 27. Получение и измерение сверхкоротких импульсов света
- § 2. СИНХРОНИЗАЦИЯ МОД ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
- § 3. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРОВ НА КРАСИТЕЛЯХ
- § 4. СИНХРОНИЗАЦИЯ МОД ИМПУЛЬСНЫХ ЛАЗЕРОВ НА КРАСИТЕЛЯХ С НАКАЧКОЙ ИМПУЛЬСНЫМИ ЛАМПАМИ
- § 5. СИНХРОНИЗАЦИЯ МОД ЛАЗЕРА НЕПРЕРЫВНОГО ДЕЙСТВИЯ НА КРАСИТЕЛЕ
- § 6. ИЗМЕРЕНИЕ ДЛИТЕЛЬНОСТИ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
- б. Сверхскоростная электронно-оптическая камера с линейной разверткой
- в. Примеры использования камеры с разверткой
- § 7. СЕЛЕКЦИЯ И УСИЛЕНИЕ ПИКОСЕКУНДНЫХ СВЕТОВЫХ ИМПУЛЬСОВ
- § 8. ЗАКЛЮЧЕНИЕ
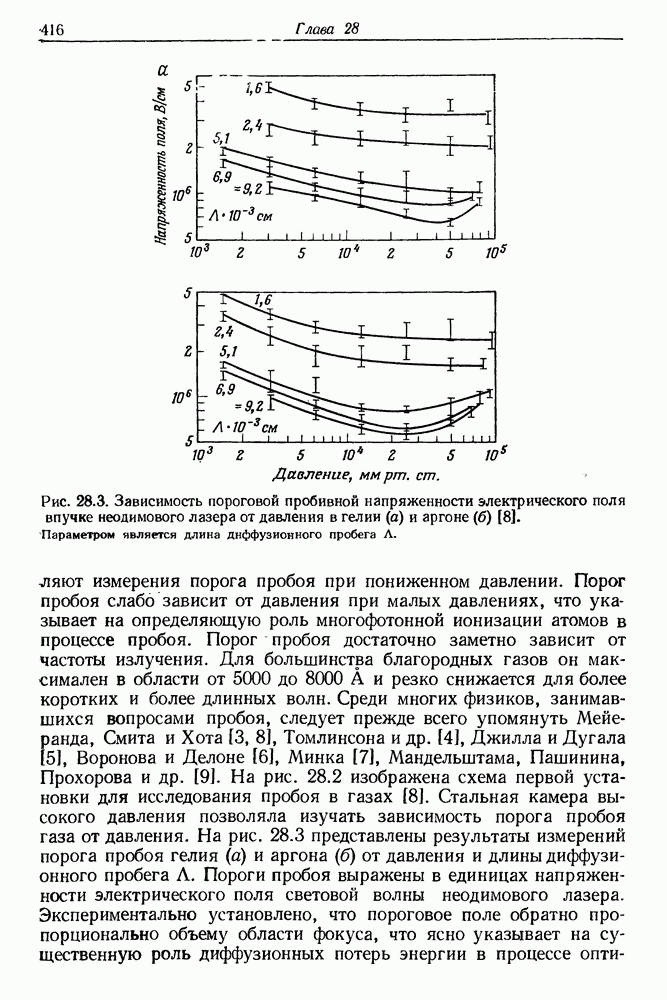
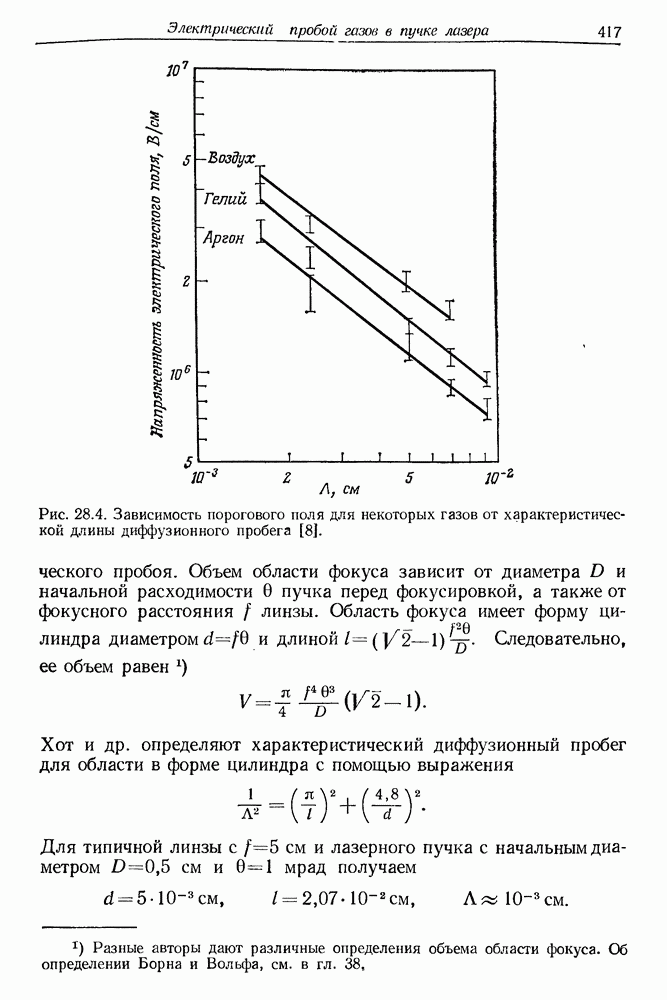
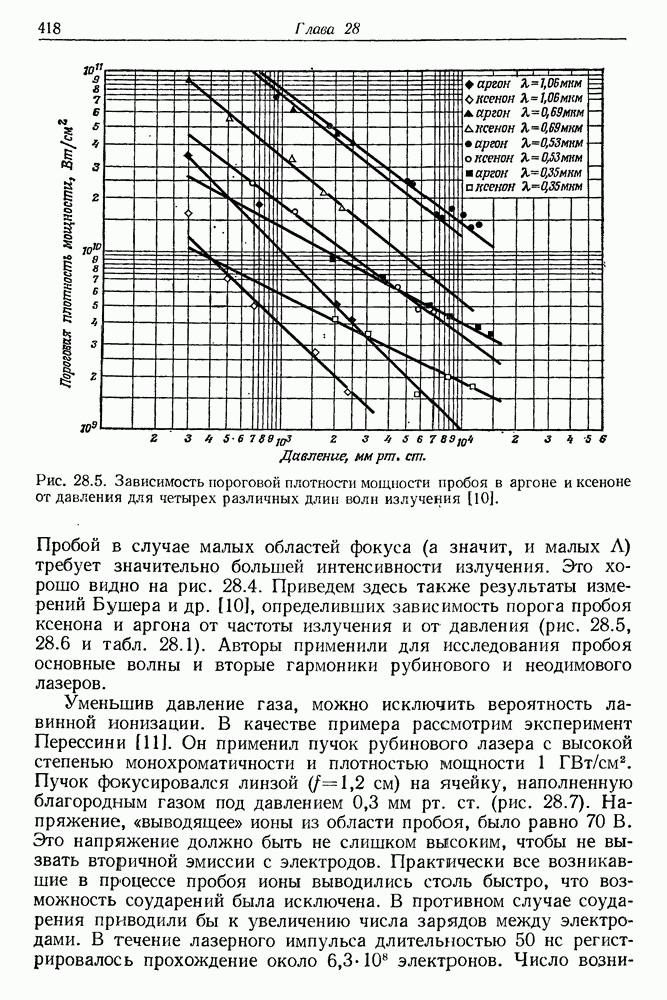
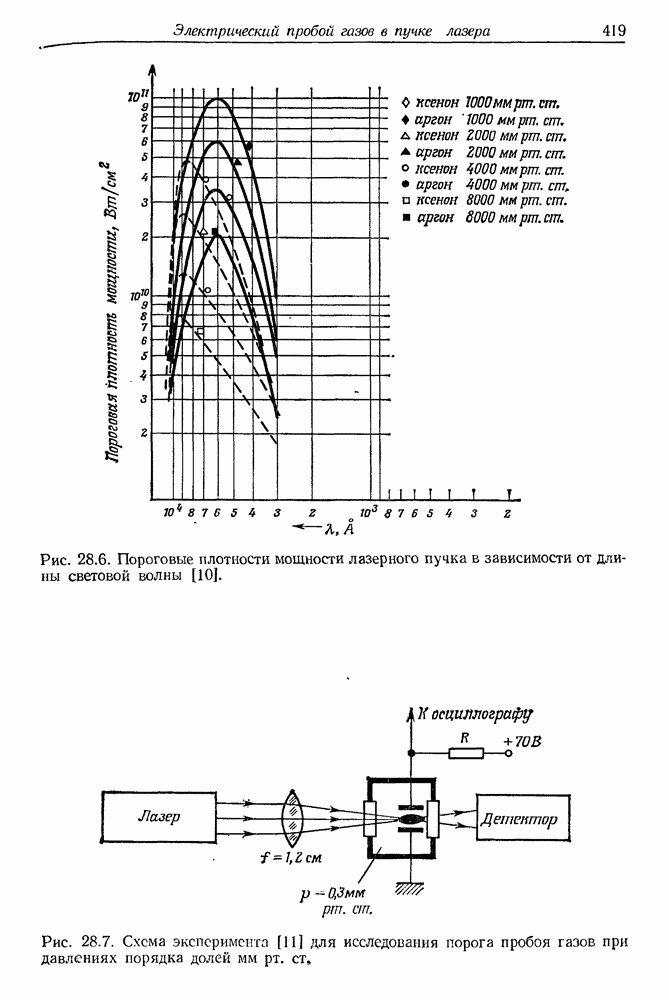
- 28. Электрический пробой газов в пучке лазерного излучения
- § 2. ВАЖНЕЙШИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
- § 3. ОЧЕРК ТЕОРИИ ИОНИЗАЦИИ АТОМОВ В ПОЛЕ МОЩНОГО ЛАЗЕРНОГО ПУЧКА
- б. Туннельный эффект
- в. Лавинная ионизация. Электрический пробой
- 29. Поверхностные и внутренние повреждения диэлектриков интенсивным световым пучком импульсного лазера
- 30. Создание плазмы и нейтронов сфокусированными пучками мощных лазеров
- § 2. ВОЗМОЖНОСТИ ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНОЙ РЕАКЦИИ С ПОМОЩЬЮ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 31 «Лунный» лазер
- § 2. ДЕЙСТВИЕ СИСТЕМ ЛАЗЕРНОЙ ЛОКАЦИИ ЛУНЫ И РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
- § 3. ЗАКЛЮЧЕНИЕ
- 32. Элементы голографии
- § 2. РЕГИСТРАЦИЯ ГОЛОГРАММЫ
- 33. Исследование спектров испускания и поглощения с помощью нано- и пикосекундных импульсов света
- § 2. СПЕКТРОСКОПИЯ ОБРАЩЕННОГО КОМБИНАЦИОННОГО РАССЕЯНИЯ СВЕТА
- § 3. ПИКОСЕКУНДНАЯ СПЕКТРОСКОПИЯ
- 34. Рентгеновские и гамма-лазеры
- § 2. ГАММА-ЛАЗЕР
- 35. Лазеры на центрах окраски
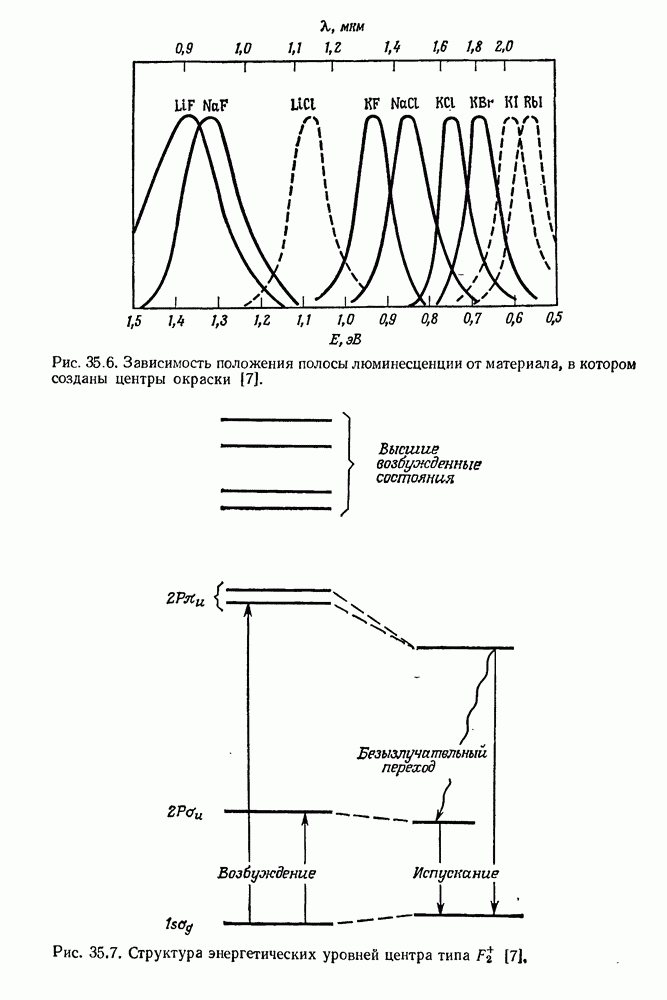
- § 2. КРАТКИЙ ОБЗОР СВОЙСТВ ВАЖНЕЙШИХ ЦЕНТРОВ ОКРАСКИ
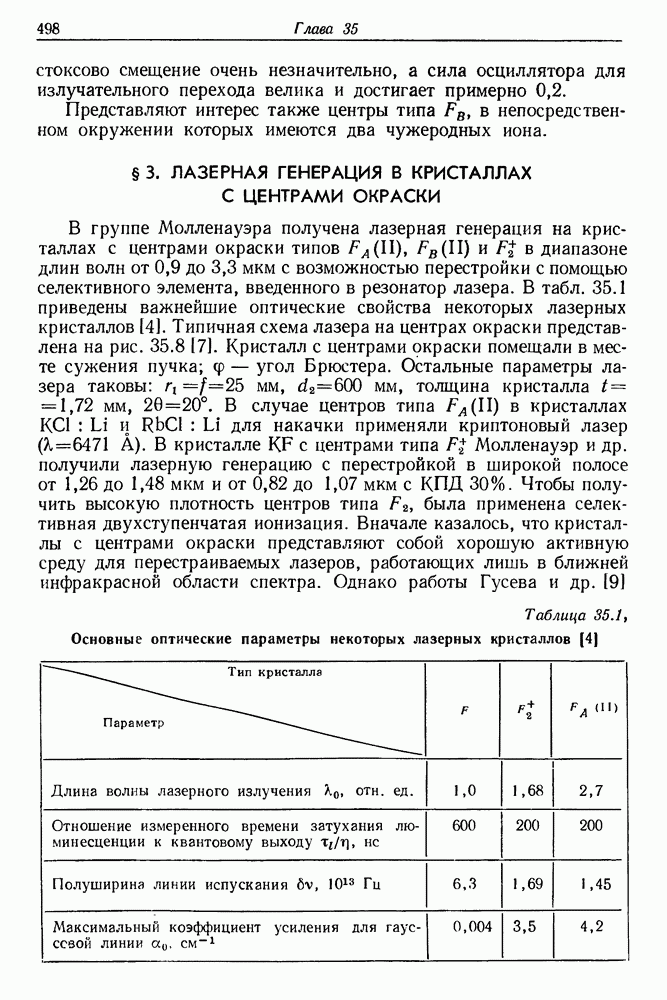
- § 3. ЛАЗЕРНАЯ ГЕНЕРАЦИЯ В КРИСТАЛЛАХ С ЦЕНТРАМИ ОКРАСКИ
- Дополнения
- § 1. УРАВНЕНИЯ МАКСВЕЛЛА И ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 3. КОГЕРЕНТНОСТЬ И СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 4. МАТРИЦА ПЛОТНОСТИ
- 37. Когерентность света
- § 1. КОГЕРЕНТНОСТЬ СВЕТА С ТОЧКИ ЗРЕНИЯ ЭЛЕМЕНТАРНОГО АКТА ИСПУСКАНИЯ АТОМА
- § 2. ОСНОВНЫЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ КОГЕРЕНТНОСТЬ СВЕТА
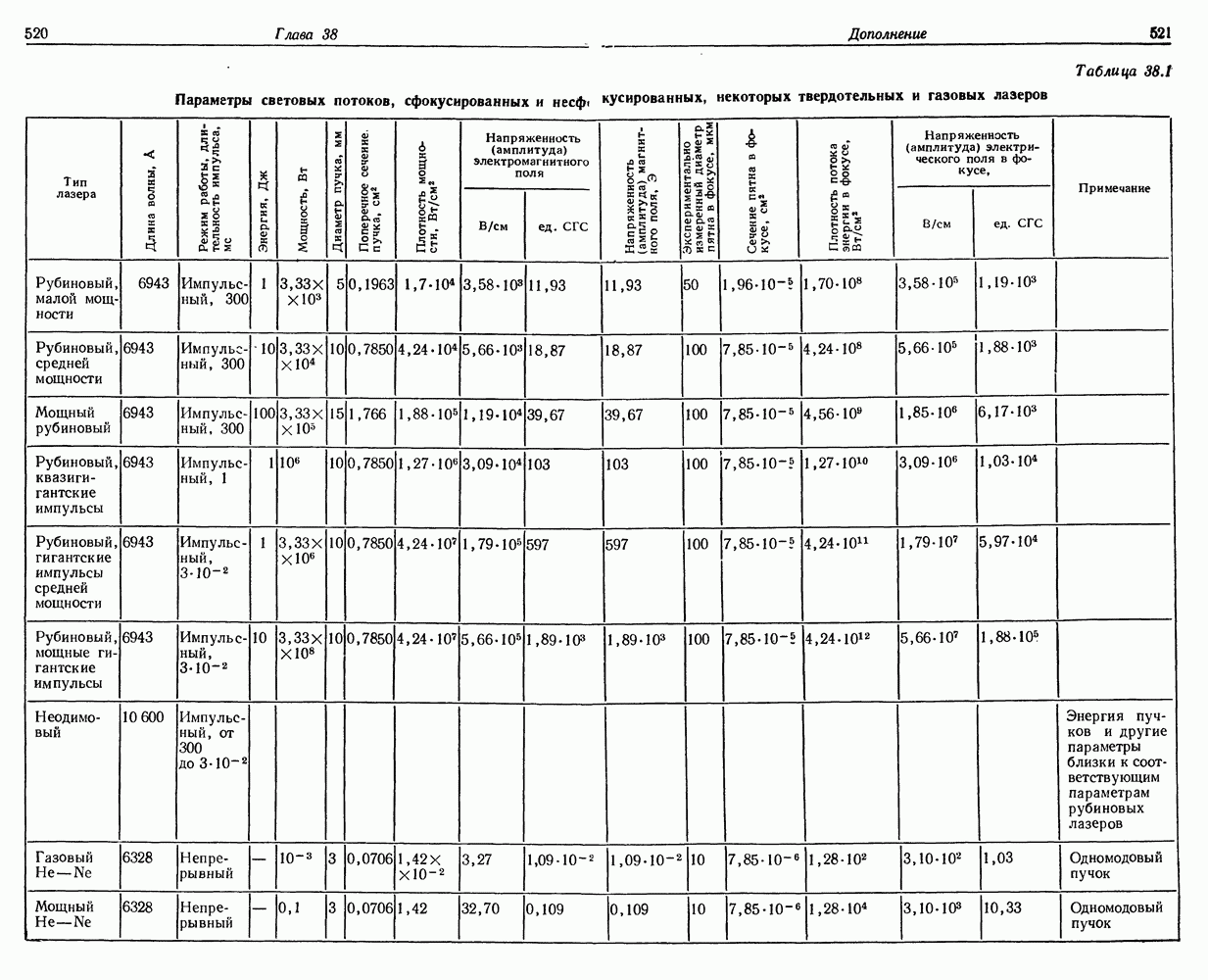
- 38. Плотность лучистой энергии и напряженности электрического и магнитного полей в лазерном световом пучке
- § 2. РАСХОДИМОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 3. ФОКУСИРОВКА ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 4. МОНОХРОМАТИЧНОСТЬ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 5. УСИЛЕНИЕ ЛАЗЕРНОГО СВЕТОВОГО ПУЧКА
- § 6. ПОТОК ЛУЧИСТОЙ ЭНЕРГИИ
- Таблицы