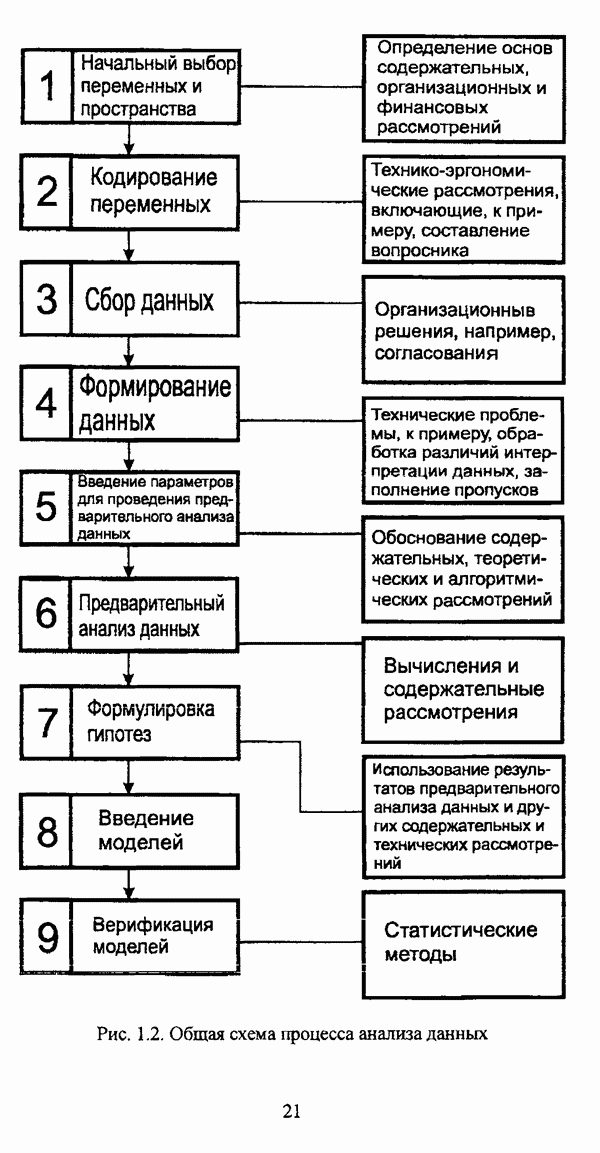
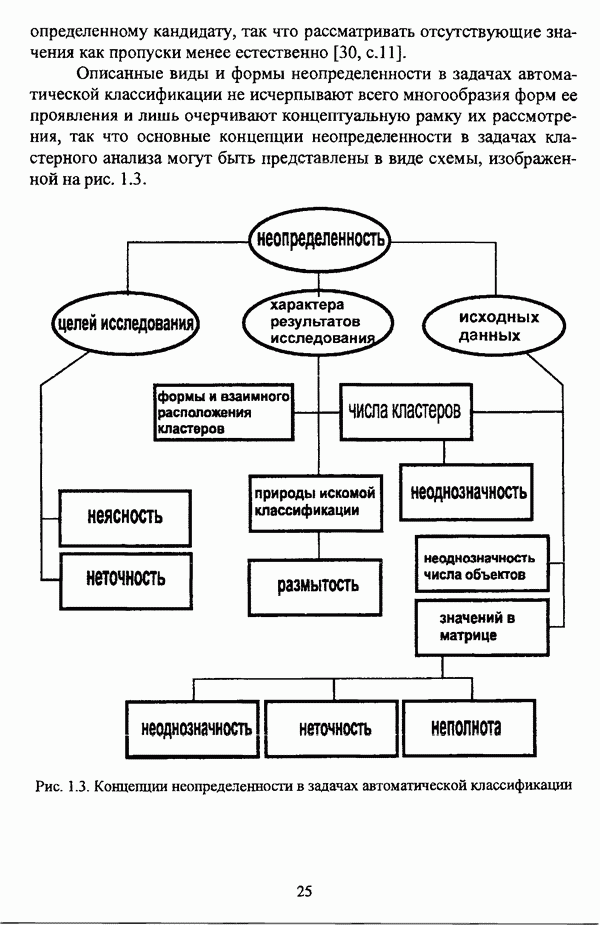
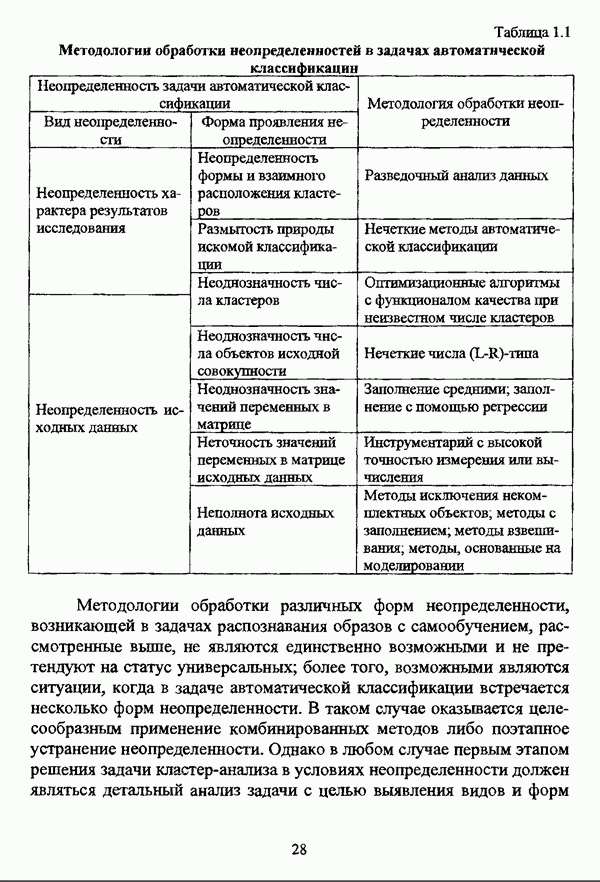
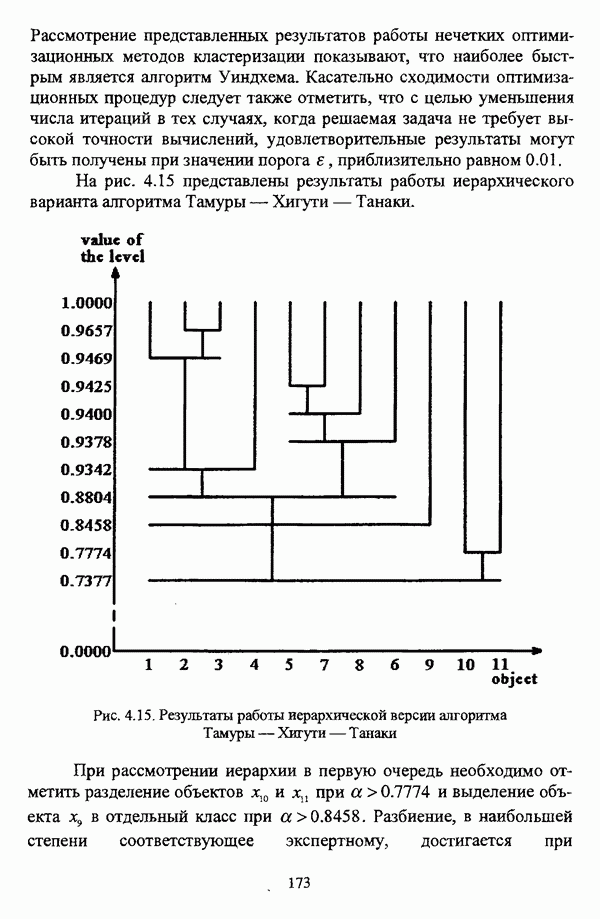
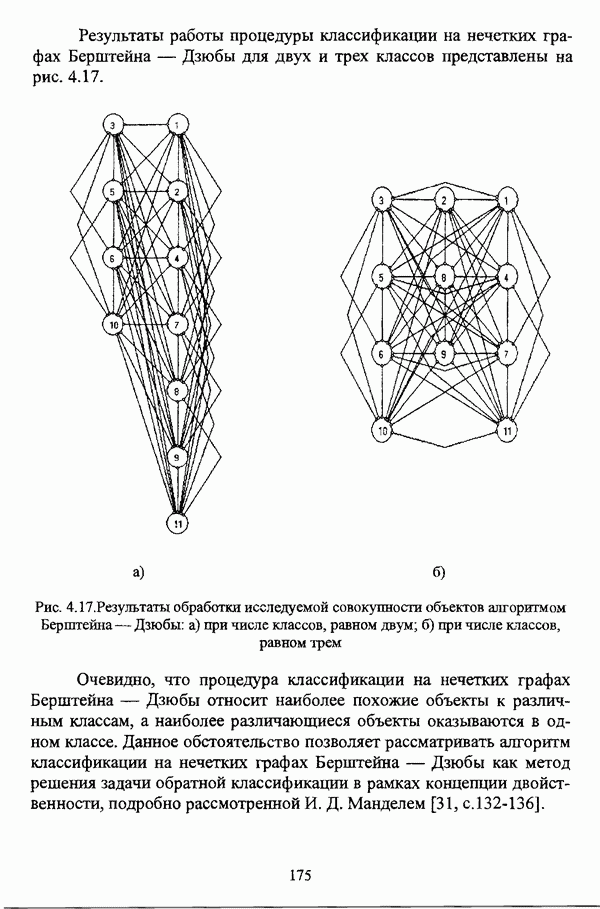
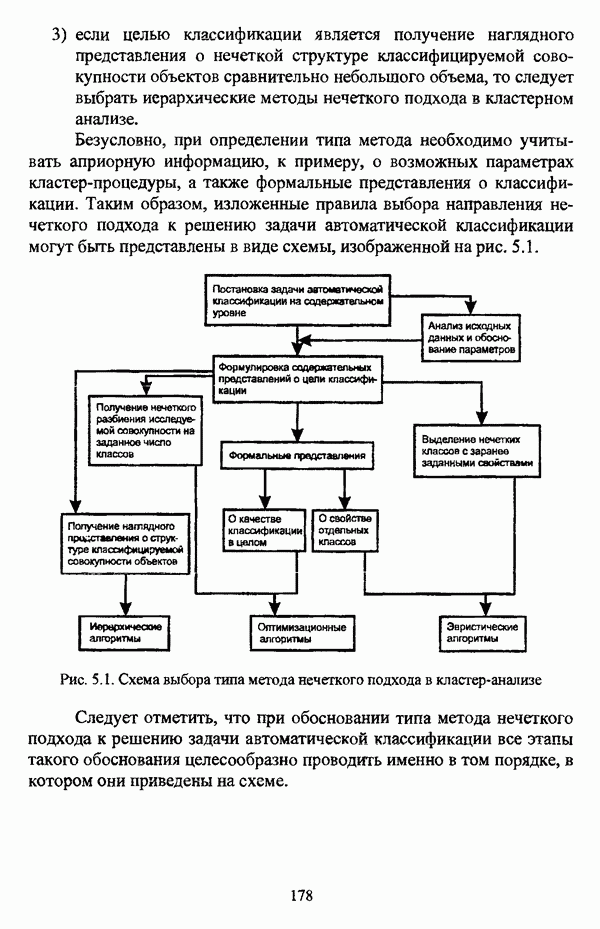
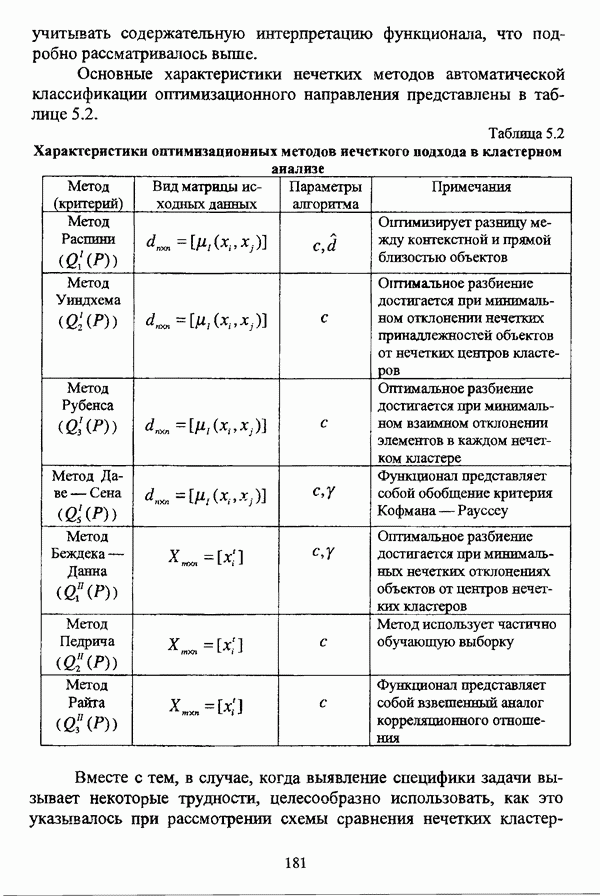
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
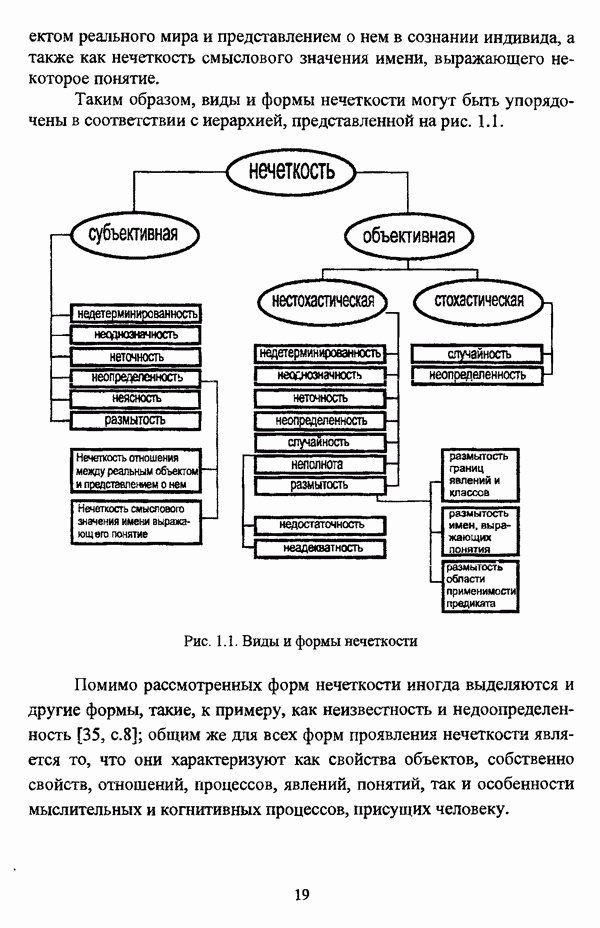
2.2.2. Основные операции над нечеткими отношениями
Пусть R и S — два произвольных бинарных нечетких отношения на множестве 
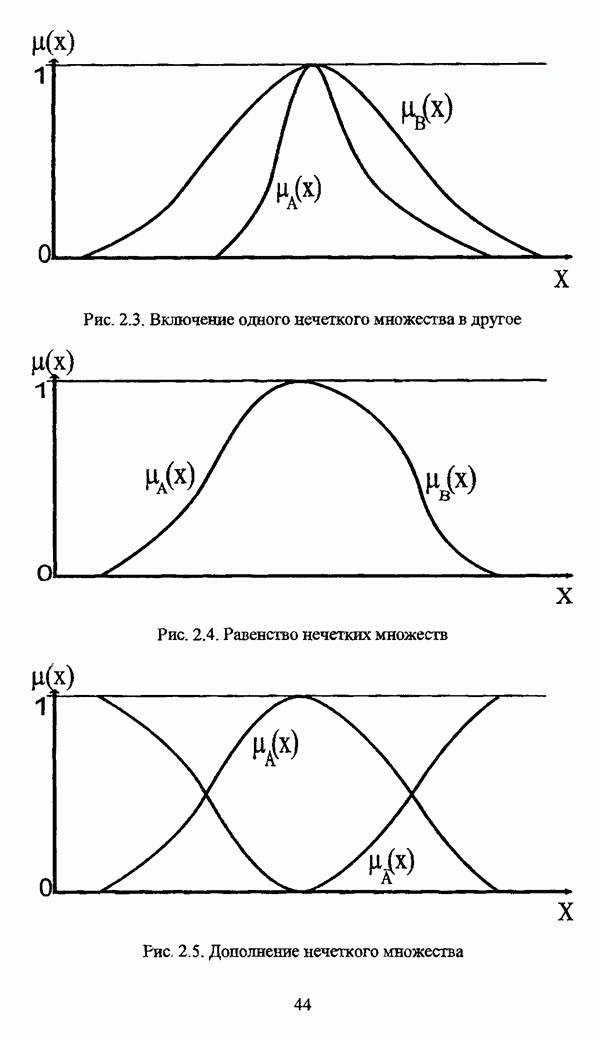
Включение нечеткого отношения R в нечеткое отношение S определяется условием

Дополнение R нечеткого отношения R определяется условием

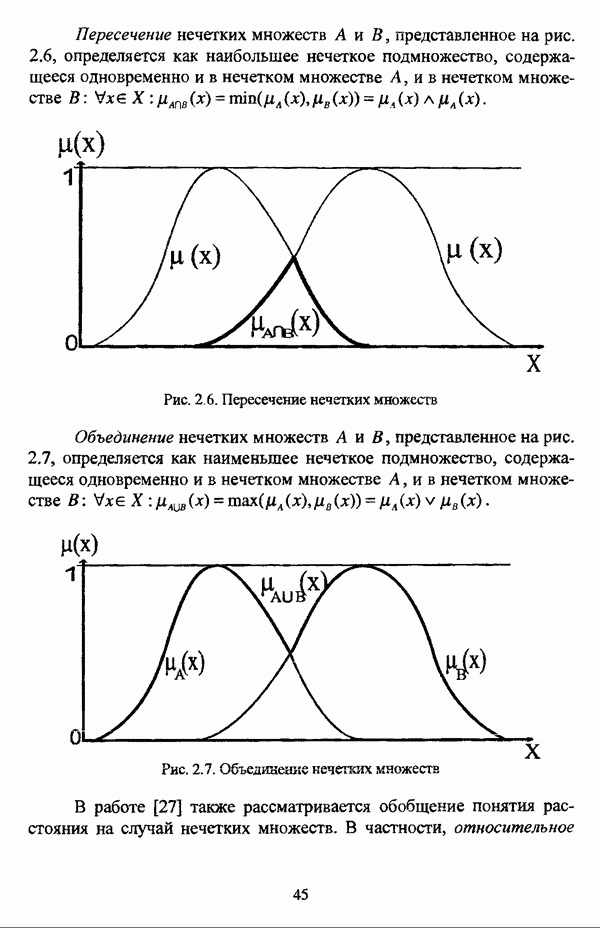
Пересечение нечетких отношений R и S определяется условием

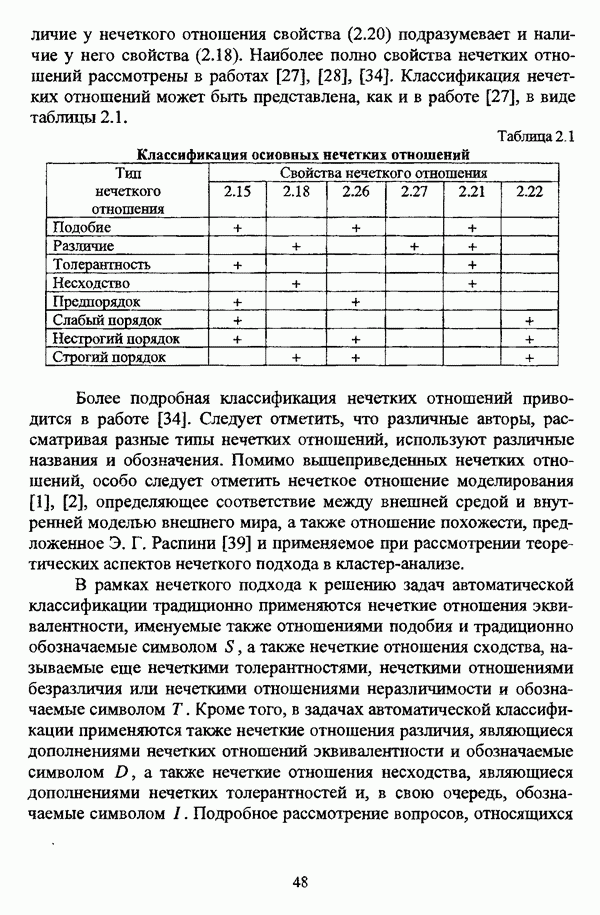
Объединение нечсгких отношений R и S определяется условием

Пусть  — универсальные множества, так что нечеткое отношение R определено на
— универсальные множества, так что нечеткое отношение R определено на  а нечеткое отношение S — соответственно на
а нечеткое отношение S — соответственно на  тогда
тогда  -композицией нечетких отношений
-композицией нечетких отношений  называется отношение
называется отношение  , определяемое условием
, определяемое условием

Свойство транзитивности нечетких отношений (2.26) может быть выражено, таким образом, в виде условия

Если в условии (2.34) операцию взятия минимума а заменить на операцию взятия среднего арифметического, получится следующее определение операции композиции:

именуемое (max-sum)-композицией. Возможны также и другие определения операции композиции нечетких отношений; например, в работе [9] рассмотрена операция (max-)-композиции:

полученная заменой в условии (2.34) операции взятия минимума а на операцию умножения.
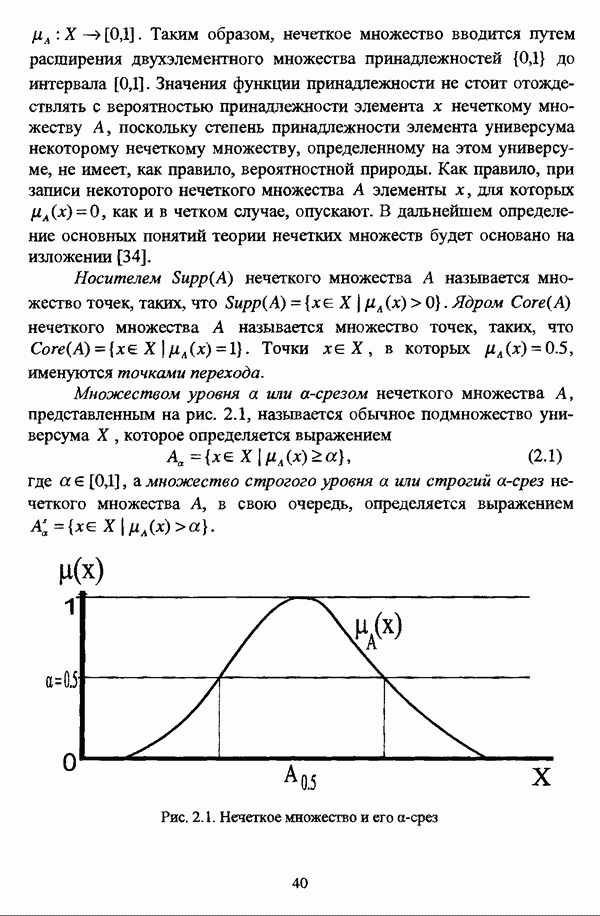
Как и при рассмотрении нечетких множеств, при рассмотрении нечетких отношений вводится понятие  -среза, так что
-среза, так что  -срезом
-срезом  некоторого бинарного нечеткого отношения R называется обычное отношение на универсуме
некоторого бинарного нечеткого отношения R называется обычное отношение на универсуме  которое определяется выражением
которое определяется выражением

где  , что, в свою очередь, в соответствии с теоремой декомпозиции [27, с. 75], позволяет представить нечеткое отношение R в виде иерархии обычных отношений:
, что, в свою очередь, в соответствии с теоремой декомпозиции [27, с. 75], позволяет представить нечеткое отношение R в виде иерархии обычных отношений:

Естественно, что смысл термина «декомпозиция» в этом случае отличается от смысла данного термина, когда речь идет о композиции нечетких отношений. В работе [9] подробно рассматриваются особенности операции декомпозиции нечетких отношений эквивалентности, которая находит обширное применение в задачах кластерного анализа. Поскольку большое значение в приложениях теории нечетких отношений играют транзитивные нечеткие отношения, необходимо рассмотреть операцию преобразования исходного нетранзитивного отношения в транзитивное. Данная операция, именуемая транзитивным замыканием, впервые была рассмотрена в работах [163], [193].
(max-min)-транзитивным замыканием бинарного нечеткого отношения R на множестве  где
где  называется бинарное нечеткое отношение R на множестве X, определяемое следующим образом:
называется бинарное нечеткое отношение R на множестве X, определяемое следующим образом:

где отношения  определяются рекурсивно:
определяются рекурсивно:

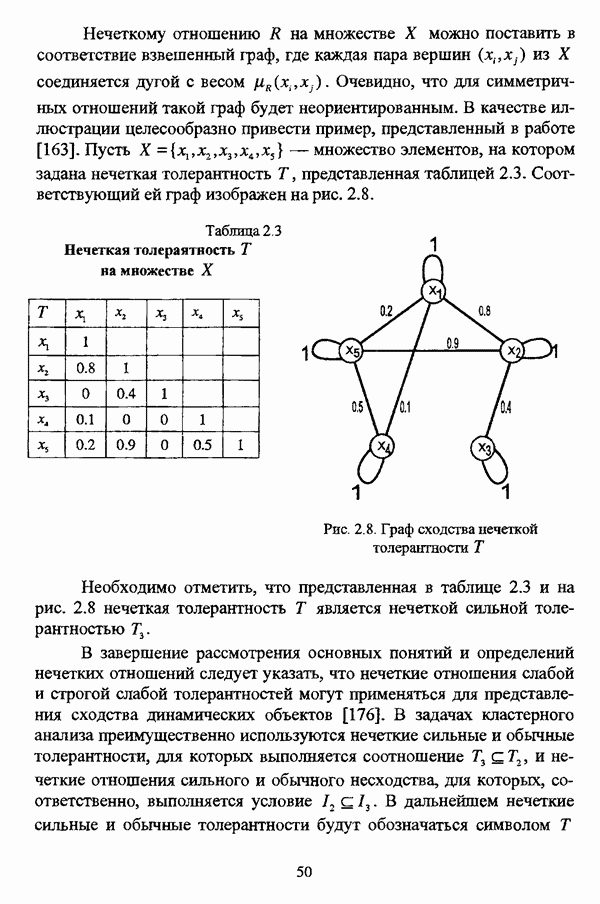
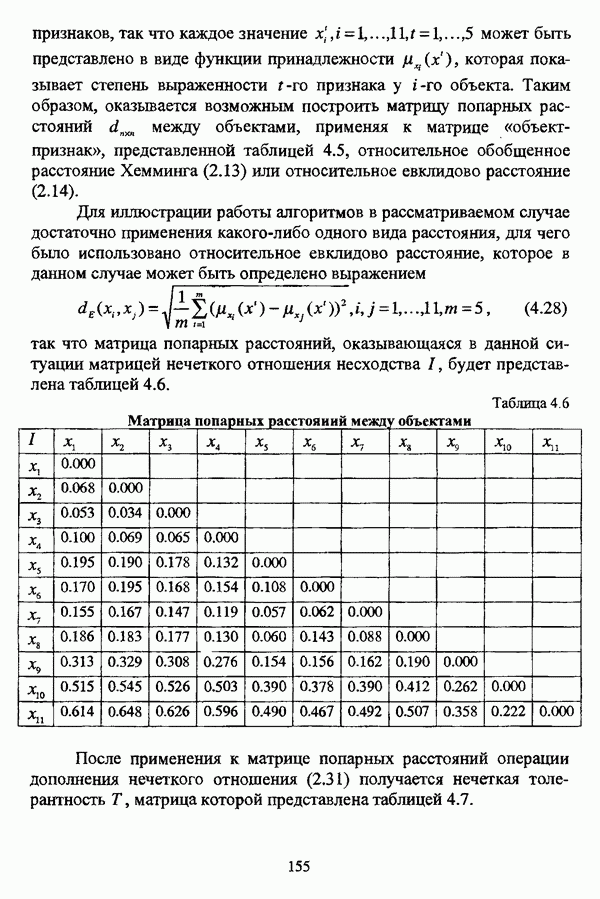
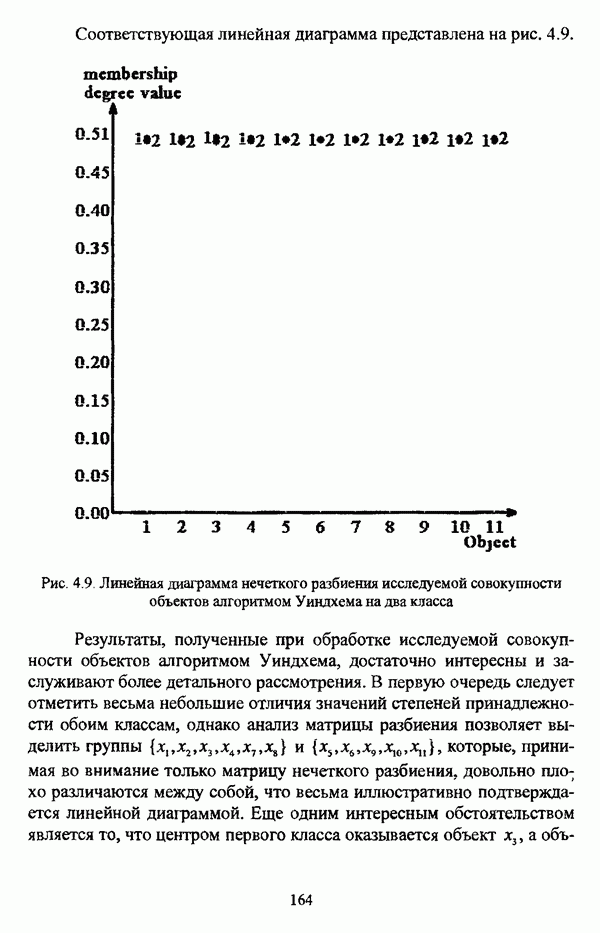
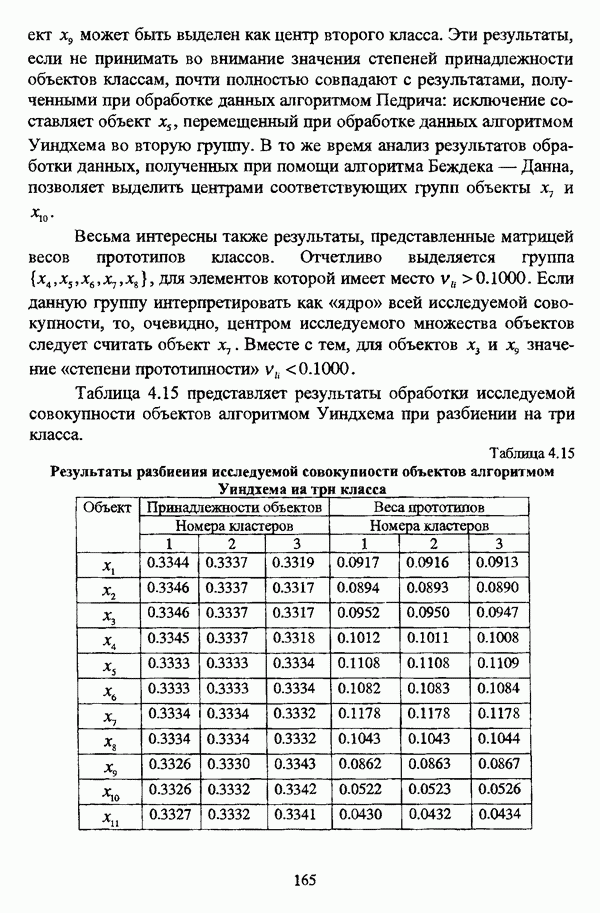
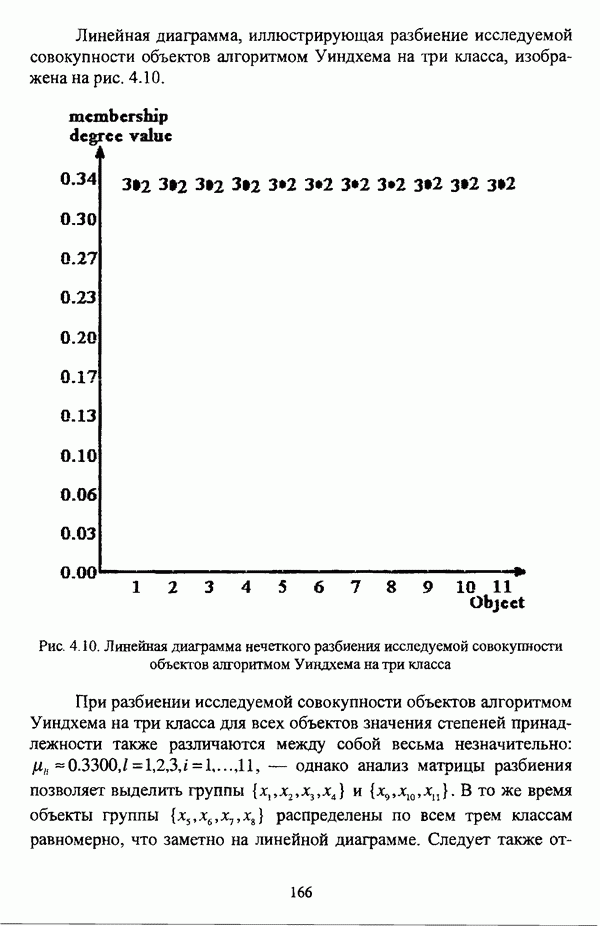
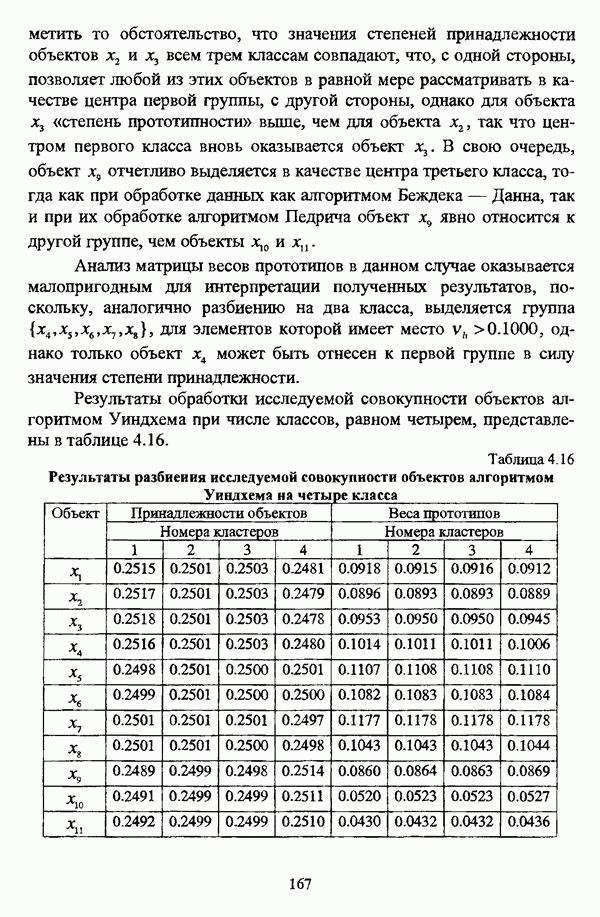
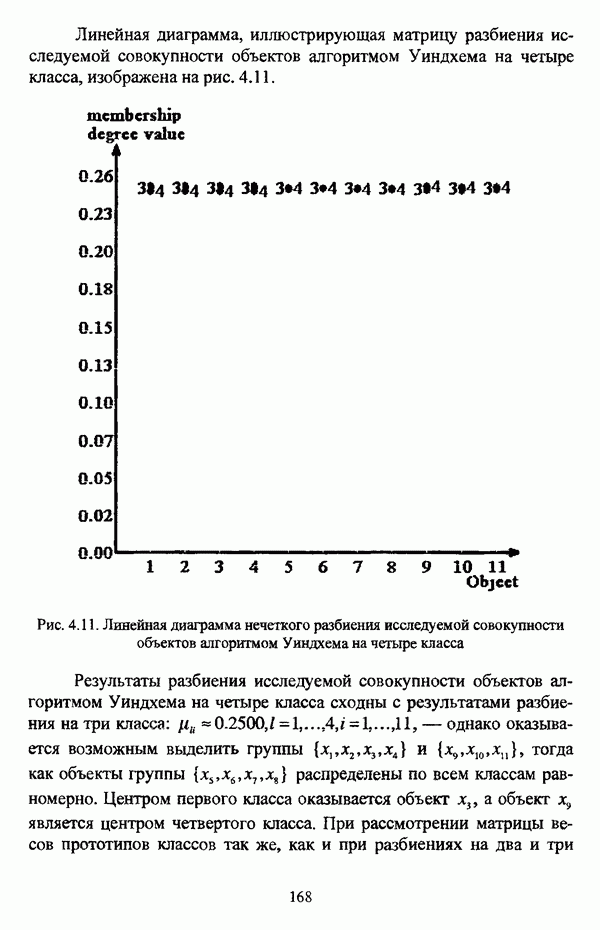
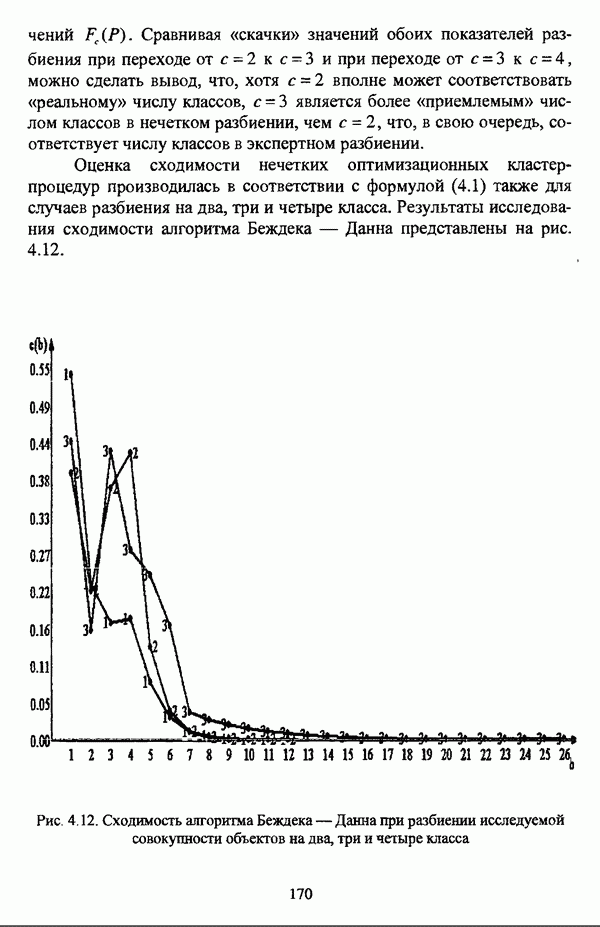
Иллюстративным примером данной операции может послужить нечеткое отношение, представленное таблицей 2.4 и являющееся (max-min)-транзитивным замыканием нечеткой толерантности Т, представленной таблицей 2.3. Соответствующий (max-min)-транзитивному замыканию Т нечеткой толерантности Т граф изображен на рис. 2.9.
Таблица 2.4. (max-min)-транзитивное замыкание Т нечеткой толерантности Т


Рис. 2.9. Граф нечеткого отношения Т
В работе [34] формулируется теорема, в соответствии с которой транзитивное замыкание R любого бинарного нечеткого отношения R транзитивно и является наименьшим транзитивным отношением, включающим  то есть
то есть  , и для любого транзитивного отношения S, такого, что R с S, следует
, и для любого транзитивного отношения S, такого, что R с S, следует 
Следует отметить [34, с. 45], что при транзитивном замыкании некоторого нечеткого отношения из свойств (2.15) — (227) сохраняются только свойства (2.15), (2.21), (2.24), (2.25), (2.26), (2.27).
(min-max)-транзитивным замыканием [27, с. 137-138] бинарного нечеткого отношения R на множестве  где
где  называется бинарное нечеткое отношение R на множестве X, определяемое следующим образом:
называется бинарное нечеткое отношение R на множестве X, определяемое следующим образом:

где отношения  определяются рекурсивно:
определяются рекурсивно:

Полное рассмотрение операций над нечеткими отношениями содержится в [27], а применение аппарата нечетких графов к решению задач кластерного анализа рассматривается в работе [190].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
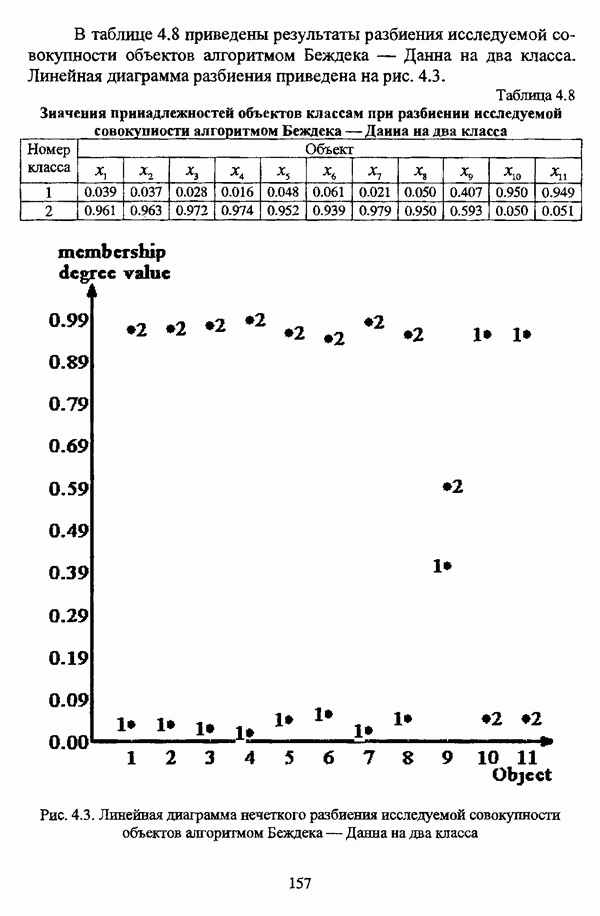
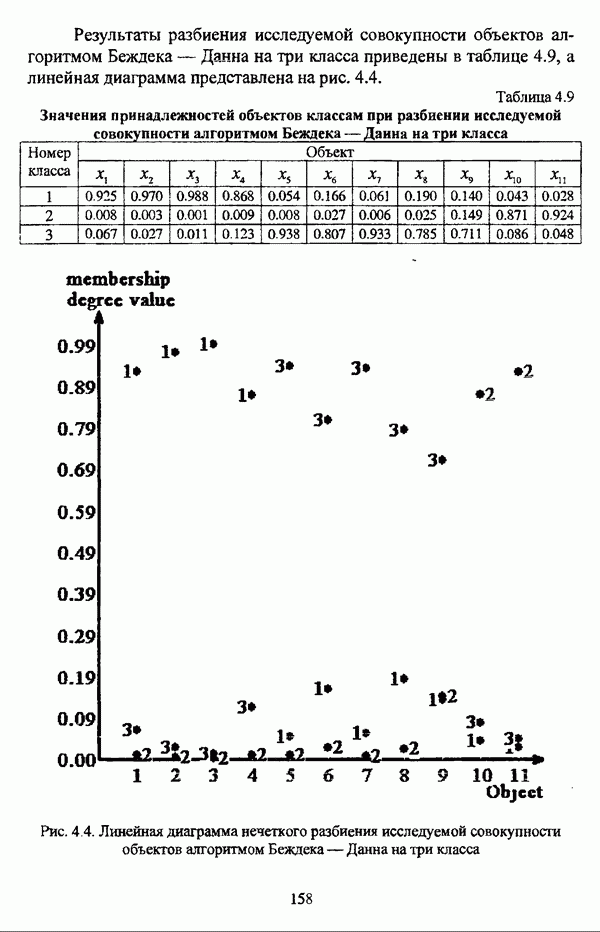
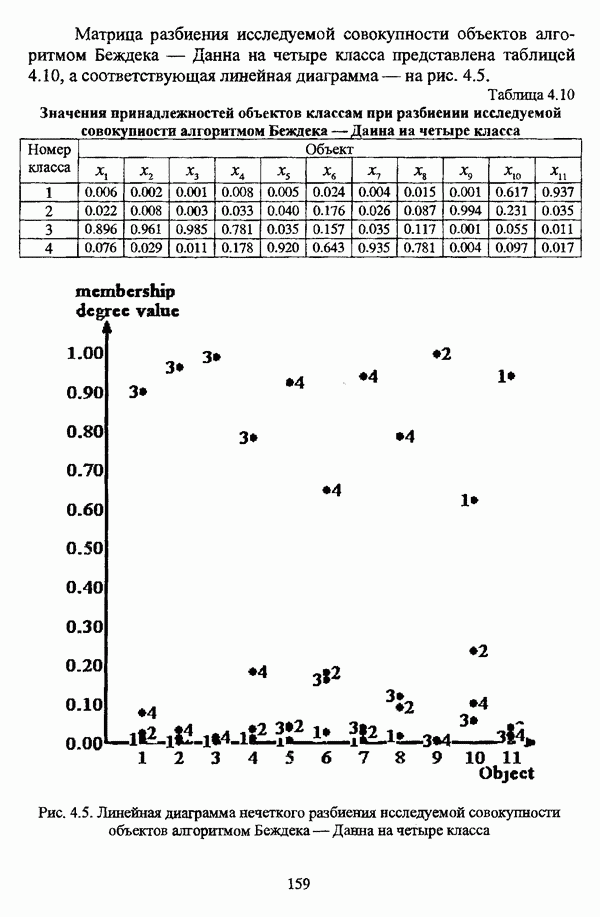
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
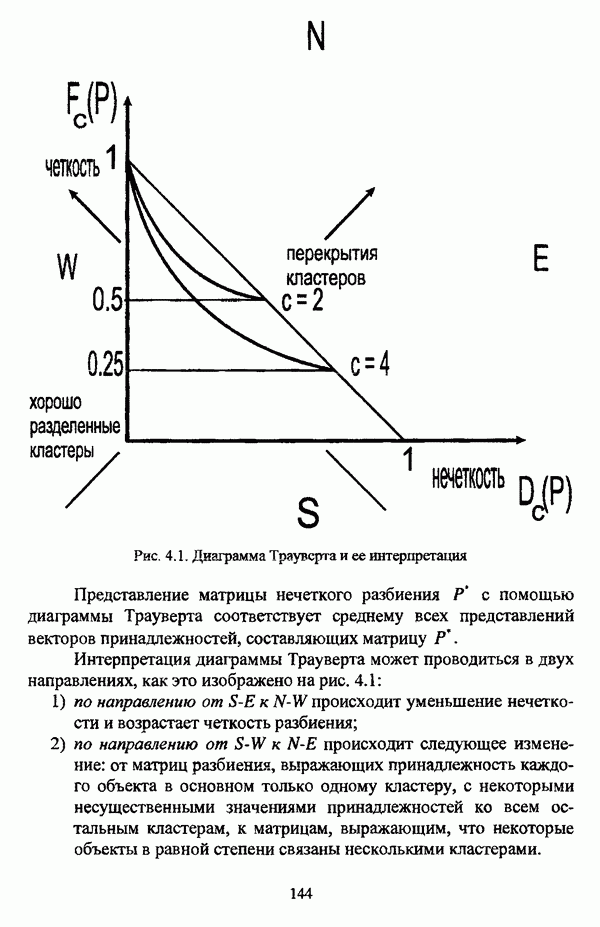
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
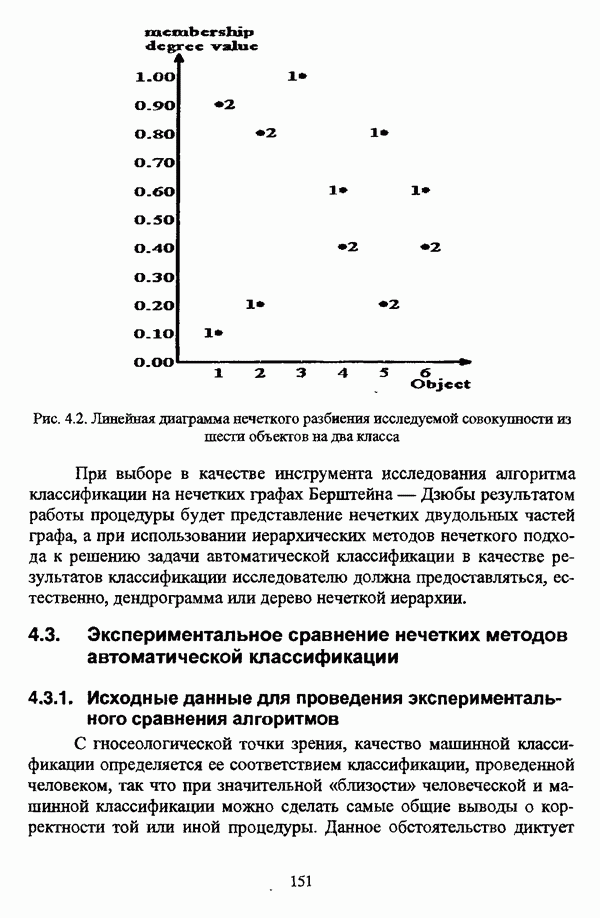
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
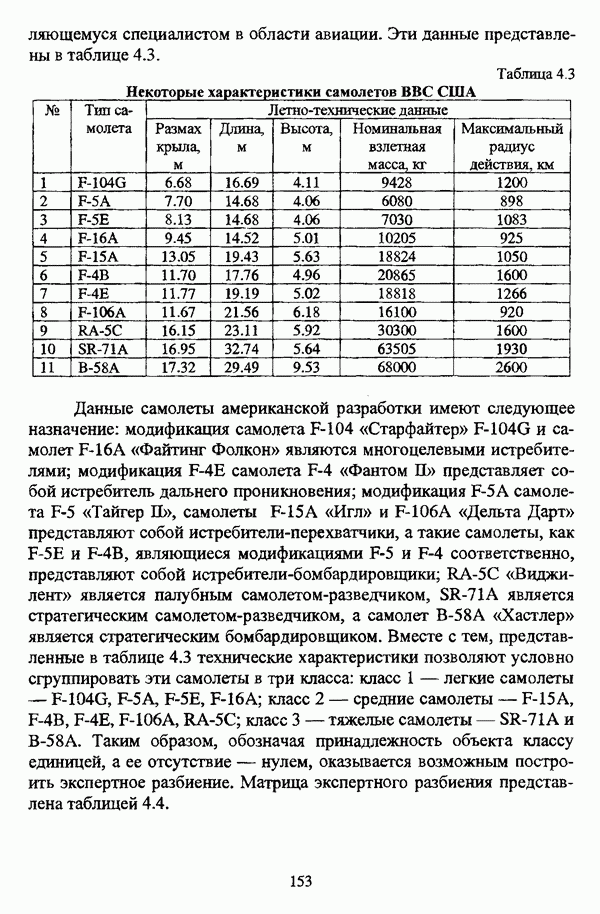
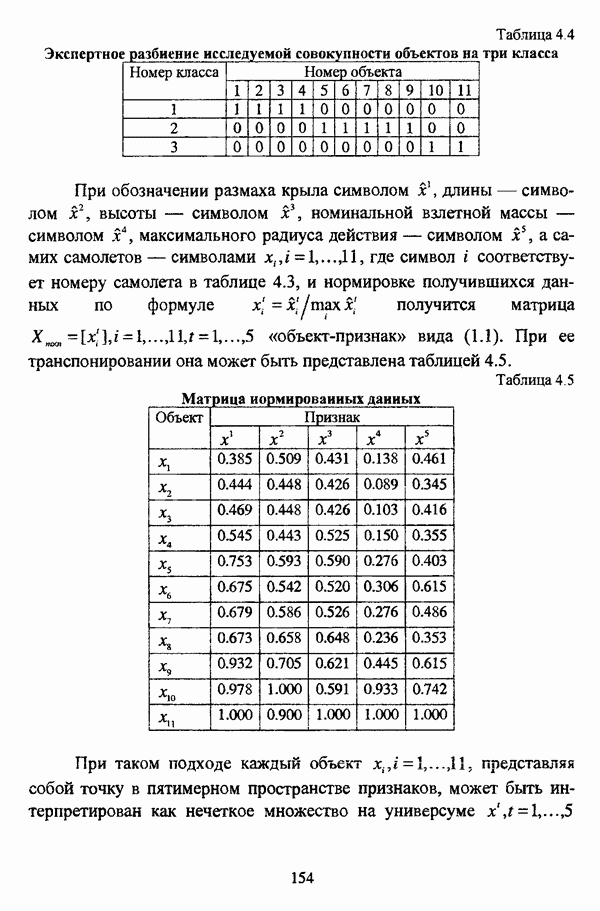
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы