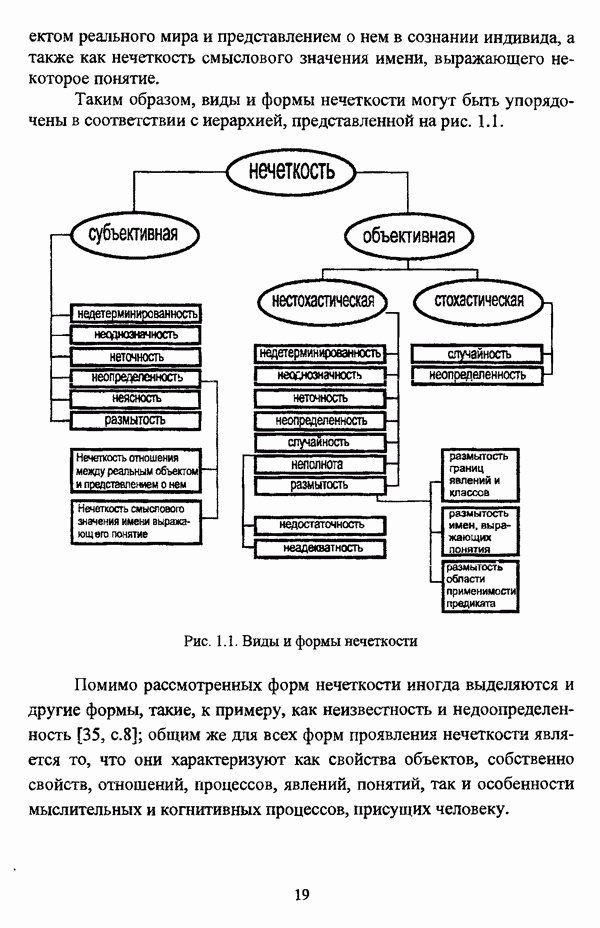
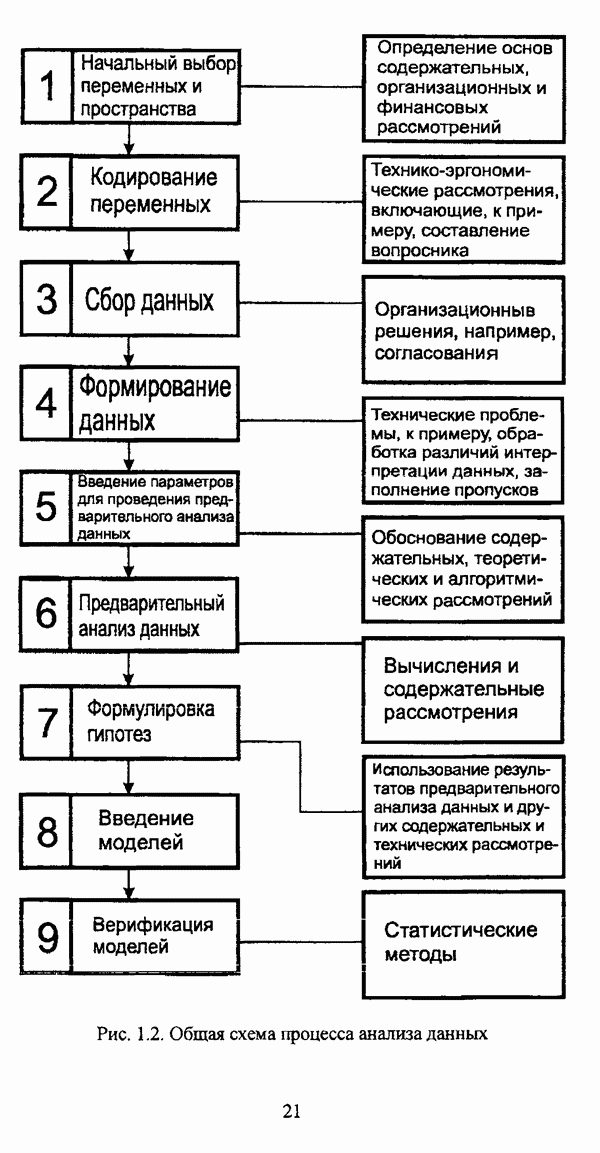
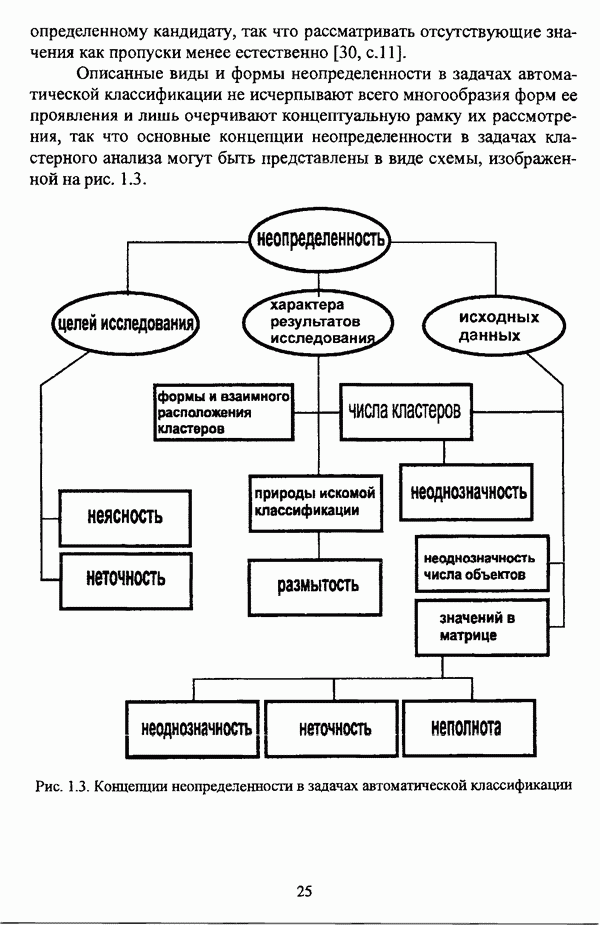
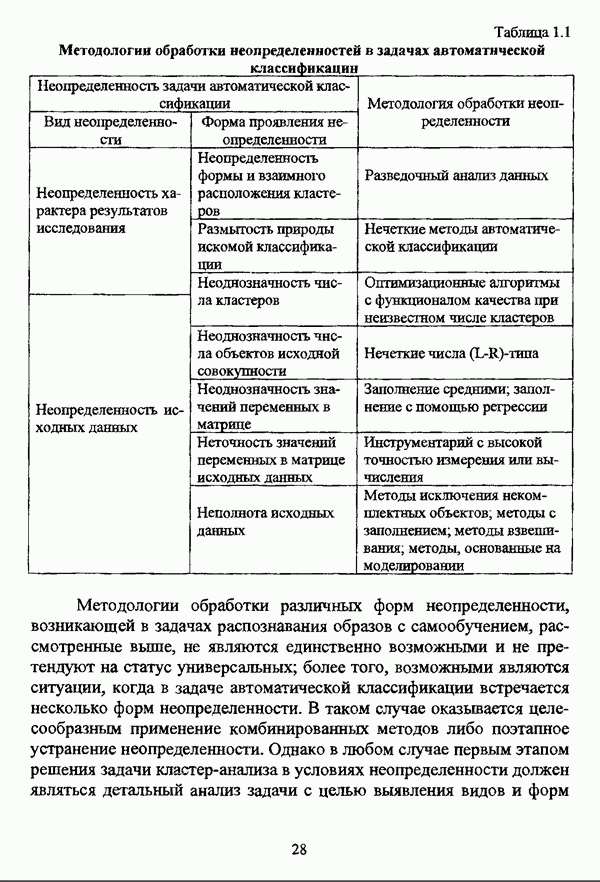
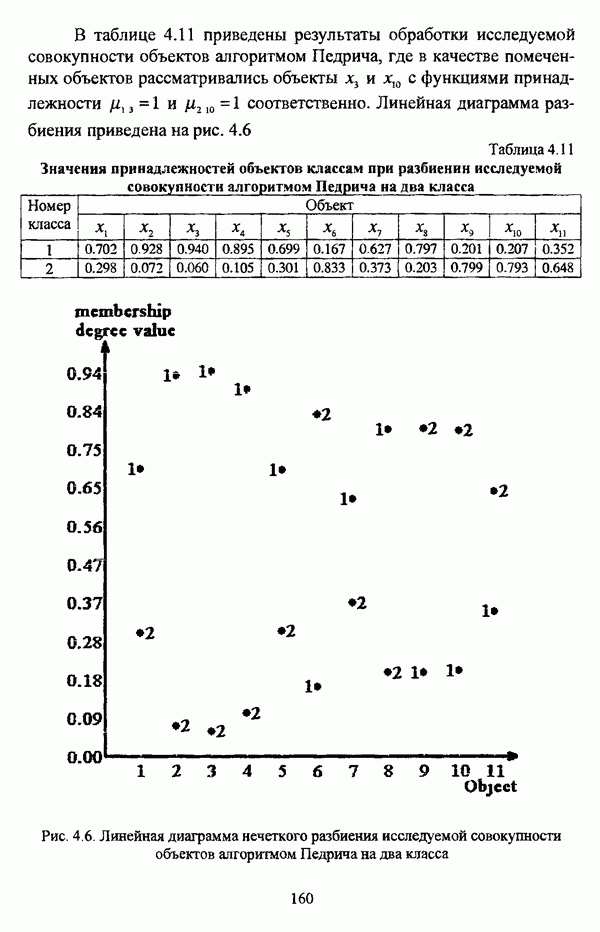
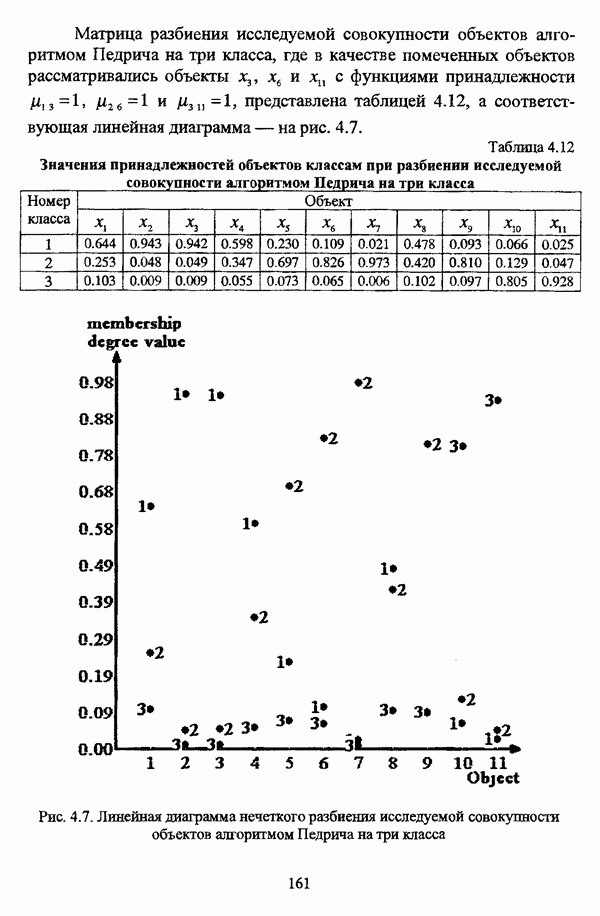
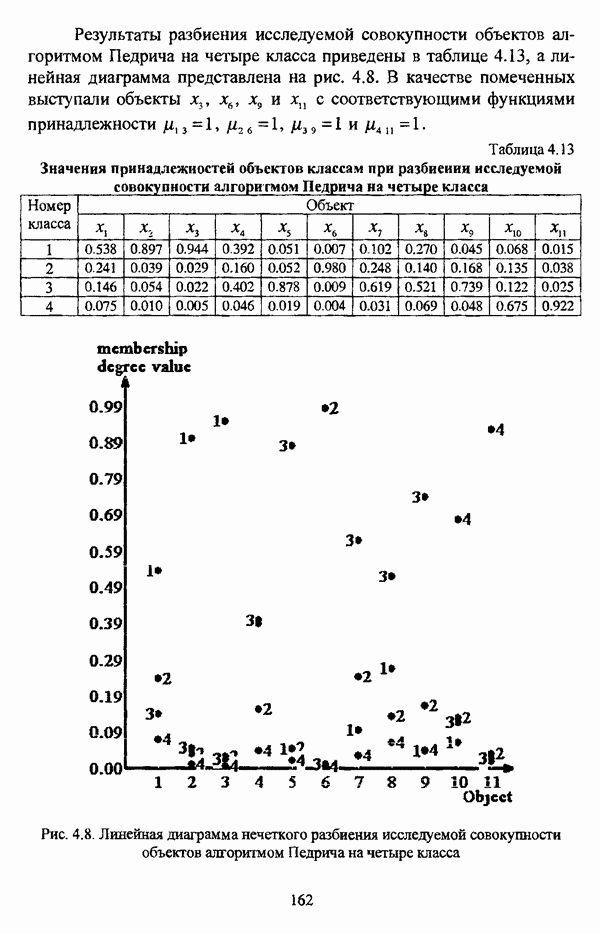
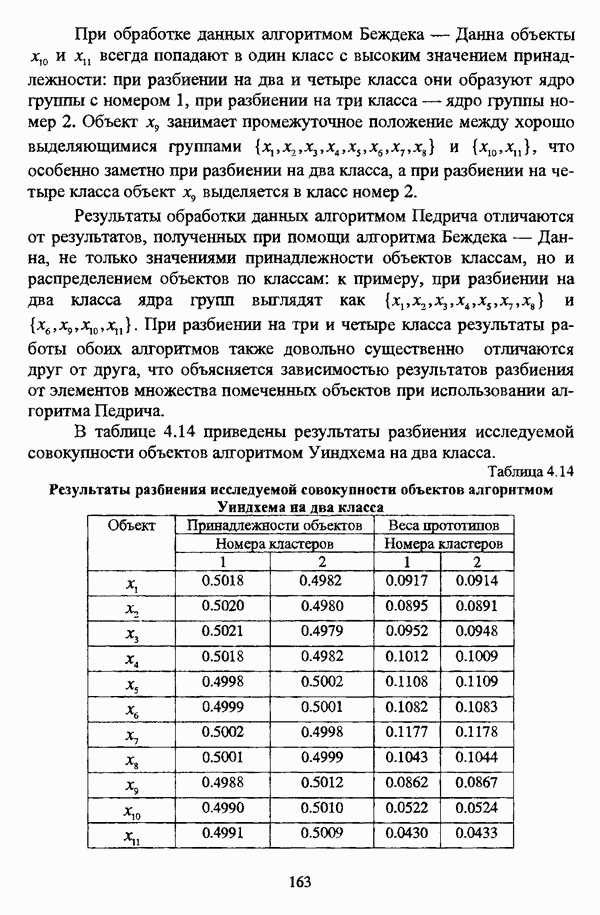
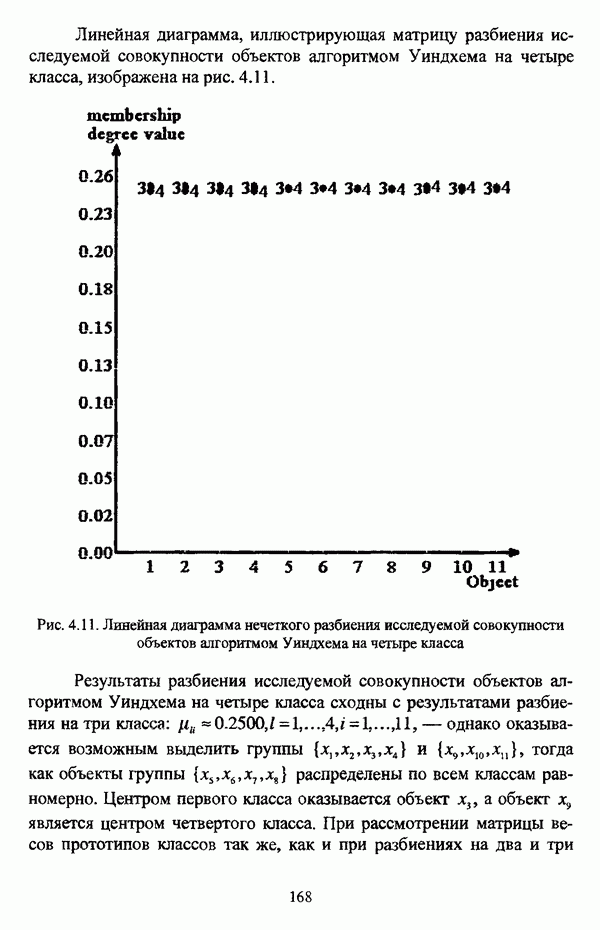
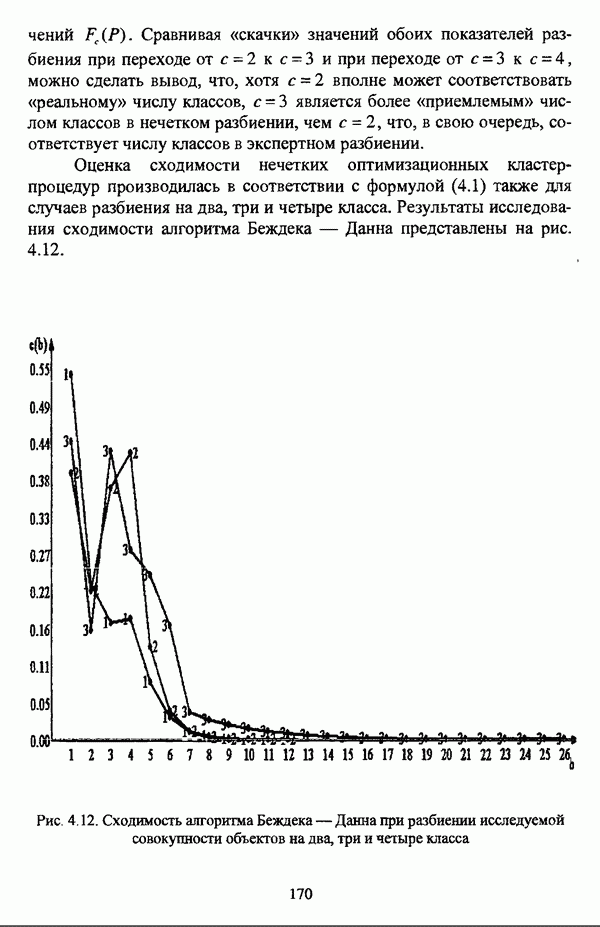
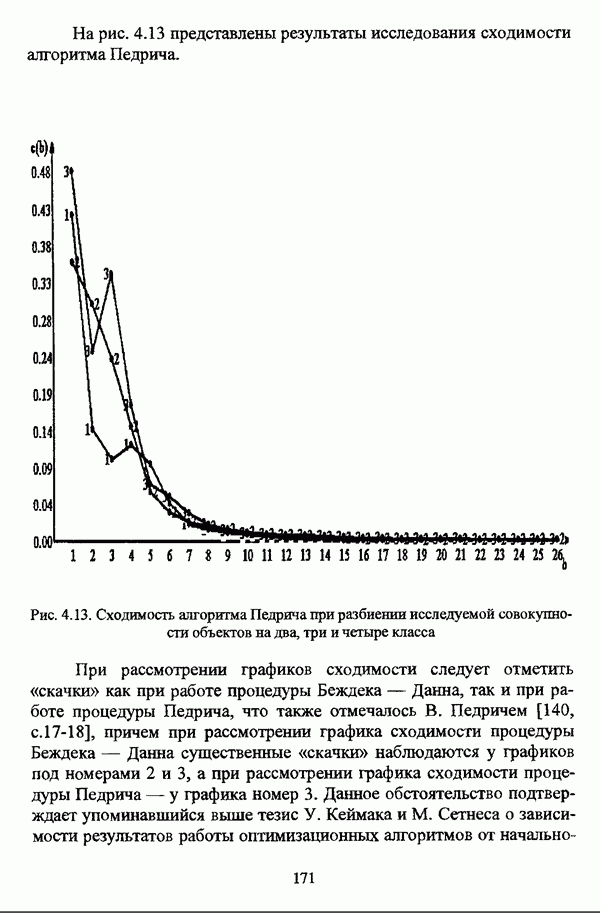
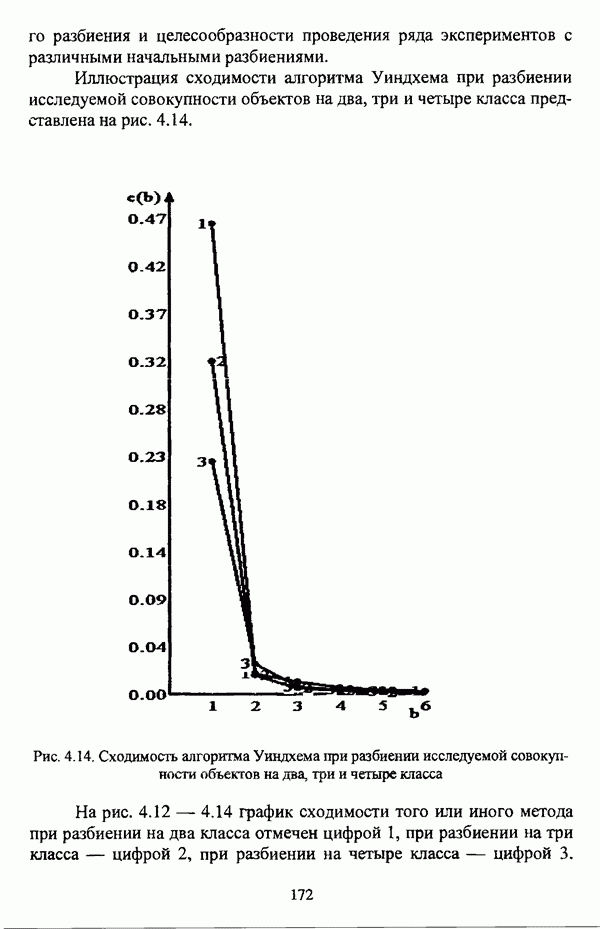
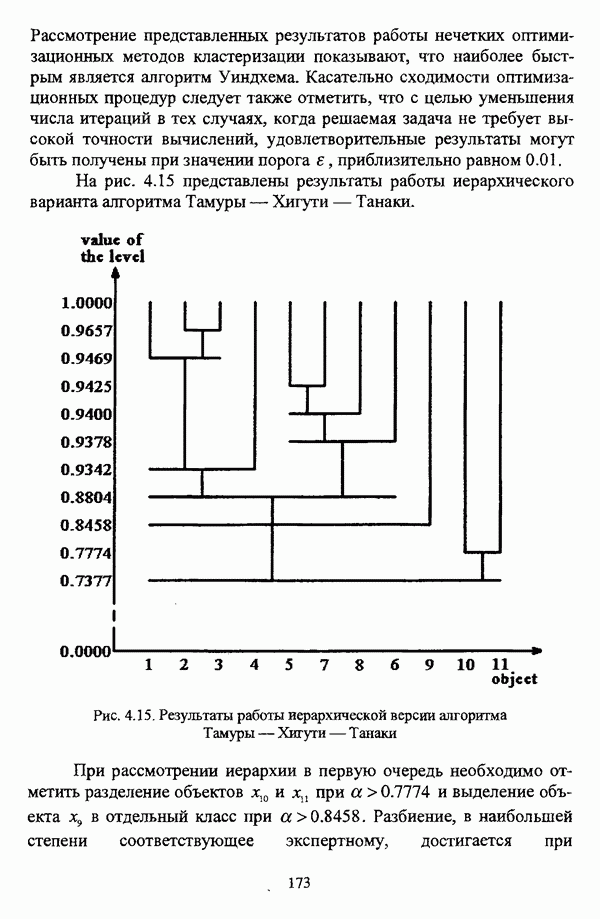
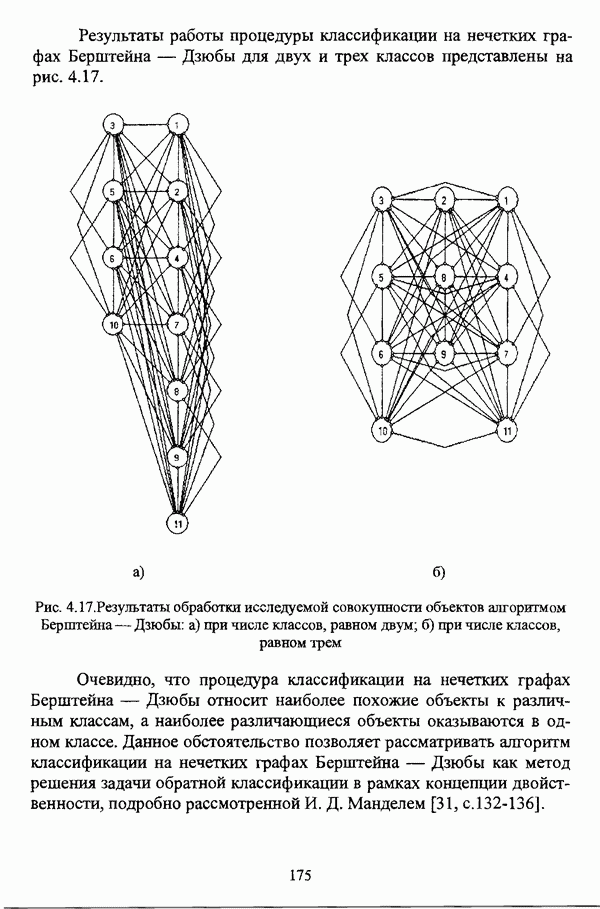
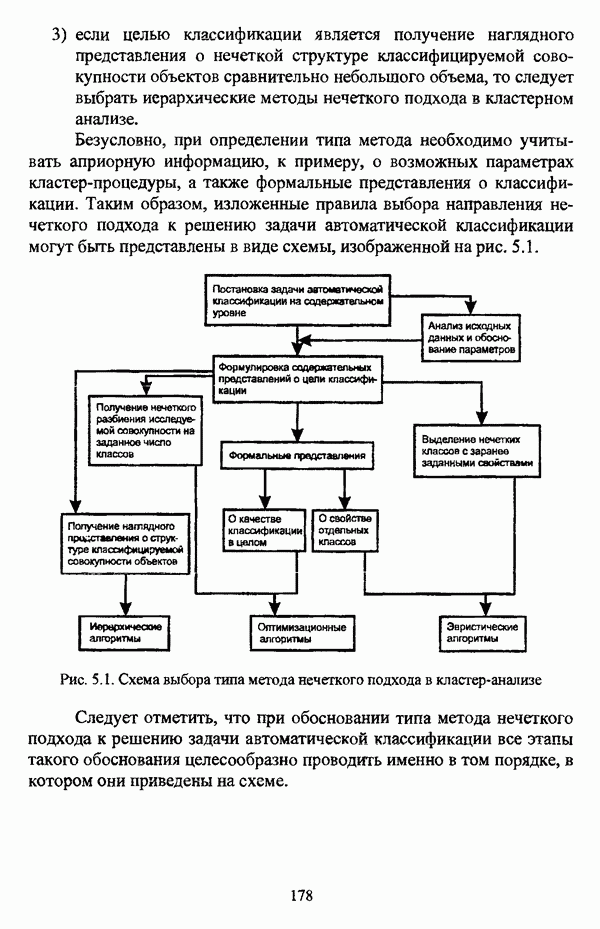
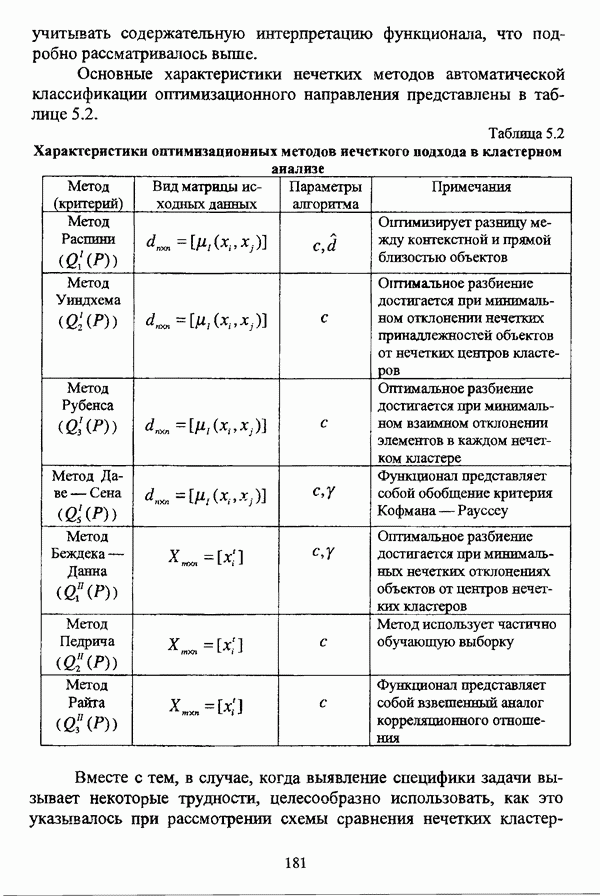
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
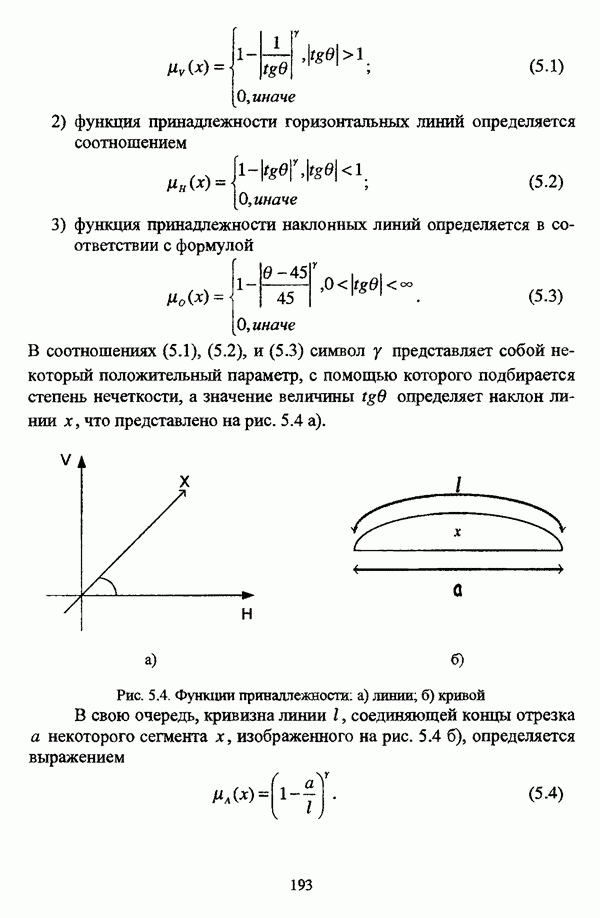
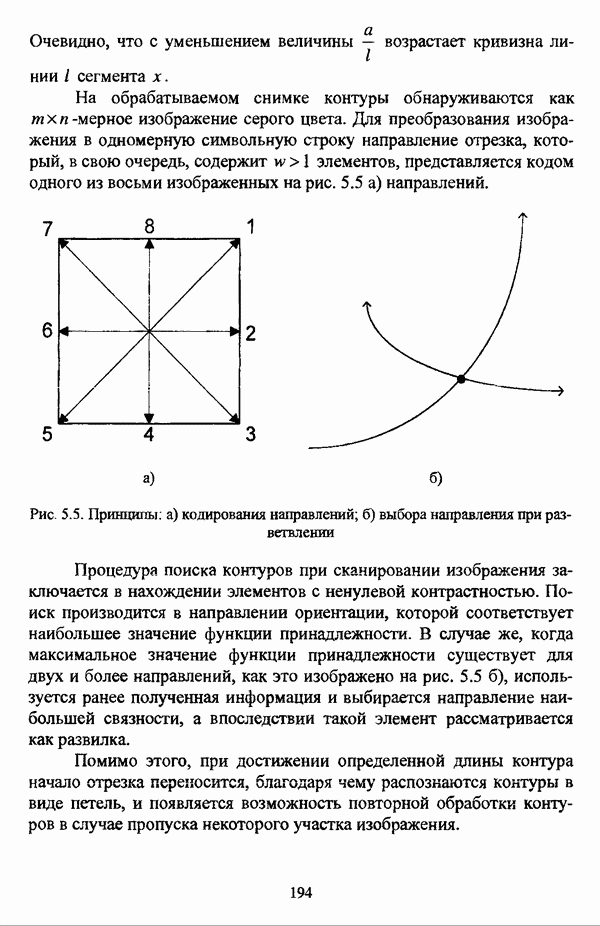
3.2.2. Описание алгоритмов
Во всех исследованиях, как правило, приводятся не только функционалы качества разбиения, но и алгоритмы поиска экстремума рассматриваемого функционала.
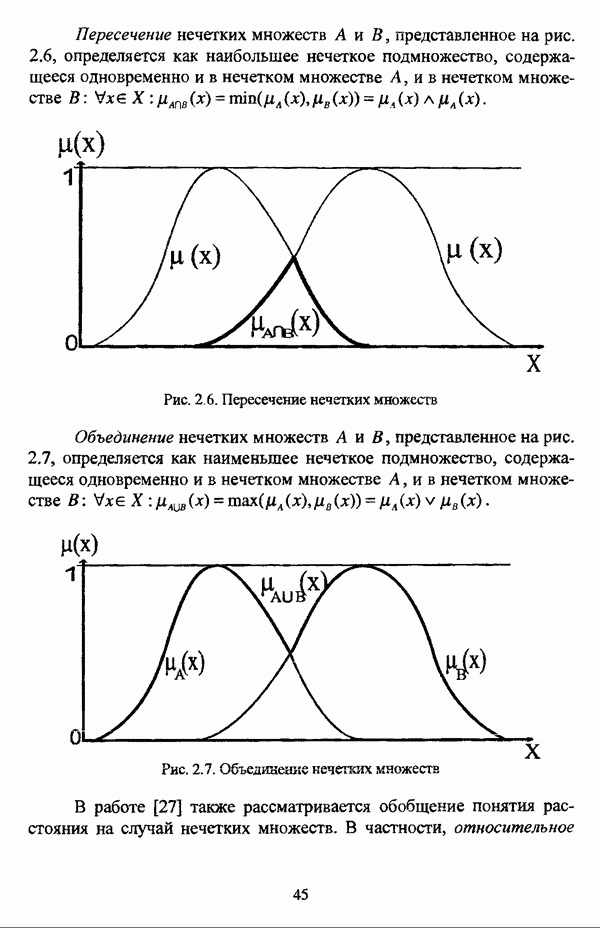
3.2.2.1. Алгоритм Распини
[150] минимизирует критерий  в виде (3.27), так что находится решение
в виде (3.27), так что находится решение

Как отмечали И. И. Елисеева и В. О. Рукавишников касательно функционала Э. Г. Распини, «поиск экстремального значения критерия качества целесообразно проводить с использованием градиентных методов, обеспечивающих быструю сходимость алгоритмов»  Дальнейшее изложение алгоритма, минимизирующего функционал
Дальнейшее изложение алгоритма, минимизирующего функционал  , основано на описании процедуры, представленном в работе [22].
, основано на описании процедуры, представленном в работе [22].
Пусть  где
где  вычисляется по формуле (3.25), а функция
вычисляется по формуле (3.25), а функция  вычисляется в соответствии с соотношением
вычисляется в соответствии с соотношением  Кроме того,
Кроме того,
для удобства преобразований можно ввести также следующие обо значения:

выражающее значение  на
на  шаге вычислительного процесса
шаге вычислительного процесса

где символом  обозначается
обозначается  на
на  шаге вычислительного процесса а также
шаге вычислительного процесса а также

так что на  шаге вычислительного процесса задача будет заключаться в нахождении
шаге вычислительного процесса задача будет заключаться в нахождении

Следует отметить, что  представляет собой дифференцируемую функцию, частные производные которой находятся по следующим формулам:
представляет собой дифференцируемую функцию, частные производные которой находятся по следующим формулам:

и, поскольку  — полином четвертой степени, то его частная производная в точке
— полином четвертой степени, то его частная производная в точке  на
на  шаге вычислительного процесса будет определяться следующим соотношением:
шаге вычислительного процесса будет определяться следующим соотношением:

где, в свою очередь,  — значение принадлежности
— значение принадлежности  объекта
объекта  кластеру на b
кластеру на b  шаге вычислительного процесса.
шаге вычислительного процесса.
Параметры алгоритма:
с — число нечетких кластеров в искомом разбиении Р;
 — порог расстояния между объектами;
— порог расстояния между объектами;
Схема алгоритма:
1. Выбираются начальное разбиение  на с нечетких классов, описываемое с непустыми функциями принадлежности, так что матрица начального разбиения
на с нечетких классов, описываемое с непустыми функциями принадлежности, так что матрица начального разбиения  имеет с строк и
имеет с строк и  столбцов; присваиваются значения
столбцов; присваиваются значения 
2. Вычисляется  в соответствии с соотношением (3.86) и
в соответствии с соотношением (3.86) и  соответствии с соотношением (3.87); вычисляется значение
соответствии с соотношением (3.87); вычисляется значение  и сравнивается со значением
и сравнивается со значением  : вычисляется некоторое пороговое значение
: вычисляется некоторое пороговое значение  если
если  )
)  , так что
, так что  алгоритм прекращает работу;
алгоритм прекращает работу;
3. Полагается  для
для  объекта вычисляются значения частных производных
объекта вычисляются значения частных производных  по формулам (3.92), (3.90), (3.91) соответственно;
по формулам (3.92), (3.90), (3.91) соответственно;
4. Если выполняется приближенное равенство  то осуществляется переход на шаг 7; в противном случае осуществляется переход на шаг 5;
то осуществляется переход на шаг 7; в противном случае осуществляется переход на шаг 5;
5. Для определения направления движения отыскивается наименьший положительный корень полинома  где
где

где, в свою очередь,

причем относительные размеры  нечетких кластеров, номера которых устанавливаются по формулам (3.93) и (3.94), определяются по формуле
нечетких кластеров, номера которых устанавливаются по формулам (3.93) и (3.94), определяются по формуле 
Поскольку  то в силу правила Декарта полином
то в силу правила Декарта полином  имеет один или три положительных корня; отыскивается наименьший положительный корень
имеет один или три положительных корня; отыскивается наименьший положительный корень  полинома
полинома  и сопоставляется с
и сопоставляется с  так что
так что 
6. Производится коррекция вектора степеней принадлежности  объекта в соответствии со следующим правилом:
объекта в соответствии со следующим правилом:

где символами  обозначены измененные значения наибольшей и наименьшей степеней принадлежности
обозначены измененные значения наибольшей и наименьшей степеней принадлежности  объекта; с учетом коррекции степеней принадлежности (3.95) и (3.96) производится также коррекция соответствующих
объекта; с учетом коррекции степеней принадлежности (3.95) и (3.96) производится также коррекция соответствующих  полагается
полагается 
7. Если просмотрены не все  то полагается
то полагается  и осуществляется переход на шаг 3, в противном случае производится проверка изменения матрицы разбиения
и осуществляется переход на шаг 3, в противном случае производится проверка изменения матрицы разбиения  если имели место изменения
если имели место изменения  то полагается
то полагается  и осуществляется переход на шаг 2, в противном случае полагается
и осуществляется переход на шаг 2, в противном случае полагается  и алгоритм прекращает работу.
и алгоритм прекращает работу.
В работах [151], [152], [39] представлены результаты, развивающие идеи, изложенные в [149], [150].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
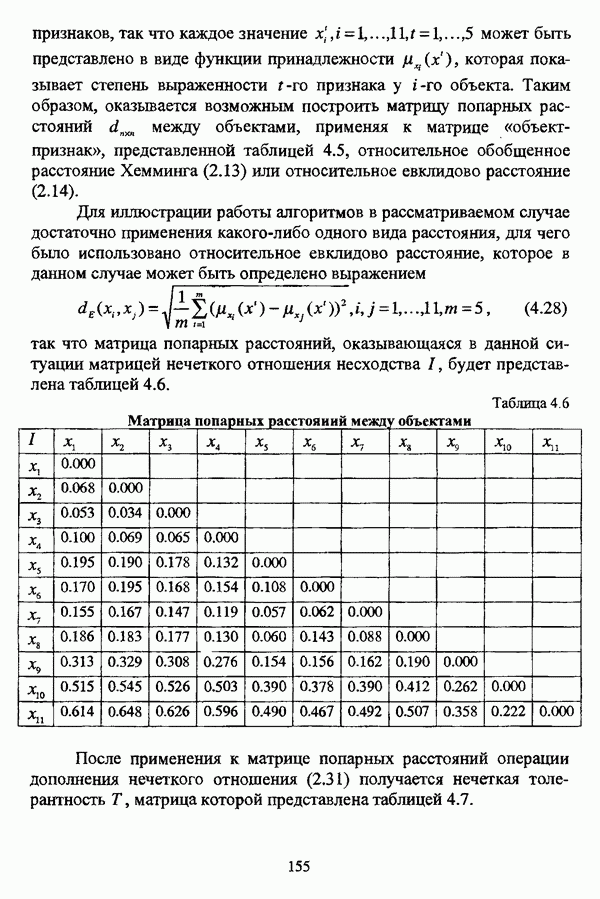
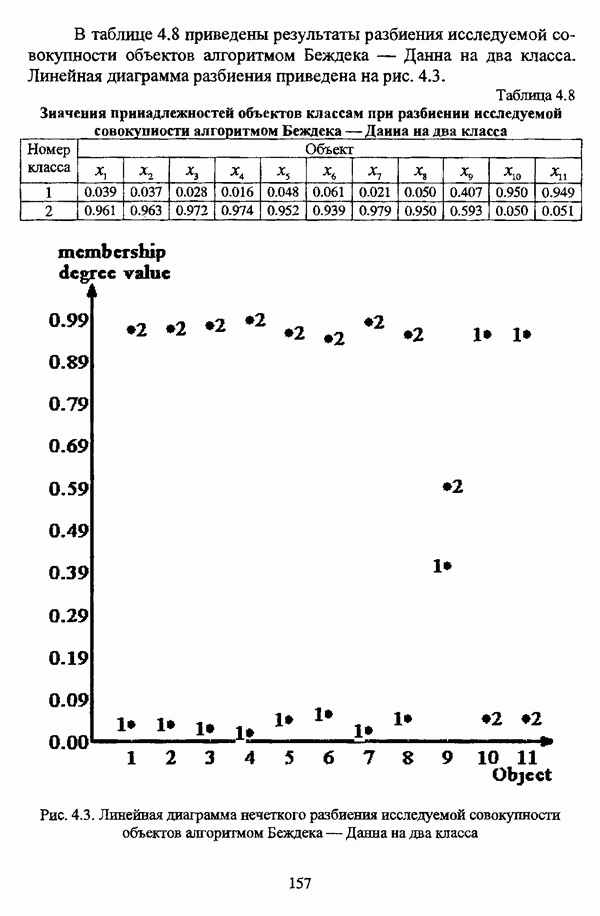
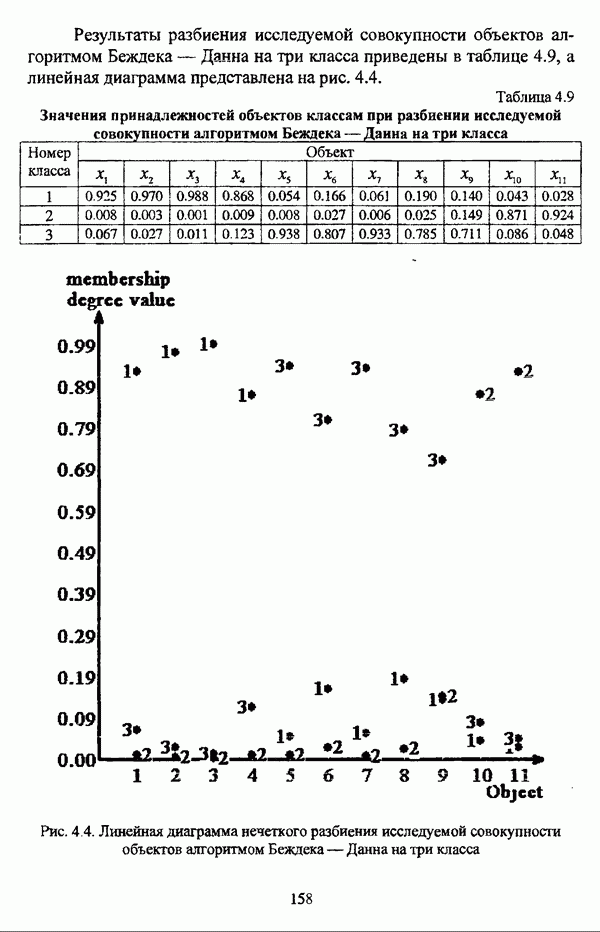
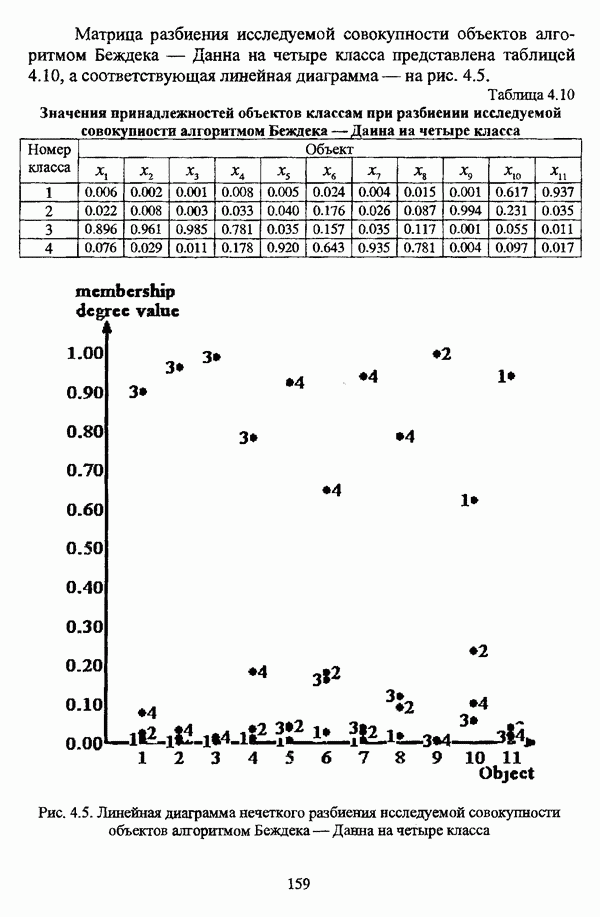
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
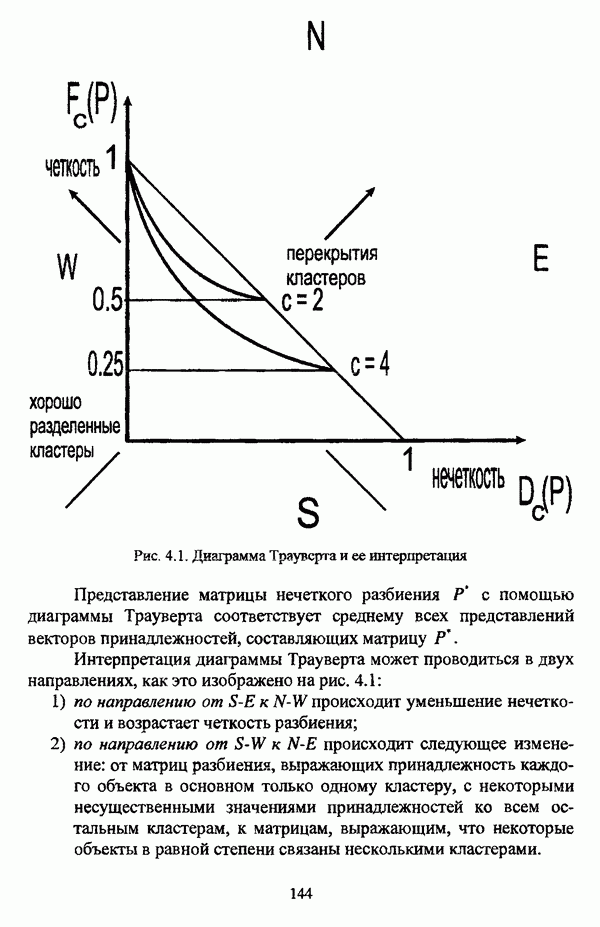
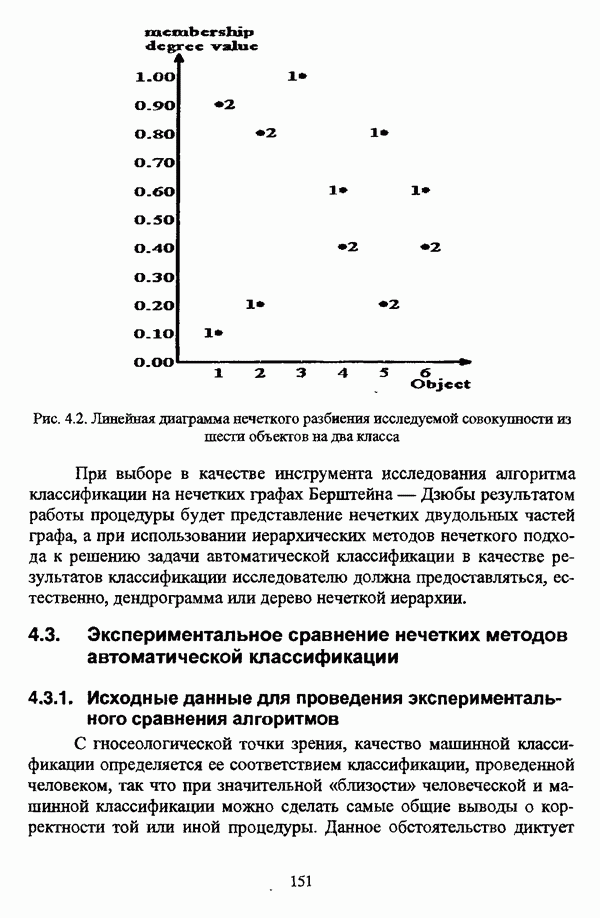
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
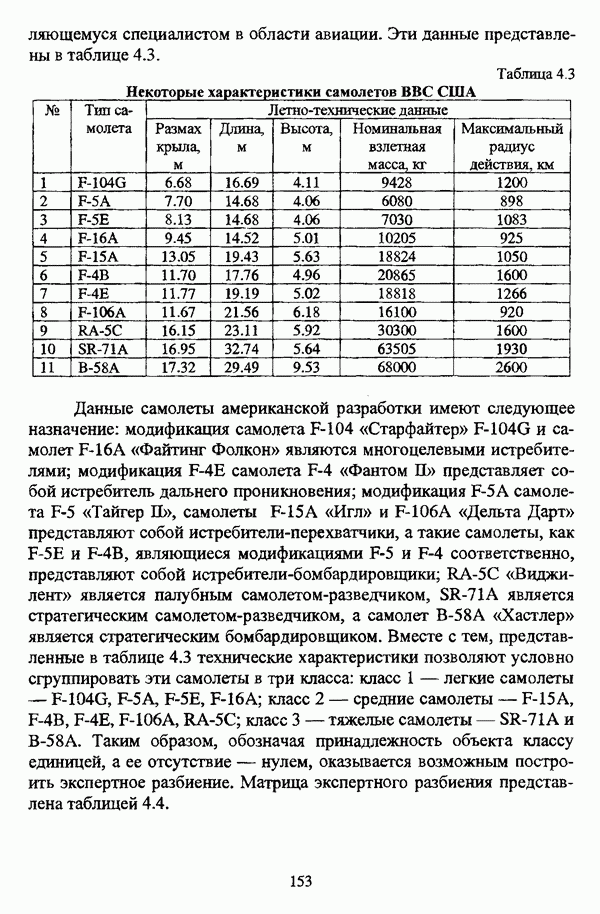
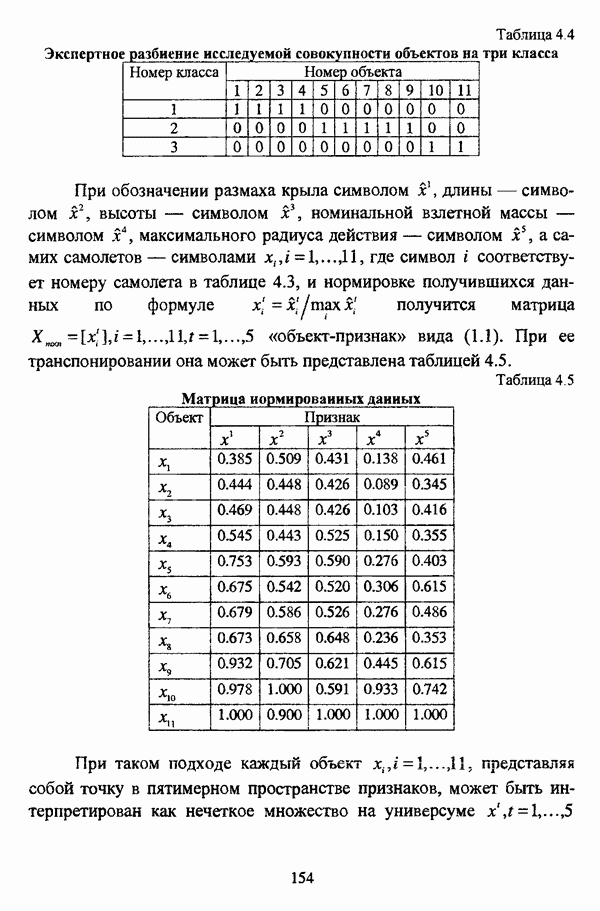
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы