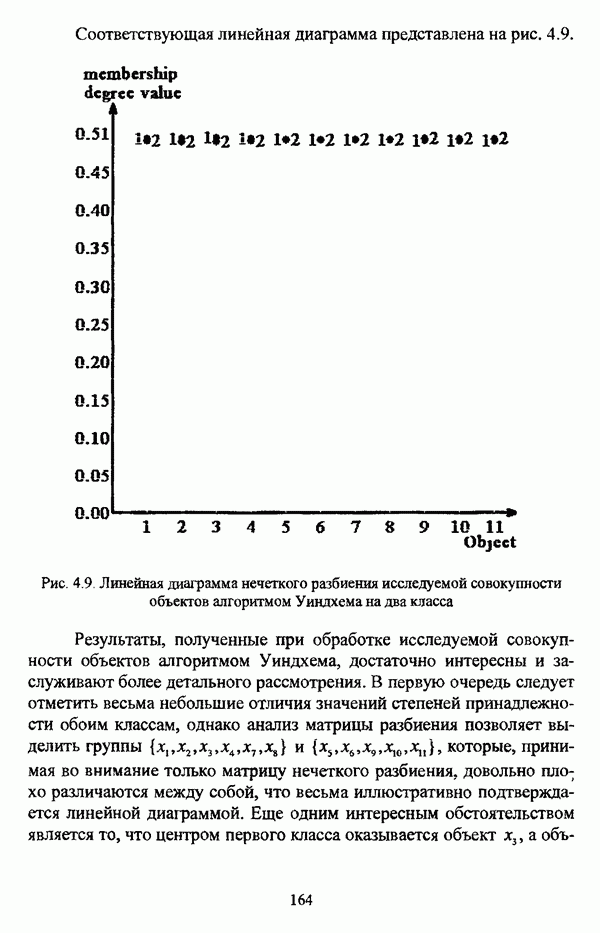
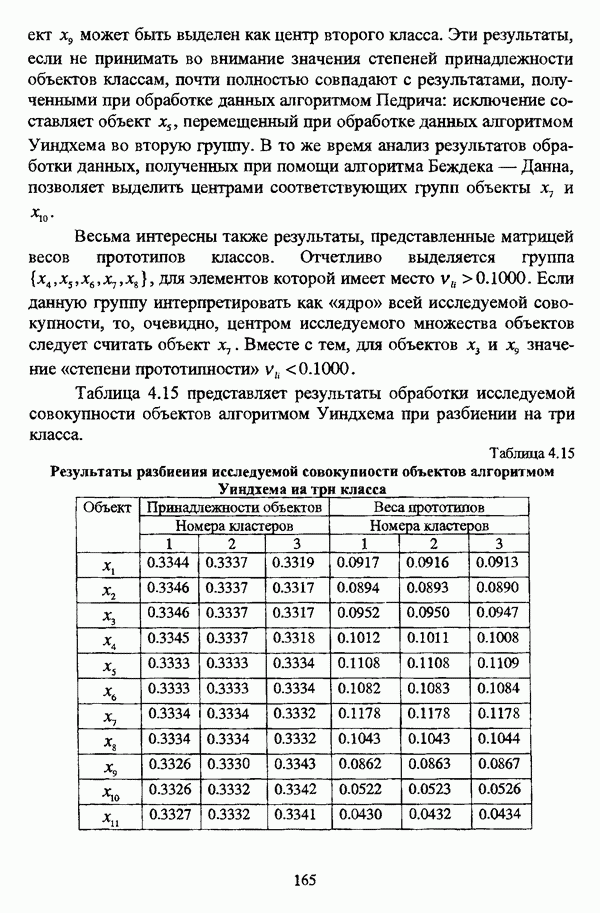
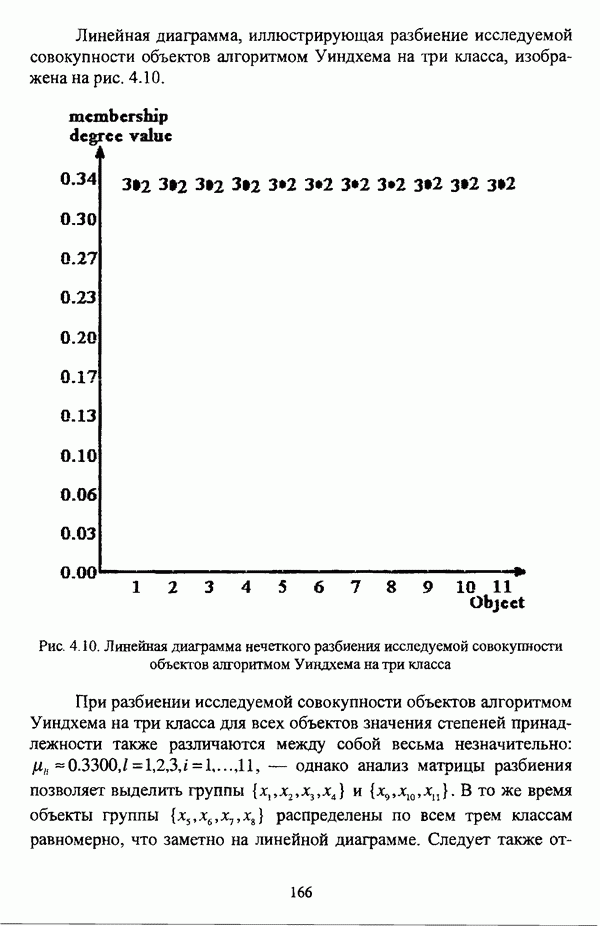
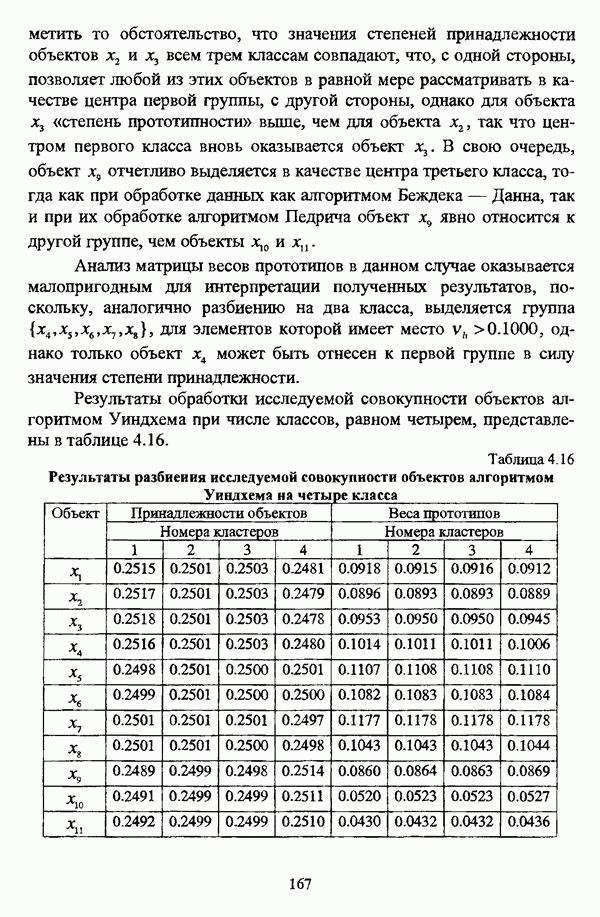
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Список литературы
1. Аверкин А Н. Нечеткое отношение моделирования и его использование для классификации и аппроксимации в нечетких лингвистических пространствах // Известия АН СССР. Техническая кибернетика. — 1982.— № 2.— с.215-217.
2. Аверкин А.Н., Тарасов В.Б. Нечеткое отношение моделирования и его применение в психологии и искусственном интеллекте. — М.: Вычислительный центр АН СССР, 1986. —36с.
3. Батыршин И.З. Кластеризация на основе размытых отношений сходства // Управление при наличии расплывчатых категорий: Тезисы докладов 3-го научно-технического семинара. — Пермь, 1980,- с.25-27.
4. Батыршин И.З., Вагин В.Н. Алгоритмы кластеризации, основывающиеся на понятии неразличимости объектов Н Управление при наличии расплывчатых категорий: Тезисы докладов 4-го научно-технического семинара, — Фрунзе, 1981.— с.79.
5. Батыршин И.З. Иерархическая кластеризация на основе нечисловой информации о близости // Нечисловая статистика, экспертные оценки и смежные вопросы: Тезнсы докладов П Всесоюзной конференции по статистическому и дискретному анализу нечисловой информации и экспертным оценкам. — Таллинн, 1984.— е.277.
6. Батыршин И.З. Иерархические алгоритмы выделения классов толерантности в задачах классификации // Применение вероятностно-статистических методов в бурении и нефтедобыче: Тезисы докладов IV Всесоюзной конференции. — Баку, 1984.— с. 16-17.
7. Батыршин И.З., Халитов Р.Г. Иерархические алгоритмы кластеризации на базе классов толерантности // Повышение эффективности технологических процессов химических, нефтехимических и биотехнологических производств: Тезисы докладов Республиканской научно-практической конференции. — Казань: КХТИ, 1986.—с.109.
8. Батыршин И.З., Халитов Р.Г. Иерархическая классификация на базе классов толерантности // Исследование операций и аналитическое проектирование в технике.—Казань: КАИ, 1987.— с. 105-110.
9. Батыршин И.З. О декомпозиции нечетких отношений эквивалентности // Математические и экспериментальные методы синтеза технических систем. — Казань: КАИ, 1989.— с.21-27.
10. Батыршин И.З., Морозов В.А., Халитов Р.Г. КЛАСТИЕР — программная система иерархической классификации // Статистический и дискретный анализ данных и экспертное оценивание: Материалы IV Всесоюзной школы-семинара.— Одесса, 1991.— с.319-321.
И. Берштейн Л.С., Дзюба ТА. Решение задач классификации на нечетких графах И Новости искусственного интеллекта.— 2000.— № 3.— с. 113-121.
12. Блишун А.Ф. Отношение сходства нечетких понятий-классов // Управление при наличии расплывчатых категорий И Тезисы докладов 4-го научно-технического семинара.— Фрунзе, 1981.— с,79.
13. Бородкин Л И. Алгоритм построения линейной разделяющей функции с использованием нечетких разбиений // Компьютерный анализ данных и
моделирование: Сборник ваучгых статей V Международной конференции (8-12 июня 1998 года, Минск). 4&vib 3: А-К / Под ред. проф. С.А. Айвазяна и проф. Ю.С. Харина. — Мн.: БГУ, 1998.— с.69-76.
14. Вятченин Д. А. Формы проявления нечеткости // Гуманитарно-экономический вестник. —1998. —№ 1. — с.66-69.
15. Вятченин Д.А. Гносеологические аспекты применения теории нечетких множеств в кластер-анализе // «Великие преобразователи естествознания: Исаак Ньютон»: Тезисы докладов XVI Международных чтений. 29-30 ноября 2000 г., Минск / БГУИР — Минск, 2000.-е. 130-133.
16. Вятченин Д. А. Содержательная интерпретация иечетких отношении сходства. // Полигнозис. — 2001. —№ 1. — с. 20-25.
17. Вятченин Д. А. О пересечении нечетких кластеров // Интегрированные модели и мягкие вычисления в искусственном интеллекте: Сборник трудов Международного научно-практического семинара, Коломна, 17-18 мая 2001. — М.: Наука, Физматлиг, 2001.—с. 122-126.
18. Вятченин Д.А. Общая схема выбора типа метода и алгоритма нечеткого подхода в кластерном анализе // Новые информационные технологии: Материалы V Международной научной конференции НИТэ’2002 (Минск, 29-31 октября 2002 г.). Т.1. / Под ред. А Н. Морозевича, Н.Н. Говядиновой, А.М. Зеневич, Л.С. Черепицы. — Минск: БГЭУ, 2002. — с.102-107.
19. Вятченин Д А Основные концепции неопределенности в задачах автоматической классификации // Полигнозис. — 2002. — № 3. — с. 160-167.
20. Давидовская И.A., Kovalik S. Применение нечеткого дерева решений для задач классификации // Новые информационные технологии: Материалы V Международной Научной Конференции НИТэ’2002 (Минск, 29-31 октября 2002 г.). Т.1. / Под ред. А.Н. Морозевича, Н.Н. Говядиновой, А.М. Зеневич, Л.С. Черепицы. —Минск: БГЭУ, 2002. —с. 179-183.
21. Данлоп С. Азбука звездного неба / Пер. с англ. — М.: Мир, 1990.— 240 с.
22. Елисеева И.И., Рукавшпников В.О. Грушшровка, корреляция, распознавание образов (Статистические методы классификации и измерения связей) — М.: Статистика, 1977.— 144 с.
23. Жук Е Е., Харин Ю.С. Устойчивость в кластер-анализе многомерных наблюдений. — Мн.: Белгосуниверситет,1998.— 240 с.
24. Заде Л А. Понятие лингвистической переменной и его применение к принятию приближенных решений / Пер. с англ.; под ред. Н.Н.Моисеева и С.А.Орловского. —М: Мир, 1976.—165 с.
25. Заде Л.А. Размытые множества и их применение в распознавании образов и кластер-анализе // Классификация и кластер / Под ред. Дж. Вэн Райзина; пер с англ.; под ред. Ю.И.Журавлева. — М: Мир, 1980.— с. 208-247.
26. Каркищенко А.Н., Бутенков С А., Кривша В.В. Нечеткие геометрические признаки в задачах классификации и кластеризации // Новости искусственного интеллекта.— 2000.— №3.— с. 129-133.
27. Кофман А. Введение в теорию иечетких множеств / Пер. с фр.; Под ред. С.И. Травкина.— М.: Радио и связь, 1982. —432 с.
28. Кузьмин В.Б. Построение групповых решений в пространствах четких и нечетких бинарных отношений. — М.: Наука, Гл. ред. физ.-мат. лит., 1982. — 168 с.
29. Лейбкинд А.Р., Рудник Б.Л., Тихомиров А.А. Математические методы и модели формирования организационных структур управления. — М.: МГУ, 1982.
— 232 с.
30. Литтл Р.Дж.А., Рубин Д.Б. Статистический анализ данных с пропусками / Пер. с англ. —М.: Финансы и статистика, 1990.— 336 с.
31. Мандель И.Д. Кластерный анализ.— М.: Финансы и статистика, 1988.
— 176 с.
32. Миленький А. В. Классификация сигналов в условиях неопределенности. — М.: Сов. радио, 1975—328 с.
33. Нгуен М.Х. Применение нечетких отношений в классификации // Нечеткие системы поддержки принятия решений: Сборник научных трудов.— Калинин: Калининский государственный университет, 1989. •— с. 99-107.
34. Нечеткие множества в моделях управления и искусственного интеллекта / А.Н.Аверкин, И.З.Батыршин, А.Ф.Блишун и др.; под ред. Д.А.Поспелова. — М.: Наука, гл. ред. физ.-мат. лит., 1986. — 312с.
35. Обработка нечеткой информации в системах принятия решений / А.Н Борисов, А,В. Алексеев. Г.В. Меркурьева и др. — М/ Радио и связь, 1989 —304с.
36. Ожегов С.И. Словарь русского языка: Ок. 57000 слов / Под ред. Н.Ю.Шведовой. — 17-е изд., стереотип. — М.: Русский язык, 1985. —797с.
37. Прикладная статистика: Классификация и снижение размерности: Справ, изд./ С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин; Под ред. С.А. Айвазяна.— М.: Финансы и статистика, 1989.— 607 с.
38. Прикладные нечеткие системы: Пер. с япон. / К.Асаи, Д.Ватада, С.Иваи и др.; под ред. Т.Тэрано, К.Асаи, М.Сугэно. — М.: Мир, 1993. —368с.
39. Руспини Э.Г. Последние достижения в нечетком кластер-анализе // Нечеткие множества и теория возможностей: Последние достижения / Под ред. Рональда Р. Ягера; Пер. с англ. В.Б. Кузьмина; Под ред. С.И. Травкина.— М: Радио и связь, 1986.— с. 114-132.
40. Смоляк С.А., Титаренко Б.Н. Устойчивые методы оценивания. — М.: Статистика, 1982.— 208 с.
41. Тарасов В.Б., Желтов С.Ю., Степанов А.А. Нечеткие модели в обработке изображений: обзор зарубежных достижений if Новости искусственного интеллекта.— 1993.— № 3.— с.40-64.
42. Фукунага К. Введение в статистическую теорию распознавания образов / Пер. с англ. — М.: Наука, 1979.— 368 с.
43. Цихош Э. Сверхзвуковые самолеты: Справочное руководство / Пер. с польск.; под ред. В.Г. Микеладзе и Е.В. Зябрева. — М.: Мир, 1983.— 432 с.
44. Шлезингер М. И. О самопроизвольном различении образов // Читающие автоматы. — Ю*ев: Навукова думка 1965.— с. 38-65.
45. Anderson Е. The Irises of the Gaspe Peninsula // Bulletin of the American Iris Society.— 1935.—Vol. 59.—pp.2-5.
46. Backer E. Cluster Analysis by Optimal Decomposition of Induced Fuzzy Sets. Delft: Delft University Press; 1978.
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы