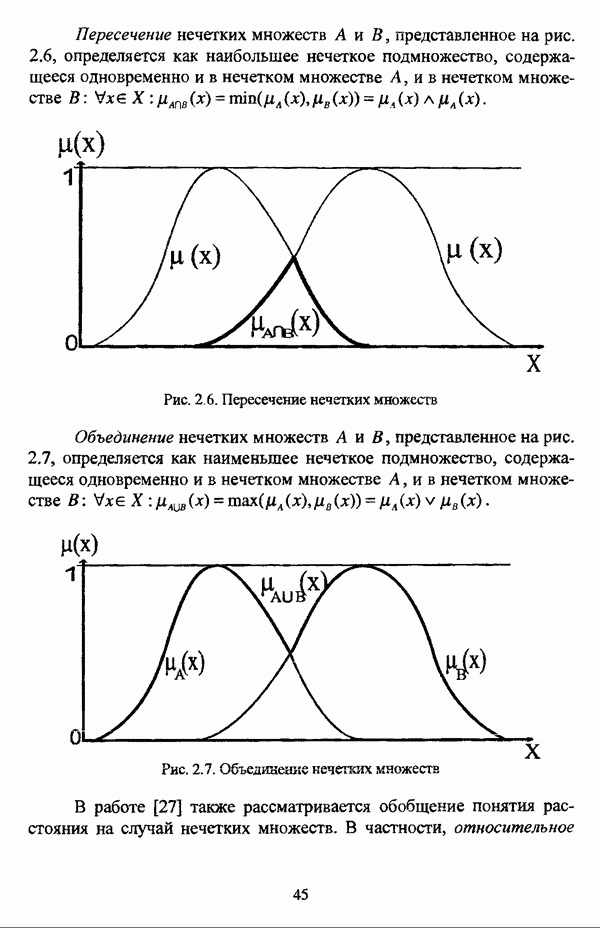
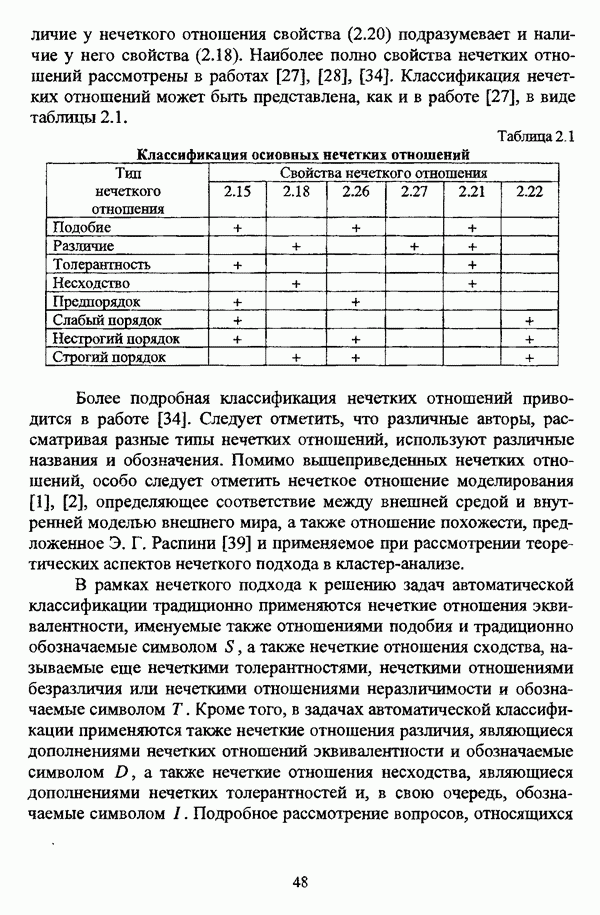
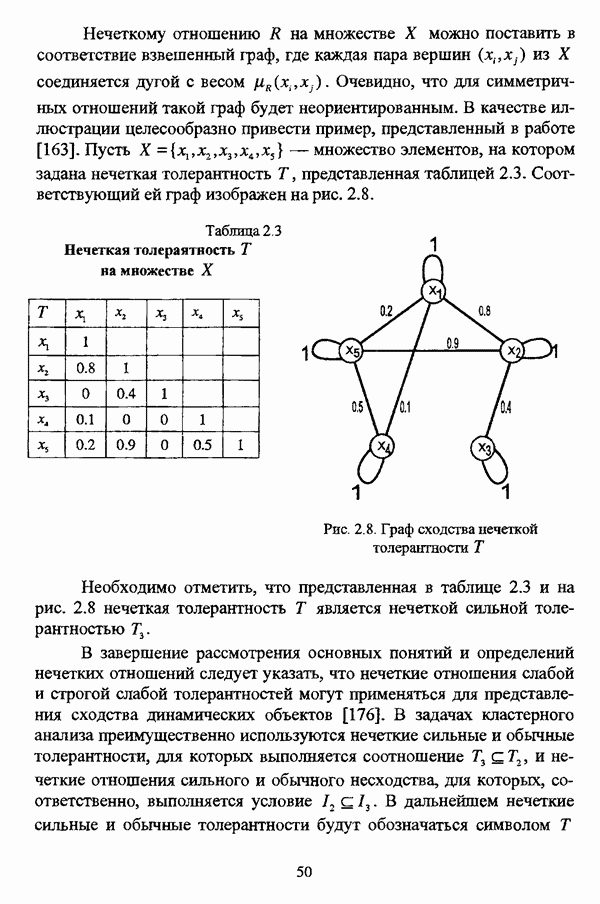
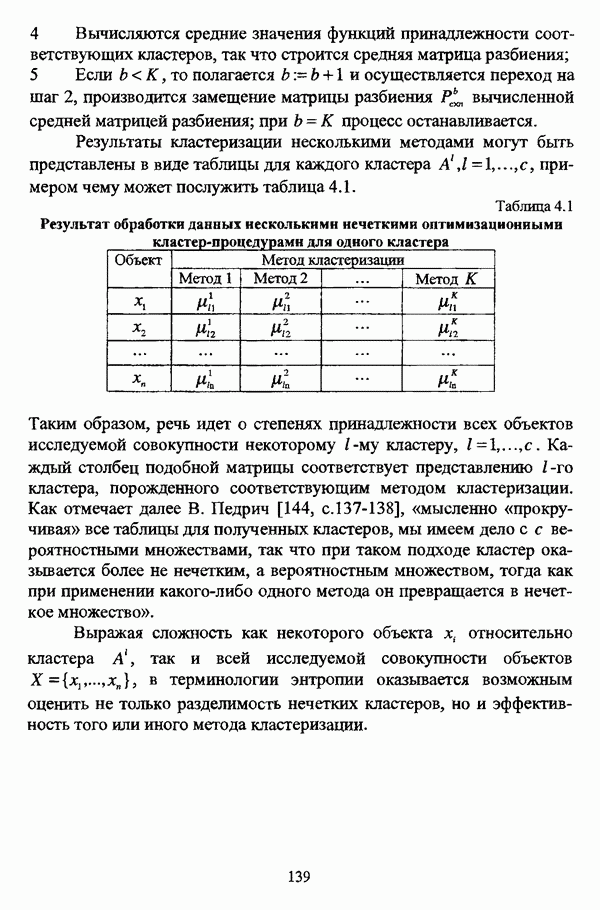
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2.2.7. Другие алгоритмы оптимизационного подхода
подробно рассматриваются в работах [46], [64], [85], [101], [108], [167], [185] и, в основном, представляют собой различные версии рассмотренных выше нечетких оптимизационных кластер-процедур. Дж. Беждеком [59] рассматриваются различные модификации критерия Q” (Р) и соответствующие им алгоритмы нахождения оптимума, такие, к примеру, как FCV алгоритм (fuzzy с-varieties). Алгоритм, предложенный Д. Е. Густафсоном и В. С. Кесселем [92] и минимизирующий критерий  , где в качестве функции
, где в качестве функции  используется квадрат расстояния Махаланобиса (3,47), известен в литературе как GK алгоритм [109].
используется квадрат расстояния Махаланобиса (3,47), известен в литературе как GK алгоритм [109].
Некоторые подходы используют методы нечеткой математики для усовершенствования статистических процедур; наиболее интересным с этой точки зрения представляется метод, предложенный Я. В. Овсиньским и С. Задрожным в работе [133], совершенствующий процедуру, отыскивающую субоптимум целевой функции [132], на основе шести предложенных правил.
Ниже рассмотрены некоторые малоизвестные процедуры, представляющие интерес с теоретической точки зрения, а также ряд модификаций рассмотренных выше методов.
Алгоритм Распини, минимизирующий один из функционалов  или
или  предложен в работе [150, с.324] и используется в описанном выше алгоритме минимизации критерия
предложен в работе [150, с.324] и используется в описанном выше алгоритме минимизации критерия  , так что его
, так что его
рассмотрение оказывается нелишним с теоретической точки зрения. Однако перед изложением общей схемы процедуры следует привести формулировки двух теорем, используемых в ней.
Как и функционал  , функционалы
, функционалы  представляют собой дифференцируемые функции, частные производные которых находятся по формулам (3.70), (3.71), (3.72):
представляют собой дифференцируемые функции, частные производные которых находятся по формулам (3.70), (3.71), (3.72):

Теорема 3.1. Если для некоторого разбиения  описываемого функциями принадлежности
описываемого функциями принадлежности  выполняется равенство
выполняется равенство  то данное разбиение Р определяет стационарную точку функции
то данное разбиение Р определяет стационарную точку функции  или
или  есть для всех возможных направлений
есть для всех возможных направлений  , таких, что
, таких, что

выполняется 
Теорема 3.2. Если при условиях предыдущей теоремы для некоторого  вьшолняется
вьшолняется  то выбираются
то выбираются  , а также
, а также  такие, что
такие, что  и ивдекс I не совпадает с индексами
и ивдекс I не совпадает с индексами  нечеткого кластера, и
нечеткого кластера, и 
Параметры алгоритма:
с — число нечетких кластеров в искомом разбиении Р;
Схема алгоритма:
1. Для некоторого разбиения  описываемого функциями принадлежности
описываемого функциями принадлежности  некоторая точка
некоторая точка  фиксируется, так что
фиксируется, так что  и для
и для  объекта вычисляются значения частных производных
объекта вычисляются значения частных производных 
2. Из множества значений частных производных  вычисляются
вычисляются 
3. Если выполняется равенство  то шаги 1 и 2 повторяются для всех
то шаги 1 и 2 повторяются для всех 
4. Если для некоторой j-й точки,  выполняется
выполняется  то выполняются вычисления в соответствии с
то выполняются вычисления в соответствии с
условием теоремы 3.2;
5. Если для всех  выполняется равенство
выполняется равенство  то найденная точка является оптимальной.
то найденная точка является оптимальной.
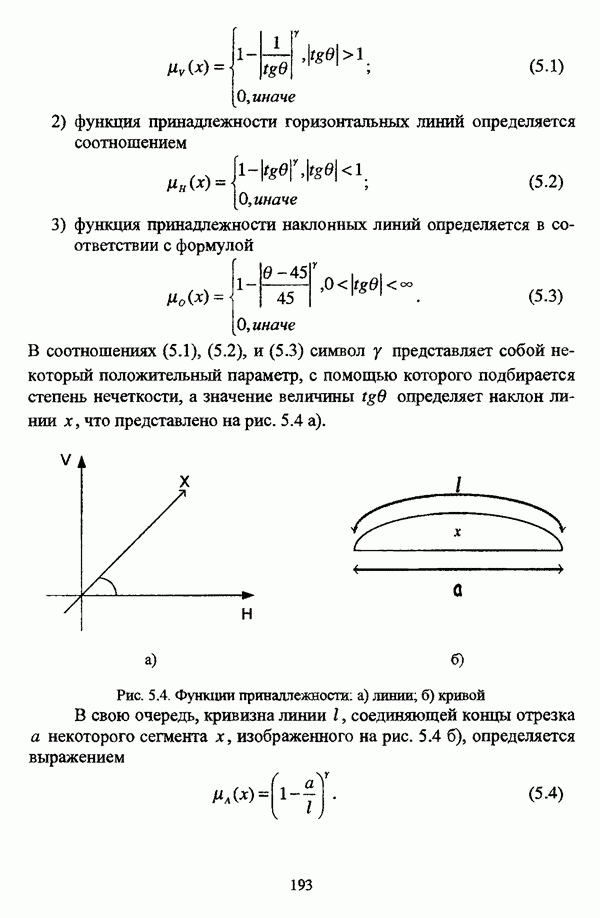
Теоремы 3.1 и 3.2 показывают, что предложенный градиентный метод сходится при указанных ограничениях. Важность рассмотренного метода заключается в том, что минимизация функционала достигается изменением значений принадлежности  в некоторой точке
в некоторой точке  при фиксированных значениях
при фиксированных значениях  а значение
а значение  последовательно изменяется на каждом шаге. Усовершенствованный вариант процедуры предусматривает цикл, повторяющий шаг 4 процедуры для фиксированной точки
последовательно изменяется на каждом шаге. Усовершенствованный вариант процедуры предусматривает цикл, повторяющий шаг 4 процедуры для фиксированной точки  до тех пор, пока не выполняется равенство
до тех пор, пока не выполняется равенство  после чего происходит изменение значения
после чего происходит изменение значения 
В работе  также рассматривается процедура, минимизирующая функционалы
также рассматривается процедура, минимизирующая функционалы  одновременно. Данная процедура устанавливает связь между рассмотренной процедурой минимизации одного из функционалов
одновременно. Данная процедура устанавливает связь между рассмотренной процедурой минимизации одного из функционалов  или
или  с одной стороны, и процедурой минимизации функционала
с одной стороны, и процедурой минимизации функционала  — с другой, и, хотя и представляет интерес с теоретической точки зрения, ее детальное рассмотрение из-за достаточно высокой сложности и громоздкости нецелесообразно.
— с другой, и, хотя и представляет интерес с теоретической точки зрения, ее детальное рассмотрение из-за достаточно высокой сложности и громоздкости нецелесообразно.
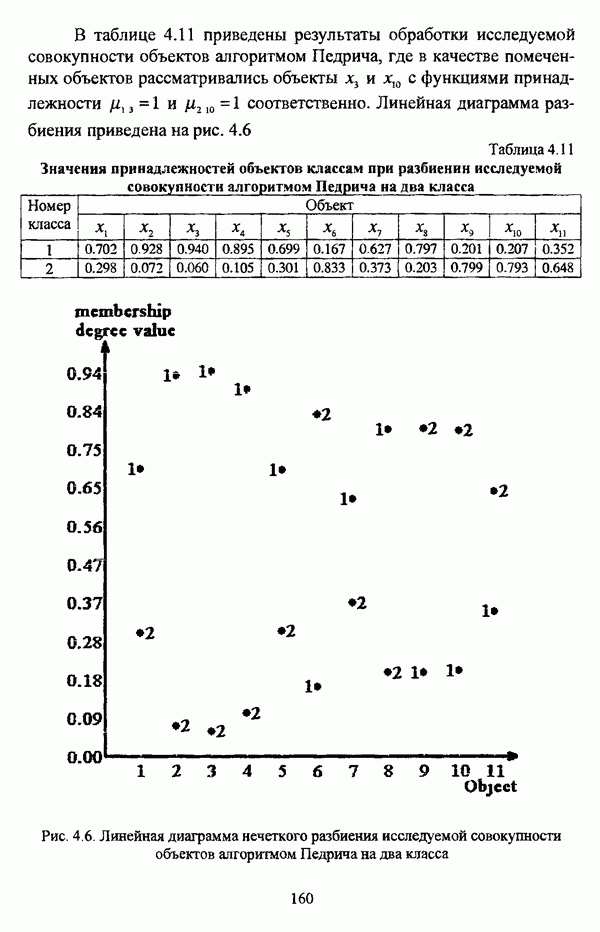
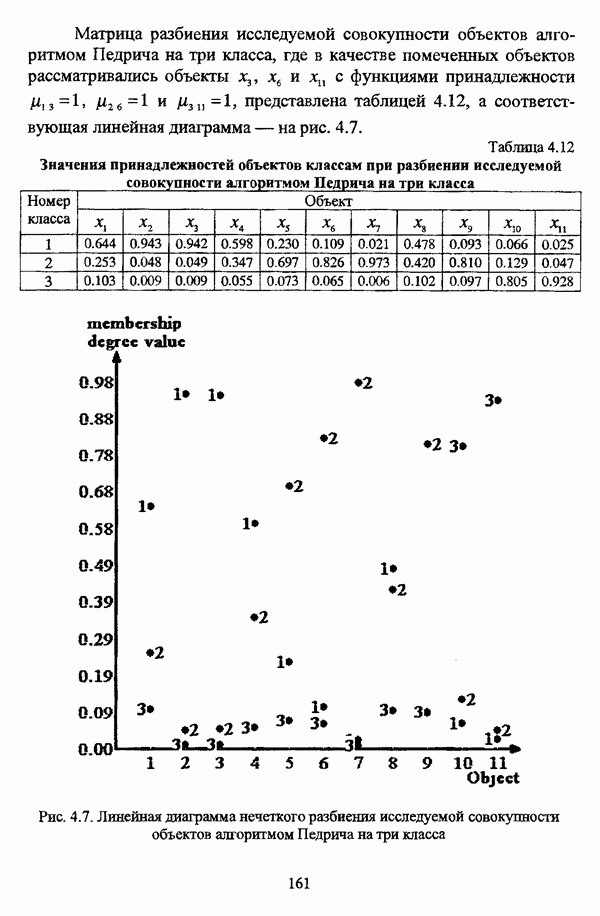
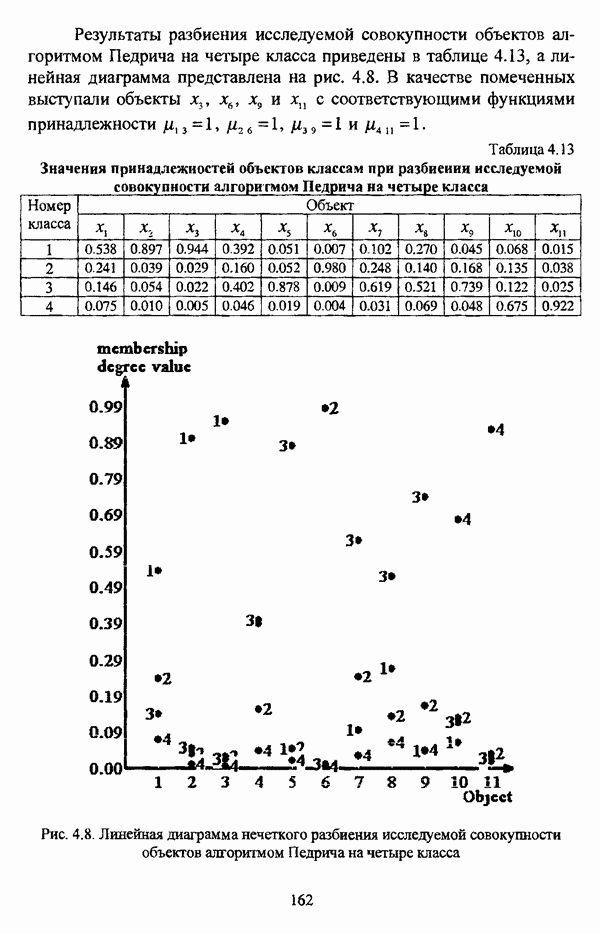
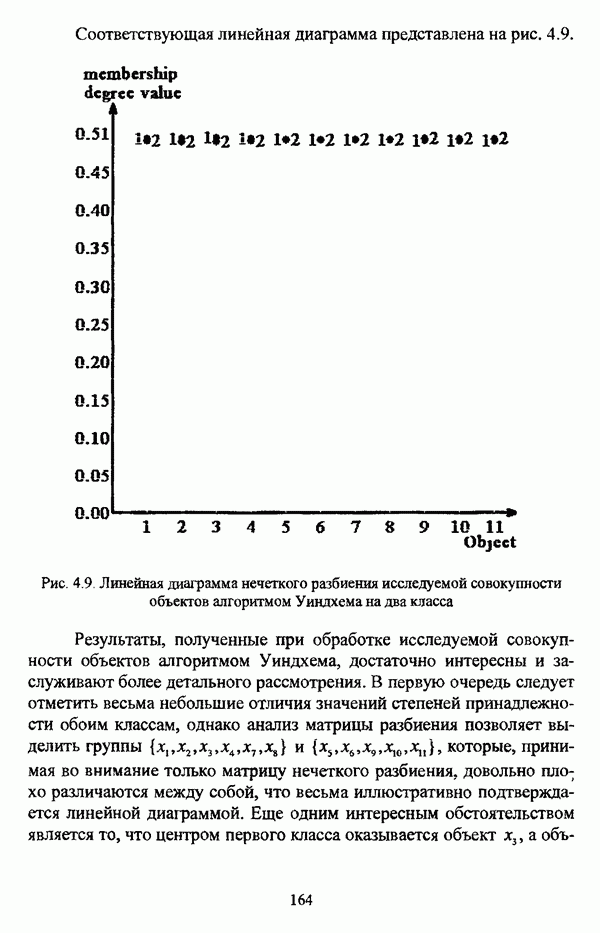
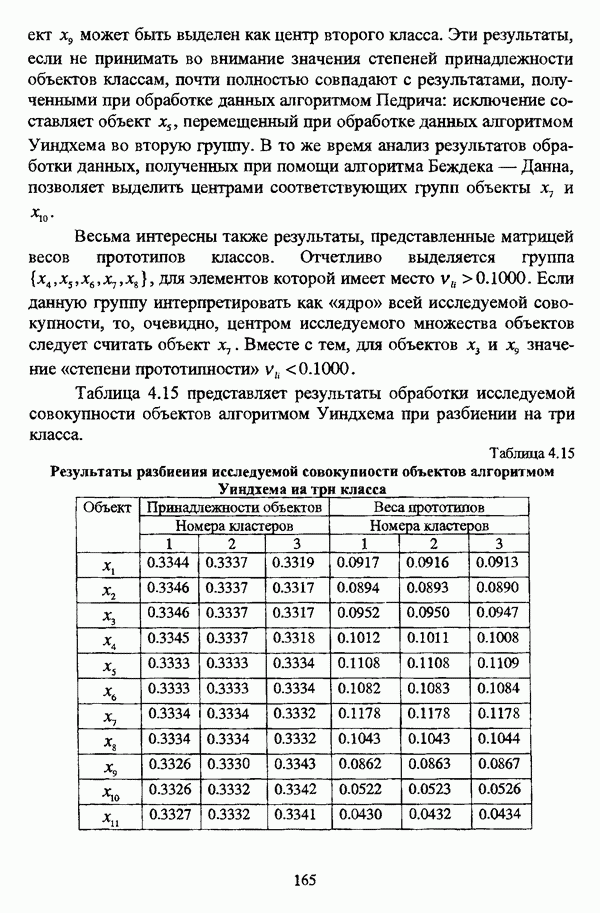
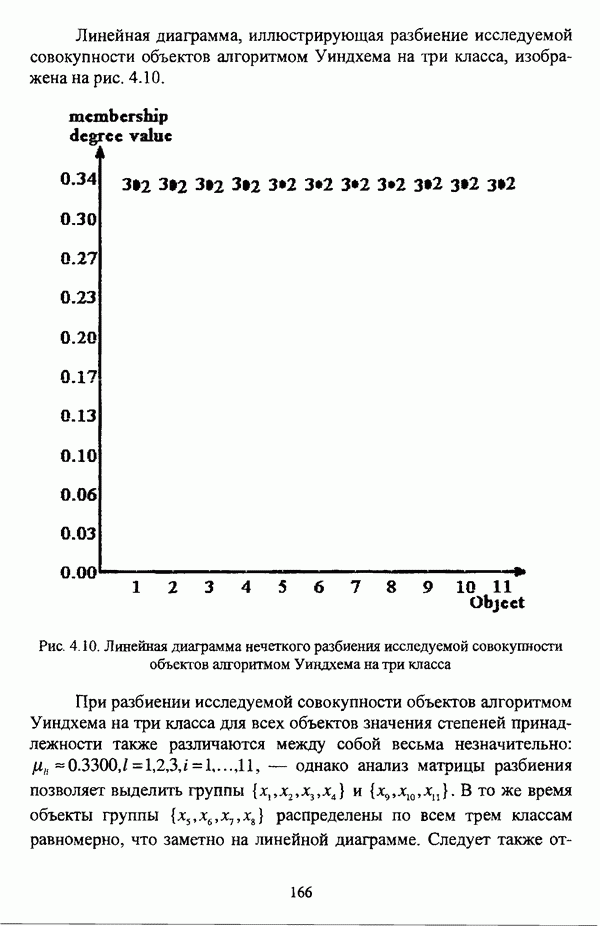
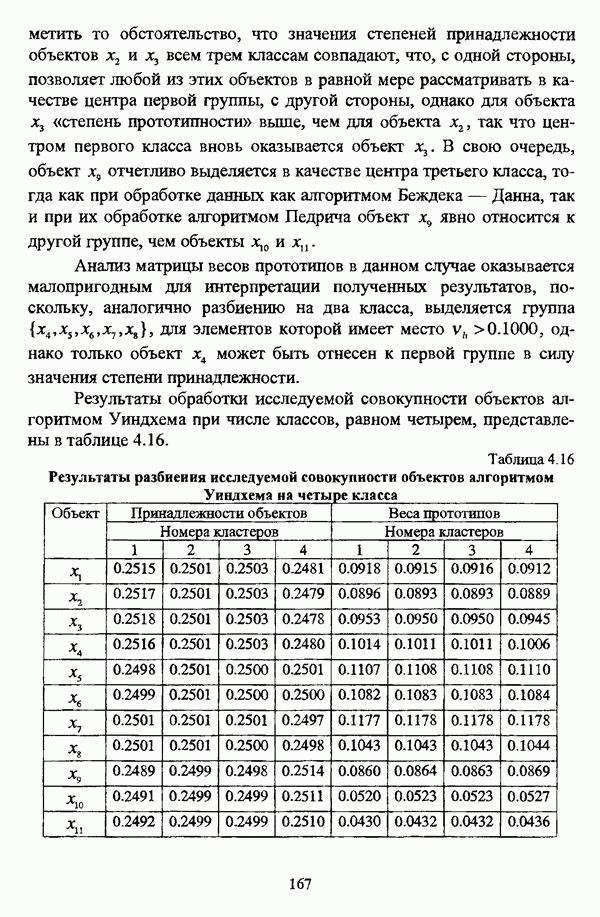
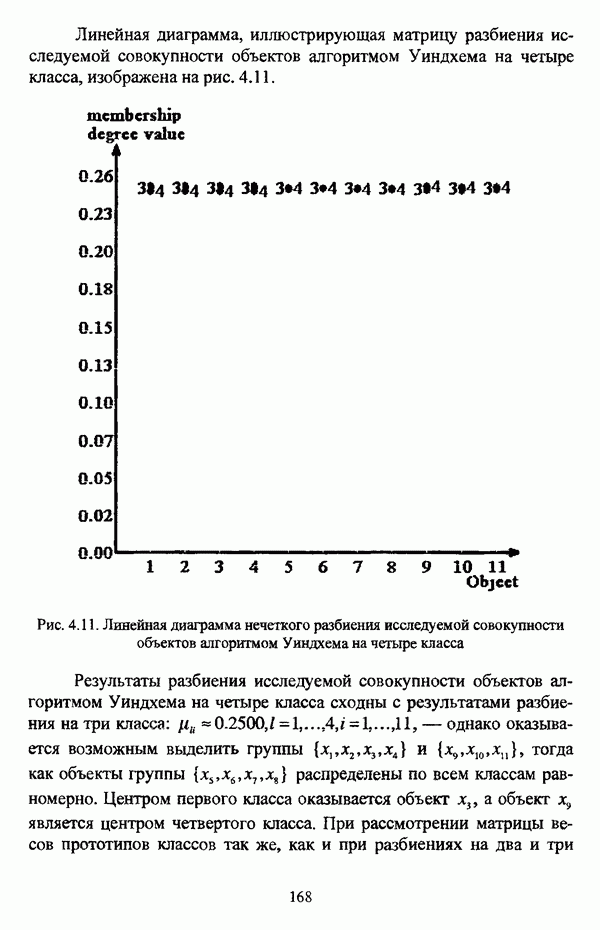
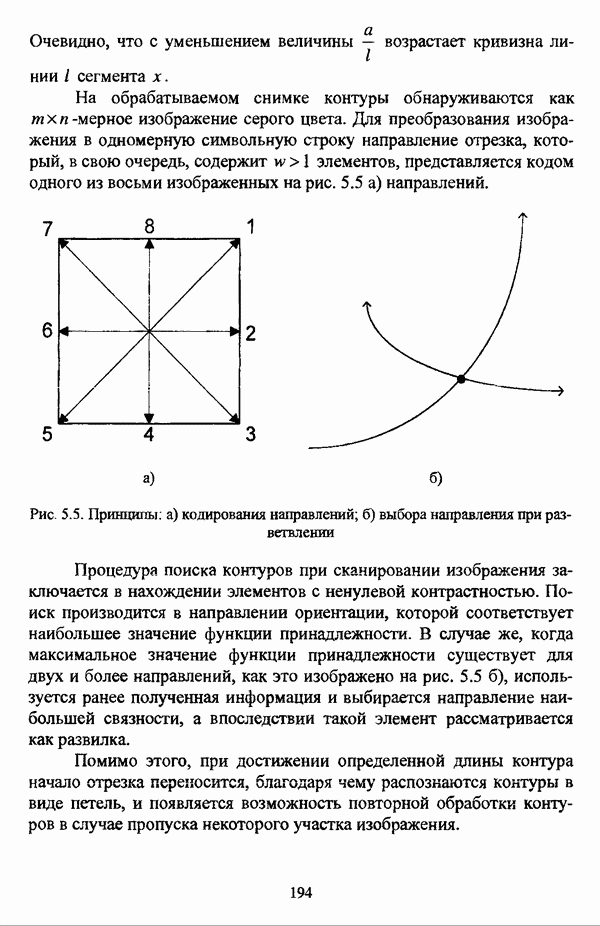
Алгоритм расстановки меток [72, с. 173-174] применяется для присвоения названий классов центрам нечетких кластеров, что в значительной степени облегчает интерпретацию результатов. Обычно хотя бы для части объектов исследуемой совокупности точно известно, какой объект принадлежит какому классу. Данная информация может послужить основой процесса присвоения названий классов центрам нечетких кластеров, именуемым расстановкой меток (labeling). В случае, когда априорная информация о принадлежности некоторых объектов классам отсутствует, то она может быть получена уже после процедуры классификации объектов, в данном случае методом нечетких с-средних.
Пусть в результате работы алгоритма Беждека — Данна построено нечеткое разбиение на с классов и результат представлен в виде соответствующей матрицы  некоторое подмножество классифицированных объектов,
некоторое подмножество классифицированных объектов,  так что
так что  инициализируется матрица меток
инициализируется матрица меток 
Параметры алгоритма:
с — число нечетких кластеров в разбиении Р;
у — показатель нечеткости классификации, 
Схема алгоритма:
1. Всем элементам матрицы меток  присваивается значение
присваивается значение 
2. Вычисляется значение функции принадлежности  объекта
объекта  для всех центров кластеров
для всех центров кластеров  в соответствии со следующей формулой:
в соответствии со следующей формулой:

3. Полагается  для всех
для всех 
4. Если  то полагается
то полагается  и осуществляется переход на шаг 2;
и осуществляется переход на шаг 2;
5. Определяется метка  для всех
для всех 
6. Производится присвоение меток  центрам кластеров
центрам кластеров 
Следует указать, что процедура расстановки меток терпит неудачу, если метка присвоена двум или более классам, что означает, что центр кластера не найден для всех меток классов. Иногда может случиться, что максимальное значение матрицы меток на шаге 5 однозначно не устанавливается. В обеих указанных ситуациях алгоритм останавливает работу и выдает сообщение об ошибке.
Модификация Либерта — Рубенса MND2 алгоритма [119, с. 418], в которой полагается, что  при
при  незначительно отличается от приведенной выше версии метода MND2.
незначительно отличается от приведенной выше версии метода MND2.
Параметры алгоритма:
с — число нечетких кластеров в искомом разбиении Р;
Схема алгоритма:
1. Выбирается начальное разбиение  на с нечетких классов, описываемое с непустыми функциями принадлежности, так что матрица начального разбиения
на с нечетких классов, описываемое с непустыми функциями принадлежности, так что матрица начального разбиения  имеет с строк и
имеет с строк и  столбцов;
столбцов;
2. Полагается 
3. Полагается  вычисляется функция расстояния
вычисляется функция расстояния  для
для  с и решается следующая задача квадратичного программирования: при
с и решается следующая задача квадратичного программирования: при  с использованием множителей Лагранжа:
с использованием множителей Лагранжа:

что приводит К

4. Полагается  для
для 
5. Если  то осуществляется переход на шаг 3;
то осуществляется переход на шаг 3;
6. В зависимости от результата сравнения полученного разбиения с предыдущим разбиением осуществляется переход на шаг 2 или останов алгоритма.
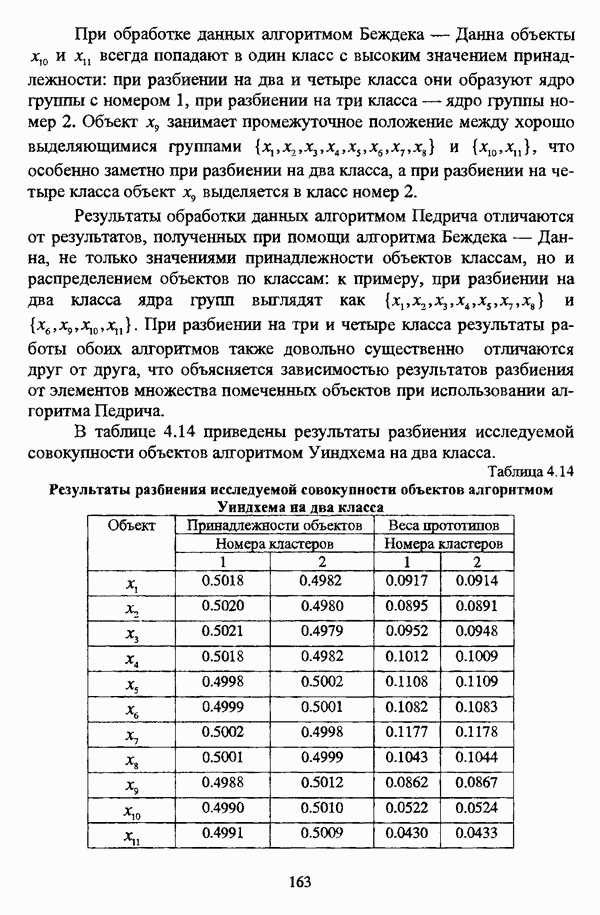
М. П. Уиндхем отмечал, что «алгоритм Рубенса основан на очень простом оптимизационном критерии, но первоначально сформулированная численная процедура неустойчива. Модификации, описанные Либертом и Рубенсом, приводят к более стабильной технике, но если типы явно неотличимы друг от друга, полезные результаты могут не быть получены» [186, с. 159].
Модификация Даве — Сена FCM алгоритма (R-FCM algorithm) [73, с. 716] минимизирует функционал  и практически не отличается от схемы FCM алгоритма, представляя собой его робастную версию: формула для вычисления центров классов остается
и практически не отличается от схемы FCM алгоритма, представляя собой его робастную версию: формула для вычисления центров классов остается
неизменной, тогда как значения принадлежностей вычисляются по формуле (3.70).
Модификация Даве — Сена MND2 алгоритма (R-MND2 algorithm) [73, с. 716] минимизирует функционал  и отличается от рассмотренной выше схемы MND2 алгоритма тем, что введение класса «выбросов» А обусловливает определение для него функции расстояния в виде
и отличается от рассмотренной выше схемы MND2 алгоритма тем, что введение класса «выбросов» А обусловливает определение для него функции расстояния в виде  где
где  значения принадлежностей вычисляются по формуле
значения принадлежностей вычисляются по формуле

Модификация Даве — Сеиа FRC алгоритма (R-FRC algorithm) [73, с. 716] является робастной версией FRC алгоритма и минимизирует функционал  так что схема R-FRC алгоритма отличается от схемы FRC алгоритма тем, что значения принадлежностей вычисляются в соответствии с формулой
так что схема R-FRC алгоритма отличается от схемы FRC алгоритма тем, что значения принадлежностей вычисляются в соответствии с формулой  в свою очередь, значения
в свою очередь, значения  вычисляются, как и на шаге 3 FRC алгоритма.
вычисляются, как и на шаге 3 FRC алгоритма.
В работе [73] представлена также робастная версия функционала, предложенного Р. Дж. Гэтевеем, Дж. В. Девенпортом и Дж. Беждеком, так что минимизирующий робастную версию функционала Р. Дж. Гэтевея, Дж. В. Девенпорта и Дж. Беждека алгоритм получил название R-RFCM алгоритма. Кроме того, Р. Н. Даве и С. Сеном рассматривается версия FRC алгоритма, отыскивающая оптимальное разбиение при условии, что для расстояния  между объектами исследуемой совокупности
между объектами исследуемой совокупности  имеет место
имеет место  получившая название NE-FRC алгоритма, а также робастная версия NE-FRC алгоритма (R-NE-FRC algorithm).
получившая название NE-FRC алгоритма, а также робастная версия NE-FRC алгоритма (R-NE-FRC algorithm).
Модификация Кеймака — Сетнеса GK алгоритма (E-GK algorithm) [109, с. 708-709] минимизирует критерий  где в качестве функции расстояния используется квадрат расстояния Махаланобиса (3.47).
где в качестве функции расстояния используется квадрат расстояния Махаланобиса (3.47).
Параметры алгоритма:
с — число нечетких кластеров в разбиении;
 — показатель нечеткости классификации,
— показатель нечеткости классификации, 
Схема алгоритма:
1. Выбирается начальное число кластеров  меры отклонения
меры отклонения  и строится начальное разбиение
и строится начальное разбиение  на
на  нечетких классов, описываемое
нечетких классов, описываемое  непустыми функциями принадлежности, так что полученная матрица начального разбиения
непустыми функциями принадлежности, так что полученная матрица начального разбиения  имеет
имеет  строк и
строк и  столбцов; полагается и
столбцов; полагается и 
2. Полагается 
3. Пусть построено некоторое  разбиение
разбиение  в виде массива
в виде массива  столбцов; вычисляется набор центров в соответствии с формулой
столбцов; вычисляется набор центров в соответствии с формулой 
4. На основании ковариационной матрицы  вычисляется радиус прототипов кластеров
вычисляется радиус прототипов кластеров 
5. Вычисляются расстояния до объемных прототипов кластеров:

6. Производится пересчет значений принадлежности в матрице разбиения  в соответствии со следующим правилом: для
в соответствии со следующим правилом: для  полагается
полагается  так что
так что

7. Выбирается пара наиболее близких кластеров:

8. Производится объединение наиболее близких кластеров в соответствии с правилом: при -  полагается
полагается  если
если  то
то  из матрицы b)
из матрицы b)  удаляется строка, соответствующая кластеру
удаляется строка, соответствующая кластеру  и полагается
и полагается  иначе
иначе 
9. Производится сравнение  по правилу: если
по правилу: если  то
то  и алгоритм заканчивает работу; в противном случае полагается
и алгоритм заканчивает работу; в противном случае полагается  и осуществляется переход на шаг 3.
и осуществляется переход на шаг 3.
Модификация Кеймака — Сетнееа FCM алгоритма (E-FCM algorithm) [109, с. 708-709] минимизирует критерий  где в качестве функции расстояния используется квадрат евклидова расстояния (3.45), так что
где в качестве функции расстояния используется квадрат евклидова расстояния (3.45), так что  алгоритм отличается от
алгоритм отличается от  алгоритма только способом вычисления расстояния на шаге 5:
алгоритма только способом вычисления расстояния на шаге 5:

Результаты вычислительных экспериментов, представленные У. Кеймаком и М. Сетнесом [109, с. 709], демонстрируют высокую эффективность расширенных версий нечетких кластер-процедур оптимизационного направления по сравнению с обычными нечеткими оптимизационными методами кластер-анализа. При проведении экспериментов У. Кеймаком и М, Сетнесом полагалось 
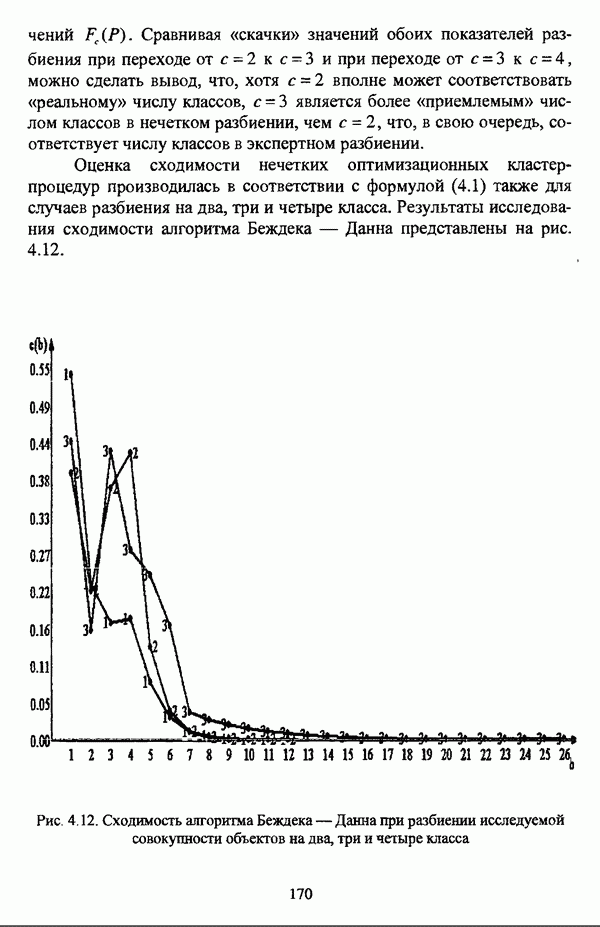
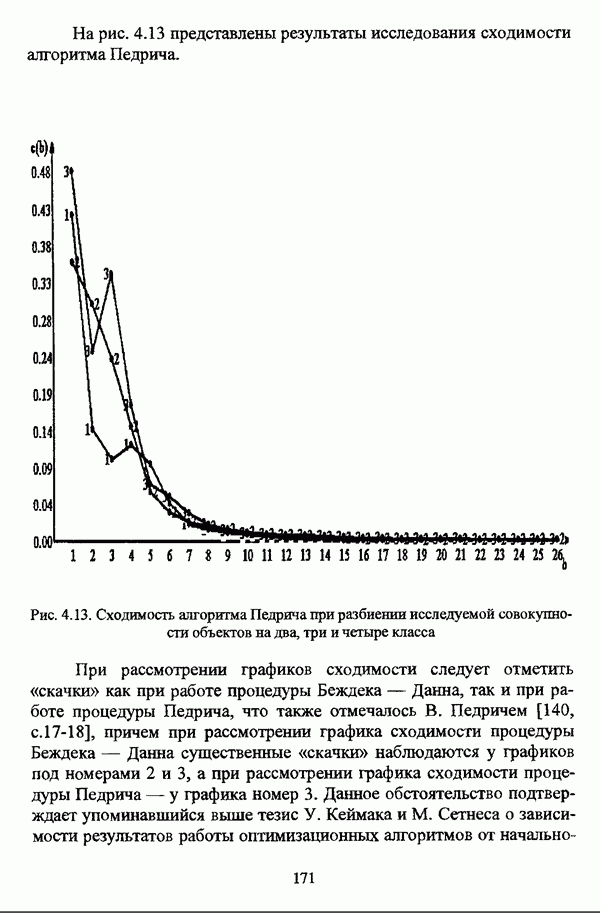
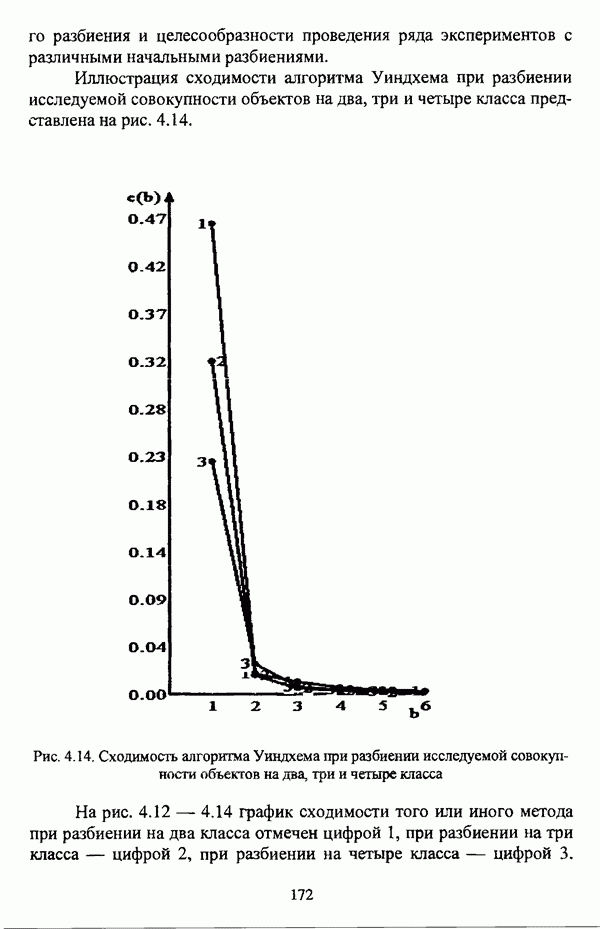
В заключение рассмотрения оптимизационных алгоритмов нечеткого подхода к решению задачи кластер-анализа следует отметить общую особенность всех рассмотренных кластер-процедур [109, с. 705]: результаты работы оптимизационных алгоритмов зависят от начального разбиения, которое инициализируется, как правило, случайным образом, так что при неудовлетворительном начальном разбиении могут быть получены некорректные результаты. В связи с этим У. Кеймак и М. Сетнес отмечают, что для получения корректных результатов целесообразно проведение ряда экспериментов с различными начальными разбиениями [109, с. 705].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
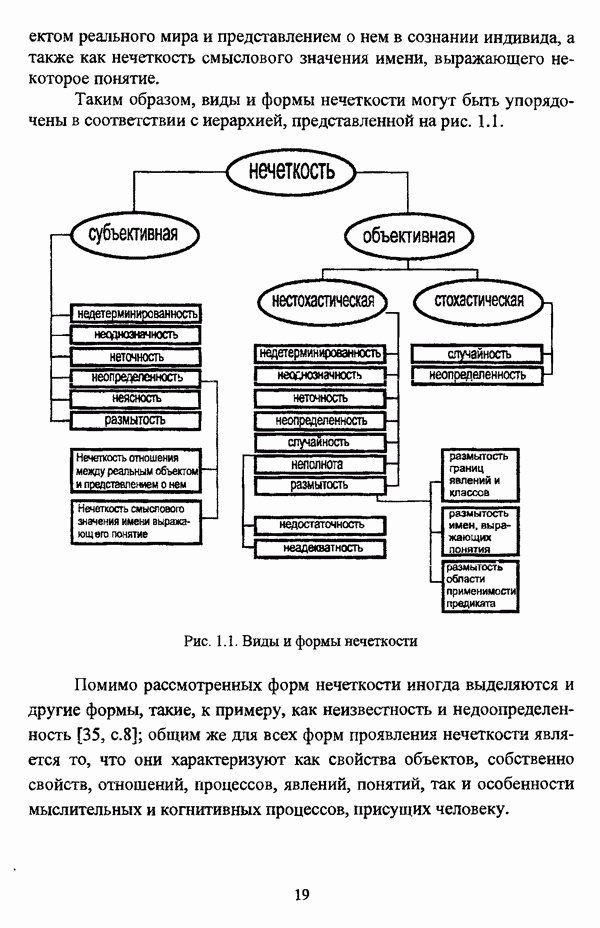
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
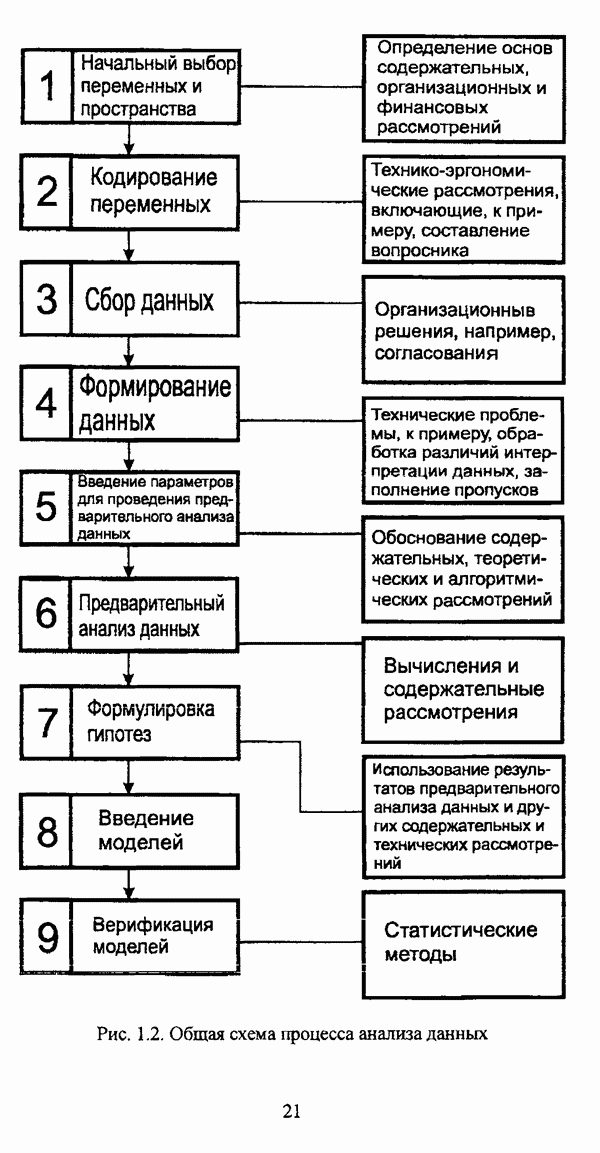
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
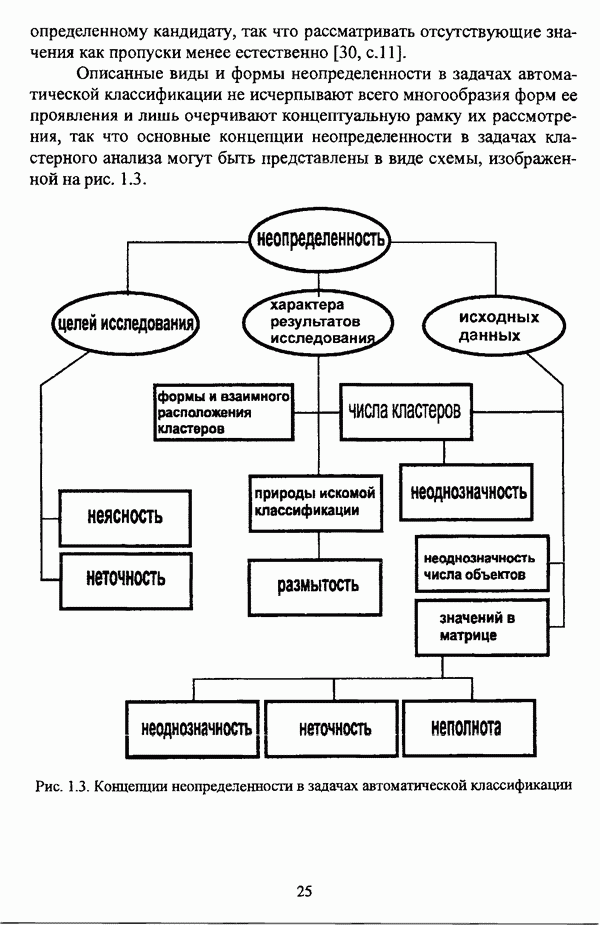
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
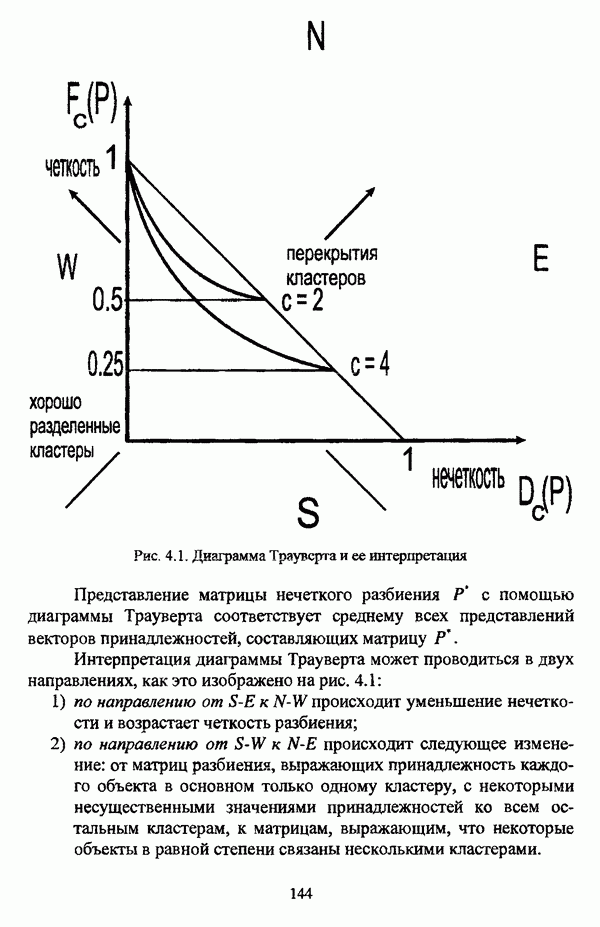
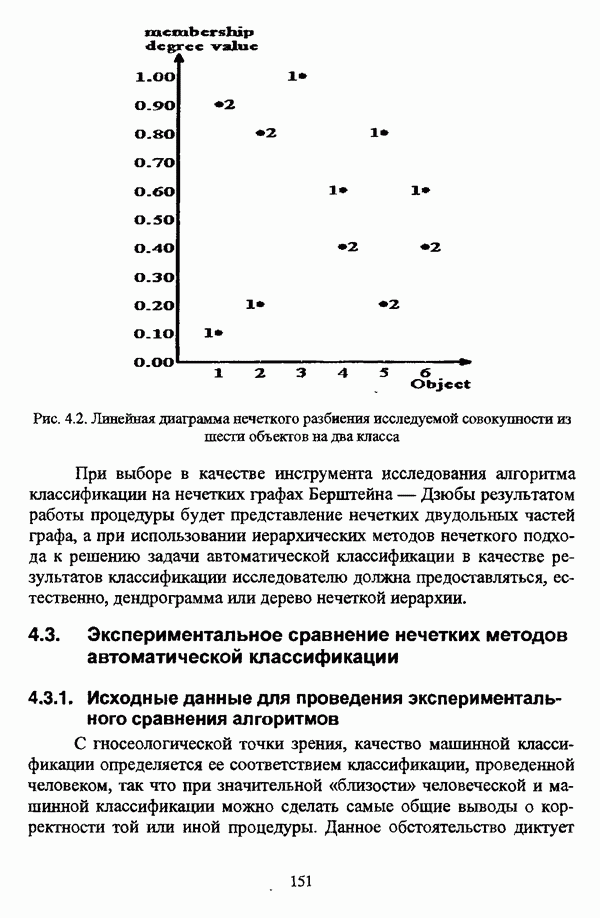
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
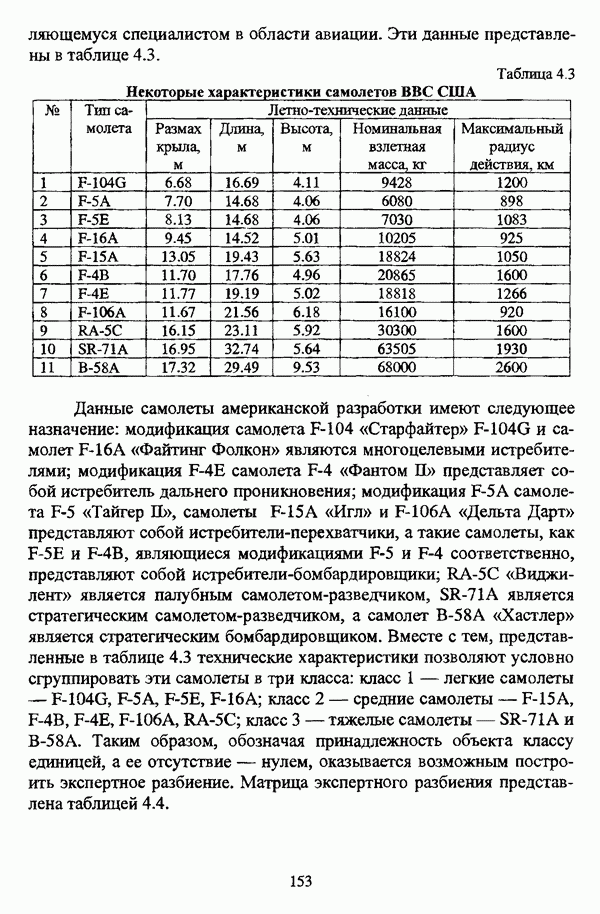
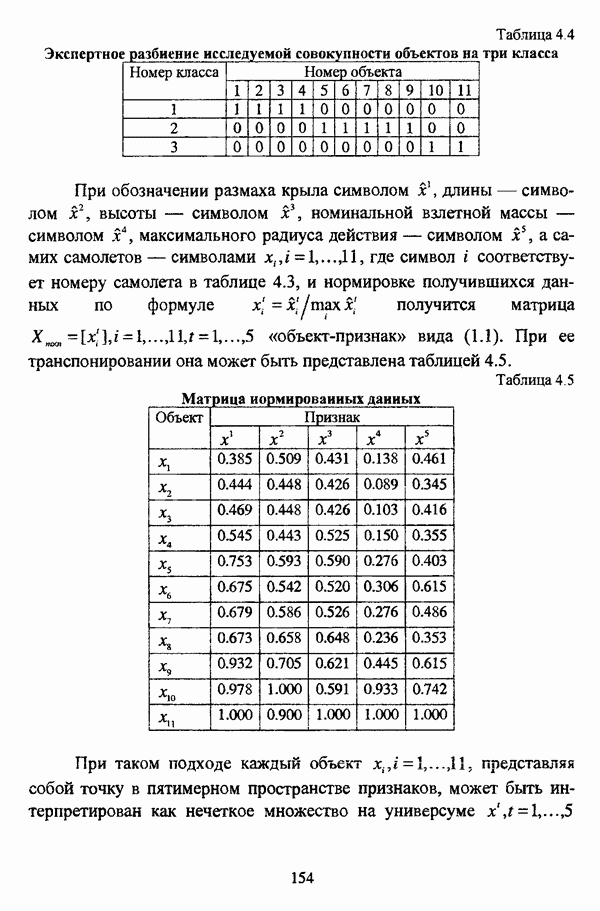
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
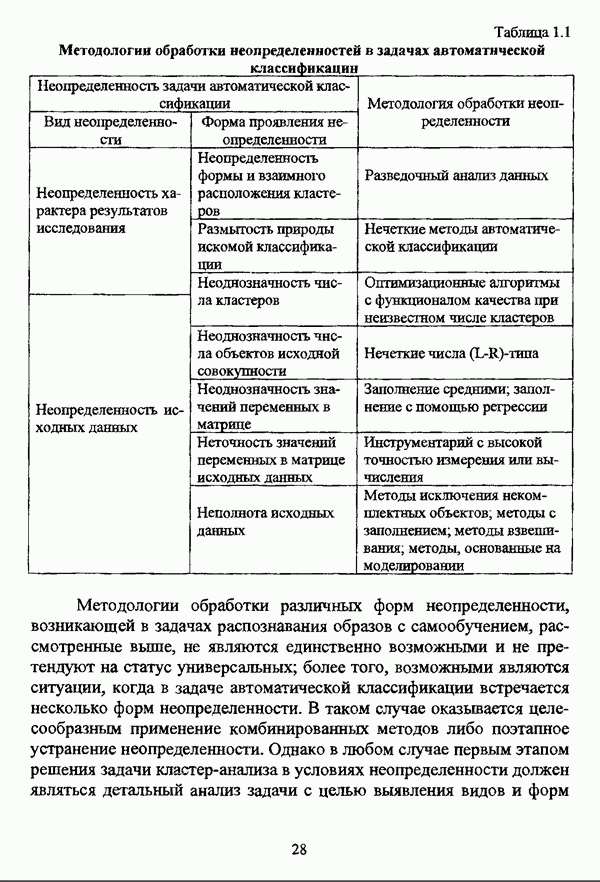
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы