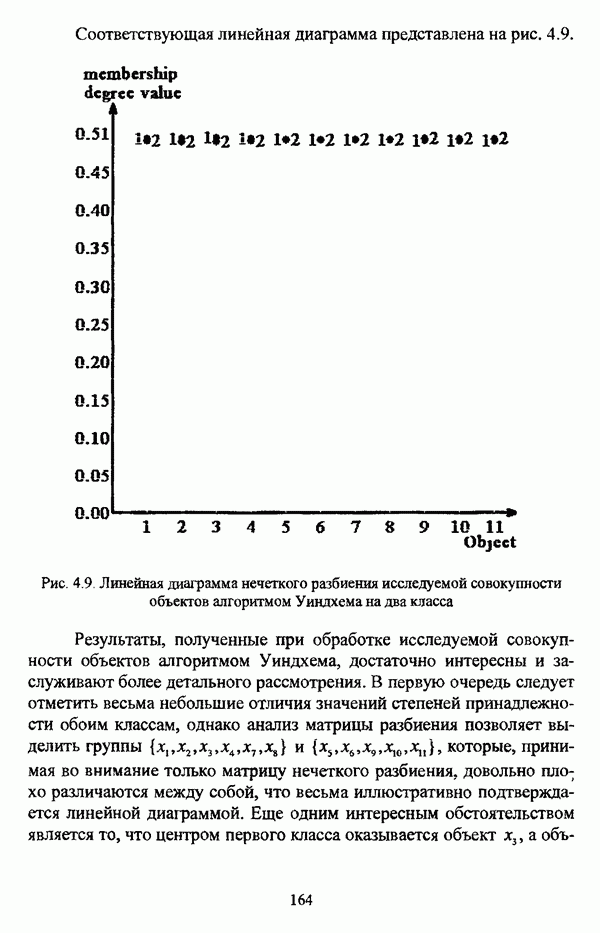
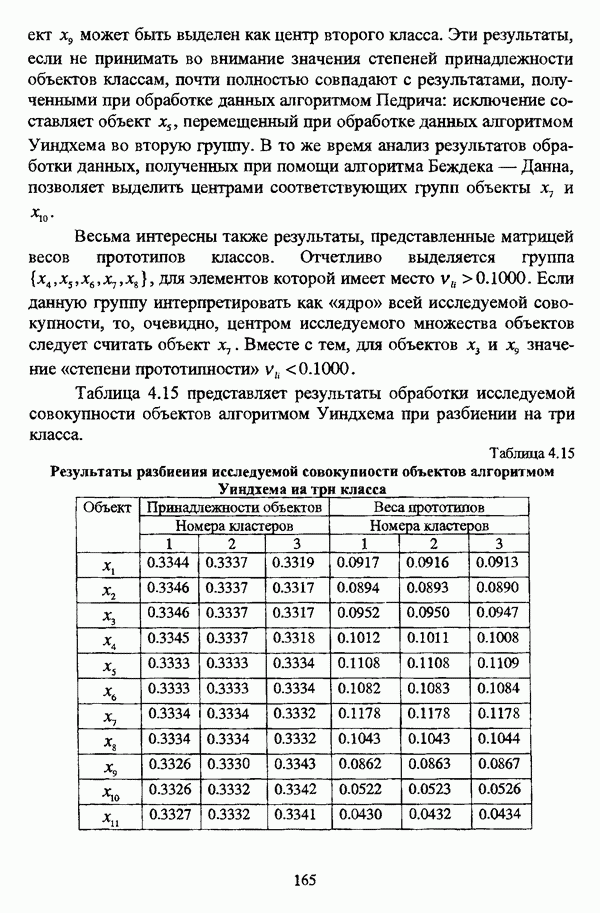
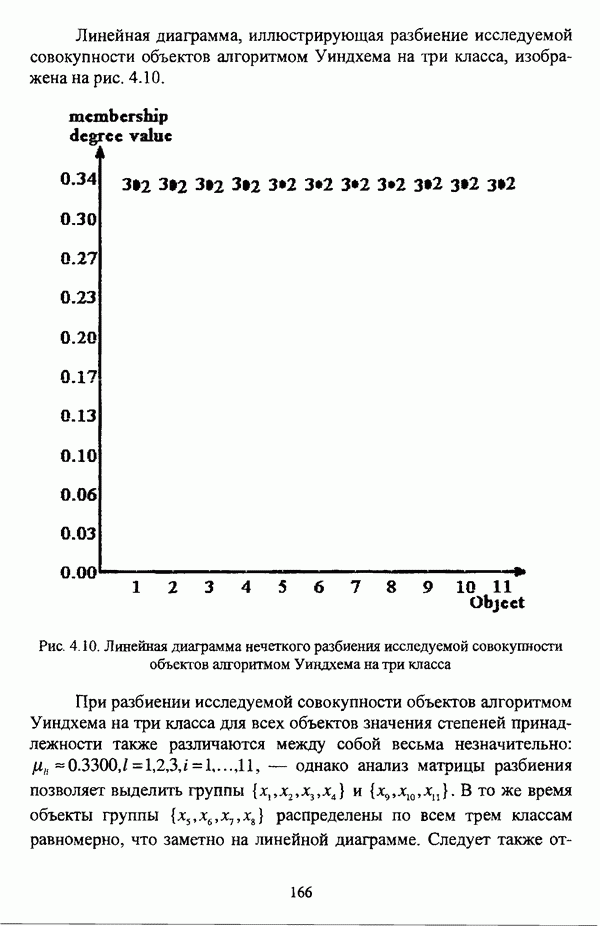
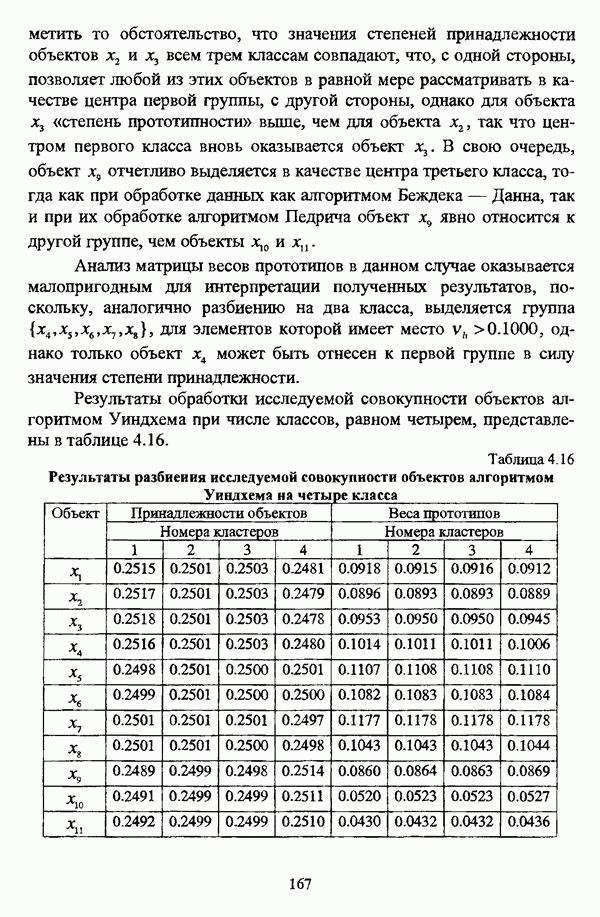
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
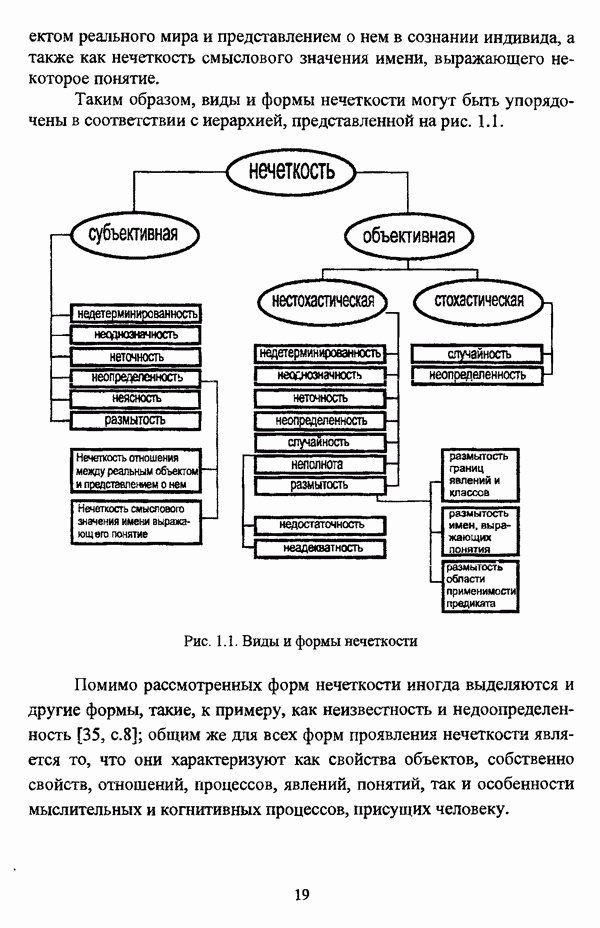
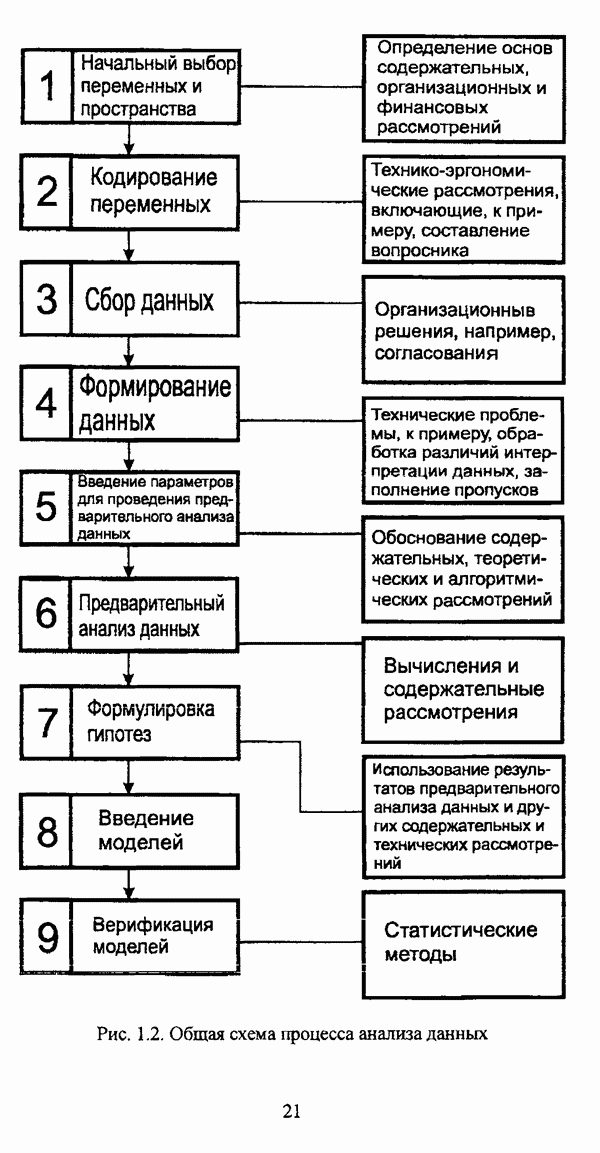
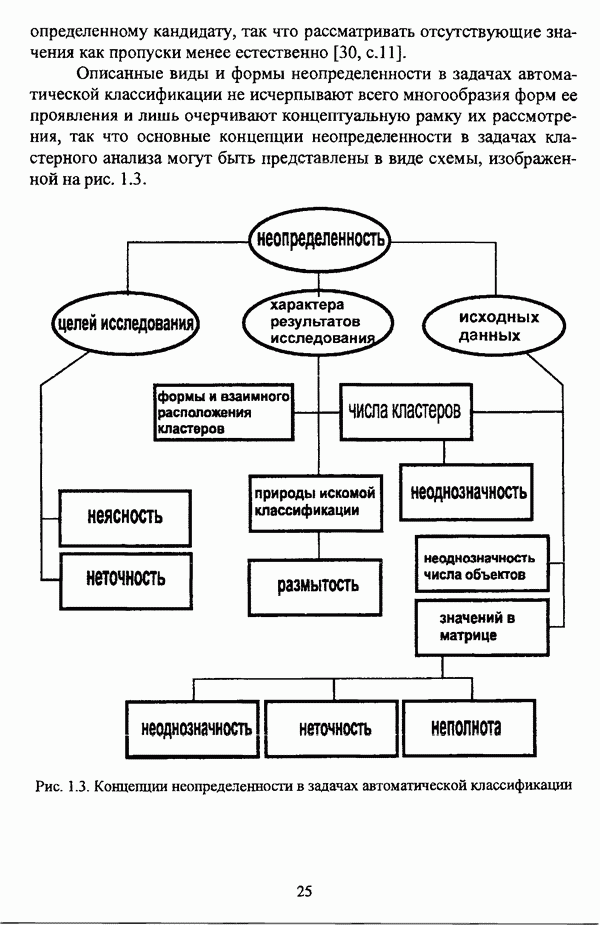
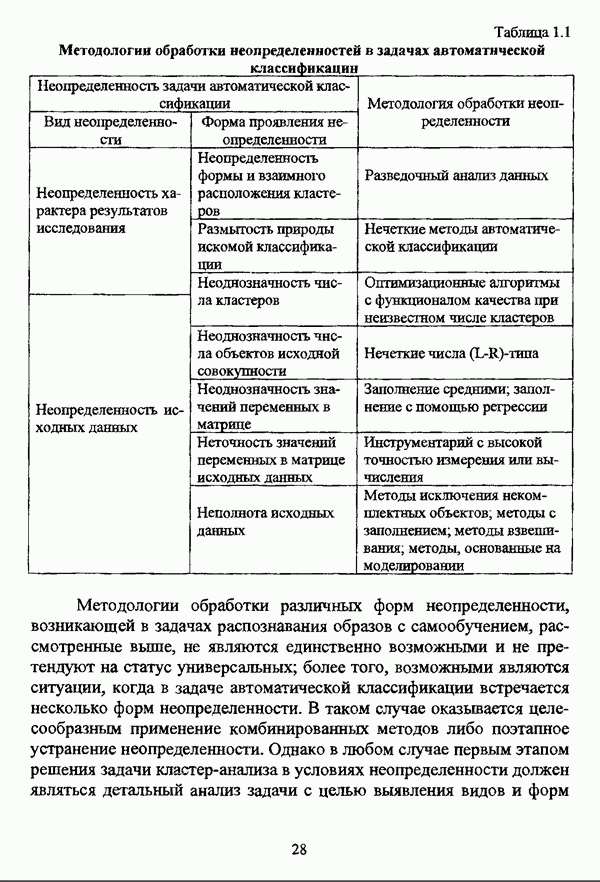
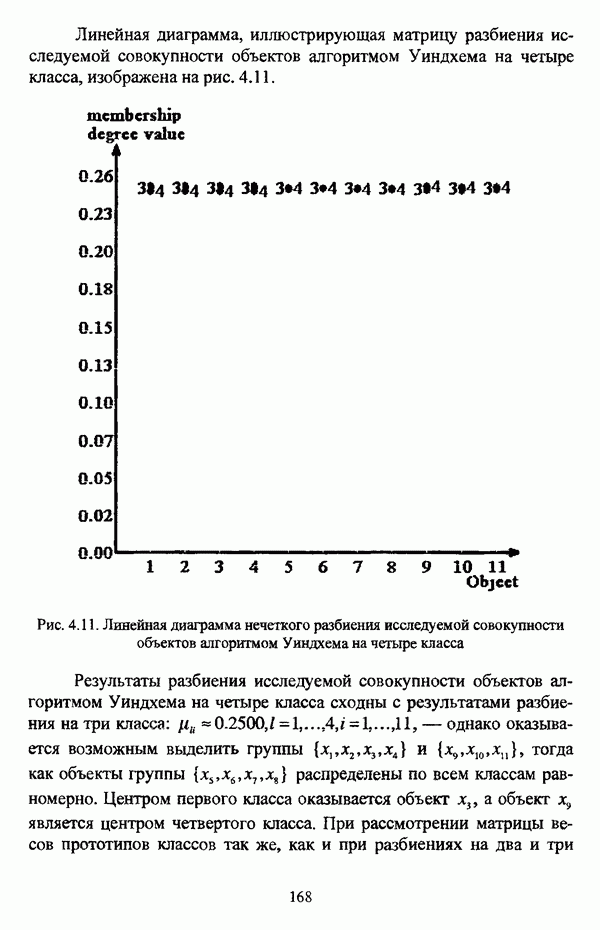
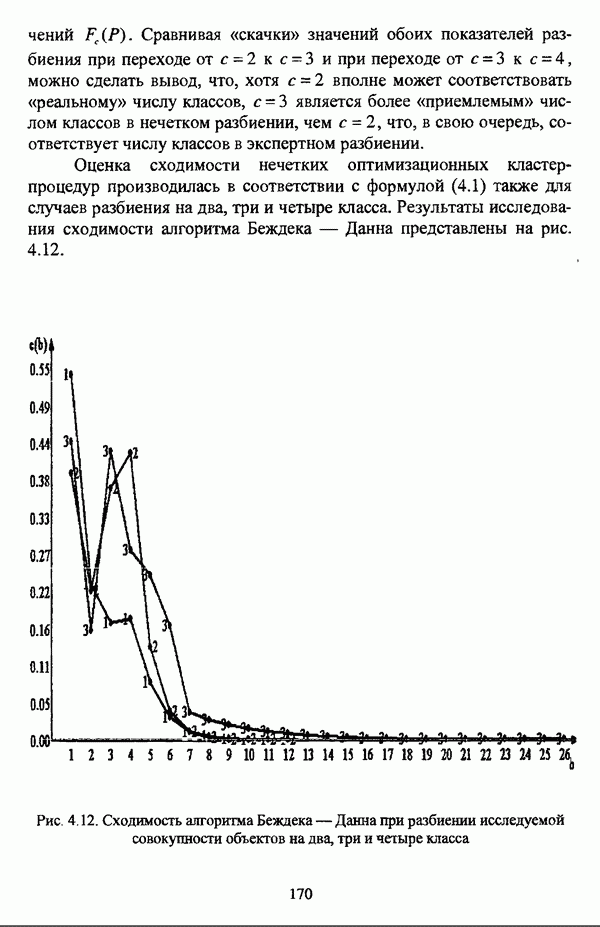
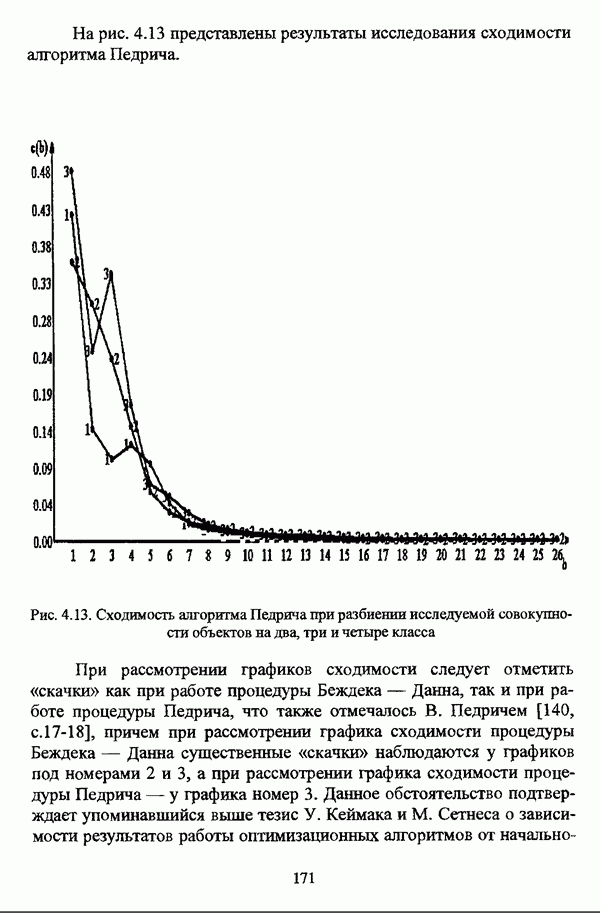
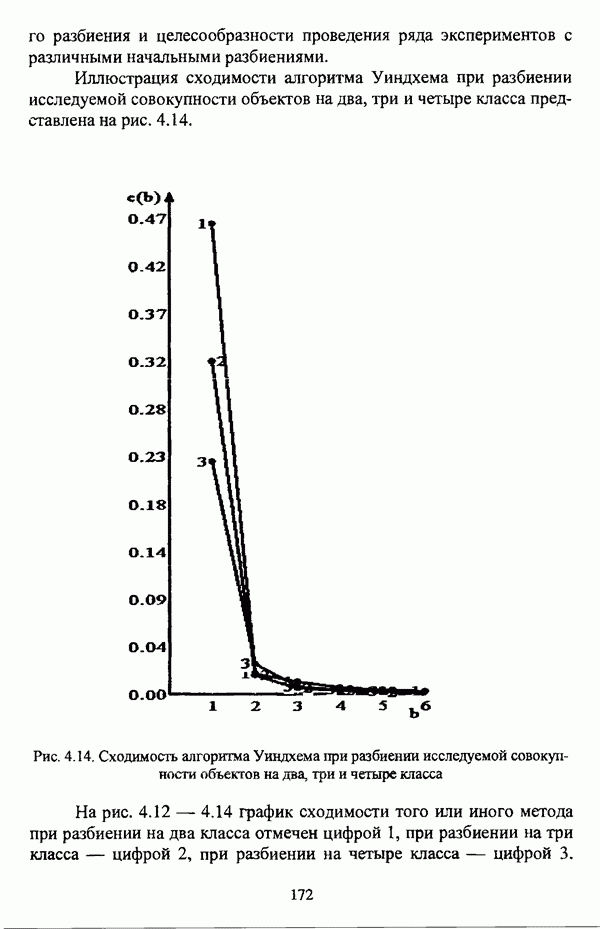
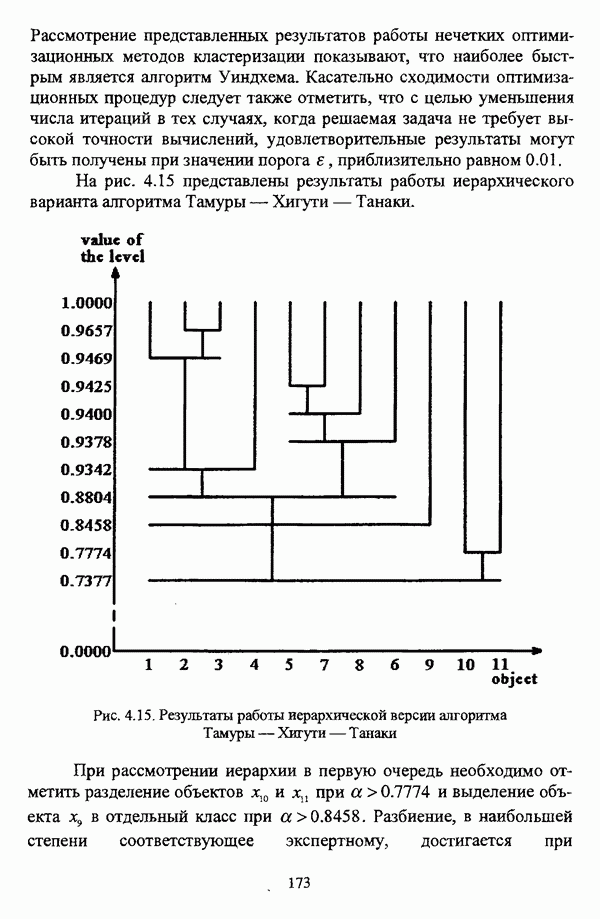
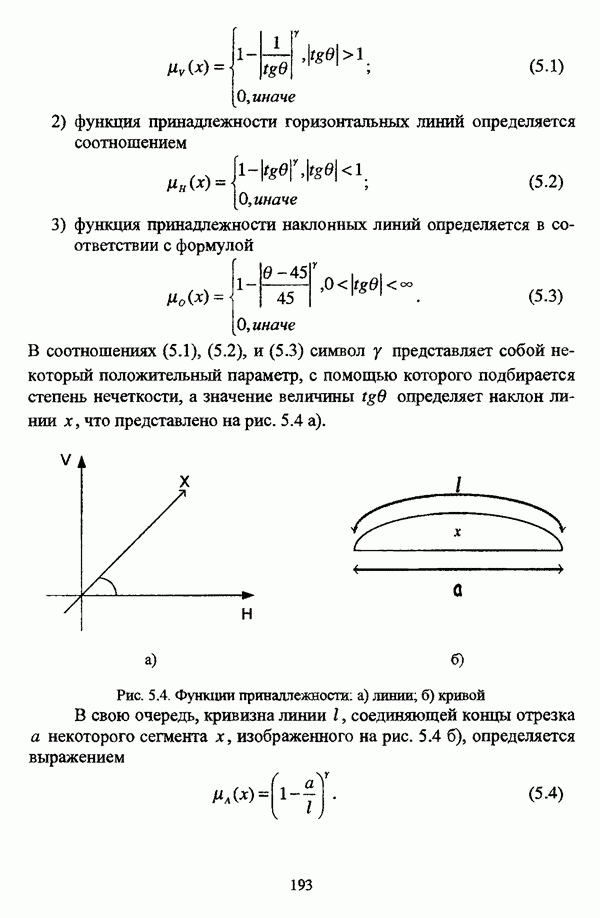
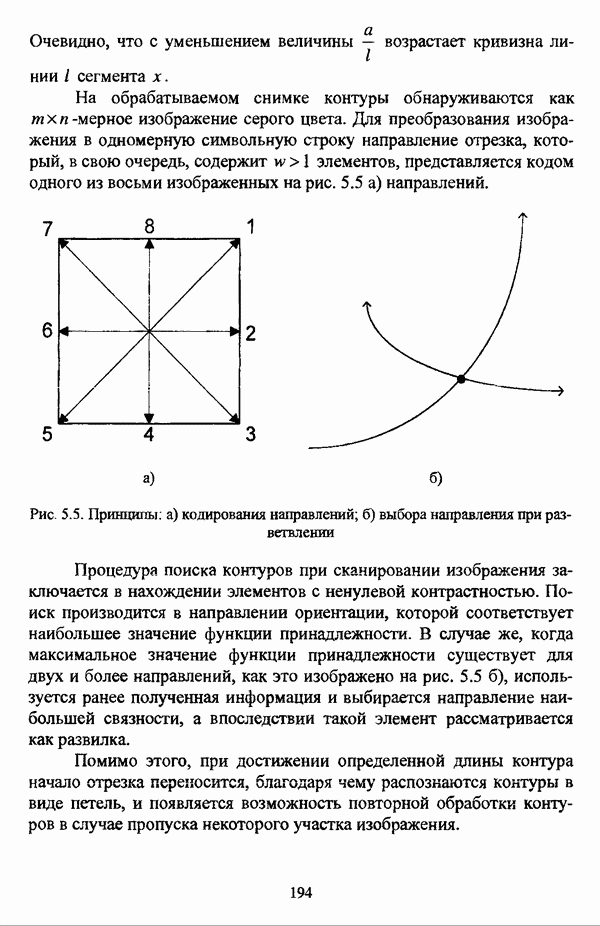
1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
Кластер-анализ представляет собой структурный подход к решению проблемы группировки многомерных объектов, основа которого заключается в представлении результатов отдельных наблюдений точками геометрического пространства с последующим выделением групп как «сгустков» этих точек, именуемых кластерами. Большинство существующих на сегодняшний день подходов и методов к решению задач кластер-анализа имеют своей основой эвристические соображения, которые возникают из конкретных приложений понятия классификации к некоторым частным классам однотипных задач, так что применение различных методов для конкретной задачи приводит к различным классификациям. Таким образом, механическое расширение области применимости частных процедур приводит к неудовлетворительным результатам и не позволяет постичь сущность причин, вызывающих таксономические различия. Зачастую это оказывается следствием различающихся между собой определений кластера, основывающихся на интуитивном представлении о кластере как о множестве объектов, подобных друг другу и отличных от объектов, не принадлежащих этому множеству. Традиционно формулируются требования, согласно которым кластер должен представлять собой непустое подмножество объектов, разные кластеры должны отличаться друг от друга и все объекты исходного множества должны быть расклассифицированы. В случае детерминистской постановки задачи последние два требования формулируются более жестко: оказывается необходимой дизъюнкгивность кластеров и образы кластеров не должны пересекаться, то есть каждый объект исходного множества должен принадлежать только одному кластеру.
Подобные требования, в частности, требование об однозначности классификации, оказываются чрезмерно жесткими при анализе
сложных динамических систем, к которым можно отнести социально-экономические, биологические и иные виды систем, в которых центральное место занимают живые объекты, к примеру, человек. Такие системы профессор Л. А. Заде предложил именовать гуманистическими [24]. При подобного рода исследованиях возможность формулировки точных и в то же время содержательно значимых высказываний сводится к минимуму, за которым точность и релевантность становятся взаимоисключающими характеристиками подобных высказывании. Практика показывает, что традиционные статистические методы автоматической классификации зачастую не дают устойчивых результатов в случае, когда два или более кластеров соединяются цепочкой из внутренне связанных объектов выборки, когда кластеры имеют несферическую форму, когда кластеры являются линейно-несепарабельными множествами либо когда различаются плотности или объемы кластеров.

Рис. 1.4. Различные формы кластеров
На рис. 1.4 первый случай иллюстрируется кластерами А и В, второй случай представлен кластерами С и D, кластер Е демонстрирует третий из описанных выше случаев, а кластеры G и Н — четвертый.
Еще более сложным оказывается случай пересечения кластеров, который иллюстрируется кластерами I и J.
Подобные примеры наглядно демонстрируют, что многие реальные системы обладают структурой, описание которой в рамках традиционных математических формализмов оказывается невозможным, так что человеческие суждения о поведении или состоянии подобных систем в действительности относятся не к какому-либо конкретному состоянию системы, а к совокупности различных состояний системы, границы между которыми оказываются объективно размыты, что, в свою очередь, можно продемонстрировать на следующем примере.
Предположим, что основой для классификации группы объектов выбран такой признак, как цвет объекта. В терминах разговорного языка описание значений переменной «цвет» является неточным, в отличие от численного представления диапазона длин волн, присущих каждому цвету. В процессе различения цветов человек основывается не на эталонном, а на собственном восприятии того или иного цвета, а этот субъективный диапазон длин волн, как показывают физиологические исследования, может колебаться в весьма значительных пределах. Таким образом, цвет, одним человеком воспринимаемый как «оранжевый», другим человеком воспринимается как «желтый», что с медицинской точки зрения оказывается вполне нормальным, поскольку патологией, в специальной литературе именуемой дальтонизмом, является неспособность человека различать три основных цвета — красный, зеленый и синий. Данный пример демонстрирует, что границы интервала длин волн, в естественном языке обозначаемого одним и тем же словом, для разных людей оказываются различными, то есть и множество волн, обозначаемое этим термином, оказывается размытым.
Вместе с тем, нечеткость может быть не только субъективной, но и объективной характеристикой. Нечеткость как характеристика собственно объектов является следствием многообразия признаков, характеризующих объект, а также динамики их изменения вследствие изменения структуры объекта. Примерами таких объектов могут служить, хамелеон — в зоологии, переменные звезды — в астрономии, самолет с изменяемой геометрией крыла — в технике. Касательно последнего примера можно указать, что для человека, не являющегося специалистом в области авиационной техники, один и тот же самолет, но при различных углах стреловидности передней кромки крыла,
соответствующих различным режимам полета, может быть воспринят как два совершенно разных типа самолетов, и если в качестве основы для классификации выбрать такие признаки, как размах крыла или угол стреловидности передней кромки крыла, то один и тот же самолет, взятый в различных ситуациях, попадет в различные кластеры.
Подобные примеры подтверждают тезис, выдвинутый профессором Л. А. Заде, что «большинство реальных кластеров размыты по своей природе в том смысле, что переход от принадлежности к непринадлежности для этих классов скорее постепенен, чем скачкообразен» [25, с. 208]. Теория нечетких множеств, вводя понятие взвешенной принадлежности объекта множеству, предлагает гибкий аппарат для формального описания подобного рода ситуаций, так что вопрос заключается не в том, принадлежит ли объект классу, а в том, какова степень принадлежности объекта тому или иному классу.
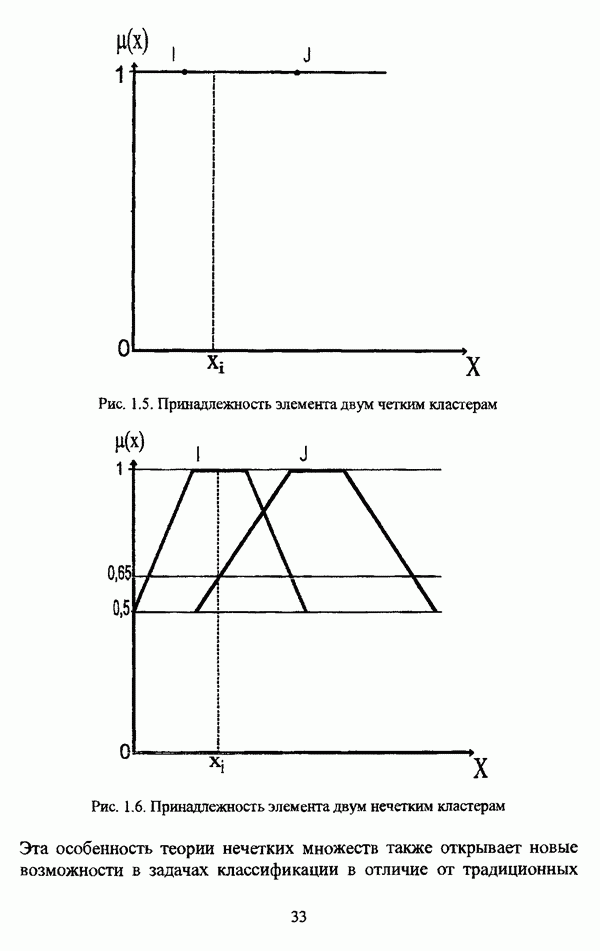
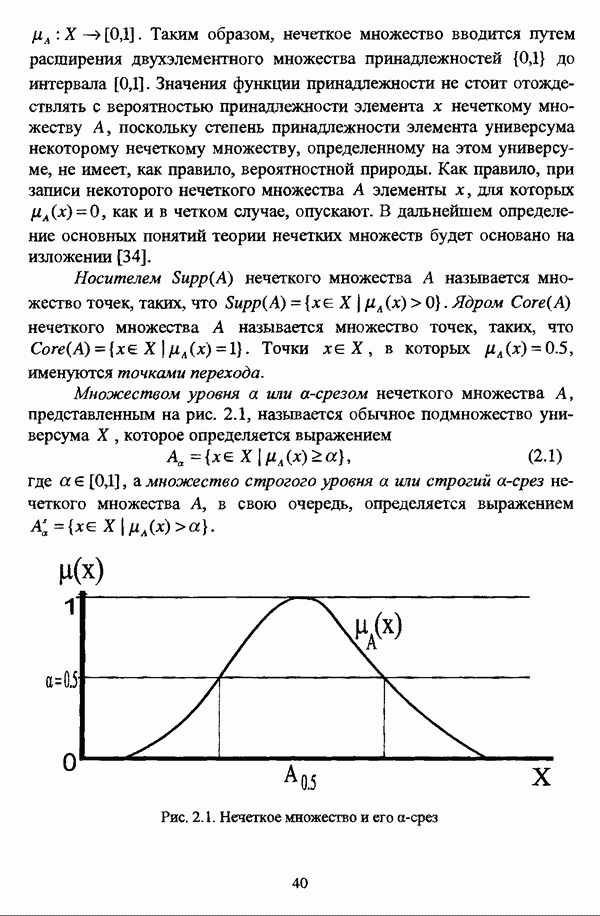
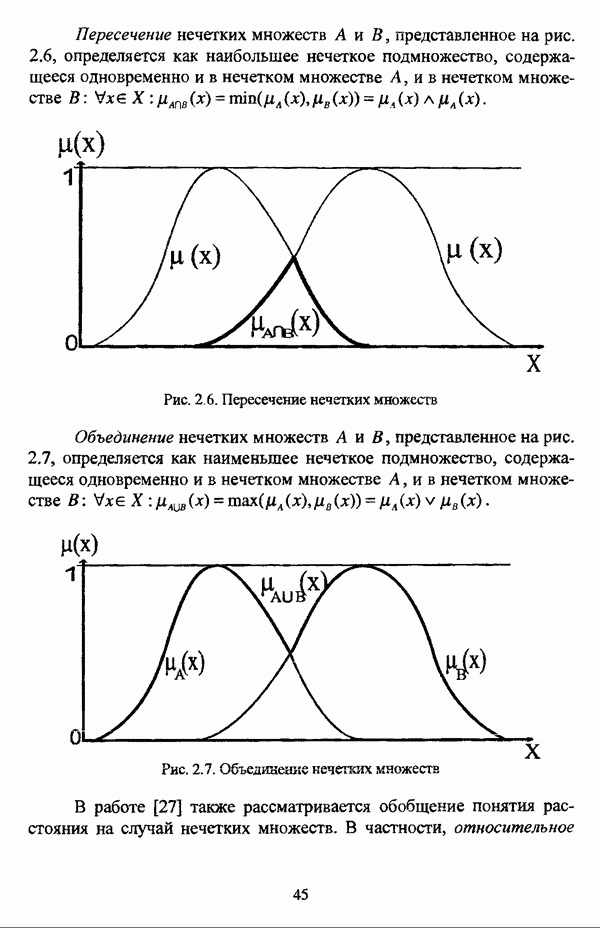
Здесь целесообразно кратко рассмотреть логический аспект проблемы. Если в случае обычной, или, как еще именуют в специальной литературе, четкой классификации, объекты, находящиеся в области пересечения кластеров, оказываются однозначно принадлежащими обоим кластерам в равной степени, что схематически изображено на рис. 1.5, то в случае нечеткого подхода к решению задачи автоматической классификации кластеры представляют собой нечеткие множества, так что о принадлежности объекта тому или иному кластеру можно судить по его функции принадлежности, которая в данном случае будет выражать степень сходства объекта с типичным элементом кластера, что изображено, соответственно, на рис. 1.6.
Таким образом, нечеткий подход к решению задачи классификации в ряде случаев позволяет разделить кластеры сложной формы и открывает новые возможности интерпретации результатов классификации. Более того, следует отметить, что в отличие от вероятностного пространства структура нечетких множеств представлена не булевой решеткой, а векторной, так что с точки зрения формальной логики для нечетких классов не выполняются такие законы, как закон противоречия и закон исключенного третьего.
(см. скан)
Рис. 1.5. Принадлежность элемента двум четким кластерам
(см. скан)
Рис. 1.6. Принадлежность элемента двум нечетким кластерам
Эта особенность теории нечетких множеств также открывает новые возможности в задачах классификации в отличие от традиционных
статистических методов и позволяет использовать более гибкие методы для представления начальной структуры данных, подлежащих классификации.
Возвращаясь к рассмотрению гносеологических аспектов вопроса о применимости теории нечетких множеств к задачам кластер-анализа, необходимо указать на следующее обстоятельство. Для того чтобы современные автоматические системы могли эффективно заменить человека в управлении, к примеру, производством, и результаты работы подобных систем были бы интерпретируемы естественным образом, необходимо, чтобы математическое обеспечение соответствующих автоматических или автоматизированных систем было основано на принципах, используемых человеком в подобных процессах. Однако данный тезис не следует понимать буквально, тем более, когда речь идет о задачах классификации. К примеру, как показывают результаты экспериментов, человек в многомерных пространствах признаков может различать только такие множества объектов, которые отличаются друг от друга линейными решающими функциями. Если способность человека к идентификации зрительных или речевых сигналов формировалась на протяжении длительного процесса эволюции, то его способность к анализу и классификации абстрактной информации формировалась на протяжении последних нескольких тысячелетий, поэтому человек блестяще классифицирует звуки и символы и гораздо хуже — абстрактные объекты. Алгоритмы же автоматической классификации, работая в подобного рода пространствах, должны классифицировать именно абстрактные объекты, то есть решать весьма трудную для человека задачу. Поэтому при разработке алгоритмов кластер-анализа нет необходимости выявлять класс решающих правил, используемых человеком при решении соответствующих задач. Достаточным в таких условиях оказывается воспроизведение свойств человеческого способа мышления и решения задач, а одним из главных таких свойств, как показывают философско-методологические исследования [162], [164], [173], является нечеткость.
Теория нечетких множеств, вводя вместо строгой принадлежности объекта множеству понятие взвешенной принадлежности, позволяет более адекватно представить точки, находящиеся вне типичной части каждого кластера. Далее, как отмечал американский исследователь Э. Г. Распини, «теория нечетких множеств обеспечивает желаемый перенос выборов таксономических решений из дискретного
метрического пространства в непрерывное пространство, в котором понятие «похожая классификация» можно определить более содержательно» [39, с. 116]. Различные аспекты нечеткой классификации детально исследуются также в работах [48], [111], [139], [179].
Таким образом, краткое логико-гносеологическое рассмотрение проблемы применимости теории нечетких множеств к задачам кластер-анализа показывает, что эта теория оказывается гибким инструментом для представления данных, когда исходная структура оказывается нечеткой, и более адекватным аппаратом для представления непрерывных кластеров, чем теория вероятностей. Кроме того, теория нечетких множеств позволяет воспроизводить человеческий подход к проблеме классификации и открывает богатые возможности для естественной интерпретации результатов процесса классификации [15]. Вместе с тем, несмотря на специфику теории нечетких множеств, использование аппарата нечетких множеств при решении задач распознавания образов с самообучением не приводит к принципиальному изменению общей постановки задачи классификации объектов в условиях отсутствия обучающих выборок, так что имеет смысл рассуждать не о задаче нечеткой автоматической классификации, что подразумевает выделение задач классификации без обучения при размытости структуры классифицируемых объектов и, соответственно, размытости искомой классификации в самостоятельную область научных исследований, а только о нечеткой модификации задачи автоматической классификации и, соответственно, о нечетких методах решения задачи классификации объектов в условиях отсутствия обучающих выборок, которые и составляют предмет исследования. Подобное различение терминологии позволяет избежать путаницы при определении характера конкретной задачи и, следовательно, способствует выбору наиболее приемлемого метода классификации для решения задачи.
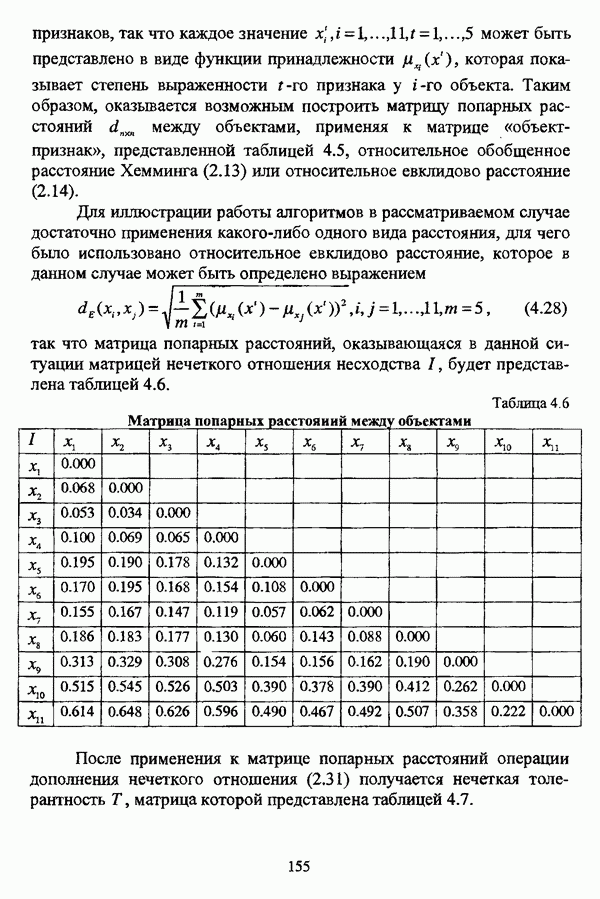
Итак, на содержательном уровне нечеткая модификация задачи автоматической классификации может быть сформулирована следующим образом: представить исходное множество объектов  структура которого характеризуется размытостью и информация о котором задана в виде матрицы «объект-свойство» или матрицы «объект-объект», заранее известным либо нет числом однородных, в некотором смысле нечетких классов адекватным образом. Адекватность представления исследуемой совокупности объектов нечеткими классами определяется, в первую очередь, целями
структура которого характеризуется размытостью и информация о котором задана в виде матрицы «объект-свойство» или матрицы «объект-объект», заранее известным либо нет числом однородных, в некотором смысле нечетких классов адекватным образом. Адекватность представления исследуемой совокупности объектов нечеткими классами определяется, в первую очередь, целями
исследования, видом искомой структуры классификации и содержательными рассмотрениями проблемы классификации в каждом конкретном случае.
Идея и основные принципы применения аппарата теории нечетких множеств к решению задач классификации были выдвинуты в фундаментальной работе Р. Беллмана, Р. Кэлабы и Л. А. Заде [49], а математическая постановка нечеткой модификации задачи кластерного анализа впервые была рассмотрена Э. Г. Распини в работе [149]. Первым систематическим исследованием, посвященным проблеме применения средств нечеткой математики к решению задач распознавания образов, была диссертация Дж. Беждека [51], после чего были предложены самые разнообразные нечеткие методы распознавания образов, в том числе нечеткие методы автоматической классификации. Однако перед рассмотрением схем алгоритмов нечеткого подхода к решению задачи кластер-анализа, нелишним будет обратиться к основным понятиям теории нечетких множеств.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
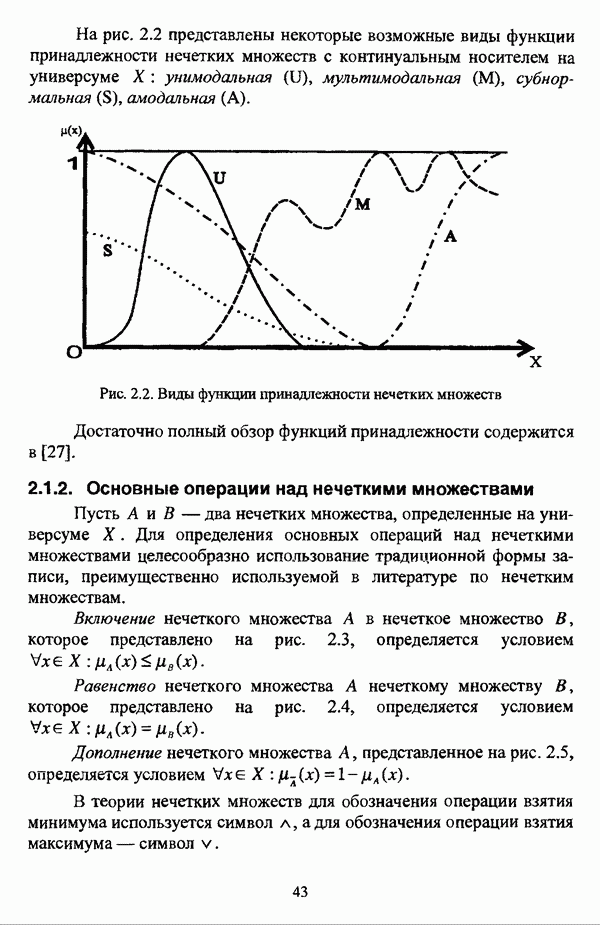
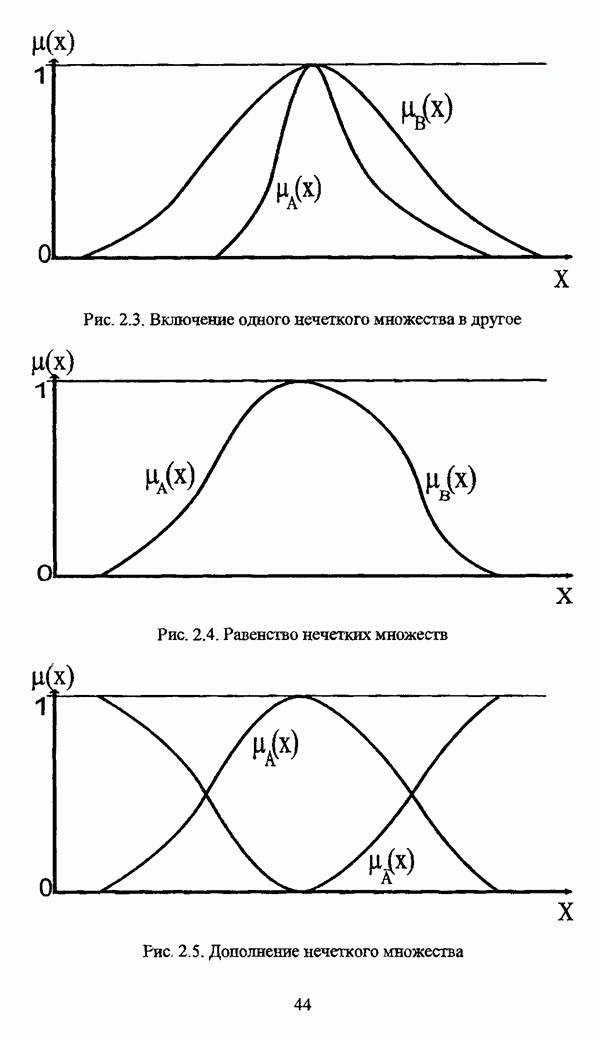
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы