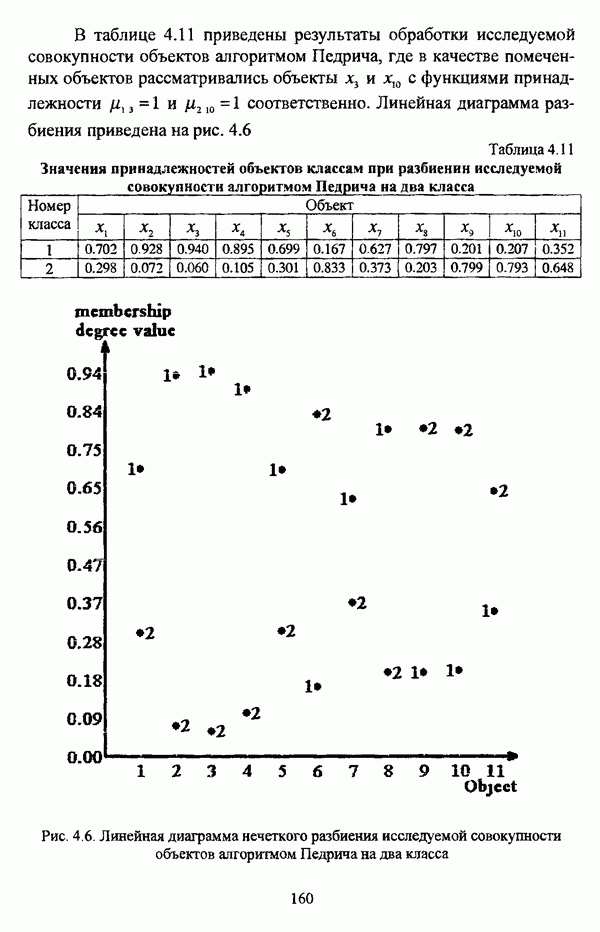
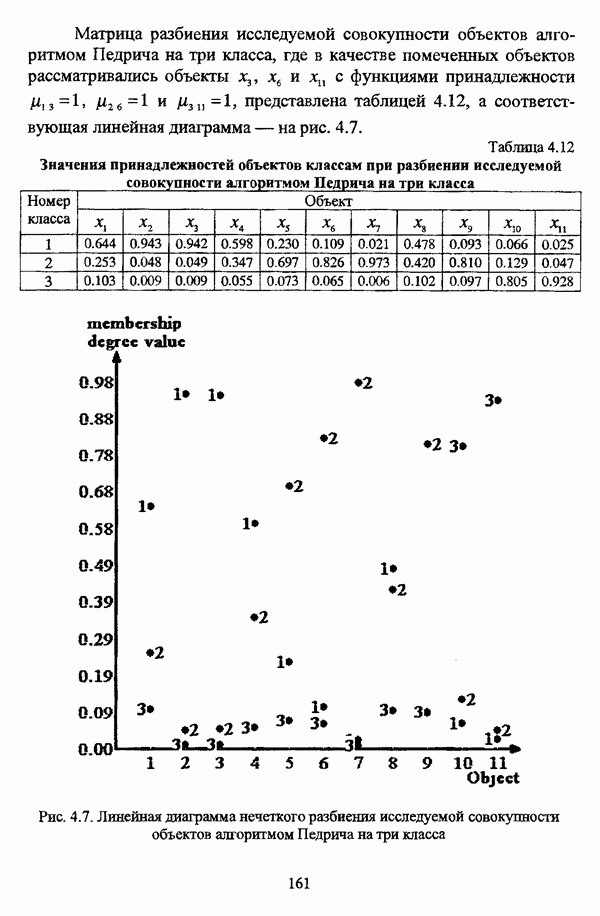
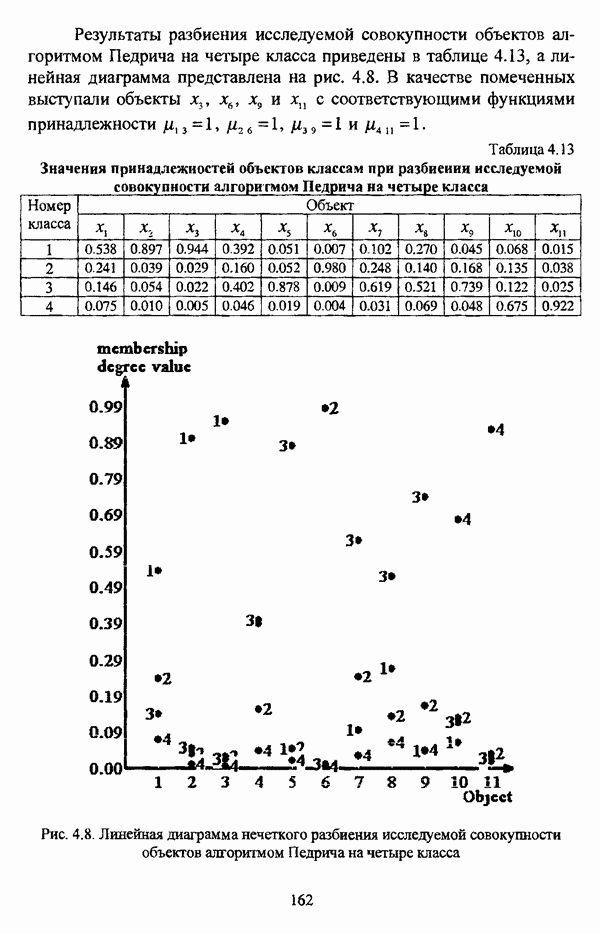
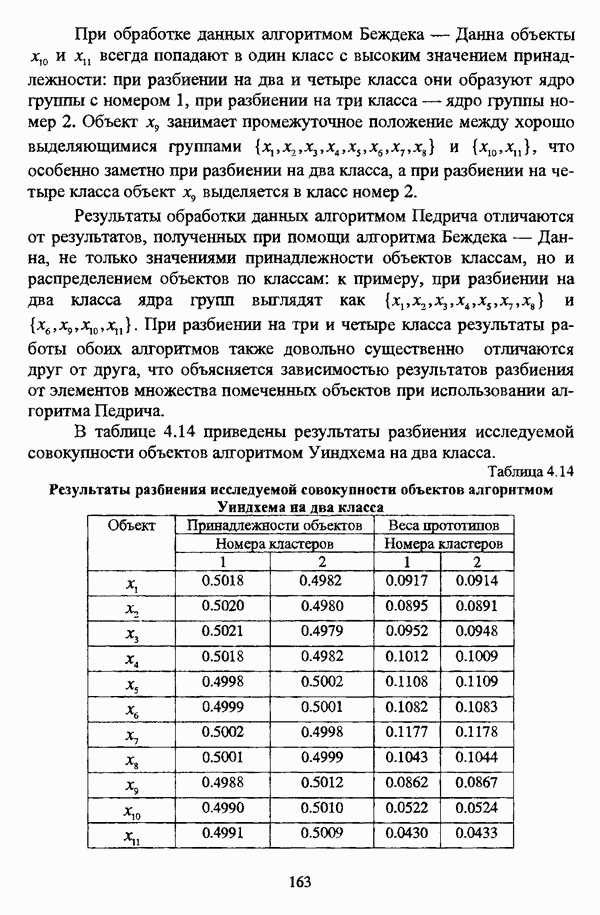
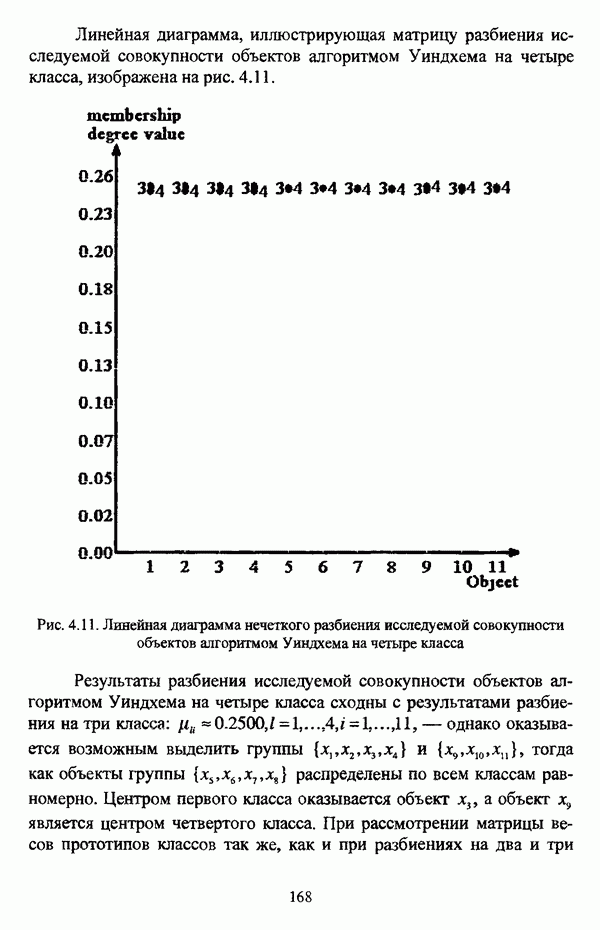
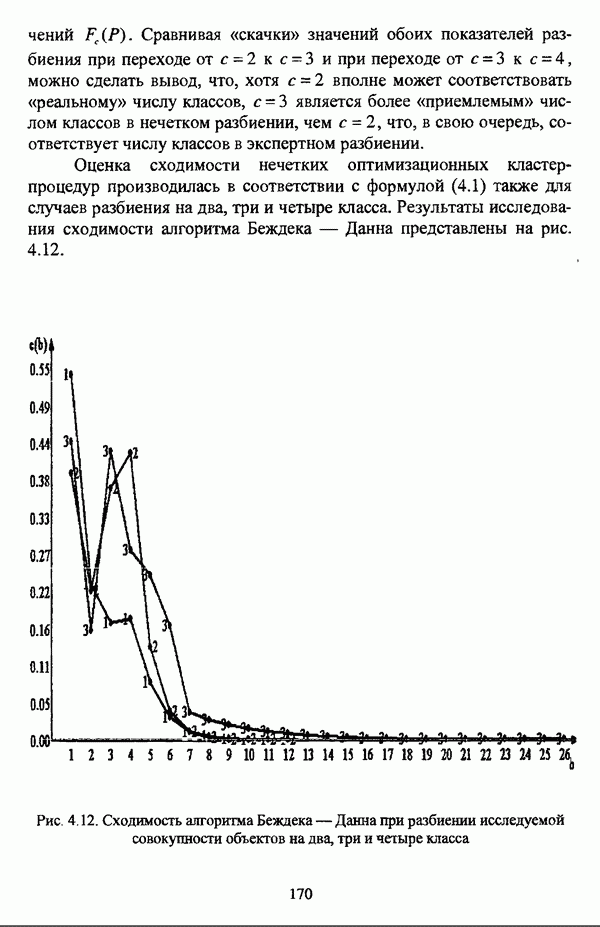
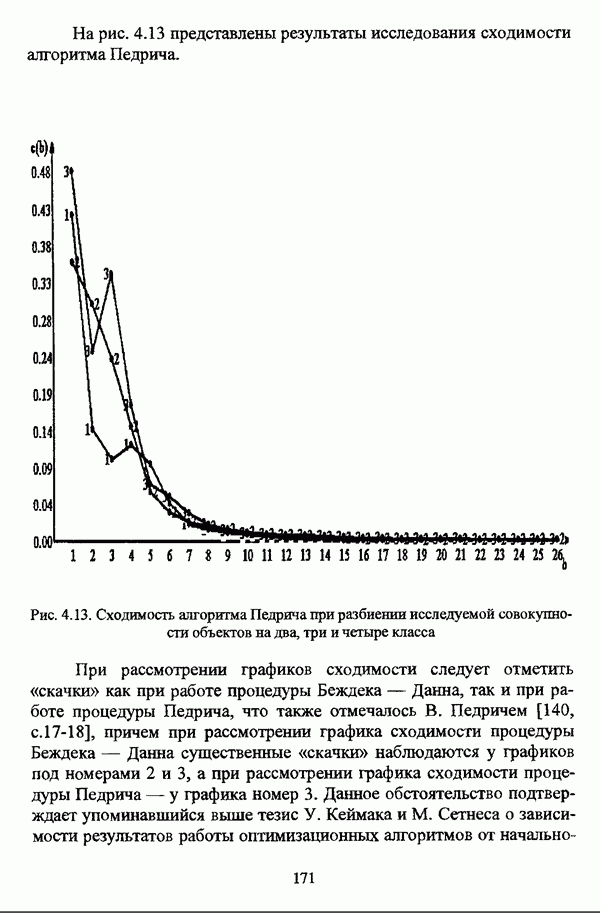
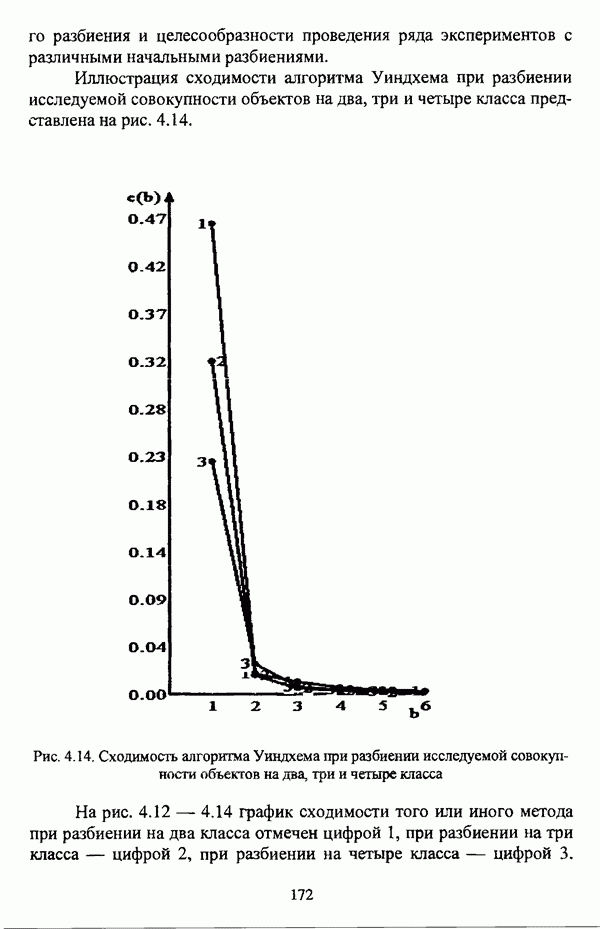
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
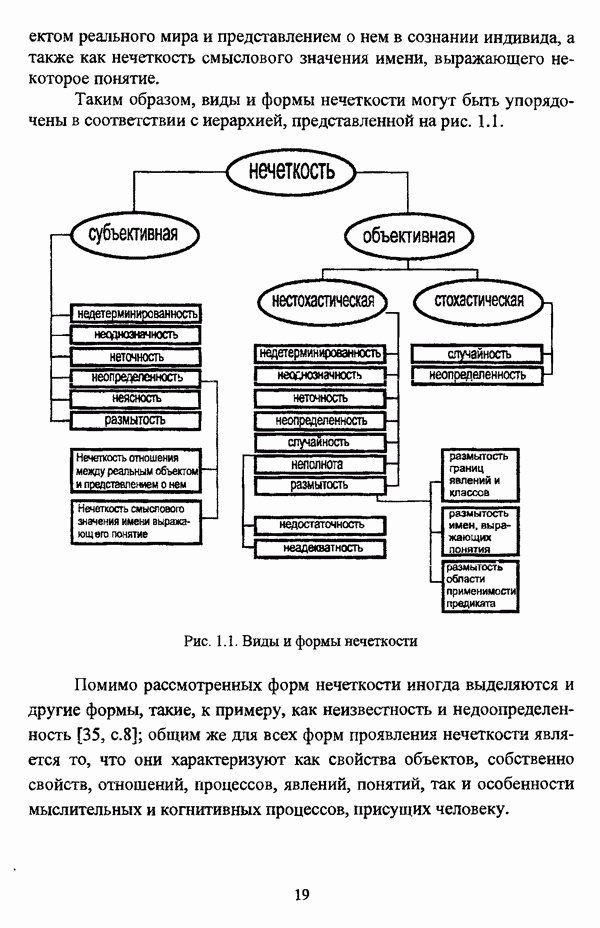
4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
4.2.1. Оценка качества нечеткой классификации
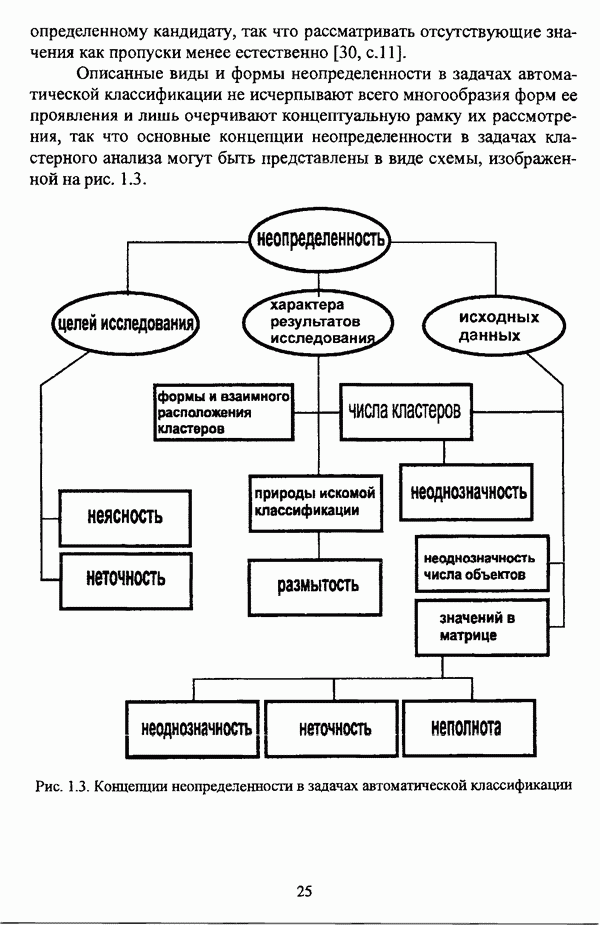
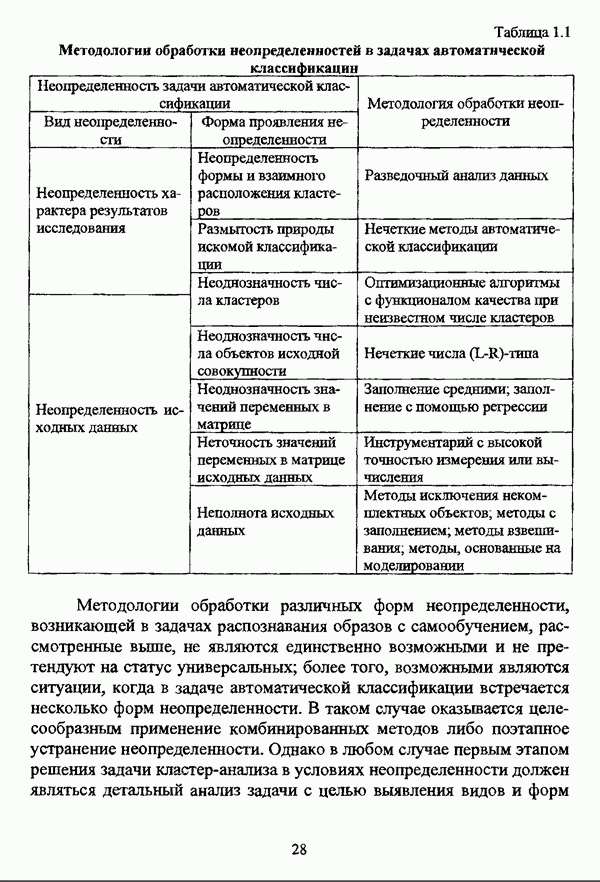
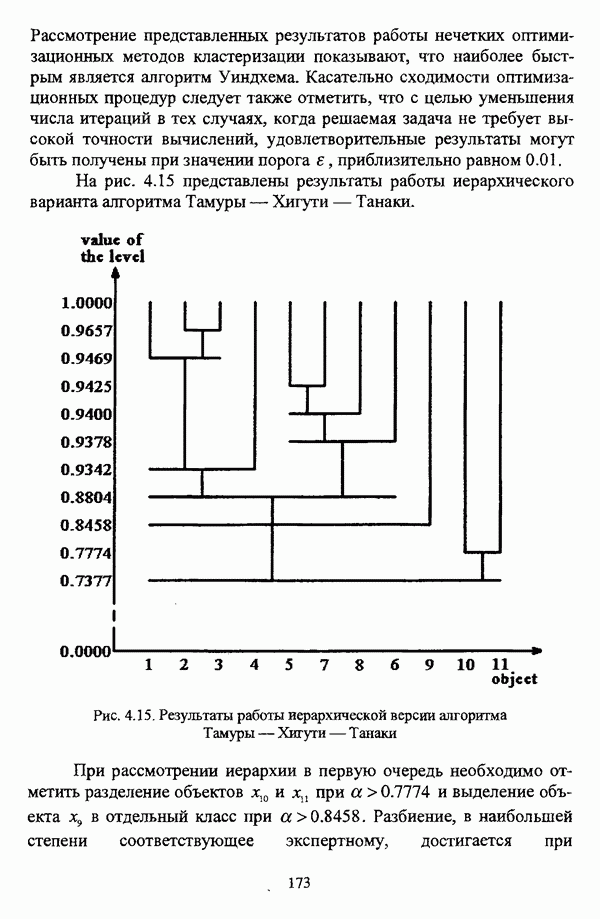
Как правило, результаты классификации, помимо содержательного осмысления и интерпретации, подлежат некоторой объективной оценке. В силу разнородности нечетких методов автоматической классификации, что особенно характерно для группы эвристических методов, каких-либо универсальных показателей качества полученной классификации не предлагается. В случае эвристических алгоритмов методы оценки классификации иногда предлагаются вместе с конкретным алгоритмом классификации. В частности, для оценки классификации С. Тамура, С. Хигути и К. Танака [163, с. 64-65] используют такие показатели, как коэффициент корректно классифицированных объектов, коэффициент некорректно классифицированных объектов и коэффициент нерасклассифицированных объектов. Следует, однако, указать, что для вычисления подобных коэффициентов необходимо знать реальную структуру данных или, в крайнем случае, иметь в наличии экспертное разбиение, так что эти коэффициенты могут быть использованы для оценки собственно метода классификации, а не результатов его применения к некоторым данным с неизвестной структурой.
В отличие от эвристических методов нечеткого подхода к решению задачи кластерного анализа, для группы оптимизационных методов предложены несколько показателей, характеризующих полученное нечеткое разбиение  которое описывается следующей матрицей:
которое описывается следующей матрицей:

где, как и ранее,  — значение принадлежности элемента
— значение принадлежности элемента  некоторому нечеткому кластеру
некоторому нечеткому кластеру  — количество элементов классифицируемого множества, или, иными словами, универсума
— количество элементов классифицируемого множества, или, иными словами, универсума
 а с — число нечетких кластеров в полученном разбиении.
а с — число нечетких кластеров в полученном разбиении.
Наиболее известными из предложенных показателей является коэффициент разбиения, предложенный в работе [85] и подробно обсуждавшийся в работах [58], [166]:

а также энтропия разбиения, предложенная в работе [58]:

Данные показатели обладают следующими свойствами:
1) В случае, когда полученное разбиение является четким, то есть  принимает значения на двухэлементном множестве
принимает значения на двухэлементном множестве  характеризующем принадлежность
характеризующем принадлежность  элемента
элемента  кластеру,
кластеру, 
2) В случае, когда полученное разбиение является наиболее неопределенным, то есть когда  для всех
для всех  показатели принимают значения
показатели принимают значения  и, соответственно,
и, соответственно, 
Таким образом, диапазон значений коэффициента разбиения определяется неравенством  а диапазон значений энтропии разбиения — неравенством
а диапазон значений энтропии разбиения — неравенством  .
.
Главной целью использования коэффициента разбиения  и энтропии разбиения
и энтропии разбиения  «является отыскание наиболее «приемлемого» числа кластеров»
«является отыскание наиболее «приемлемого» числа кластеров»  в нечетком разбиении Р. Вместе с тем, необходимо отметить, что диапазон значений
в нечетком разбиении Р. Вместе с тем, необходимо отметить, что диапазон значений  зависит от числа нечетких кластеров с, то есть при изменении числа кластеров в нечетком разбиении соответствующим образом изменяются и значения обоих показателей, так что коэффициент разбиения
зависит от числа нечетких кластеров с, то есть при изменении числа кластеров в нечетком разбиении соответствующим образом изменяются и значения обоих показателей, так что коэффициент разбиения  и энтропия разбиения
и энтропия разбиения  оказываются непригодными для сравнения разбиений с различным числом кластеров одной исследуемой совокупности. В. Педрич по этому поводу отмечал, что «минимальное или максимальное значение показателей может быть найдено, или, в крайнем случае, может наблюдаться существенный скачок их значений. Тем не менее их поведение не находит теоретического обоснования. Вычислительные эксперименты показывают, главным
оказываются непригодными для сравнения разбиений с различным числом кластеров одной исследуемой совокупности. В. Педрич по этому поводу отмечал, что «минимальное или максимальное значение показателей может быть найдено, или, в крайнем случае, может наблюдаться существенный скачок их значений. Тем не менее их поведение не находит теоретического обоснования. Вычислительные эксперименты показывают, главным
образом, их полезность, однако невозможно судить, какое значение показателей является наилучшим и наиболее соответствующим числу классов» [144, с.135]. Таким образом, целесообразным оказывается использование пропорциональной экспоненты, предложенной в работе [184]:

диапазон значений которой не зависит от числа нечетких кластеров в нечетком разбиении и выражается неравенством 
Коэффициент разбиения  энтропия разбиения
энтропия разбиения  а также другие показатели, характеризующие нечеткое разбиение, подробно исследуются в работах [58], [119]; кроме того, проблеме обоснования числа кластеров посвящены работы [52], [120]. Вместе с тем, некоторыми исследователями предлагаются либо модификации существующих показателей для оценки предлагаемых ими процедур, либо специальные методы оценки эффективности предлагаемой нечеткой кластер-процедуры. К примеру, М. Рубенсом
а также другие показатели, характеризующие нечеткое разбиение, подробно исследуются в работах [58], [119]; кроме того, проблеме обоснования числа кластеров посвящены работы [52], [120]. Вместе с тем, некоторыми исследователями предлагаются либо модификации существующих показателей для оценки предлагаемых ими процедур, либо специальные методы оценки эффективности предлагаемой нечеткой кластер-процедуры. К примеру, М. Рубенсом  была предложена следующая модификация коэффициента разбиения
была предложена следующая модификация коэффициента разбиения 

что можно переписать в виде 
Помимо модификации коэффициента разбиения  в этой же работе [148] М. Рубенсом была предложена также следующая оценка разбиения:
в этой же работе [148] М. Рубенсом была предложена также следующая оценка разбиения:

где  представляет индекс различия пары кластеров
представляет индекс различия пары кластеров  так что
так что  Как и для коэффициента разбиения
Как и для коэффициента разбиения
 для показателей разбиения М. Рубенса вьшолняются неравенства
для показателей разбиения М. Рубенса вьшолняются неравенства 
Исследуя коэффициент разбиения  , Е. Трауверт отмечает, что
, Е. Трауверт отмечает, что  измеряет четкость, но не ее точные предельные значения, выраженные соотношением (4.3), а ряд ее полностью определенных значений»
измеряет четкость, но не ее точные предельные значения, выраженные соотношением (4.3), а ряд ее полностью определенных значений»  При рассмотрении взаимосвязи между наименьшим и наибольшим значениями
При рассмотрении взаимосвязи между наименьшим и наибольшим значениями  Е. Трауверт вводит коэффициент нечеткости
Е. Трауверт вводит коэффициент нечеткости  разбиения
разбиения  вычисляемый по формуле
вычисляемый по формуле

где W — матрица четкого разбиения, имеющая, так же, как и матрица Р, размерность с 

элементы которой определяются следующим образом:

Взаимосвязь между коэффициентом четкости  и коэффициентом нечеткости
и коэффициентом нечеткости  в свою очередь, определяется выражением
в свою очередь, определяется выражением

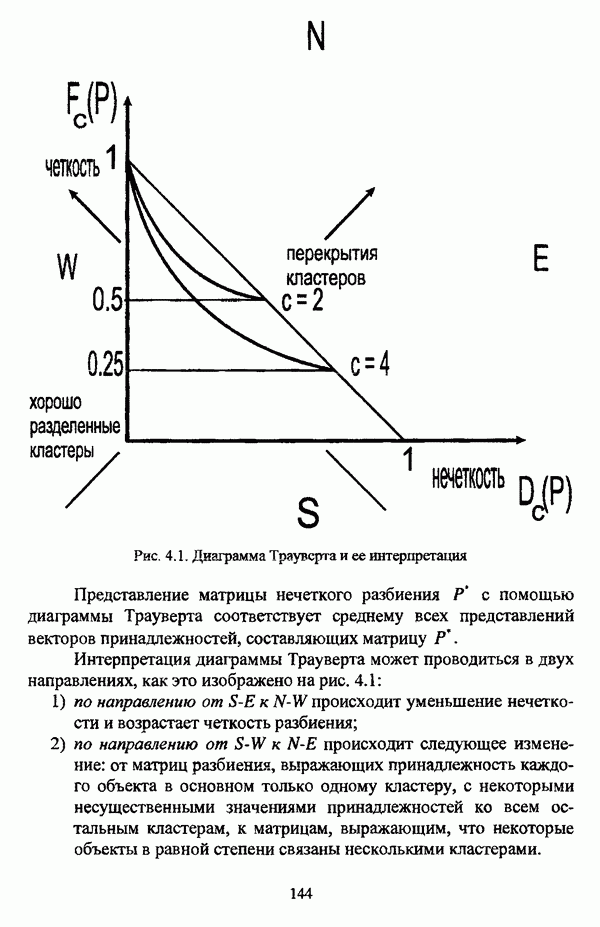
Используя методологию, детально рассмотренную в работе [166], можно построить соответствующий график, называемый Е. Траувертом ( -диаграммой, схематический пример которой приведен на рис. 4.1.
-диаграммой, схематический пример которой приведен на рис. 4.1.
(см. скан)
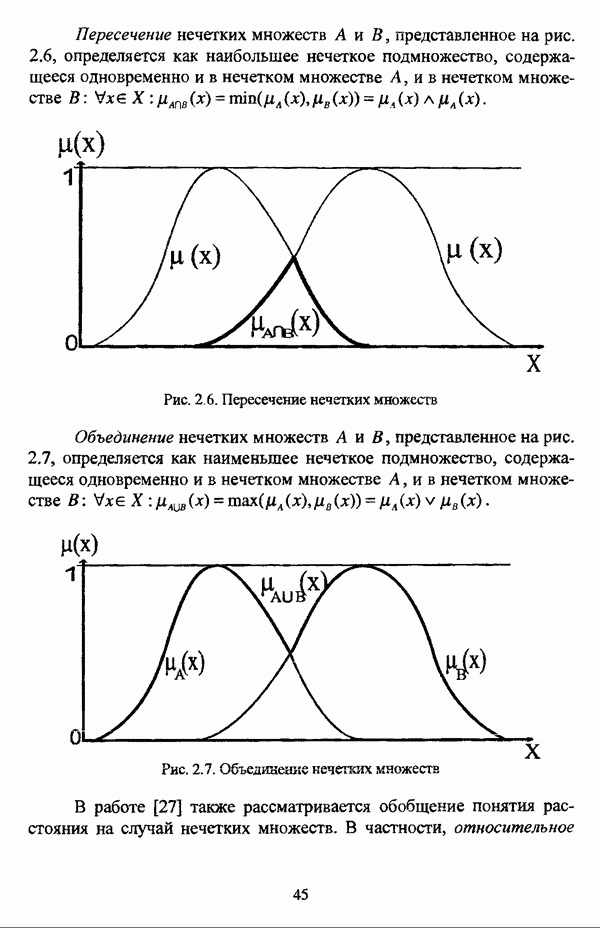
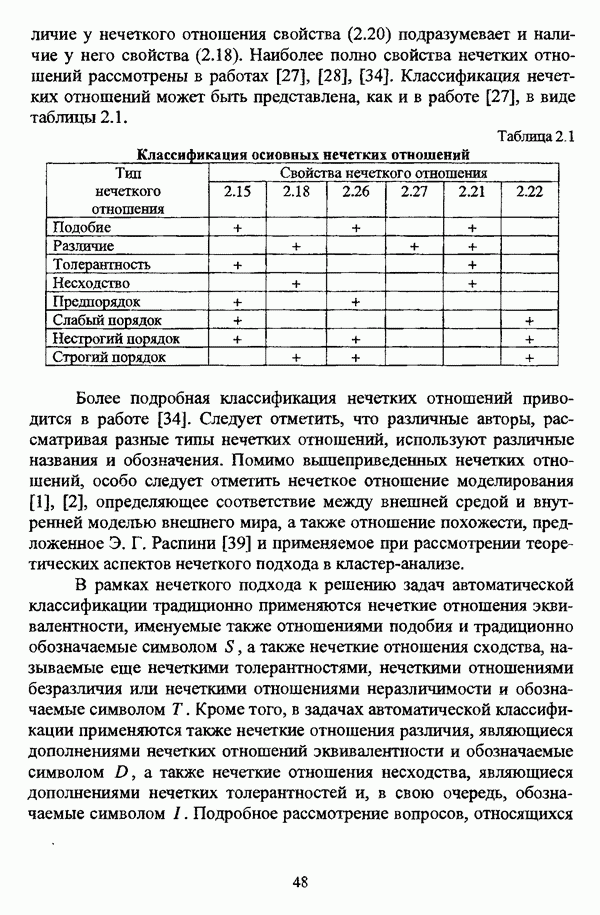
Рис. 4.1. Диаграмма Траувсрта и ее интерпретация
Представление матрицы нечеткого разбиения Р с помощью диаграммы Трауверта соответствует среднему всех представлений векторов принадлежностей, составляющих матрицу Р.
Интерпретация диаграммы Трауверта может проводиться в двух направлениях, как это изображено на рис. 4.1:
1) по направлению от  происходит уменьшение нечеткости и возрастает четкость разбиения;
происходит уменьшение нечеткости и возрастает четкость разбиения;
2) по направлению от  происходит следующее изменение: от матриц разбиения, выражающих принадлежность каждого объекта в основном только одному кластеру, с некоторыми несущественными значениями принадлежностей ко всем остальным кластерам, к матрицам, выражающим, что некоторые объекты в равной степени связаны несколькими кластерами.
происходит следующее изменение: от матриц разбиения, выражающих принадлежность каждого объекта в основном только одному кластеру, с некоторыми несущественными значениями принадлежностей ко всем остальным кластерам, к матрицам, выражающим, что некоторые объекты в равной степени связаны несколькими кластерами.
Последняя ситуация известна также, как случай «цепочек», «мостиков» между кластерами и схематически изображена на рис. 1.4 в виде кластеров А и В.
Е. Трауверт отмечал, что  -диаграмма проявляет себя как интересное новое средство, характеризующее задачу кластер-анализа или алгоритм нечеткой кластеризации, но не выбирающее обоснование нечеткого решения» [166, с. 235].
-диаграмма проявляет себя как интересное новое средство, характеризующее задачу кластер-анализа или алгоритм нечеткой кластеризации, но не выбирающее обоснование нечеткого решения» [166, с. 235].
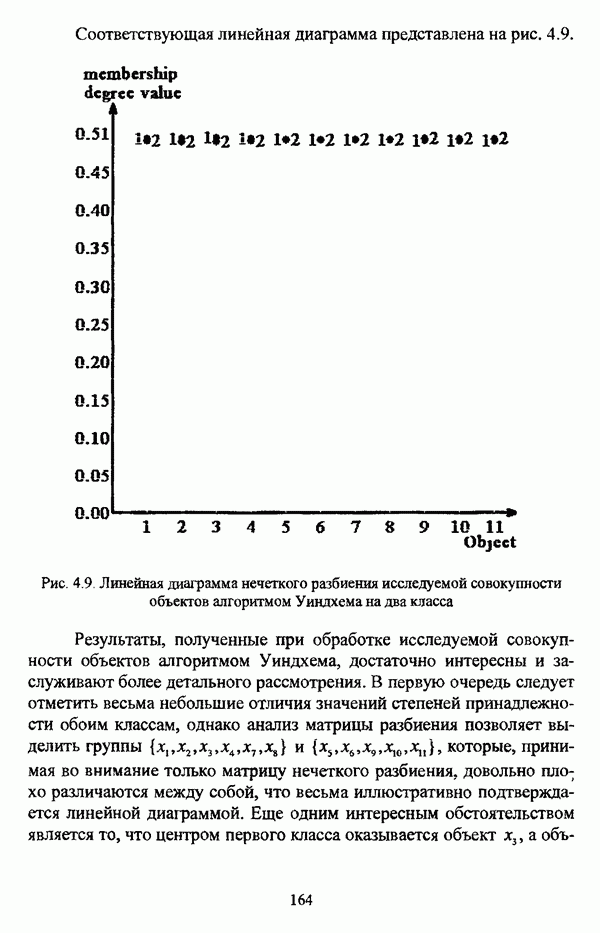
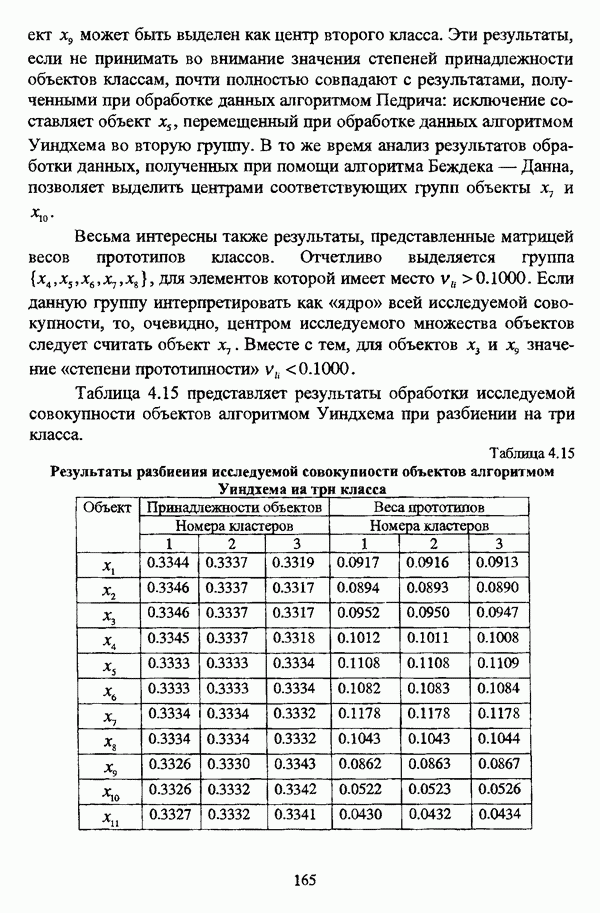
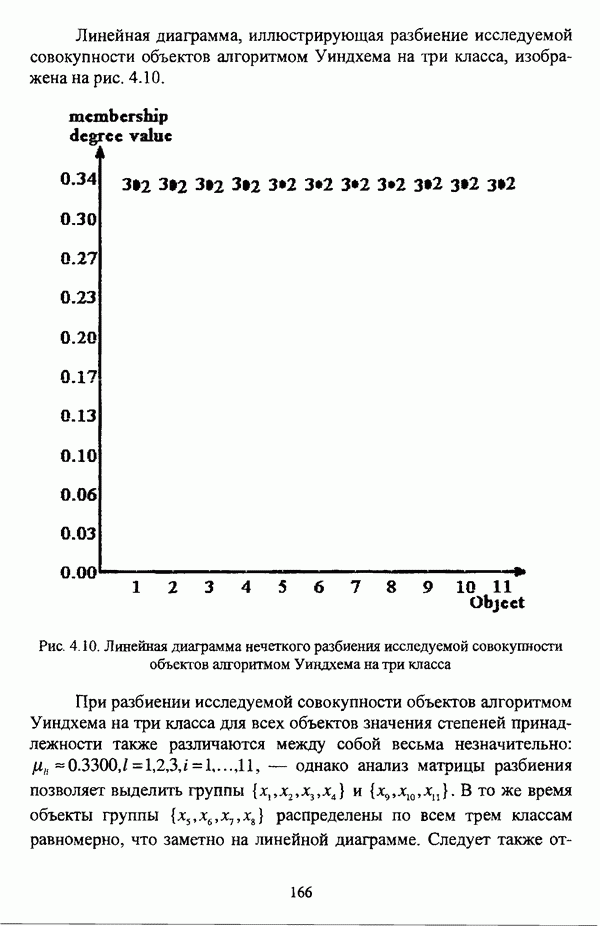
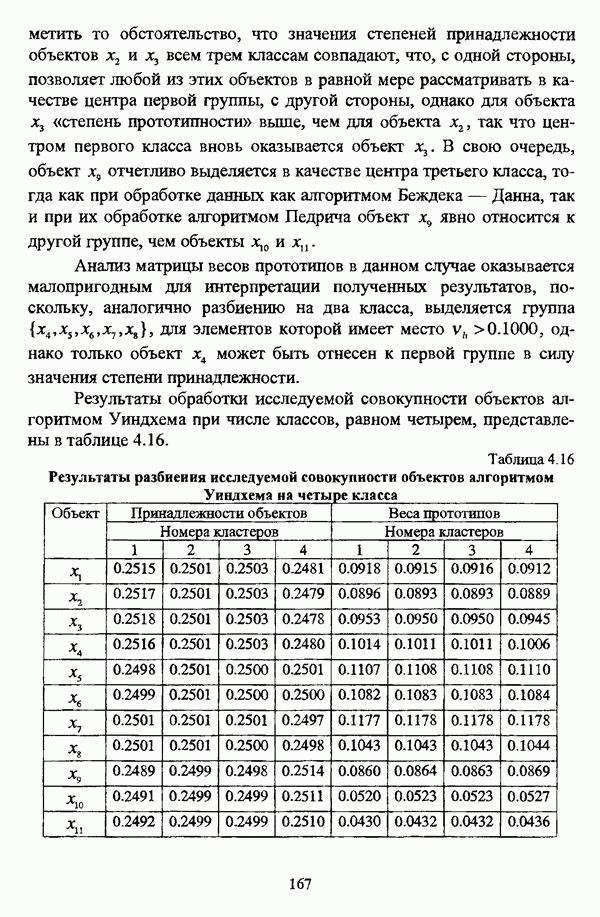
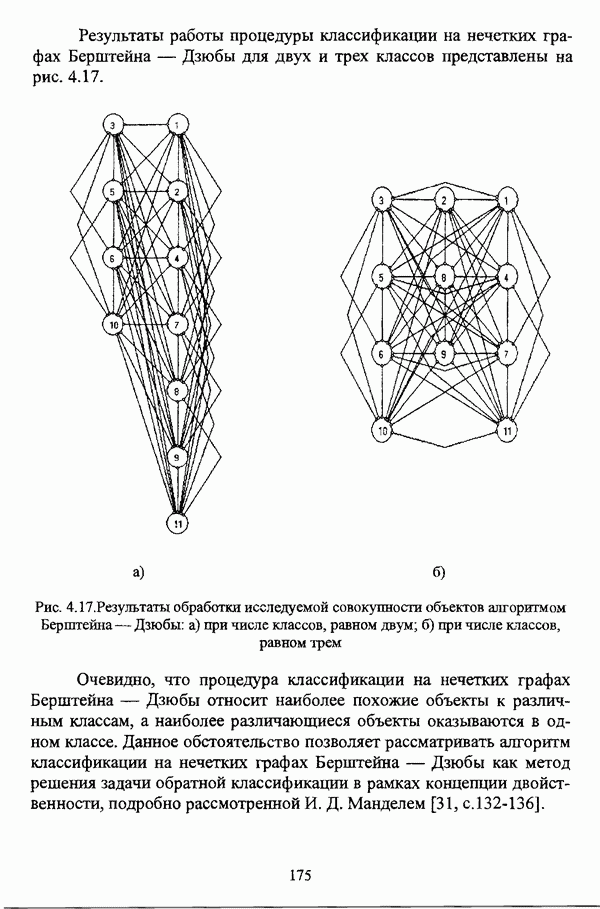
Предпринятое рассмотрение различных методов оценки нечеткой классификации наглядно демонстрирует, что показатели, характеризующие нечеткое разбиение, несмотря на их полезность для анализа полученной классификации, не могут быть использованы для выявления действительной структуры исследуемой совокупности объектов, так что нельзя не согласиться с В. Педричем, отмечавшим, что при решении задачи нечеткой классификации «будет разумным использовать различные методы и сравнивать полученные результаты» [144, с. 135]. Соображения, подобные приведенному замечанию, просматриваются также в работах [96], [97], [98].
В свою очередь, помимо оценки качества разбиения, можно также исследовать некоторые характеристики отдельных кластеров для детального рассмотрения их структуры. К примеру, Э. Г. Распини [149], [150] для исследования свойств отдельных кластеров использовал уже упоминавшееся соотношение

выражающее относительный размер кластера  а также соотношение
а также соотношение

показывающее среднюю плотность точек вокруг некоторой точки  Кроме того, для оценки средней плотности точек вокруг точки х в нечетком кластере
Кроме того, для оценки средней плотности точек вокруг точки х в нечетком кластере  Э. Г. Распини предложил также соотношение
Э. Г. Распини предложил также соотношение

В. Педричем [144] предлагается весьма интересный и многообещающий подход к решению проблемы представления структуры
нечетких кластеров, так что целесообразно его рассмотреть подробнее. Поскольку значение функции  представляющее собой элемент матрицы разбиения
представляющее собой элемент матрицы разбиения  выражает степень принадлежности
выражает степень принадлежности  элемента
элемента  кластеру, то элемент
кластеру, то элемент  может рассматриваться как элемент ядра нечеткого кластера
может рассматриваться как элемент ядра нечеткого кластера  если, по меньшей мере, это значение
если, по меньшей мере, это значение  превышает некоторый порог, который в дальнейшем будет обозначаться символом
превышает некоторый порог, который в дальнейшем будет обозначаться символом  . Далее, рассматривая для каждой точки
. Далее, рассматривая для каждой точки  ее структурное отношение ко всем кластерам
ее структурное отношение ко всем кластерам  принимают во внимание функции принадлежности точки
принимают во внимание функции принадлежности точки  всем остальным нечетким кластерам, за исключением рассматриваемого нечеткого кластера
всем остальным нечетким кластерам, за исключением рассматриваемого нечеткого кластера  Поскольку число кластеров равно с, можно отметить, что любая точка
Поскольку число кластеров равно с, можно отметить, что любая точка  , для которой
, для которой  не способствует выявлению сущности кластерной структуры. Мерой структурного свойства некоторой точки
не способствует выявлению сущности кластерной структуры. Мерой структурного свойства некоторой точки  может послужить показатель
может послужить показатель

так что, производя нормализацию этого показателя умножением правой части выражения (4.16) на константу с  можно получить
можно получить

то есть  , и из выражения (4.17) и свойств матрицы разбиения
, и из выражения (4.17) и свойств матрицы разбиения  следует, что если точка
следует, что если точка  принадлежит одному из кластеров
принадлежит одному из кластеров  со степенью принадлежности, равной 1, то значение показателя (4.17) в этой точке достигает максимума, то есть
со степенью принадлежности, равной 1, то значение показателя (4.17) в этой точке достигает максимума, то есть  Структурная сущность ядра нечеткого кластера может определяться некоторым пороговым значением
Структурная сущность ядра нечеткого кластера может определяться некоторым пороговым значением  так что точка
так что точка  может быть элементом ядра нечеткого кластера, только если
может быть элементом ядра нечеткого кластера, только если  превышает
превышает  Комбинация этих рассуждений приводит к определению понятия
Комбинация этих рассуждений приводит к определению понятия  -ядра нечеткого кластера
-ядра нечеткого кластера  как подмножества Х универсума
как подмножества Х универсума  при
при  , если оно содержит множество
, если оно содержит множество  то есть
то есть

Таким образом, получается множество ядер  резидуальное множество данных
резидуальное множество данных  содержащее все оставшиеся элементы универсума X, так что вьшолняется соотношение
содержащее все оставшиеся элементы универсума X, так что вьшолняется соотношение

где первая составляющая правой части представляет собой существенную для рассмотрения структуру, а вторая соответствует малосущественной структуре множества 
Для аналитического представления  -ядра нечеткого кластера
-ядра нечеткого кластера  в
в  -мерном пространстве целесообразно рассматривать гиперсферы, описываемые, в общем, выражением
-мерном пространстве целесообразно рассматривать гиперсферы, описываемые, в общем, выражением

где символ Т обозначает операцию транспонирования, так что центрами гиперсфер будут точки  а радиусами, соответственно, значения для всех
а радиусами, соответственно, значения для всех  . При рассмотрении
. При рассмотрении  гиперсферы точка
гиперсферы точка  как точка, являющаяся прототипом
как точка, являющаяся прототипом  кластера, может быть опущена, либо она может трактоваться как некоторая точка
кластера, может быть опущена, либо она может трактоваться как некоторая точка  , такая, что функция принадлежности
, такая, что функция принадлежности  кластеру для нее является максимальной. Значение
кластеру для нее является максимальной. Значение  выбирается таким образом, что положение точек, являющихся элементами ядра X минимизирует взвешенную сумму квадратов ошибок, которая определяется выражением
выбирается таким образом, что положение точек, являющихся элементами ядра X минимизирует взвешенную сумму квадратов ошибок, которая определяется выражением

При взятии первой производной  для соответствующего
для соответствующего  решение системы уравнений
решение системы уравнений

дает решение

где

Налагая дополнительные ограничения в форме системы уравнений

где  устанавливает евклидово расстояние между точками
устанавливает евклидово расстояние между точками  у так что, варьируя значения
у так что, варьируя значения  и/или
и/или  , оказывается возможным определить невыделенные гиперсферы, представляющие ядра. Более того, следует отметить, что при фиксированном параметре
, оказывается возможным определить невыделенные гиперсферы, представляющие ядра. Более того, следует отметить, что при фиксированном параметре  для каждой пары
для каждой пары  упорядоченных так, что
упорядоченных так, что  соответствующие радиусы будут упорядочены как
соответствующие радиусы будут упорядочены как  . С точки зрения статистического подхода, гиперсферическая форма кластеров соответствует ситуации, когда кластеры описываются средним значением
. С точки зрения статистического подхода, гиперсферическая форма кластеров соответствует ситуации, когда кластеры описываются средним значением  и ковариационной матрицей
и ковариационной матрицей

Таким образом, построение аналитического представления ядер  позволяет идентифицировать резидуальное множество данных
позволяет идентифицировать резидуальное множество данных 
Наряду с гиперсферической формой, в работе [144] также рассматривается ситуация гиперзллиптической формы ядер нечетких кластеров, рассуждения для которой незначительно отличаются от приведенных выше. Порог  для каждого кластера
для каждого кластера  обычно соответствует среднему значению функции принадлежности точек кластеру, так что
обычно соответствует среднему значению функции принадлежности точек кластеру, так что

Следует отметить, что величина, определяемая выражением (4.27), соответствует мощности нечеткого множества  При таком выборе порога центром ядра некоторого нечеткого кластера будет точка, имеющая максимальное значение принадлежности этому кластеру, так что во внимание будут приниматься только те точки, значения принадлежности которых превышают средние, так
При таком выборе порога центром ядра некоторого нечеткого кластера будет точка, имеющая максимальное значение принадлежности этому кластеру, так что во внимание будут приниматься только те точки, значения принадлежности которых превышают средние, так
что в результате ядра нечетких кластеров автоматически устанавливаются распределением значений принадлежностей. Вместе с тем, как указывает В. Педрич, порог  может выбираться произвольно.
может выбираться произвольно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРОБЛЕМА НЕОПРЕДЕЛЕННОСТИ В ЗАДАЧАХ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 1.1. Понятие однородности и проблема классификации объектов
- 1.1.2. Общая постановка задачи автоматической классификации и основные направления ее решения
- 1.2. Подход к решению задачи автоматической классификации с позиции теории нечетких множеств
- 1.2.2. Гносеологические аспекты подхода к решению задач классификации с позиции теории нечетких множеств
- Резюме
- ГЛАВА 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
- 2.1. Нечеткие множества
- 2.1.2. Основные операции над нечеткими множествами
- 2.2. Нечеткие отношения
- 2.2.2. Основные операции над нечеткими отношениями
- Резюме
- ГЛАВА 3. МЕТОДЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 3.1.2. Описание алгоритмов
- 3.2. Оптимизационные методы
- 3.2.2. Описание алгоритмов
- 3.2.2.2. Алгоритм Уиндхема
- 3.2.2.3. Алгоритм Рубенса
- 3.2.2.4. Алгоритм Беждека — Данна
- 3.2.2.5. Алгоритм Педрича
- 3.2.2.6. Алгоритм Даве — Сена
- 3.2.2.7. Другие алгоритмы оптимизационного подхода
- 3.3. Иерархические методы
- 3.3.2. Описание алгоритмов
- 3.3.2.2. Алгоритм Думитреску (FDH algorithm)
- 3.3.2.3. Другие алгоритмы иерархического подхода
- Резюме
- ГЛАВА 4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕЧЕТКИХ МЕТОДОВ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 4.1.2. Виды исходных данных и общая схема проведения сравнительного анализа
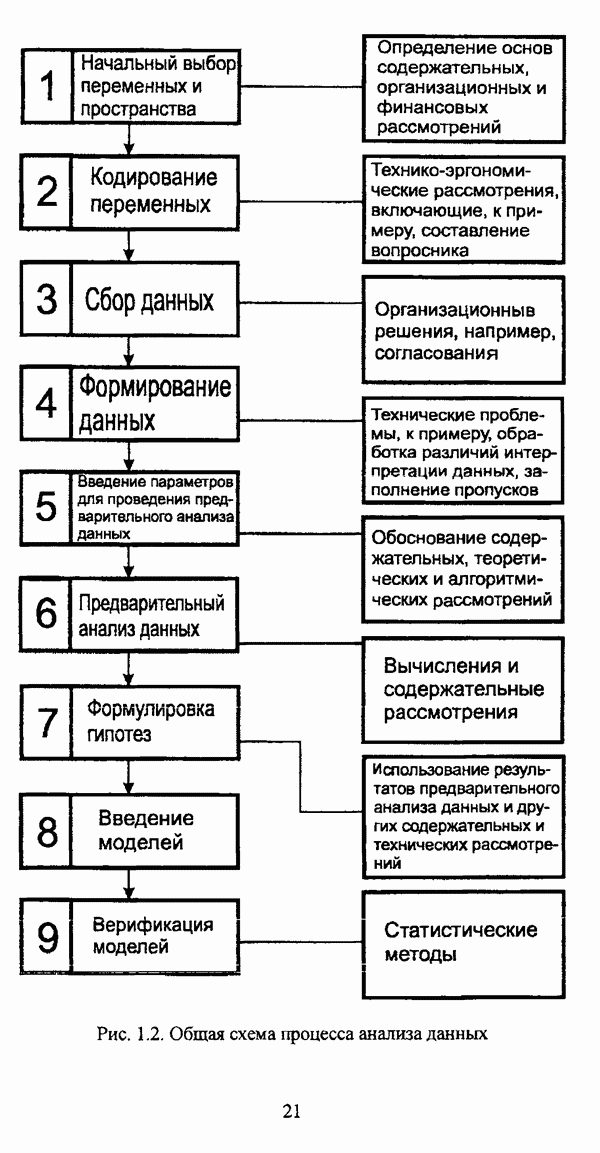
- 4.2. Оценка и представление результатов обработки данных нечеткими методами автоматической классификации
- 4.2.2. Представление и интерпретация результатов нечеткой классификации
- 4.3. Экспериментальное сравнение нечетких методов автоматической классификации
- 4.3.2. Результаты вычислительных экспериментов
- Резюме
- ГЛАВА 5. МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ НЕЧЕТКОГО ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ
- 5.1.2. Выбор алгоритма нечеткого подхода к решению задачи автоматической классификации и обоснование параметров
- 5.2. Прикладные аспекты нечеткой классификации
- 5.2.2. Нечеткие методы автоматической классификации и другие нечеткие методы распознавания образов
- Резюме
- ЗАКЛЮЧЕНИЕ
- Основные обозначения
- Список литературы